1. Introduction
One of the more often-asked questions in surface catalysis is: how are surface reactions driven, and how can these driving mechanisms be optimized [
1]? In importance, these questions are comparable to the more fundamental question of how catalytic processes themselves can be defined in terms of the active site [
2] or surface equilibration. The terms of optimization are not always clearly defined, but the focus is generally on the yield and purity of the product, the hidden carbon and energy costs of each process, and the longevity of the supporting materials, such as the catalysts.
Transition metal (TM) catalysts remain a common choice for surface catalysts [
3]. Their relatively developed technology and their reasonable abundance mean they can be reliably deployed in production environments. Their diversity means that they can be somewhat tuned to promote reactions or to behave in an enhanced way to support other parameters in the reaction, such as the temperature required for the process, which can heavily affect the financial and carbon costs of a process, or how stable the catalyst can remain. This latter parameter is often overlooked in catalyst design experiments, which is odd as the rate at which the catalyst itself becomes consumed or corrupted during an industrial process can significantly influence their viability, particularly for the more expensive catalysts like Pt. Accelerated durability testing (ADT) is used to investigate the degradation of catalysts in operational circumstances [
4]. Materials used in many processes that involve atom exchange, such as membrane fuel cells, undergo significant structural changes during their operation. Corruption of the catalyst may further be exacerbated by the temperatures used during normal operation; often, operating temperatures of several hundred degrees centigrade are required, which are a hidden carbon cost as well as providing a mechanism for structural damage, such as grain boundary diffusion, which can potentially significantly alter the magnetic as well as the morphological character of the catalyst. Pt is one of the most ubiquitous catalysts and, consequently, has a relatively developed literature concerning its durability. Stress testing of Pt/C catalysts for the oxygen reduction reaction (ORR) has shown that oxide formation [
5] is one of the key mechanisms of performance loss. This result is not surprising when considering the fundamental surface science of O/Pt. Oxygen reactions require quite high thermal activation on Pt surfaces, but once adsorbed, they cannot easily be removed by subsequent thermal cycling. Generally, catalysts that are, by design and use, not expected to behave identically to ideal single-crystal systems can still be analyzed using fundamental studies, and this fact highlights the importance of fundamental investigations.
Effective metrics for the degradation of catalysts are also important. Liquid half-cell measurements [
6] have defined the electrochemically active surface area (ESCA) as a useful parameter for describing Pt/Vulcan performance. Reliable reporting of degradation studies does still require the inclusion of supporting data for these metrics, such as voltammograms and, generally, transmission electron microscopy (TEM) of the reacted surfaces. The metric does provide an effective and transferable measure of performance for catalysts under different reaction conditions and for different processes.
The development of standardized test protocols is a related process. Studies of Ir performance for the ORR [
7] have shown that normalized ESCA parameters provide a better comparison of performance across the literature. This was achieved by integrating the total average charge from cyclic voltammetry data and was proven to be a better way of assessing the performance of Ir-based electrocatalysts. A full review of this field is beyond the scope of the current manuscript, particularly given its theoretical focus, but future work in this experimental field would be valuable.
Returning to catalyst design, one further parameter that can be considered in catalyst design is spin. The systematic investigation of magnetic materials for heterogeneous catalysis and specific spin-sensitive modeling of heterogeneous catalysis processes is relatively novel [
8,
9,
10]. However, the topic is burgeoning and affects a number of other topics within the broader field of heterogeneous catalysis, including the hydrogenation, oxidation, and polymerization of alkanes, including the steam-reforming process [
11], the Haber-Bosh process for ammonia production, hydrogen evolution (HER), oxygen reduction (ORR), and oxygen evolution (OER) fuel cell reactions. The inclusion of spin is particularly germane for reactions including oxygen, such as those mentioned above or, for example, in water splitting [
12], where the key reactants, oxygen, are in a spin-polarized state, so modeling of their interactions with the catalyst becomes more specialized than modeling of reactants that are not polarized.
These observations are supported by spin catalysis [
13,
14]. In chemical reactions, the energy and the angular momentum (spin) of the reactants are the parameters that control the reaction. Spin catalysis stimulates the reaction and, in this way, overcomes the barrier imposed by spin conservation. One cogent example of how spin-forbidden reactions have significant effects in catalysis is CH activation, where a complex is inserted into the C–H bond of a simple alkane such as methane. Co, Rh, and Ir complexes exist in triplets and singlets. The triplet states create a spin barrier that requires significant energy to overcome, and the Co complex is comparatively difficult to insert in this sequence.
Catalysts are generally deployed in nanoparticle form, and significant literature already exists for non-magnetic materials; see, for example, refs. [
15,
16,
17,
18] for an up-to-date review. The reason for this deployment is because it increases the surface area available to reactants while still providing sufficient stability, even in hostile environments, to allow the catalysis to perform. An example of this could be for a biological application where the catalyst needs to maintain structural integrity during a digestive process. Though the technology of magnetic nanoparticles is developing rapidly, there are significant comparisons with non-magnetic particles. Nanoparticles have sizes in the order of 10–1000 Å. Their chemistry is sensitive to size and shape, and the ability to grow tubular or otherwise hollowed particles has significantly improved the design and diversity of these materials, in particular since the discovery of graphene and the realization that the material can be manipulated and folded. The growth of nanoparticles therefore focuses not only on their geometry but also on their surface composition. Core-shell materials, such as Pt-Ni, are effective in processes such as the oxygen reduction reaction (ORR) and have outer’shell’ layers, which are pure metals. This is effected by sintering the materials during growth and allows a mechanism of controllably straining the surface layer of the particle. The topic of the effect of strain on these materials will be reviewed later in this manuscript. Equally, the morphology of the particles and the development of edges, defects, and step profiles can also critically affect the activity of the particle. Simplistically, this arises as the presence of discontinuities gives rise to unsaturated, or dangling, bonds, which are inherently more reactive than their saturated counterparts.
Magnetism is related to the magnetic moments of atoms. Generally, magnetism can be thought of as either the orbital or spin magnetic moment of electrons giving rise to orbital or spin magnetization, respectively. No general theory for magnetism exists, which means that modern contributions to the field often rely on approximate approaches such as the Density Functional Theory (DFT, outlined below) to model magnetic systems. However, the key features of magnetic materials are well known and will be summarized here.
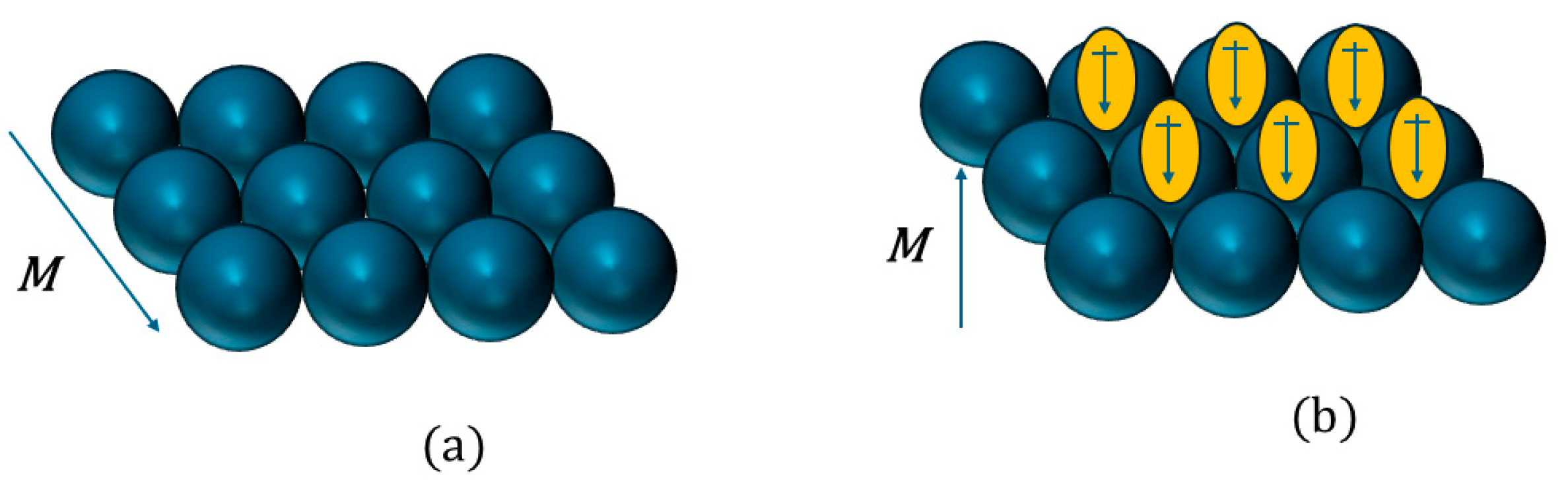
Magnetic materials can be classified according to their response to an applied magnetic field. This is quantified by the magnetic susceptibility of the material in the following equation:
M is the magnetization of the material. Materials with positive susceptibility will enhance or strengthen the applied magnetic field by aligning their magnetic moments in the direction of the field. These materials are paramagnets. Conversely, materials with a zero or negative susceptibility are diamagnets and tend to oppose or weaken an applied field. This happens because their magnetic moments align anti-parallel to the applied field.
The effect of applying a magnetic field to diamagnetic and paramagnetic materials is summarized in
Figure 1. With no applied magnetic field, a diamagnet does not contain magnetic moments. Conversely, a paramagnetic material will contain moments, but these will be randomly arranged, only becoming ordered when the magnetic field is applied. The magnetic field induces moments in the atoms of the diamagnet, which oppose the applied field.
A third type of magnetic material exists, where the atoms again contain magnetic spin moments in the absence of an applied field. These are ferromagnetic, anti-ferromagnetic, and ferrimagnetic materials, and they differ from paramagnets as their moments are aligned with one another even in the absence of a magnetic field. This is different from the behavior of paramagnets, where moments are randomly aligned in the absence of an applied field.
Diamagnetism is present to some degree in all materials but is overcome in paramagetic and ferromagnetic materials by the interactions between the dipoles. Diamagnets are considered to be non-magnetic materials, such as wood and glass, whereas materials such as cobalt and iron are permanently magnetized and treated as magnets. To understand what causes the alignment of the dipoles, the concept of exchange is used. Before discussing this concept, it is beneficial to review some of the modern methods used to model magnetic materials, in particular to highlight the use of spin Hamiltonians and the Density Functional Theory (DFT) approaches to this problem.
The Heisenberg model was originally proposed to predict the development of ferromagnetism in Fe, Co, and Ni. The Heisenberg exchange Hamiltonian [
19] is shown in Equation (2).
is the effective exchange integral between atoms i and j and is positive (negative) for ferromagnetic (anti-ferromagnetic) coupling. and are the spin angular moments between the two orbitals. The model is impressive in its simplicity, but it does not perform well in systems where there is indirect coupling, such as rare earth metals or dilute metal alloys. The latter case is particularly of interest in the current manuscript, as catalytically, many of the successful catalytic systems are, e.g., alloys, so a more accurate model for these systems is required.
The Heisenberg model can be refined to more accurately describe electrons moving in a periodic potential, and this approach is the Hubbard model:
The summations xy in Equation (3) extend over nearest neighbors only; the c’s are spin eigenfunctions, and and are single-particle kinetic (hopping) and two-particle (correlation) parameters, respectively. The model is better at describing delocalized systems than the Heisenberg model but requires further refinement to include the effects of higher neighbor interactions and exchange.
The implementation of spin in density functional theory (DFT) has provided some solution to this problem [
20,
21]. The DFT Hamiltonian can take the form
Equation (4) shows that the total energy of the Hamiltonian is made of terms describing the kinetic
, Coulomb
, external
and exchange-correlation
interactions. The first four of these terms are given in Equations (5)–(7), respectively.
Physically, these are the kinetic energy
of the non-interacting electron wavefunctions, the Coulomb interaction energy
acting between electrons, the external energy
between the electrons and the atomic lattice, and the exchange-correlation energy, which describes the Pauli interaction between the electron wavefunctions and their correlated motion. For the spin-polarized case, this latter term can be written in a number of ways, depending on the level of approximation used to describe the interaction. In the Local Spin-Density Approximation (LSDA), which is good for materials that have a homogeneous electron gas, the exchange correlation interaction is given in Equation (8).
For non-homogeneous systems, the Generalised Gradient Approximation is an improved approximation, and the exchange-correlation function is given in Equation (9).
The function
can be written as the linear combination of the exchange and correlation parts, and this formulation is shown in Equation (10).
A self-consistent solution of Equation (4) using terms presented in Equations (5)–(10) will then generate a solution set of electron wavefunctions and, through simple transformation, the spatially defined electron density. These can be converted—again, through a simple transformation—into the electron density of state functions used in the d-band model, which will be discussed in more detail later in this review.
summarizes the limitations of the Density Functional Theory, a form of must exist by the Hohenberg-Kohn theorem, which, when used in a full self-consistent solution of Equation (4), will yield electron wavefunctions that have exact energies and spatial distributions. However, this form of is not known, and therefore approximations must be used. The level of approximation affects both the computational efficiency and accuracy of the resulting electron wavefunctions . One of the more common approximations is the use of tight binding, which assumes that the electron wavefunctions are strongly localized on the atoms or ion cores of an extended system. Like all the approximations in DFT, this has a range of validity; however, it is generally considered chemically accurate—i.e., accurate to meV energies—which is generally considered to be the accuracy of the DFT. Numerically, this approximation is accurate for the d and f orbitals, which are tightly bound to ion cores when compared with the more delocalized s orbitals. Consequently, the DFT is an appropriate approximation to be used for the d-band model of adsorption.
Once a self-consistent field has been determined, there are a number of post-processing procedures that can be used to extract useful physical information from the simulation results. Central to this are the charge and spin densities, which are and , respectively. and are the number of spin up and down charge carriers. Once these quantities have been calculated, much of the post-processing can be completed, such as the deduction of the density of states and the estimation of the charge density distributions. Returning to the terms used in the DFT Hamiltonian to deduce these quantities, one of the more instructive for spin-polarized or magnetic systems is the exchange energy. Exchange interactions, generally in physics, are quantum mechanical terms that arise from the requirement for symmetry. For systems of fermions, these interactions are more commonly called the Pauli exclusion principle, which places restrictions on how the sign of the wavefunction describing the particle must change if the particles are interchanged.
There are two types of exchange mechanisms: short-range, or direct, mechanisms and long-range, indirect mechanisms. In the short-range case, the orbitals of electrons bound at adjacent sites are close enough for there to be orbital overlap, and the electrons have a mechanism by which they can ‘hop’ between sites. This hopping can be between two electrons with differing spins, resulting in a final state that has a spin-up/down electron pair at the same energy, or it can be between two electrons of the same spin with the second electron shifting to a third unoccupied site, leaving two electrons at two different sites.
In materials where the electrons have a delocalized character, e.g., metals, indirect mechanisms become viable. In the RKKY (Ruderman, Kittel, Kasuya, and Yosida) exchange interaction, or itinerant exchange, there is no direct overlap between the electrons involved in the exchange. Computationally, this can be modeled by creating electron wavefunctions that have separate spatial and spin components, i.e.:
and are the spatial and spin coordinates, respectively. The interaction depends on the distance between the spin centers and tends to spread spin alignment. These alignments can be either ferromagnetic or anti-ferromagnetic, and consequently, the interaction tends to create magnetic ordering.
There are further exchange mechanisms, which include the prototypical super- and double-exchange. In these mechanisms, the hopping of electrons between non-neighboring magnetic centers is assisted by an interaction with an intermediate non-magnetic center. Superexchange is shown schematically in
Figure 2.
The mechanism works by allowing electrons to hop between atomic centers, resulting in a final ordering that is either ferromagnetic or antiferromagnetic. Mechanistically, three different mechanisms are possible. Common to all three mechanisms is the starting state: that two TM centers have one electron each and one with the electron spinning up, while the second has the electron spinning down. These two TM atoms are separated by an oxygen p-orbital with two electrons, one spinning up and the other spinning down. In the first mechanism, the p-orbital is stripped of electrons, leaving both TM atoms with two electrons that spin up and spin down. In the second mechanism, one electron from the oxygen atom hops to one of the TM centers, while the electron from the second TM atom hops onto the oxygen atom. This leaves the electronic state of the oxygen atom unchanged, but the TM atoms have changed configuration, with one left with no electrons and the other with a pair of electrons. The final mechanism allows the hopping of just one electron from the oxygen atom to one of the TM centers, resulting in a ferromagnetic final state. Superexchange is generally controlled by the Goodenough-Kanamori rules, which determine the exchange energy of the final interactions and are dependent on the angle θ between the spin states and consequently the form of the exchange mechanism. Alternate mechanisms such as double exchange and semicovalent exchange are mechanistically similar. Which mechanism dominates is controlled by the energy operators for the individual system and by the filling of the d-states. What can be generally understood is that these provide the electronic mechanisms that control reactive catalytic processes on surfaces. The importance of the mechanisms can be seen experimentally by measuring the magnetization of the surface during reaction and identifying that changes in this magnetization must be explained by changes in the ordering of the surface spin states, as outlined above. The state of the theory at the moment is too young to allow a further discussion; models are currently in development to describe the interactions in stable materials, and it will be sometime before the mechanisms can be confidently applied to reactive systems.
Beyond the DFT, there are a number of computationally expensive but more accurate formulations that could be used to describe surface catalysis. Exact exchange can be used but is computationally significantly more expensive—by perhaps up to an order of magnitude in terms of processing time—than the non-exact formulation. Further, standard DFT can only poorly describe non-local behavior such as the van der Waals interaction. However, these terms are not generally significant for transition metal alloys.
Post-DFT, however, further refinements to the description of magnetism in catalytic systems are not widely in use. The modern theory of magnetization [
23] can potentially describe fully and exactly the interactions involved in surface catalysis. Their use may be more appropriate for some materials, e.g., strongly correlated materials, but this has not been thoroughly investigated for surface catalysis to date. However, their use is not widespread, so their consideration will be precluded from this review.
The current review will highlight how the understanding of spin-polarized processes has developed recently in surface catalysis, with a particular focus on transition metal (TM) and TM oxide surfaces. The key fundamental advances that will be addressed in this work are primarily centered around the transition of surfaces between non-magnetic and permanently magnetized surfaces through the adsorption of conjugated organic molecules. Refinements to these models—such as the onset of super-magnetism as the system reduces to nanoparticle dimensions [
24]—are potentially of interest, as is the use of externally applied magnetic fields in catalysis [
25]. However, their application to the onset of magnetization by organic adsorption has not been significantly investigated, so it is excluded from the current review manuscript.
A review of the current theoretical understanding of these systems will be made with a focus on the fundamental models of spin-polarized adsorption. This will be developed with a survey of the method of moments in describing adsorbate-substrate bonding, and some discussion will be made about how these models could be applied to the case of spin-polarized adsorption.
2. Experimental Studies of Small Particle Reactions with Magnetic Surfaces
Pt, Ir, and Ru-based catalysts are of particular interest in the current work. Pt-based materials are very common catalysts for the oxygen reduction reaction (ORR), and Ir and Ru have similar importance in the oxygen evolution reaction (OER) [
26]. Non-metallic surfaces [
27] are contenders for this role. The magnetic properties of graphene [
28] and the so-called ‘magnetic graphene’ [
29] have only recently been identified. Their impact on catalysis is consequently quite limited, so it will not be discussed in the current survey.
Pt, Ir, and Ru are expensive components. Alternatives have been suggested, including oxides, hydroxides, and hydroxyl oxides [
26] and sulfide layers. The mechanism of reaction does not alter fundamentally for these alternative surfaces; the reaction center is at the transition metal atom, which can accept electrons or electron pairs. Moreover, the reactivity of these surfaces can be tuned by either applying strain—tensile or compressive—or by creating defects or vacancies [
30]. These modifications can potentially improve the effectiveness of the surfaces by upshifting the
d-band. This promotes the adsorption of active intermediates, which in turn enhances the reactivity of the surfaces.
Within the same group of materials lie the perovskites. Thin films of LaNiO
3 contain highly correlated electrons that are sensitive to reduced dimensionality and epitaxial strain, i.e., their characteristics can be ‘tuned’ through thin film growth. Hydrogen reduction of LaNiO
3 [
31] perovskite electrocatalysts produces a material that has a large current density at low overpotential compared with earlier versions of the catalyst. The mechanism for this enhanced performance has been assigned to the formation of surface oxygen defects. A similar enhancement has been seen for holey TiN-LDH [
32], which is shown schematically in
Figure 3. The holey TiN−LDH activates the Fe and Ni ions—both ferromagnetic—during electrocatalysis, which increases the number of active sites and improves charge transfer kinetics.
A comparative example is monolayer tantalum disulfide (TaS
2) [
33], which shows multiple structural defects in experimental samples, and these defects are seen to significantly affect the catalytic performance of the layer. In this case, the effectiveness of the layer correlates to the center of the p or d band of the Ta or S atom. These examples demonstrate that the geometric modification of these surfaces can affect their activity and improve their catalytic performance by modifying the surface electronic structure of the materials. The remaining geometric parameter, that of the strain state of the surface, will be discussed in the next section, along with a more detailed discussion of the theoretical modeling of these surfaces.
The previous examples have briefly demonstrated how geometric factors can affect the activity of a surface, even for strongly correlated systems. It is noted that the changes in the geometry of the surface directly alter the surface electronic structure, which then itself changes the activity. Spin is a purely electronic factor that can also modify the activity. Its effect can be seen in ammonia synthesis. Adding alkali atoms to the surface usually promotes the synthesis, and electrostatic mechanisms between the dissociating N
2 and the alkali-modified surface and between adsorbed NH
x intermediates are accepted as the primary mechanisms for this type of interaction. Reports that Ba-promoted Co is higher than the usual Fe or Ru-based catalysts for this process [
34] have been explained by the lowering of the N adsorption energy and the N
2 dissociation energy on the promoted Co surface, as well as the as the observation that other promoters lower the spin moment close to where they are adsorbed, consequently stabilizing the N and N–N transition states. These effects were seen for the other ferromagnetic surfaces of Ni and Fe, indicating that spin-tuning was effective in improving the activity of these catalysts.
Fundamentally, first-principles investigations of RuO
2(110) [
35] have shown this surface to be magnetic despite the bulk system being non-magnetic. This magnetism satisfies the conservation of angular momentum required for reactions between the surface and oxygen to progress. Moreover, it also provides a mechanism to produce oxygen in its magnetic ground state, which is facilitated by the surface spin moments rearranging themselves during their interaction with the reacting oxygen. This mechanism allows the surface to be used as an effective electrocatalyst and is similar in form to the mechanism of O
2 interaction with clean and Au-doped rutile TiO
2(110) [
36].
The improvement of catalysis activity or of its precursors—for example, the adsorption energy or the energy barrier to adsorption—can also be modified on a pure metal surface without the inclusion of promoter atoms. An example of this is the FCC(111) Fe film [
37]. For this material, the surface can exist in a ferromagnetic or anti-ferromagnetic state, and its state affects its reactivity towards H
2. In an antiferromagnetic stage, H
2 can undergo barrierless adsorption and has a metastable molecular adsorption state. This compares to the usual high energies needed to dissociate H
2 across a metal surface and highlights how applying a magnetic field to a surface can change the magnetic state and, consequently, the activity of the surface.
Fe, Co, Ni, and Ru are the most common choices of catalysts for the Fischer-Tropsch (FTS) process, which converts CO + H
2 (syngas) into long-chain hydrocarbons and oxygenates. It is notable that three of the metals—Fe, Co, and Ni—are ferromagnets, but the exact reasoning is difficult to establish. The Fischer-Tropsh process is complex, and particular hydrogenations can require dozens of intermediate steps. Fe carbides have a different activity than the pure metal surfaces and arise as part of the FTS, so some effort has been expended in exploring both the fundamental structure and the resulting catalytic behavior of these surfaces. Swarm intelligence calculations [
38] have investigated the carbonization of Fe(100), (110) and (210) and have identified that C tends to stay on the surface of these facets. The chemical potential of carbon
(i.e., the experimental surface energy or stability of the surface) tends to increase with the number of (100) and (210) facets and decrease with the number of (110) facets. This effect is shown in
Figure 4. A micro-kinetic analysis of the carbonized surfaces showed that Fe(110) had the highest overall selectivity towards long-chain hydrocarbons but that the overall activity was not significantly increased by carbonization.
Fe–N–C catalysts are strong contemporaries to the more usual Pt-based catalysts used for the oxygen reduction reaction (ORR). Spin-polarized studies of atomically dispersed Fe–N–C catalysts [
25] have shown that electron spin-state modulation of the Fe active centers can selectively improve the ORR performance. Mechanistically, this is achieved by electron migration into the Fe 3D orbitals, which changes the valence state of the Fe center. The improvement to device performance is shown in
Figure 5 and compares the high-spin Fe–N
4 catalyst to the platinum carbide surface. Both the power density and voltage of the Fe-based device are better supported by increasing current density when compared with the non-ferrous device.
Comparative studies were made of the oxidation of CO to CO
2 on iron oxide surfaces [
40], and though they elucidated the oxidation mechanism, they did not identify spin as a driving force in the mechanism. Fundamental studies of the Fe-NiO(001) [
41] and Fe/Ir(100) [
42] surfaces have gone some way toward elucidating the magnetic character of the surfaces, with the Fe/Ir study in particular critically comparing the stability of the ferromagnetic and antiferromagnetic surfaces. Further investigation of the catalytic behavior of these surfaces may be productive, as the chemical potential of the Ni and Ir centers is close to that of Fe and Pt, suggesting that their performance may at least be comparable. The consideration of further experimental parameters, e.g., the method of heating the reacting system [
43], is precluded from the current survey.
These examples have demonstrated how Fe-based materials are rapidly emerging as effective alternatives to non-spin-polarized materials. This concept can be extended by looking at other materials that contain ferromagnetic components. Recent studies of Ni-Co alloys [
44] have demonstrated that these materials can effectively hydrogenate benzene. The mechanism of
d-orbital overlap across the surface of the material, which leads to this activity, is also seen across the surface facets of Pt-Ni nanoclusters [
45]. These clusters are shown to be particularly effective in promoting the water-gas shift (WGS) reaction, which is summarized in
Figure 6.
The study uses the
d-band model to predict the activities of Pt
13−nNi
n (
n = 0, 3, 6, 9, 13) nanoclusters using the d-band, bandwidth-corrected d-band, and effective d-band center approaches [
15]. The following activity series were obtained:
(1) Ni13 < Pt4Ni9 < Pt7Ni6 < Pt10Ni3 < Pt13 for the d-band and effective d-band center approaches; and
(2) Ni13 < Pt7Ni6 < Pt4Ni9 < Pt10Ni3 < Pt13 for the bandwidth-corrected d-band center approach.
The results of a full simulated reaction cycle using density functional theory (DFT) are shown in
Figure 7. These simulations show that the Pt
10Ni
3 clusters are the most effective catalyst, which is supported by all three variants of the
d-band model. However, the study further shows that though the catalytic performance of the Pt
4Ni
9 and Pt
7Ni
6 is inferior, they suffer lower structural changes per cycle, suggesting that they would survive more cycle rounds keeping their catalytic activity, and more specifically, that due to their higher turnover frequency, the Pt
4Ni
9 is expected to be a better catalyst than Pt
7Ni
6.
The authors of [
45] provide an exceptional insight into the durability of the nanoclusters as well as identifying that a Pt-rich stoichiometry provides the best environment for WGS catalysis in terms of the reaction energetics. These conclusions are somewhat supported by spin-polarized DFT calculations [
46] of the Pt
0.5Ni
0.5 bimetal, which show that H
2O binding occurs at the Ni atom. This is suggestive that the most effective catalyst in this sequence relies on geometric separation of the reaction centers, i.e., on the surface of the Pt
10Ni
3 nanoparticles, the Ni centers will be separated from one another, allowing reactants to move more easily between them. The precise mechanisms of this reaction mechanism and the reasoning why it is more effective than on a more ‘crowded’ reaction surface are currently not determined.
The examples presented above have shown that the magnetic state of the surface can significantly affect its activity and how, by mixing the
d-states of bimetallic surfaces, the activity of the catalyst can be controlled, particularly in the case of spin-polarized surfaces. These effects have been seen for the permanent ferromagnets Fe, Ni, and Co, as well as being discussed for other closely related systems, particularly those including Pt. Comparative changes in activity can be seen with other metals such as vanadium [
47], V–Cr [
48], and more complex tri-metallics such as Co
2VGa, Co
2MnGa, and Mn
2CoGa [
49], as well as in photochemical systems such as FeCoSe
2 [
50] and BiVO
4/Fe
0.4Co
0.6Se
2/Co(Fe)O
xH
y [
51]. What links all these studies is that they can be analyzed using the
d-band model. Therefore, in the next part of this survey, we will review some of the current metrics and reductions used to analyze catalytic processes and then consider how the
d-band model can be applied. We will also consider how the
d-band model can be developed to both predict processes as well as provide physical insight into the systems.
3. Theoretical Approaches to Adsorbate-Surface Bonding in Catalytic Systems
The previous section highlighted examples of spin-polarized surface adsorption and their consequences for catalytic processes, particularly those that use spin-polarized adsorbates such as oxygen. The previous part also highlighted the utility of surfaces that are spin-polarized and the effects these surfaces can have on catalysis. Overall, the utility of spin as a comparatively novel and viable design parameter in surface catalysis has been demonstrated, so the current section will move on to focus on approaches to rationalizing and reducing these design parameters.
Modeling catalytic processes is a challenging task. The reason for this is because of the length scales involved for the different types of processes involved [
52]. Real processes demand that a larger-scale approach be taken. The reason for this is because real catalysts contain defects and impurities that cannot usually be included in small unit cell calculations. Catalysts are also often in nanoparticle form, which means that they are necessarily generated with a size distribution that requires some form of averaging to determine behavior. Consequently, effective modeling of processes requires a multiscale approach, and in the current manuscript, the parts of this modeling that have been developed to describe magnetic systems will be highlighted.
The
d-band model of surface adsorption [
53] is one of the foremost descriptors of adsorption. The model describes the bonding between an adsorbate and the surface in terms of the center of the surface
d-band and is a development of the Newns-Anderson model, in the narrow
d-band limit, and of the effective medium theory. The model relates the movement of the
d-band center relative to the Fermi level
Ef during adsorption to the adsorption energy. An upward motion of the
d-band center relative to
Ef allows more anti-bonding states to become available, whereas a downward motion reduces the number of anti-bonding states and therefore the adsorption energy.
It is cogent to now highlight the use of strain as a controllable parameter in surface catalysis. This concept was highlighted in the previous section. Strain in the current context generally refers to strain within the surface or selvedge layers of the catalyst or substrate material being used. The methods of applying strain are reasonably diverse; in more fundamental studies, the strain can be applied mechanically, for example, by using a cantilever approach [
54], though more commonly, stain is applied by epitaxial growth and develops from the lattice mismatch between the epitaxial layer and the support. The latter approach is more convenient experimentally and can generate large yields of strained surfaces for catalytic processes. However, the approach is prone to interference in the surface bonding by the selvedge and support layers. This effect has been investigated for (111)-Pt/Ni/Pt
3Ni and (111)-Pt/Ni/PtNi
3 [
55] using spin-polarized DFT, which has shown explicitly that changes in the magnetic character of the support layers—in this case, Pt
3Ni and PtNi
3—alter the binding energy of oxygen and hydrogen atoms to the surface.
The effect of strain can be thought of in terms of the position of the d-band center of the substrate. In the case of tensile (compressive) strain, the
d-band will tend to narrow (broaden). The mechanism for this charge conservation is shown in
Figure 8.
This simple model has been used to discuss the adsorption of O and CO on Ru(0001) [
42] and to explain differences in the reactivity of the early transition metals, i.e., those with less than half-filled
d-bands [
56]. More recently, the model has been applicable to a more extensive survey of H bonding to strained Fe, Co, Ni, Cu, Ru, Rh, Pd, Ag, Os, Ir, and Au surfaces [
57] and in particular Pt [
58], where an extremely distinctive set of binding site transitions were observed as a function of the strain state of the surface.
Other surveys of the same group of metals have identified that the surface susceptibilities to strain are (Au, Pt) > Pd > (Ag, Cu) [
59]. This survey also showed that N- and O-containing adsorbates are more prone to changes in their binding than those that contain C. Further studies for the full hydrogen evolution reaction (HER) and the oxygen reduction reaction (ORR) [
60] on a more limited set of these metals have shown that the catalytic performance of certain metals can be enhanced by strain. What is noted throughout these studies is that the selvedge effects—highlighted in [
55]—have been neglected. This has been in part because the surveys have focused on pure metals. However, the actual mechanism of applying strain has been left as an experimental concern. Mechanistically, the studies have also focused on higher-level observables such as binding energy. More insight into the actual driving forces for the mechanisms seen under strain may be possible, perhaps through a simplified theoretical approach. This latter approach has been successfully applied to strained CeNi
5 [
61], where an RKKY analysis fully elucidated the complex interplay between the Ce 4f and Ni 3d states and the Ce 6s–Ni 4s, Ni 3d–Ce 6s/Ni 4s, and Ni 3d–Ni 3d states, providing information for how this system might be adapted in the future.
The
d-band model is not inherently spin-polarized. When it is therefore applied to magnetic systems, the level of agreement between the conventional d-band model and the spin-polarized system may therefore be improved by decoupling the spin up and down components and then treating each as an independent d-band system [
62]. This is shown schematically in
Figure 9.
The effects of strain as a design tool have been seen to be successful in some cases, and the mechanisms of the improvements in activity have been analyzed using the spin-polarized
d-band model. The reduction of nitrogen on strained Ti
2CO
2 [
63] uses surface Ti as the active site. The
dx2 and
dxz/dyz states of the surface Ti allow charge exchange into the surface bonding and anti-bonding states, providing the mechanism for improved catalytic performance when compared with the unstrained surface. However, alternative mechanisms to explain surface catalytic performance have been considered.
So far in this review, surface magnetization has been limited to cases where the magnetization exists in the absence of adsorbates or of externally applied magnetic fields. There is a body of evidence to show that magnetization can be induced on non-ferromagnetic transition metal surfaces by adsorption. Modeling magnetism in transition metals is complex because the
d electrons are neither completely localized nor delocalized. The accepted itinerant (delocalized) models of these systems use the Stoner criterion, Equation (12).
is the density of states at the Fermi level
and
is Stoner parameter. The model predicts that the polarization
P of the system is controllable. P is given in Equation (13).
and are the number of spin-up and spin-down electrons at , respectively, and is the total number of electrons. If the criteria in Equation (12) are satisfied, then an unpolarized system (P = 0) will become polarized, and P will be non-zero. The Stoner parameter plays a similar role in this model to the U parameter in the Hubbard model, which is formally estimated in spin polarized DFT calculations.
The Stoner model establishes criteria for the onset of magnetization in itinerant systems. One form of behavior for adsorption onto surfaces that are already ferromagnetic is shown schematically in
Figure 10.
Figure 10 shows the potential effect of adsorption on the surface magneto-crystalline anisotropy (MCA). Changes in the MCA have been recently predicted for organic adsorption of ferromagnetic surfaces—for example, for benzene, cyclooctatetraene, naphthalene, pyrene, and coronene adsorption on Co [
64]. In this study, the mechanism for changes in the MCA was assigned to orbital interactions between the C
p and Co
d states. Changes in the surface magnetization have been observed during PCP adsorption on Fe/W(110) [
65], though the magnitude rather than the direction of the surface magnetization was seen to be most affected. In this latter example, changes in the magneto-crystalline anisotropy energy (MAE) were assigned to interactions between the adsorbate
π and substrate
d states. Energetically, these changes corresponded to shifts in the exchange energy, which supports a more localized spin-focused model.
Experimental investigations of supported C
60 [
66] have shown that some non-ferromagnetic Cu surfaces may be made ferromagnetic at room temperature by covering them with C
60. The experimental data focuses on low-energy muon spin spectroscopy, a magnetic probe that shows that localized spin states exist close to the Cu/C
60 interface. The explanation for this behavior in Cu/C
60 has focused on the Stoner model and adaptations of the model to improve its description of the experimental data. This has been achieved by modifying the interaction between localized and itinerant states at the interface by a Newns-Anderson-Grimley term [
67]. The revised model does improve agreement between the calculated and experimental adsorption energies. However, it does highlight the difficulties involved in treating transition metal
d-states, which are neither fully localized nor fully itinerant.
The theoretical models presented so far have focused on single electron formulations, and the consequential results have highlighted that modification of the exchange interaction can improve the agreement between experiment and theory. Cutting-edge models [
68] have investigated the many-body effect and its effect on the correlation energy using dynamical mean field theory (DMFT) [
69]. The theory replaces the average approach to the many body interactions used in DFT with a more exact, multi-dimensional approach. The manuscript highlights the importance of taking this more exact approach for the case of oxygen adsorption on Fe surfaces, where it explicitly shows that the
U and
J system parameters, which describe the electron-electron interaction, are underestimated. Noting the importance of these parameters in both the Hubbard and the DFT treatments of these systems, accurate revisions of their values are expected to be of significance in the future.
An equally fundamental work has investigated the presence of topological surface states in certain metal diborides [
70], which have been identified as mechanisms for the enhanced HER performance of those materials. Comparatively, Quantum Spin Exchange Interactions (QSEI) [
71] are a quantitative approach to describing the stabilization energy between two electrons with the same spin by allowing them to exchange orbitals, positions, and momentum. Using this correction, metals like Cr and Mn, which have high spin, can be shown to be more inert than Au towards covalently bound H. Both of these methods may provide predictive alternatives to the
d-band approach, though both are in comparative infancy.
The computational limitations of the spin-polarized formulation of Bhattacharjee et al. [
72] are similar to those of the non-polarized model. Both assume that the reactivity of a surface is determined by the position of the center of the surface
d-band. Mathematically, we can write this position as the first moment of the surface
d-band
. This means that, mathematically, there will exist a higher sequence of moments. For this case,
these are defined as follows [
72,
73]:
is the center of the electronic density of states
. Equation (14) is written in the general form, so it defines the higher moments for atom A and orbital O but reduces to the
d-band case with an appropriate choice of O. For this case,
we have
Physically,
corresponds to the center of the orbital band, and the higher moments
,
, and
correspond to the width, skewness, and bimodality of the band, respectively [
74,
75,
76]. The adsorption energy
can then be written in the form shown in Equation (16).
The expression for
given in Equation (13) is a polynomial series in ascending powers of the moments of the electronic density of states. The numerical coefficients
and the
in Equation (14) have then been determined by fitting to a database of adsorption energies [
72,
73] for metal, oxygen, and hydrogen adsorption in high symmetry positions on strained low Miller index Ni, Cu, Rh, Pd, Ag, Ir, Pt, Au surfaces, and on Co(0001), Ru(0001), and Os(0001). These adsorption energies were determined using a combination of spin-polarized and non-spin-polarized DFT. The quality-of-fit functions
and
used in the original work are shown in
Figure 11.
The convergence testing presented in
Figure 11 shows that polynomials of degree 2, which include moments up to and including and
are required to give a satisfactory fit between the polynomial and the data set. Further refinement was not attempted as qualitatively the curves in
Figure 11 show convergence, and a quantitative analysis of the fitted polynomials determined at
Nm = 4 and
D = 2 showed that the fitted polynomials agreed with the data set within chemical accuracy, which itself is seen as the limiting accuracy of DFT.
The success of the formulation in Equation (16) has been the demonstration that chemical accuracy can be obtained by modeling adsorption using a description of the adsorbate-substrate interaction, which includes terms up to , including magnetic systems. This has tested numerically one of the original assumptions of the d-band model that the adsorbate-substrate interaction can be accurately modeled by using only terms in .
The relationship between the moments of a particular band and the atomic orbitals in that band is given in Equation (17) [
74,
75,
76].
Equation (17) shows that
is equivalent to the hopping parameters between orbitals [
77]. The results in
Figure 11 are particularly significant for simulations of catalytic processes using small to medium units of cells. It shows that the hopping parameters of up to the 4th nearest neighbors are significant at the DFT/spin-polarized DFT level. Consequently, this level of interaction should be included to maintain DFT accuracy, and the size of the unit cell used in these simulations should be scaled appropriately.