Doping Effects on the Multiferroic Properties of KNbO₃ Nanoparticles

Abstract

The magnetization, polarization, and band-gap energy in pure and ion-doped ${\mathrm{KNbO}}_3$ (KNO) bulk and nanoparticles (NPs) are investigated theoretically using a microscopic model and Green’s function theory. It is shown that KNO NPs are multiferroic. The size dependence of M and P is studied. The magnetization M increases with decreasing NP size, whereas the polarization P decreases slightly. The properties of KNO can be tuned by ion doping, for example, through the substitution of transition metal ions at the Nb site or Na ions at the K site. By ion doping, depending on the relation between the doping and host ion radii, different strains appear. They lead to changes in the exchange interaction constants, which are inversely proportional to the lattice parameters. So, we studied the macroscopic properties on a microscopic level. By doping with transition metal ions (Co, Mn, Cr) at the Nb site, M increases, whereas P decreases. Doped KNO NPs exhibit the same behavior as doped bulk KNO, but the values of the magnetization and polarization in KNO NPs are somewhat enhanced or reduced due to the size effects compared to the doped bulk KNO. In order to increase P, we substituted the K ions with Na ions. The polarization increases with increasing magnetic field, which is evidence of the multiferroic behavior of doped KNO bulk and NPs. The behavior of the band-gap energy $E_g$ also depends on the dopants. $E_g$ decreases with increasing Co, Mn, and Cr ion doping, whereas it increases with Zn doping. The results are compared with existing experimental data, showing good qualitative agreement.

1. Introduction

Potassium niobate ${\mathrm{KNbO}}_3$ (KNO) is a well-known ferroelectric material with a high Curie temperature of about 435 $°$C, which is widely studied because of its ferroelectricity, piezoelectricity, and optical properties [1]. It is one of the candidate materials for lead-free piezoelectric applications because of its large piezoelectricity and high Curie temperature [2]. KNO has an orthorhombic symmetry at room temperature and exhibits phase transitions at −10, 225, and 435 $°$C, corresponding to rhombohedral → orthorhombic → tetragonal → cubic phases [3]. For the perovskite oxide KNO, the ferroelectricity originates from the displacement of ${\mathrm{Nb}}^{5+}$, causing them to deviate from the center of the symmetry within the ${\mathrm{NbO}}_6$ octahedron, which leads to the destruction of the spatial inversion symmetry. It must be noted that ${\mathrm{K}}^{+}$ and ${\mathrm{Nb}}^{5+}$ are paramagnetic ions. Therefore, pure bulk KNO is nonmagnetic; it is only ferroelectric.

We emphasize that there are two ways for KNO to become magnetic, i.e., to be multiferroic. One method involves doping with magnetic ions, which leads to weak ferromagnetism. The other method is the generation of ferromagnetism due to surface and size effects. It should be noted that doping KNO nanoparticles with magnetic ions would enhance their magnetic properties. Moreover, doping KNO bulk and NPs with different ions of different sizes can change all properties, for example, magnetic, electric, and optical ones.

In recent years, the multiferroic properties of ion-doped KNO ceramics have been observed in a few works, i.e., existing magnetic and electric properties coexist within the same phase. Weak ferromagnetic behavior in ion-doped (Co, Fe, Mn, Cr, Al) KNO on the Nb site at room temperature was reported in [1,4,5,6,7,8,9,10]. Therefore, it is a promising candidate for room-temperature multiferroic applications. Density functional theory, using ultra-soft pseudo-potential, was used to study the structural, electronic, magnetic, and optical properties of Sr-doped KNO by Jameel et al. [11]. The authors showed that Sr-doped KNO has enhanced band gap, optical conductivity, energy absorption, and refractive index, making it an appropriate material for perovskite solar cell applications. We would like to point out that the transition metal ion doping on the Nb site leads to a decrease in polarization, as reported by Min et al. [1] and Zhang et al. [12]. Moreover, it was observed by Astu et al. [8] that the application of an external magnetic field leads to enhanced polarization, which is also evidence of the multiferroic behavior of KNO.

Ion doping on the K site with Na, Li, Rb, and Cs ions [13,14,15] leads to increasing polarization and band gap, contrary to the case of Nb ion substitution with transition metal ions. The ferroelectric properties of Na-doped KNO were studied within first-principles calculations by Wang et al. [13].

The magnetic and electric properties of KNO nanostructures were investigated in [10,16,17,18,19]. It was observed that although the bulk crystals of KNO are nonmagnetic, the nanoparticles (NPs) show a ferromagnetic behavior. The magnetization increases with decreasing NP size. Based on the magnetic percolation theory, Golovina et al. [20] considered the appearance of ferromagnetic ordering in KNO NPs. For polarization in KNO NPs, an increase [18,19] and a decrease [17] with decreasing NP size have been reported. We will try to clarify this different behavior and these discrepancies.

Like most ferroelectric materials, pure KNO shows semiconducting properties, with a bandwidth of around 3.22 eV [21]. It has a low utilization rate of sunlight; therefore, the problem of how to increase its absorption response to visible light has become a popular research direction for KNO materials, e.g., through doping, ion substitution, or composition adjustments, which are effective for adjusting the optical band gap and electrical property, as reported with Mn doping by Manikandan et al. [6] and Cr doping by Raja et al. [5]. Transition metal ion doping at the Nb site can lead to a decrease in the bandwidth energy [5,12]. First-principles calculations were performed by Liang and Shao [22] to investigate the electronic structures and band-gap energies of KNO with 3D transition metal substitutions (V, Mn, Fe, Ti, Cr, Ni, Cu) at the Nb site. The authors showed that perovskite oxides are potential key materials for photovoltaic applications.

The majority of theoretical papers that have studied the properties of ion-doped KNO are based on density functional theory [11,13,15]. DFT is a very powerful tool for investigating many-body problems. However, DFT is mostly concerned with ground-state properties at zero temperature. In our approach, we are able to cover the whole temperature regime. It is a finite temperature analysis and includes the entire excitation spectrum. In particular, the method allows us to study the total phase diagram, which is based on the different excitation energies realized in the system. The disadvantage of our approach lies in the consideration of collective properties from the beginning. Our basic quantities are not the naked electrons but effective spins of the underlying quasi-particles. However, with DFT, all parameters of the system can—at least in principle—be calculated, so we are forced to use additional models to determine these parameters. We are convinced that both approaches, DFT and the Green’s function method, are appropriate and, to a certain extent, can be alternatives for describing many-body systems. Therefore, in the present work, we show that ion-doped KNO NPs manifest ferroelectricity and ferromagnetism simultaneously at room temperature, using a microscopic model and the Green’s function technique. Moreover, the ion-substitution effects of the Nb and K sites on magnetization, polarization, and band-gap energy are demonstrated. The results are compared with existing experimental data, showing good qualitative agreement.

2. Model and Method

The multiferroic properties are described by the following Hamiltonian:

$$H=H_f+H_m+H_{mf}.$$

(1)

For the ferroelectric subsystem, we use the transverse Ising model:

$$H_f=-\mathsf{\Omega }\sum _i{B}_i^x-\frac{1}{2}\sum _{ij}(1-x^{\prime })J_{ij}^{\prime }{B}_i^z{B}_j^z-\mu E\sum _i{B}_i^z,$$

(2)

where $B_i^x$ and $B_i^z$ are the spin-1/2 operators of the pseudo-spins at site i. The pseudo-spin operator $B_i^z$ determines the two positions of the ferroelectric unit. $J_{ij}^{\prime }$ is the pseudo-spin exchange interaction constant. The transverse term with the flipping rate $\mathsf{\Omega }$ and the operator $B_i^x$ gives the dynamics of the ferroelectric part. E is an electric field. $x^{\prime }$ is the ion-doping concentration on the K site.

The relative polarization P is calculated from $\langle B^z\rangle$:

$$P=\langle B^z\rangle =\frac{1}{2N}\sum _{ij}tanh\frac{E_{fij}}{2k_{B}T}.$$

(3)

$E_{fij}$ is the pseudo-spin excitation energy observed from the poles of the Green’s function $G_{ij}$ = $\ll B_i^{+};B_j^{-}\gg .$

The magnetic properties of the transition metal (TM) ion-doped KNO are given by the Heisenberg model:

$$H_m=-\sum _{ij}x{J}_{ij}{\mathbf{S}}_i·{\mathbf{S}}_j-\sum _i{D}_i{\left(S_i^z\right)}^2-g{\mu }_{B}h\sum _i{\mathbf{S}}_i,$$

(4)

where ${\mathbf{S}}_i$ is the Heisenberg spin operator of the TM ion at site i. $J_{ij}$ is the exchange interaction constant between the TM ions, $D_i$ is the single-ion anisotropy constant, and h is an external magnetic field.

The magnetization $M=\langle S^z\rangle$ is calculated as follows:

$$M=\langle S^z\rangle =\frac{1}{N}\sum _{ij}\left[(S+0.5)coth\left[(S+0.5)\beta E_{mij}\right)]-0.5coth\left(0.5\beta E_{mij}\right)\right],$$

(5)

where S is the spin value and $\beta =1/k_{B}T$. $E_{mij}$ represents the spin excitations calculated from the spin Green’s function ${\tilde{G}}_{ij}$ = $\ll S_i^{+};S_j^{-}\gg$:

$$E_{ij}=\frac{\langle [[S_i^{+},H_m],S_j^{-}]\rangle }{\langle [S_i^{+},S_j^{-}]\rangle }.$$

(6)

The two subsystems (2) and (4) are coupled through the magnetoelectric coupling g:

$$H_{mf}=-g\sum _{iklm}{B}_i^z{B}_k^z{\mathbf{S}}_l·{\mathbf{S}}_m.$$

(7)

In order to calculate the band-gap energy, we use the following s–d model: $H_{s-d}=H_m+H_{el}+H_{m-el}$. The Hamiltonian of the conduction band electrons is:

$$H_{el}=\sum _{ij\sigma }{t}_{ij}{c}_{i\sigma }^{+}{c}_{j\sigma }.$$

(8)

$t_{ij}$ is the hopping integral and $c_{i\sigma }^{+}$ and $c_{i\sigma }$ are the Fermi-creation and -annihilation operators.

The s–d coupling term $H_{m-el}$ is expressed as follows:

$$H_{m-el}=\sum _i{I}_i{\mathbf{S}}_i{\mathbf{s}}_i,$$

(9)

where I is the s–d interaction constant. The spin operators ${\mathbf{s}}_i$ of the conduction electrons at site i can be expressed as $s_i^{+}=c_{i+}^{+}{c}_{i-}$, $s_i^z=(c_{i+}^{+}{c}_{i+}-c_{i-}^{+}{c}_{i-})/2$.

The band-gap energy $E_g$ of KNO is studied by the difference between the valence and conduction bands:

$$E_g={\omega }^{+}(\mathbf{k}=0)-{\omega }^{-}(\mathbf{k}={\mathbf{k}}_{\sigma })$$

(10)

with the electronic energies

$${\omega }^{\pm }\left(\mathbf{k}\right)={ϵ}_{\mathbf{k}}-0.5\sigma I\langle S^z\rangle ,$$

(11)

where $\sigma =\pm 1$, ${ϵ}_{\mathbf{k}}$ is the conduction band energy in the paramagnetic state.

3. Numerical Results and Discussion

KNO is a perovskite-structured crystal that crystallizes in the cubic Pm3m space group. The structure is three-dimensional, where the ${\mathrm{K}}^{1+}$ ions bond to twelve equivalent ${\mathrm{O}}^{2-}$ ones to form KO12 cuboctahedra. KNO exists in different phases, like cubic, orthorhombic, rhombohedral, and tetragonal. On cooling from high temperatures, the crystal symmetry of KNO changes from cubic centrosymmetric (Pm3m) to tetragonal non-centrosymmetric (P4mm). On further cooling, at 225 $°$C, the crystal symmetry changes from tetragonal (P4mm) to orthorhombic (Amm2), and at −50 $°$C, from orthorhombic (Amm2) to rhombohedral (R3m).

Here, we present and discuss our numerical results, which are obtained using the following model parameters: J(Mn-Mn) = −1.07 meV, D = 0.02 meV [23], J(Cr-Cr) = −3.348 meV, D = 0.03 meV [24], J(Co-Co) = −0.237 meV, D = 0.01 meV [25], I = 0.2 eV, g = 15 K, $J^{\prime }$ = 550 K, and $\mathsf{\Omega }$ = 20 K. It should be mentioned that the numerical results provide an opportunity for qualitative analysis of the behavior of systems at the microscopic level, prediction of their behavior, explanation of experimental results in the presence of contradictory behavior, and their use in explaining or predicting results in similar systems.

3.1. Ion-Doping Dependence of the Magnetization of Bulk KNO

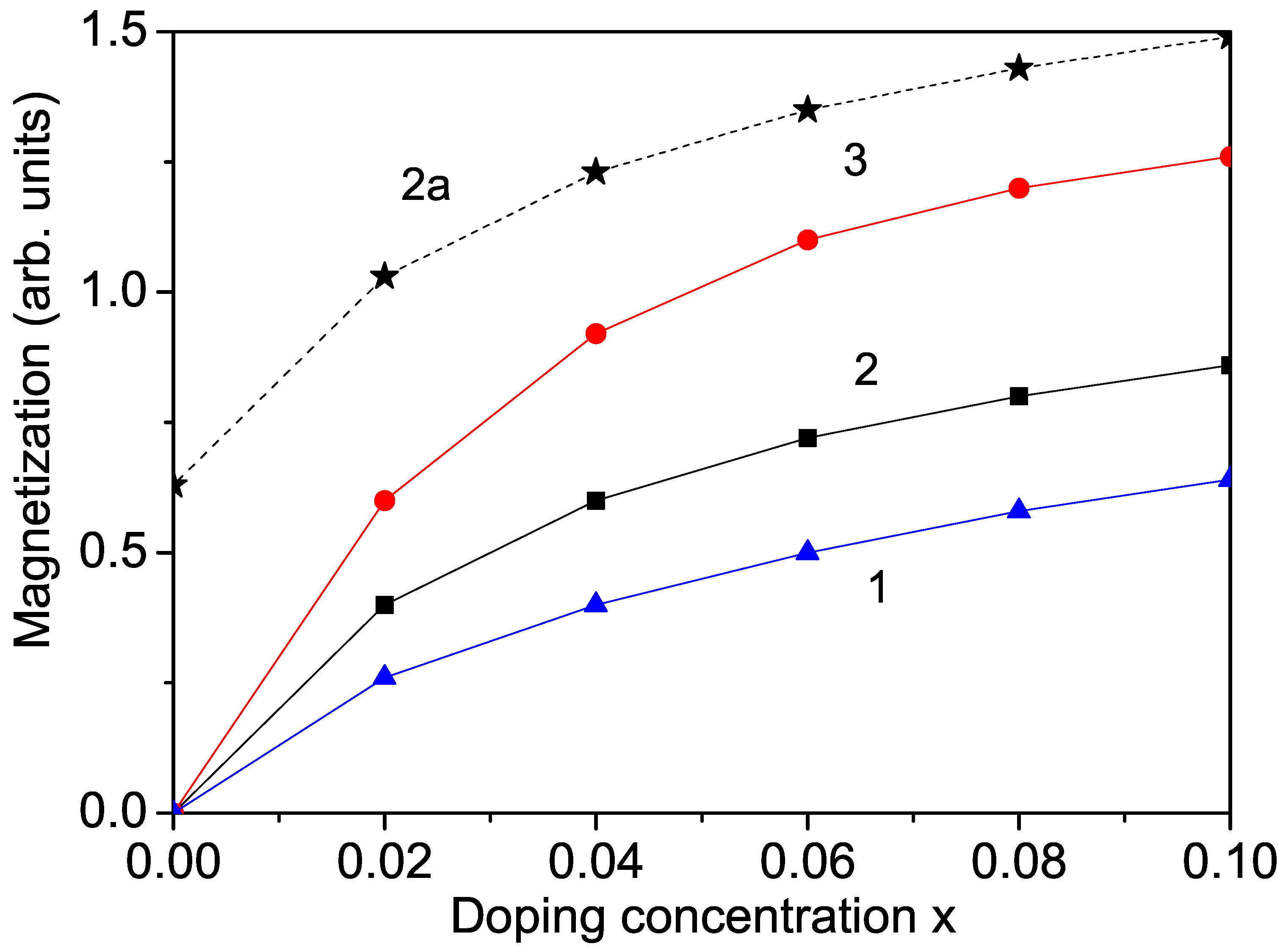
Firstly, we calculate the ion-doping dependence of the magnetization of bulk KNO for different transition metal ions. Bulk undoped KNO is nonmagnetic. But after substitution with transition metal ions, ferromagnetic behavior appears. For example, ${\mathrm{Mn}}^{4+}$ ion doping at the ${\mathrm{Nb}}^{5+}$ site creates oxygen vacancies in order to balance the charge state. When comparing the cell parameters of pure and doped samples, there is a decrease in the lattice parameters. This is due to the difference in the ionic radii of ${\mathrm{Mn}}^{4+}$ (0.53 Å) and ${\mathrm{Nb}}^{5+}$ (0.69 Å) in the octahedral coordination [6]. The smaller ionic radius of ${\mathrm{Mn}}^{4+}$ compared to that of ${\mathrm{Nb}}^{5+}$ leads to a decrease in the cell volume and the lattice parameters, i.e., to a compressive strain. The exchange interaction constants, for example, $J(r_i-r_j)$, depend on the distance between the spins and the lattice parameters. They are inversely proportional to both the distance between the spins and the lattice parameters. With compressive strain, the exchange interaction constant in the doped state, denoted as $J_d$, is larger compared to that in the undoped state, $J_d>J$. Conversely, with tensile strain, we have the relation $J_d<J$, which allows for the study of the macroscopic properties on a microscopic level. In our case, the Mn substitution induces compressive strain, leading to an increase in the exchange interaction constants $J_d>J$ and the appearance of ferromagnetic behavior (see Figure 1, curve 2), in agreement with the experimental data of Manikandan et al. [6]. Similar ferromagnetic behavior is observed with ${\mathrm{Cr}}^{3+}$ (r = 0.61 Å) substitution of the Nb ions in bulk KNO (see Figure 1. curve 3), in agreement with the results of Raja et al. [5], and through ${\mathrm{Co}}^{2+}$ ion doping (Figure 1, curve 1), as reported by Astudillo et al. [7].

We emphasize that compositions containing elements with multi-oxidation states (e.g., manganese, antimony, niobium, iron) can lead to the formation of substitutional defect centers [26]. This is accompanied by the formation of charge-compensating holes, further contributing to the increase in oxygen vacancy concentration. An example of such a process is the reduction of ${\mathrm{Nb}}^{5+}$ to ${\mathrm{Nb}}^{4+}$. It should be noted that the experimental determination of the point defects is difficult and requires a combination of several complementary techniques, for example, impedance spectroscopy, electron paramagnetic resonance, positron annihilation spectroscopy, Moessbauer spectroscopy, and X-ray photoelectron spectroscopy. Moreover, the exact charge-compensating mechanisms strongly depend on the processing atmosphere, temperature, and chemical composition.

3.2. Ion-Doping Dependence of the Polarization of Bulk KNO

When ${\mathrm{Co}}^{2+}$ ions replace part of the ${\mathrm{Nb}}^{5+}$ ions in the KNO lattice, it causes octahedral deformation. According to the Raman results of Zhang et al. [12], this deformation reduces the degree of distortion along the polar axis. We emphasize that the polarization in perovskite oxide KNO is due to the displacement of ${\mathrm{Nb}}^{5+}$ deviating from the center of symmetry of the ${\mathrm{NbO}}_6$ octahedron, which leads to the destruction of spatial inversion symmetry. Therefore, the ferroelectric polarization is weakened after doping with Co or other transition metals (Cr, Mn) at the Nb sites. The phase transition temperature also decreases, as reported by Lin et al. 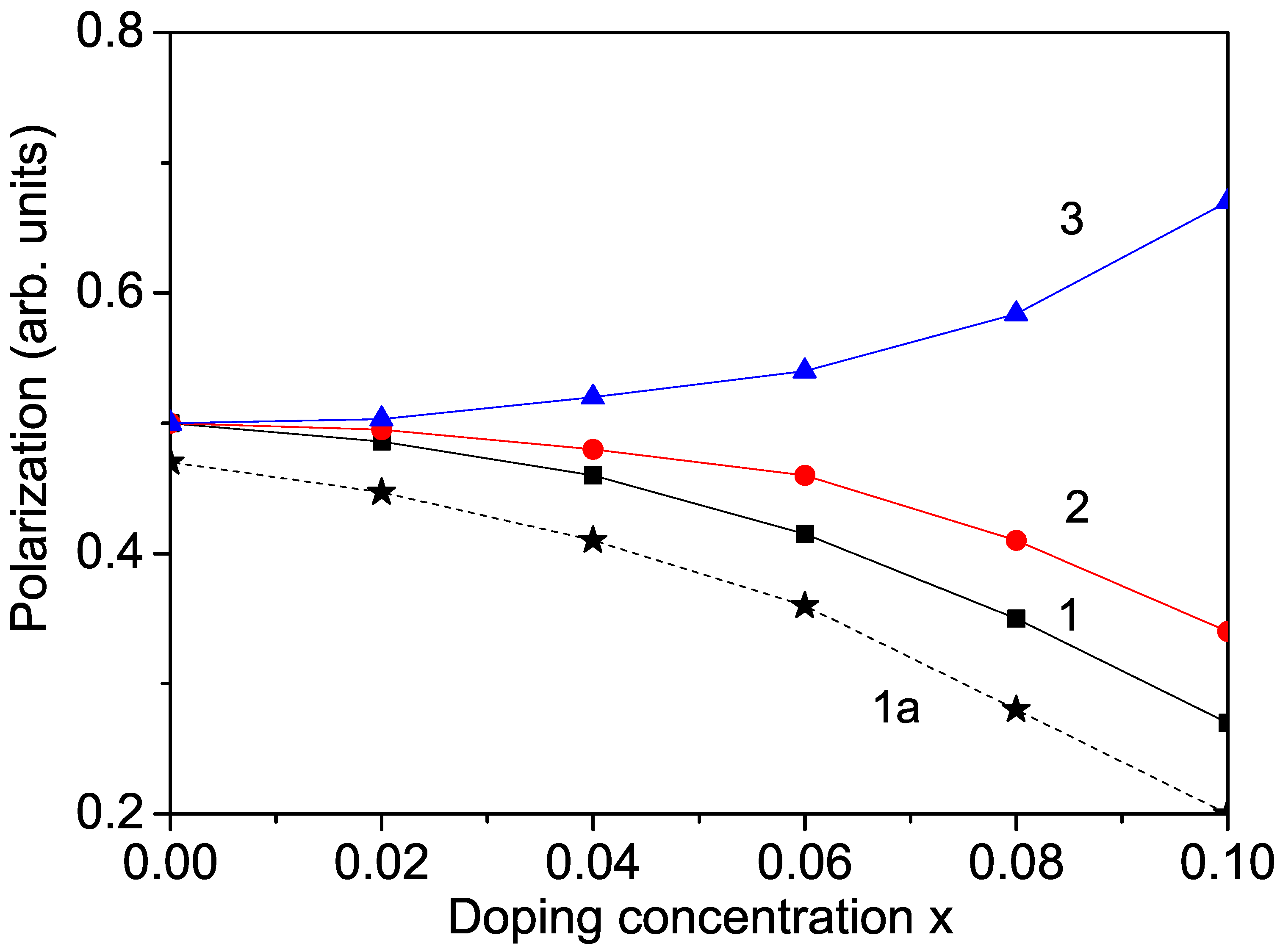[27], for Mn-doped KNO. The numerical results for $P\left(x\right)$ are demonstrated in Figure 2, curves 1 and 2, for example, for Co and Cr ion substitution. The decrease in P for Mn-doped KNO is not shown here. A similar reduction in the polarization in transition metal ion-doped KNO was reported in [1,5,9,12].

To observe an increase in the polarization, we substituted Na or Li ions at the K site. The radius of the Na (1.16 Å) and Li (0.90 Å) ions is smaller than that of the K ion (1.52 Å), i.e., compressive strain appears. This leads to enhancing the pseudo-spin exchange interaction $J^{\prime }$ and to a larger polarization P with increasing doping concentration compared to the undoped case. We calculated the polarization for Na-doped KNO. The results are demonstrated in Figure 2, curve 3. A similar increase in the electric properties in Na- and Li-doped KNO was reported in [13,15].

3.3. Magnetic and Electric Properties of KNO Nanoparticles

Next, we consider the magnetic and electric properties of pure and ion-doped KNO NP. An NP is defined by fixing the origin at a certain Fe spin in the center of the particle and including all spins within the particle into shells numbered by $n=1,\dots ,N$, where $n=1$ is the central spin and $n=N$-the surface shell. In our case, the NP offers icosahedral symmetry [28], i.e., there are 12 spherical particles in the first shell, 42 in the second shell, 92 in the third shell, etc.

The exchange interaction $J_{ij}\equiv J(r_i-r_j)$ depends on the lattice parameters, which are inversely proportional. The surface effects ($n=N$) are included by the exchange interaction constant on the surface layer $J_s$, which differs from the bulk constant J. We emphasize that J in the bulk pure KNO is zero, but in the NP, $J_s$ is non-zero. The index s is used for all model parameters.

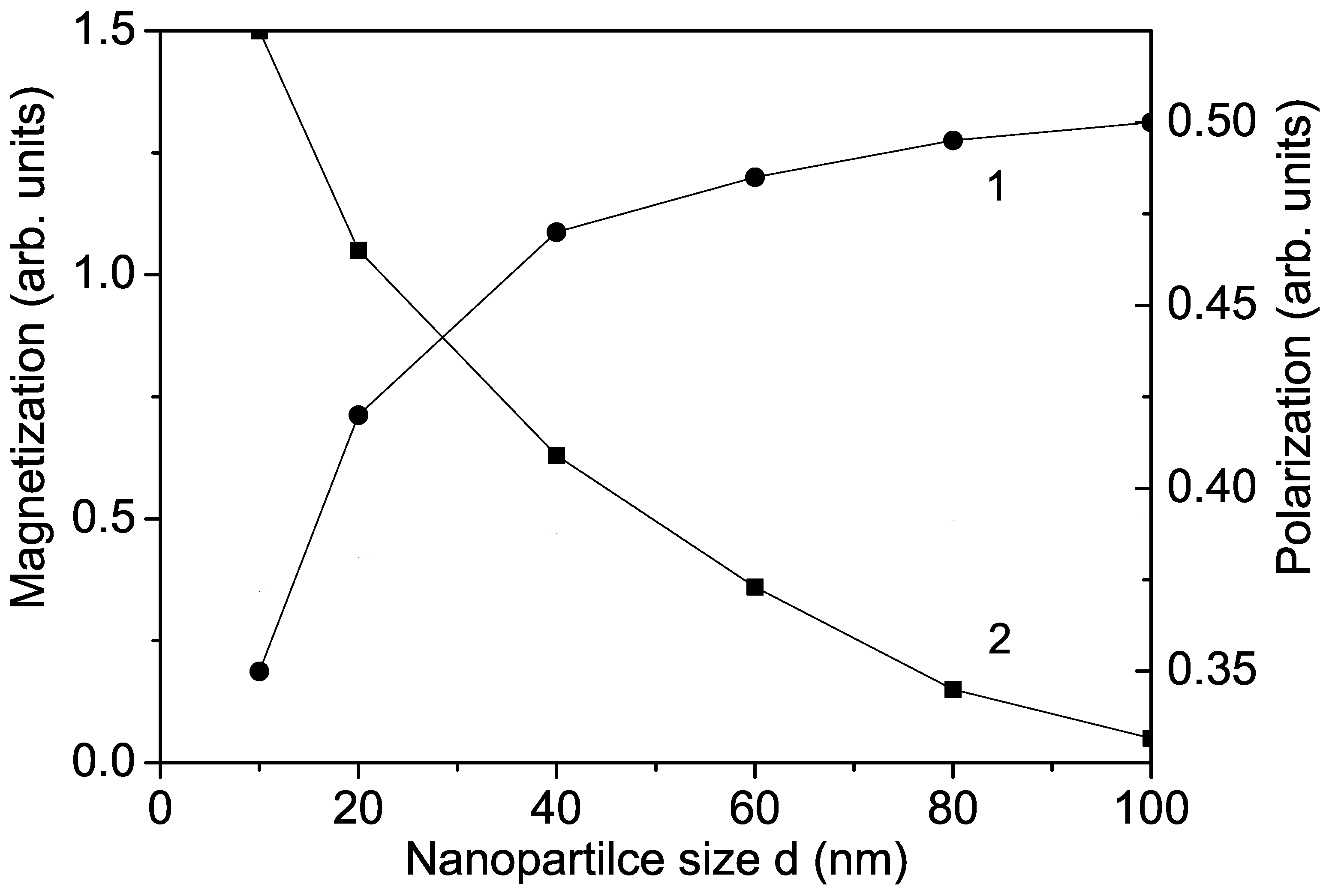
It is important to note that ${\mathrm{Nb}}^{5+}$ is nonmagnetic, and bulk undoped KNO is also nonmagnetic. But in KNO NPs, oxygen vacancies appear on the surface, leading to the appearance of different valence states of ${\mathrm{Nb}}^{4+}$ and/or ${\mathrm{Nb}}^{3+}$, which are paramagnetic (S = 1) [29,30]. They cause a non-zero magnetization in an external magnetic field, which increases with decreasing particle size (see Figure 3, curve 1), in agreement with the results of Diaz-Moreno et al. [30] and Golovina et al. [10]. There is weak surface ferromagnetism in KNO NPs, which increases after ion doping (see Figure 1, curve 2a). A similar increase in the magnetization M was reported in Fe-doped KNO NPs in [10].

There are some discrepancies in the experimental data about the size dependence of the polarization P in KNO NPs. We observe that due to surface effects, the polarization P decreases with decreasing NP size d (see Figure 3, curve 2). This is in agreement with the results of Dudhe et al. [17] but contrasts with the increase in P with decreasing d reported by Ge et al. [18] and Lee et al. [19]. We emphasize that small KNO NPs remain ferroelectric, in agreement with Dudhe et al. [17]. The Curie temperature $T_C$ is also reduced in KNO NPs by about 30 $°$C compared with bulk KNO, which is attributed to surface and size effects. By ion doping, the polarization also decreases with increasing transition metal ion concentration but more significantly compared to undoped KNO NP due to the surface effects (see Figure 2, curve 1a).

3.4. Magnetic Field Dependence of the Polarization of KNO Bulk and NPs

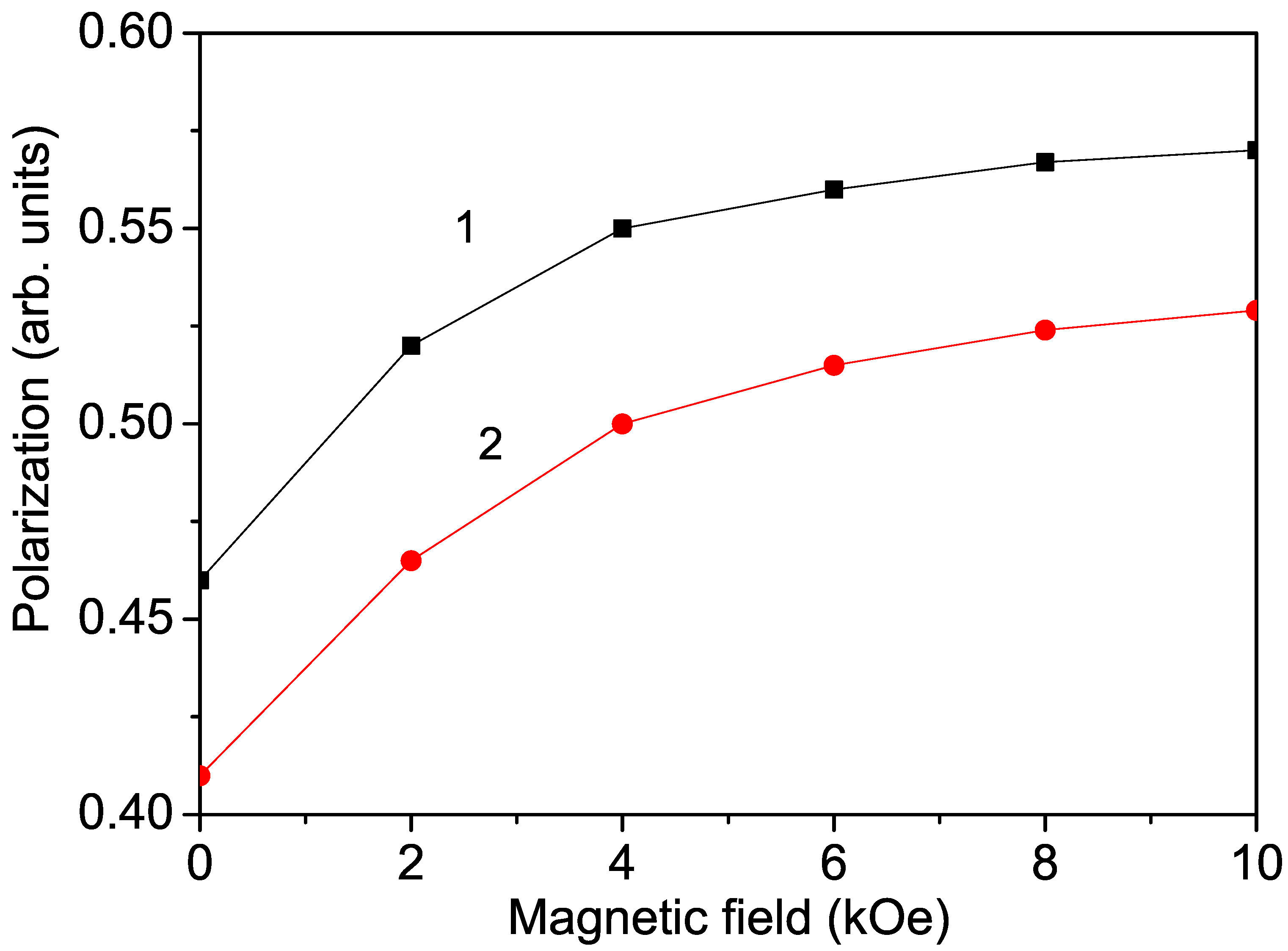
We have shown that bulk ion-doped KNO exhibits magnetic and electric properties, i.e., it is a multiferroic compound. It must be mentioned that one of the most important properties of multiferroics is the change in polarization due to an external magnetic field, and conversely, the change in magnetization due to an external electric field. Therefore, we calculated the magnetic field dependence of the polarization in Co-doped KNO. The results are presented in Figure 4, curve 1. It can be seen that P increases with increasing h, in agreement with Astudillo et al. [8]. This behavior is indicative of the coupling between the two order parameters—polarization and magnetization. Increasing h results in a non-linear increase in magnetization M due to the magnetoelectric interaction, which also leads to a non-linear increase in P. The increase in polarization is stronger at higher temperatures near $T_N$. At low temperatures, the polarization is saturated and nearly independent of the applied magnetic field. Moreover, when a magnetic field is applied to a magnetoelectric material, the material undergoes strain. This strain induces stress on the piezoelectrics (all ferroelectrics are piezoelectrics), which generates an electric field. This field can then orient the ferroelectric domains, leading to an increase in the polarization value. This magnetoelectric coupling and large polarization, i.e., large dielectric constant, could be useful in device applications.

After applying an external magnetic field, enhanced polarization was also observed in Cr- and Mn-doped KNO NPs. Curve 2 in Figure 4 shows the magnetic field dependence of the polarization P in a Co-doped KNO NP with d = 40 nm. This behavior is also evidence of the multiferroicity of ion-doped KNO NPs.

It must be noted that undoped KNO NPs, which show ferromagnetic and ferroelectric properties due to surface effects, are also multiferroic compounds, whose polarization also increases with the enhancement of the external magnetic field h.

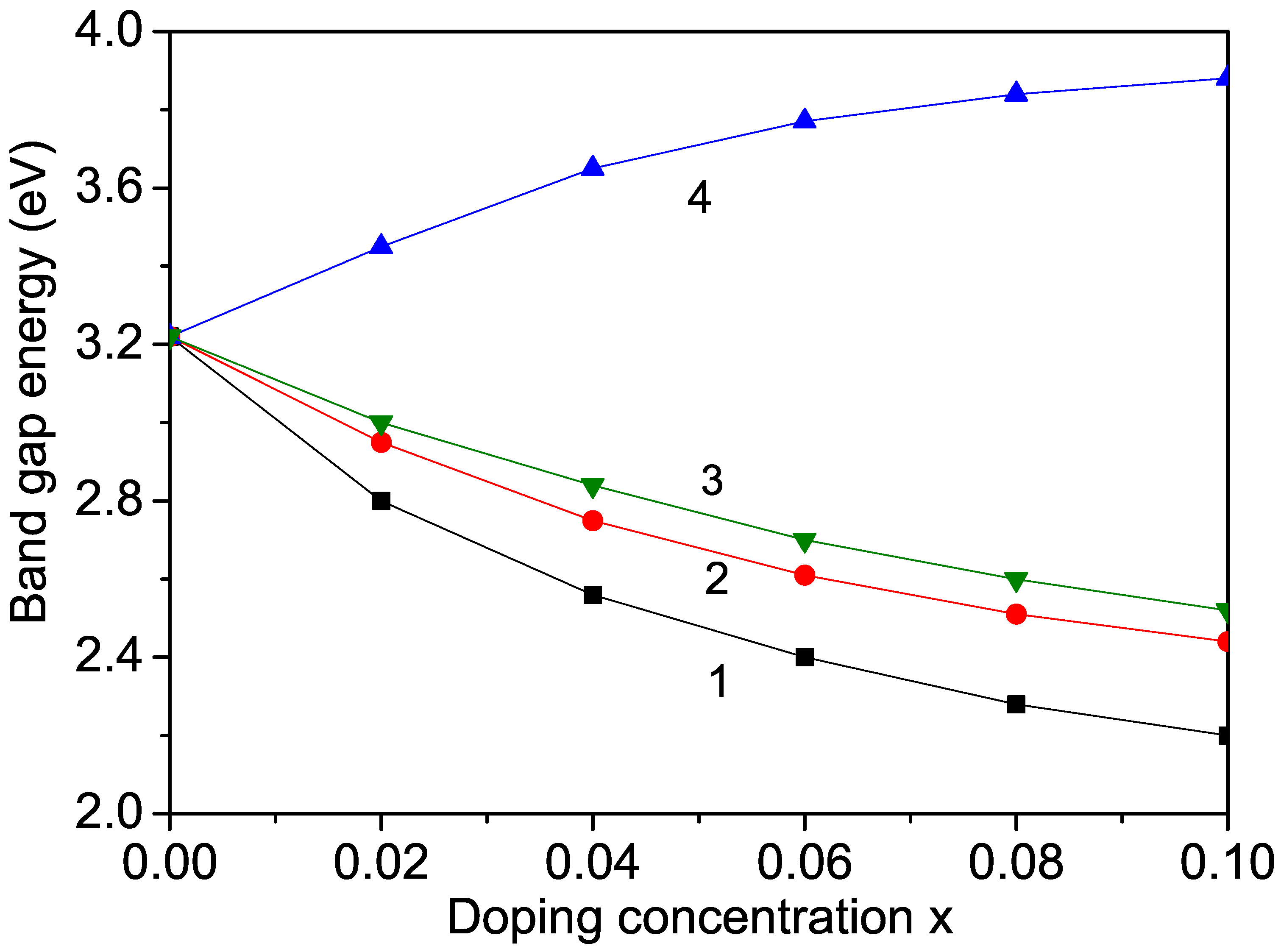
3.5. Ion-Doping Dependence of the Band Gap of Bulk KNO

KNO is not widely used in photocatalytic applications because of its large band gap ($E_g$ = 3.2–3.3 eV), which is not appropriate for the visible range of the solar spectrum. However, doping KNO may reduce its band gap. Therefore, using Equations (10) and (11), we calculated the band-gap energy $E_g$ in KNO and studied the effects of Cr, Co, and Mn ion doping on $E_g$. The doping induced the transformation from the orthorhombic to the cubic phase of KNO and significantly reduced the optical band gap. The results are presented in Figure 5. When using Equation (11), it can be seen that increasing the magnetization $\langle S^z\rangle$ by increasing the doping concentration x (see Figure 1) led to a lowering of the band-gap energy $E_g$, as shown in Figure 5, curves 1–3. A similar behavior in Cr- and Co-doped KNO nanostructures was observed experimentally by Raja et al. [5] and Zhang et al. [12]. Thus, the modified band gap can be used for applications in solar photovoltaics.

It must be mentioned that through ${\mathrm{Zn}}^{2+}$ ion substitution of the ${\mathrm{Nb}}^{5+}$ ions in KNO NPs, we observed an increase in the band-gap energy $E_g$ (see Figure 5, curve 4), which is in agreement with the results of Liang et al. [22]. This behavior could be caused by the lattice distortion due to the larger ionic radius of the Zn ion (0.88 Å) in comparison with that of the Nb ion, i.e., there appears to be tensile strain. A similar increase in $E_g$ was also reported by Jameel et al. [11] in ${\mathrm{Sr}}^{2+}$ (1.32 Å) ion-doped KNO.

We emphasize that our microscopic model and approximation method could be applied to describe the multiferroic properties of ion-doped ${\mathrm{LiNbO}}_3$, another perovskite oxide compound, as reported by Zeng et al. using first-principles calculations [31] (Fe doping) and recently by Lin et al. [32,33] (Fe, Ni, Ga doping), which will be considered in a future paper.

4. Conclusions

In conclusion, using a microscopic model and Green’s function theory, the magnetization, polarization, and band-gap energy in pure and ion-doped KNO bulk and NPs were investigated. Although the bulk KNO was nonmagnetic, the undoped KNO NP exhibited magnetic properties that increased after doping with Co, Mn, and Cr at the Nb site. The polarization decreased with decreasing NP size and with increasing doping concentration. In doped KNO NPs, we observed the same behavior as in doped bulk KNO, but the values of the magnetization and polarization in KNO NPs were somewhat enhanced or reduced due to the size effects. The polarization could be enhanced by the substitution of the K ion with the Na ion. In order to show the multiferroic properties of doped KNO, we calculated the magnetic field dependence of the polarization. It increased with increasing h. The band-gap energy decreased with increasing Co, Mn, and Cr ion doping and increased with Zn doping.

In future work, it will be of interest to study co-substitution on the K and Nb sites with different or the same doping ions. Some recent studies have shown that Mn-doped structures, with Mn entering both Nb and K sites, are more stable [34]. This will be also considered in a future paper.