Analysis of Magnetization Dynamics in NiFe Thin Films with Growth-Induced Magnetic Anisotropies
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. X-ray Reflectivity
3.2. FMR: Field-Swept Absorption
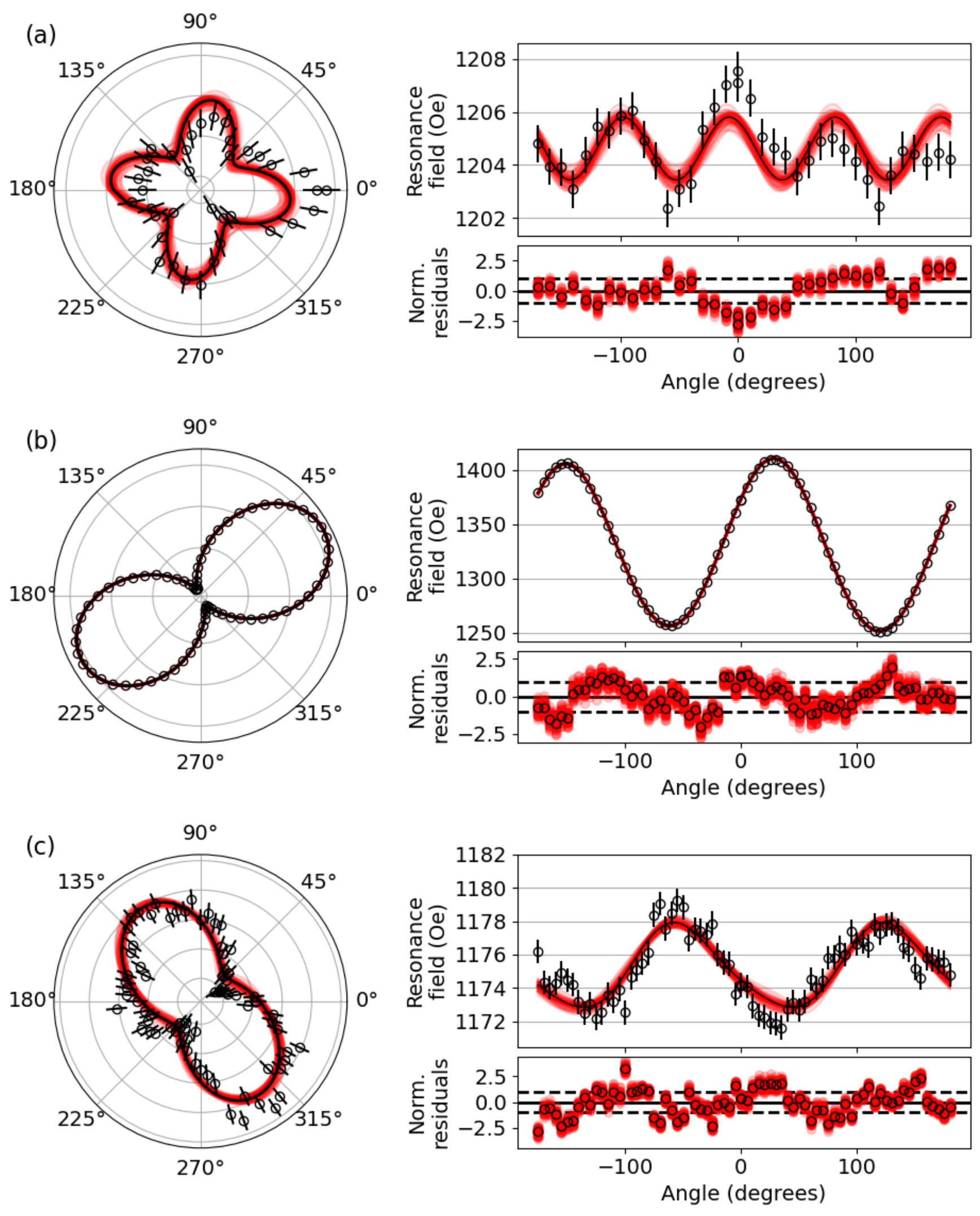
3.3. FMR: In-Plane Angular Dependence
3.4. FMR: Frequency Dependence
3.4.1. Out-of-Plane Field
3.4.2. In-Plane Field
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hirohata, A.; Yamada, K.; Nakatani, Y.; Prejbeanu, I.L.; Diény, B.; Pirro, P.; Hillebrands, B. Review on spintronics: Principles and device applications. J. Magn. Magn. Mater. 2020, 509, 166711. [Google Scholar] [CrossRef]
- Blois, M.S., Jr. Preparation of Thin Magnetic Films and Their Properties. J. Appl. Phys. 1955, 26, 975–980. [Google Scholar] [CrossRef]
- Suits, F. Bilayer Permalloy films grown in orthogonal applied fields. IEEE Trans. Magn. 1990, 26, 2353–2355. [Google Scholar] [CrossRef]
- Hindmarch, A.T.; Kinane, C.J.; MacKenzie, M.; Chapman, J.N.; Henini, M.; Taylor, D.; Arena, D.A.; Dvorak, J.; Hickey, B.J.; Marrows, C.H. Interface induced uniaxial magnetic anisotropy in amorphous CoFeB films on AlGaAs(001). Phys. Rev. Lett. 2008, 100, 117201. [Google Scholar] [CrossRef]
- Hindmarch, A.T.; Rushforth, A.W.; Campion, R.P.; Marrows, C.H.; Gallagher, B.L. Origin of in-plane uniaxial magnetic anisotropy in CoFeB amorphous ferromagnetic thin films. Phys. Rev. B 2011, 83, 212404. [Google Scholar] [CrossRef]
- Seeger, R.L.; Millo, F.; Mouhoub, A.; de Loubens, G.; Solignac, A.; Devolder, T. Inducing or suppressing the anisotropy in multilayers based on CoFeB. Phys. Rev. Mater. 2023, 7, 054409. [Google Scholar] [CrossRef]
- Atkinson, D.; Searle, S.; Jefferies, M.; Levy, J.; Cramman, H. Controlling Anisotropy of NiFe Thin Films During Deposition for Device Applications. Sens. Lett. 2013, 11, 13–20. [Google Scholar] [CrossRef]
- Zhan, Q.f.; Van Haesendonck, C.; Vandezande, S.; Temst, K. Surface morphology and magnetic anisotropy of Fe/MgO(001) films deposited at oblique incidence. Appl. Phys. Lett. 2009, 94, 042504. [Google Scholar] [CrossRef]
- Frisk, A.; Achinuq, B.; Newman, D.G.; Heppell, E.; Dąbrowski, M.; Hicken, R.J.; van der Laan, G.; Hesjedal, T. Controlling In-Plane Magnetic Anisotropy of Co Films on MgO Substrates using Glancing Angle Deposition. Phys. Status Solidi A 2023, 220, 2300010. [Google Scholar] [CrossRef]
- Chowdhury, N.; Bedanta, S. Controlling the anisotropy and domain structure with oblique deposition and substrate rotation. AIP Adv. 2014, 4, 027104. [Google Scholar] [CrossRef]
- Farle, M. Ferromagnetic resonance of ultrathin metallic layers. Rep. Prog. Phys. 1998, 61, 755. [Google Scholar] [CrossRef]
- Shaw, J.M.; Knut, R.; Armstrong, A.; Bhandary, S.; Kvashnin, Y.; Thonig, D.; Delczeg-Czirjak, E.K.; Karis, O.; Silva, T.J.; Weschke, E.; et al. Quantifying Spin-Mixed States in Ferromagnets. Phys. Rev. Lett. 2021, 127, 207201. [Google Scholar] [CrossRef]
- Azzawi, S.; Hindmarch, A.T.; Atkinson, D. Magnetic damping phenomena in ferromagnetic thin-films and multilayers. J. Phys. Appl. Phys. 2017, 50, 473001. [Google Scholar] [CrossRef]
- Glavic, A.; Björck, M. GenX 3: The latest generation of an established tool. J. Appl. Crystallogr. 2022, 55, 1063–1071. [Google Scholar] [CrossRef]
- Montoya, E.; McKinnon, T.; Zamani, A.; Girt, E.; Heinrich, B. Broadband ferromagnetic resonance system and methods for ultrathin magnetic films. J. Magn. Magn. Mater. 2014, 356, 12–20. [Google Scholar] [CrossRef]
- Swindells, C.; Hindmarch, A.T.; Gallant, A.J.; Atkinson, D. Spin current propagation through ultra-thin insulating layers in multilayered ferromagnetic systems. Appl. Phys. Lett. 2020, 116, 042403. [Google Scholar] [CrossRef]
- Edwards, E.R.; Nembach, H.T.; Shaw, J.M. Co25Fe75 Thin Films with Ultralow Total Damping of Ferromagnetic Resonance. Phys. Rev. Appl. 2019, 11, 054036. [Google Scholar] [CrossRef]
- Kienzle, P.; Krycka, J.; Patel, N.; Sahin, I. Bumps (Version 0.9.1) [Computer Software]; University of Maryland: College Park, MD, USA. Available online: https://github.com/bumps/bumps (accessed on 16 October 2024).
- Vrugt, J.A.; ter Braak, C.J.F.; Clark, M.P.; Hyman, J.M.; Robinson, B.A. Treatment of input uncertainty in hydrologic modeling: Doing hydrology backward with Markov chain Monte Carlo simulation. Water Resour. Res. 2008, 44, W00B09. [Google Scholar] [CrossRef]
- Vrugt, J.A.; ter Braak, C.J.F.; Gupta, H.V.; Robinson, B.A. Equifinality of formal (DREAM) and informal (GLUE) Bayesian approaches in hydrologic modeling? Stoch. Environ. Res. Risk Assess. 2009, 23, 1011. [Google Scholar] [CrossRef]
- Kienzle, P.; Krycka, J.; Patel, N.; Sahin, I. Refl1D [Computer Software]; University of Maryland: College Park, MD, USA. Available online: https://github.com/reflectometry/refl1d (accessed on 16 October 2024).
- Omelchenko, P.; Girt, E.; Heinrich, B. Test of spin pumping into proximity-polarized Pt by in-phase and out-of-phase pumping in Py/Pt/Py. Phys. Rev. B 2019, 100, 144418. [Google Scholar] [CrossRef]
- Chechenin, N.G.; Dzhun, I.O.; Babaytsev, G.V.; Kozin, M.G.; Makunin, A.V.; Romashkina, I.L. FMR Damping in Thin Films with Exchange Bias. Magnetochemistry 2021, 7, 70. [Google Scholar] [CrossRef]
- Layadi, A.; Artman, J. Ferromagnetic resonance in a coupled two-layer system. J. Magn. Magn. Mater. 1990, 92, 143–154. [Google Scholar] [CrossRef]
- Stenning, G.B.G.; Shelford, L.R.; Cavill, S.A.; Hoffmann, F.; Haertinger, M.; Hesjedal, T.; Woltersdorf, G.; Bowden, G.J.; Gregory, S.A.; Back, C.H.; et al. Magnetization dynamics in an exchange-coupled NiFe/CoFe bilayer studied by x-ray detected ferromagnetic resonance. New J. Phys. 2015, 17, 013019. [Google Scholar] [CrossRef]
- Arias, R.; Mills, D.L. Extrinsic contributions to the ferromagnetic resonance response of ultrathin films. Phys. Rev. B 1999, 60, 7395–7409. [Google Scholar] [CrossRef]
- Lindner, J.; Barsukov, I.; Raeder, C.; Hassel, C.; Posth, O.; Meckenstock, R.; Landeros, P.; Mills, D.L. Two-magnon damping in thin films in case of canted magnetization: Theory versus experiment. Phys. Rev. B 2009, 80, 224421. [Google Scholar] [CrossRef]
- Tokaç, M.; Kazan, S.; Özkal, B.; Al-jawfi, N.; Rameev, B.; Nicholson, B.; Hindmarch, A.T. Two Magnon Scattering Contribution to the Ferromagnetic Resonance Linewidth of Pt(Ir)/CoFeTaB/Ir(Pt) Thin Films. Appl. Magn. Reson. 2023, 54, 1053. [Google Scholar] [CrossRef]
- Waring, H.J.; Li, Y.; Johansson, N.A.B.; Moutafis, C.; Vera-Marun, I.J.; Thomson, T. Exchange stiffness constant determination using multiple-mode FMR perpendicular standing spin waves. J. Appl. Phys. 2023, 133, 063901. [Google Scholar] [CrossRef]
- Shaw, J.M.; Nembach, H.T.; Silva, T.J.; Boone, C.T. Precise determination of the spectroscopic g-factor by use of broadband ferromagnetic resonance spectroscopy. J. Appl. Phys. 2013, 114, 243906. [Google Scholar] [CrossRef]
- Tokaç, M.; Bunyaev, S.A.; Kakazei, G.N.; Schmool, D.S.; Atkinson, D.; Hindmarch, A.T. Interfacial Structure Dependent Spin Mixing Conductance in Cobalt Thin Films. Phys. Rev. Lett. 2015, 115, 056601. [Google Scholar] [CrossRef]





| Sample | (Oe) | (Oe) | (degrees) | (Oe) | (degrees) | (Oe) | (degrees) |
|---|---|---|---|---|---|---|---|
| Rotated | — | — | — | — | |||
| Static | |||||||
| Two-step | — | — |
| Sample | OOP | OOP g-Factor | IP | IP g-Factor | |
|---|---|---|---|---|---|
| (G) | (G) | 0 Degrees | 90 Degrees | ||
| Rotated | – | ||||
| Static | |||||
| Two-step | – | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Merryweather, L.; Hindmarch, A.T. Analysis of Magnetization Dynamics in NiFe Thin Films with Growth-Induced Magnetic Anisotropies. Magnetochemistry 2024, 10, 80. https://doi.org/10.3390/magnetochemistry10100080
Merryweather L, Hindmarch AT. Analysis of Magnetization Dynamics in NiFe Thin Films with Growth-Induced Magnetic Anisotropies. Magnetochemistry. 2024; 10(10):80. https://doi.org/10.3390/magnetochemistry10100080
Chicago/Turabian StyleMerryweather, Leah, and Aidan T. Hindmarch. 2024. "Analysis of Magnetization Dynamics in NiFe Thin Films with Growth-Induced Magnetic Anisotropies" Magnetochemistry 10, no. 10: 80. https://doi.org/10.3390/magnetochemistry10100080
APA StyleMerryweather, L., & Hindmarch, A. T. (2024). Analysis of Magnetization Dynamics in NiFe Thin Films with Growth-Induced Magnetic Anisotropies. Magnetochemistry, 10(10), 80. https://doi.org/10.3390/magnetochemistry10100080






