The Creation of Remote Spin Entanglement with a Nanomechanical Cantilever

Abstract

We consider the creation of entanglement between remote electron spins using a magnetic nanoparticle attached to a cantilever tip (CT). We assume that the frequency of the CT vibrations matches the Larmor frequency of the spin (CT–spin resonance). Under the conditions of CT–spin resonance, the CT–spin system is described using the Jaynes–Cummings model. In this work, using the evolution operator of the Jaynes–Cummings model, we show that a movable CT can create an entangled state between remote spins. The most striking result is that the entanglement between the remote spins can be achieved without measuring the vibrational state of the CT.

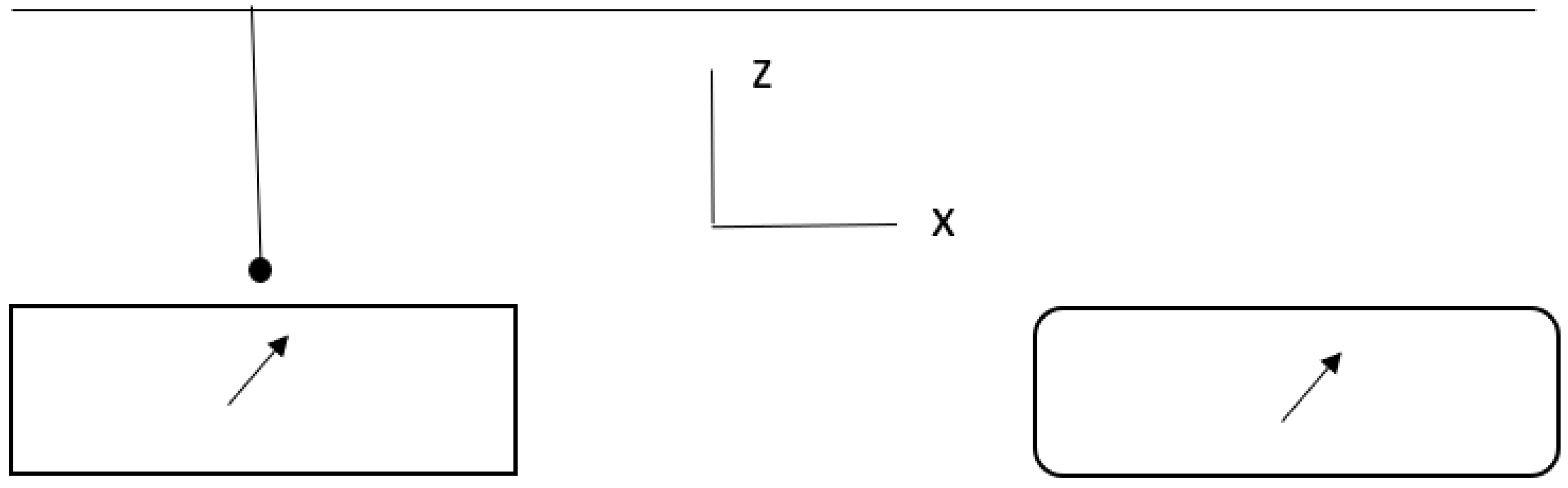
1. Introduction

Entanglement between remote particles is probably the most spectacular phenomenon in quantum physics. Since the publication of the seminal article of Einstein, Podolsky, and Rosen [1], this phenomenon has attracted the unrelenting attention of scientists and the general public. Today, remote entanglement not only presents deep philosophical significance but also profound practical importance. For example, entanglement between remote electron spins can be used for developing secure quantum communication and quantum internet (see, for example, a recent review [2]).

In this work, we consider the creation of remote spin entanglement using a movable nanomechanical cantilever with a magnetic nanoparticle at the cantilever tip (CT). It was shown recently [3,4,5] that the Larmor frequency of electron spin could be reduced to the fundamental frequency of the cantilever vibrations (the CT frequency). This phenomenon was called CT–spin resonance. It was shown that, under the conditions of CT–spin resonance, the evolution of the CT–spin system can be described using the Jaynes–Cummings model [6,7].

We use the evolution operator of the Jaynes–Cummings model to describe the creation of entanglement between remote spins using CT–spin resonance. There are many studies addressing entanglement generation between remote spins (see, for example, [2,8,9,10,11,12,13,14,15]). To the best of our knowledge, if the isolated remote spins are initially independent, the suggested schemes generate the entanglement by measuring the state of an intermediate object, e.g., the state of a photon which initially interacts with the first spin and later with the second spin. We show that, in our case, where the intermediate object is the CT, the entanglement can be created without measuring the CT state.

2. Results

We consider two remote spins and a movable nanomechanical cantilever with a magnetic nanoparticle at the CT (see Figure 1). We explore the magnetic dipole interaction between the oscillating magnetic nanoparticle and the spin. This interaction couples the CT oscillations with the Larmor precession of the electron spin (the details are described in Ref. [4]). We assume that the CT can be placed at a small vertical distance from the first spin, the second spin, or far away from both spins which we call the “neutral position”. The CT can oscillate along the horizontal x-axis. Both spins experience the external magnetic field, which points in the positive z-direction and controls the Larmor frequency of the spin.

We assume that if the CT is placed near the first or the second spin, the Larmor frequency of the corresponding spin ${\omega }_k \left(k=1,2\right)$ matches the CT frequency $\omega$ (the CT–spin resonance), as described in Refs. [3,4,5]. Then, the Hamiltonian of the CT–spin system can be described using the Jaynes–Cummings model as follows:

$$\begin{array}{l}\widehat{H}=\hslash \omega \left(\widehat{n}+{\displaystyle \frac{1}{2}}\right)+{\displaystyle \frac{\hslash \omega }{2}}{\widehat{\sigma }}_z-{\displaystyle \frac{\hslash \lambda }{2}}\left({\widehat{a}}^{†}{\widehat{\sigma }}_{-}+\widehat{a}{\widehat{\sigma }}_{+}\right) \\ \end{array}$$

(1)

where $\widehat{n}={\widehat{a}}^{†}\widehat{a}$, ${\widehat{a}}^{†}$, and $\widehat{a}$ are the creation and annihilation operators for the CT; ${\widehat{\sigma }}_{\pm }={\widehat{\sigma }}_x\pm i{\widehat{\sigma }}_y,{\widehat{\sigma }}_{xz,y,z}$ are the Pauli operators for spin; and $\lambda$ is the CT–spin interaction constant. Certainly, we assume that when the CT is placed near one spin, we can ignore its interaction with the other one.

The evolution operator ${\widehat{U}}_k(t)$ in the Jaynes–Cummings model with a single spin $“k”(k=1,2)$ can be written as a product of two operators [7]: ${\widehat{U}}_k\left(t\right)={\widehat{U}}_{0k}\left(t\right){\widehat{U}}_{Ik}\left(t\right)$, where ${\widehat{U}}_{0k}(t)$ describes the evolution of the CT–spin system with no CT–spin interaction:

$$\begin{array}{l}{\widehat{U}}_{0k}\left(t\right)=\exp \left\{-i\omega \left(\widehat{n}+1/2\right)+\left(-i{\omega }_k{\widehat{\sigma }}_{zk}t/2\right)\right\},\\ \end{array}$$

(2)

Operator ${\widehat{U}}_{0k}(t)$ only changes the phase factors in the CT–spin state, which we will ignore in our computations.

Operator ${\widehat{U}}_{Ik}(t)$ describes the evolution caused by the CT–spin interaction in the condition of the CT–spin resonance when the CT is placed near the spin $“k”$ as follows:

$$\begin{array}{l} {\widehat{U}}_{Ik}\left(t\right)=\cos \left(\lambda t\sqrt{\widehat{n}+1}\right){\mathrm{X}}_k^{11}+i\widehat{a}{\displaystyle \frac{\sin \left(\lambda t\sqrt{{\widehat{a}}^{†}\widehat{a}}\right)}{\sqrt{{\widehat{a}}^{†}\widehat{a}}}}{\mathrm{X}}_k^{10}\\ +i{\displaystyle \frac{\sin \left(\lambda t\sqrt{{\widehat{a}}^{†}\widehat{a}}\right)}{\sqrt{{\widehat{a}}^{†}\widehat{a}}}}{\widehat{a}}^{†}{\mathrm{X}}_k^{01}+\cos \left(\lambda t\sqrt{{\widehat{a}}^{†}\widehat{a}}\right){\mathrm{X}}_k^{00} . \end{array}$$

(3)

where the Hubbard operator $X_k^{pq}={\left(\left|p\right.〉\left.〈q\right|\right)}_k$, $p,q=0,1$, and the ground state $\left|0\right.〉$ corresponds to the spin direction “down” (the negative z-direction). Note that the operators ${\widehat{U}}_{0k}\left(t\right)$ and ${\widehat{U}}_{Ik}\left(t\right)$ commute.

Now, we describe the protocol for the creation of entanglement between the remote spins. The basis states for the CT–spin system are $\left|n,s_1,s_2\right.〉$, where $n=0,1,2,3\dots$ describes the CT state, and $s_k=0_k,1_k$ describes the state of spin $“k”$. Initially, the CT is in a neutral position, and the CT–spin system is in its ground state $\left|{\psi }_a\right.〉=\left|0,0_1,0_2\right.〉$. Next, one drives the CT to the first excited state, so the vector of state changes to $\left|{\psi }_b\right.〉=\left|1,0_1,0_2\right.〉$. Then, one quickly moves (during the time much smaller than $1/\lambda$) the cantilever from a neutral position toward the first spin where the CT interacts with the spin under the conditions of CT–spin resonance. After time interval $t_1$, CT is quickly moved back to a neutral position. Using direct computation, we obtain the vector of state after the interaction between the CT and the first spin as follows:

$$\begin{array}{l}\left|{\psi }_c\right.〉=U_{I1}(t_1)\left|{\psi }_b\right.〉\\ =\cos \left(\lambda t_1\right)\left|1,0_1,0_2\right.〉+i\sin \left(\lambda t_1\right)\left|0,1_1,0_2\right.〉\end{array}$$

(4)

Next, one quickly moves the cantilever toward the second spin so that the CT interacts with the second spin under the conditions of CT–spin resonance. After time interval $t_2$, CT is moved back to the neutral position. The resulting vector of state is expressed as follows:

$$\begin{array}{l}\left|{\psi }_d\right.〉=U_{I2}(t_2)\left|{\psi }_c\right.〉\\ =\cos \left(\lambda t_1\right)\cos \left(\lambda t_2\right)\left|1,0_1,0_2\right.〉+i\sin \left(\lambda t_1\right)\left|0,1_1,0_2\right.〉\\ +i\cos \left(\lambda t_1\right)\sin \left(\lambda t_2\right)\left|0,0_1,1_2\right.〉\end{array}$$

(5)

Next, $t_1=\pi /4\lambda ,t_2=\pi /2\lambda$ is chosen in order to obtain an entangled state for the remote spins, while the CT returns to its ground state. In this case:

$$\begin{array}{l}\left|{\psi }_d\right.〉=\left(i/\sqrt{2}\right)\left(\left|0,1_1,0_2\right.〉+\left|0,0_1,1_2\right.〉\right)\\ =\left|0\right.〉\otimes \left(i/\sqrt{2}\right)\left(\left|1_1,0_2\right.〉+\left|0_1,1_2\right.〉\right)\end{array}$$

(6)

Taking the value of the interaction constant $\lambda =1.28\times {10}^4 \mathrm{rad}/\mathrm{s}$ from Ref. [4], we obtain the experimentally achievable times $t_1=61.4 \mathrm{\mu }\mathrm{s}$ and $t_2=123 \mathrm{\mu }\mathrm{s}$. Note that the entanglement between the remote spins is achieved without measuring the CT state. Certainly, we assume that the decoherence time in our system is much greater than $t_1$ and $t_2$. (In this work, we do not study the impact of decoherence on the fidelity of entanglement).

From an experimental perspective, we should estimate the accuracy of assuming that when the CT is placed near one spin, the interaction with the other one can be ignored. Let the CT is placed near spin $“k”$. The dipole magnetic field produced by the magnetic nanoparticle on the other spin can be estimated as ${\mu }_{0}m/4\pi r^3$, where ${\mu }_0$ is the permeability of free space, $m$ is the magnetic moment of the magnetic nanoparticle, and $r$ is the distance between the spins. We assume that during time $t_k$ of the interaction between the CT and spin $“k”$, we can ignore the change in the direction of the other spin, i.e., $\gamma \left({\mu }_{0}m/4\pi r^3\right)t_k<<1$, where $\gamma$ is the electron gyromagnetic ratio. From this expression, we obtain the requirement for the distance between the spins: $r\gg {\left(\gamma {\mu }_{0}m{t}_k/4\pi \right)}^{1/3}$. Taking the value of magnetic moment $m=5.41\times {10}^{-16} \mathrm{J}/\mathrm{T}$ from Ref. [4], we obtain $r\gg 10 \mu \mathrm{m}$.

For estimation, the cantilever parameters are assumed to be the same as in Ref. [4]: the dimensions is $600\times 400\times 100 \mathrm{nm}$, and the vibrational frequency of the cantilever with the magnetic nanoparticle of mass is $2.71\times {10}^{-18} \mathrm{kg}$ (the CT frequency) $\omega /2\pi =124 \mathrm{MHz}$. The time constant of the CT vibrations must be much greater than $t_k$. Thus, the requirement for the quality factor of the cantilever is $Q\gg \omega t_k$. For our parameters, we obtain $Q\gg {10}^5$.

3. Conclusions

In conclusion, we study the creation of entanglement between remote spins using a nanomechanical cantilever with a magnetic nanoparticle at the CT. The CT and spin interact when the cantilever is moved toward the spin. The CT–spin interaction takes place in the condition of the CT–spin resonance when the CT frequency matches the frequency of the Larmor precession of the spin. In this case, the evolution of the CT–spin system can be described using the Jaynes–Cummings model. With direct computation, we show that choosing the appropriate interaction time can create remote spin entanglement without measuring the CT state.