Evaluation of the Storage Performance of ‘Valencia’ Oranges and Generation of Shelf-Life Prediction Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Plant Material
2.2. Postharvest Storage Conditions
2.3. Evaluations of Fruit Quality
2.3.1. Firmness
2.3.2. Weight Loss
2.3.3. Peel Color
2.3.4. Peel Damage, Decay, and Internal Dryness
2.3.5. Total Soluble Solids (TSS) and Titratable Acidity (TA)
2.3.6. Vitamin C
2.3.7. Ethanol Levels
2.3.8. Flavor
2.3.9. Acceptance Scores
2.4. Statistical Analysis
2.5. Quality-Prediction Models
2.5.1. Data-Set Preparation
2.5.2. Prediction Models
- Multiple Linear Regression (MLR)—This basic model attempts to establish a linear relationship between the features and the label [25]. The model finds the optimal parameters that minimize the mean squared error for the predicted quality scores;
- Support Vector Regression (SVR)—SVR is a generalization of the support vector machine (SVM) for regression tasks [26,27]. Unlike other models, SVR attempts to predict the label within a small range of allowed error. In other words, while MLR punishes every prediction error, SVR tolerates small errors as long as they fall within a predefined range. SVR models often employ kernels, which enable the model to handle non-linearity in the input space. Non-linearity is achieved by transforming the data to a higher-dimensional space, in which the relation between the inputs and the label is a linear one. In this work, two kernels were used: a linear kernel, and a radial basis function (RBF) kernel that enables non-linearity [28];
- Random Forests (RF)—RF is a supervised ensemble method that is widely used for regression problems [29]. The RF model employs multiple regression trees (i.e., forests) to reduce the variance error [30]. For each tree, the model introduces different subsets of samples and features with replacements, also known as the bagging approach [31]. At the prediction time (inference), each individual tree predicts a different value and the average of all of the predictions is used. The tree structure enables non-linearity and, by averaging multiple predictions of different trees, RF decreases the variance of the model, which often leads to more accurate results than SVR or MLR;
- Extreme Gradient Boosting (XGBoost)—This is a state-of-the-art ensemble method that has become popular in recent years for tabular data predictions [32]. Similar to RF, this model is based on regression trees. However, unlike RF, it uses a boosting approach instead of bagging. In boosting, the trees are built sequentially, with each tree trying to minimize the remaining error of all previous trees [33].
2.5.3. Evaluation of the Models
2.5.4. Duplication as a Way to Deal with Unbalanced Data Sets
3. Results
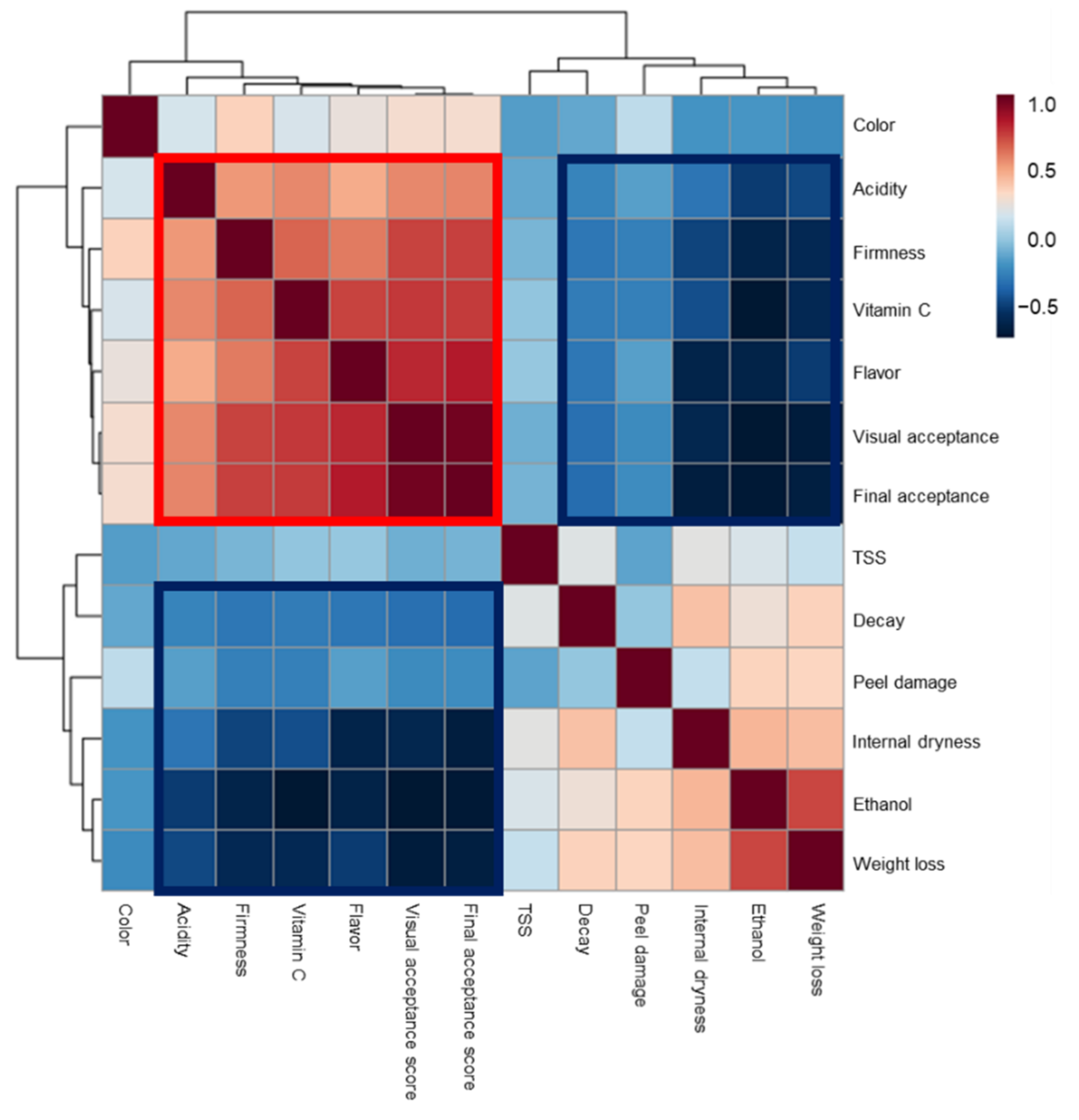
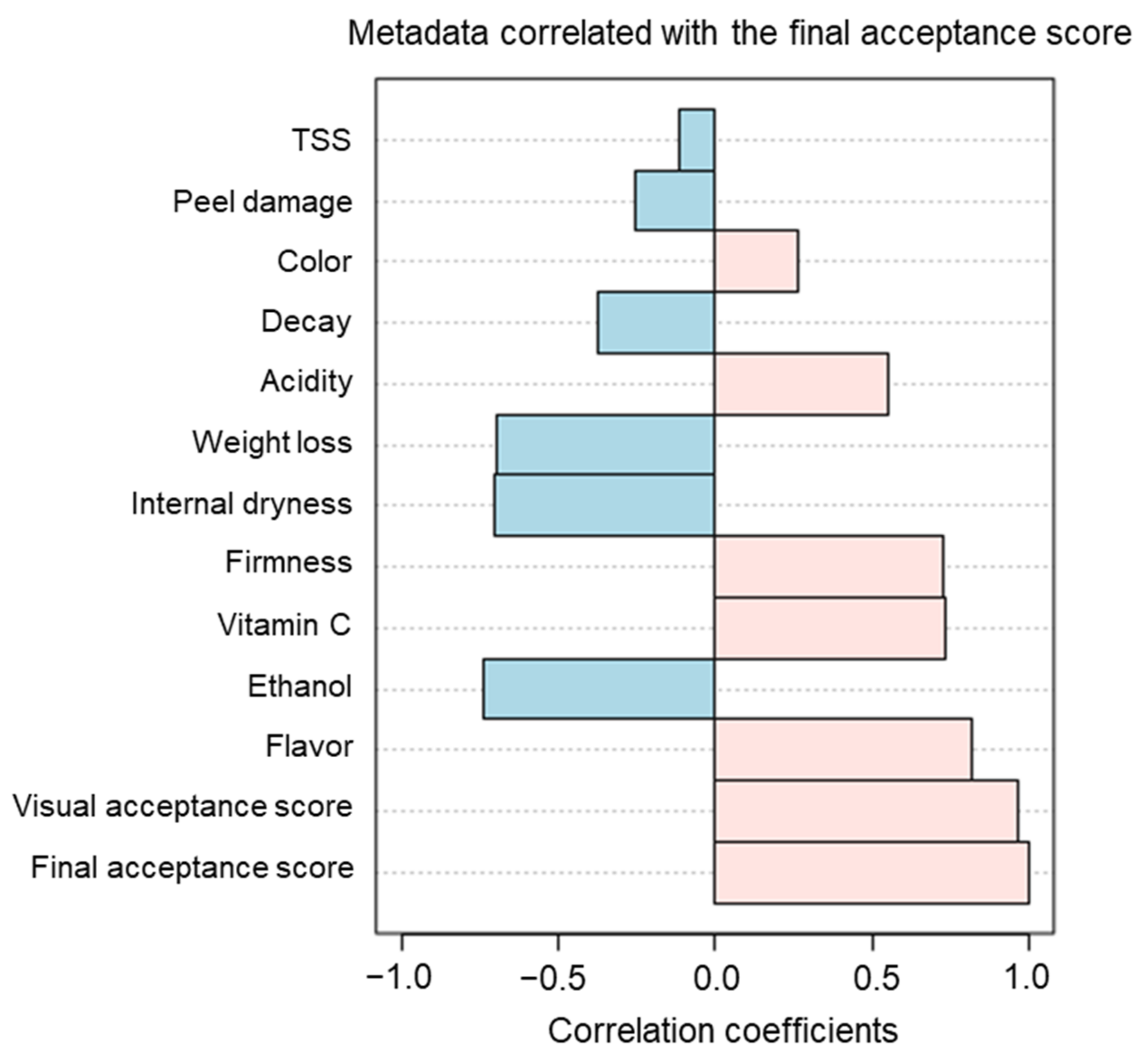
3.1. Effects of Preharvest and Postharvest Features on the Quality of ‘Valencia’ Oranges
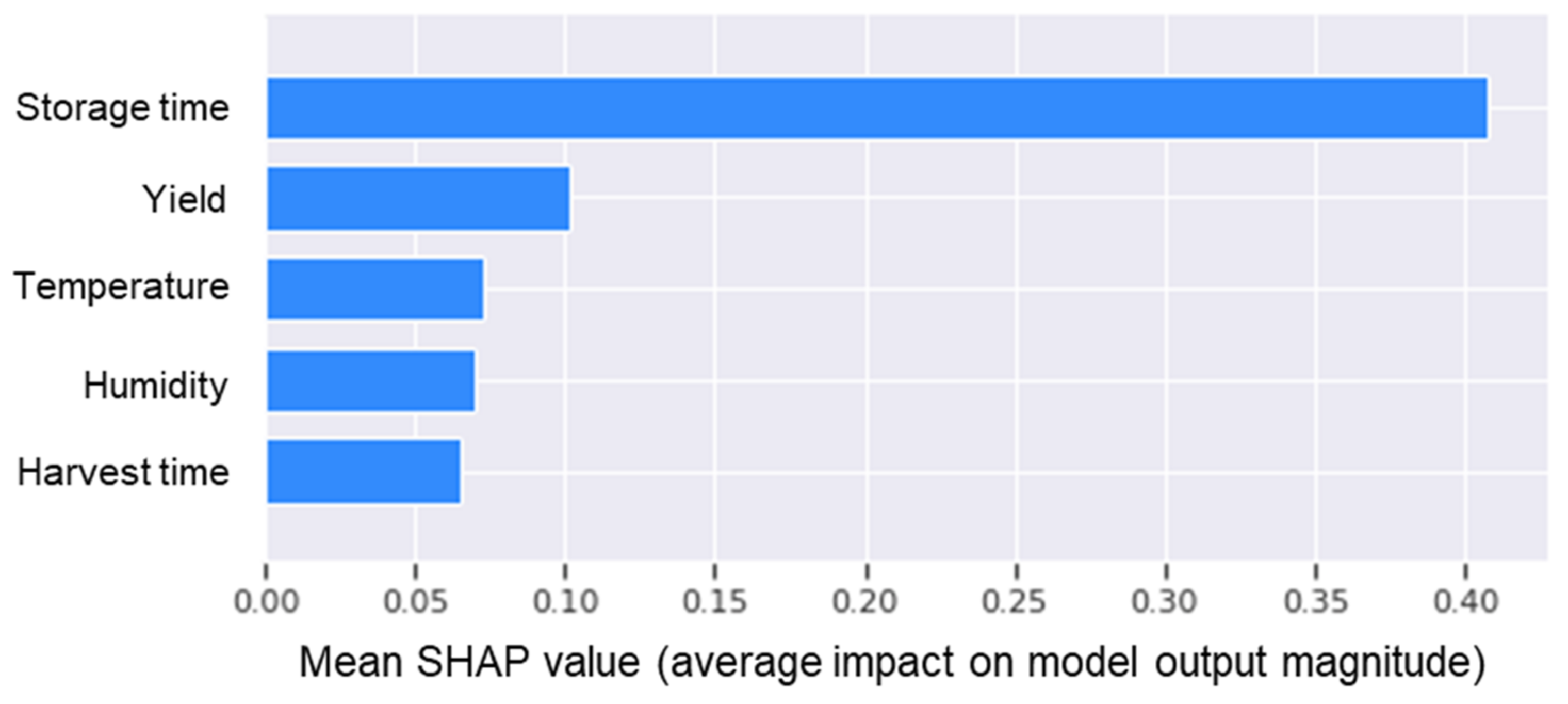
3.2. Quality-Prediction Models
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Statista. Fruit: World Production by Type 2020. Available online: https://www.statista.com/statistics/264001/worldwide-production-of-fruit-by-variety/ (accessed on 19 May 2022).
- Ranganna, S.; Govindarajan, V.S.; Ramana, K.V.R. Citrus fruits—Varieties, chemistry, technology, and quality evaluation. Part II. Chemistry, technology, and quality evaluation. A. Chemistry. Crit. Rev. Food Sci. Nutr. 1983, 18, 313–386. [Google Scholar] [CrossRef] [PubMed]
- Hodgson, R.W. Horticultural varieties of citrus. In Citrus Ind.; Reuther, W., Webber, H.J., Batchelor, L.D., Eds.; University of California Press: Berkeley, CA, USA, 1967; pp. 431–591. [Google Scholar] [CrossRef] [Green Version]
- Pekmezci, M.; Erkan, M.; Demirkol, A. The effects of harvest time and different postharvest applications on the storage of “Valencia” oranges. Acta Hortic. 1995, 398, 277–284. [Google Scholar] [CrossRef]
- Ozdemir, A.E.; Dundar, O. Effect of different postharvest applications on storage of “Valencia” oranges. Acta Hortic. 2001, 553, 561–564. [Google Scholar] [CrossRef]
- Kader, A.A.; Arpaia, M.L. Postharvest handling systems: Subtropical fruit. In Postharvest Technology of Horticultural Crops, 3rd ed.; Kader, A.A., Ed.; University of California, Agriculture and Natural Resources: Oakland, CA, USA, 2002; pp. 375–384. [Google Scholar]
- Arpaia, M.L. Preharvest Factors Influencing Postharvest Quality of Tropical and Subtropical Fruit. HortScience 1994, 29, 982–985. [Google Scholar] [CrossRef] [Green Version]
- Tyagi, S.; Sahay, S.; Imran, M.; Rashmi, K.; Mahesh, S. Pre-harvest Factors Influencing the Postharvest Quality of Fruits: A Review. Curr. J. Appl. Sci. Technol 2017, 23, 1–12. [Google Scholar] [CrossRef]
- El-Zeftawi, B.M.; Peggie, I.D.; Minnis, D.C. Postharvest treatments, storage temperature and rootstocks in relation to storage disorders and fruit quality of ‘Valencia’ oranges. J. Hortic. Sci. 1989, 64, 373–378. [Google Scholar] [CrossRef]
- Khalid, S.; Malik, U.A.; Khan, A.S.; Khan, M.N.; Ullah, M.I.; Abbas, T.; Khalid, M.S. Tree age and fruit size in relation to postharvest respiration and quality changes in ‘Kinnow’ mandarin fruit under ambient storage. Sci. Hortic. 2017, 220, 183–192. [Google Scholar] [CrossRef]
- Paull, R. Effect of temperature and relative humidity on fresh commodity quality. Postharvest Biol. Technol. 1999, 15, 263–277. [Google Scholar] [CrossRef]
- Hertog, M.L.A.T.M.; Uysal, I.; McCarthy, U.; Verlinden, B.M.; Nicolaï, B.M. Shelf life modelling for first-expired-first-out warehouse management. Philos. Trans. R. Soc. A 2014, 372, 20130306. [Google Scholar] [CrossRef]
- Jedermann, R.; Nicometo, M.; Uysal, I.; Lang, W. Reducing food losses by intelligent food logistics. Philos. Trans. R. Soc. A 2014, 372, 20130302. [Google Scholar] [CrossRef]
- Li, Y.; Chu, X.; Fu, Z.; Feng, J.; Mu, W. Shelf life prediction model of postharvest table grape using optimized radial basis function (RBF) neural network. Br. Food J. 2019, 121, 2919–2936. [Google Scholar] [CrossRef]
- Song, Y.; Hu, Q.; Wu, Y.; Pei, F.; Kimatu, B.M.; Su, A.; Yang, W. Storage time assessment and shelf-life prediction models for postharvest Agaricus bisporus. LWT 2019, 101, 360–365. [Google Scholar] [CrossRef]
- Jalali, A.; Linke, M.; Geyer, M.; Mahajan, P.V. Shelf life prediction model for strawberry based on respiration and transpiration processes. Food Packag. Shelf Life 2020, 25, 100525. [Google Scholar] [CrossRef]
- Salehi, F. Recent Advances in the Modeling and Predicting Quality Parameters of Fruits and Vegetables during Postharvest Storage: A Review. Int. J. Fruit Sci. 2020, 20, 506–520. [Google Scholar] [CrossRef]
- Cammarota, G.; Ianiro, G.; Ahern, A.; Carbone, C.; Temko, A.; Claesson, M.J.; Gasbarrini, A.; Tortora, G. Gut microbiome, big data and machine learning to promote precision medicine for cancer. Nat. Rev. Gastroenterol. Hepatol. 2020, 17, 635–648. [Google Scholar] [CrossRef]
- Neethirajan, S. The role of sensors, big data and machine learning in modern animal farming. Sens. Bio Sens. Res. 2020, 29, 100367. [Google Scholar] [CrossRef]
- La Scalia, G.; Nasca, A.; Corona, O.; Settanni, L.; Micale, R. An Innovative Shelf Life Model Based on Smart Logistic Unit for an Efficient Management of the Perishable Food Supply Chain. J. Food Process Eng. 2017, 40, e12311. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Dukovska-Popovska, I.; Subramanian, N.; Chan, H.K.; Bai, R. Decision-making in cold chain logistics using data analytics: A literature review. Int. J. Logist. Manag. 2018, 29, 839–861. [Google Scholar] [CrossRef] [Green Version]
- Davis, P.L.; Chace, W.G. Determination of alcohol in citrus juice by gas chromatographic analysis of headspace. Hortscience 1969, 2, 168–169. [Google Scholar]
- Lundberg, S.I.; Lee, S.M. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Metsalu, T.; Vilo, J. ClustVis: A web tool for visualizing clustering of multivariate data using Principal Component Analysis and heatmap. Nucleic Acids Res. 2015, 43, W566–W570. [Google Scholar] [CrossRef] [PubMed]
- Lewis-Beck, C.; Lewis-Beck, M. Applied Regression: An Introduction; Sage Publications: Thousand Oaks, CA, USA, 2015. [Google Scholar]
- Drucker, H.; Surges, C.J.C.; Kaufman, L.A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 1, 155–161. [Google Scholar]
- Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines; Apress: New York, NY, USA, 2015; pp. 67–80. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, S.F.; Esteki, M.; Mostafazadeh-Fard, B.; Dehghani, S.; Khorvash, M. Linear and nonlinear modeling for predicting nickel removal from aqueous solutions. Environ. Eng. Sci. 2012, 29, 765–775. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Guestrin, T. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Polikar, R. Ensemble based systems in decision making. IEEE Circuits Syst. Mag. 2006, 6, 21–44. [Google Scholar] [CrossRef]
- Lin, Y.; Guan, Y.; Asudeh, A.; Jagadish, H.V. Identifying insufficient data coverage in databases with multiple relations. Proc. VLDB Endow. 2020, 13, 2229–2242. [Google Scholar] [CrossRef]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross Validation, Encyclopedia of Database Systems (EDBS); Arizona State University Springer: Phoenix, AZ, USA, 2009; Volume 6. [Google Scholar]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. In Breakthroughs in Statistics; Springer: New York, NY, USA, 1992; pp. 196–202. [Google Scholar] [CrossRef]
- Casagrande, E.; Génard, M.; Lurol, S.; Charles, F.; Plénet, D.; Lescourret, F. A process-based model of nectarine quality development during pre- and post-harvest. Postharvest Biol. Technol. 2021, 175, 111458. [Google Scholar] [CrossRef]
- Amodio, M.L.; Derossi, A.; Mastrandrea, L.; Colelli, G. A study of the estimated shelf life of fresh rocket using a non-linear model. J. Food Eng. 2015, 150, 19–28. [Google Scholar] [CrossRef]
- Wang, W.; Hu, W.; Ding, T.; Ye, X.; Liu, D. Shelf-life prediction of strawberry at different temperatures during storage using kinetic analysis and model development. J. Food Proc. Preserv. 2018, 42, 1–9. [Google Scholar] [CrossRef]
- Niu, Y.; Yun, J.; Bi, Y.; Wang, T.; Zhang, Y.; Liu, H.; Zhao, F. Predicting the shelf life of postharvest Flammulina velutipes at various temperatures based on mushroom quality and specific spoilage organisms. Postharvest Biol. Technol. 2020, 167, 111235. [Google Scholar] [CrossRef]
- Ktenioudaki, A.; O’Donnell, C.P.; do Nascimento Nunes, M.C. Modelling the biochemical and sensory changes of strawberries during storage under diverse relative humidity conditions. Postharvest Biol. Technol. 2019, 154, 148–158. [Google Scholar] [CrossRef]
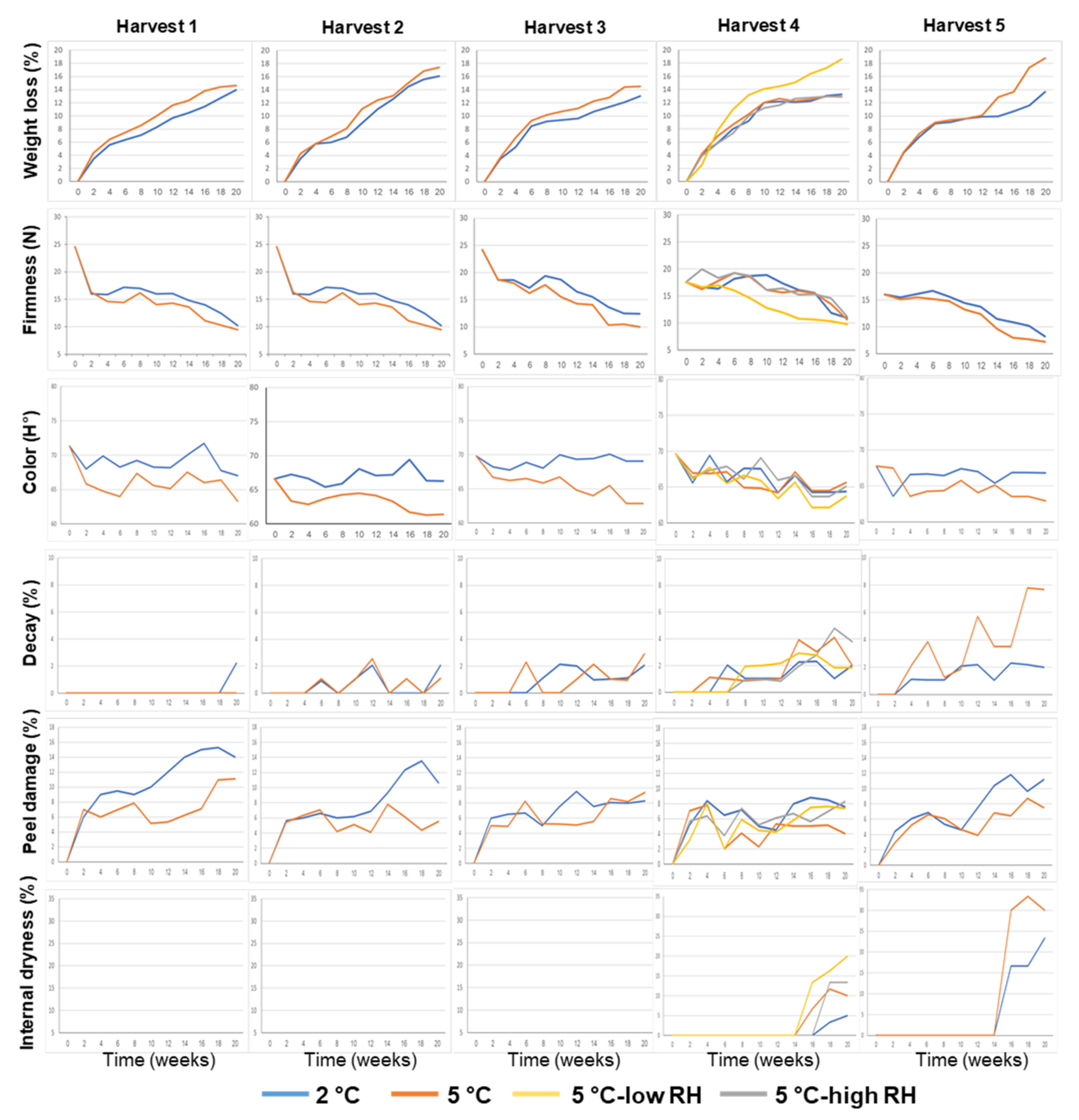

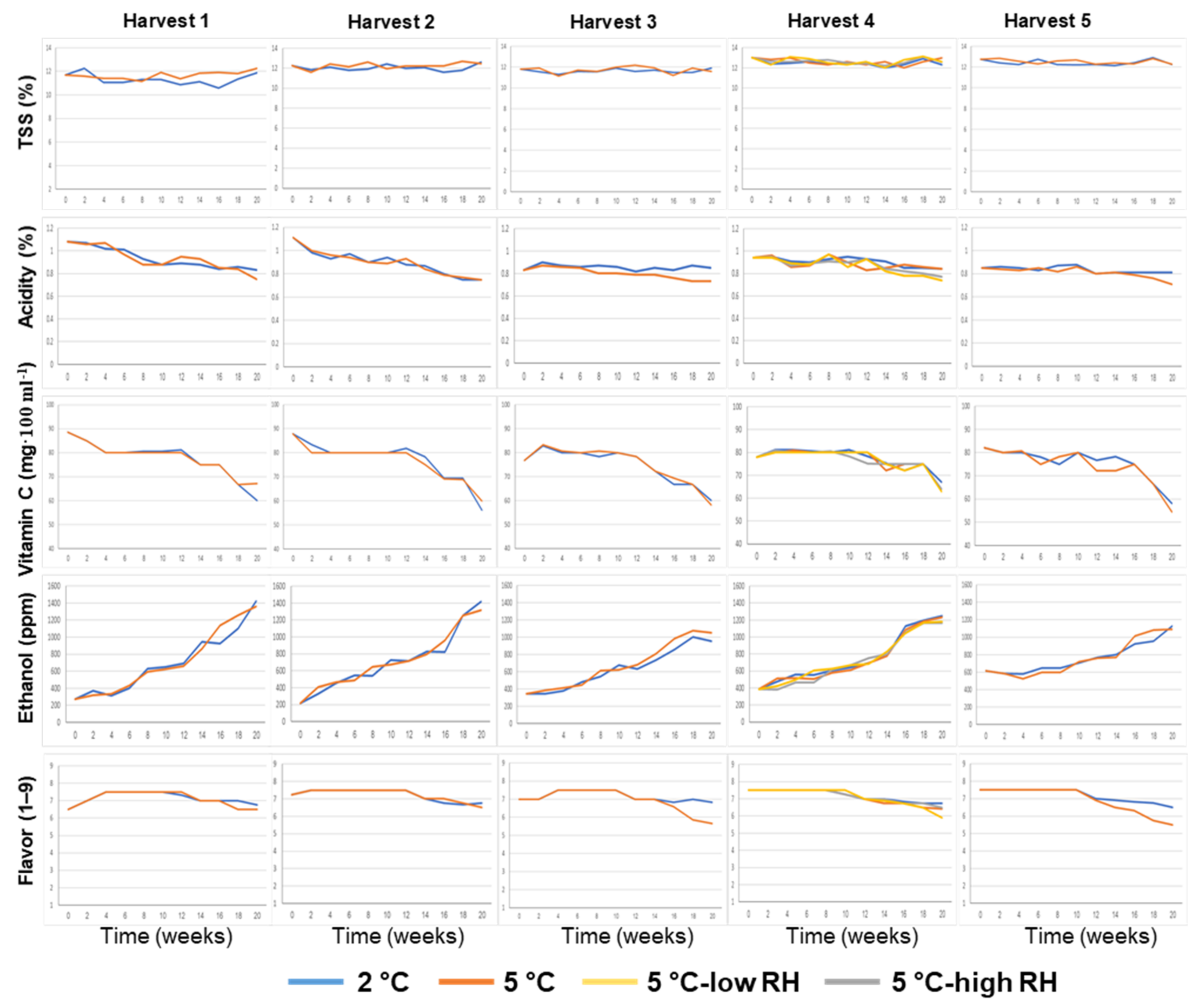
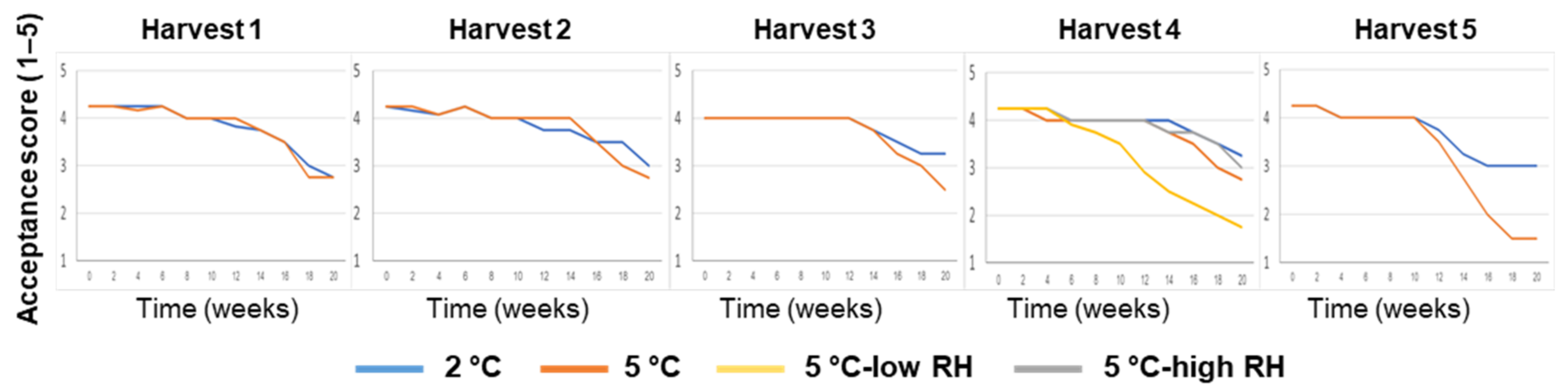
| Harvest Time (Weeks from Blooming) | Yield (Ton/Hectare) | Tree Age (Years) | Rootstock | |
|---|---|---|---|---|
| Harvest 1 (18 April 2021) | 56 | 47 | 6 | SO |
| Harvest 2 (19 April 2021) | 56 | 31 | 6 | VOL |
| Harvest 3 (26 April 2021) | 57 | 19 | 25 | SO |
| Harvest 4 (11 May 2021) | 59 | 47 | 6 | SO |
| Harvest 5 (12 May 2021) | 59 | 19 | 25 | SO |
| Harvest Time | Yield | Tree Age | Rootstock | Storage Time | Storage Temperature | RH | |
|---|---|---|---|---|---|---|---|
| Acidity | 0.027 | 2.01 × 10−10 | 5.54 × 10−12 | - | 1.42 × 10−24 | 0.001 | - |
| Vitamin C | 1.54 × 10−13 | 0.003 | - | 5.06 × 10−121 | 0.001 | - | |
| Internal dryness | 2.05 × 10−7 | 0.002 | 1.49 × 10−5 | 0.002 | 2.93 × 10−26 | 0.012 | - |
| Decay | 2.55 × 10−8 | 0.001 | 5.42 × 10−6 | - | 2.37 × 10−5 | 0.022 | - |
| Flavor | - | 3.55 × 10−5 | 0.018 | - | 2.12 × 10−93 | 0.044 | - |
| Final acceptance score | 0.017 | 0.003 | 0.013 | - | 3.89 × 10−85 | 2.83 × 10−5 | 4.37 × 10−7 |
| Firmness | 0.011 | - | 0.023 | - | 3.52 × 10−55 | 4.67 × 10−14 | 0.001 |
| Ethanol | - | 0.002 | - | - | 2.38 × 10−133 | 3.48 × 10−6 | - |
| Visual acceptance score | 0.012 | 0.035 | - | - | 8.80 × 10−90 | 9.82 × 10−5 | 1.72 × 10−9 |
| Weight loss | - | 1.58 × 10−16 | - | - | 5.78 × 10−85 | 1.55 × 10−17 | 0.001 |
| Peel damage | 0.001 | 8.33 × 10−6 | - | - | 7.72 × 10−14 | 1.27 × 10−16 | - |
| Color (hue angle) | 0.004 | 0.001 | - | - | 0.001 | 3.48 × 10−13 | - |
| TSS | 1.87 × 10−39 | - | - | - | 1.42 × 10−24 | 5.70 × 10−6 | 1.11 × 10−9 |
| Full Set | Low-Score Subset | |||
|---|---|---|---|---|
| Algorithm | RMSE | RMSE | ||
| MLR | 0.341 | 0.677 | 0.488 | 0.047 |
| Linear SVR | 0.362 | 0.646 | 0.641 | −0.640 |
| Non-linear SVR | 0.235 | 0.846 | 0.387 | 0.401 |
| RF | 0.242 | 0.834 | 0.447 | 0.201 |
| XGBoost | 0.220 | 0.859 | 0.396 | 0.373 |
| Full Set | Low-Score Subset | |||
|---|---|---|---|---|
| Number of Duplications | RMSE | RMSE | ||
| Non-linear SVR | ||||
| 0 | 0.235 | 0.846 | 0.387 | 0.401 |
| 1 | 0.199 | 0.883 | 0.248 | 0.755 |
| 2 | 0.195 | 0.885 | 0.224 | 0.799 |
| 3 | 0.195 | 0.884 | 0.210 | 0.823 |
| RF | ||||
| 0 | 0.242 | 0.834 | 0.447 | 0.201 |
| 1 | 0.225 | 0.856 | 0.400 | 0.360 |
| 2 | 0.221 | 0.860 | 0.384 | 0.411 |
| 3 | 0.217 | 0.864 | 0.369 | 0.455 |
| XGBoost | ||||
| 0 | 0.220 | 0.859 | 0.396 | 0.373 |
| 1 | 0.228 | 0.849 | 0.393 | 0.383 |
| 2 | 0.235 | 0.836 | 0.389 | 0.396 |
| 3 | 0.239 | 0.830 | 0.386 | 0.405 |
| Subgroup | Full Set | Low-Score Subset | ||
|---|---|---|---|---|
| RMSE | RMSE | |||
| 0.383 | 0.595 | 0.640 | −0.640 |
| 0.420 | 0.489 | 0.662 | −0.752 |
| 0.269 | 0.801 | 0.466 | 0.132 |
| 0.195 | 0.884 | 0.210 | 0.823 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Owoyemi, A.; Porat, R.; Lichter, A.; Doron-Faigenboim, A.; Jovani, O.; Koenigstein, N.; Salzer, Y. Evaluation of the Storage Performance of ‘Valencia’ Oranges and Generation of Shelf-Life Prediction Models. Horticulturae 2022, 8, 570. https://doi.org/10.3390/horticulturae8070570
Owoyemi A, Porat R, Lichter A, Doron-Faigenboim A, Jovani O, Koenigstein N, Salzer Y. Evaluation of the Storage Performance of ‘Valencia’ Oranges and Generation of Shelf-Life Prediction Models. Horticulturae. 2022; 8(7):570. https://doi.org/10.3390/horticulturae8070570
Chicago/Turabian StyleOwoyemi, Abiola, Ron Porat, Amnon Lichter, Adi Doron-Faigenboim, Omri Jovani, Noam Koenigstein, and Yael Salzer. 2022. "Evaluation of the Storage Performance of ‘Valencia’ Oranges and Generation of Shelf-Life Prediction Models" Horticulturae 8, no. 7: 570. https://doi.org/10.3390/horticulturae8070570
APA StyleOwoyemi, A., Porat, R., Lichter, A., Doron-Faigenboim, A., Jovani, O., Koenigstein, N., & Salzer, Y. (2022). Evaluation of the Storage Performance of ‘Valencia’ Oranges and Generation of Shelf-Life Prediction Models. Horticulturae, 8(7), 570. https://doi.org/10.3390/horticulturae8070570








