Continuous Third Phase Fruit Monitoring in Olive with Regulated Deficit Irrigation to Set a Quantitative Index of Water Stress
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Description and Phenology
2.2. Irrigation
2.3. Fruit Maturation Monitoring
2.4. Fruit Measurement and Experimental Design
2.5. Fruit Growth Parameters
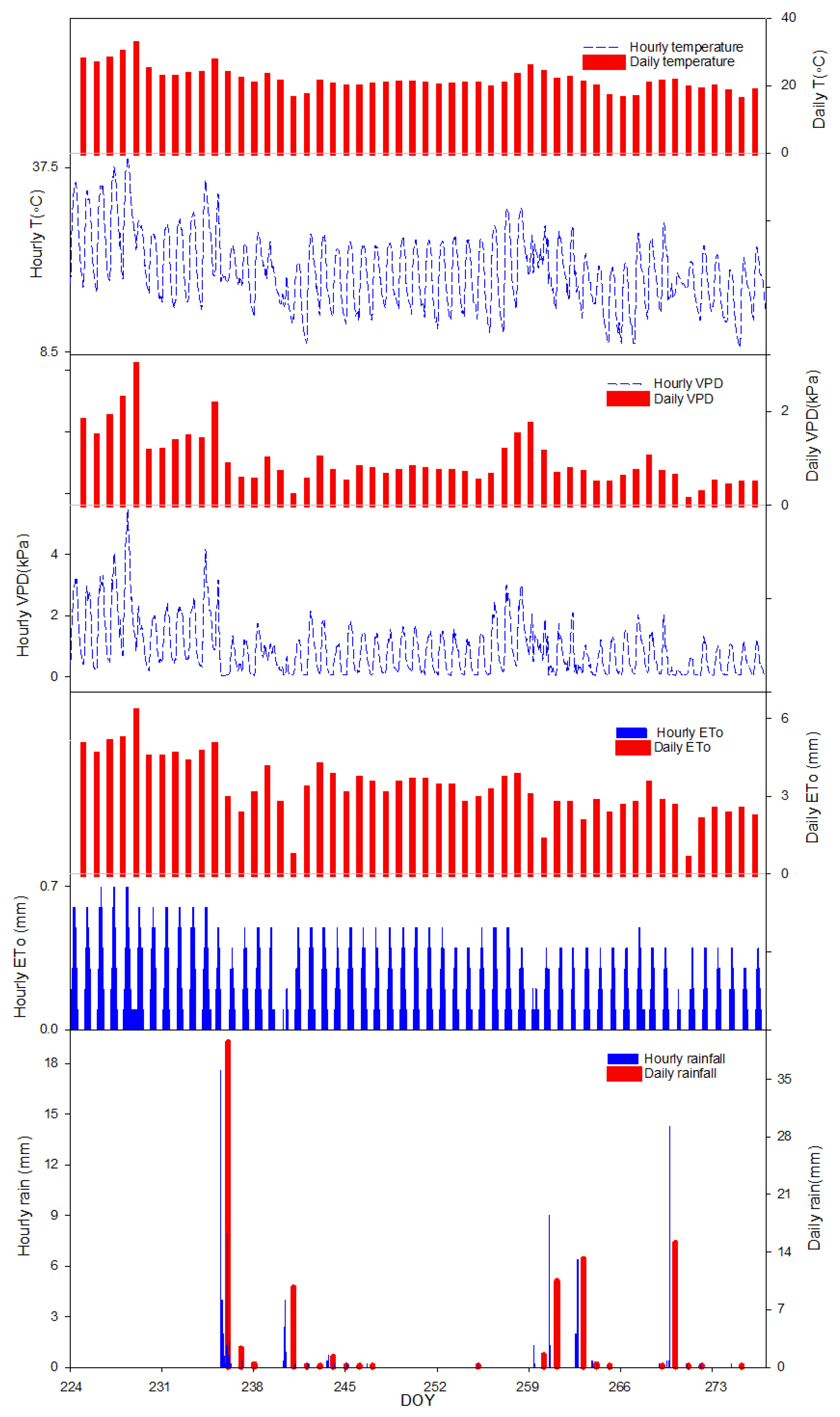
2.6. Meteorological Data
2.7. Hysteresis Curves
2.8. Data Analysis and Presentation
3. Results
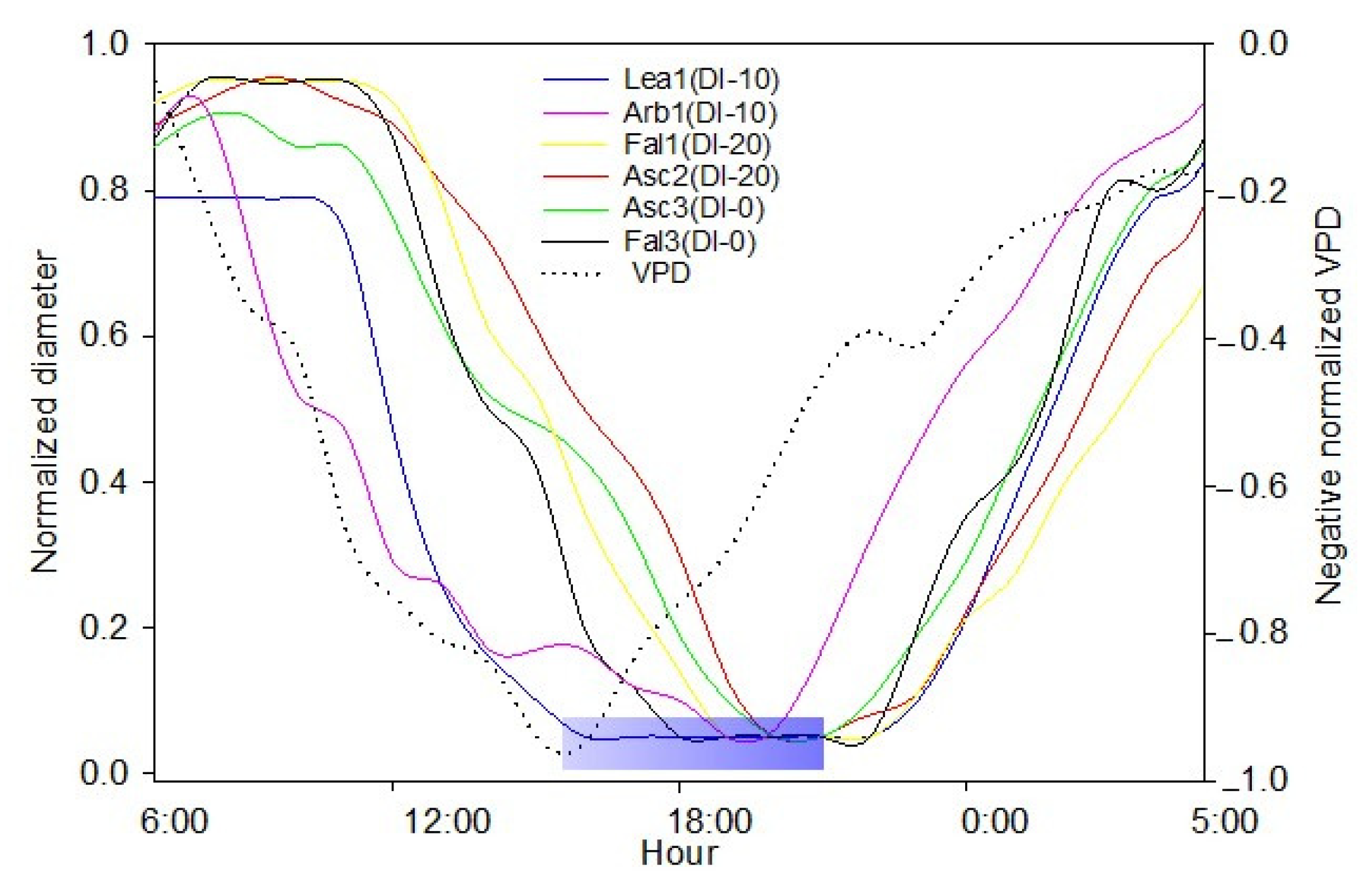
3.1. Environmental Data Analysis and VPD Evolution
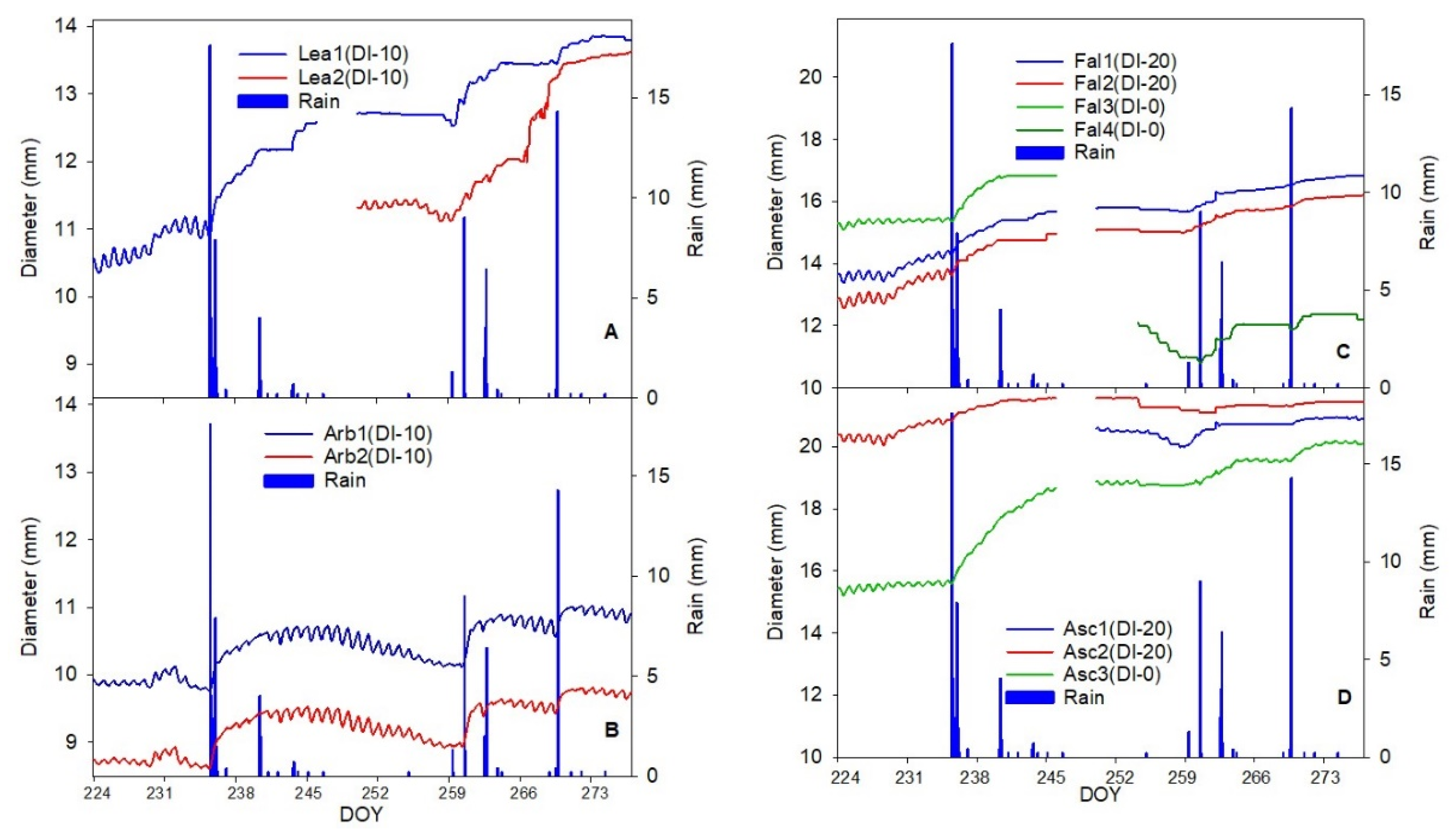
3.2. Fruit Growth
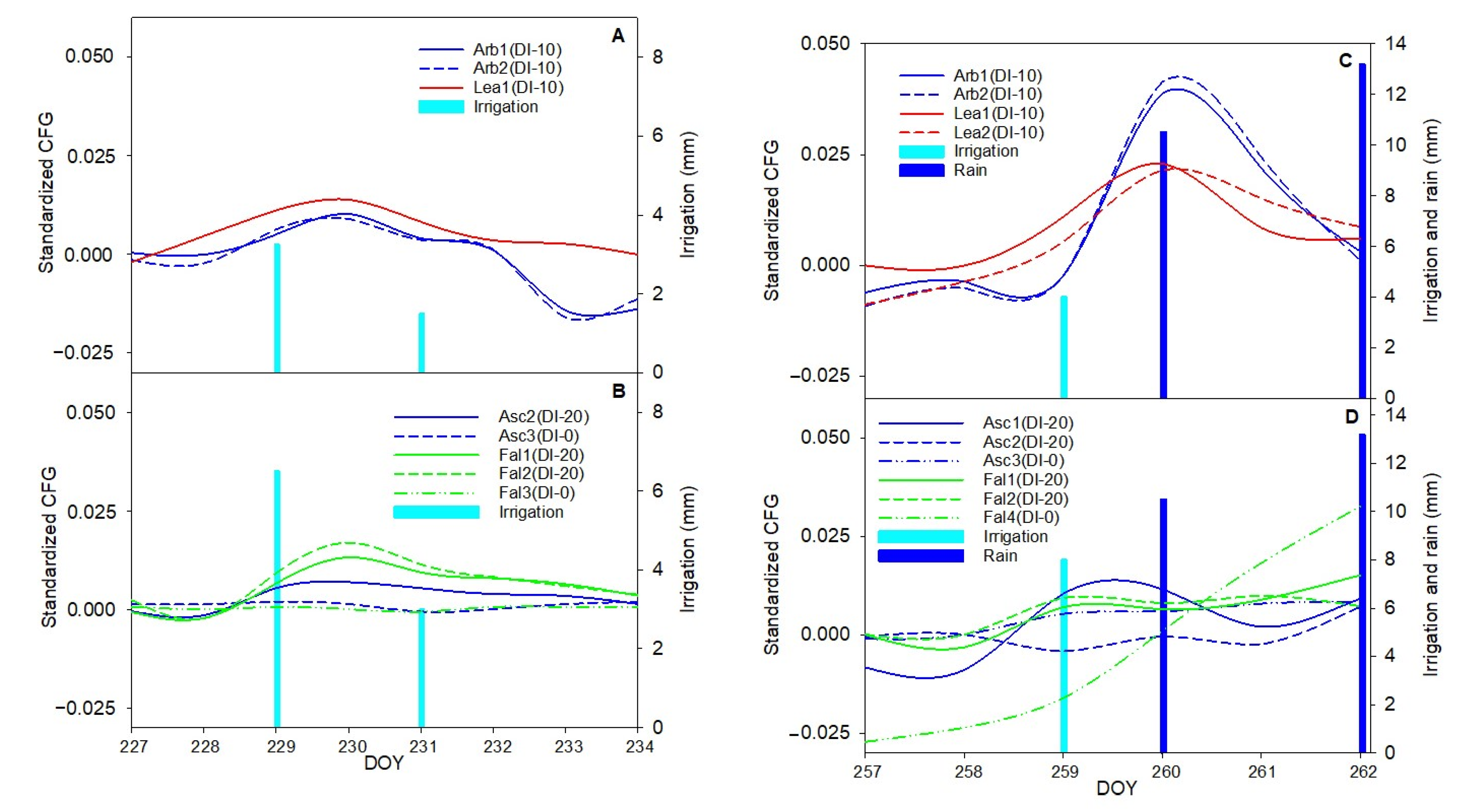
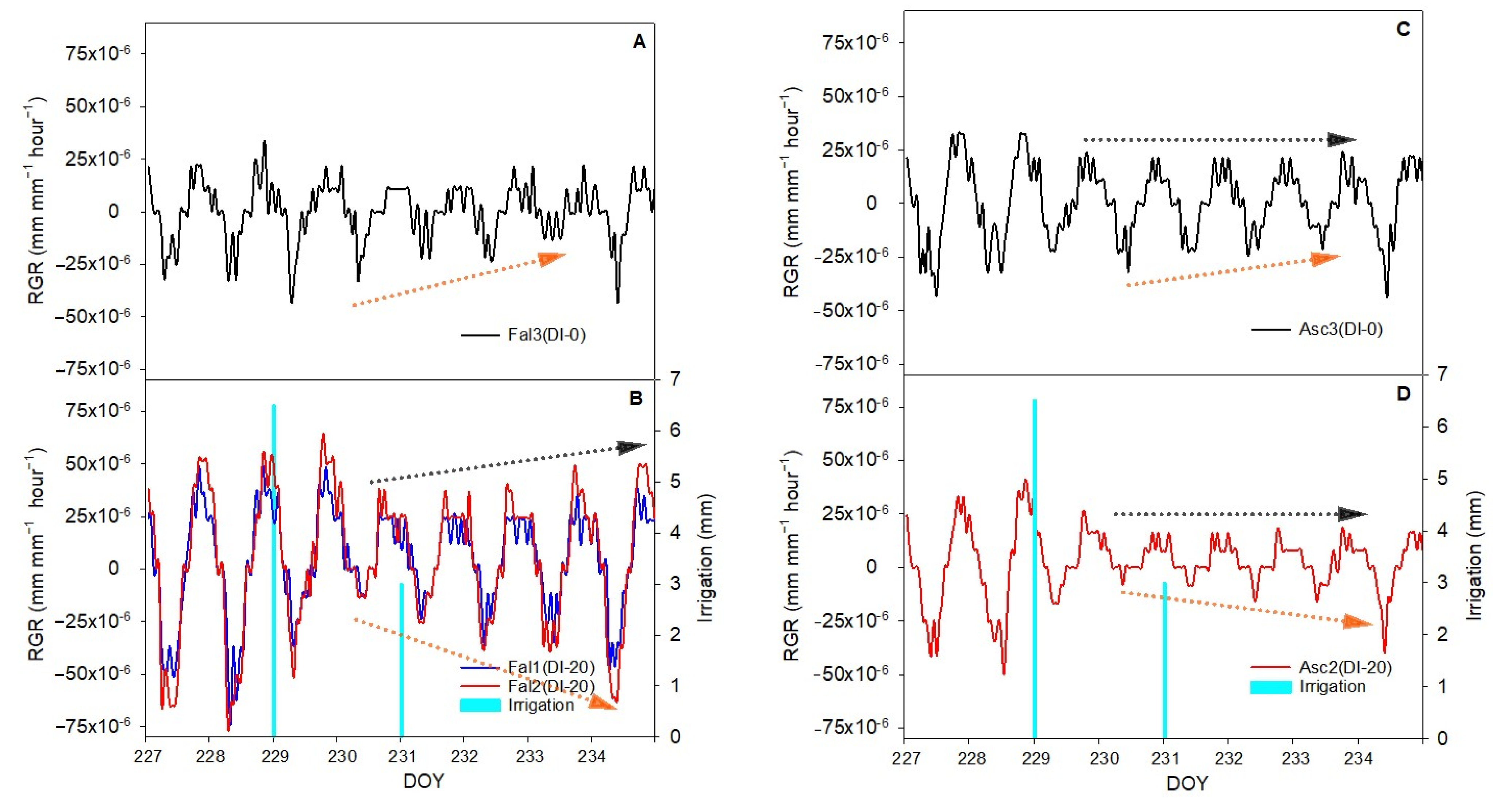
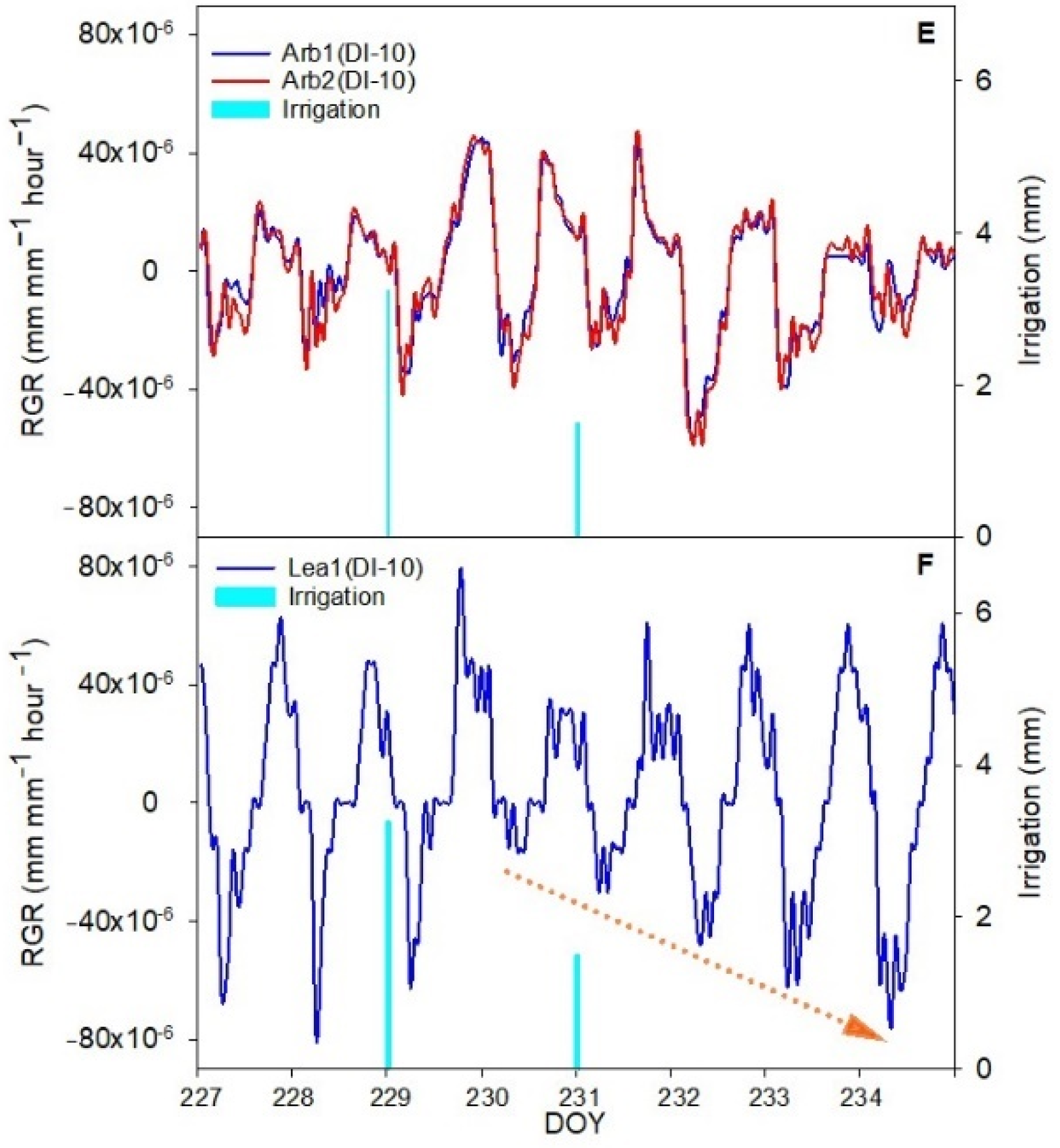
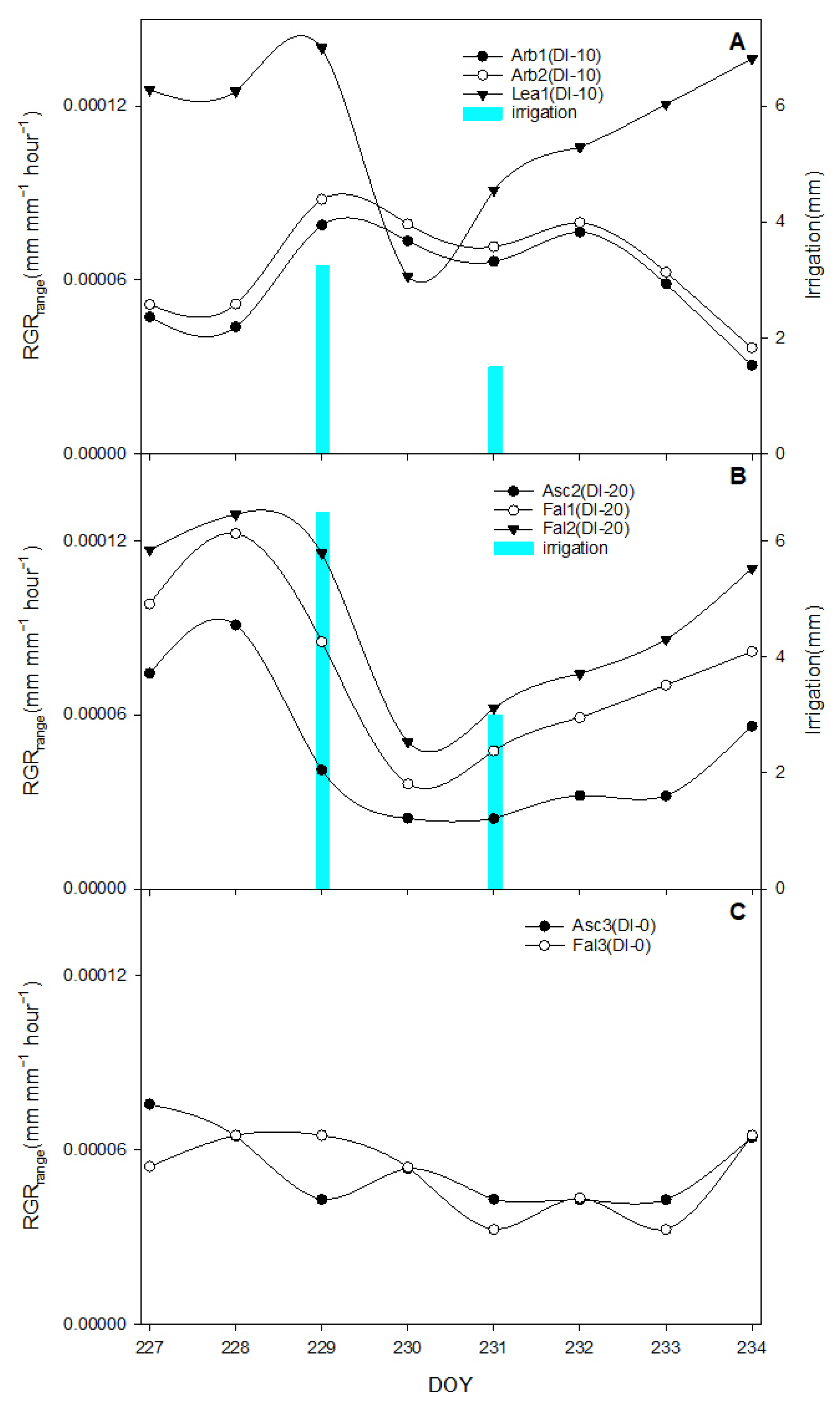
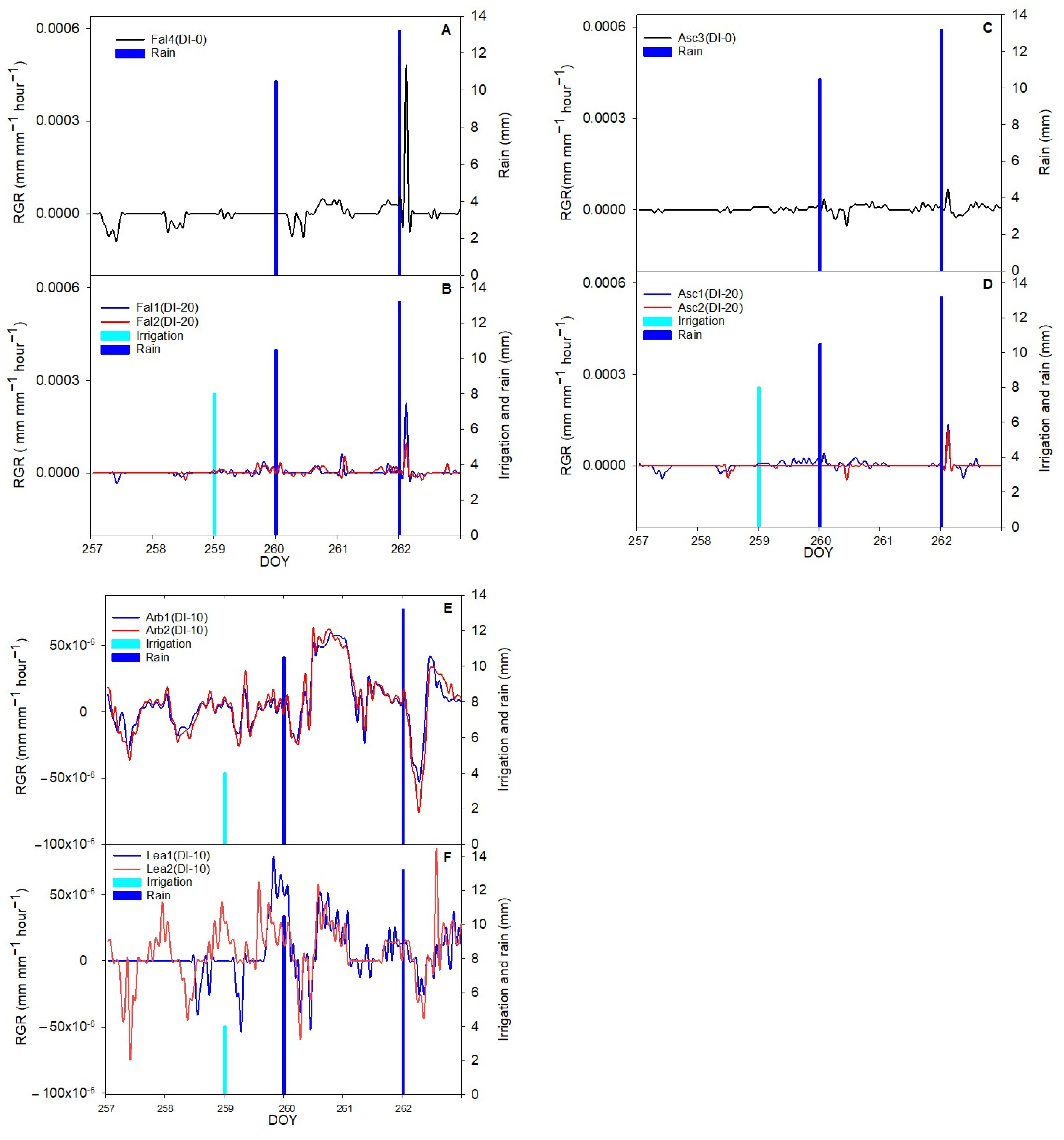
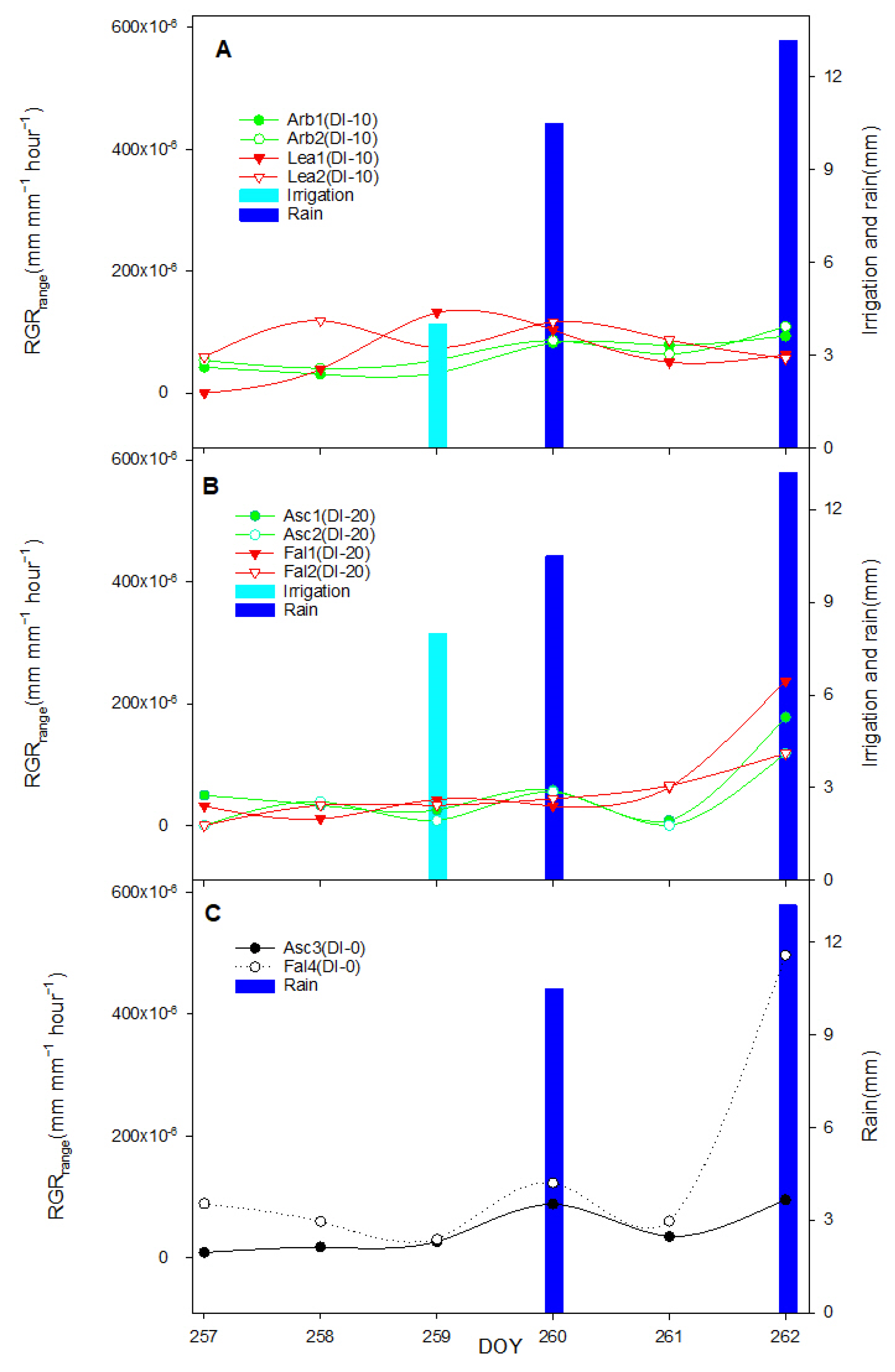
3.3. Irrigation Response
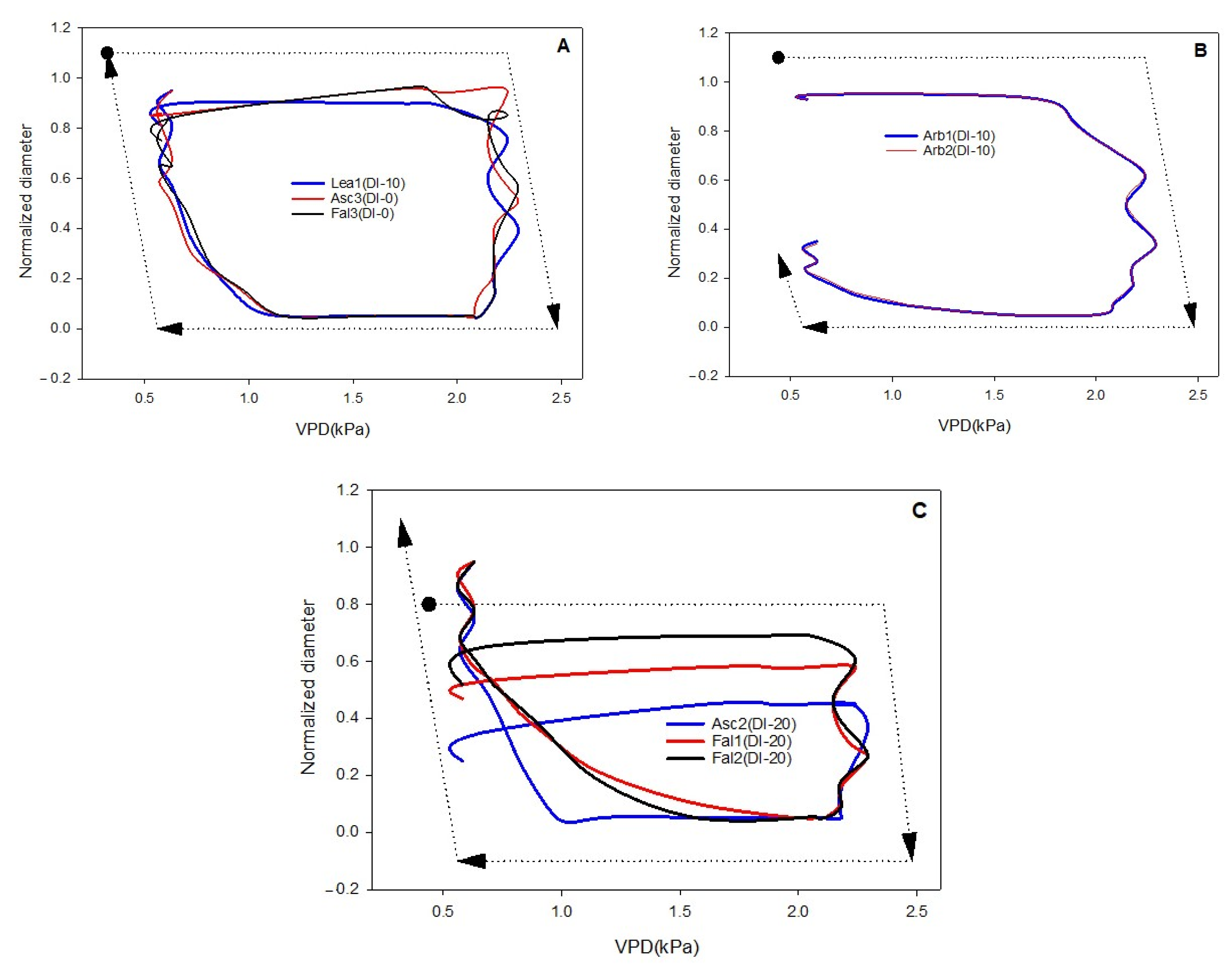
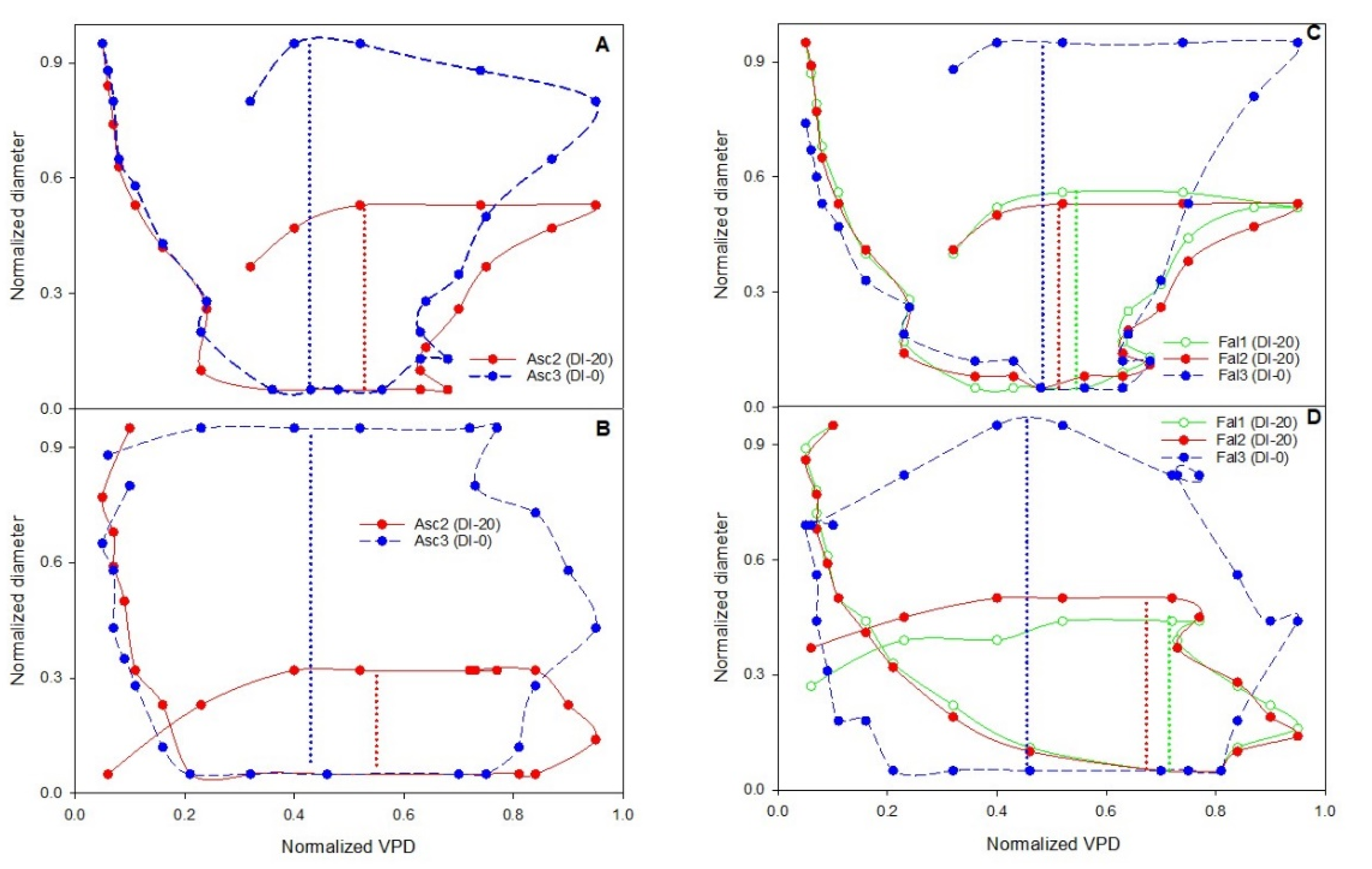
3.4. Hysteresis Curves of Fruit Growth versus VPD
4. Discussion
4.1. Response of Fruit Growth to Deficit Irrigation and Rain
4.2. Hysteresis Curves Variations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seifi, E.; Guerin, J.; Kaiser, B.; Sedgley, M. Flowering and fruit set in olive: A review. Iran. J. Plant Physiol. 2015, 5, 1263–1272. [Google Scholar]
- Rodrigues, N.; Casal, S.; Peres, A.M.; Baptista, P.; Bento, A.; Martín, H.; Manzanera, M.C.A.S.; Pereira, J.A. Effect of olive trees density on the quality and composition of olive oil from cv. Arbequina. Sci. Hortic. 2018, 238, 222–233. [Google Scholar] [CrossRef]
- Fraga, H.; Pinto, J.G.; Viola, F.; Santos, J.A. Climate change projections for olive yields in the Mediterranean Basin. Int. J. Climatol. 2020, 40, 769–781. [Google Scholar] [CrossRef]
- Romero-Trigueros, C.; Vivaldi, G.A.; Nicolás, E.N.; Paduano, A.; Salcedo, F.P.; Camposeo, S. Ripening indices, olive yield and oil quality in response to irrigation with saline reclaimed water and deficit strategies. Front. Plant Sci. 2019, 10, 1243. [Google Scholar] [CrossRef] [PubMed]
- Fernández, J.E. Plant-based sensing to monitor water stress: Applicability to commercial orchards. Agric. Water Manag. 2014, 142, 99–109. [Google Scholar] [CrossRef]
- Ahumada-Orellana, L.E.; Ortega-Farías, S.; Searles, P.S.; Retamales, J.B. Yield and water productivity responses to irrigation cut-off strategies after fruit set using stem water potential thresholds in a super-high density olive orchard. Front. Plant Sci. 2017, 8, 1280. [Google Scholar] [CrossRef]
- Romero-Trigueros, C.; Parra, M.; Bayona Gambín, J.M.; Nortes Tortosa, P.; Alarcon Cabañero, J.J.; Nicolás, E. Effect of deficit irrigation and reclaimed water on yield and quality of grapefruits at harvest and postharvest. LWT—Food Sci. Technol. 2017, 85, 405–411. [Google Scholar] [CrossRef]
- Lodolini, E.M.; Morini, F.; Polverigiani, S.; Neri, D. Olive fruit and root growth on different irrigation regimes in central Italy. Acta Hortic. 2011, 924, 63–68. [Google Scholar] [CrossRef]
- Lodolini, E.M.; Ali, S.; Mutawea, M.; Qutub, M.; Arabasi, T.; Pierini, F.; Neri, D. Complementary irrigation for sustainable production in olive groves in Palestine. Agric. Water Manag. 2014, 134, 104–109. [Google Scholar] [CrossRef]
- Lodolini, E.M.; Polverigiani, S.; Ali, S.; Mutawea, M.; Qutub, M.; Pierini, F.; Neri, D. Effect of complementary irrigation on yield components and alternate bearing of a traditional olive orchard in semi-arid conditions. Spanish J. Agric. Res. 2016, 14, e1203. [Google Scholar] [CrossRef]
- Goldhamer, D.A. Regulated deficit irrigation for California canning olives. Acta Hortic. 1999, 474, 369–372. [Google Scholar] [CrossRef]
- Gómez-del-Campo, M. Summer deficit irrigation in a hedgerow olive orchard cv. Arbequina: Relationship between soil and tree water status, and growth and yield components. Spanish J. Agric. Res. 2013, 11, 547–557. [Google Scholar] [CrossRef]
- Rodríguez Sousa, A.A.; Barandica, J.M.; Rescia, A.J. Estimation of soil loss tolerance in olive groves as an indicator of sustainability: The case of the Estepa Region (Andalusia, Spain). Agronomy 2019, 9, 785. [Google Scholar] [CrossRef]
- Scalisi, A.; Marino, G.; Marra, F.P.; Caruso, T.; Lo Bianco, R. A Cultivar-Sensitive Approach for the Continuous Monitoring of Olive (Olea europaea L.) Tree Water Status by Fruit and Leaf Sensing. Front. Plant Sci. 2020, 11, 340. [Google Scholar] [CrossRef]
- Marino, G.; Scalisi, A.; Guzmán-Delgado, P.; Caruso, T.; Marra, F.P.; Lo Bianco, R. Detecting Mild Water Stress in Olive with Multiple Plant-Based Continuous Sensors. Plants 2021, 10, 131. [Google Scholar] [CrossRef]
- Caruso, G.; Palai, G.; Gucci, R.; Priori, S. Remote and Proximal Sensing Techniques for Site-Specific Irrigation Management in the Olive Orchard. Appl. Sci. 2022, 12, 1309. [Google Scholar] [CrossRef]
- Caruso, G.; Palai, G.; Gucci, R.; D’Onofrio, C. The effect of regulated deficit irrigation on growth, yield, and berry quality of grapevines (cv. Sangiovese) grafted on rootstocks with different resistance to water deficit. Irrig. Sci. 2022, 40, 1–15. [Google Scholar] [CrossRef]
- Measham, P.F.; Wilson, S.J.; Gracie, A.J.; Bound, S.A. Tree water relations: Flow and fruit. Agric. Water Manag. 2014, 137, 59–67. [Google Scholar] [CrossRef]
- Fernández, J.E. Plant-based methods for irrigation scheduling of woody crops. Horticulturae 2017, 3, 35. [Google Scholar] [CrossRef]
- Lo Bianco, R.; Scalisi, A. Water relations and carbohydrate partitioning of four greenhouse-grown olive genotypes under long-term drought. Trees 2017, 31, 717–727. [Google Scholar] [CrossRef]
- Marino, G.; Caruso, T.; Ferguson, L.; Marra, F.P. Gas exchanges and stem water potential define stress thresholds for efficient irrigation management in olive (Olea europea L.). Water 2018, 10, 342. [Google Scholar] [CrossRef]
- Scalisi, A.; O’Connell, M.G.; Stefanelli, D.; Lo Bianco, R. Fruit and Leaf Sensing for Continuous Detection of Nectarine Water Status. Front. Plant Sci. 2019, 10, 805. [Google Scholar] [CrossRef] [PubMed]
- Boini, A.; Manfrini, L.; Bortolotti, G.; Corelli-Grappadelli, L.; Morandi, B. Monitoring fruit daily growth indicates the onset of mild drought stress in apple. Sci. Hortic. 2019, 256, 108520. [Google Scholar] [CrossRef]
- Jones, H.G. Irrigation scheduling: Advantages and pitfalls of plant-based methods. J. Exp. Bot. 2004, 407, 2427–2436. [Google Scholar] [CrossRef]
- Scalisi, A.; Bresilla, K.; Simões Grilo, F. Continuous determination of fruit tree water-status by plant-based sensors. Italus Hortus 2017, 24, 39–50. [Google Scholar] [CrossRef]
- Fernandes, R.D.M.; Cuevas, M.V.; Diaz-Espejo, A.; Hernandez-Santana, V. Effects of water stress on fruit growth and water relations between fruits and leaves in a hedgerow olive orchard. Agric. Water Manag. 2018, 210, 32–40. [Google Scholar] [CrossRef]
- Khosravi, A.; Zucchini, M.; Giorgi, V.; Mancini, A.; Neri, D. Continuous Monitoring of Olive Fruit Growth by Automatic Extensimeter in Response to Vapor Pressure Deficit from Pit Hardening to Harvest. Horticulturae 2021, 7, 349. [Google Scholar] [CrossRef]
- Gucci, R.; Lodolini, E.M.; Rapoport, H.F. Water deficit-induced changes in mesocarp cellular processes and the relationship between mesocarp and endocarp during olive fruit development. Tree Physiol. 2009, 29, 1575–1585. [Google Scholar] [CrossRef]
- Giorgi, V.; Neri, D.; Maria Lodolini, E.; Massetani, F. Olive (Olea europaea L.) root growth in soil sectors with olive husks and hay residues. Int. J. Fruit Sci. 2008, 7, 19–32. [Google Scholar] [CrossRef]
- Lodolini, E.M.; Falleroni, P.; Polverigiani, S.; Neri, D. Fertigation of young olive trees in Marche region, central Italy: Preliminary study results. Acta Hortic 2011, 888, 289–294. [Google Scholar] [CrossRef]
- Polverigiani, S.; Lodolini, E.M.; Neri, D. Olive root growth observed by field rhizotron. Acta Hortic. 2012, 949, 271–278. [Google Scholar] [CrossRef]
- Lakso, A.N.; Corelli Grappadelli, L.; Barnard, J.; Goffinet, M.C. An expolinear model of the growth pattern of the apple fruit. J. Hortic. 1995, 70, 389–394. [Google Scholar] [CrossRef]
- Morandi, B.; Losciale, P.; Manfrini, L.; Zibordi, M.; Anconelli, S.; Galli, F.; Pierpaoli, E.; Grappadelli, L.C. Increasing water stress negatively affects pear fruit growth by reducing first its xylem and then its phloem inflow. J. Plant Physiol. 2014, 171, 1500–1509. [Google Scholar] [CrossRef]
- Brüggenwirth, M.; Winkler, A.; Knoche, M. Xylem, phloem, and transpiration flows in developing sweet cherry fruit. Trees 2016, 30, 1822–1830. [Google Scholar] [CrossRef]
- Mancini, A.; Zucchini, M.; Polverigiani, S.; Marcheggiani, E.; Casavecchia, S.; Neri, D. Cherry fruit growth: Monitoring and ‘tweeting’. Acta Hortic. 2021, 1314, 399–408. [Google Scholar] [CrossRef]
- Zucchini, M.; Khosravi, A.; Giorgi, V.; Mancini, A.; Neri, D. Is There Daily Growth Hysteresis versus Vapor Pressure Deficit in Cherry Fruit? Horticulturae 2021, 7, 131. [Google Scholar] [CrossRef]
- Carella, A.; Gianguzzi, G.; Scalisi, A.; Farina, V.; Inglese, P.; Bianco, R.L. Fruit Growth Stage Transitions in Two Mango Cultivars Grown in a Mediterranean Environment. Plants 2021, 10, 1332. [Google Scholar] [CrossRef]
- Grilo, F.S.; Scalisi, A.; Pernice, F.; Morandi, B.; Lo Bianco, R. Recurrent deficit irrigation and fruit harvest affect tree water relations and fruitlet growth in ‘Valencia’orange. Eur. J. Hortic. Sci. 2019, 84, 177–187. [Google Scholar] [CrossRef]
- Tuzet, A.; Perrier, A.; Leuning, R. A coupled model of stomatal conductance, photosynthesis and transpiration. Plant Cell Environ. 2003, 26, 1097–1116. [Google Scholar] [CrossRef]
- Zhang, Q.; Manzoni, S.; Katul, G.; Porporato, A.; Yang, D. The hysteretic evapotranspiration—Vapor pressure deficit relation. J. Geophys. Res. Biogeosciences 2014, 119, 125–140. [Google Scholar] [CrossRef]
- Mayergoyz, I.D. Mathematical Models of Hysteresis and Their Applications, 2nd ed.; Electromagnetism; Academic Press: Cambridge, MA, USA, 2003; ISBN 978-0-12-480873-7. [Google Scholar]
- Phillips, J.D. Sources of nonlinearity and complexity in geomorphic systems. Prog. Phys. Geogr. 2003, 27, 1–23. [Google Scholar] [CrossRef]
- O’Kane, J.P. Hysteresis in hydrology. Acta Geophys. Pol. 2005, 53, 373–383. [Google Scholar]
- Zeppel, M.J.B.; Murray, B.R.; Barton, C.; Eamus, D. Seasonal responses of xylem sap velocity to VPD and solar radiation during drought in a stand of native trees in temperate Australia. Funct. Plant Biol. 2004, 31, 461–470. [Google Scholar] [CrossRef] [PubMed]
- O’Brien, J.J.; Oberbauer, S.F.; Clark, D.B. Whole tree xylem sap flow responses to multiple environmental variables in a wet tropical forest. Plant Cell Environ. 2004, 27, 551–567. [Google Scholar] [CrossRef]
- Bai, Y.; Li, X.; Liu, S.; Wang, P. Modelling diurnal and seasonal hysteresis phenomena of canopy conductance in an oasis forest ecosystem. Agric. For. Meteorol. 2017, 246, 98–110. [Google Scholar] [CrossRef]
- Perez-Martin, A.; Flexas, J.; Ribas-Carbó, M.; Bota, J.; Tomàs, M.; Infante, J.M.; Diaz-Espejo, A. Interactive effects of soil water deficit and air vapour pressure deficit on mesophyll conductance to CO2 in Vitis vinifera and Olea europaea. J. Exp. Bot. 2009, 60, 2391–2405. [Google Scholar] [CrossRef]
- Assirelli, A.; Romano, E.; Bisaglia, C.; Lodolini, E.M.; Neri, D.; Brambilla, M. Canopy Index Evaluation for Precision Management in an Intensive Olive Orchard. Sustainability 2021, 13, 8266. [Google Scholar] [CrossRef]
- Agenzia Servizi Settore Agroalimentare delle Marche (ASSAM). Available online: http://www.meteo.marche.it/pi/#produzioneintegrata_discliplinare (accessed on 12 September 2022).
- COI (International Olive Council). Guide for the Determination of the Characteristics of Oil Olives, COI/OH/Doc. No 1 November 2011. Available online: http://www.internationaloliveoil.org (accessed on 15 September 2021).
- Morandi, B.; Manfrini, L.; Zibordi, M.; Noferini, M.; Fiori, G.; Grappadelli, L.C. A Low-cost Device for Accurate and Continuous Measurements of Fruit Diameter. HortScience 2007, 42, 1380–1382. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Monteith, J.; Unsworth, M. Principles of Environmental Physics: Plants, Animals, and the Atmosphere, 4th ed.; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Zhang, R.; Xu, X.; Liu, M.; Zhang, Y.; Xu, C.; Yi, R.; Luo, W.; Soulsby, C. Hysteresis in sap flow and its controlling mechanisms for a deciduous broad-leaved tree species in a humid karst region. Sci. China Earth Sci. 2019, 62, 1744–1755. [Google Scholar] [CrossRef]
- Zuecco, G.; Penna, D.; Borga, M.A.R.C.O.; van Meerveld, H.J. A versatile index to characterize hysteresis between hydrological variables at the runoff event timescale. Hydrol. Process. 2016, 30, 1449–1466. [Google Scholar] [CrossRef]
- Fishman, S.; Génard, M. A biophysical model of fruit growth: Simulation of seasonal and diurnal dynamics of mass. Plant Cell Environ. 1998, 21, 739–752. [Google Scholar] [CrossRef]
- Morandi, B.; Manfrini, L.; Losciale, P.; Zibordi, M.; Corelli Grappadelli, L. Changes in vascular and transpiration flows affect the seasonal and daily growth of kiwifruit (Actinidia deliciosa) berry. Ann. Bot. 2010, 105, 913–923. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Santana, V.; Perez-Arcoiza, A.; Gomez-Jimenez, M.C.; Diaz-Espejo, A. Disentangling the link between leaf photosynthesis and turgor in fruit growth. Plant Sci. J. 2021, 107, 1788–1801. [Google Scholar] [CrossRef]
- Morandi, B.; Rieger, M.; Grappadelli, L.C. Vascular flows and transpiration affect peach (Prunus persica Batsch.) fruit daily growth. J. Exp. Bot. 2007, 58, 3941–3947. [Google Scholar] [CrossRef]
| DOY | Arb1(DI-10) | Arb2(DI-10) | Lea1(DI-10) | Lea2(DI-10) | Asc1(DI-20) | Asc2(DI-20) | Asc3(DI-0) | Fal1(DI-20) | Fal2(DI-20) | Fal4(DI-0) |
|---|---|---|---|---|---|---|---|---|---|---|
| 262 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 269 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 2 |
| 276 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 2 | 1 | 2 |
| 284 | 0 | 0 | 1 | 3 | 1 | 1 | 1 | 3 | 2 | 2 |
| 291 | 1 | 1 | 1 | 3 | 1 | 1 | 1 | 3 | 3 | 3 |
| 299 | 1 | 1 | 2 | 4 | 3 | 2 | 2 | 4 | 3 | 3 |
| DOY | Arb1(DI-10) | Arb2(DI-10) | Lea1(DI-10) | Lea2(DI-10) | Asc1(DI-20) | Asc2(DI-20) | Asc3(DI-0) | Fal1(DI-20) | Fal2(DI-20) | Fal3(DI-0) | Fal4(DI-0) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| First and second irrigation treatment (DOYs 229 &231) | |||||||||||
| 227 | 0.4 | 0.46 | 0.29 | - | - | 0.41 | 0.62 | 0.34 | 0.32 | 0.72 | - |
| 234 | 0.13 | 0.15 | 0.79 | - | - | 0.91 | 0.9 | 0.95 | 0.95 | 0.89 | - |
| Third irrigation treatment (DOY 259) | - | ||||||||||
| 257 | 0.19 | 0.2 | 0.23 | 0.24 | 0.38 | 0.95 | 0.1 | 0.17 | 0.08 | - | 0.81 |
| 262 | 0.95 | 0.91 | 0.95 | 0.83 | 0.89 | 0.95 | 0.95 | 0.92 | 0.92 | - | 0.95 |
| DOY | Arb1(DI-10) | Arb2(DI-10) | Lea1(DI-10) | Lea2(DI-10) | Asc1(DI-20) | Asc2(DI-10) | Asc3(DI-0) | Fal1(DI-20) | Fal2(DI-20) | Fal3(DI-0) | Fal4(DI-0) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 227 | 0.0004 | 0.0021 | 0.0019 | - | - | −0.0029 | −0.0006 | −0.0029 | −0.0031 | 0.0000 | - |
| 228 | −0.0005 | 0.0021 | 0.0028 | - | - | 0.0000 | 0.0013 | −0.0044 | −0.0054 | 0.0006 | - |
| 229 | −0.0050 | −0.0086 | 0.0102 | - | - | 0.0054 | 0.0013 | 0.0102 | 0.0139 | −0.0013 | - |
| 230 | −0.0076 | −0.0066 | 0.0119 | - | - | 0.0063 | −0.0013 | 0.0116 | 0.0144 | −0.0013 | - |
| 231 | −0.0034 | −0.0029 | 0.0073 | - | - | 0.0048 | −0.0006 | 0.0086 | 0.0097 | 0.0000 | - |
| 232 | 0.0158 | 0.0177 | 0.0027 | - | - | 0.0034 | 0.0006 | 0.0064 | 0.0074 | 0.0006 | - |
| 233 | 0.0134 | 0.0113 | −0.0018 | - | - | 0.0029 | 0.0006 | 0.0049 | 0.0044 | 0.0006 | - |
| 234 | 0.0029 | 0.0029 | −0.0090 | - | - | −0.0010 | 0.0000 | 0.0021 | 0.0022 | 0.0000 | - |
| 257 | 0.0043 | 0.0059 | 0.0000 | −0.0044 | −0.0089 | 0.0000 | −0.0011 | −0.0032 | 0.0000 | - | −0.0236 |
| 258 | 0.0030 | 0.0041 | −0.0063 | 0.0018 | −0.0045 | −0.0042 | 0.0011 | −0.0019 | −0.0007 | - | −0.0170 |
| 259 | 0.0008 | −0.0017 | 0.0174 | 0.0116 | 0.0145 | −0.0005 | 0.0048 | 0.0089 | 0.0100 | - | −0.0009 |
| 260 | −0.0395 | −0.0408 | 0.0194 | 0.0159 | 0.0108 | −0.0024 | 0.0058 | 0.0063 | 0.0072 | - | 0.0027 |
| 261 | −0.0177 | −0.0204 | 0.0076 | 0.0201 | 0.0015 | 0.0000 | 0.0074 | 0.0088 | 0.0098 | - | 0.0154 |
| 262 | −0.0022 | 0.0020 | 0.0053 | 0.0009 | 0.0068 | 0.0071 | 0.0084 | 0.0137 | 0.0052 | - | 0.0294 |
| Type ofhysteresis | Arb1(DI-10) | Arb2(DI-10) | Lea1(DI-10) | Lea2(DI-10) | Asc1(DI-20) | Asc2(DI-20) | Asc3(DI-0) | Fal1(DI-20) | Fal2(DI-20) | Fal3(DI-0) | Fal4(DI-0) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Complete | 27.45 | 15.69 | 19.05 | 12.50 | 15.00 | 12.82 | 27.66 | 6.67 | 10.26 | 35.29 | 0.00 |
| Incomplete | 41.18 | 50.98 | 23.81 | 62.50 | 50.00 | 25.64 | 19.15 | 42.22 | 15.38 | 17.65 | 33.33 |
| Partial | 23.53 | 25.49 | 42.86 | 16.67 | 15.00 | 30.77 | 34.04 | 26.67 | 48.72 | 23.53 | 50.00 |
| No hysteresis | 7.84 | 7.84 | 14.29 | 8.33 | 20.00 | 30.77 | 19.15 | 24.44 | 25.64 | 23.53 | 16.67 |
| DOY | Arb1(DI-10) | Arb2(DI-10) | Lea1(DI-10) | Lea2(DI-10) | Asc1(DI-20) | Asc2(DI-20) | Asc3(DI-0) | Fal1(DI-20) | Fal2(DI-20) | Fal3(DI-0) | Fal4(DI-0) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 227 | Complete | Incomplete | Complete | - | - | Incomplete | Complete | Incomplete | Incomplete | Complete | - |
| 228 | Complete | Incomplete | Complete | - | - | Complete | Complete | Incomplete | Incomplete | Complete | - |
| 229 | Partial | Partial | Partial | - | - | Partial | Partial | Partial | Partial | Incomplete | - |
| 230 | Partial | Partial | Partial | - | - | Partial | Incomplete | Partial | Partial | Incomplete | - |
| 231 | Partial | Partial | Partial | - | - | Partial | Complete | Partial | Partial | Complete | - |
| 232 | Incomplete | Incomplete | Complete | - | - | Partial | Complete | Partial | Partial | Complete | - |
| 233 | Incomplete | Incomplete | Incomplete | - | - | Partial | Incomplete | Partial | Partial | Partial | - |
| 234 | Incomplete | Incomplete | Incomplete | - | - | Incomplete | Complete | Complete | Complete | Complete | - |
| 257 | Incomplete | Incomplete | # | Incomplete | Incomplete | # | Incomplete | Incomplete | # | - | Incomplete |
| 258 | Incomplete | Incomplete | Incomplete | Complete | Incomplete | Incomplete | Complete | Incomplete | Incomplete | - | Incomplete |
| 259 | No | No | No | No | No | No | No | No | No | - | No |
| 260 | Partial | Partial | No | Partial | No | No | Partial | No | No | - | Complete |
| 261 | No | No | Partial | Incomplete | Partial | # | Partial | Incomplete | Partial | - | Partial |
| 262 | Partial | Incomplete | Partial | Chaos | Partial | Partial | Partial | Partial | Partial | - | Partial |
| Treatment Name | N | Mean | Std Dev | SEM | Student-Newman-Keuls test |
|---|---|---|---|---|---|
| Fal1 (DI-20) | 8 | 62.125 | 25.503 | 9.017 | a |
| Fal2 (DI-20) | 8 | 70 | 18.83 | 6.657 | a |
| Fal3 (DI-0) | 8 | 90 | 0 | 0 | b |
| Asc2 (DI-20) | 8 | 56.125 | 31.692 | 11.205 | A |
| Asc3 (DI-0) | 8 | 90 | 0 | 0 | B |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khosravi, A.; Zucchini, M.; Mancini, A.; Neri, D. Continuous Third Phase Fruit Monitoring in Olive with Regulated Deficit Irrigation to Set a Quantitative Index of Water Stress. Horticulturae 2022, 8, 1221. https://doi.org/10.3390/horticulturae8121221
Khosravi A, Zucchini M, Mancini A, Neri D. Continuous Third Phase Fruit Monitoring in Olive with Regulated Deficit Irrigation to Set a Quantitative Index of Water Stress. Horticulturae. 2022; 8(12):1221. https://doi.org/10.3390/horticulturae8121221
Chicago/Turabian StyleKhosravi, Arash, Matteo Zucchini, Adriano Mancini, and Davide Neri. 2022. "Continuous Third Phase Fruit Monitoring in Olive with Regulated Deficit Irrigation to Set a Quantitative Index of Water Stress" Horticulturae 8, no. 12: 1221. https://doi.org/10.3390/horticulturae8121221
APA StyleKhosravi, A., Zucchini, M., Mancini, A., & Neri, D. (2022). Continuous Third Phase Fruit Monitoring in Olive with Regulated Deficit Irrigation to Set a Quantitative Index of Water Stress. Horticulturae, 8(12), 1221. https://doi.org/10.3390/horticulturae8121221






