Abstract
Endotherapy is a potential eco-friendly alternative to conventional pesticide application techniques in coconut (Cocos nucifera Linn.) palms. Field trials applying cyproconazole by vegetative endotherapy using two different injection methods, pressurized and nonpressurized, were tested. Stem samples above the injection point were collected 2 to 45 days after application, and fruits were collected up to 45 to 120 days after application. Residue analyses on the coconut fruit and stem above the point of application of cyproconazole were performed on different days using modified QuEChERS (an acronym for “quick, easy, cheap, effective, rugged, and safe”) and LC-MS/MS MS (liquid chromatography–tandem mass spectrometry). For cyproconazole application in 2 m tall hybrid coconut palms, the residue analysis results revealed that the pressurized method achieves faster translocation and higher concentrations of cyproconazole in the upper part than the nonpressurized method, even when applying half the volume. After 120 days of application, both methods showed residue-free fruits, ensuring fruit quality. Based on these experimental results, mathematical models were developed to aid in interpreting translocation in the stem. The modeling was extrapolated for taller coconut palms, and a prediction was simulated for coconut leaf disease. The modeling was fitted to the stem translocation data, indicating that the pressurized method performs better in translocation efficiency.
1. Introduction
Good Agricultural Practices (GAP) have required modern and precision agriculture associated with the improvement of more efficient, sustainable, and ecologically safe production systems. Because of this, vegetative endotherapy has become a counterpoint to conventional control techniques [1,2]. The process begins by opening a port on the stem, followed by applying the control product directly into the plant’s vascular system, with distribution occurring due to sap translocation driven by evapotranspiration in the leaves [3,4,5]. This endogenous treatment has the advantages of avoiding product exposure to external factors such as rain, wind, and sun; reducing contamination of the environment; having more outstanding durability of action on the plant; and overcoming the challenge of application in tall trees, in addition to facilitating the treatment of plants in areas of difficult access [2,6]. Vegetative endotherapy has been employed to overcome the difficulties faced in the control of diseases and pests [6], in the correction of nutritional deficiencies in plants [7], in the application of phytohormones [8], and resistance-inducing products [9] to several types of trees, such as arboreal, urban, forest, ornamental, and fruit trees. This method has shown satisfactory agricultural results due to its faster and more durable action. It has attracted increasing attention from researchers and producers of tall and perennial crops for use in large plantations. This practice is safer for the environment, operators, and fruit consumers [10,11].
Endotherapy is not considered a recent technique. Ibn al-Awwam, in the 12th century, used it by introducing substances to induce new flavors, odors, and colors in fruits. Leonardo da Vinci, in the 15th century, reported systemic action after applying an arsenic solution to the trunk of apple trees to scare possible fruit thieves [12]. Innovations in the field and investment in technological resources have stimulated the sector to replace conventional techniques with endotherapy, especially in managing diseases and pests. Its market has grown progressively, although it is still tiny compared to conventional techniques [2,11]. In high-value monoculture systems, such as the coconut palm tree (Cocos nucifera Linn.), large areas are deforested for cultivation, which alters ecosystems and causes damage to biodiversity by stimulating disease outbreaks and agricultural pests [6,13,14]. Phytosanitary products such as pesticides, antibiotics, nutrients, and fertilizers used to protect crops with conventional application techniques increase production but may also damage the environment. The dispersive form of crop spraying techniques may expose workers, animals, and communities close to the treated areas. Pesticide residues can be leached into the soil and reach water sources and groundwater when applied to the soil through rainwater or in the irrigation process [15]. When applied directly on fruits and floral branches in fruit trees, systemic and/or translaminar action products can lead to fruit contamination, affecting food safety and consumer health [16].
Unlike dicotyledonous trees that cannot have their cambium perforated, endotherapy in coconut palms is facilitated by the numerous vascular bundles distributed along its length. For this reason, it allows the stem to be perforated as long as it does not reach its single growth point, the apical meristem [17,18]. Each vascular bundle is composed of xylem and phloem vessels responsible for sap translocation, which occurs due to the pressure gradient generated in the roots. This allows the soil water to be pumped into the leaves.
Coconut palm is highly economically, socially, and environmentally important in cultivated regions. All parts of the plant are used for the most diverse purposes, and its products can supply almost all basic needs for subsistence, being classified as the Tree of Life [19]. However, the demand for fruit drives the main economic interest in the agricultural and industrial sectors, for example, the importance of coconut water in the healthy food segment, given its nutritional qualities and low glycemic index, and of coconut pulp as a raw material for the food, pharmaceutical, and cosmetic industries [20,21]. In Brazil, leaf diseases have been of concern to producers, such as coconut leaf blight caused by the ascomycete fungus Botryosphaeria cocogena Subileau, which usually arises after the incidence of small verrucosis caused by the fungus Camarotella torrendiella (Batista) Bezerra & Vitória and the larger verrucosis caused by the fungus Coccostromopsis palmicola (Speg) K.D. Hyde & P.F. Cannon causes the gradual drying of leaves from the basal leaves. This complex of fungal diseases causes premature death of the leaves, reducing the number of leaves by up to 50%. As the older leaves lose the support of the leaves below in the spiral in which they hang, the sap flow and fruit feeding are interrupted, which causes a total loss of the fruits, leading to significant production losses [22].
The main objectives of this work were to study the translocation of cyproconazole applied by two endotherapeutic methods into coconut palm tree stems. We performed residue analysis using modified QuEChERS (an acronym for “quick, easy, cheap, effective, rugged, and safe”) and LC-MS/MS (liquid chromatography–tandem mass spectrometry) in coconut stem and fruit, established mechanistic mathematical models for explained cyproconazole translocation along the stem, and simulated for predictions of the disease dynamics within the leaf. The model was fitted to the residue analysis data and applied to the coconut palm tree’s different endotherapy protocols, pressurized and nonpressurized.
2. Materials and Methods
2.1. Sampling Sites
The experiments were conducted at the Sococo S/A Agroindustry coconut hybrid plantation located in the municipality of Moju/PA in the northern region of Brazil (11°07′ S and 37°11′ W). The coconut cultivar used was PB 121 (Port Bouet 121—Malaysian yellow dwarf x West African tall), eight years of age, in a complete state of production, and with an excellent phytosanitary appearance. The experiment was conducted between September 2015 (spring) and February 2016 (summer), a significant drought period in the region. Thirty-six plants in the total production state were randomly selected to evaluate cyproconazole translocation in coconut trunk palms from 1.80 m or 2.31 m in height. From those, 24 plants were selected to analyze the concentration of cyproconazole at different points using modified QuEChERS as the extraction method and LC-MS/MS for analyses proposed by Ferreira et al. [16] above the application point up to the base of the leaves. Furthermore, 12 others analyzed cyproconazole residues in the commercial components of coconut fruits, i.e., water and pulp, using modified QuEChERS and LC-MS/MS proposed by Ferreira et al. [23].
2.2. Cyproconazole Solution for Endotherapeutic Applications
The commercial fungicide selected was Alto 100 (Syngenta, Basel, Switzerland), containing the active ingredient cyproconazole (10%, w/v) as well as inert ingredients (102% w/v). Table S1 shows the characteristics and physicochemical properties of cyproconazole. The adjuvant Break-thru® (Evonik, Essen, Germany) was added to a pure concentration of cyproconazole [11] to potentiate product translocation into the trunk, based on previous studies [9]. Table 1 shows the preparation of cyproconazole solutions used in the respective treatments.

Table 1.
Preparation of the solutions used in pressurized and nonpressurized endotherapeutic treatments.
In both treatments, formulations were prepared with dilutions made in proportion to a 1:1 (v/v) ratio of the commercial product cyproconazole in Break-thru®. After formulation was prepared by dilution, a volume of 10 mL was applied in the pressurized treatment, and 20 mL was used in the non-pressurized treatment.
2.3. Endotherapeutic Systems
The experiments used the following injection methods: (a) nonpressurized treatment, which consisted of using a machine with a sharp spiral drill bit to open the trunk, followed by the application of the solution containing cyproconazole in this hole in each plant with the aid of a polyethylene syringe; (b) pressurized treatment, using the commercial equipment Bite Infusion® version Di Palma (Figure S1), consists of a blade for opening the trunk driven by a sliding hammer coupled to the equipment system that forced the introduction of the blade into the trunk. The blade is hollow with small holes in its extension inside the trunk through which the solution was introduced under pressure exerted through the syringe plunger. The blade was only removed when the entire syringe content was applied.
2.4. Application and Sample Collection—Field Trials
The application point on coconut palm trunks was standardized and established at 80 cm above the ground to contemplate the most significant number of vascular bundles during the application and become more comfortable for the operators. In the nonpressurized treatment, the entry hole is made in a downward slope at an angle of 45 degrees about the trunk position, approximately 15 cm deep and 2 cm wide. After being filled by the product, it is sealed with a small piece of wood. The pressurized treatment introduced the equipment blade into the coconut palm trunk.
The experimental design consisted of three plants for treatment and four sample collection intervals of 2, 15, 30, and 45 days after application, resulting in 12 coconut palms for the nonpressurized treatment and 12 for the pressurized treatment. These intervals were established to standardize the days after the application of cyproconazole formulations through spatiotemporal translocation. The standardization of sample collections for translocation analysis at each sampled interval was set at 50 and 100 cm above the application point and in four and five holes around the trunk of the coconut palm. At each collection interval, three new plants were used since the vegetal tissue was removed at the collection points, disrupting many vascular bundles responsible for the translocation of the internal fluids of the plants. Samples were collected with a drill machine using a 10 mm drill bit with holes 10–15 cm deep. The drill bit was disinfected after each sample was taken and between palms. All samples were stored in individual sterile plastic bags, identified, and refrigerated in a thermal box containing bags of frozen water to minimize sample oxidation. To be safe, sent to the laboratory for freezing (Figure S2). At the end of the work, all the holes were sealed and treated with vegetable tar to avoid attracting pests or microorganisms.
Samples for fruit residue analysis were collected from (a) bunch nine on leaf 19, fruits six months after fecundation and intended for the consumption of coconut water, the maturity stage in which the coconut water undergoes enzymatic reactions starting pulp formation, and (b) dry coconut bunch, fruits with 12 months of maturity addressed mainly to industrial uses, such as copra for oil extraction or fresh pulp for the food industry and domestic consumption.
The fruit samples were collected at intervals of 45 days, 90 days, and 120 days after fungicide applications. Three fruits from these bunches were harvested for sample collection, and the coconut water and pulp were homogenized separately, corresponding to one sample for each palm. The coconut water was collected through a hole in the fruit, transferred to a beaker, and then placed in sterilized polyethylene bottles. The coconut pulp was collected with a spatula, and each sample was transferred to a sterile plastic bag.
The sampled fruits for residue analyses were continuously collected in bunch 19 (fruits suitable for coconut water consumption) and the fully matured bunch with fruits ideal for industrial purposes. The fruits harvested in bunch 19 at 45 days after cyproconazole treatment was in a position of bunch 17 during the time of solution application. Those harvested at 90 days were in the position of bunch 15, and those harvested at 120 days were in the position of bunch 14. For the dry coconut bunch, the fruits harvested after 45 days were bunches 20 during the application of the cyproconazole solution, those harvested at 90 days were bunches 18, and those harvested at 120 days were bunches 17.
All stem, coconut water, and pulp samples were maintained in a freezer at a temperature of −17 °C, interrupting the oxidation process, and were thawed only for analysis.
2.5. Residual Analysis
After collection, all samples were frozen, packed, and prepared for shipment in thermal boxes and sent to the Institute of Chemistry at the University of Campinas, Campinas-SP, Brazil. The cyproconazole concentration was determined through residue analyses developed for the stem [23], and fruits, coconut water, and pulp were evaluated separately [16] using modified QuEChERS and LC-MS/MS. The conditions of the analyses were the same as those in references [23] and [16].
For all pesticides, the instrumental limits of detection (LOD) and limits of quantification (LOQ) were 0.75 and 2.5 μg L−1, respectively. The LOQs of the method was satisfactory for quantifying pesticides considering the maximum residue limits (MRL) adopted by regulatory agencies such as the European Union. LOQ for the coconut water and pulp were spiked from the matrices ‘free of interference or blank’ at a concentration of 10 μg kg−1 and 40 μg kg−1 for the stem for all pesticides and had recovery values between 50–120% and RSD below 20%. Three analytical curves were constructed from the standard solution in the extract of the “blank” matrices (stem, pulp, and coconut water), with each matrix spiked at eight concentration levels that varied to concentrations 2.5–250.0 μg L−1 for the pulp and coconut water, and for the stem at concentrations of 10.0–1000.0 μg L−1, with linearity from 0.99.
2.6. Mathematical Modeling
Modeling the dynamics of cyproconazole translocation along the trunk (trunk model).
We developed a mathematical model based on partial differential equations (PDEs) to describe cyproconazole translocation along the stem. The model assumes that cyproconazole inside the plant stem is present in two different states: bioconcentrated and bioavailable. The bioconcentrated state represents the product concentration still accumulated in high concentrations within the vegetal tissues close to the application point. The bioavailable state represents the product concentration delivered to the vascular bundles and is now mixed with the sap and subject to translocation due to sap flow. The following PDE system gives the model:
where w(z,t) and u(z,t) represent the distributions (measured in mL/cm) of bioconcentrated and bioavailable cyproconazole along the trunk, respectively, at time t (measured in days) and at height z∈[0,h] (measured in cm); h is the coconut palm height.
The model assumes the following hypothesis: (i) the initial cyproconazole concentration is zero, and the application of bioconcentrated cyproconazole is described by a function i(z,t), which depends on the application method (pressurized or nonpressurized) and is presented below; (ii) the bioconcentrated cyproconazole becomes bioavailable at a rate kw; (iii) cyproconazole has a natural chemical degradation with rate m; (iv) the bioconcentrated and bioavailable cyproconazole distributions diffuse along the trunk with diffusion coefficients dw and d, respectively; (iv) due to the sap flow, bioavailable cyproconazole is subject to transport along the trunk with velocity v(z,t). To model v(z,t), we follow the cohesion-tension or Dixon-Joly theory (details below).
The model assumes zero-flux boundary conditions for bioconcentrated cyproconazole at the trunk bottom and top. For bioavailable cyproconazole, we assume zero-flux at the trunk bottom and absorbent conditions at the trunk top, reflecting that the bioavailable cyproconazole reaches the trunk top and flows to the crown leaves through the vascular bundles. These boundary conditions are written as , , , and We observe that the bioavailable cyproconazole flux at a point z is given by
According to the cohesion-tension or Dixon-Joly theory, the sap molecules are driven toward regions of lower pressure due to evaporation and transpiration occurring in the leaves, which pushes the sap from the roots (z = 0) up to the tree crown (z = h) due the adhesion to the vascular bundles’ walls and capillarity. We assume that the transport velocity v(z,t) for bioavailable cyproconazole results from the sap flow and is modeled using Darcy’s Law, where p(z,t) represents the pressure at height z and time t, pz is the pressure gradient, and k1 is a positive constant.
For the sake of simplicity, we assume a linear profile for the pressure , ranging from a minimum at the tree crown to a maximum at the roots, i.e., . Thus, the cyproconazole transport velocity is , where . Note that is not equal but proportional to the sap flow velocity, since the cyproconazole molecular weight and size, associated with the diverse physical barriers along the xylem, decrease its velocity in comparison to the sap velocity.
The cyproconazole application is described by the expression where represents the initial dose, is the application time, describes the application method (see below), and is given by
and describes the application point: a hole centered at height z0 and width b; here, H(z) is the unit-step function. In the pressurized method, the mixture with cyproconazole is applied inside the trunk with external pressure from the syringe plunger. For this case, we assume that the entire cyproconazole quantity enters the trunk in a single instant, i.e., the application is described by an impulse, , where is the Dirac delta function. On the other hand, in the nonpressurized method, the mixture is applied with a syringe in this orifice. In this case, the effective entry of cyproconazole is slow since it needs to be absorbed from the orifice to the trunk. Thus, the nonpressurized method is described by where is related to the time spent for cyproconazole entering the trunk; and is the unit step function.
With the above hypotheses, the PDE system modeling the cyproconazole dynamics along the trunk becomes
The following model parameters were set to fixed values obtained from (i) field experiments data, (ii) knowledge of the physical characteristics of the coconut palm, or (iii) after several simulations and tests of the model: height of application point, m; hole width, m; quantity of cyproconazole applied, L in the pressurized method and L for the nonpressurized; application time, (12 PM, day 0); injection constant for the nonpressurized method, (half of the cyproconazole enters the trunk within 6 h).
Five parameters were not fixed a priori and were fitted to the experimental data: . A parameter estimation method was used to minimize the quadratic error between the model simulations and data (cyproconazole measured at days 2, 15, 30, 45). Due to the computational cost and a high number of free parameters, a search method based on a Monte Carlo strategy was adopted. Initially, using several test simulations for each of the 5 parameters, we determined a set or an interval of plausible values. For the least sensitive parameters , and , we defined a discrete set of search values: , , and . Note that , where is the mean time necessary for half of the bioconcentrated cyproconazole to become bioavailable, and , where is the mean time necessary to half of the cyproconazole to be chemically degraded. For parameters and , which are the most sensitive in the model dynamics, we defined the following search intervals: and . Thus, the search set for parameter fits is . In the search method, we sorted parameter tuples and, for each , we simulated the model and calculated the quadratic error between field data and model simulations, given by
In the above expression, and are values related to the data collected from field experiments; is the cyproconazole density (mL/cm) simulated at position and time ; is the cyproconazole density in units of µg/L measured at position and time ; and is a conversion factor from µg/L to mL/cm, where mL/(µg/L) was obtained by stoichiometric calculations and m is the diameter of the hole made in the trunk.
After simulating the model for each parameter tuple and calculating , the optimal parameter set was chosen, i.e., such that . To measure the fit quality, the determination coefficient was calculated, for each
where
Thus, for each coconut palm set for which we collected data, optimal parameter values were found, which provided the best fit of the model to the data; these optimal values and corresponding determination coefficients are shown in Table S2. The fitted simulations are presented in Figure S3A (pressurized) and Figure S3B (nonpressurized) for each of 6 sets (3 for each application method).
The field data were collected using coconut trees 2 m tall. Using the adjusted parameter values, the model was simulated for different tree heights (3 m, 5 m, 10 m, 15 m), and the translocation profiles predicted by the model for trees with these heights were obtained as follows. The cyproconazole flow (mL/day) reaching the trunk top and passing to the leaves is calculated by setting in Equation (1) for the bioavailable cyproconazole flow, i.e.,
Cyproconazole delivery rate for both methods and different tree heights. We observe that the translocation is faster in the pressurized method, even though this method uses half the cyproconazole quantity of the nonpressurized method. The percentage of the initial cyproconazole that effectively reaches the tree crown after days is calculated by
Calculating for each method and each of the four tree heights, we found that cyproconazole delivery was consistently lower in the nonpressurized method. We suppose this happens because cyproconazole takes more time to be absorbed and moved along the trunk in the nonpressurized method and is thus more subject to natural chemical degradation inside the trunk. Additionally, the taller the tree is, the more time it takes for cyproconazole to reach the treetop.
2.7. Modeling the Disease Dynamics along the Leaves (Leaf Model)
We present a model for the dynamics within each leaf (leaf model), where the fungi causing the coconut leaf blight disease are potentially expanding. We assume that once the translocated cyproconazole reaches the treetop, it enters the leaves through the vessels connecting the trunk and leaf and then confers protection to the healthy leaflets remaining in the leaf.
The leaf model is based on a mixed partial and ordinary differential equations system. For the sake of simplicity, we considered a single leaf, idealized as a line segment with a length centimeters, where the position is denoted by , with representing the side connected to the tree crown and representing the opposite side. Within the leaf, we consider five populations (or densities) varying with time and position : (i) the fraction of healthy leaflets, i.e., the leaflets in the natural state, subject to burn by the fungi, described by ; the fraction of burnt/diseased leaflets, described by ; the fraction of protected leaflets, which are the healthy leaflets that received protection by the cyproconazole effect, described by ; the fungal density, described by ; and the cyproconazole density within the leaf, described by
The following hypothesis is assumed for the dynamics of the fungal population: (i) the fungi proliferate according to logistic growth with carrying capacity ; we normalize so that denotes the fungal density; (ii) the fungi need to colonize the healthy unprotected leaflets to proliferate, therefore, its proliferation rate depends on the density of healthy leaflets and is given by ; (iii) the fungal population propagates itself along the leaf through diffusion mediated by the burn of healthy leaflets; thus the diffusion coefficient for the fungal population is proportional to the density of burnt leaflets, . Hence, the dynamics of the fungal population are described by the following PDE:
The following hypotheses are assumed for leaflet populations: (i) the healthy leaflets are burnt with rate by the fungi present; (ii) in the presence of cyproconazole, the healthy leaflets pass to the protected state at a rate ; (iii) the protected leaflets lose their protection after a mean time , returning to the state of nonprotected healthy leaflets. Therefore, the dynamics of the leaflet populations are described by the following ODEs:
The following hypotheses are assumed for cyproconazole dynamics: (i) cyproconazole diffuses along the leaf through the living leaflets; thus, the cyproconazole diffusion coefficient is proportional to the density of living leaflets, healthy or protected, and is given by ; (ii) the cyproconazole density within the leaf has a natural degradation rate given by . Therefore, the cyproconazole dynamics within the leaf are described by the following PDE:
The leaf model consists of Equations (4)–(8) together with the following boundary and initial conditions: the cyproconazole entering the leaf at is described by , where is the cyproconazole flow at the trunk top, described by Equation (2); the remaining boundary conditions are of zero-flux type, The initial conditions for the model are as follows: initially, there is no cyproconazole at the leaf, ; the initial fungal density is ; the initial distribution for burnt leaflets is ; the initial distribution for healthy leaflets is given by the fraction that is not burnt, initially, there are no protected leaflets, . Note that the rate of change for the total leaflet density is zero, i.e., , and thus the total leaflets density remains constant with time, , while only changes between the states take place.
Due to a lack of data, it is difficult to estimate the parameter values for the leaf model. After simulating it with different values, we found a set of values for which the model reasonably represents field observations, i.e., fungal invasion and total leaf burn after approximately 90 days in the absence of cyproconazole application. The parameter values are as follows: for the cyproconazole diffusion coefficient and natural degradation rate , we adopted the same value obtained in the trunk model, given by the values of and (see Table S2); the fungal proliferation rate was set to ; the fungal diffusion coefficient was set to ; the rate of burnt of healthy leaflets was set to ; the rate of gain of cyproconazole protection of healthy leaflets was set to ; the rate of loss of cyproconazole protection of protected leaflets was set to
The simulations of the leaf model are presented in Figure S4. In the nontreated situation (Figure S5A), the leaf was burned entirely in 90 days. When treatment is applied (we simulate this with the trunk model), cyproconazole enters the leaf after some days and blocks fungal invasion and subsequent burning of the entire leaf (Figure S5B,C).
To assess the protection provided by cyproconazole application, we calculated, for each model simulation, the fraction of burnt leaflets present at day 90 after application. This amount is given by
The higher the value of , the lower the cyproconazole protection effect on the leaflets. The value of was compared for different tree highs and methods.
3. Results and Discussions
Cyproconazole is a systemic broad-spectrum fungicide with different effects on nontarget organisms, environmental fate, and toxicity activity. Its systemic, associated with its physical-chemical properties, gives cyproconazole a high capacity for bio-accumulation. It shows nondissociation, moderate solubility in water, and stability at pH 4–9, which are suitable product characteristics to be selected for this study. It is moderately soluble in water, has a high risk of leaching into groundwater, and can persist in both soil and water systems. It is moderately toxic to most aquatic organisms, earthworms, and honeybees but highly toxic to birds [24]. The adjuvant used in the solution was an organosilicone permeabilizing agent with penetrating action [11]. Cyproconazole applied directly to 14 axils of coconut palm leaves and by endotherapy showed satisfactory results in preventing and controlling foliar diseases in work previously proposed by Siqueira [25] and Silva [26]. Based on these results, this fungicide was selected for this translocation study and fruit contamination assessment to support these agronomic efficiency results. However, it is essential to emphasize that LC-MS/MS analyzed only concentrations of cyproconazole. Cyproconazole and adjuvant solutions for endotherapeutic applications were prepared from commercial products.
After the results of concentrations in µg kg−1 from coconut stem samples were collected above the application point on different days, it was possible to build the mathematical model to facilitate the interpretation of the results performed in field trials. Additionally, it was possible to extrapolate the model to taller coconut palm trees and make a prediction to simulate the disease in the leaves.
3.1. Stem Translocation—Modeling Based on Field Trials and LC-MS/MS
Cyproconazole translocation along the stem was described using a system of advection-diffusion partial differential equations explained by the theory of Dixon and Joly (1894), which is the most accepted theory using the physicochemical properties of water known as cohesion-tension-adhesion [27,28,29]. The model considers two movement stages of the pesticide inside the stem. Bioconcentrated cyproconazole accumulated and adsorbed in the stem tissues, and bioavailable cyproconazole entered the vascular bundles and was subject to translocation through the sap flow. The model parameters were fitted using the pesticide concentration data collected in field trials with 2 m tall coconut palms (Table S2). The resulting model simulations show that in the pressurized method, the product quickly passes from the bioconcentrated to the bioavailable state, leading to a faster translocation and higher translocated concentrations in comparison with the nonpressurized method, for which the model predicts a slow transition to the bioavailable state, as well as product saturation at the point of application (smaller availability rate kw, Table S2, compare the right panels on Figure 1). Figure 1 shows the optimal fits for the “mean trees” generated using the mean cyproconazole data of the three sets in each application method.
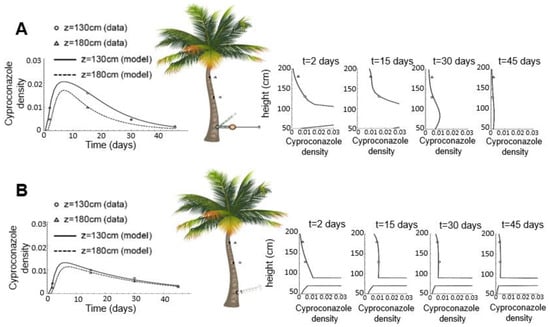
Figure 1.
“Stem Model” simulations fitted to plant average data using the pressurized (A) and nonpressurized (B) methods. Triangles and circles represent the results collected in the field, and lines represent the concentrations predicted by the model. On the left, graphs show the cyproconazole concentration over time at 130 cm and 180 cm above the ground. On the right, graphs show the cyproconazole concentration profile along the stem at days 2, 15, 30, and 45 after application.
Higher cyproconazole losses were observed in the nonpressurized method. Despite the simple operation of this method, the results indicated that the lack of pressure slows product absorption and promptly precipitates it at the point of entry, thus requiring a larger volume in the application and becoming more expensive for producers. Since the drill machine damages the internal bundles, this technique makes the application point susceptible to attack by diseases and pests and hinders successive applications in necrotic areas.
3.2. Stem Translocation—Modeling Extrapolation for Taller Palms
Cyproconazole delivery to the canopy was calculated using the model fit for plants of different heights (Figure 2). The palms with 3 m and 5 m in the pressurized method showed the highest release rate of cyproconazole for the leaves, which occurred up to 15 days after application, followed by a decrease in delivery until 60 days, indicating that approximately 95% of the applied concentration was released to the leaves, while the other 5% was naturally degraded (Figure 2A and Figure S3A). The results for the nonpressurized method indicated that part of the applied product remained concentrated at the entry points and slowly became bioavailable to be translocated to the leaves, leading to an elongated and flattened translocation profile (Figure 2B and Figure S3B).
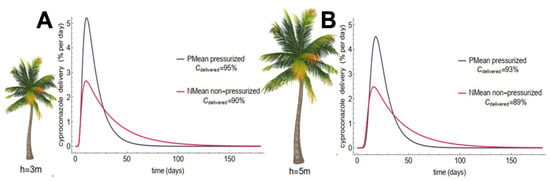
Figure 2.
Dynamics of cyproconazole translocation from stem to leaves for coconut palms of different heights using pressurized (A) and nonpressurized methods (B). The release rate was calculated using Equation (2) (Video S1). The percentage of cyproconazole applied to the leaves after 180 days for each simulation is indicated by the cdelivered and was calculated using Equation (3) (Video S2).
Due to the release delay and the natural degradation that occurred over time, higher cyproconazole losses were observed in the nonpressurized method (compare values of in Figure 2A,B). Together, these factors led to an expression trend in the translocation profile of the pressurized method, which used half the volume applied in the nonpressurized method. The bioavailability of the product’s translocation showed that the speed with which the systemic active ingredient reaches the canopy strongly depends on the sap flow and the application pressure. This finding certifies that the pressure exerted on the application methods is a functionally essential commitment for endotherapy in coconut palms and promotes higher dissipation rates with a longer fungicide life (Figure S3A). The pressurized method showed the best results, giving a comprehensive view of the treatment efficiency with the advantages of applying a smaller volume, larger concentrations, and speedier translocations. The highest release rate from the stem to the leaves, in trees at 3 m and 5 m, occurred up to 15 days after application, followed by a decrease in the release until 60 days.
3.3. Leaf Translocation—Simulation/Prediction for Disease in Coconut Leaf
Plants do not have a heart as a muscle to pump sap throughout their vascular system, so the leaves play this role [30]. The coconut palm leaves are organized into five spirals, and the arrangement of the leaves in the stem is five leaves in each spiral, synchronized by a mathematical phenomenon known as the Fibonacci Sequence, in which any two consecutive leaves subtend a 137.5° angle (Figure S5). This sequence demonstrates the demand by this palm species to find the best angle for the use of sunlight so that the photosynthetic surfaces do not overlap in the capture of energy. For each new leaf formation in the region of the plant’s meristem, a bunch is formed with its vascular bundles distributed in the main branch and floral branches following a spiral pattern [17]. For these reasons, leaf diseases and fruit quality greatly concern producers.
Cyproconazole entering through the leaves spreads and tends to protect the healthy leaflets. To understand the effect of cyproconazole on disease progression, we developed a second mathematical model. The leaf model considered sap movement into the vessels and the fungus population on leaves since this pathogen reproduces according to the availability of healthy leaflets and tends to disperse within leaves as the healthy leaflets become burnt. This model describes (i) the dynamics of the disease in the leaves considering scenarios with and without the application of cyproconazole (Figure 3); (ii) the dynamics at trees of different heights (Figure 2), and (iii) the effect of cyproconazole protection to estimate the percentage of burnt leaflets on the leaf 90 days after pesticide application (Figure 4). Comparing both application methods, the modeling results show that taller trees have more burnt leaflets 90 days after cyproconazole application due to the longer time required for cyproconazole to reach the tree canopy pressurized method offers similar protection than the nonpressurized method for trees with smaller than 5 m. However, it is essential to highlight that the pressurized method requires less product than the nonpressurized method. For coconut palms over 5 m, it is vital to assess the need to adjust the dosage volume for both methods. The active translocation associated with the passage mechanisms of the product crossing the barriers of the tissues of the vascular bundles is characterized by a transfer of molecules against gravity and its concentration gradient. The distribution of the product through the sap flow along the coconut palm stem alters the product concentration in its site of action, which may interfere with its effectiveness (Videos S3–S6) [28,31].
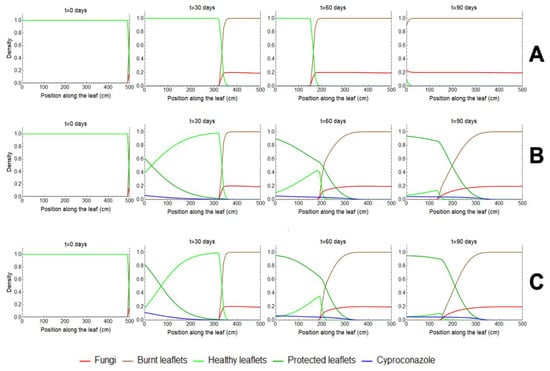
Figure 3.
“Leaf model” simulations. Each panel shows snapshots of the leaf profile at a given time, with the leaflet/fungi/cyproconazole densities varying along the leaf. (A) The first row shows the leaf for the nontreated situation, i.e., the “leaf model” without cyproconazole entering the leaf. (B,C). The second and third rows showed leaf snapshots when 10 mL of cyproconazole was applied at day 0 with the nonpressurized (B) or pressurized (C) methods for a 5 m tall tree. In all panels, the cyproconazole densities are multiplied by 103.
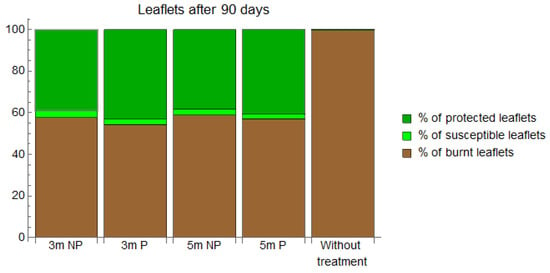
Figure 4.
Percentage of burnt (brown), susceptible (light green), and protected (dark green) leaflets at day 90 after standard cyproconazole application for different methods of application (NP = nonpressurized, P = pressurized) and palm heights (3 m and 5 m).
The simulation results show that taller palms have more burnt leaflets 90 days after cyproconazole application due to the longer time required for cyproconazole to reach the tree canopy. The pressurized method offers similar protection to the nonpressurized method for palms smaller than 5 m. However, these predicted data need to be confirmed after experimental field trials. The magnitude of the effects predicted by our models depends heavily on the cultivated area, the higher temperature of the day, the greater plant transpiration, and the better bioavailability of the product for dynamic translocation in the sap [2,32,33].
3.4. Cyproconazole Residue in Coconut Fruit Treated by Endotherapy
The maturity phase of the sampled bunches was strategically selected since their fruits are intended for human consumption. This study assesses fruit contamination of cyproconazole residues and may help guarantee food security.
Cyproconazole may contaminate the commercial components of coconut palm nuts (coconut water and pulp). Residues found in the coconut water and coconut pulp were below the limit of quantification (LOQ) of the analytical method and the maximum residue limit (MRL) established by the European Union (EU) [34] (Figure S6). These results suggest three possibilities: (i) the coconut palm is vascularized, and the vascular bundles communicate by diluting the concentrations along the stem, leaves, and inflorescence (Figure S7); (ii) the physicochemical properties of cyproconazole (log Kow 2.90, and pKa no dissociation) and the formulation of the commercial product was not developed for phloematic translocation, only in the xylem [17]; or (iii) cyproconazole did not reach the fruit of the coconut palm because the elaborate sap that fills the fruit cavity or the embryonic sac passes through a single bundle in the functional pore that nourishes the embryo until six months of age (Figure 5). For this reason, the probability of the pesticide applied by endotherapy entering the fruit cavity is small, characterizing the peculiarity of this fruit [35]. However, pesticide residues are detected in coconut fruit treated by the spraying method, which increases the direct contact of the product with the surface of the leaves, floral branches, and fruits [22,23,36].

Figure 5.
Scheme of the application of cyproconazole to coconut palm, showing translocation through the vascular bundles following the flow of sap from the roots/soil to the leaves, without contamination of the fruit.
Cyproconazole translocation-transpiration cycle in coconut palms occurs through the sap in the vascular bundles upward to the leaves, with non-contamination of the fruit because of the physiology of the palm.
Studies using the endotherapeutic treatment in fruit trees showed the detection of pesticides in apples [6], penicillin G in citrus [37], and insecticides in avocados [38], indicating the importance of evaluating residues due to different translocation dynamics in other fruit trees.
4. Conclusions
Endotherapeutic techniques have potential applications for extended use in any perennial crop. Although the nonpressurized method was simpler to execute, a larger opening in the stem was necessary for applying the product, causing more significant damage to the stem than the pressurized method. Based on residue analyses, our experimental field results proved through the translocation study that pressurized endotherapy was faster using fewer products than the nonpressurized method. In addition, for both endotherapeutic methods, coconut fruits evaluated up to 120 days after applications showed residue-free fruits. The spatial-temporal translocation of cyproconazole in coconut palms documented here presents the possibility of reducing environmental impacts by replacing the techniques of conventional product application methods.
While the mathematical model proposed was based on general hypotheses on chemical translocation mediated by sap flow, it was evaluated with numerical parameter values considering cyproconazole and coconut properties. Therefore, the prevailing model structure (equations) has the potential to be applied to other types of fruit trees or chemical compounds but takes into account parameter values for the considered cases.
Incentives to invest in research with endotherapeutic approaches will result in a change in perspectives for more sustainable practices in agriculture.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/horticulturae8121099/s1, Figure S1: The procedure was performed in pressurized endotherapeutic treatment using Bite Infusion® equipment.; Figure S2: Strategy of heights of application points and sample collections; Figure S3A: Model fits and data for trees where the pressurized method was applied; Figure S3B: Model fits and data for trees where the nonpressurized method was applied; Figure S4: “Leaf model” simulations; Figure S5: Profile of the phyllotaxy of the coconut palm tree with a view of the leaf distribution from the top to the basal leaves based on the Fibonacci Sequence; Figure S6: Chromatograms of the selected ions obtained by UHPLC–MS/MS.; Figure S7: Stem tissue images; Table S1: Physicochemical properties and main characteristics of cyproconazole; Table S2: Optimal parameter values fitted for each coconut tree title; Video S1: Simulation for cyproconazole after application in the stem for 3 m tall coconut palm up to 90 days, being pressurized on the left and nonpressurized on the right; Video S2: Simulation for cyproconazole after application in the stem for 5 m tall coconut palm up to 90 days, being pressurized on the left and nonpressurized on the right; Video S3: Simulation for cyproconazole in 3 m tall coconut palm to 90 days using the pressurized method; Video S4: Simulation for cyproconazole in 3 m tall coconut palm to 90 days using the nonpressurized method for the stem; Video S5: Simulation for cyproconazole in 5 m tall coconut palm to 90 days using the pressurized method for the stem in the graph on the left; Video S6: Simulation for cyproconazole in 5 m tall coconut palm to 90 days using the nonpressurized method for the stem in the graph on the left.
Author Contributions
Conceptualization and methodology: J.A.F., A.C.F., J.M.S.F., C.B.G.B. and P.M.P.L.; software, A.C.F.; validation, J.A.F. and A.C.F.; formal analysis and investigation, J.A.F. and C.B.G.B.; resources, J.A.F., C.B.G.B. and P.M.P.L.; data curation, J.A.F. and A.C.F.; writing—original draft preparation, J.A.F., A.C.F. and J.M.S.F.; writing—review and editing, A.C.F., J.M.S.F., C.B.G.B. and P.M.P.L.; supervision, J.M.S.F., C.B.G.B. and P.M.P.L.; project administration, C.B.G.B.; funding acquisition, J.A.F., C.B.G.B. and P.M.P.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by São Paulo Research Foundation—FAPESP, grant number 2012/18318-4, Conselho Nacional de Desenvolvimento Científico e Tecnológico—CNPq by 309363/2018-7, Instituto Nacional de Ciência e Tecnologia—INCT/Bioanalítica, grant numbers: FAPESP/INCT 2014/50867-3, CNPq 465389/2014-7.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
J.A.F. thanks the São Paulo Research Foundation—FAPESP (2012/18318-4) for the Ph.D. scholarship. C.B.G.B. thanks Conselho Nacional de Desenvolvimento Científico e Tecnológico—CNPq (309363/2018-7) for research fellowship and Instituto Nacional de Ciência e Tecnologia—INCT/Bioanalítica for funding support (grant numbers: FAPESP/INCT 2014/50867 CNPq 465389/2014-7). We thank Hyun Yang for initial suggestions for the mathematical models, Carol Collins (in memorian) for valuable comments and suggestions, Lais da Silva for comments and suggestions, and Maksuel Fernandes for sending us cytological sections of the coconut palm.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Piñeiro, V.; Arias, J.; Dürr, J.; Elverdin, P.; Ibáñez, A.M.; Kinengyere, A.; Opazo, C.M.; Owoo, N.; Page, J.R.; Prager, S.D.; et al. A scoping review on incentives for adoption of sustainable agricultural practices and their outcomes. Nat. Sustain. 2020, 3, 809–820. [Google Scholar] [CrossRef]
- Berger, C.; Laurent, F. Trunk injection of plant protection products to protect trees from pests and diseases. Crop. Prot. 2019, 124, 104831. [Google Scholar] [CrossRef]
- Gardner, C.L.; da Silva, D.R.; Pagliai, F.A.; Pan, L.; Padgett-Pagliai, K.A.; Blaustein, R.A.; Merli, M.L.; Zhang, D.; Pereira, C.; Teplitski, M.; et al. Assessment of unconventional antimicrobial compounds for the control of ‘Candidatus Liberibacter asiaticus’, the causative agent of citrus greening disease. Sci Rep. 2020, 10, 5395. [Google Scholar] [CrossRef] [PubMed]
- Montecchio, L. A venturi effect can help cure our trees. J. Vis. Exp. 2013, 80, e51199. [Google Scholar] [CrossRef] [PubMed]
- Beerling, D.J.; Franks, P.J. The hidden cost of transpiration reconfigurable colloids. Nature. 2010, 464, 495–496. [Google Scholar] [CrossRef]
- VanWoerkom, A.H.; Aćimović, S.G.; Sundin, G.W.; Cregg, B.M.; Mota-Sanchez, D.; Vandervoort, C.; Wise, J.C. Trunk injection, An alternative technique for pesticide delivery in apples. Crop. Prot. 2014, 65, 173–185. [Google Scholar] [CrossRef]
- Hesami, A.; Jafari, N.; Shahriari, M.H.; Zolfi, M. Yield and Physico-Chemical Composition of Date-Palm (Phoenix Dactylifera) as Affected by Nitrogen and Zinc Application. Commun. Soil Sci. Plant. Anal. 2017, 48, 1943–1954. [Google Scholar] [CrossRef]
- Corina, V.A.; Dempsey, D.A.; Klessig, D.F. Salicylic acid, a multifaceted hormone to combat disease. Annu. Rev. Phytopathol. 2009, 47, 177–206. [Google Scholar] [CrossRef]
- Hu, J.; Jiang, J.; Wang, N. Control of citrus huanglongbing via trunk injection of plant defense activators and antibiotics. Phytopathology 2018, 108, 186–195. [Google Scholar] [CrossRef]
- Byrne, F.J.; Almanzor, J.; Tellez, I.; Eskalen, A.; Grosman, D.M.; Morse, J.G. Evaluation of trunk-injected emamectin benzoate as a potential management strategy for Kuroshio shot hole borer in avocado trees. Crop. Prot. 2020, 132, 105136. [Google Scholar] [CrossRef]
- Ferreira, J.A.; Ferreira, J.M.S.; Talamini, V.; Lins, P.M.P.; Farias, S.C.C.; Bottoli, C.B.G. Translocation of pesticides in coconut palm by endotherapy with the addition of different adjuvants. Ciência E Nat. 2020, 42, e56. [Google Scholar] [CrossRef]
- Ainsworth, G.C. Introduction to the History of Plant Pathology, 1st ed.; Cambridge University Press: Cambridge, UK, 1981. [Google Scholar]
- Chihaoui-Meridja, S.; Harbi, A.; Abbes, K.; Chaabane, H.; La Pergola, A.; Chermiti, B.; Suma, P. Systematicity, persistence and efficacy of selected insecticides used in endotherapy to control the red palm weevil Rhynchophorus ferrugineus (Olivier, 1790) on Phoenix canariensis. Phytoparasitica 2020, 48, 75–85. [Google Scholar] [CrossRef]
- Maso, E.D.; Linaldeddu, B.T.; Fanchin, G.; Faccoli, M.; Montecchio, L. The potential for pesticide trunk injections for control of thousand cankers disease of walnut. Phytopathol. Mediterr. 2019, 58, 73–79. [Google Scholar] [CrossRef]
- Carles, C.; Bouvier, G.; Lebailly, P.; Baldi, I. Use of job-exposure matrices to estimate occupational exposure to pesticides A review. J. Expo. Sci. Environ. Epidemiol. 2016, 27, 125–140. [Google Scholar] [CrossRef]
- Ferreira, J.A.; Talamine, V.; Facco, J.F.; Rizzetti, T.M.; Ferreira, J.M.S.; Oliveira, F.A.; Prestes, O.D.; Zanella, R.; Martins, M.L.; Adaime, M.B.; et al. Determination of pesticide residues in coconut tree trunks by modified QuEChERS method and ultrahigh-performance liquid chromatography coupled to triple quadrupole tandem mass spectrometry. Anal. Methods 2015, 7, 4237–4245. [Google Scholar] [CrossRef]
- Davis, T.A.; Sudasrip, H.; Darwis, S.N. Coconut Research Institute Manado Indonesia, An Overview of Research Activities; CRI: Manado, Indonesia, 1985. [Google Scholar]
- Ferry, M.; Gomez, S. Assessment of risks and potential of injection techniques in integrated programs to eradicate the red palm weevil, Review and new perspectives. Fruits 2014, 69, 143–157. [Google Scholar] [CrossRef]
- Foale, M.A.; Nguyen, Q.T.; Adkins, S.W. iCocos Nucifera/i Coconut. In Biotechnology of Fruit and Nut Crops, 2nd ed.; Litz, R.E., Pliego-Alfaro, F., Hormaza, J.I., Eds.; CAB eBooks—CABI: London, UK, 2020; p. 79. [Google Scholar] [CrossRef]
- Yalegama, L.L.W.C.; Karunaratne, D.N.; Sivakanesan, R.; Jayasekara, C. Chemical and functional properties of fiber concentrates obtained from byproducts of coconut kernel. Food Chem. 2013, 141, 124–130. [Google Scholar] [CrossRef]
- Ferreira, J.A.; Santos, J.M.; Breitkreitz, M.C.; Ferreira, J.M.S.; Lins, P.M.P.; Farias, S.C.; de Morais, D.R.; Eberlin, M.N.; Bottoli, C.B.G. Characterization of the lipid profile from coconut (Cocos nucifera L.) oil of different varieties by electrospray ionization mass spectrometry associated with principal component analysis and independent component analysis. Food Res. Int. 2019, 123, 189–197. [Google Scholar] [CrossRef]
- Warwick, D.R.N.; Talamini, V.; Leal, E.C.; Ram, C. Principais Doenças. In A Cultura do Coqueiro no Brasil, 3rd ed.; Ferreira, J.M.S., Warwick, D.R.N., Siqueira, L.A., Eds.; Embrapa: Brasília, Brazil, 2018; p. 447. [Google Scholar]
- Ferreira, J.A.; Ferreira, J.M.S.; Talamini, V.; Facco, J.d.F.; Rizzetti, T.M.; Prestes, O.D.; Adaime, M.B.; Zanella, R.; Bottoli, C.B.G. Determination of pesticides in coconut (Cocos nucifera Linn. ) water and pulp using modified QuEChERS and LC–MS/MS. Food Chem. 2016, 213, 616–624. [Google Scholar] [CrossRef]
- Lewis, K.; Tzilivakis, J. Development of a data set of pesticide dissipation rates in/on various plant matrices for the pesticide properties database (PPDB). Data 2017, 2, 28. [Google Scholar] [CrossRef]
- Siqueira, J.A.M.; Eficiência da Aplicação axilar de Ciproconazole no Controle de Doenças Foliares do Coqueiro-anão. Universidade Estadual do Norte Fluminense. 2013. Available online: https://uenf.br/posgraduacao/producao-vegetal/wp-content/uploads/sites/10/2014/03/Disserta%C3%A7%C3%A3o-M.Sc_.-Jackeline-Ara%C3%BAjo-Mota-Siqueira-2013.pdf (accessed on 14 June 2020).
- da Silva, J.M.; Complexo lixa e queima das folhas em coqueiro anão, Avaliação de germoplasma e estratégias de controle químico por cyproconazole. Universidade Federal de Sergipe. 2016. Available online: https://ri.ufs.br/handle/riufs/6782 (accessed on 14 June 2020).
- Holbrook, N.M.; Zwieniecki, M.A. Vascular Transport in Plants; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Taiz, L.; Zeiger, E. Plant Physiology, 3rd ed.; Sinauer Associates: Sunderland, MA, USA, 2002. [Google Scholar]
- Wheeler, T.D.; Stroock, A.D. The transpiration of water at negative pressures in a synthetic tree. Nature 2008, 455, 208–212. [Google Scholar] [CrossRef] [PubMed]
- McElrone, A.J.; Choat, B.; Gambetta, G.A.; Brodersen, C.R. Water uptake and transport in vascular plants. Nat. Educ. Knowl. 2013, 4, 6. [Google Scholar] [CrossRef]
- Bhosle, V.K.; Altit, G.; Autmizguine, J.; Chemtob, S. 18—Basic Pharmacologic Principles, 5th ed.; Fetal and Neonatal Physiology, 2-Volume Set; Elsevier Inc.: Amsterdam, The Netherlands, 2017. [Google Scholar] [CrossRef]
- Darrieutort, G.; Lecomte, P. Evaluation of a trunk injection technique to control grapevine wood diseases. Phytopathol. Mediterr. 2007, 46, 50–57. [Google Scholar]
- Koch, G.W.; Sillett, S.C.; Jennings, G.M. The limit to tree height. Nature 2004, 428, 851–854. [Google Scholar] [CrossRef]
- European Union Pesticides Database. Pesticide Residues. 2021. Available online: https://ec.europa.eu/food/plant/pesticides/eu-pesticides-database/start/screen/mrls (accessed on 20 February 2020).
- Roth, I. Fruits of Angiosperms. Encyclopedia of Plant Anatomy, 1st ed.; Gebruder Borntraeger: Berlin, Germany, 1977; p. 675. [Google Scholar]
- Ferreira, J.A.; Queiroz, S.C.N. Multiresidue method for determination of pesticides in coconut (Cocos nucifera Linn.) endosperm by using GC—MS/MS and UHPLC—MS/MS analysis. J. Food Compos. Anal. 2021, 97, 103764. [Google Scholar] [CrossRef]
- McVay, J.; Sun, X.; Jones, D.; Urbina, H.; Aldeek, F.; Cook, J.M.; Jeyaprakash, A.; Hodges, G.; Smith, T. Limited persistence of residues and metabolites in fruit and juice following penicillin trunk infusion in citrus affected by Huanglongbing. Crop. Prot. 2019, 125, 104753. [Google Scholar] [CrossRef]
- Byrne, F.J.; Krieger, R.I.; Doccola, J.; Morse, J.G. Seasonal timing of neonicotinoid and organophosphate trunk injections to optimize the management of avocado thrips in California avocado groves. Crop. Prot. 2014, 57, 20–26. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).