Using Sigmoid Growth Curves to Establish Growth Models of Tomato and Eggplant Stems Suitable for Grafting in Subtropical Countries
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources
2.2. Growth Model Establishment
2.3. Model Assumption Verification
2.4. Model Performance Evaluation
2.5. Model Parameter Comparison between Two Growing Seasons
2.6. Statistical Analysis
3. Results and Discussion
3.1. Verifying the Model Assumptions
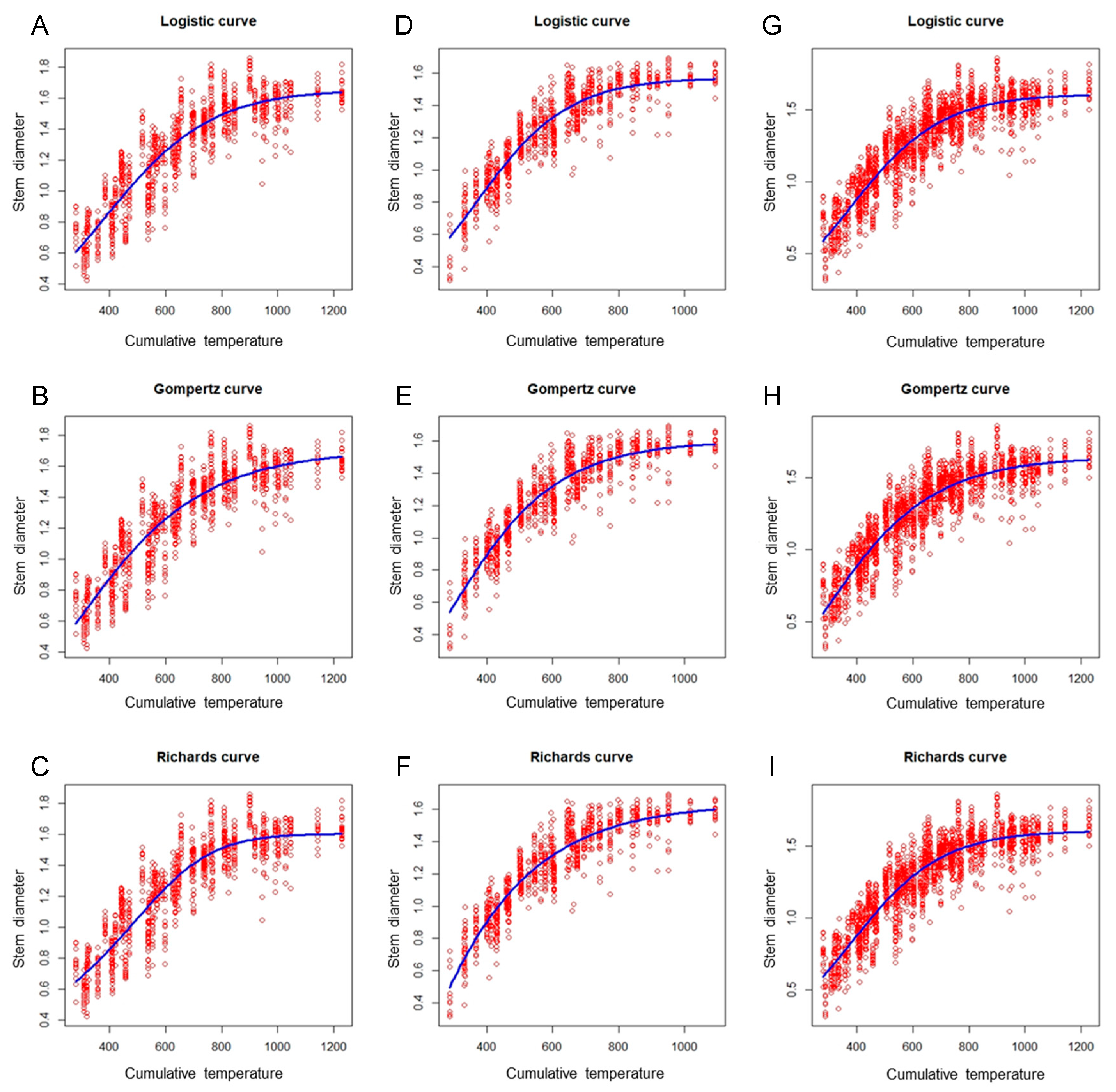
3.2. Model Training and Validation
3.3. Comparison of Model Parameters for Data from Different Growing Seasons
3.4. Estimation of a Suitable Grafting Standard by Using the Cumulative Daily Temperature
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- García-Alonso, F.J.; Bravo, S.; Casas, J.; Pérez-Conesa, D.; Jacob, K.; Periago, M.J. Changes in antioxidant compounds during the shelf life of commercial tomato juices in different packaging materials. J. Agric. Food Chem. 2009, 57, 6815–6822. [Google Scholar] [CrossRef]
- Manickam, R.; Chen, J.R.; Sotelo-Cardona, P.; Kenyon, L.; Srinivasan, R. Evaluation of different bacterial wilt resistant eggplant rootstocks for grafting tomato. Plants 2021, 10, 75. [Google Scholar] [CrossRef] [PubMed]
- Perveen, R.; Suleria, H.A.R.; Anjum, F.M.; Butt, M.S.; Pasha, I.; Ahmad, S. Tomato (Solanum lycopersicum) carotenoids and lycopenes chemistry; metabolism, absorption, nutrition, and allied health claims—A comprehensive review. Crit. Rev. Food Sci. Nutr. 2015, 55, 919–929. [Google Scholar] [CrossRef]
- Rosales, M.A.; Cervilla, L.M.; Sánchez-Rodríguez, E.; Rubio-Wilhelmi, M.; Blasco, B.; Ríos, J.J.; Soriano, T.; Castilla, N.; Romero, L.; Ruiz, J.M. The effect of environmental conditions on nutritional quality of cherry tomato fruits: Evaluation of two experimental Mediterranean greenhouses. J. Sci. Food Agric. 2011, 91, 152–162. [Google Scholar] [CrossRef] [PubMed]
- Norday, T.; Shem, E.; Huat, J. Impacts of temperature and rootstocks on tomato grafting success rates. HortScience 2020, 55, 136–140. [Google Scholar] [CrossRef]
- Kubota, C.; McClure, M.A.; Kokalis-Burelle, N.; Bausher, M.G.; Rosskopf, E.N. Vegetable grafting: History, use, and current technology status in North America. HortScience 2008, 43, 1664–1669. [Google Scholar] [CrossRef]
- Lee, J.M.; Kubota, C.; Tsao, S.J.; Bie, Z.; Echevarria, P.H.; Morra, L.; Oda, M. Current status of vegetable grafting: Diffusion, grafting techniques, automation. Scientia Hort. 2010, 127, 93–105. [Google Scholar] [CrossRef]
- Lee, J.M. Cultivation of grafted vegetables. I. Current status, grafting methods, and benefits. HortScience 1994, 29, 235–239. [Google Scholar] [CrossRef]
- Lee, J.M.; Oda, M. Grafting of herbaceous vegetable and ornamental crops. Hortic. Rev. 2003, 28, 61–124. [Google Scholar]
- Morra, L. Potential and limits of grafting in horticulture. Inf. Agrar. 1998, 54, 39–42. [Google Scholar]
- Xu, Q.; Guo, S.R.; Li, H.; Du, N.S.; Shu, S.; Sun, J. Physiological aspects of compatibility and incompatibility in grafted cucumber seedlings. J. Am. Soc. Hort. Sci. 2015, 140, 299–307. [Google Scholar] [CrossRef]
- Kumar, P.; Rouphael, Y.; Cardarelli, M.; Colla, G. Vegetable grafting as a tool to improve drought resistance and water use efficiency. Front. Plant Sci. 2017, 8, 1130. [Google Scholar] [CrossRef]
- Rouphael, Y.; Cardarelli, M.; Rea, E.; Colla, G. Improving melon and cucumber photosynthetic activity, mineral composition, and growth performance under salinity stress by grafting onto Cucurbita hybrid rootstocks. Photosynthetica 2012, 50, 180–188. [Google Scholar] [CrossRef]
- Savvas, D.; Colla, G.; Rouphael, Y.; Schwarz, D. Amelioration of heavy metal and nutrient stress in fruit vegetables by grafting. Sci. Hort. 2010, 127, 156–161. [Google Scholar] [CrossRef]
- Schwarz, D.; Rouphael, Y.; Colla, G.; Venema, J.H. Grafting as a tool to improve tolerance of vegetables to abiotic stresses: Thermal stress, water stress and organic pollutants. Sci. Hort. 2010, 127, 162–171. [Google Scholar] [CrossRef]
- Venema, J.H.; Dijk, B.E.; Bax, J.M.; van Hasselt, P.R.; Elzenga, J.T.M. Grafting tomato (Solanum lycopersicum) onto the rootstock of a high-altitude accession of Solanum habrochaites improves suboptimal-temperature tolerance. Environ. Expt. Bot. 2008, 63, 359–367. [Google Scholar] [CrossRef]
- Morikawa, C.K. Reducing cadmium accumulation in fresh pepper fruits by grafting. Hort. J. 2017, 86, 45–51. [Google Scholar] [CrossRef]
- Xie, Y.D.; Tan, H.Q.; Sun, G.C.; Li, H.X.; Liang, D.; Xia, H.; Wang, X.; Liao, M.A.; Deng, H.H.; Wang, J.; et al. Grafting alleviates cadmium toxicity and reduces its absorption by tomato. Soil Sci. Plant Nutr. 2020, 20, 2222–2229. [Google Scholar] [CrossRef]
- Naik, S.A.T.S.; Hongal, S.; Harshavardhan, M.; Chandan, K.; Kumar, A.J.S.; Ashok; Kyriacou, M.C.; Rouphael, Y.; Kumar, P. Productive characteristics and fruit quality traits of cherry tomato hybrids as modulated by grafting on different Solanum spp. rootstocks under Ralstonia solanacearum infested greenhouse soil. Agronomy 2021, 11, 1311. [Google Scholar] [CrossRef]
- Singh, H.; Kumar, P.; Chaudhari, S.; Edelstein, M. Tomato grafting: A global perspective. HortScience 2017, 52, 1328–1336. [Google Scholar] [CrossRef]
- Singh, H.; Kumar, P.; Kumar, A.; Kyriacou, M.C.; Colla, G.; Rouphael, Y. Grafting tomato as a tool to improve salt tolerance. Agronomy 2020, 10, 263. [Google Scholar] [CrossRef]
- Bumgarner, N.R.; Kleinhenz, M.D. Grafting guide—A pictorial guide to the cleft and splice graft methods. Ohio Agr. Res. Dev. Ctr. Bul. 2014, 950. [Google Scholar]
- Rivard, C.L.; Louws, F.J. Grafting for disease resistance in heirloom tomatoes. Ext. Folder NC Agric. Ext. Serv. 2006, 8. [Google Scholar]
- Guzmán, G.; Morales, M.; Pukkala, T.; de-Miguel, S. A model for predicting the growth of Eucalyptus globulus seedling stands in Bolivia. For. Syst. 2012, 21, 205–209. [Google Scholar] [CrossRef][Green Version]
- Streck, N.; Bosco, L.C.; Lucas, D.D.P.; Lago, I. Modelagem da emissão de folhas em arroz. Pesqui. Agropecu. Bras. 2008, 43, 559–567. [Google Scholar] [CrossRef]
- Bem, C.M.; Cargnelutti Filho, A.; Facco, G.; Schabarum, D.E.; Silveira, D.L.; Simões, F.M.; Uliana, D.B. Growth models for morphological traits of sunn hemp. Semin. Cienc. Agrar. 2017, 38, 2933–2944. [Google Scholar] [CrossRef]
- Gomes, A.C.S.; Robaina, A.D.; Peiter, M.X.; Soares, F.C.; Parizi, A.R.C. Modelo para estimativa da produtividade para a cultura da soja. Cienc. Rural 2014, 44, 43–49. [Google Scholar] [CrossRef][Green Version]
- Archontoulis, S.A.; Miguez, F.E. Nonlinear regression models and applications in agricultural research. Agron. J. 2015, 107, 786–798. [Google Scholar] [CrossRef]
- Gan, Y.; Stobbe, E.H.; Njue, C. Evaluation of selected nonlinear regression models in quantifying seedling emergence rate of spring wheat. Crop Sci. 1996, 36, 165–168. [Google Scholar] [CrossRef]
- Miguez, F.E.; Zhu, X.; Humphries, S.; Bollero, G.A.; Long, S.P. A semimechanistic model predicting growth and production of the bioenergy crop Miscanthus × giganteus: Description, parameterization and validation. Glob. Change Biol. Bioenergy 2009, 1, 282–296. [Google Scholar] [CrossRef]
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc. 1825, 115, 513–585. [Google Scholar]
- Verhulst, P.F. A note on population growth. Corresp. Math. Phys. 1838, 10, 113–121. [Google Scholar]
- Lucio, A.D.; Nunes, L.F.; Rego, F. Nonlinear models to describe production of fruit in Cucurbita pepo and Capiscum annuum. Sci. Hortic. 2015, 193, 286–293. [Google Scholar] [CrossRef]
- Gonzaga, T.W.C.; Mata, M.E.; Silva, H.; Duarte, M.E. Crioconservação de sementes de aroeira (Astronium urundeuva Engl.), e baraúna (Schinopsis brasiliensis Engl.). Rev. Bras. Prod. Agroind. 2003, 5, 145–154. [Google Scholar] [CrossRef]
- Martins Filho, S.; Silva, F.F.; Carneiro, A.P.; Muniz, J.A. Abordagem bayesiana das curvas de crescimento de duas cultivares de feijoeiro. Cienc. Rural 2008, 38, 1516–1521. [Google Scholar] [CrossRef]
- Richards, F.J. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–300. [Google Scholar] [CrossRef]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Filliben, J.J. The probability plot correlation coefficient test for normality. Technometrics 1975, 17, 111–117. [Google Scholar] [CrossRef]
- Bem, C.M.; Cargnelutti Filho, A.; Chaves, G.G.; Kleinpaul, J.A.; Lavezo, A. Gompertz and Logistic models to the productive traits of sunn hemp. J. Agric. Sci. 2018, 10, 225–238. [Google Scholar] [CrossRef]
- Shah, D.A.; Molineros, J.E.; Paul, P.A.; Willyerd, K.T.; Madden, L.V.; De Wolf, E.D. Predicting Fusarium head blight epidemics with weather-driven pre-and post-anthesis Logistic regression models. Phytopathology 2013, 103, 906–919. [Google Scholar] [CrossRef]
- Hu, B.; Bennett, M.A.; Kleinhenz, M.D. A new method to estimate vegetable seedling vigor, piloted with tomato, for use in grafting and other contexts. HortTechnology 2016, 26, 767–775. [Google Scholar] [CrossRef]
- Oda, M.; Tsuji, K.; Sasaki, H. Effect of hypocotyl morphology on survival rate and growth of cucumber seedlings grafted on Cucurbita spp. Jpn. Agr. Res. Qrtly. 1993, 26, 259–263. [Google Scholar]
- Yetisxir, H.; Sari, N. Effect of hypocotyl morphology on survival rate and growth of watermelon seedlings grafted on rootstocks with different emergence performance at various temperatures. Turk. J. Agr. For. 2004, 28, 231–237. [Google Scholar]
- Jones, J.W.; Kenig, A.; Vallejos, C.E. Reduced state-variable tomato growth model. Trans. ASAE 1999, 42, 255–265. [Google Scholar] [CrossRef]
- Yuan, F.M.; Bland, W.L. Comparison of light and temperature based index models for potato (Solanum tuberosum L.) growth and development. Am. J. Potato. Res. 2005, 82, 345–352. [Google Scholar] [CrossRef]





| Data Set | Eggplant | Tomato | ||||
|---|---|---|---|---|---|---|
| T (°C) | RH (%) | Light Intensity (μmol m−2 s−1) | T (°C) | RH (%) | Light Intensity (μmol m−2 s−1) | |
| Spring–summer | 27.25 (2.68) | 80.96 (5.59) | 79.42 (27.10) | 27.50 (2.39) | 81.39 (5.60) | 78.99 (27.01) |
| Autumn–winter | 23.82 (2.61) | 78.13 (6.03) | 58.42 (24.48) | 23.47 (2.51) | 78.23 (6.06) | 57.64 (21.17) |
| Combined | 25.68 (3.15) | 79.67 (5.96) | 69.83 (27.94) | 25.72 (3.16) | 80.00 (6.01) | 69.57 (26.77) |
| Data Set | Model | Eggplant | Tomato | ||
|---|---|---|---|---|---|
| PPCC | p-Value | PPCC | p-Value | ||
| Spring–summer | Logistic | 0.9966 | 0.0001 | 0.9984 | 0.0385 |
| Gompertz | 0.9964 | 0.0000 | 0.9984 | 0.0379 | |
| Richards | 0.9975 | 0.0019 | 0.9984 | 0.0407 | |
| Autumn–winter | Logistic | 0.9931 | 0.0000 | 0.9947 | 0.0000 |
| Gompertz | 0.9942 | 0.0000 | 0.9945 | 0.0000 | |
| Richards | 0.9948 | 0.0001 | 0.9948 | 0.0000 | |
| Combined | Logistic | 0.9926 | 0.0000 | 0.9945 | 0.0000 |
| Gompertz | 0.9924 | 0.0000 | 0.9946 | 0.0000 | |
| Richards | 0.9926 | 0.0000 | 0.9945 | 0.0000 | |
| Data Set | Model | R2 | AIC | RMSE | MAE |
|---|---|---|---|---|---|
| Spring–summer | Logistic | 0.8184 | −1.2573 | 0.1406 | 0.1077 |
| Gompertz | 0.8157 | −1.2426 | 0.1416 | 0.1084 | |
| Richards | 0.8203 | −1.4335 | 0.1399 | 0.1080 | |
| Autumn–winter | Logistic | 0.8518 | −1.8066 | 0.1068 | 0.0837 |
| Gompertz | 0.8540 | −1.8217 | 0.1060 | 0.0831 | |
| Richards | 0.8548 | −1.9924 | 0.1058 | 0.0829 | |
| Combined | Logistic | 0.8316 | −1.4828 | 0.1256 | 0.0958 |
| Gompertz | 0.8306 | −1.4769 | 0.1260 | 0.0959 | |
| Richards | 0.8316 | −1.6490 | 0.1256 | 0.0959 |
| Data Set | Model | R2 | AIC | RMSE | MAE |
|---|---|---|---|---|---|
| Spring–summer | Logistic | 0.7459 | −0.9653 | 0.1627 | 0.1307 |
| Gompertz | 0.7455 | −0.9637 | 0.1628 | 0.1309 | |
| Richards | 0.7459 | −1.1310 | 0.1628 | 0.1308 | |
| Autumn–winter | Logistic | 0.8038 | −1.5461 | 0.1217 | 0.0946 |
| Gompertz | 0.8029 | −1.5416 | 0.1220 | 0.0948 | |
| Richards | 0.8041 | −1.7130 | 0.1217 | 0.0946 | |
| Combined | Logistic | 0.7516 | −1.1499 | 0.1483 | 0.1177 |
| Gompertz | 0.7509 | −1.1471 | 0.1485 | 0.1178 | |
| Richards | 0.7516 | −1.3161 | 0.1484 | 0.1177 |
| Data Set | Model | R2 | AIC | RMSE | MAE |
|---|---|---|---|---|---|
| Spring–summer | Logistic | 0.8012 | −1.2114 | 0.1438 | 0.1090 |
| Gompertz | 0.7962 | −1.1867 | 0.1456 | 0.1103 | |
| Richards | 0.8070 | −1.4054 | 0.1419 | 0.1082 | |
| Autumn–winter | Logistic | 0.8558 | −1.8070 | 0.1068 | 0.0848 |
| Gompertz | 0.8573 | −1.8177 | 0.1062 | 0.0841 | |
| Richards | 0.8572 | −1.9813 | 0.1064 | 0.0845 | |
| Combined | Logistic | 0.8030 | −1.3278 | 0.1357 | 0.1046 |
| Gompertz | 0.8014 | −1.3198 | 0.1363 | 0.1046 | |
| Richards | 0.8031 | −1.4938 | 0.1358 | 0.1047 |
| Data Set | Model | R2 | AIC | RMSE | MAE |
|---|---|---|---|---|---|
| Spring–summer | Logistic | 0.7219 | −0.9929 | 0.1605 | 0.1292 |
| Gompertz | 0.7225 | −0.9952 | 0.1603 | 0.1291 | |
| Richards | 0.7220 | −1.1576 | 0.1606 | 0.1295 | |
| Autumn–winter | Logistic | 0.8305 | −1.7108 | 0.1121 | 0.0913 |
| Gompertz | 0.8293 | −1.7041 | 0.1124 | 0.0918 | |
| Richards | 0.8309 | −1.8769 | 0.1121 | 0.0914 | |
| Combined | Logistic | 0.7524 | −1.1338 | 0.1495 | 0.1186 |
| Gompertz | 0.7517 | −1.1309 | 0.1497 | 0.1186 | |
| Richards | 0.7524 | −1.2993 | 0.1496 | 0.1187 |
| Model | Parameter | Eggplant (Spring–Summer) | Eggplant (Autumn–Winter) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | SE | Lower Limit | Upper Limit | Estimate | SE | Lower Limit | Upper Limit | ||
| Logistic | a * | 1.6559 | 0.0144 | 1.6275 | 1.6842 | 1.5702 | 0.0110 | 1.5486 | 1.5917 |
| b * | −2.0222 | 0.0693 | −2.1582 | −1.8863 | −2.5662 | 0.0880 | −2.7389 | −2.3935 | |
| c * | 0.0053 | 0.0002 | 0.0049 | 0.0057 | 0.0071 | 0.0002 | 0.0066 | 0.0075 | |
| Gompertz | a * | 1.7021 | 0.0186 | 1.6656 | 1.7386 | 1.5986 | 0.0128 | 1.5734 | 1.6238 |
| b * | 3.2076 | 0.1764 | 2.8615 | 3.5537 | 5.3383 | 0.3802 | 4.5921 | 6.0844 | |
| c * | 0.0039 | 0.0002 | 0.0036 | 0.0043 | 0.0055 | 0.0002 | 0.0052 | 0.0059 | |
| Richards | a | 1.6040 | 0.0147 | 1.5753 | 1.6328 | 1.6375 | 0.0255 | 1.5876 | 1.6875 |
| b * | −4.3237 | 0.8051 | −5.9034 | −2.7439 | −0.9572 | 0.2814 | −1.5095 | −0.405 | |
| c * | 0.0088 | 0.0012 | 0.0064 | 0.0111 | 0.0043 | 0.0005 | 0.0032 | 0.0053 | |
| d * | 3.5041 | 0.8306 | 1.8743 | 5.1339 | −0.8156 | 0.3103 | −1.4247 | −0.2065 | |
| Model | Parameter | Tomato (Spring–Summer) | Tomato (Autumn–Winter) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | SE | Lower Limit | Upper Limit | Estimate | SE | Lower Limit | Upper Limit | ||
| Logistic | a | 1.5000 | 0.0174 | 1.4660 | 1.5341 | 1.5012 | 0.0232 | 1.4556 | 1.5468 |
| b | −1.9437 | 0.0878 | −2.1160 | −1.7714 | −1.9607 | 0.0823 | −2.1222 | −1.7993 | |
| c | 0.0061 | 0.0003 | 0.0055 | 0.0066 | 0.0067 | 0.0003 | 0.0061 | 0.0074 | |
| Gompertz | a | 1.5377 | 0.0219 | 1.4947 | 1.5806 | 1.5749 | 0.0337 | 1.5089 | 1.6410 |
| b | 3.1026 | 0.2217 | 2.6676 | 3.5376 | 2.9736 | 0.2025 | 2.5761 | 3.3711 | |
| c | 0.0046 | 0.0003 | 0.0041 | 0.0051 | 0.0048 | 0.0003 | 0.0042 | 0.0054 | |
| Richards | a | 1.5035 | 0.0292 | 1.4461 | 1.5608 | 1.4710 | 0.0419 | 1.3888 | 1.5532 |
| b | −1.8477 | 0.6408 | −3.1052 | −0.5902 | −2.4943 | 0.9138 | −4.2877 | −0.7008 | |
| c | 0.0059 | 0.0012 | 0.0036 | 0.0082 | 0.0079 | 0.0020 | 0.0041 | 0.0118 | |
| d | 0.8839 | 0.7698 | −0.6266 | 2.3944 | 1.6152 | 1.0238 | −0.3942 | 3.6246 | |
| Model | Parameter | Eggplant (Global) | Tomato (Global) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate | SE | Lower Limit | Upper Limit | Estimate | SE | Lower Limit | Upper Limit | ||
| Logistic | a | 1.6108 * | 0.0086 | 1.5940 | 1.6277 | 1.3871+ | 0.0084 | 1.3706 | 1.4036 |
| b | −2.2376 * | 0.0546 | −2.3447 | −2.1305 | −3.1616+ | 0.0842 | −3.3267 | −2.9964 | |
| c | 0.0061 * | 0.0001 | 0.0058 | 0.0063 | 0.0102+ | 0.0003 | 0.0097 | 0.0107 | |
| Gompertz | a | 1.6463 * | 0.0106 | 1.6256 | 1.6671 | 1.5171 | 0.0153 | 1.4871 | 1.5471 |
| b | 3.9172 * | 0.1709 | 3.5821 | 4.2523 | 3.1341 | 0.1591 | 2.8221 | 3.4460 | |
| c | 0.0046 * | 0.0001 | 0.0044 | 0.0049 | 0.0049 | 0.0002 | 0.0046 | 0.0053 | |
| Richards | a | 1.6070 | 0.0125 | 1.5824 | 1.6316 | 1.4783 | 0.0187 | 1.4416 | 1.5151 |
| b | −2.3698 * | 0.3341 | −3.0249 | −1.7146 | −2.0085 | 0.4494 | −2.8898 | −1.1272 | |
| c | 0.0063 * | 0.0006 | 0.0052 | 0.0074 | 0.0066 | 0.0009 | 0.0049 | 0.0083 | |
| d | 1.1490 * | 0.3697 | 0.4240 | 1.8740 | 1.0766 | 0.5444 | 0.0090 | 2.1442 | |
| Plant | Data Set | Model | Cumulative Temperature (°C) | |
|---|---|---|---|---|
| 1.5 mm | 2.0 mm | |||
| Eggplant | Spring–summer | Logistic | 579.5 | 716.1 |
| Gompertz | 578.2 | 724.1 | ||
| Richards | 584.4 | 703.3 | ||
| Autumn–winter | Logistic | 542.2 | 675.1 | |
| Gompertz | 541.4 | 681.7 | ||
| Richards | 541.5 | 688.5 | ||
| Combined | Logistic | 559.7 | 694.7 | |
| Gompertz | 558.8 | 702.8 | ||
| Richards | 559.9 | 693.7 | ||
| Tomato | Spring–summer | Logistic | 567.4 | 783.6 |
| Gompertz | 570.7 | 789.2 | ||
| Richards | 567.7 | 784.3 | ||
| Autumn–winter | Logistic | 511.3 | 707.1 | |
| Gompertz | 514.5 | 694.2 | ||
| Richards | 509.6 | 718.6 | ||
| Combined | Logistic | 540.5 | 770.5 | |
| Gompertz | 544.1 | 770.0 | ||
| Richards | 540.3 | 770.6 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsieh, C.-Y.; Fang, S.-L.; Wu, Y.-F.; Chu, Y.-C.; Kuo, B.-J. Using Sigmoid Growth Curves to Establish Growth Models of Tomato and Eggplant Stems Suitable for Grafting in Subtropical Countries. Horticulturae 2021, 7, 537. https://doi.org/10.3390/horticulturae7120537
Hsieh C-Y, Fang S-L, Wu Y-F, Chu Y-C, Kuo B-J. Using Sigmoid Growth Curves to Establish Growth Models of Tomato and Eggplant Stems Suitable for Grafting in Subtropical Countries. Horticulturae. 2021; 7(12):537. https://doi.org/10.3390/horticulturae7120537
Chicago/Turabian StyleHsieh, Chih-Yu, Shih-Lun Fang, Yea-Fang Wu, Yung-Chu Chu, and Bo-Jein Kuo. 2021. "Using Sigmoid Growth Curves to Establish Growth Models of Tomato and Eggplant Stems Suitable for Grafting in Subtropical Countries" Horticulturae 7, no. 12: 537. https://doi.org/10.3390/horticulturae7120537
APA StyleHsieh, C.-Y., Fang, S.-L., Wu, Y.-F., Chu, Y.-C., & Kuo, B.-J. (2021). Using Sigmoid Growth Curves to Establish Growth Models of Tomato and Eggplant Stems Suitable for Grafting in Subtropical Countries. Horticulturae, 7(12), 537. https://doi.org/10.3390/horticulturae7120537






