Abstract
Electrostatic droplets can enhance deposition on target leaves. To comprehensively investigate the main factors affecting droplet adhesion and splashing after electrostatic droplet impact on pepper leaves, a specialized experimental platform was developed to capture the impact behavior of charged droplets on pepper leaves. The following four variables were examined: the applied voltage of the electrode ring, droplet size, impact velocity, and the relative distance from the impact point to the leaf tip (expressed as a percentage of the total leaf length). The results showed that all four factors had significant effects on droplet adhesion. The effect sizes (partial η2) of the four factors, in descending order, were impact velocity (0.935), applied voltage (0.907), impact position (0.895), and droplet size (0.505). Compared with non-electrostatic droplets, the increase in the maximum spreading factor of charged droplets was positively correlated with droplet size, impact velocity, and applied voltage but showed no significant correlation with the relative distance to the leaf tip. The critical velocity for splashing of electrostatic droplets decreased to a certain extent but increased with higher applied voltages. The influence of the four factors on droplet splashing decreases in the following order: impact velocity (odds ratio ≫ 1), charging voltage (odds ratio = 1.246), droplet size (odds ratio = 1.023), and impact position (odds ratio < 1). Among these, impact velocity has the most significant effect on splashing behavior. This study reveals the adhesion and splashing mechanisms of electrostatic droplets on flexible pepper leaves, providing theoretical support for the design of electrostatic spraying systems and the selection of operational parameters. The findings offer a scientific basis for optimizing droplet deposition, minimizing splash losses, and improving application efficiency in precision spraying.
1. Introduction
Pepper is a common and important vegetable in daily life. However, its yield is significantly reduced each year due to pest and disease infestations affecting pepper plants [1]. Currently, pesticide spraying remains one of the most effective methods for pest control in crops [2]. However, not all droplets sprayed from pesticide nozzles successfully reach the leaf surface; droplet drift and other losses often lead to considerable pesticide waste [3]. In response to this issue, electrostatic spraying has been explored. A series of studies have demonstrated that electrostatic spraying can effectively reduce droplet drift and thereby improve pesticide utilization efficiency [4,5]. Nevertheless, even when charged droplets reach the target surface, they may still exhibit splashing, rebounding, or adhesion behaviors [6,7]. Among these, splashing and rebounding hinder the effective deposition of droplets on the target surface, whereas only adhesion ensures that droplets remain on the leaf surface [8]. Therefore, studying the impact behavior of charged droplets on pepper leaves is essential for understanding the wetting mechanism of charged droplets on leaf surfaces, which provides theoretical guidance for enhancing the efficiency of electrostatic spraying.
In agricultural applications, droplet charging methods include contact charging [9], inductive charging [10], and corona charging technologies [11]. Among these, inductive charging has achieved broader commercialization in agricultural spraying due to its operational stability and practicality [12]. Research on electrostatic spraying in agriculture has primarily focused on improving electrostatic systems and components [13], such as electrode positioning, materials used for spray charging, liquid flow rate, the balance between airflow and liquid flow, the resistivity range of the spray solution, high-voltage generation, and energy consumption [14,15]. Patel et al. [16] conducted a comparative study using annular electrodes made of various materials, including nickel, copper, stainless steel, brass, and aluminum. They characterized the outcomes of the induction charging process by examining the charge-to-mass ratio as a function of electrode material. The results showed that both the electrode material and position significantly influenced the charging performance. Lin et al. [17] designed an electrostatic spraying system based on induction charging and found that when the charging voltage reached a certain threshold, the charge-to-mass ratio of the droplets first stabilized and then gradually declined. Sánchez-Hermosilla et al. [18] evaluated the spray deposition of a non-electrostatic and an electrostatic handheld sprayer on greenhouse pepper canopies. The results showed that the electrostatic sprayer increased canopy deposition by 1.48 times compared to the handheld sprayer and reduced pesticide usage by 48%. The motion behavior of a droplet upon impacting a target surface is primarily influenced by the following three categories of factors: droplet properties (e.g., impact velocity, droplet size, and the physicochemical properties of the spray liquid) [19,20,21,22], target surface characteristics (e.g., inclination angle, mechanical properties, and surface microstructure) [23,24,25], and external field conditions (e.g., wind fields [26], electric fields [7], and magnetic fields) [27] at the time of impact. In previous studies on the impact of charged droplets, the focus has primarily been on rigid substrates with varying surface properties [28,29], or on leaf surfaces that were fixed onto rigid bases. Although electrostatic spraying is an effective technique for improving pesticide deposition, the dynamic behavior of charged droplets impacting flexible plant surfaces—particularly pepper leaves—remains insufficiently investigated. This study aims to fill this gap by examining how droplet charge, impact velocity, and leaf surface characteristics influence droplet deposition and splashing behavior.
To gain a deeper understanding of the motion behavior of charged droplets upon impacting the surface of living pepper leaves, this study investigates droplet adhesion and splashing behavior by considering the following four experimental variables: applied voltage to the electrode ring, droplet size, impact velocity, and the relative distance from the impact point to the leaf tip. The effects of different applied voltages on the maximum spreading factor (i.e., the extent of droplet adhesion) were analyzed, and the critical splashing velocity for droplets of various sizes under different voltages was determined. The findings of this study provide theoretical guidance for the practical application of electrostatically charged droplets, with the goals of reducing pesticide usage, enhancing pesticide efficacy, and contributing to environmental sustainability.
2. Materials and Methods
2.1. Experimental Crop
In this study, pepper (Capsicum annuum L., Tianshuai 101) was selected as the experimental subject. The seedlings were cultivated in a sunlight greenhouse in Zhenjiang, Jiangsu Province, China, for 90 days under controlled conditions (relative humidity: 60–75%, temperature: 20–25 °C, and photoperiod: 16 h light/8 h dark). Upon reaching the fruiting stage, ten healthy plants without any signs of pests or diseases were selected for the experiment. Before the experiment, the plants were adequately watered and placed in the experimental environment for over 48 h to acclimate and ensure that the leaves were in optimal condition. All experiments were conducted in the laboratory of Jiangsu University, and three well-developed leaves were selected from each plant as test samples.
Since rapid changes in temperature and humidity can affect the physical state and dry matter content of leaves [30,31,32], the experimental conditions were controlled based on the average greenhouse temperature of 26 ± 6 °C and relative humidity of 57–72% recorded during the 10 days preceding the test. Prior to the experiment, a constant-temperature air conditioning system (temperature accuracy ± 1 °C and relative humidity accuracy ± 5%) was used to maintain the laboratory environment. After more than 6 h of preconditioning, the air temperature was stabilized at 26 °C and relative humidity at 65%, ensuring that the conditions closely resembled the typical growth environment of pepper plants.
To characterize leaf mass and size, the average fresh weight of the leaves was measured as 1195 ± 200 mg using a high-precision electronic balance (AL204, Mettler Toledo, Greifensee, Switzerland), and the average leaf area was determined to be 2086 ± 300 mm2 using an AM-350 leaf area meter (Zealquest Technology Co., Ltd., Shanghai, China). The surface topography of pepper leaves was characterized using a 3D digital microscope (VHX-900F, Keyence Corporation, Osaka, Japan). The average surface roughness (Ra) of the leaf surface was measured to be 5.24 μm. Notably, no significant trichomes or hair-like structures were observed on the scanned regions of the leaf surface. This relatively smooth and trichome-free surface may influence the interaction dynamics between electrostatic droplets and the leaf, particularly in terms of spreading and adhesion behaviors.
2.2. Leaf Division
To ensure that droplet impact behavior on the leaf surface reflects actual spraying conditions, the experiments were conducted on intact leaves in their natural growth state, with impact and measurement points kept consistent. According to the study by Wang et al. [33], leaf elasticity affects the distribution of droplet deposition across different regions of the leaf. To avoid interference from curvature near the petiole and preferential deposition near the leaf tip, the leaf length was proportionally divided, and four impact points were selected at 20%, 40%, 60%, and 80% of the distance from the leaf tip, as shown in Figure 1.

Figure 1.
Segmentation of pepper leaves into different regions based on relative distance from the tip.
2.3. Measurement of the Static Contact Angle on the Leaf Surface
Static contact angle measurements were conducted on different regions of the cut pepper leaves using an OCA video optical contact angle meter (Data Physics Instruments GmbH, Filderstadt, Germany) equipped with a syringe needle (Model SNS-052). Distilled water was loaded into the syringe, and droplets with a fixed volume of 2 μL were dispensed using the sessile drop method under computer control. The instrument’s built-in analysis software was used to determine the contact angle of each droplet on the leaf surface, and the average value was calculated. According to the segmentation shown in Figure 1, contact angles were measured on each region while avoiding the midrib and lateral veins. For each region (corresponding to 20%, 40%, 60%, and 80% of the distance from the impact point to the leaf tip), ten different points were selected, and each was measured three times. The average static contact angles at these regions were found to be 94.9°, 89.3°, 87.1°, and 84.5°, respectively.
2.4. Electrostatic Single-Droplet Generation System
To investigate the behavior of charged single droplets, an inductive charging method was employed. In this setup, each droplet passed through a ring-shaped electrode, where it acquired charge via electrostatic induction [4]. The experimental system consisted of a single-droplet generation device composed of a syringe pump (NE-1000, New Era Pump Systems, Inc., Wantagh, NY, USA), a syringe, and a needle. The syringe pump controlled the liquid flow rate to form individual droplets at the needle tip, which then detached under the influence of gravity. The droplet size was controlled by selecting needles of different inner diameters. As the droplets passed through the ring electrode, they became charged through electrostatic induction. Since the falling droplets approximated an ellipsoidal shape, the equivalent diameter D0 was used to characterize droplet size.
where Dv and Dh represent the vertical and horizontal diameters of the droplet, respectively.
In the experiment, four types of syringe needles with inner diameters of 0.1 mm, 0.2 mm, 0.3 mm, and 0.4 mm were selected, generating droplets with corresponding equivalent diameters (D0) of 1051 μm, 1413 μm, 1647 μm, and 1741 μm, respectively. The droplet size was determined by capturing images of the droplets prior to impact using a high-speed camera and analyzing them with ImageJ software (version 1.54g, National Institutes of Health, USA). To ensure the consistency of droplet size controlled by needle gauge, 20 droplets were measured for each condition, and the size uncertainty was within ±10 μm.
When the same voltage is applied to the ring electrode, droplets passing through different positions within the inner cavity of the electrode acquire different amounts of charge [34]. To ensure uniform charging, a composite PMMA induction electrode plate with a central circular hole (diameter 2.5 ± 0.1 mm) was designed (as shown in Figure 2), allowing each droplet to pass through the same region of the electrode. The applied charging voltages were set to 0, 14, 16, and 18 kV. All experiments were conducted in a sealed laboratory to eliminate interference from ambient airflow. Since the electric field near the needle tip can influence the surface tension of the liquid, it may cause variations in droplet size generated by the device [35]. After repeated testing, it was determined that when the distance between the needle tip and the induction electrode exceeded 12.0 mm, the size deviation between charged and uncharged droplets remained within 1%. Therefore, the distance h between the needle and the charging electrode was fixed at 15.0 mm.
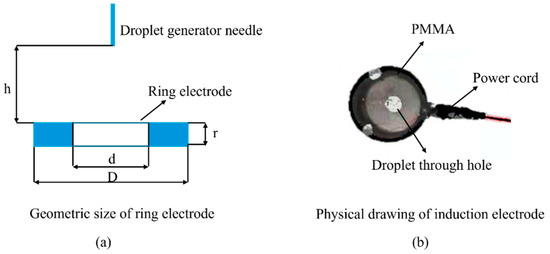
Figure 2.
(a) Schematic diagram of the ring electrode geometry. (b) Photograph of the induction electrode charging device.
2.5. Experimental Platform
High-speed imaging technology has been widely used to capture droplet impact behavior [36]. To investigate the behavior of electrostatic droplets impacting the surface of pepper leaves, an experimental platform was constructed, consisting of a high-speed camera, a light source, and a computer, as shown in Figure 3. The electrostatic single-droplet generator was positioned above the target leaf, and the distance between the droplet release point and the pepper leaf surface was adjusted to achieve the desired impact velocity. The lens of the high-speed camera (OLYMPUS i-Speed 3, manufactured by Navitar, Rochester, NY, USA) was aligned directly in front of the pepper leaf, forming a 15° angle with the horizontal plane, with a horizontal distance of 932 mm between the camera and the leaf. An OSRAM high-brightness light source (230 V, 1000 W) was used to assist illumination. The camera settings were adjusted to a frame rate of 5000 fps and a resolution of 1024 × 512 pixels. Prior to each test, the high-speed camera was calibrated using the Zhang Zhengyou calibration method [37]. It is important to note that the position of both the camera and the target leaf must remain fixed after calibration. During the experiments, doors and windows were kept closed to minimize airflow interference with the droplet trajectory. The accompanying i-Speed Suite software (version 3.0.3.1, Olympus, Center Valley, PA, USA) was used to process the captured videos and extract pixel data in the X–Y plane.
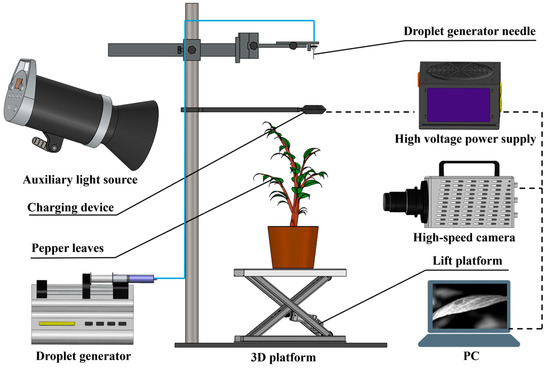
Figure 3.
Experimental setup for the impact of charged droplets on flexible pepper leaves.
2.6. Test Method for Droplet Impact Behavior
Previous studies have examined the effects of droplet particle size, impact velocity, and impact angle on droplet impact behavior [38,39,40]. To investigate the effect of charge on the impact behavior of droplets on pepper leaves, this study used the following four test variables: applied voltage to the composite electrode ring, droplet impact velocity, droplet particle size, and impact position. The charge effect was investigated by adjusting the applied voltage to the composite inductive electrode plate to 0, 14, 16, and 18 kV, respectively. Droplet impact velocity was varied by changing the vertical distance between the needle and the leaf surface. The velocity was determined by analyzing high-speed video footage frame-by-frame. The frame where the droplet was just about to hit the leaf surface was recorded as the first frame, and another frame was selected such that the droplet was approximately 1 mm above the surface. The impact velocity was calculated based on the known time interval and distance between these two frames. Four impact velocities—1.389, 1.931, 2.370, and 2.750 m/s—were tested. Droplet size was controlled by selecting syringe needles with different inner diameters (0.1 mm, 0.2 mm, 0.3 mm, and 0.4 mm), corresponding to average droplet diameters of 1051 μm, 1413 μm, 1712 μm, and 2071 μm, respectively.
At present, composite pesticide formulations with added adjuvants are commonly used in pepper crop protection sprays. These formulations are complex in composition and may possess certain levels of toxicity. After electrostatic charging, changes in physical properties (such as surface tension and adhesiveness) and chemical composition may occur, increasing the uncertainty of the experimental system. To eliminate the influence of multi-component interference and better quantify the effect of electric charge on droplet adhesion and spreading behavior, distilled water—characterized by stable physical properties, simple composition, and safety—was selected as the experimental liquid in this study. The surface tension (σ) of distilled water was measured using a surface tensiometer (DCAT25, Beijing ODELINO Instruments Co., Ltd., Beijing, China) via the pendant drop method, yielding values ranging from 0.070 to 0.074 N/m. The dynamic viscosity (μ) and density (ρ) of water were taken as standard values of 0.00089 Pa·s and 998 kg/m3, respectively.
To improve the applicability of the experimental results under practical spraying conditions, this study employed a dimensionless similarity approach. By adjusting droplet diameter and impact velocity, the Weber number (We) of the experimental droplets was matched to that of pesticide droplets containing adjuvants during field spraying. In this way, the impact dynamics of distilled water droplets in the experiments were made reasonably representative of actual pesticide droplet–leaf interactions.
Due to the flexible nature of pepper leaves, different parts of the leaf exhibit varying inclination angles under natural growth conditions. As shown in Figure 1, four impact positions were selected based on their relative distance from the leaf tip as follows: 20%, 40%, 60%, and 80%. As shown in Figure 4a, the leaf was maintained in its natural orientation during the droplet impact experiments. The average inclination angles at the 20%, 40%, 60%, and 80% positions were measured to be 20.1°, 18.4°, 15.2°, and 11.7°, respectively. Accordingly, the calculated droplet impact angles (α) at these positions were 69.9°, 71.6°, 74.8°, and 78.3°, respectively.
Figure 4.
Droplet impact on a flexible pepper leaf: (a) definition of the impact angle and (b) measurement of the spreading diameter.
During the impact behavior tests, the leaf was maintained in its natural growth state, and droplet impact was positioned close to—but not on—the midvein to ensure that spreading occurred without overflow or interference from the vein. As shown in Figure 4b, the maximum spreading diameter (Dm) of the droplet after impacting the leaf surface was determined using the i-Speed Suite software. The coordinates of the two endpoints of the droplet spread, denoted as (X1, Y1) and (X2, Y2), were identified, and the maximum spreading diameter was calculated as the straight-line distance between these two points using Equation (2):
where X1 and X2 are the X-axis coordinates of the two endpoints of the droplet’s maximum spreading, and Y1 and Y2 are the corresponding Y-axis coordinates.
To evaluate the differences in droplet behavior during adhesion, the maximum spreading factor (β) was introduced, as defined in Equation (3).
where β is the maximum diffusion factor of the droplet and D0 is the initial particle size of the droplet.
2.7. Data Processing and Analysis
All statistical analyses were performed using SPSS software (version 22, IBM Corp., Armonk, NY, USA). Experimental results were expressed as means ± standard deviation (SD). To evaluate differences among multiple groups, a one-way analysis of variance (ANOVA) was conducted, followed by Duncan’s multiple range test for post hoc comparisons. This method was selected for its ability to detect significant differences between treatment means while controlling for Type I errors in multiple comparisons. A significance level of p < 0.05 was used to determine statistical significance.
3. Results and Discussion
In actual pesticide spraying, especially when using contact insecticides and fungicides, droplet deposition on both the upper and lower surfaces of leaves is crucial. This study focused on the behavior of electrostatic droplets impacting the adaxial (upper) surface of pepper leaves, systematically observing adhesion, fragmentation, and splashing phenomena, and analyzing the effects of charging voltage, impact velocity, impact location, and droplet size on deposition performance.
In the impact test of electrostatic droplets, the following three behaviors were observed: droplet adhesion, fragmentation, and splashing, with no rebound behavior occurring. Adhesive droplets are those that remain intact after impacting the leaf surface and are deposited on the leaf; fragmented droplets are droplets from which fine, small droplets are ejected from the boundary layer after impact but remain attached to the main droplet body, presenting small droplets protruding from the main body while still being deposited on the leaf surface; splashed droplets are those in which small droplets detach from the main droplet body upon impact with the leaf surface and scatter around, failing to be efficiently deposited on the leaf surface. In the electrostatic droplet impact test, it was found that adhesive droplets were predominant, with fragmentation and splashing occurring only at high impact velocities.
3.1. Droplet Spreading Behavior Under Different Applied Voltages
To investigate the effect of applied voltage on droplet impact behavior, the theoretical model of the maximum spreading factor previously developed by our group [41] was employed. In earlier studies involving uncharged droplets, it was found that the theoretical predictions of the maximum spreading factor on pepper leaves were generally higher than the experimental results [42]. This discrepancy was attributed to the model’s omission of air resistance caused by leaf bending and the variation in surface wettability at different leaf positions. Despite this deviation, the model remains valid for evaluating the influence of droplet charging on impact dynamics. The experimental results obtained under different applied voltages revealed the relationship between the theoretical and measured maximum spreading factors for both uncharged and electrostatically charged droplets, as shown in Figure 5. The red and blue lines in Figure 5 represent the error margins between the experimental and theoretical values of the maximum diffusion factor of the droplets. Specifically, in Figure 5a, the +10% line (blue line) corresponds to 1.1 times the actual test value compared to the theoretical predicted value, while the −4% line (red line) is 0.96 times the theoretical predicted value. In Figure 5b, the +11.5% line (blue line) represents 1.15 times the actual test value, and the 1:1 line (red line) indicates equality between the actual test value and the theoretical predicted value. In Figure 5c, the +12% line (blue line) is 1.12 times the actual test value, while the −3.5% line (red line) is 0.97 times the theoretical predicted value. From the experimental results, it can be observed that when the applied voltage is 14 kV, the error deviation between the theoretical and actual values ranges from −4% to 10%. As the applied electric field voltage increases, the theoretical model’s predicted value gradually exceeds the actual measured value. This phenomenon occurs because electrostatic droplets spread over a larger area than non-electrostatic droplets. In this study, the maximum spreading factor of charged droplets upon impact with pepper leaves was found to increase, indicating that droplet charging enhances wettability on the leaf surface. This observation is consistent with the findings of Chen et al. [43], who reported that electrostatic charging reduces the surface tension of droplets and decreases the contact angle on the leaf surface, thereby improving their wettability.
Figure 5.
Deviation of βT and βE at (a) 14 kV, (b) 16 kV, and (c) 18 kV charged voltage.
3.2. Behavior Analysis of Adherent Droplets
The droplet impact position, impact speed, droplet particle size, and the applied voltage to the composite inductive electrode plate all influence the droplet motion behavior. It was observed that with varying droplet particle sizes, impact speeds, applied voltages, and impact positions on the blade, the droplets exhibited three behaviors—adhesion, fragmentation, and splashing—after impacting the blade. No rebound behavior was observed.
3.2.1. Effects of Impact Position, Impact Velocity, Droplet Size, and Applied Voltage on Droplet Adhesion
To investigate the effect of each factor on droplet adhesion, the test results for all adherent droplets were extracted and analyzed using ANOVA in SPSS software. The results of the main effect analysis for the multiple factors are presented in Table 1. The four test factors—impact position, impact velocity, droplet size, and applied voltage—had significant effects on the maximum diffusion factor of the adherent droplets (p < 0.05). The adjusted R2 was 0.962, indicating that the ANOVA model explained 96.2% of the experimental results. The effect sizes of the four factors, listed in descending order of η2 deviations, were as follows: impact velocity (0.935), applied voltage (0.907), impact position (0.895), and droplet size (0.505). All four factors passed the significance test. According to the analysis results, among the four factors investigated in this study, impact velocity exhibited the most significant contribution to the overall variation in the maximum spreading factor, with a coefficient of determination (R2) of 0.935. This was followed by applied voltage (R2 = 0.907) and impact position (R2 = 0.895), while droplet diameter had the least influence (R2 = 0.505). These results indicate that the dynamic characteristics of droplet impact, such as velocity and charge, play a more dominant role in spreading behavior compared to geometric parameters like droplet size.

Table 1.
Analysis of variance (ANOVA) of the four factors selected in the experiment on the effect of the maximum diffusion factor.
To further understand the differences between the different levels of each factor, post hoc tests were conducted on the averages of each factor level using Duncan’s new complex polarity method. The four factors—droplet impact position, impact velocity, droplet particle size, and applied voltage—were examined individually. During the post hoc tests, the maximum diffusion factor of the droplet was calculated as the average of all levels of the other two factors. The results of the post hoc tests are shown in Table 2.

Table 2.
Post hoc test for the four factors selected in the experiment.
From the data in Table 2, it can be observed that there is a positive correlation between the impact location and the maximum diffusion factor of the droplet. The growth rate of the maximum diffusion factor between the impact point and the tip of the leaf, when the distance from the impact point to the tip of the leaf is between 20% and 40%, is 7.692%. The average increase in the maximum diffusion factor across different impact locations, from 20% to 80%, is 5.141%. Because the impact angle of droplets when they hit different positions of the blade changes and the elastic deformation of different positions of the blade is different after being impacted, the diffusion behavior of droplets is affected.
The impact velocity exhibited a positive correlation with the maximum spreading factor of the droplets. An increase in droplet impact velocity significantly enhances its spreading behavior on the leaf surface. When the impact velocity increased from 1.389 m/s to 2.750 m/s, the maximum spreading factor rose from 2.658 to 3.021, indicating that higher kinetic energy promotes greater spreading upon impact. A linear fit of the data yielded the equation y = 0.395x + 2.1331 with a coefficient of determination R2 = 0.986, indicating that for every 1 m/s increase in impact velocity, the maximum spreading factor increased by an average of 0.395. Within the selected experimental range, the droplet size also showed a positive correlation with the maximum spreading factor. The linear fitting equation was y = 0.0002x + 2.687, with an R2 value of 0.909, indicating that the maximum spreading factor increased by an average of 0.02 for every 100 μm increase in droplet size. As shown in Table 2, the maximum spreading factor of all charged droplets is higher than that of the uncharged droplets (2.732). With the increase in charging voltage from 14 kV to 18 kV, the maximum spreading factor on the leaf surface increases continuously, showing a clear linear positive correlation. The fitted linear equation was y = 0.068x + 1.956, with a coefficient of determination R2 = 0.999. This suggests that the maximum diffusion factor of the droplets increases by 0.068 for every 1 kV increase in charge voltage. In summary, all four factors exert a significant influence on the maximum spreading factor of droplets. Based on the average change in the spreading factor per unit increase, the order of influence from highest to lowest is impact velocity (0.395), charging voltage (0.068), impact position (0.051), and droplet diameter (0.002).
3.2.2. Growth Rate of Maximum Diffusion Factor of Droplet
To investigate the differences in adhesion behavior between electrostatic and non-electrostatic droplets upon impacting flexible pepper leaves, it is essential to compare the maximum diffusion factors of droplets with varying particle sizes at different impact positions on the leaves under different applied voltages. For ease of analysis and comparison, the difference between the maximum diffusion factor of electrostatic droplets and that of non-electrostatic droplets is defined as the growth rate of the maximum diffusion factor (βg). The growth rate of the maximum diffusion factor under different conditions and levels is shown in Figure 6.
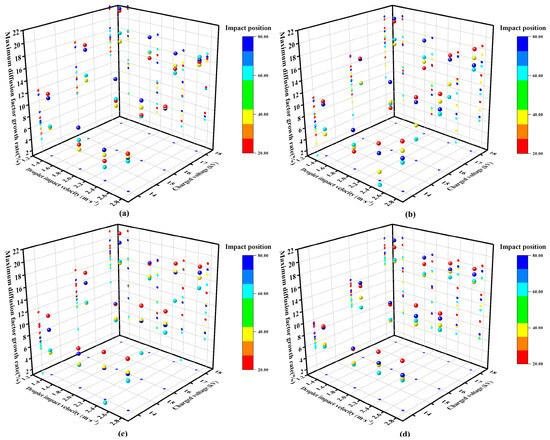
Figure 6.
Growth rates of the maximum diffusion factor for droplets of (a) 1051 μm, (b) 1413 μm, (c) 1647 μm, and (d) 1741 μm impacting flexible chili pepper blades at varying charging voltages.
The projections of the droplet maximum diffusion factor growth rate values on different surfaces in Figure 6 illustrate the correlation between each factor and the droplet’s maximum diffusion factor growth rate. The colors of the data points reflect the relationship between the droplet maximum diffusion factor and the impact location. From Figure 6, it is evident that the growth rate of the maximum diffusion factor for electrostatic droplets exhibits a clear positive correlation with the charging voltage compared to uncharged droplets. Additionally, the growth rate of the maximum diffusion factor first decreases and then increases with the droplet impact velocity. A slight increase in the growth rate is observed at an impact velocity of 2.750 m/s. This phenomenon may be related to the droplet approaching the splash threshold, with some droplets breaking through the boundary layer and fragmenting slightly. The growth rate of the maximum diffusion factor does not show a significant correlation with the impact location. This lack of correlation may be attributed to the varying dielectric constants of different parts of the leaf, leading to a more unpredictable effect on the charged droplets. Furthermore, the growth rate of the maximum diffusion factor is negatively correlated with the droplet particle size.
3.3. Analysis of Splash Behavior in Droplets
The effect of different charging voltages on the splash threshold of droplets was investigated by comparing the impact behavior of charged and uncharged droplets. It was found that, although charging the droplets leads to splashing, the fine droplets generated during the splash are more likely to adhere to the leaf surface, as shown in Figure 7.

Figure 7.
Droplet impact and splash behavior at a charge voltage of 14 kV: (a) initial state, (b) initial spreading, (c) onset of fragmentation, and (d) steady state.
3.3.1. Effects of Droplet Size, Impact Velocity, Impact Position, and Charge Voltage on Droplet Splashing
To investigate the correlation between the initial droplet size, impact velocity, impact location, and applied voltage with droplet splashing behavior, the experimental data for both adherent and splashing droplets were extracted and combined. Adherent droplets were labeled as 0, and splashing droplets were labeled as 1. The labeled data were analyzed using the Kruskal–Wallis rank-sum test for non-parametric correlation analysis. The p-values for all four tested factors were less than 0.001, indicating that each factor was significantly correlated with droplet splashing. Subsequently, a binary logistic regression analysis was performed on the combined dataset. The Hosmer–Lemeshow test yielded a significance value of 0.520, which is greater than 0.05, indicating a good model fit and statistical validity of the data. Table 3 presents the results of the binary logistic regression analysis. The p-values for all four factors influencing droplet splashing were less than 0.05, confirming their significant effects. Based on the partial regression coefficients, it can be concluded that larger charge voltage, larger droplet size, and higher impact velocity all increase the likelihood of droplet splashing upon impact. Furthermore, using the impact point located at 20% of the distance to the leaf tip as the reference category, it was found that the farther the impact location from the leaf tip, the more likely splashing occurred. The odds ratio represents the change in the likelihood of droplet splashing versus non-splashing for each unit increase in the independent variable. According to the data presented in Table 3, the odds ratios for the four experimental factors affecting droplet splashing are ranked in descending order as follows: impact velocity (odds ratio >> 1), charging voltage (odds ratio = 1.246), droplet size (odds ratio = 1.023), and impact location (odds ratio < 1).

Table 3.
Binary logistic regression analysis of droplet splash behavior based on four experimental factors.
3.3.2. Splash Critical Value Analysis
Mundo et al. [44] investigated the impact behavior of droplets on stainless steel surfaces through experimental and theoretical analyses and established a dimensionless number, Kcrit = Oh · Re1.25, to define the boundary between droplet adhesion and splashing, with a critical value of 57.7. However, the critical value varies depending on the surface characteristics and liquid properties [45]. For instance, the critical K value increases as surface roughness decreases, and Yoon et al. [46] found that when droplets impact a paraffin surface, the critical value reaches 152. In practical agricultural spray applications, droplet impacts are often not strictly perpendicular to surfaces, and the surface properties are more complex [47]. In their study, Forster et al. [48] found that for hydrophilic surfaces (static contact angle < 90°), Kcrit can be predicted based on the static contact angle CA20%acetone of a 20% acetone solution on the target surface using the model Kcrit = −0.584(CA20%acetone) + 147. Using the above contact angle measurement method, the contact angles of the 20% acetone solution measured at 20%, 40%, 60%, and 80% distances from the base to the tip of the leaf were 92.1°, 88.9°, 86.0°, and 83.1°, respectively. The corresponding contact angles for distilled water were 94.9°, 89.3°, 87.1°, and 84.5°, respectively.
To investigate the critical splashing behavior of droplets on flexible chili pepper leaves, this study defines the critical splashing velocity as the minimum impact velocity at which a droplet transitions from deposition or spreading to splashing. This is characterized by the ejection of secondary droplets from the impact region. To quantitatively describe this critical condition, we refer to the splash characterization parameter K = We0.5·Re0.25 established in the previous literature [44], where We is the Weber number and Re is the Reynolds number of the droplet at the moment of impact on the target surface. The critical splashing velocities of charged droplets under different charging voltages were experimentally determined, and the results are presented in Figure 8. Based on previous research findings, charging droplets typically reduces their surface tension, viscosity, and contact angle as the applied voltage increases [6]. Therefore, the observed decrease in the critical splashing velocity of charged droplets aligns well with theoretical expectations. Figure 8 compares the critical splashing velocities of droplets impacting different positions on pepper leaves for both charged and uncharged droplets across four particle sizes. As shown in Figure 8, with the increase in droplet diameter, both mass and impact kinetic energy increase, making it easier for the droplet to overcome surface tension and induce splashing, thus reducing the critical splashing velocity. However, due to the flexible structure of chili pepper leaves, larger droplets cause local bending or twisting upon impact, which absorbs part of the kinetic energy and suppresses the splashing tendency, leading to a reduced rate of decline in the critical velocity. At different impact positions, the critical splashing curves of charged droplets exhibit a similar overall trend to those of uncharged droplets. However, the critical curves for charged droplets lie consistently below those of uncharged ones, indicating that charging the droplets reduces their critical splashing threshold. In addition, within the tested voltage range, the critical splashing velocity shows a slight increase with rising charging voltage. This phenomenon is attributed to the fact that, when droplets are near the transition between breakup and splashing states, the broken droplets can still adhere rapidly to the leaf surface due to the electrostatic attraction.
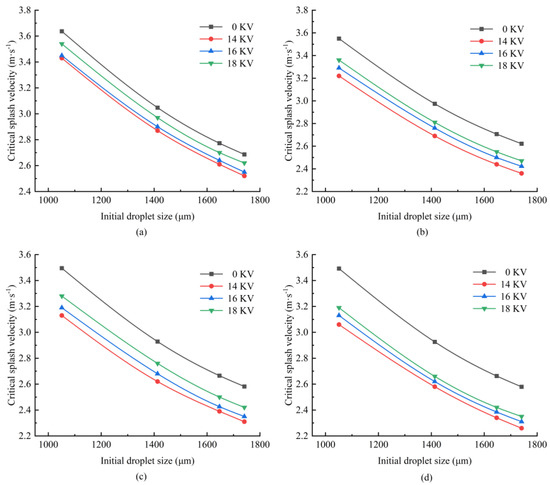
Figure 8.
Critical splashing velocity of droplets at different charging voltages impacting pepper leaves at (a) 20% of the distance to the leaf tip, (b) 40% of the distance to the leaf tip, (c) 60% of the distance to the leaf tip, and (d) 80% of the distance to the leaf tip.
4. Conclusions
This study investigated the impact behavior of electrostatically charged droplets on flexible pepper leaves under varying charging voltages, impact velocities, droplet sizes, and impact locations. The main conclusions are as follows:
(1) Three distinct behaviors—adhesion, fragmentation, and splashing—were observed when charged droplets impacted the pepper leaf surface. During fragmentation, fine secondary droplets were effectively re-deposited onto the leaf surface due to electrostatic attraction.
(2) The maximum spreading factor of charged droplets increased with the applied voltage. Analysis of variance (ANOVA) showed that all four factors had a significant effect on droplet spreading (p < 0.05). The effect sizes (partial η2) were as follows: impact velocity (0.935) > charging voltage (0.907) > impact location (0.895) > droplet size (0.505), indicating that charging voltage had the second greatest influence on spreading behavior after impact velocity.
(3) Charging the droplets reduced their critical splashing velocity to a certain extent, although this critical velocity increased with higher charging voltages. The relative importance of the four factors on droplet splashing was ranked as follows: impact velocity (>>1) > charging voltage (1.246) > droplet size (1.023) > impact location (<1).
Author Contributions
Conceptualization, K.W.; Methodology, K.W., S.W. and T.W.; Software, K.W., X.D., L.D., X.W., X.L. and B.Q.; Validation, X.L.; Formal analysis, K.W., S.W., Z.G. and T.W.; Investigation, K.W. and X.L.; Resources, X.D.; Data curation, K.W., S.W., L.D. and X.W.; Writing—original draft, K.W.; Writing—review & editing, K.W., X.D. and S.W.; Visualization, Z.G. and X.W.; Supervision, Z.G.; Project administration, X.D., L.D. and B.Q.; Funding acquisition, X.D. and B.Q. All authors have read and agreed to the published version of the manuscript.
Funding
The present study was supported by grants from the Project Funded by the Priority Academic Program Development of Jiangsu Higher Education Institutions (No. PAPD2023-87), the National Key Research and Development Plan (No. 31971790), and the Key Research and Development Program of Jiangsu Province (No. BE2020328).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Han, D.; Yoo, D.; Kim, T. Analysis of Social Welfare Impact of Crop Pest and Disease Damages Due to Climate Change: A Case Study of Dried Red Peppers. Humanit. Soc. Sci. Commun. 2023, 10, 378. [Google Scholar] [CrossRef]
- Zheng, L.; Cao, C.; Cao, L.; Chen, Z.; Huang, Q.; Song, B. Bounce Behavior and Regulation of Pesticide Solution Droplets on Rice Leaf Surfaces. J. Agric. Food. Chem. 2018, 66, 11560–11568. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.; Yang, S.; Gao, Y.; Wang, Z.; Zhai, C.; Qiu, W. Evaluation of Spray Drift from an Electric Boom Sprayer: Impact of Boom Height and Nozzle Type. Agronomy 2025, 15, 160. [Google Scholar] [CrossRef]
- Tavares, R.M.; Cunha, J.P.; Alves, T.C.; Bueno, M.R.; Silva, S.M.; Zandonadi, C.H. Electrostatic Spraying in the Chemical Control of Triozoida Limbata (Enderlein) (Hemiptera: Triozidae) in Guava Trees (Psidium guajava L.). Pest Manag. Sci. 2017, 73, 1148–1153. [Google Scholar] [CrossRef]
- Salcedo, R.; Sánchez, E.; Zhu, H.; Fàbregas, X.; García-Ruiz, F.; Gil, E. Evaluation of an Electrostatic Spray Charge System Implemented in Three Conventional Orchard Sprayers Used on a Commercial Apple Trees Plantation. Crop Prot. 2023, 167, 106212. [Google Scholar] [CrossRef]
- Appah, S.; Zhou, H.; Wang, P.; Ou, M.; Jia, W. Charged Monosized Droplet Behaviour and Wetting Ability on Hydrophobic Leaf Surfaces Depending on Surfactant-Pesticide Concentrate Formulation. J. Electrostat. 2019, 100, 103356. [Google Scholar] [CrossRef]
- Xu, H.; Wang, J.; Wang, Z.; Yu, K.; Xu, H.; Wang, D.; Zhang, W. Impact Dynamics of a Charged Droplet onto Different Substrates. Phys. Fluids 2021, 33, 102111. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, B.; Huang, K.; Wang, S.; Quirino, R.L.; Zhang, Z.; Zhang, C. Eco-Friendly Castor Oil-Based Delivery System with Sustained Pesticide Release and Enhanced Retention. ACS Appl. Mater. Interfaces 2020, 12, 37607–37618. [Google Scholar] [CrossRef]
- Sun, Y.; Huang, X.; Soh, S. Solid-to-liquid Charge Transfer for Generating Droplets with Tunable Charge. Angew. Chem. Int. Ed. 2016, 55, 9956–9960. [Google Scholar] [CrossRef]
- Appah, S.; Jia, W.; Ou, M.; Wang, P.; Gong, C. Investigation of Optimum Applied Voltage, Liquid Flow Pressure, and Spraying Height for Pesticide Application by Induction Charging. Appl. Eng. Agric. 2019, 35, 795–804. [Google Scholar] [CrossRef]
- Higuera, F.J. Neutralization of a Spray of Electrically Charged Droplets by a Corona Discharge. J. Fluid Mech. 2016, 801, 130–149. [Google Scholar] [CrossRef]
- Hislop, E.C. Electrostatic Ground-Rig Spraying: An Overview. Weed Technol. 1988, 2, 94–105. [Google Scholar] [CrossRef]
- Appah, S.; Wang, P.; Ou, M.; Gong, C.; Jia, W. Review of Electrostatic System Parameters, Charged Droplets Characteristics and Substrate Impact Behavior from Pesticides Spraying. Int. J. Agric. Biol. Eng. 2019, 12, 1–9. [Google Scholar] [CrossRef]
- Gao, J.; Xu, K.; He, R.; Chen, X.; Hussain Tunio, M. Development and Experiments of Low Frequency Ultrasonic Electrostatic Atomizing Nozzle with Double Resonators. Int. J. Agric. Biol. Eng. 2022, 15, 39–48. [Google Scholar] [CrossRef]
- Dai, S.; Zhang, J.; Jia, W.; Ou, M.; Zhou, H.; Dong, X.; Chen, H.; Wang, M.; Chen, Y.; Yang, S. Experimental Study on the Droplet Size and Charge-to-Mass Ratio of an Air-Assisted Electrostatic Nozzle. Agriculture 2022, 12, 889. [Google Scholar] [CrossRef]
- Patel, M.K.; Ghanshyam, C.; Kapur, P. Characterization of Electrode Material for Electrostatic Spray Charging: Theoretical and Engineering Practices. J. Electrostat. 2013, 71, 55–60. [Google Scholar] [CrossRef]
- Lin, Z.; Xie, J.; Tian, S.; Wang, X.; Sun, W.; Mo, X. Research and Experiment of Electrostatic Spraying System for Agricultural Plant Protection Unmanned Vehicle. Front. Ecol. Evol. 2023, 11, 1138180. [Google Scholar] [CrossRef]
- Sánchez-Hermosilla, J.; Pérez-Alonso, J.; Martínez-Carricondo, P.; Carvajal-Ramírez, F.; Agüera-Vega, F. Evaluation of Electrostatic Spraying Equipment in a Greenhouse Pepper Crop. Horticulturae 2022, 8, 541. [Google Scholar] [CrossRef]
- Deng, Q.; Wang, H.; Xie, Z.; Zhou, X.; Tian, Y.; Zhang, Q.; Zhu, X.; Chen, R.; Liao, Q. Behaviors of the Water Droplet Impacting on Subcooled Superhydrophobic Surfaces in the Electrostatic Field. Chem. Eng. Sci. 2023, 266, 118282. [Google Scholar] [CrossRef]
- Kumar, A.; Ahmad, I.; Pathak, M. Droplet Impact on a Hydrophobic Surface Integrated with Electrowetting Technique. Colloids Surf. A 2023, 656, 130423. [Google Scholar] [CrossRef]
- Appah, S.; Jia, W.; Ou, M.; Wang, P.; Asante, E.A. Analysis of Potential Impaction and Phytotoxicity of Surfactant-Plant Surface Interaction in Pesticide Application. Crop Prot. 2020, 127, 104961. [Google Scholar] [CrossRef]
- Gong, C.; Jia, F.; Kang, C. Deposition of Water and Emulsion Hollow Droplets on Hydrophilic and Hydrophobic Surfaces. Agriculture 2024, 14, 960. [Google Scholar] [CrossRef]
- Srivastava, T.; Jena, S.K.; Kondaraju, S. Droplet Impact and Spreading on Inclined Surfaces. Langmuir 2021, 37, 13737–13745. [Google Scholar] [CrossRef]
- He, Y.; Wu, J.; Xiao, S.; Fang, H.; Zheng, Q. Investigating the Wettability of Rapeseed Leaves. Appl. Eng. Agric. 2021, 37, 399–409. [Google Scholar] [CrossRef]
- Hu, B.; Li, H.; Jiang, Y.; Tang, P.; Du, L. Review of the Interaction Mechanism for Droplets and Foliage under Sprinkler Irrigation and Water-Fertilizer Integration. Int. J. Agric. Biol. Eng. 2024, 17, 31–43. [Google Scholar] [CrossRef]
- Wu, S.; Liu, J.; Wang, J.; Hao, D.; Wang, R. The Motion of Strawberry Leaves in an Air-Assisted Spray Field and Its Influence on Droplet Deposition. Trans. Asabe 2021, 64, 83–93. [Google Scholar] [CrossRef]
- Li, Q.-P.; Ouyang, Y.; Niu, X.-D.; Jiang, Y.; Wen, M.-F.; Li, Z.-Q.; Chen, M.-F.; Li, D.-C.; Yamaguchi, H. Maximum Spreading of Impacting Ferrofluid Droplets under the Effect of Nonuniform Magnetic Field. Langmuir 2022, 38, 2601–2607. [Google Scholar] [CrossRef]
- Tan, J.; Wang, H.; Sun, M.; Tian, P.; Wang, Y.; Wang, K.; Jiang, D. Regulating Droplet Impact on a Solid Hydrophobic Surface through Alternating Current Electrowetting-on-Dielectric. Phys. Fluids 2021, 33, 42101. [Google Scholar] [CrossRef]
- Pan, L.; Chen, Y.; Li, Z.; Xie, X. Dynamical Behaviors of Nanodroplets Impinging on Solid Surfaces in the Presence of Electric Fields. Nanoscale 2023, 15, 6215–6224. [Google Scholar] [CrossRef]
- Kaiser, E.; Morales, A.; Harbinson, J.; Kromdijk, J.; Heuvelink, E.; Marcelis, L.F.M. Dynamic Photosynthesis in Different Environmental Conditions. J. Exp. Bot. 2015, 66, 2415–2426. [Google Scholar] [CrossRef]
- Myster, J.; Moe, R. Effect of Diurnal Temperature Alternations on Plant Morphology in Some Greenhouse Crops—A Mini Review. Sci. Hortic. 1995, 62, 205–215. [Google Scholar] [CrossRef]
- Stuerz, S.; Asch, F. Responses of Rice Growth to Day and Night Temperature and Relative Air Humidity—Dry Matter, Leaf Area, and Partitioning. Plants 2019, 8, 521. [Google Scholar] [CrossRef]
- Wang, Z.; Zheng, C.; Li, T.; He, X. Analysing the Preference for Pesticide Spray to Be Deposited at Leaf-Tips. Biosyst. Eng. 2021, 204, 247–256. [Google Scholar] [CrossRef]
- Cerkanowicz, A.E. Rayleigh Limit for Nonstationary Charged Drops. In Proceedings of the 1981 Annual Meeting Industry Applications Society, Philadelphia, PA, USA, 5–9 October 1981; pp. 1161–1165. [Google Scholar]
- Ding, S.; Hu, Z.; Dai, L.; Zhang, X.; Wu, X. Droplet Impact Dynamics on Single-Pillar Superhydrophobic Surfaces. Phys. Fluids 2021, 33, 102108. [Google Scholar] [CrossRef]
- Qiu, W.; Guo, H.B.; Zheng, H.; Cao, Y.B.; Lv, X.; Fang, J.; Zhai, C.Y.; Yu, H.F. CFD Modelling to Analyze the Droplets Deposition Behavior on Vibrating Rice Leaves. Comput. Electron. Agric. 2022, 201, 107330. [Google Scholar] [CrossRef]
- Zhang, Z. A Flexible New Technique for Camera Calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Liu, D.; Zhou, H.; Zheng, J.; Ru, Y. Study on oblique impact behavior of spray droplets on tea leaf surface. J. Agric. Mach. 2019, 50, 96–103. [Google Scholar]
- Massinon, M.; Lebeau, F. Experimental Method for the Assessment of Agricultural Spray Retention Based on High-Speed Imaging of Drop Impact on a Synthetic Superhydrophobic Surface. Biosyst. Eng. 2012, 112, 56–64. [Google Scholar] [CrossRef]
- Yarin, A.L. DROP IMPACT DYNAMICS: Splashing, Spreading, Receding, Bouncing…. Annu. Rev. Fluid Mech. 2006, 38, 159–192. [Google Scholar] [CrossRef]
- Wang, S.; Zhao, X.; Gao, Z.; Zhu, C.; Dong, L.; Qiu, B. Study on the impact behavior of droplets on the surface of flexible pepper leaves. J. Agric. Mach. 2024, 55, 188–201. [Google Scholar] [CrossRef]
- Dong, X.; Dong, L.; Gao, Z.; Wang, K.; Wang, X.; Wang, S.; Qiu, B.; Wang, X. Droplet Deposition Behavior on the Surface of Flexible Pepper Leaves. Agronomy 2025, 15, 708. [Google Scholar] [CrossRef]
- Chen, D.-R.; Pui, D.Y.H. Experimental Investigation of Scaling Laws for Electrospraying: Dielectric Constant Effect. Aerosol Sci. Technol. 1997, 27, 367–380. [Google Scholar] [CrossRef]
- Mundo, C.; Sommerfeld, M.; Tropea, C. Droplet-Wall Collisions: Experimental Studies of the Deformation and Breakup Process. Int. J. Multiph. Flow 1995, 21, 151–173. [Google Scholar] [CrossRef]
- Wal, R.L.V.; Berger, G.M.; Mozes, S.D. The Splash/Non-Splash Boundary upon a Dry Surface and Thin Fluid Film. Exp. Fluids 2006, 40, 53–59. [Google Scholar] [CrossRef]
- Yoon, S.S.; DesJardin, P.E.; Presser, C.; Hewson, J.C.; Avedisian, C.T. Numerical Modeling and Experimental Measurements of Water Spray Impact and Transport over a Cylinder. Int. J. Multiph. Flow 2006, 32, 132–157. [Google Scholar] [CrossRef]
- Delele, M.A.; Nuyttens, D.; Duga, A.T.; Ambaw, A.; Lebeau, F.; Nicolai, B.M.; Verboven, P. Predicting the Dynamic Impact Behaviour of Spray Droplets on Flat Plant Surfaces. Soft Matter 2016, 12, 7195–7211. [Google Scholar] [CrossRef]
- Forster, W.; Mercer, G.N.; Schou, W. Process-Driven Models for Spray Droplet Shatter, Adhesion or Bounce. In Proceedings of the 9th International Symposium on Adjuvants for Agrochemicals, Freising, Germany, 16–20 August 2010; p. 285. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).