Human-Following Strategy for Orchard Mobile Robot Based on the KCF-YOLO Algorithm

Abstract

Autonomous mobile robots play a vital role in the mechanized production of orchards, where human-following is a crucial collaborative function. In unstructured orchard environments, obstacles often obscure the path, and personnel may overlap, leading to significant disruptions to human-following. This paper introduces the KCF-YOLO fusion visual tracking method to ensure stable tracking in interference environments. The YOLO algorithm provides the main framework, and the KCF algorithm intervenes in assistant tracking. A three-dimensional binocular-vision reconstruction method was used to acquire personnel positions, achieving stabilized visual tracking in disturbed environments. The robot was guided by fitting the personnel’s trajectory using an unscented Kalman filter algorithm. The experimental results show that, with 30 trials in multi-person scenarios, the average tracking success rate is 96.66%, with an average frame rate of 8 FPS. Additionally, the mobile robot is capable of maintaining a stable following speed with the target individuals. Across three human-following experiments, the horizontal offset Error Y does not exceed 1.03 m. The proposed KCF-YOLO tracking method significantly bolsters the stability and robustness of the mobile robot for human-following in intricate orchard scenarios, offering an effective solution for tracking tasks.

1. Introduction

The increasing use of autonomous mobile robots in collaborative transportation tasks has positioned this field as a rapidly advancing research area [1,2,3,4,5,6,7]. Over the past two decades, significant advancements in sensor technology, robotic hardware, and software have driven the widespread adoption of mobile robots in diverse industries [8,9,10,11,12,13]. In agriculture, collaborative mobile robots have emerged as key replacements for labor-intensive tasks, highlighting their potential as essential servo technologies. Human-following technology has attracted considerable attention in structured environments, such as factory logistics, transportation, and airport operations, and has seen partial commercialization [14,15,16]. However, this technology is still experimental in complex orchard environments. The complex nature of an orchard environment, coupled with numerous obstacles and occlusions, makes the human tracking process susceptible to recognition failure, target loss, and other problems. These challenges lead to the failure of the mobile tracking function of robots, which is a significant obstacle to the successful operation of mobile robots.

To handle the aforementioned challenges, this paper proposes a human-following strategy for an orchard mobile robot based on KCF-YOLO. The method includes two main components: personnel detection and tracking, and human-following. The KCF algorithm, as a traditional visual tracking method, mainly achieves target tracking by adopting a histogram of oriented gradients (HOG) features, which results in higher tracking accuracy compared to grayscale or color feature methods. The YOLO v5s algorithm, as an efficient object detection algorithm, boasts excellent detection speed and accuracy. Therefore, this method combines the strengths of both the KCF and YOLO v5s algorithms, achieving continuous and stable tracking of target individuals in orchard environments (Section 3.3). Building upon stable visual tracking, spatial information of individuals is obtained through binocular stereo vision methods and transformed into coordinates in the vehicle’s frame. Due to the potential positional oscillations in the three-dimensional spatial information acquired through cameras, dynamic modeling of target trajectories is implemented. The unscented Kalman filter (UKF) is introduced to predict the trajectories of individuals (Section 3.4), thereby enhancing the stability of following. Simultaneously, multi-person interference experiments are conducted on the KCF-YOLO algorithm to evaluate its robustness. Furthermore, the integration of the KCF-YOLO algorithm onto a mobile robot is performed to assess its performance in real orchard environments (Section 4.2).

This study aimed to devise a method for accurately recognizing and tracking a target within a complex scene, thereby achieving stable mobile robots in such intricate environments. The main contributions of this paper are summarized as follows:

• A visual tracking algorithm is proposed in the paper, with the YOLO algorithm as the main framework and the KCF algorithm introduced for auxiliary tracking, aiming to achieve continuous and stable tracking of targets in orchard environments.
• A KCF-YOLO human-following framework has been constructed in the paper, which can be employed for human-following based on visual mobile robots in real orchard scenarios.

The remainder of this paper is organized as follows: In Section 2, related works are discussed. Section 3 provides a detailed description of the proposed KCF-YOLO visual tracking algorithm, along with the human-following method. Section 4 describes the experimental validation of the proposed algorithm and discusses the experimental results. Finally, Section 5 concludes the paper with a summary and outlook on the proposed methodology.

2. Related Works

With the rapid development of computer vision technology, human-following methods based on machine vision have received widespread attention [17,18,19]. These methods involve two crucial steps: the first is target detection and tracking, and the second is human-following. For target detection and visual tracking, Bolme et al. [20] proposed a minimum output sum of squares of error filter that generates a stable correlation filter via single-frame initialization to enhance the tracking robustness against rotation, scale variation, and partial occlusion. However, this method is sensitive to changes in the target color and brightness, making it prone to tracking errors when the target moves rapidly or closely resembles the background. Henriques et al. [21] proposed a high-speed kernel correlation factor (KCF) algorithm that uses a cyclically shifted ridge regression method to reduce memory and computation significantly, thereby improving the execution speed of the algorithm. When encountering changes in the appearance of non-rigid targets, such as the human body, adaptation through the online updating of the tracking model is essential.

Nonetheless, online updating can lead to drifts in tracking. To solve the drift problem, Liu et al. proposed a real-time target response-adaptive and scale-adaptive KCF tracker that can detect and recover from drifts [22]. Despite this, drift errors persist in long-term target tracking, impacting the system robustness owing to frequent changes in the target attitude and appearance. To mitigate the error caused by tracking drift and enhance system robustness, Huan et al. proposed a tracking method using a structured support vector machine and the KCF algorithm [23]. This approach optimizes the search strategy for tracking the motion characteristics of a target, thereby reducing the search time for dense sampling. Consequently, it improves the search efficiency and classifier accuracy compared with the traditional KCF algorithm in the setting of a dense sample. Search efficiency and classifier accuracy in dense sampling improve computational efficiency and target tracking performance in complex environments, solving the problem of failing to accurately track the target owing to the drift caused by changes in target size and rapid movement. Nevertheless, the KCF algorithm faces the significant drawback of poor tracking robustness owing to obstacle occlusion. Bai et al. introduced the KCF-AO algorithm to solve the tracking failure problem caused by occlusion in the KCF algorithm [24]. This algorithm employs the confidence level of the response map to assess the tracking result of each frame. In cases where the target disappearance is detected, it employs the A-KAZE feature point matching algorithm and the normalized correlation coefficient matching algorithm to complete the redetection of the target. The position information is then fed back to KCF to resume tracking, which improves the robustness of the tracking performance of the KCF algorithm. Mbelwa et al. proposed a tracker based on object proposals and co-kernelized correlation filters (Co-KCF) [25]. This tracker utilizes object proposals and global predictions estimated using a kernelized correlation filter scheme. Through a spatial weight strategy, it selects the optimal proposal as prior information to enhance tracking performance in scenarios involving fast motion and motion blur. Moreover, it effectively handles target occlusions, overcoming issues such as drift caused by illumination variations and deformations. The studies mentioned underscore researchers’ substantial contributions to overcome challenges related to obstacle occlusion, target size variation, and the rapid movement faced by the KCF algorithm in mobile robot tracking. These findings pave the way for novel advancements in visually guided human-following techniques. However, the KCF target-tracking algorithm is computationally complex, and detection accuracy based on artificially designed features is unsatisfactory for partially occluded human bodies.

In contrast, deep learning methods offer innovative approaches in the realm of people detection and following. Gupta et al. proposed the use of the mask region-based convolutional neural network (mask RCNN) and YOLO v2-based CNN architectures for personnel localization, along with speed-controlled tracking algorithms [26]. Boudjit et al. introduced a target-detecting unmanned aerial vehicle (UAV) following a method based on the YOLO-v2 architecture and achieved UAV target tracking by combining detection algorithms with proportional–integral–derivative control [27]. Additionally, the single-shot multi-box detector (SSD) target detection algorithm proposed by Liu et al. is even faster than the so-called faster RCNN detection method. It offers a significant advantage in the mean average precision achieved compared with YOLO [28]. Algabri et al. presented a framework combining an SSD detection algorithm and state-machine control to identify a target person by extracting color features from video sequences using H-S histograms [29]. This framework enables a mobile robot to effectively identify and track a target person. The aforementioned methods involve integrating deep learning with traditional computer vision techniques for fine-grained target detection and tracking.

Stably following a target person in complex scenarios poses a significant challenge in human-following. In the following problem, effectively avoiding obstacles while continuously following a target and keeping the target within the robot’s field of view is an important part of realizing a human-following task. Han et al. utilized the correlation filter tracking algorithm to track the target individual [30]. In instances of tracking failure, they introduced facial matching technology for re-tracking, achieving continuous tracking of the target person in indoor environments and improving the stability of the tracking process. Cheng-An et al. obtained obstacle and human features using an RGB-D camera and estimated the next moment state of pedestrians using the extended Kalman filter (EKF) algorithm to achieve stable human-following in indoor environments [31]. However, outdoor environments are more complex than indoor environments. Human stability is affected by various factors, including diverse terrains, unstructured obstacles, and dynamic pedestrian movements. Gong et al. proposed a point cloud-based algorithm, employing a particle filter to continuously track the target’s position. This enables the robot to detect and track the target individual in outdoor environments [32]. Tsai et al. achieved human-following in outdoor scenes using depth sensors to determine the distance between the tracking target and obstacles [33]. A Kalman filter predicts the target person’s position based on the relative distance between the mobile robot and the target person. However, the applicability of this method is limited to relatively simple scenes, making it unstable in complex orchard environments.

Human-following techniques for orchard environments face a lack of effective solutions. The traditional KCF algorithm exhibits instability when confronted with challenges, such as obstacle occlusion, variations in target size, and rapid movements. Consequently, they lack persistent tracking capabilities for specific individuals or targets, which restricts their effectiveness in orchards. Although the YOLO target detection algorithm demonstrated high accuracy in orchards, its role as a detection tool limited its ability to track specific individuals, limiting its applicability in complex scenarios. Ensuring stability and devising effective strategies for robots are paramount in an unstructured orchard environment. The absence of state estimation and prediction capabilities in robots operating in uncertain and complex environments results in a lack of stability in target following. Therefore, a novel human-following strategy is proposed to enhance the robustness of target tracking and improve the adaptability and stability of robot movements in orchard scenarios.

3. Algorithm

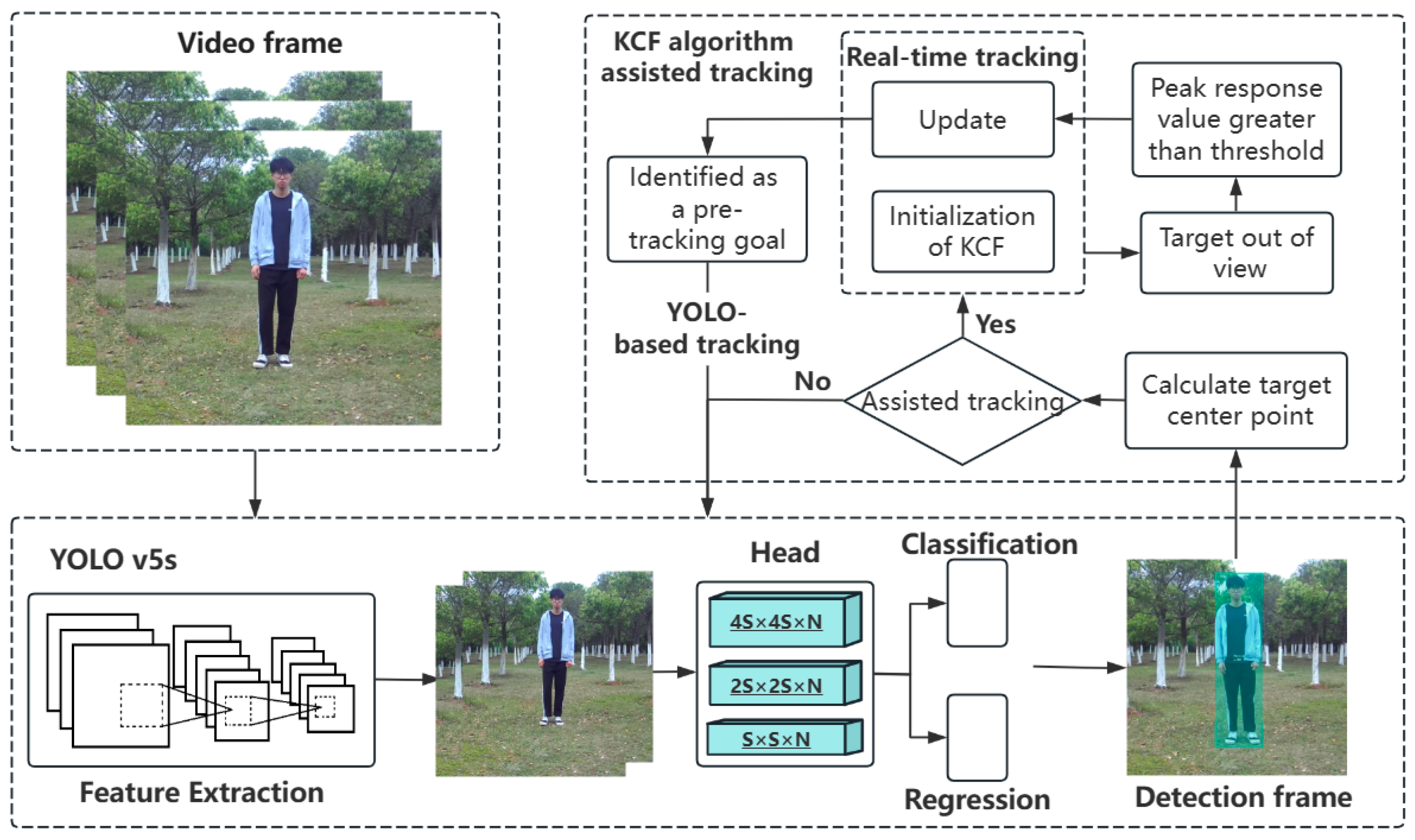
Based on the KCF and the YOLO v5s algorithms, this paper proposes a comprehensive human-following system framework. This framework utilizes camera sensors to acquire three-dimensional spatial information of individuals, which is then transformed into the coordinate system of a mobile robot. The unscented Kalman filter (UKF) algorithm is employed to predict the trajectory of individuals based on their three-dimensional information. When the target individual moves out of the robot’s field of view, the KCF-YOLO algorithm is used to retrack the target individual upon re-entry into the field of view, enabling continuous tracking of individuals. The overall framework of the human-following system is illustrated in Figure 1.

3.1. Kernel Correlation Filter (KCF)

The KCF is a target-tracking algorithm based on online learning that encompasses three key steps: feature extraction, online learning, and template updating. Initially, the algorithm extracts HOG features from the target, generating a Fourier response. Subsequently, the correlation of the Fourier response is computed to estimate the target location. Following that, the classifier is trained by cyclically shifting image blocks around the target location and adjusting the weights of the KCFs through a ridge regression formulation. Continuous target tracking is achieved through online learning and updating, leveraging the real-time detected target position and adjusted filter weights. The flow of the KCF algorithm is illustrated in Figure 2.

In Step 1, the HOG feature extraction process is illustrated. In Step 2, F (u, v), a complex-valued spectrum in the frequency domain, represents information regarding the frequency component (u, v). f (x, y) denotes the pixel intensity value at coordinates (x, y) in the image, and R (x, y) signifies the response at position (x, y) in the image. In Step 3, the template update process in the KCF algorithm is elucidated, where FFT represents the fast Fourier transform, and IFFT represents the inverse Fourier transform. The Gaussian kernel function in the KCF algorithm plays a crucial role in modeling the similarity between the target and candidate regions. The sigma value, an essential parameter of the Gaussian kernel function, determines the bandwidth of the Gaussian kernel function, thereby directly affecting the stability of the KCF algorithm. The Gaussian kernel function in the frequency domain is typically represented as shown in Equation (1).

$$K\left(u,v\right)=e^{-2{\pi }^2{\sigma }^2\left(u^2+v^2\right)}$$

(1)

The KCF algorithm demonstrates robust real-time capabilities and accuracy in practical applications, particularly in real-time video target tracking, and effectively addresses the challenges associated with target deformation and scale changes. However, in complex orchard environments, the robustness of the tracking performance of the KCF algorithm diminishes because of factors such as occlusions between trees. Therefore, the integration of additional techniques is essential to enhance the tracking performance in specific application scenarios.

3.2. YOLO

The YOLO series of algorithms is a fast and efficient object detection algorithm that can perform object detection and classification directly in the entire image. It provides both the position and category probability for each detected object box [34]. The network structure of the YOLO v5s algorithm was categorized into four modules: input, backbone, neck, and prediction. The network architecture is shown in Figure 3.

Initially, the preprocessed image undergoes characterization and a series of convolutional processes in the backbone layer. Subsequently, the neck layer integrates the feature pyramid network and path aggregation network to construct multi-scale feature information. Finally, the prediction layer utilizes three feature maps to predict the target class and generate information regarding the target box location.

The algorithm proposed in this paper serves as a framework, not limited to a specific version of YOLO. The YOLOv5s algorithm strikes a balance between performance and speed, catering to specific scenarios and the requirements of existing hardware. Simultaneously, its deployment is more straightforward on mobile robots. While higher versions may offer additional features, they demand increased computational resources. In the context of mobile robot tracking tasks, real-time information is crucial for system stability. Therefore, this study harnesses the advantages of YOLO v5s regarding target detection accuracy, coupled with its real-time capabilities and adaptability to the continuous tracking of KCF. A target detection algorithm that integrates the strengths of both approaches to enhance the stability and reliability of target visual tracking is proposed.

3.3. Proposed KCF-YOLO Algorithm

The KCF algorithm is known for its high efficiency and accuracy in real-time tracking, excelling when the target size remains relatively constant and there are no occlusions. However, in intricate orchard environments characterized by occlusions, such as trees and overlapping pedestrians, the KCF algorithm faces challenges that lead to failures in target tracking. Conversely, the YOLO v5s algorithm demonstrates a rapid and accurate response in target recognition yet encounters difficulties in distinguishing and localizing specific objects among similar targets. To address the limitations of both algorithms in specific target tracking, this section introduces the KCF-YOLO fusion visual tracking algorithm. The implementation of this algorithm is illustrated in Figure 4.

The KCF-YOLO algorithm leverages the YOLO v5s algorithm for target detection. The algorithm identifies the target detection box and determines the position of the target center in the image. Through the continuous calculation of the range between the real-time target center and the edges of the field of view, the algorithm evaluates whether the detected target is on the verge of leaving the field of view. Based on this evaluation, the algorithm determines whether the KCF algorithm should intervene to provide auxiliary tracking. Suppose the algorithm determines that the tracked target is positioned at the edge of the field-of-view window. In that case, the KCF-YOLO algorithm utilizes the target detection frame obtained by the YOLO v5s algorithm as the region of interest to initialize the KCF algorithm for auxiliary tracking. Notably, the parameters distance serves as the trigger region for the KCF algorithm, denoted as dis, which represents a certain distance from the left or right boundary of the image to the image center, as shown in Figure 5. It is primarily used to determine whether the target individual is about to leave the frame and initiate the KCF algorithm for auxiliary tracking, directly impacting the detection efficiency of the KCF-YOLO algorithm. This study experimentally validated the KCF-YOLO algorithm using different dis and sigma values as test variables.

There are two common target-loss scenarios during personnel visual tracking. Tracking loss occurs when the target is positioned at the edge of the image. To address this problem, the KCF algorithm calculates the response value by performing correlation operations in the region surrounding the region of interest. If the peak response value exceeds a preset threshold, the KCF-YOLO algorithm considers the position as a new tracking position. It continuously updates the tracking region of the target until the personnel exit the edge of the image. Second, in the complex environment of an orchard, the target is prone to tracking loss owing to obscuration and other circumstances. The system captures the frame of the image before the target leaves its field of view and performs a response value calculation. When the target-tracking frame is at the edge of the image, waiting for the target to re-enter the tracking area, the system waits for and monitors the target. If the target re-enters the image field of view area and the peak response value exceeds the set threshold, the system recognizes it as a specific target that has previously lost its field of view. The KCF is used to accomplish assisted visual tracking. Once a specific target returns to the field of view and retracing is confirmed, the system turns to the YOLO algorithm to complete the detection and tracking of that target. The process is illustrated in Figure 6.

In complex orchard environments, the KCF algorithm may encounter difficulties in tracking owing to obstructions, such as bushes and fruit trees, or issues with pedestrian overlap. In contrast, the YOLO v5s algorithm struggles to determine whether the target re-entering the field of view after being lost is the original target. However, the KCF algorithm supports target tracking under specific conditions. When the target is lost and re-enters the field of view, YOLO v5s, as the primary tracker, can identify and continue tracking the previously lost target by combining it with the KCF. This addresses the deficiency of YOLO v5, which cannot confirm the original target when it re-enters the field of view. Consequently, this integration improves the stability and robustness of visual tracking in a complex orchard environment.

3.4. Human-Following Control Strategy

To maintain personnel within the field of view of the robot’s camera, appropriate control commands must be generated based on the personnel’s positional information. The human-following control strategy includes personnel moving trajectory acquisition, offset calculation of the personnel positions, and subsequent control. The process is described below.

3.4.1. Obtaining Personnel Trajectory

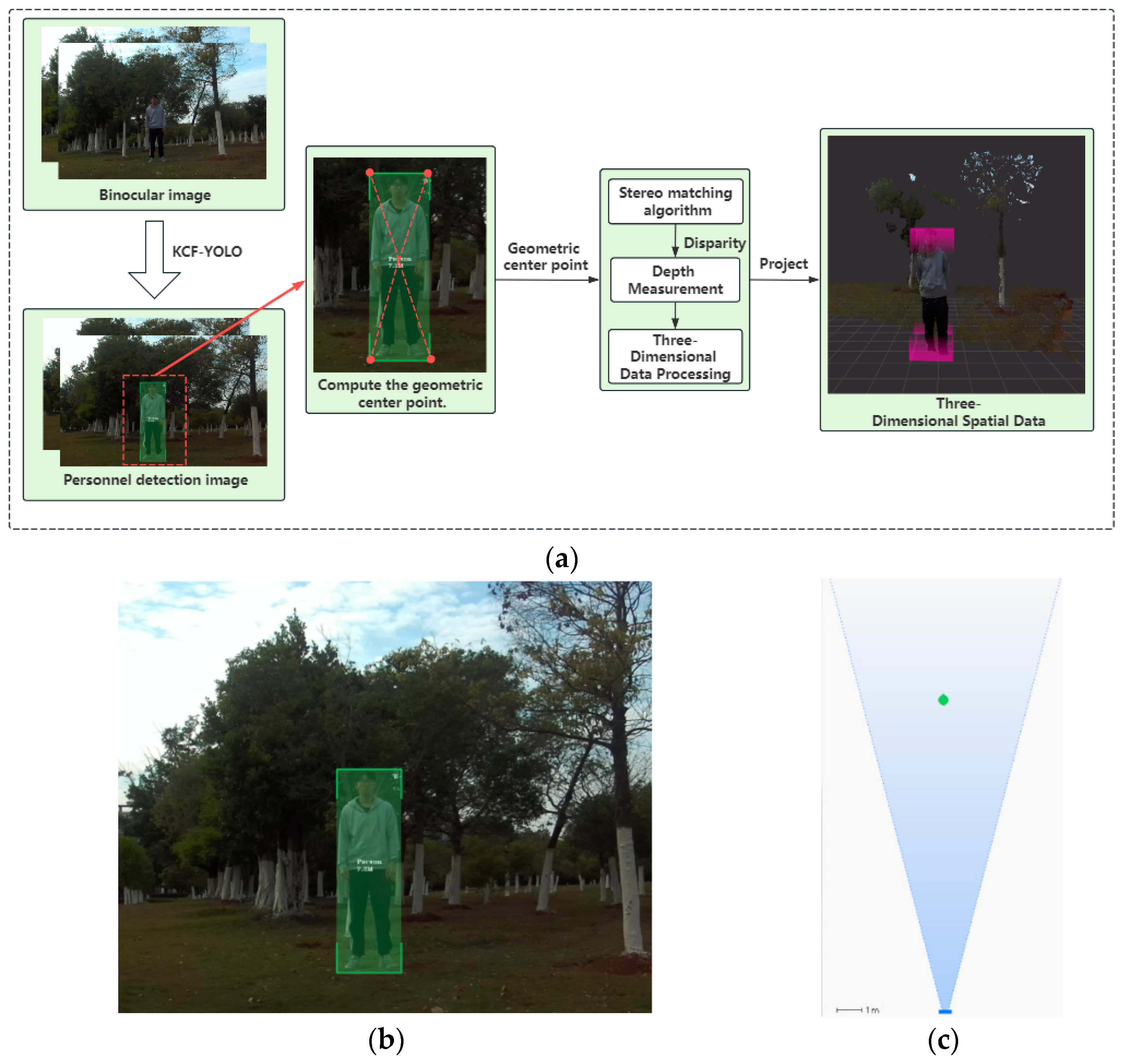
Human-following requires acquiring the position information of the target person and executing the corresponding behavior based on that person’s spatial information. This study utilizes the software development kit (SDK) provided by the camera, version ZED 3.8.2, to extract 3D spatial information from two-dimensional (2D) image data, as illustrated in Figure 7a. This process stabilizes the tracking of the target person through the KCF-YOLO fusion algorithm, producing a target-tracking detection box, as shown in Figure 7b. The geometric center of the detection box is calculated based on its four corners. The coordinates of this geometric center in the 2D plane image are defined as the mapped 3D spatial information of the person in the camera coordinate system. After obtaining the geometric center of the person in the 2D plane image, a stereo-matching algorithm is used to find the corresponding feature points in the image, establishing the relationship between the feature points in the 2D image and the actual positions in the 3D space. Finally, the spatial position of the tracking target in the camera coordinate system is determined based on the binocular disparity parameters. The spatial position of the person is shown in Figure 7c.

3.4.2. Personnel Trajectory Calculation

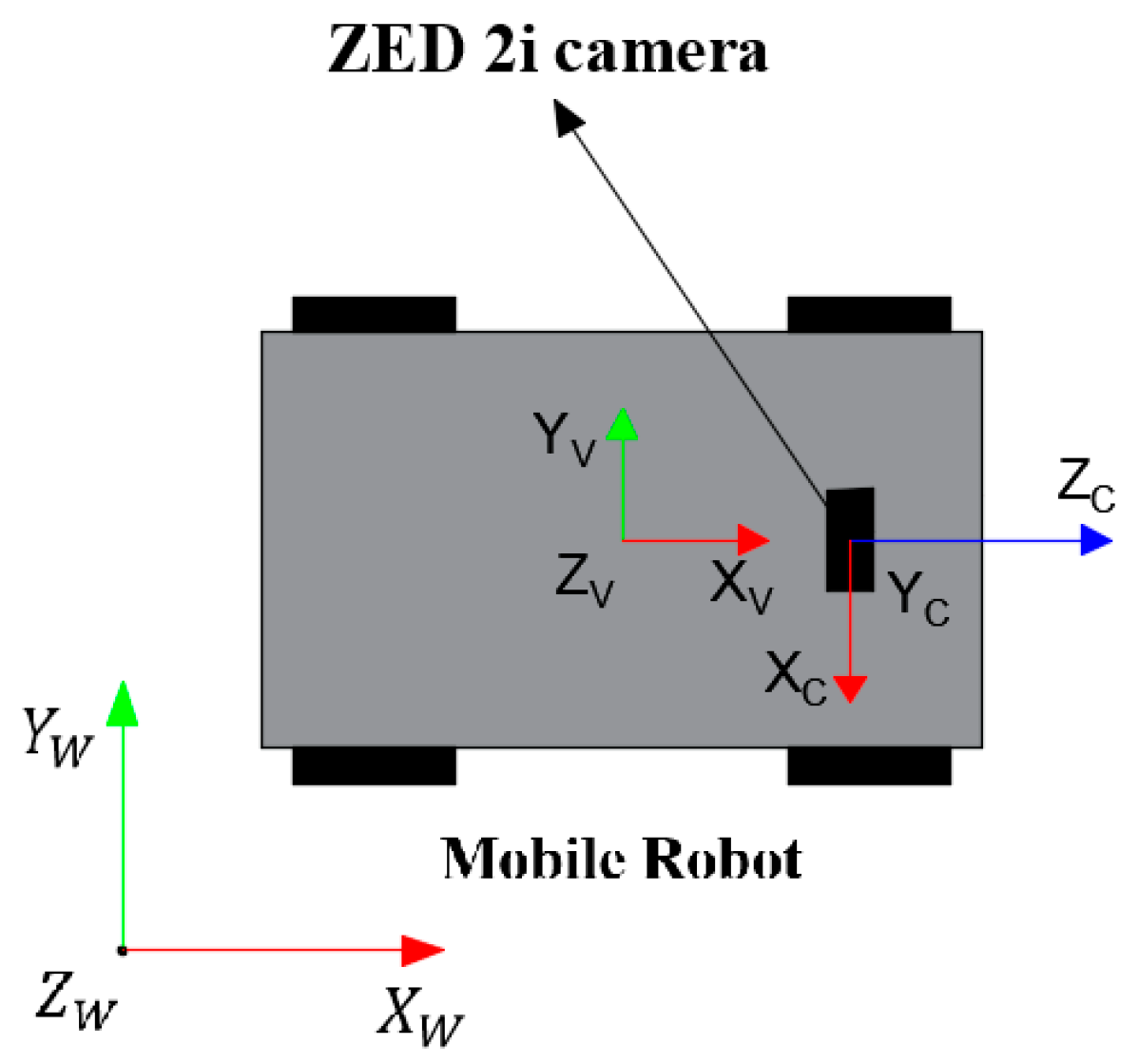
The task of human-following involves the processing of multiple coordinate systems. These encompass the world coordinate system W, the vehicle coordinate system V of the mobile robot, and the camera coordinate system C of the binocular camera, as illustrated in Figure 8.

The origins of the camera and vehicle coordinate systems are defined as the geometric centers of the stereoscopic camera and mobile robot structure, respectively. The rotation relationship R and translation relationship T of the two coordinate systems are known. The spatial information of the individuals in the camera coordinate system can be transformed into the vehicle coordinate system through coordinate transformation, as expressed in Equation (2). The mobile robot can then acquire the spatial information of the dynamic personnel.

$$P_V=\left[\begin{array}{cc}R& T\\ {\mathbf{0}}^{\mathbf{T}}& \mathbf{1}\end{array}\right]P_C$$

(2)

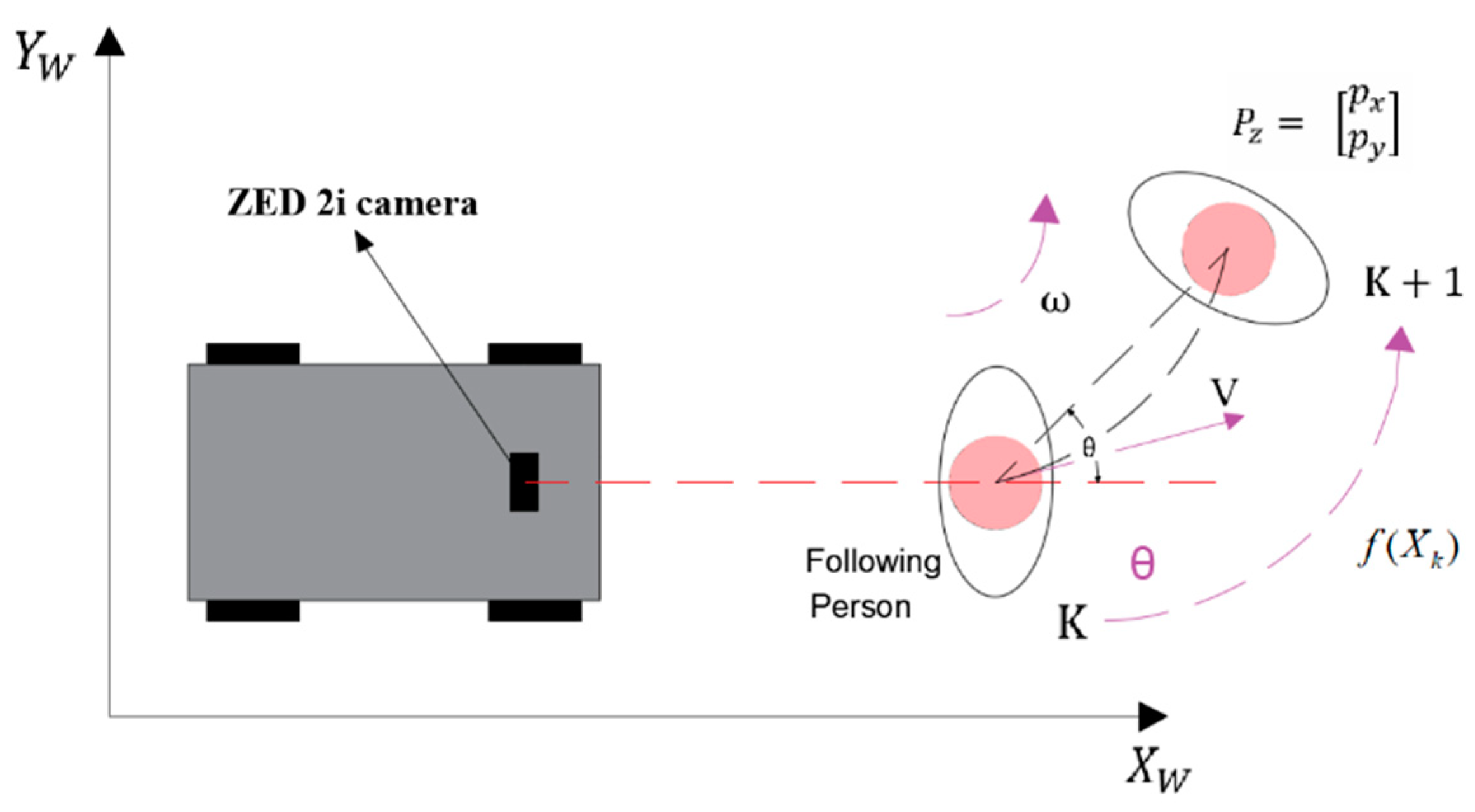
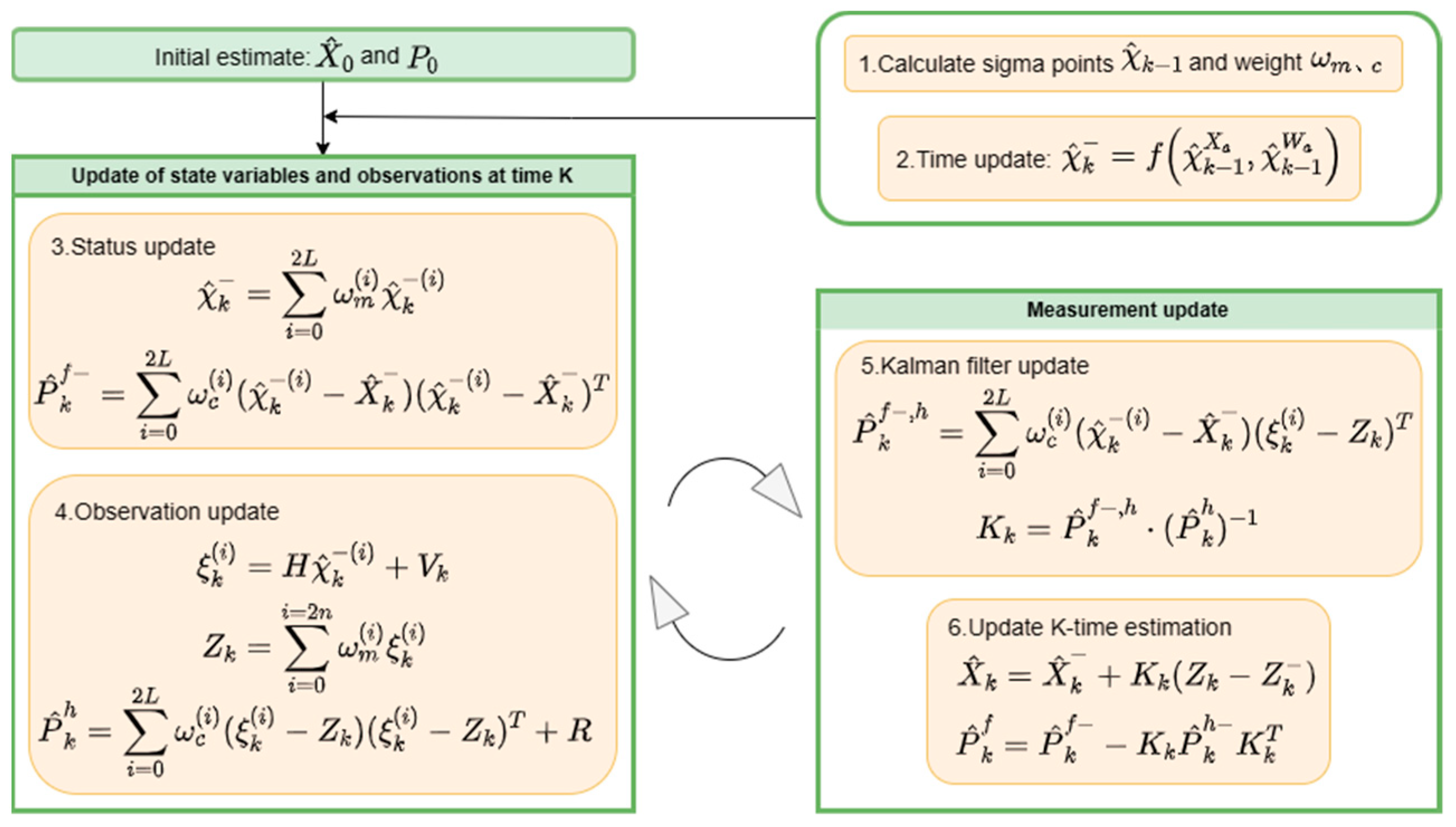
Owing to the uncertainty in the personnel trajectory, relying solely on the spatial position obtained from the stereo camera is prone to result in positional oscillations, making real-time human-following tasks challenging. The UKF algorithm proves to be effective in predicting the trajectory of a target person. Even if the target exits the field of view of the camera, the mobile robot can track the target based on the predicted trajectory, guiding it back into the field of view. This significantly enhances the stability and robustness of human-following in uncertain environments. The trajectory of a target person’s movement can be conceptualized as a combination of multiple curves and straight-line trajectories. For simplicity, the target person is assumed to travel along a straight line and move at a fixed turning rate. This motion model is defined as a constant turn rate and velocity (CTRV) motion model, as shown in Figure 9.

In the CTRV model, the state of the target person can be defined using Equation (3),

$$X={[p_x{p}_y\nu \theta \omega ]}^T$$

(3)

where $p_x$ and $p_y$ are the coordinates of the target person in the vehicle coordinate system, v is the linear velocity of the target, $\theta$ is the heading angle of the target moving in the vehicle coordinate system, and $\omega$ is the angular velocity of the target heading.

In real-world scenarios, achieving a uniform speed state for the target person is challenging. Therefore, it becomes necessary to introduce perturbations in the target person’s motion model through noise simulation. The line acceleration $\alpha$ and angular acceleration $\dot{\omega }$ are considered to be process noise. The two are assumed to follow Gaussian distributions with a mean of 0 and variances of ${\sigma }_a^2$ and ${\sigma }_{\dot{\omega }}^2$, respectively. In other words, there exist $a~N(0,{\sigma }_a^2)$ and $a~N(0,{\sigma }_{\dot{\omega }}^2)$ such that the state transfer process noise is denoted as $W={\left[\begin{array}{cc}a& \dot{\omega }\end{array}\right]}^T$, and the covariance of W can be expressed as shown in Equation (4).

$$Q=\left[\begin{array}{c}{\sigma }_a^2\\ 0\end{array}\begin{array}{c}0\\ {\sigma }_{\dot{\omega }}^2\end{array}\right]$$

(4)

The human-following motion model can be expressed as $X_{\mathrm{k}}=f(X_{k-1},W_k)$, as shown in Equation (5).

$$X_k=\{\begin{array}{ll}{X}_{k-1}+\left[\begin{array}{c}\frac{v}{\omega }\left[\sin ({\omega }_{k-1}\cdot \mathsf{\Delta }t+{\theta }_{k-1})\right]-\sin ({\theta }_{k-1})\\ -\frac{v}{\omega }\left[\cos ({\omega }_{k-1}\cdot \mathsf{\Delta }t+{\theta }_{k-1})\right]-\cos ({\theta }_{k-1})\\ 0\\ {\omega }_{k-1}\cdot \mathsf{\Delta }t\\ 0\end{array}\right]+\left[\begin{array}{c}\frac{1}{2}\mathsf{\Delta }{t}^2\cos ({\theta }_{k-1})a_k\\ \frac{1}{2}\mathsf{\Delta }{t}^2\sin ({\theta }_{k-1})a_k\\ \mathsf{\Delta }t\cdot a_k\\ \frac{1}{2}\mathsf{\Delta }{t}^2\cdot {\dot{\omega }}_k\\ \mathsf{\Delta }t\cdot {\dot{\omega }}_k\end{array}\right]\hfill & \omega \ne 0\hfill \\ X_{k-1}+\left[\begin{array}{c}v\cos ({\theta }_{k-1})\\ v\sin ({\theta }_{k-1})\\ 0\\ {\omega }_{k-1}\cdot \mathsf{\Delta }t\\ 0\end{array}\right]+\left[\begin{array}{c}\frac{1}{2}\mathsf{\Delta }{t}^2\cos ({\theta }_{k-1})a_k\\ \frac{1}{2}\mathsf{\Delta }{t}^2\sin ({\theta }_{k-1})a_k\\ \mathsf{\Delta }t\cdot a_k\\ \frac{1}{2}\mathsf{\Delta }{t}^2\cdot {\dot{\omega }}_k\\ \mathsf{\Delta }t\cdot {\dot{\omega }}_k\end{array}\right]\hfill & \omega =0\hfill \end{array}$$

(5)

The observation equation for the stereo camera of the target pedestrian is given by Equation (6):

$$Z_k=\left[\begin{array}{l}{p}_x\\ p_y\end{array}\right]=H{X}_k+V_k=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& 1& 0& 0& 0\end{array}\right]\left[\begin{array}{l}{p}_x\\ p_y\\ v\\ \theta \\ \omega \end{array}\right]+{\left[\begin{array}{l}{r}_k\\ r_y\end{array}\right]}_k$$

(6)

where $V_k={\left[\begin{array}{cc}{r}_x& r_y\end{array}\right]}^T$ is the observation noise satisfying $r_x~N(0,{\sigma }_{r_x}^2)$ and $r_y~N(0,{\sigma }_{r_y}^2)$. Therefore, $V_k~N(0,R),R=\left[\begin{array}{cc}{\sigma }_{r_x}^2& 0\\ 0& {\sigma }_{r_y}^2\end{array}\right]$.

In this paper, the Q and R matrices are set according to default parameters, with a value of 0.8 for ${\sigma }_a$, 0.55 for ${\sigma }_{\dot{\omega }}$, and 0.15 for both ${\sigma }_{r_x}$ and ${\sigma }_{r_y}$. In this process, the system state $X_0$ is first initialized, and a set of sigma points ${\chi }_i$ is generated based on the personnel k − 1 moment states. The corresponding weights $W_i$ for ${\chi }_i$ are constructed, and a nonlinear state function is used to predict the k-moment sigma points. The mean and covariance of the state at moment k are calculated. Subsequently, the means and covariances of the measurements are predicted. Finally, the Kalman filter gain $K_k$ is derived from the measurements at moment k to estimate the state and variance at moment k. A flowchart of the process is shown in Figure 10.

3.4.3. Human-Following Control

After obtaining the predicted value of the personnel space, the x-axis of the robot is defined as the positive forward direction of the mobile robot. The angular offset between the personnel position and the robot is then calculated using Equation (7). $p_x^v$ and $p_y^v$ represent the personnel distances along the x- and y-axes, respectively, in the mobile-robot coordinate system.

$${\theta }_{\mathrm{p}}=\arctan (\frac{p_y^v}{p_x^v})$$

(7)

The mobile robot controls the steering angle according to the offset, thus keeping the target person in the field of view and following it at a safe distance. The strategy for the mobile robot is shown in Figure 11.

During the human-following process, the deviation angle from the robot when the target person is on one side of the field of view of the camera is ${\theta }_{\mathrm{p}}$, where there exists a heading-angle error threshold $\theta$ between the target and the robot. The robot does not need to execute steering commands within this threshold range. When the deviation angle ${\theta }_{\mathrm{p}}$ exceeds a certain heading-angle error threshold, the robot controls the steering angle based on the magnitude of the deviation angle, which is denoted as ${\theta }_{\mathrm{p}}$. Simultaneously, the safe distance between the target person and the robot is defined as $X_{safe}$. When the distance $p_z^v$ between the person being followed and the robot is larger than the predefined $X_{safe}$, the mobile robot continues to follow. Steering commands are executed to adjust the body position, ensuring the personnel returns to the center of the field of view of the camera. When the personnel stops moving and the distance $p_z^v$ is less than or equal to $X_{safe}$, the mobile robot brakes slowly until it stops. By this process, a mobile robot can automatically track the target person.

4. Experiments and Discussions

4.1. Experimental Platform and Equipment

This study is based on an experimental design executed by a self-developed mobile robot in an orchard. The robot achieves intelligent autonomous following by integrating environmental sensors and an underlying control module. The overall test platform is illustrated in Figure 12. The key parameters are listed in

Table 1. Main parameters of the test platform.

Parameter	Value
Length	160 mm
Width	80 mm
Height	120 mm
Maximum grade	20°
Running speed	0–3.6 km/h

. In addition, the mobile robot is outfitted with a binocular stereo camera with a resolution of 1920 × 1080 pixels and a frame rate of 30 FPS.

Table 2. Main parameters of the binocular stereo camera.

Parameter	Value
Resolution	1920 × 1080 px
Frame rate	30 FPS
Baseline	12 cm (4.72 in)
Field of view (H × V × D)	Max. 72° (H) × 44° (V) × 81° (D)

shows the main parameters of the binocular stereo camera.

To assess the robustness and stability of the proposed method, an experiment was conducted in a complex orchard environment. The ground in the orchard exhibits a firm texture, and simultaneously, it is covered with a dense layer of grass, comprising both herbaceous species and other low vegetation, as illustrated in Figure 13. The robot operating system platform was used for data processing. The evaluation of the tracking robustness of the KCF-YOLO algorithm and the stability of the mobile robot are discussed in the following subsections.

4.2. Experimental Results

To assess the recognition effectiveness of the KCF-YOLO algorithm in an orchard setting, experiments were conducted on two major modules: visual tracking and human-following. In the visual tracking section, we conducted three sets of experiments: tracking experiments under multi-person interference, investigations of the effects of different dis and sigma values on the efficiency of the KCF-YOLO algorithm, and comparisons between the KCF-YOLO algorithm and other algorithms. The evaluation indices for the algorithm performance included the average frame rate and recognition success rate. The reason for choosing the average frame rate as a quality metric is because it directly reflects the real-time performance evaluation of the system and its responsiveness. The average frame rate represents the average number of image frames displayed per second during the KCF-assisted tracking. When the algorithm fails to track a person, the FPS is recorded as 0 and is not included in the calculation of the average frame rate. This metric serves as a crucial indicator for measuring system real-time performance. A higher frame rate implies a more timely system response, consequently enhancing the robot’s tracking performance of personnel. The recognition success rate is the ratio of the successful tracking of the target person when entering and leaving the field of view of the camera to the total number of entries and exits. The human-following experiment evaluates the stability of following through two different paths.

4.2.1. Visual Tracking Experiments under Multiple Interferences

In practical applications of human-following in orchard environments, encountering situations with multiple people simultaneously is common. To evaluate the impact of personnel interference on the recognition accuracy of the KCF-YOLO algorithm, tests were conducted in orchard scenarios with different numbers of individuals. Four sets of experiments were carried out with varying numbers of individuals: 1, 2, and 3, respectively. One of the experiments focused on visual tracking under different environmental conditions, potentially affecting detection stability and other factors. Tests were conducted in overcast weather conditions. The dis of the KCF-YOLO algorithm is set to 200 pixels, along with a sigma value of 0.2 for the Gaussian kernel function. Each set of experiments comprised 30 tests.

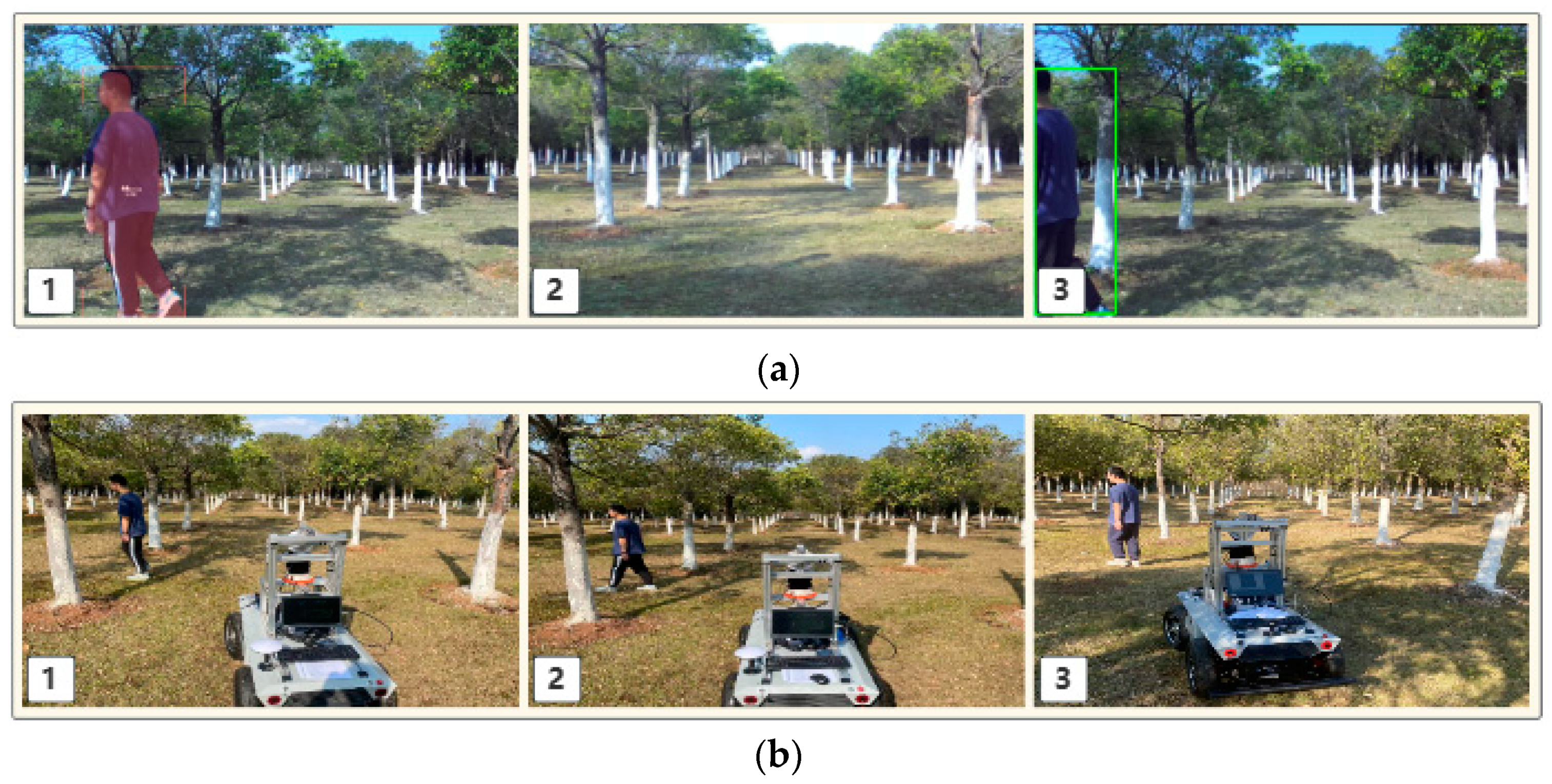
At the onset of the experiment, the personnel are positioned at the center of the field of view of the camera. Subsequently, the personnel gradually shift from the center to the edge of the field of view. As the target person approaches the edge of the frame, the KCF algorithm assists in tracking. The target person continues to move leftward, eventually exiting the field of view of the image. Once out of sight, the system enters a waiting state for the target person’s re-entry into the field of view. Upon re-entry, the system re-identifies the target person. Finally, the system reverts to the YOLO algorithm to resume tracking the target person. The entire process is deemed as successful tracking by the KCF-YOLO algorithm. The detection effect of the algorithm on the target person is shown in Figure 14.

As shown in

Table 3. Performance of the algorithm with different numbers of persons.

Number of Persons	FPS	Success Rate/%
1	9	100
2	9	96.667
3	8	96.667
3 (overcast)	6	93.333

, the average frame rate for the four sets of trials reaches 9 FPS, 9 FPS, 8 FPS, and 6 FPS, respectively. The recognition success rates are 100%, 96.667%, 96.667%, and 93.333%, respectively. These data indicate that the KCF-YOLO algorithm can reliably and accurately recognize a target despite personnel interference. Additionally, it exhibits good recognition speed with minimal impact from the interfering individuals. Meanwhile, the tracking performance of the algorithm is minimally affected under overcast conditions.

4.2.2. Effects of Different dis and sigma Values on the Efficiency of the KCF-YOLO Algorithm

In the KCF-YOLO algorithm, the dis and sigma values are crucial parameters that substantially influence the detection efficiency and stability of the algorithm. To validate the efficiency and stability of the KCF-YOLO algorithm, experiments were conducted using various dis and sigma values. The experiment includes a total of three participants, with each group conducting 30 trials.

During the experiment, setting the dis value to 175 pixels while maintaining the sigma value at 0.1 resulted in the relatively low effectiveness of the KCF-YOLO algorithm, with a recognition success rate of only 86.667%. The small dis value prompted the early intervention of the KCF algorithm for tracking assistance, causing the peak response value in the region of interest (ROI) calculation correlation to fall below the set threshold, resulting in the failure of the mobile robot to track the target. In addition, with a sigma value of 0.1, the Gaussian kernel function proved to be excessively sensitive to the input samples, affecting the stability of the algorithm. The recognition success rate of the KCF-YOLO algorithm reached 100% when the dis value was set to 200 pixels, and the sigma values were taken as 0.1 and 0.2, respectively. A higher recognition speed was observed when the sigma value was set to 0.2. However, at a sigma value of 0.3, the recognition success rate of the KCF-YOLO algorithm is only 86.667%. Owing to the large sigma value, the discriminative ability of the KCF-YOLO algorithm toward target details decreased, thereby affecting the recognition accuracy. Efficient recognition efficiency was achieved by setting the dis value to 225 pixels and using sigma values of 0.1, 0.2, and 0.3 for optimal performance of the KCF-YOLO algorithm. The experimental results are presented in

Table 4. Algorithm performance for different dis and sigma values.

dis/Pixel	sigma	FPS	Success Rate/%
175	0.1	9	86.667
	0.2	9	90
	0.3	11	93.33
200	0.1	11	100
	0.2	9	100
	0.3	8	86.667
225	0.1	8	96.667
	0.2	9	96.667
	0.3	12	96.667

.

The experimental results demonstrate that the KCF-YOLO algorithm performs well in recognition and tracking. Specifically, when the dis is set to 200 pixels and sigma is set to 0.1, the tracking performance is optimal, with an average frame rate of 11 FPS and a recognition success rate of 100%.

4.2.3. A Comparative Experiment with Other Algorithms

To compare the performance of different algorithms, experiments were conducted to compare the YOLO v5s algorithm, the KCF algorithm, and the KCF-YOLO algorithm in similar scenarios. In this study, the YOLO v5s algorithm utilizes the official provided code. The KCF algorithm employed the official version provided by OpenCV. Simultaneously, the KCF-YOLO algorithm utilized the optimal parameters obtained from the aforementioned experiments, with a dis set to 200 pixels and sigma set to 0.1.

In the YOLO experiment, targets were detected using a pre-trained YOLO v5s model. Subsequently, attempts were made to track the targets based on the detected target position information in consecutive frames. In the KCF experiment, person A was set as the target for tracking and designated as the initial target. Afterwards, the scenario was simulated where individual A moved out of the camera’s field of view, representing the target leaving the view. After a certain period, individual A re-entered the camera’s field of view, simulating the target reappearing. The tracking performance of the KCF algorithm was recorded and analyzed. The KCF-YOLO experiment process was similar to that under multiple person interference. The experimental process is illustrated in Figure 15.

The experimental results indicate that the YOLOv5s algorithm only performs target detection on individuals. However, due to its inherent design characteristics, it lacks the capability for continuous target tracking. While the KCF algorithm is capable of tracking target individuals, it suffers from issues such as target bounding box loss and drifting, resulting in poor stability. In contrast, the KCF-YOLO algorithm combines the strengths of the YOLOv5s and KCF algorithms. It not only leverages the precise target detection capability of YOLOv5s but also effectively tracks targets using the KCF algorithm. It demonstrates excellent performance in terms of tracking stability and resistance to interference.

4.2.4. Human-Following Experiment

In intricate orchard scenarios, challenges arise because of factors such as the varying heights of fruit trees, narrow passages, and randomly distributed obstacles, which intensify the complexity of human-following tasks. Consequently, this study integrates the human-following function into a test scenario by synergizing the KCF-YOLO algorithm with a mobile robot control chassis. This study explored human-following performance when personnel were in a dynamic state. In the experiment, the safe following distance between personnel and the robot was set to 3 m. When the mobile robot detected a distance less than 3 m from the personnel, it would cease following. The human-following experiment involved two participants and included following scenarios under target loss, occlusion, and overcast weather conditions.

In the first scenario, when the target person A exits the robot’s field of view, the robot temporarily halts following target A. Concurrently, the robot activates the KCF-YOLO algorithm for assisted localization of the target person A. Upon the target person A’s re-entry into the robot’s field of view and recognition as the previously tracked target, the robot resumes its tracking program to continue following the movement trajectory of the target person A, as shown in Figure 16.

In the second scenario, even when the target individual is occluded by fruit trees, the system can still identify the person using the YOLO v5s algorithm, as shown in Figure 17a. When the distance between the target individuals falls below the safety threshold, the mobile robot stops following them. When a person appears from the side, the mobile robot resumes following, as illustrated in Figure 17b.

Furthermore, in addressing the issue of human-following effectiveness in different environments, the stability of mobile robot following was further evaluated under overcast weather conditions. The experimental process is illustrated in Figure 18.

The mobile robot is equipped with a SLAM module to record its own position. Based on this module, after the stereo camera captures the spatial coordinates of the personnel, the personnel’s spatial information is transformed into the world coordinate system through the static spatial relationship between the stereo camera and the robot, as well as the rotation matrix of the robot in the world coordinate system. Consequently, the complete trajectory of the personnel in the spatial environment is obtained. 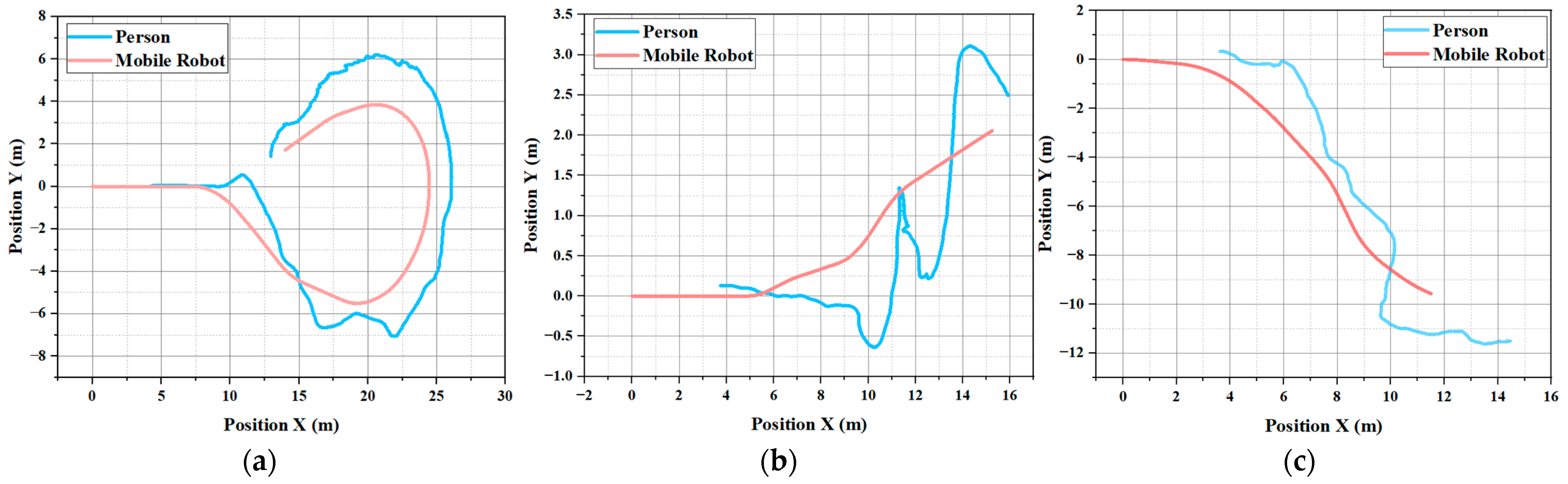Figure 19 shows the motion trajectories of the target and robot in the human-following experiment. The red line segment denotes the following trajectory of the mobile robot, and the blue line segment illustrates the actual movement trajectory of the personnel.

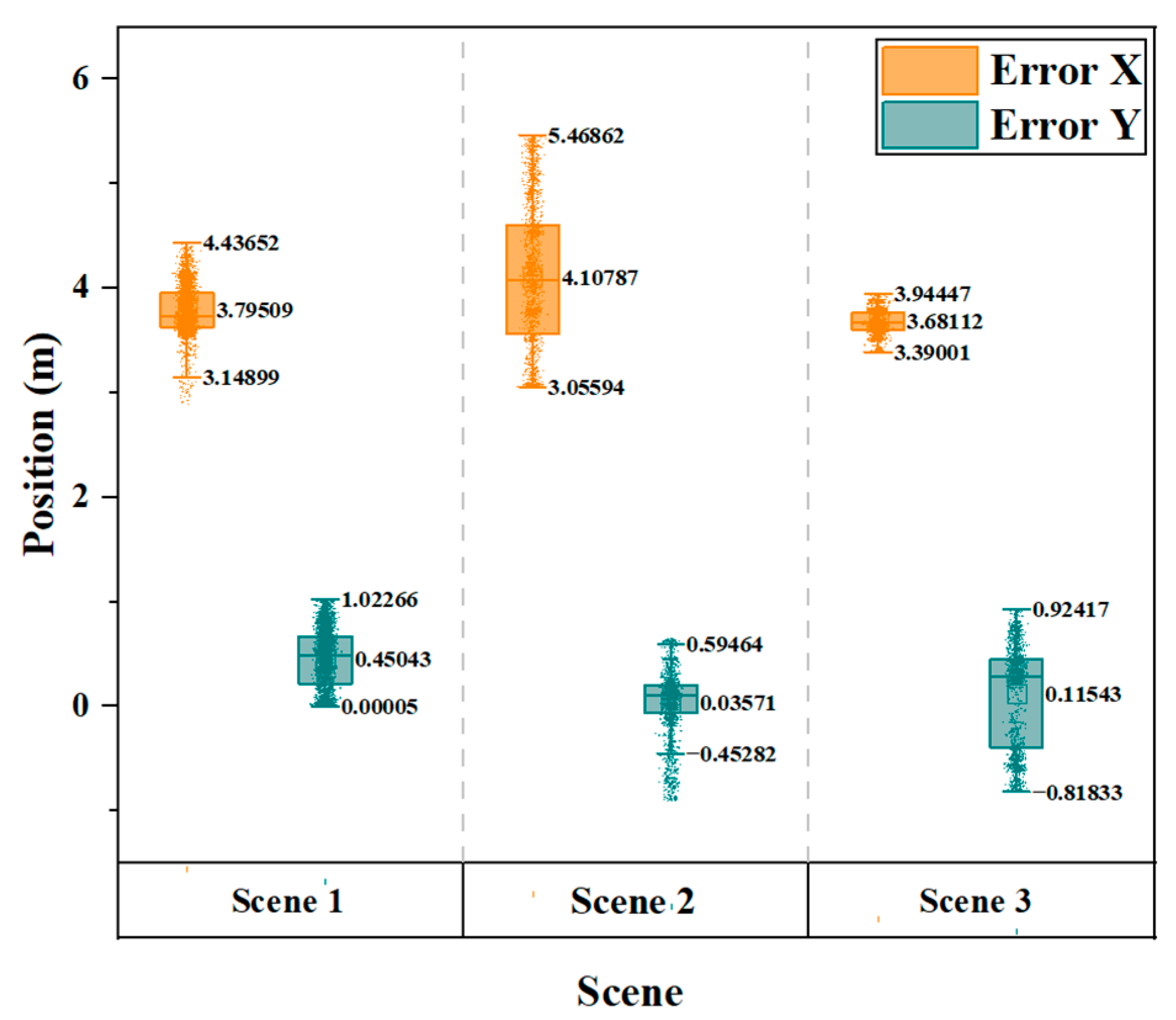
Figure 20 illustrates the distribution of the spatial positional offsets for the X- and Y-components in the motion trajectories of the follower and mobile robot. Error X represents the variance in the vertical distance between the personnel and the mobile robot, whereas Error Y indicates the degree of deviation in the horizontal distance during the mobile human-following process.

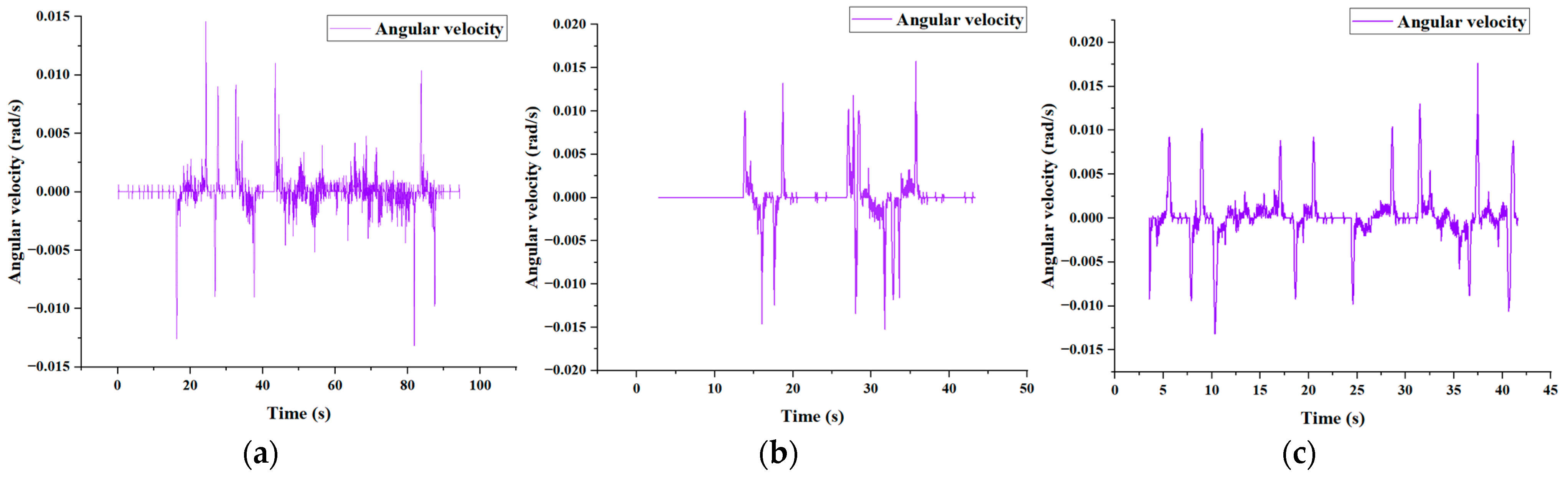
To ensure the stability of human-following in an orchard environment, the UKF algorithm predicts the trajectories of personnel. This prediction allows the mobile robot to stabilize the movement trend of the personnel during the following process, thereby minimizing the lateral swaying of the robot. The average angular velocity of the steering joint of the robot is shown in Figure 21. The dense part of the illustration represents the robot executing steering commands. However, owing to the complexity of the orchard terrain, the angular velocity of the steering joint is affected by the landscape during the following phase, resulting in some noise. Overall, the steering joint of the robot maintains a relatively stable angular acceleration during the following process. 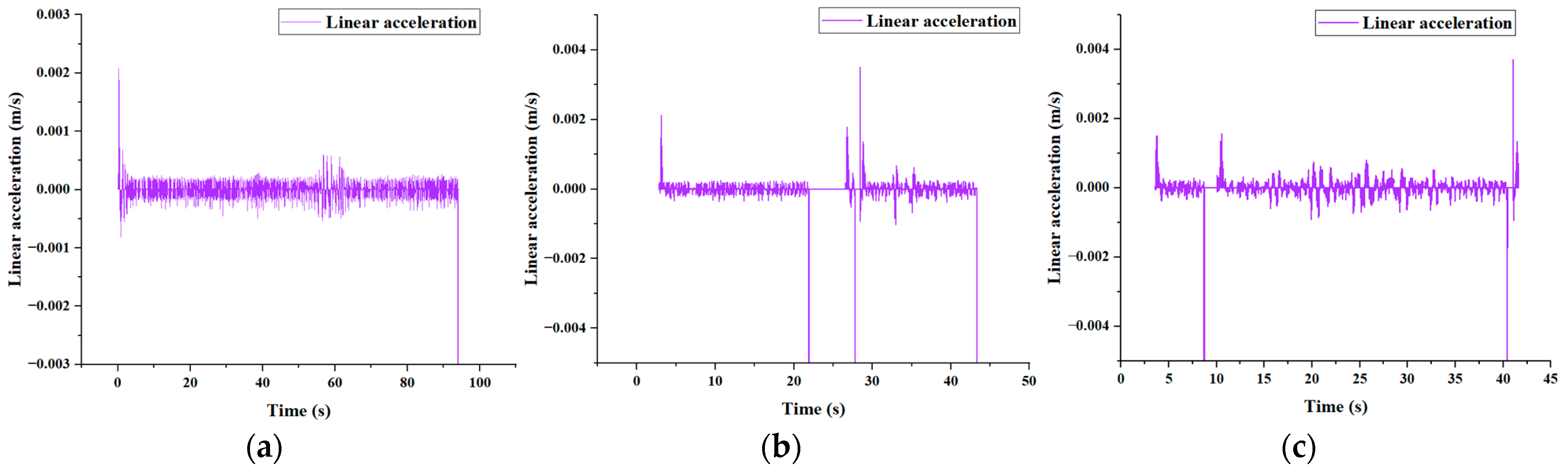Figure 22 shows the linear acceleration situations during the following processes of the mobile robot in three groups. The illustration indicates that the linear acceleration of the robot remains within a certain range, suggesting stable following at a consistent average speed.

In all three different human-following experiments under varying conditions, the maximum horizontal distance Error Y does not exceed 1.03 m. The robot’s following trajectory is relatively smooth, allowing it to follow the target at a steady pace until the end of the follow-up task, demonstrating good reliability and stability.

4.3. Results Analysis and Discussion

In the above-mentioned experiments, this study primarily validates the stability and feasibility of the KCF-YOLO algorithm from experiments conducted in two major modules: visual tracking and human-following. In the multi-person interference experiments, when the number of subjects is two or three, during the recognition process, the fluctuation in the scale of the target individuals and the similarity between the features identified from interfering persons and those of the target individuals affect the algorithm’s decision mechanism. Consequently, there is a decrease in the recognition success rate. The KCF-YOLO algorithm can still stably track target individuals, demonstrating good robustness in detection performance. Under overcast conditions, both the success rate and the frame rate have decreased, possibly due to the dim lighting in overcast scenes, leading to a blurred background. This increases the computational load for processing the background in the KCF-YOLO algorithm. The algorithm requires more computational resources to identify and filter targets, thereby reducing tracking efficiency and frame rate. However, the ability to track target individuals has not been significantly affected, with a success rate reaching 93.33%. Thus, the KCF-YOLO algorithm still maintains good stability.

In terms of the impact of different dis and sigma values on the algorithm, this study experimented with various values of dis and sigma for validation. When the dis value was set to 200 pixels and the sigma value to 0.1, the KCF-YOLO algorithm demonstrated the best performance. For sigma values of 0.2 and 0.3, the Gaussian kernel function performs poorly in processing target feature information. The reason might be that when the sigma value is large, the blurring effect of the Gaussian kernel function leads to loss of target feature information, thereby reducing the expressive power of the algorithm. By combining the optimal solutions for dis and sigma values, the algorithm in this study effectively captured target individual features, leading to the best overall performance. By adjusting the dis and sigma values according to specific scenes, the algorithm can meet diverse scene requirements, thereby enhancing its robustness and accuracy. In order to better evaluate the tracking stability and anti-interference ability of the algorithm, this paper conducted comparative experiments between the YOLO v5s algorithm and the KCF algorithm. The experimental results indicate that the YOLO v5s algorithm can only recognize target individuals but lacks the ability to track them, while the KCF algorithm exhibits instability and poor tracking performance. In contrast, the proposed KCF-YOLO algorithm not only achieves accurate tracking of target individuals but also possesses real-time detection capabilities, demonstrating excellent performance in both tracking and detection.

Building upon the visual experiments, this paper conducted experiments focused on human-following to assess the practicality and reliability of the KCF-YOLO algorithm in real-world scenarios. Due to the slightly faster movement speed of the target individual compared to the constant speed maintained by the mobile robot, there may be differences in the Error X between the mobile robot and the target individual. However, this does not affect the stability of the KCF-YOLO algorithm during the following process. Meanwhile, it is evident that the prediction of personnel trajectories through UKF reduces the lateral swaying of the robot, resulting in smoother following paths for the robot. The horizontal distance Error Y between the three trajectories does not exceed 1.03 m. However, due to terrain effects, there is relative jitter between the personnel and the mobile robot, leading to some errors in the obtained personnel trajectories. In particular, Figure 22b illustrates the linear acceleration of the mobile robot when personnel following are obstructed by fruit trees. During the period from 20 s to 30 s, there is a segment where the acceleration value is 0, indicating that the mobile robot has stopped following. The linear accelerations of the three axes remain within a certain range without significant fluctuations, indicating that the speed of the mobile robot following is smooth. Compared to sunny conditions, the tracking error under overcast conditions may slightly increase. This could be due to changes in lighting conditions, resulting in less clear visual features of the target person and causing some delay in the steering of the mobile robot. Although lighting conditions under overcast skies may affect the tracking accuracy of the mobile robot to some extent, the experimental results demonstrate that the mobile robot system is still capable of effectively tracking the target person.

In summary, the algorithm combines the strengths of the KCF and YOLO v5s algorithm. By integrating the YOLO v5s algorithm into the target detection module, precise identification of target individuals is achieved. When the target individual is about to leave the field of view, the KCF algorithm is introduced to accurately track the target individual, ensuring that when the target person returns to the center of the field of view, YOLO v5s can identify and continue tracking the lost target. The algorithm effectively utilizes the advantages of both algorithms, thereby enhancing the stability of following within complex orchard environments.

5. Conclusions and Future Work

5.1. Conclusions

To address the stability challenges faced by autonomous mobile robots in orchard scenarios during human-following functions, this study proposes a vision-tracking method based on KCF-YOLO fusion. This method aimed to overcome issues, such as obstacle occlusion and overlapping personnel in unstructured orchard environments. First, target localization and specific person identification were achieved by leveraging the target detection accuracy advantage of YOLO v5s, combined with the real-time capabilities of KCF and its adaptability to continuous tracking. Second, fusion with the unscented Kalman filter algorithm to fit the personnel movement trajectory achieved human-following in a complex orchard scenario. Experiments were conducted in a complex orchard environment to verify the effectiveness of the method in practical applications. The experimental results showed that the KCF-YOLO algorithm performed well in tracking in orchard scenarios, with an average tracking success rate of 96.66% and an average frame rate of 8 FPS. The mobile robot maintained a constant speed and followed the target person steadily, maintaining the horizontal offset from the followed person within a certain range. These results suggest that the KCF-YOLO vision fusion human-following method proposed in this paper offers an innovative solution for achieving human-following tasks in complex orchard environments, providing more efficient and reliable assistance tools for fruit farmers.

5.2. Future Work

The proposed KCF-YOLO vision fusion method can effectively address the problems of target tracking loss and repositioning failure of mobile robots in complex environments. However, setting different dis values in different scenarios to ensure the robustness of the algorithm is a crucial task. The reason lies in the difficulty of determining the optimal value of this parameter across different scenes. Meanwhile, the dis value has a certain impact on the stability of the subsequent human-following. In future work, further research and adoption of adaptive algorithms are needed to enable the system to dynamically adjust parameters based on real-time scenarios, thereby improving the robustness and adaptability of the algorithm. Although the KCF-YOLO vision fusion method performs well in target tracking, it lacks autonomous obstacle avoidance functionality. To enhance the practicality and safety of mobile robots in orchard environments, future work will focus on researching the autonomous navigation capabilities of robots to achieve obstacle avoidance during the human-following. By delving into advanced navigation algorithms and sensor technologies, and leveraging the characteristics of orchard terrain, robots will be able to accurately identify and evade obstacles, ensuring smooth progress during the human-following.