Abstract
The decrease in arable land, water scarcity, and climate change increase the pressure on natural resources and agricultural production systems. In this context, agriculture must ensure food production for the rapidly growing and increasingly urban population of the world. Efforts must be made to obtain the highest yield from the unit area and promote the transition to more sustainable production systems Hydroponics is a modern growing technology mainly applied in greenhouses, which has developed rapidly over the past 30–40 years. Substrate-free hydroponic vertical crops (VC) can reduce the pressure conventional agriculture exerts on resources, saving water and nutrients, and increasing crop yields per unit area. Therefore, this study aimed to validate a proposed predictive model (PM) to simulate water and nutrient uptake in vertical crops under greenhouse conditions. On the basis of the Penman–Monteith equation, the PM estimates transpiration, while nutrient uptake was estimated using the Carmassi–Sonneveld submodel. The PM was experimentally evaluated for vertically grown lettuce under Mediterranean greenhouse conditions during spring 2023. The irrigation technique was a closed-loop fertigation circuit. The experiment consisted of testing two densities (50 and 80 plants·m−2) and three plant positions (low, medium, and upper). ANOVA (p < 0.05) and R2 were used to evaluate the PM performance and crop behavior. The low density and the upper position had significantly higher mass values. The results suggest a high degree of performance for the PM, as the R2 ranged from 0.7 to 0.9 for water and nutrient uptake. Both densities had a yield 17–20 times higher than conventional lettuce production and significant savings in water, about 85–88%. In this sense, the PM has great potential to intelligently manage VC fertigation, saving water and nutrients, which represents an advance toward reaching SDG 6 and SDG 12 within the 2030 Agenda.
1. Introduction
Rapid demographic growth will cause the world’s population to reach 10 billion people by 2050, and seven out of ten people will live in cities [1,2]. To ensure food security, agrifood systems must be able to increase production by around 3 billion tons [3,4] and reduce losses by around 30% to achieve SDG 12 of the 2030 Agenda [5]. Likewise, there is a profound concern about the depletion of resources and climate change and its relationship with agricultural activity [6]. Agriculture accounts for 37% of the land surface [7], consumes 74% of freshwater withdrawals [8], and produces 31% of greenhouse gas emissions [9]. Today, agriculture has become one of the main drivers of nutrient depletion in soil, land pollution and degradation, water shortages, and climate change [5,10]. Therefore, it is important to face these world hazards and challenges through sustainable strategies that include stopping arable land expansion, increasing crop yields, reducing waste food and land degradation, and protecting biodiversity [11]. Closed-loop fertigation systems (CLFS) for soilless crops allow for improving the efficiency of water and fertilizer use but require adequate knowledge of the behavior of the system to optimize the process with benefits for crop growth and development [12,13,14].
An innovative and sustainable alternative to food production in urban and peri-urban areas is vertical farming (VF) [15,16,17], which can reduce the high pressure of conventional agriculture. Vertical crops (VCs) require short production cycles, between 60 and 90 days, and can be produced year-round, increasing the efficiency of arable land between four and ten times [13], reducing transport costs and the carbon footprint by 60%, reducing food waste by up to 30% [18], and saving between 90 and 95% of water through accurate and efficient irrigation strategies [19,20,21]. These systems have great potential to reduce the use of water and fertilizers and are competitive and feasible, with yields of close to 500 t·ha−1 per year [22]. Currently, VFs are carried out in buildings, basements, warehouses, growth chambers, containers known as plant factories (PF), greenhouses, or even in open fields, and allow the production of a wide variety of fresh and nutritious foods, such as fruits, verdures, herbs, cereals, mushrooms, and flowers, with high profits [17,20,23,24]. In greenhouses, VCs consume 40% less energy than VF or PF because they reduce the energy demand by around 42%, just for LED lighting [25]. In addition, they reduce crop water needs by between 20 and 40% [26] and increase the yield 5–8 times compared to conventional agriculture [27]. Therefore, vertical crop production in greenhouses can increase yields even more without the need for more energy for radiation supply [27].
The plant water uptake or the crop water requirements can be forecasted through the Penman–Monteith equation, proposed by the Food and Agriculture Organization of the United Nations (FAO) since it considers both external physical drivers and physiological features of the crop; in other words, this method allows one to predict the losses as vapor in the leaf stomates as transpiration [28].
Modeling closed-loop fertigation systems (CLFS) for soilless cultures such as those used in vertical farms allows us to understand the behavior of the system and, at the same time, improve its control and optimization [29]. A model that describes crop growth in a CLFS greenhouse must be capable of simulating water and nutrient uptake by the crop as a function of its concentration and distribution on the substrate. Moreover, it must consider the accumulation of salts and the effects of salinity on crop production [29,30], which after a specific threshold can reduce the yield of crops [31].
Greenhouse crop models for salt accumulation in CLFS, such as the Giuffrida model, show a simplified management of crop fertigation based on two rules: replacing all the nutrient solution when the initial electrical conductivity reaches a threshold, or eliminating a fraction of the nutrient solution (approximately 65%) when sodium reaches a specific concentration; both strategies mean lower water consumption by 51–61% compared to open growing systems [32]. The model proposed by Silberbush and Ben-Asher is more complete but, at the same time, more complex. This includes the expected concentration of all nutritive ions (NO3−, NH4+, K+, H2PO4−, Ca2+, Mg2+, and SO42−) and non-nutritive ions (Na+ and Cl−) within a hydroponic channel. It assumes that water losses are due solely to the transpiration process and solute depletion to root absorption. In addition, it simulates plant growth parameters such as root length density and leaf area index (LAI) [33]. The conceptual model proposed by Carmassi et al. is simpler and simulates changes in the recirculating nutrient solution for CLFS for ion concentration and electrical conductivity (EC) with respect to sodium (Na+) variations. This model is derived from a balanced equation for the uptake of nutrients from crops and the equation proposed by Sonneveld et al. for estimating EC as a function of the sum of cation concentration, which is useful for estimating Na+ concentration [34,35,36]. This model is also applied to calculate leaching requirements in semi-closed systems for a soilless crop, such as rockwool tomatoes. The conceptual and mechanistic nutrient uptake submodel is based on an apparent ion uptake concentration and not on a real uptake concentration of ions; and the empirical water uptake submodel is a function of LAI and radiation intercepted by the plant, calculated through the canopy light extinction coefficient [37,38]. These mathematical and agronomic bases set up useful tools to establish an optimum algorithm to manage fertigation in closed-loop hydroponics since it allows the prediction of the amount of replacement nutrient solution over time and the adjustment of the nutrient concentration in the nutrient solution, which means a best-decision support system for the automatic function of fertigation in greenhouse closed hydroponic systems [39].
Lettuce (Lactuca sativa L.) belongs to the Asteraceae family and is a crop commonly eaten as salads around the world, due to its high nutritional value and medicinal properties. It is a rich source of polyphenols, carotenoids, fiber, antioxidant compounds such as vitamin C, and minerals such as Ca and P, among others. It is classified as one of the most relevant leaf vegetables at the economic level and one of the products of the IV-Gamma (minimally processed vegetables and fruits) with a greater demand worldwide [40,41,42]. Currently, net lettuce production around the world is approximately 27 million tons, and its main producers are China, the United States, India, and Spain [43]. This vegetable can be used as a model plant in VC due to its rapid growth, short production cycle, and small size [44].
Despite the efforts and scientific studies carried out in recent years around VC, it is important to encourage more research and development activities to determine the feasibility of implementing these VC systems in greenhouses at the economic, social, and environmental levels [19,22,45]. It is possible to use a predictive model to improve the management and refreshment needs of the recirculating nutrient solution to achieve better performance and productivity in a closed vertical farming system.
Therefore, this research aimed to prove the validity of a predictive model of water and nutrient uptake in a closed-loop fertigation system established within a vertical crop under greenhouse conditions, allowing the establishment of additional sustainable fertigation strategies through fewer resources used with high yields in greenhouse horticulture.
2. Materials and Methods
2.1. Predictive Model of Water and Nutrients Uptake
Two submodels working together compose this proposed predictive model (PM): a water uptake submodel (WUS) and a nutrient concentration submodel (NCS). The PM is adapted for vertical crops under greenhouse conditions.
2.1.1. Water Uptake Submodel
The water uptake submodel (WUS) was derived from the Penman–Monteith equation, established as the FAO standard method to measure crop evapotranspiration. This version was modified by the American Society of Civil Engineers (ASCE) to calculate the reference crop evapotranspiration (ETo) in hourly periods (mm·h−1). The model runs according to two different factors that consider daytime and nighttime hours [46,47], as follows:
where: Δ (KPa·C°−1) is the slope of the relationship of saturation vapor pressure to temperature. Rn and G (MJ·m−2·h−1) are the net radiation at the crop surface and the soil heat flux at the soil surface, respectively. γ (KPa·C°−1) is the psychrometric constant. u2 (m·s−1) is the mean hourly wind velocity. (es − ea) (KPa) represents the VPD of the air. T (°C) is the mean hourly air temperature, and Cd (s·m−1) is the day and night factor: Cd = 0.24 for hours of the day, and Cd = 0.96 for hours of the night.
ETo = [0.408Δ(Rn − G) + 37u2γ(es − ea)·(T + 273)−1][Δ + γ(1 + u2Cd)]−1
Two modifications were conducted to adapt Equation (1) to the reference crop evapotranspiration in vertical crops in the greenhouse (ETo′). The term G was assumed to be zero because soil does not exist in this type of system. Rn was calculated as the product between solar radiation (Rs) outside and the transmissivity coefficient (α) associated with the characteristics of the greenhouse film. This coefficient was estimated considering the multi-levels in vertical crops, so it did not overestimate the water requirements by lower plants. In addition, the crop coefficient used to calculate the standard evapotranspiration (ETc) was equal to the basal crop coefficient (Kcb) to consider only the transpiration (Tr) process. Finally, a new factor (Φ) was included that considers the relationship between the density of the vertical crop (a) and its equivalent in a standard horizontal density (b), so the result is (a·b−1). In this way, the proposed Tr predictive model is the following:
where: ETo′ (mm·h−1 = L·m−2·h−1) is the crop reference evapotranspiration for vertical crops in the greenhouse. Kcb (-) is the basal crop coefficient, which is calibrated by the PM. Φ is the density index. ETc′ (L·m−2·h−1) is the crop evapotranspiration under standard conditions for vertical crops in the greenhouse. A (m−2) is the land surface of the vertical crop, and Tr (L·h−1) is the hourly crop transpiration for vertical crops under greenhouse conditions.
ETc′ = ΦKcbETo′
Tr ≈ AETc′
2.1.2. Nutrient Concentration Submodel
The nutrient concentration submodel (NCS) is based on a simple model of ion concentration variations proposed by Carmassi et al. in 2003 for closed-loop hydroponic systems, which is a function of crop transpiration and other fertigation parameters [35,36,48]. The concentration (expressed as mM) of the nutritive ions can be calculated with Equation (4), while the non-nutritive ions can be computed with Equation (5), as follows:
where [I]t+1 is the concentration of ion I at time t+1. [I]t is the concentration of ion I at time t. [I]R is the recharge concentration of ion I at time t + 1. [I]U (mM) is the crop uptake concentration (CUC) of ion I, which stays constant over time. V (L) is the volume of the nutrient solution tank. p (-) is a coefficient that depends on the sensitivity of the crop to specific ions and ranges from 0.01–0.3 [34].
[I]t+1 = [I]t + TrV−1([I]R − [I]U)
[I]t+1 = ([I]t − [I]Rp−1)exp(−pTrV−1) + [I]Rp−1
This submodel includes electrical conductivity as a function of the sum of cations in the nutrient solution (Equation (6)), proposed by Sonneveld and Van der Wees in 1990, as shown below [34]:
where EC (dS·m−1) is the electrical conductivity, and [C+] (meq·L−1) is the sum of cation concentration in the nutrient solution (NH4+, K+, Ca2+, Mg2+, and Na+).
EC = 0.19 + 0.095[C+]
2.2. Modeling Process
The simulation time was 24 days, which started on day 7 and finished on day 31 after transplanting (crop time).
The WUS submodel worked with initial Kcb values equal to 0.15 for the initial crop stage and 0.9 for the midseason and final crop stages, which were later calibrated. The duration of the crop stages was as follows: 0 days for the initial stage, because the transplantation was carried out 19 days after the sowing, 30 days for the development stage, 15 days for the mid-season stage, and 0 days for the late season because the harvesting was done before this stage started [46,49]. The standard horizontal density (11 plants·m−2) was calculated from a distance between plants and furrows of 0.3 m. An adjustment of the WUS to the measured data was carried out through a nonlinear least squares process using the generalized reduced gradient (GRG) method, which tries to minimize a target value [48,50]. For this, the Microsoft Excel Solver tool [51] and mean absolute error (MAE) were used to find the target value, whose variable cells during the simulation process were Kcb values.
The NCS submodel used as initial values for crop uptake concentrations [I]u in (mM) were 5.73 K+, 3.20 Mg2+, 9.06 Ca2+, and 0.97 NH4+ [52]. Likewise, it used an initial sensitivity coefficient, p, equal to 0.2 for Na+ [36]. Both these values and initial concentrations in the nutrient solution calculated were calibrated by the PM through the Solver tool as well, where the target value was the total sum of the mean absolute error of each cation.
2.3. Location, Climatic Conditions, and Time Experiment
The experiment was conducted in a tunnel-type medium technology greenhouse (TG) of Almeria University close to the Mediterranean Sea (La Cañada de San Urbano, Almería, Spain; 36°46′37.8″ N, 2°24′20.1″ W) with a northwest–southeast orientation. The TG had a surface of 51 m2, 6.3 m wide, 8.1 m long, and 3.5 m in height up to the ridge, with polycarbonate side, front, and back walls. The roof cover material was 720 gauge low-density polyethylene with transmittances of 92.7 and 83.0% for GSR and PAR, respectively, with UV additives. Ventilation was natural and consisted of a longitudinal window mechanic with an axis on the roof (zenithal ventilation), 8.1 m in length, with an opening of 94%, and totally covered with an anti-aphid mesh of 50 × 25 threads per inch. Inside was a mobile black shade screen to a height of 2.5 m. The transmissivity coefficient (α) of the film cover was 0.2, indirectly measured relative to the measurements outside the TG by the pyranometer of an automatic climate station (ACS) and the measurements inside the TG by a luxometer, Sekonic C-7000, and the conversion factor used was 1 lx = 118 W·m−2 [53]. This coefficient was a representative mean of the multiple levels in the vertical crop to avoid overestimations at lower levels.
Within the TG, three Elitech RC-51H sensor data loggers (DT) were strategically placed in the vertical crop, which registered temperature (°C) and relative humidity (%) each 30 min at a height of 1.2 m. ACS was a greenhouse climate control system installed outside by Atenix Electronics and Automatics S.L. and placed 15 m from the TG and 4.5 m high. This device had sensors to measure irradiance (W·m−2), temperature (°C), humidity (%), and wind velocity (km·h−1), whose data also registered each 30 min.
The climate database used by the predictive model was based on information from the ACS and DT devices. The data were complemented by the European Commission Photovoltaic Geographical Information System (PVGIS) [54] and the Almería Airport automatic meteorological station (36°50′47″ N, 2°21′25″ W) of the State Meteorological Agency (AEMET) [55]. The outside wind velocity measurements were transformed into the inside greenhouse velocity measurements with a linear model by Wang, proposed for this type of greenhouse [56]. The average climate conditions of Almería belong to a hot semi-arid climate, according to Köppen’s classification, with an average monthly temperature of 19 °C, an average monthly relative humidity of 65%, an annual precipitation equal to 200 mm with 25 rain days, and an annual insolation of 2800 h [57].
Figure 1 shows the outside environmental conditions during the time experiment, spring 2023 (transplant 15 March, harvest 19 April). The average temperature for the 35 days was 17.3 °C and ranged from 21.7 to 14.4 °C. The daily humidity had an average value of 63.6% and ranged from 31.1 to 86.1%. The average irradiance was 7.2 KW·m−2 and ranged from 5.9 to 8.0 KW·m−2. The daily average wind speed was 3.3 m·s−1 and ranged from 0.9 to 7.1 m·s−1.
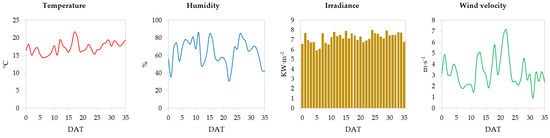
Figure 1.
External environmental conditions with daily frequency for the day after transplantation (DAT): temperature (°C), humidity (%), irradiance (KW·m−2), and wind velocity (m·s−1).
2.4. Plant Material
The vegetable used was baby lettuce, cv. Gatsby, supplied by Gautier Semences. Lettuce seeds sown on 24 February 2023, on a substrate composed of a mixture of peat moss and vermiculite, were transplanted early on the 20th day after sowing (15 March) into polystyrene foam (3 × 3 cm). At days after transplant (DAT) 0, the lettuce plants were 15.5 ± 0.2 cm in height, with a stem diameter of 4.86 ± 0.11 mm, root length of 18.4 ± 1.2 cm, and had an average of eight leaves. The harvest process was carried out 35 days after transplantation (DAT) in the morning (19 April).
2.5. Experimental Design and Vertical Crop Set-Up
Two different experimental designs were implemented. The first (ED1) aimed to evaluate the performance of the predictive model by measuring water and nutrient uptake in the vertical crop, and the second (ED2) aimed to assess the effects on physiological and development crop parameters under these environmental and system conditions.
2.5.1. Experimental Design 1 (ED1)
The experimental unit was a vertical crop tower type (VCT) of 2.25 m height, arranged in a row of 6 m length (Figure 2a), elevated 0.25 m over the ground, and mounted over a collection drainage pipe (250 mm Ø); both components were supported by a structure of anodized aluminum resting on the ground. Each vertical crop was made up of cylindrical units or towers designated as columns (CLs). In turn, 15 individual GrowPipe (GP) units (Figure 2b) formed each column. Each GP was 15 cm high and 7.5 cm in diameter; moreover, it was divided inside into two cavities by an inner septum and featured a hole in one of the sides, which supported a plant by an integrated water-collecting slide. The setup of multiple GP was conducted placing one on the other, opposing the holes for the plants 180°, while the vertical distance between plants was 30 cm (Figure 2c).

Figure 2.
Montage of vertical crops according to the experimental designs: (a) experimental unit and ED1 CD levels of ED1; (b) GrowPipes unit; (c) assembly of GP units; and (d) levels low (L), medium (M) and upper (U) of nested factor P in ED2 (d).
The performance of the predictive model was assessed under different conditions through ED1, which consisted of a completely randomized design to compare two crop densities (CDs). The two crop densities were obtained by modifying the distance between CLs. Low density (LD) comprised 20 CLs placed every 0.3 m, including 300 plants at 50 plants·m−2. High density (HD) consisted of 32 CLs placed every 0.19 m, including 480 plants at 80 plants·m−2, each with three replicates. The distance between two consecutive rows of vertical crops was 1 m. Furthermore, days after transplantation (DAT) and replications (RPs) were included as variation sources to increase the accuracy of the experiment.
2.5.2. Experimental Design 2 (ED2)
The developmental crop response to the system was evaluated with the ED2 experiment, which consisted of a nested or hierarchical design in which the relative plant position (PP) of the plant relative to the ground was nested in the CD. The PP nest factor had three levels: low (L), where plants were located between 0.25 and 1.0 m; medium (M), between 1.0 and 1.75 m, and upper (U), between 1.75 and 2.5 m above ground. In this way, the experimental VCT unit was divided into three levels (Figure 2d). Thus, the LD vertical crop contained 100 plants per level, and the HD vertical crop contained 180 plants per level. Likewise, the RPs were included to increase the accuracy of the experiment.
Lettuce plants at the U level received 100% indoor radiation (57 W·m−2 = 260 µmol·m−2·s−1), M level, 36% (21 W·m−2 = 96 µmol·m−2·s−1), and L level, 24% (14 W·m−2 = 64 µmol·m−2·s−1). The conversion factor used to transform sunlight, the units of irradiance to units of photons, was 1 µmol·m−2·s−1 = 0.219 W·m−2 [58]. The U level had an average value of sunlight photons 4% higher than ideal photosynthetically active radiation (PAR) for lettuce, established at 250 µmol·m−2·s−1 [59].
2.6. Management of Fertigation System
The fertilizer and water dosage mechanism consisted of a closed-loop fertigation system (CLFS) with drip-type irrigation. Below each experimental unit at ground level was located a 250 mm diameter PVC collection drainpipe, 6.26 m long, with a 250 L capacity, whose purpose was to collect all drainage from the vertical crop and, in turn, work as a nutrient solution tank (NST) for the fertigation system. Each NST had an automatic water replenishment mechanism composed of a plastic buoy, which allowed filtered water from the reserve tank (RT) to maintain the same level in the NST during the time experiment. Each RT had a capacity of 100 L connected to the NST by a 6 mm diameter polyurethane hose. The input of filtered water into the RT came from a reverse osmosis system (ROS), Mega Grow 1000. The water output had a pH of 7 and an electrical conductivity (EC) of 0.52 dS·m−1, with the following ion concentrations in (mM): 0.50 HCO3−, 0.13 NO3−, 0.01 NH4+, 0.86 H2PO4−, 0.01 K+, 0.11 Ca2+, 0.73 Mg2+, 1.78 Na+, 0.49 SO42−, and 1.85 Cl−.
The automatic supply and adjustment of fertilizers and pH inside the NST were conducted by a pH and EC hydroponic controller (HP) (Prosystem Aqua Europe S.L. model 04001), through three peristaltic pumps: two for fertilizers, and one for pH. The nutrient solution in the NST was pumped up to an irrigation lateral pipe of 20 mm diameter, placed over the VCT using a Monzana MZPP27 peripheral pump of 550 W, and coupled to the filter system, whose filtering material was balls of polypropylene. Each column had two flow-regulated drippers (Rivulis Supertit) with a flow rate of 2.2 L·h−1, which supplied water through a 6 mm diameter microtube connected with irrigation pickets. The LD vertical crop had an IL with 40 drippers separated by 15 cm, and the HD vertical crop had 64 drippers separated by 9.4 cm.
The fertigation frequency was established using an analog Coati irrigation timer. Irrigation programming consisted of irrigation each 15 min between 10:00 and 16:00, and then each 45 min for the rest of the day. The nutrient solution was calculated using the Nutrient Solutions Calculator developed by Incrocci et al. [60]. The ion concentrations of macronutrients in (mM) and micronutrients in (µM) of the calculated nutrient solution (NS) were: 15.0 NO3−, 1.0 NH4+, 2.0 H2PO4−, 10.0 K+, 4.5 Ca2+, 1.0 Mg2+, 2.6 SO42−, 1.78 Na+, 1.85 Cl−, 40 Fe, 5 Mn, 1 Zn, 1 Cu, 30 B, and 1 Mo. The NS was concentrated 100 times to prepare concentrated nutrient solutions (CNS) A and B. In tank A, Ca (NO3)2, and micronutrients were dissolved, while tank B contained MgSO4, NH4H2PO4, KNO3, KH2PO4, and K2SO4. The pH was regulated with HNO3 (nitric acid); as a result, the NS EC was 2.45 dS·m−1 and pH 5.5. Three intervals for the management of the nutrient solution (fertigation phases) were defined: the EC target was set at 2.45 dS·m−1 between 0 and 6 DAT to acclimatize the lettuce crop, then increased to 3.3 dS·m−1 from 7 to 31 DAT (simulation time), and finally withheld for the remaining time.
2.7. Response Variables
For ED1, water uptake from and nutrient concentration in the NST were considered as response variables. The sampling process consisted of taking 21 samples from the NST in the morning (9:00) from 7 to 31 DAT. The daily water uptake (DWU) was measured as the volume in liters of water needed to recharge the NST to the original level through a plastic bucket calibrated to 1 L accuracy. The daily variation in ion concentration in the NST was measured. For this, samples were taken in containers of 50 mL, which were maintained in a refrigerator at 4 °C until their measurement at the final experiment time. Specifically, the concentrations of nutritive cations (NH4+, K+, Ca2+, and Mg2+) and non-nutritive cations (Na+) were measured in mM, using a portable ion-selective electrode meter (ISE), Imacimus IC-5, with a precision of 0.01 mM.
The sampling in ED2 was at 35 DAT, collecting 16 plants per level of the PP factor. Leaf number (LN) and productivity parameters were determined. Productivity (g·plant−1) was measured as fresh weight (FW) for the root, shoot (leaves + stem), and harvested head, with an analytical balance of 0.01 g precision. The root/shoot ratio (R/S) was calculated for the FW as Root·Shoot−1. The fresh weight of the heads was extrapolated to express yield as t·ha−1. To determine the dry mass, the fresh mass samples were dried (in a 631 Plus forced convection oven model) at 70 °C for 48 h to obtain the dry weight (DW) of the shoots and roots. The water content of the plants was expressed as the percentage of (FW–DW),·FW−1. The shoot biomass index (SBI) was calculated as shoot FW·LN−1 (in g·leaf−1).
2.8. Statistical Analysis
Data from both statistical designs (ED1, ED2) were analyzed with IBM SPSS Statistics v.28 software (IBM, Armonk, NY, USA), using an analysis of variance (ANOVA) with statistical significance (p-value < 0.05) and Tukey test for the comparison of mean values in ED2. The fit goodness (accuracy) of the PM was measured by statistics metrics for assessing the performance of prognostic models: the coefficient of determination (R2), mean absolute error (MAE), mean square error (MSE), and root mean square error (RMSE) [61,62,63,64].
3. Results and Discussion
3.1. Statistical Performance of the Predictive Model
Table 1 shows that the PM had a better fit for water uptake, NH4+, and K+ concentrations for both densities, whose R2 ranged from 0.826 to 0.920, while the Mg2+ and Na+ concentration R2 ranged from 0.707 to 0.748, These coefficients were higher than 0.6, so can be classified as “good fit variables” [65]. For the Ca2+ concentration, the PM could not explain its variation for both densities, a fact that will be discussed later. Comparing the two densities found that NH4+, K+, and Mg2+ had a better R2 in the LD system than in the HD, while the opposite was true for water uptake and Na+ concentration, whose R2 values were better in the HD.

Table 1.
Statistical performance metrics of PM regarding water uptake and cation concentrations for low- and high-density vertical crops.
Regarding the other metrics (MAE, MSE, and RMSE), all the cation concentrations had higher values in the HD than the LD, being higher for K+ and Ca2+ concentrations, so the PM was less accurate in denser vertical crops. The MAE was less than 0.267 mM for all the cations, except for the K+ and Ca2+ concentrations, whose values ranged from 0.728 to 0.996 mM. The same occurred for the RMSE, whose value was lower than 0.337 mM for the concentrations of NH4+ Mg2+ and Na+ and ranged from 0.882 to 1.224 mM for the rest of the cations. However, with respect to water uptake, the PM was less accurate in the LD, with an MAE 40% higher and an RMSE 31% higher than the HD. Overall, the PM had a mean absolute error lower than 2 L·day−1.
Although EC is not estimated by the PM, because this is a fixed parameter along the time established by the user for the simulation process, its value was 3.3 dS·m−1 (EC target) from 7 to 31 DAT simulation time. The mean absolute error (MAE), mean square error (MSE), and root mean square error (RMSE) of the measured data with respect to the EC fixed in the PM were calculated. Therefore, in Table 1, it is shown that the LD had an average error 41% higher than the HD vertical crop with respect to the MAE and RMSE statistic metrics, but for both densities, the maximum error threshold was lower than 0.341 dS·m−1, meaning 10% of the EC target value.
3.2. Water Uptake and Cation Concentrations
Multivariate ANOVA analysis showed significant differences for all the response variables: water absorption and cation concentrations (NH4+, K+, Ca2+, Mg2+, and Na+) for CD, DAT, and their interaction. However, there were no statistically significant differences between the repetitions for any variable. Table 2 shows the mean values of variables on the NST. The HD vertical crop for all response variables was significantly higher than the LD. In the case of water uptake, the results were agreed on expected outputs because the HD crop had 60% more plants than the LD. However, for all the nutritive cation concentrations, it was expected that the LD would consume less than the HD vertical crop; in other words, the average cation concentration in the LD was higher than the HD vertical crop as a result of a smaller difference between the initial and final concentrations of each cation, but this did not happen. In the same way, this reasoning is applicable for non-nutritive cations such as Na+, because despite this being accumulated in the NST, the crop consumes small quantities over time. This fact will be explained later by analyzing how the crop was affected by the system and the climate conditions through the ED2 response variables. In addition, the management parameters of the nutrient solution (pH and EC) are also shown in Table 2, and which ones were significantly influenced by crop density: the LD had an EC statistically lower than the HD, while the opposite occurred for the pH parameter.

Table 2.
Water uptake, pH, EC, and cation concentrations by crop density (CD): high density (HD) and low density (LD) in the nutrient solution tank (NST) of the vertical crop.
3.2.1. Water Uptake
The graphs shown in Figure 3 show that the PM overestimated substantially the real water consumption using the initial values of Kcb. The PM forecasted a water consumption of roughly 105 L for the LD (Figure 3a) and 168 L for the HD (Figure 3b) at 31 DAT, while the adjusted PM adjusted with calibrated Kcb values did not exceed the 30 L consumed per day for both densities. The calibrated Kcb values for the LD were 0.01 for the initial stage and 0.21 for the midseason and late stages, meaning a decrease between 77 and 100%, while the Kcb for the HD was 0.04 for the initial stage and 0.14 for the midseason and late stages, so the basal crop coefficient reduced between 74 and 85%. In this way, the modeling process deduced that the crop basal coefficients are lower in vertical crops than in conventional agriculture.
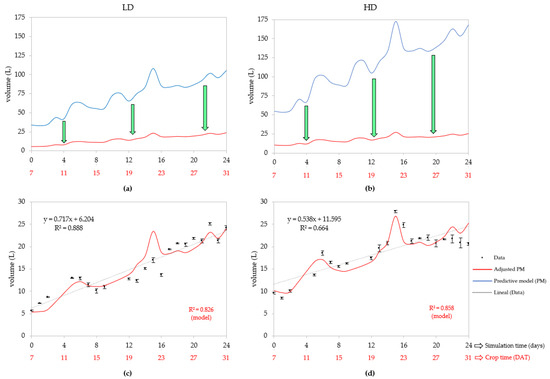
Figure 3.
Lettuce water uptake days after transplant (DAT) of the adjusted predictive model, for low (a,c) and high density (b,d), respectively. (a,b), graphs with the predictive model run with initial and adjusted parameters. (c,d), graphs of the adjusted model with linear regression of the data and R2.
According to Figure 3c, the adjusted PM forecasted a daily water consumption for the vertical LD between 5 L and 24 L, at 7 and 31 DAT, respectively, while Figure 3d shows that the daily water consumed by the HD ranged from 10 to 25 L (7–31 DAT). As a result, the compound daily growth rate (CDGR) was 6.4% for the LD and 3.9% for the HD, so the model established that the LD consumed water faster. The adjusted PM had a good fit at both densities, since the R2 was 0.826 for the LD and 0.858 for the HD, with a better performance in the HD because its R2 was higher than the linear regression.
The HD consumed significantly more water than the LD crop since it had an average daily consumption of 15 L (4 L less than the HD), whose average consumption was 19 L per day (Table 2). Therefore, the average consumption per plant was 50 mL·d−1 for the LD, which was higher than the 40 mL·d−1 for the HD system. For the same time interval, the adjusted PM estimated an average daily consumption of 12 L for the LD and 20 L for the HD, but with the same average consumption per plant of roughly 40 mL·d−1; this is proof that the tPM assumes that all the plants are healthy and have the same irrigation conditions when comparing the results with the water uptake for a lettuce crop in conventional agriculture, whose daily consumption per plant is around 334 mL·d−1 [66]. Vertical crops were found to significantly save water, as the LD system reduced the plants’ uptake by 284 mL, which represents an 85% savings, lower than the HD system, where the water reduction was roughly 294 mL, which is equal to an 88% savings. Even compared to horizontal hydroponic lettuce, whose average consumption is approximately 94 mL·plant−1·day−1 [66], vertical crops are better because the LD system saves 44 mL, equal to a 47% savings, and the HD system saves 54 mL, a 57% savings. In these ranges, water savings are close to those reported for vertical farms as plant factories, which are capable of saving water by more than 95% compared to conventional crop methods.
3.2.2. Sodium Concentration (Na+)
The initial Na+ concentration used by the PM at 0 DAT was 1.78 mM for both densities, according to the quality of the irrigation water. The initial value of the sensitivity coefficient, p, was 0.2, and later calibrated was equal to 0.27 for the LD and 0.29 for the HD, so within the range (0.01–0.3) reported by Carmassi et al. [36,48].
In Figure 4, the blue graph shows that the predictive model run with the initial values overestimated the data. The red graph, corresponding to the adjusted PM, shows that Na+ concentration at 7 DAT was 1.88 mM for the LD and 2.11 mM for the HD, and the final values were 3.39 and 3.80 mM, respectively. This establishes a difference of 1.51 mM for the LD and 1.69 mM for the HD; despite that, the CDGR values for both densities were equal to 2.5% so, based on the PM, this deduces that Na+ was accumulated in the same ratio independent of density. In both densities, adjusted PM presented a high correlation with measured data, since R2 was 0.720 for the LD and 0.743 for the HD, but no greater than linear regression, indicating that it could be feasible and simpler to use a straight line instead of an exponential function, as the PM works for non-nutritive ions.
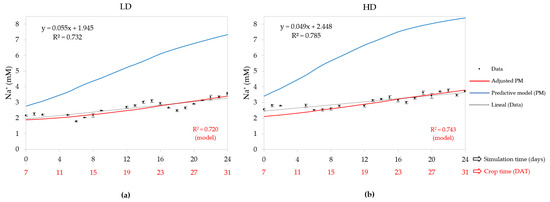
Figure 4.
Days after transplant (DAT) concentration of Na+ in the nutrient solution tank (NST) at (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM, and linear regression of measured data with their equation and R2.
The sensibility coefficients were calibrated together with the average Na+ concentration by the model fitted between 7 and 31 DAT, 2.60 mM for LD and 2.99 mM for HD. For this, we estimate that the Na+ crop uptake concentration (CUC) by the lettuce crop was 0.71 mM for LD and 0.87 mM for HD, values close to 1 mM, a value reported for the formulation of the nutrient solution for the lettuce crop [67,68]. Furthermore, the measured data indicate that the average Na+ concentration for the vertical HD crop during the experimental calibration time was 3.09 mM, significantly higher than the LD system, whose value was 2.66 mM (Table 2). This indicates that the CD of the vertical crop significantly affected this variable, suggesting increased accumulation of Na+ in the denser systems. In comparison, the average concentrations from the data and the adjusted model found that during 24 days of simulation time, there was a relative error range of 2–3%. The CUC based on the measured data was 0.72 mM for the LD and 0.90 mM for the HD.
3.2.3. Ammonium Concentration (NH4+)
Figure 5 shows the graph of the PM run with the initial values, which does not adjust to the data, while the PM run with the parameters adjusted accordingly. The adjusted model used initial concentrations (0 DAT) calibrated at 0.45 for the LD and 0.49 mM for the HD. These values differ by more than twice the initial concentration of NH4+ in the NST, set at 1 mM.
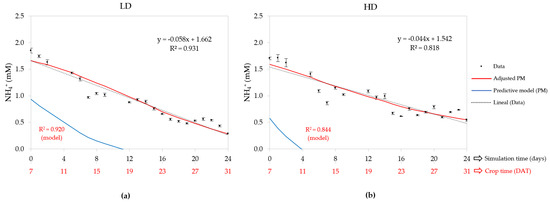
Figure 5.
Days after transplant (DAT) concentration of NH4+ in the nutrient solution tank (NST): (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM, and a linear regression of the measured data with their equation and R2.
If we analyze the model adjusted between 7 and 31 DAT, we found that the initial concentration was 1.66 mM for the LD and 1.59 mM for the HD, and their corresponding final values were 0.28 and 0.55 mM, resulting in differences of 1.38 and 1.05 mM, respectively. Both values are close to the 1 mM reported in the nutrient solution for lettuce [69,70]. As a result, the compound daily decrease rate (CDDR) was 7% for the LD and 4% for the HD. So, one deduces that the LD consumed this cation at almost double the velocity of the HD. Overall, the adjusted PM agreed well with the measured data, because R2 was 0.920 for the LD and 0.844 for the HD, and the linear regression R2 was higher than the LD.
The average NH4+ concentration for CD between 7 and 31 DAT was 0.91 mM, significantly lower in the LD than the HD, whose value was 0.97 mM (Table 2). If we compare these values with the average concentrations of the adjusted model, 0.92 mM for the LD and 0.97 mM for the HD, we find a maximum relative error of 1%. The calibrated crop uptake concentration (CUC) values were 1.72 mM for the LD and 1.12 mM for the HD. These differ by a maximum of 77% from the 0.97 mM reported for tomatoes and sweet peppers [52,71].
3.2.4. Potassium Concentration (K+)
Figure 6 shows that the model run with the initial values did not adjust to the data (blue graph). The adjusted model worked with an initial K+ concentration (0 DAT) calibrated at 3.56 mM for the LD and 4.15 mM for the HD; both values differ by more than double regarding the initial concentration in the NST, whose value was 10 mM. The initial concentration predicted by the adjusted model at 7 DAT was 13.99 mM for the LD and 14.90 mM for the HD, with their corresponding final concentrations (31 DAT) equal to 4.60 and 6.72 mM. As a result of the differences of 9.39 and 8.18 mM obtained, both values differ between 4 and 10% with respect to the K+ value reported in the nutrient solution for horizontal hydroponic lettuce, 8.5 mM [72]. The CDDR was 4.5% for the LD and 3.3% for the HD, so the conclusion is that the LD consumed K+ faster. The performance of the adjusted model was good, because R2 was 0.896 and 0.839 for the LD and HD, respectively. The linear regression in both cases had a higher R2.
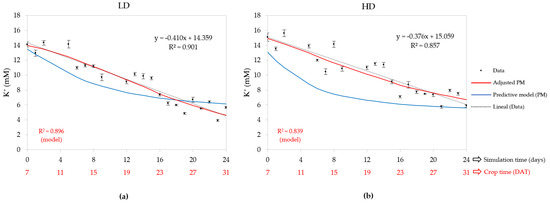
Figure 6.
Days after transplantation (DAT) K+ concentration in nutrient solution tank (NST): (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM, and linear regression of measured data with their equation and R2.
The average K+ concentration between 7 and 31 DAT for the LD was 9.05 mM, significantly lower than that of the HD system, whose value was 10.19 mM (Table 2). Comparing these values with the average concentrations of the adjusted model, 8.93 mM for the LD and 10.05 mM for the HD, finds a relative error lower than 2%. The CUC values calibrated by the model were 11.71 and 8.79 mM for the LD and HD, respectively, which compares to the literature, whose value reported is 6.6 mM for cucumber [52], resulting in a difference between 33 and 77%.
3.2.5. Calcium Concentration (Ca2+)
According to Table 2, there were statistically significant differences between the LD and HD systems, so CD was influential in the Ca2+ concentration in the NST. The average value for the LD was 4.89 mM and 5.20 mM for the HD. Figure 7 shows that the PM (blue graph) run with the initial values follows a decreasing tendency but without any adjustment of the data, whereas the adjusted model (red graph) does not follow a decreasing trend for the HD and presents a slightly decreasing tendency for the LD, a strange behavior that does not correspond to normal nutrient consumption. In contrast, in the case of the HD, it seems that the Ca2+ concentration increases along the crop time, resulting in an accumulation in the NST. The linear regression shows this unusual behavior because the slope of the straight line is positive for both densities, an indication that the Ca2+ concentration is increasing over time. Just like the PM run with the initial data, the adjusted PM did not correlate with the data because the R2 was 0.001, due to the measured data being very dispersed. The CUCs calibrated by the model were negative values or small, 0.41 mM for the LD and −0.95 mM for the HD. This unusual behavior can be explained as a system response for two reasons: a low-velocity uptake by the crop, and the crop uptake concentration was lower than the concentration replenishment in the NST by the pH and EC controller; as a result, there was an accumulation. Consequently, the lettuce plants expressed a physiological disorder known as tip burn; however, the cause could also have been deficient ventilation within the greenhouse [73].
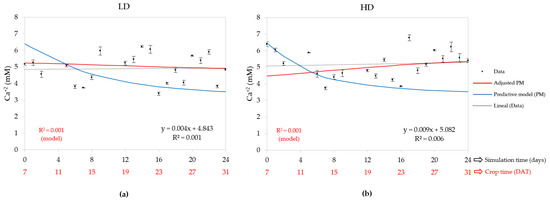
Figure 7.
Days after transplantation (DAT) calcium concentration in nutrient solution tank (NST): (a) low density (LD) and (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM, and a linear regression of measured data with their equation and R2.
3.2.6. Magnesium Concentration (Mg2+)
Figure 8 shows no correlation to the PM data (blue graph) run with the initial values. The adjusted model used initial concentrations (0 DAT) calibrated at 0.54 and 0.66 mM for the LD and HD, respectively. These values differ between 56 and 64% in terms of the initial concentration of NST, whose value was 1.50 mM. At 7 DAT, the adjusted model predicted a magnesium concentration of 2.31 mM for the LD and 2.53 mM for the HD, and final concentrations (31 DAT) of 1.28 and 1.32 mM, respectively. This resulted in differences of 1.04 mM for the LD and 1.21 mM for the HD; both values are within the range values reported for hydroponic lettuce (0.7–1.40 mM) [67,74]. The CDDR was 2.4% for the LD and 2.7% for the HD, so based on the model, it is deduced that the HD consumed this cation faster. In relation to the adjusted PM performance, this was a good fit for the data because the R2 for the LD and HD were 0.748 and 0.707, respectively, with the LD higher than the HD. The linear regression only had an R2 higher than the model for the LD crop.
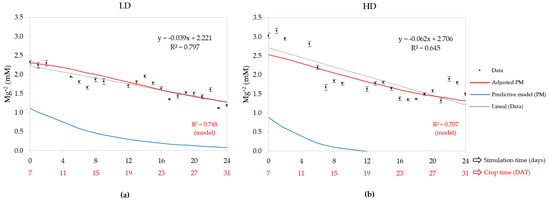
Figure 8.
Days after transplantation (DAT) magnesium concentration in nutrient solution tank: (a) low density (LD), (b) high density (HD); also contains measured data, predictive model (PM), adjusted PM, and linear regression of measured data with their equation and R2.
The average magnesium concentration for the LD between 7 and 31 DAT was 1.71 mM, significantly lower than that of the HD system, whose value was 1.90 mM (Table 2). Comparing these values with the average concentrations of the adjusted model, 1.75 and 1.81 mM for the LD and HD, results in a relative error range of 2–5%. The CUC calibrated by the model was 1.29 mM for the LD and 1.30 mM for the HD, which when comparing them to the literature, whose value is 0.9 mM for tomato [52], determines a difference of 44%.
3.3. Crop Behavior: Physiological and Production Parameters
Table 3 shows the mean values and statistical significance of lettuce crop behavior in vertical cropping systems with two planting densities (CD) nested at three levels of plant positioning (PP). Replicas of the experimental design did not show significant differences, so they can be considered homogeneous. All the variables are affected by PP in the crop column and by CD (except for water content).

Table 3.
Fresh and dry weight, yield, and related parameter behavior at 35 DAT for vertical lettuce crop growth with different crop density (CD) and plant position (PP).
The increase in CD results in a reduction in the individual fresh and dry biomass of each plant (46–47% in the shoot and 60–61% in the root), which means a reduction in the R/S ratio of 22–13% but does not affect the water content of the plant. The rate of accumulation of shoot biomass (SBI) decreases by more than half in high CD and by 40% with decreasing PP. On the other hand, the number of leaves developed per plant increases by 10% with higher CDs and by 33% with decreasing PP. This increase is progressive with the decrease in PP and is more pronounced for the LD (up to 40%) than for the HD (up to 25%). The fresh weight of the aerial part (shoot) and the shoot biomass index (SBI) show significant interactions between CD and PP. The behavior of leaf development and shoot fresh weight is responsible for the significant interaction of CD x PP for shoot FW and SBI, while these reductions are progressive for the HD, and they are only visible between the top level and the rest of the column for LD.
According to Table 3, the shoot and root fresh biomass of the LD lettuce plants, whose respective mean values were 148.6 and 14.6 g, was between 55 and 67% higher than the values of shoot FW reported for lettuce grown in horizontal hydroponic greenhouses (HHG), and between 41 and 66% higher than values of the roots of HHG, whose respective ranges in the literature are 88.8–96.1 g for the shoot and 8.78–11.5 for the root FW [75]. The HD system had a root FW between 9 and 16% lower than lettuce in HHG, and an FW of the root between 33 and 49% lower than in HHG. If we compare these values with data reported for lettuce in open field systems (OFS), which range between 5.32 and 9.07 g for shoots and 0.24–0.84 g for roots FW [76], we find that both crop densities in vertical crops had, on average, a shoot FW between 11 and 21 times higher than in OFS and a root FW between 11 and 27 times higher than in OFS.
Regarding the mean values of these variables for PP levels within the LD system, which vary between 136.3 and 172.7 g for shoot, and 12.8 and 18.1 g for root FW. These results found a major similarity to those reported by Kerbiriou et al. for lettuce in HHG (152–167 g, shoot, and 11.2–11.8 g root FW) [77], and by Gavhane et al. for lettuce in vertical hydroponic systems (VHS) (150–200 g, shoot, and 9–15 g, root FW) [78]. However, within the HD system, the mean values were lower, even below the threshold of 127 g for shoot, and 11 g for root FW, reaching values of 43.5 g for shoots and 3.4 g for roots on the lower level, close to the values reported for lettuce in HHG by Voutsinos et al. (58.1 g, shoot and 5.4 g, root FW) [44], or the values reported for lettuce in aeroponics and substrate (37.8–50.9 g, shoot and 3.9–11.5 g, root FW [75]. The mean values of the FW of the shoot for LD, and its values for each PP level, were higher than the range reported for a plant factory with artificial lighting (PFAL) of 64.9–123.3 g [44], while in the case of the HD vertical crop, they were within the range of the literature, except the mean value of the U and L levels, which were higher and lower, respectively. Regarding the root FW, the literature reports a range between 9.4 and 17.8 g [44] for a PFAL; this range includes all the mean values except the average value for the HD and the levels of the mean of the M and L in the HD, which were lower, and the mean of the U level in the LD, which was higher.
The root–shoot ratio for both the LD and HD, whose respective mean values were 0.09 and 0.07, were on average between 18 and 36% lower than the range reported for lettuce in HHG (0.10–0.12) [75,79], but equal to the 0.09 value reported by Voutsinos et al. [40,44], in the case of the LD. Compared to the VHS, whose range is 0.06–0.08 [79], the LD was 13% higher than the maximum limit of the range, and the HD was within the range, but at the same time, the LD was 36% lower than the 0.14 reported for a PFAL [44], while the HD had a mean equal to half of this. For both densities, the mean values were within the range reported for lettuce in OFS, 0.03–0.13 [76]. In relation to the mean values of PP levels for the LD, these were closer to the values reported for lettuce in HHG and, in turn, within the OFS values, while for the HD, they were closer to the VHS values.
None of the mean values of the shoot DW were within the range reported for lettuce in HHG (4.12–4.86 g) [44,75], but they were within the range reported for the VHS and PFAL systems (4.00–8.77 g) [44,78], except the mean value of the HD and the LD, and mean values of the M and L levels of the HD, since they were lower than the bottom limit of the range. The root DW of the LD and the U level in the LD were higher than the top limit of the range reported for lettuce in HHG, 0.54–0.82 g [75,77]. The mean of the M and L levels in the LD, together with the mean of the U level in the HD, were within the literature range. The rest of the values were lower. However, compared to the VHS and PFAL systems, 0.3–0.7 g [44,78], the LD and its mean values of each PP level were higher, while the average value of the HD and its mean for the U level were within the range, and the rest of the values were lower.
All the mean values of water content were within the general range published for the lettuce crop (90–99%) [80], being the more common value [81]. Likewise, they were close to the values informed for lettuce in the HHG (94–95%) [75,82,83] and the VHS systems (97%) [78].
Lettuce productivity (extrapolated to t·ha−1) differs significantly between systems (Table 3). LD systems are 13% more productive than HD systems, and their average head weight is 45% higher. Plants in the upper levels produce, on average, 94 t·ha−1, 32% more than those in the middle and 44% more than those in the lower levels. However, there is a significant interaction between CD and PP for harvesting. Analysis of this interaction significantly differentiates the behavior of both systems. First, the harvest in the LD system is more uniform than in the HD, both for the production per unit area (t·ha−1) and for the average weight of the heads (shoot FW). At 35 DAT, all the heads collected in the LD reach marketable weights (>120 g), while only those collected at the upper level for the HD reach this weight. Second, the differences in PP descend linearly for the HD (−57% for the medium and −65% for the lower level), while there are only differences between the upper level and the rest for the LD (−20%). Finally, the highest yields are obtained at the upper level of the HD (110 t·ha−1 and 127 g·head−1), followed by the upper level of the LD (86 t·ha and 173 g·head−1).
The LD system had a mean of 74.3 t·ha−1, 61% higher than the top limit of the range reported for lettuce in HHG (12–46 t·ha−1) [66,75,82,84], roughly 20 times more than the yield of the OFS systems, 3.73 t·ha−1, noted by Barbosa et al. [66], 55% higher than the value published by Orsini et al. for urban agriculture, 48 t·ha−1 [18], and two times higher than the value described by Voutsinos et al. for a PFAL (19–37 t·ha−1) [44], but 20% lower than the bottom limit of the range reported for VHS (93–125 t·ha−1) [78], which requires high energy input, while the yield of the HD vertical crop was 40% higher than that of lettuce in HHG, 17 times higher than that of the OFS, 34% higher than urban agriculture, 74% higher than that of a PFAL, but 31% lower than the VHS. The average value of the low level in the HD was within the range for lettuce in HHG, and the medium level was closer to the value reported for urban agriculture since it differed by only 20%; the mean value of the upper level in the HD was within the VHS range, and the mean values of the PP levels in the LD were closer to the VHS range since the difference was between 7 and 27%.
The production behavior at the lower levels allows us to assume that both systems can be used to obtain continuous harvests year-round (with different sowing and harvesting time schedules) in vertical systems in a Mediterranean climate, in other words, using a stepped harvest to minimize the effect of shadow-casting on the plants further down and achieve more sustainable horticultural production and greater efficiency in water and nutrient resources. Recent research [85] has shown that the use of decision support systems in CLS related to sensor-based system operations, and weather information, along with artificial intelligence and deep learning, can maintain optimal nutrient levels in real time, minimizing or even eliminating the need to discharge the NST. Consequently, considerable amounts of water and fertilizer can be saved, while the pollution of water resources can be avoided by increasing crop yields.
4. Conclusions
The predictive model is capable of forecasting the water uptake and cation concentrations in the nutrient solution tank of a closed-loop hydroponic circuit for vertical crops under greenhouse conditions, with better performance for the water uptake and the ammonium and potassium cations, followed by the sodium and magnesium cations. At the same time, it is more accurate in less-dense vertical crops. Moreover, the simulation process suggests new basal crop coefficients and crop uptake concentrations for vertical crops in these climate conditions, which can be used as a reference point to design highly efficient fertigation strategies for water and fertilizer resources. Nevertheless, the model has potential improvement points: on one hand, the addition of nutritive and non-nutritive anions, and also the regulation of the proportions among all the ions to avoid issues around disequilibrium that will affect the product.
Vertical crops under greenhouse conditions are more competitive than conventional agriculture and even horizontal hydroponics systems, due to their higher yield and development of aboveground biomass, but at the same time, are limited by the shade projection of the highest levels, so it is important to establish parameters to predict and carry out a stepped harvest year-round, those being net radiation, the canopy light extinction coefficient, and leaf area index, which are key parameters with high potential to better simulate the plant conditions in vertical crops and their relationship to the water and nutrient uptake.
Author Contributions
Writing—original draft preparation, M.F.L.M.; review and editing paper, M.F.Q.C. and M.G.; execution of experiment and methodology, M.F.L.M. and C.B.; statistical analysis and analysis of results and preparing all figures and tables, M.F.L.M. and M.d.C.S.S.; analyzing of model performance, M.F.L.M. and C.A.G.M.; agronomy interpretation of results, M.F.L.M. and M.d.C.S.S.; supervision and project administration, M.F.Q.C. and M.G. All authors have read and agreed to the published version of the manuscript.
Funding
Research project TRFE-I-2021/013 “Closed Vertical Crop System in Cascade (GroVert)” PPI 2021 funded by Almeria University (UAL) and Seed for Innovation S.L. Research project CPP2021-008801 “Production and validation of multifunctional nanoparticles for more efficient and sustainable precision agriculture”, funded by “Plan Estatal de Investigación Cientifica, Técnica y de Innovación 2021–2023”.
Data Availability Statement
Data are available in the Almería University repository: Collection: Datasets—Research Objects Dept. Agronomy, http://hdl.handle.net/10835/14861 (accessed on 19 December 2023).
Acknowledgments
The research groups RNM 151 PAIDI-UAL and UASLP-CA-236 developed the research project. Likewise, it was supported by AUIP and CONACYT.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- United Nations Department of Economic and Social Affairs. World Population Prospects 2019; UN: New York, NY, USA, 2019; ISBN 9789211483161.
- World Bank. Population Estimates and Projections|DataBank. Available online: https://databank.worldbank.org/source/population-estimates-and-projections (accessed on 18 December 2023).
- FAO. The Future of Food and Agriculture—Drivers and Triggers for Transformation; FAO: Roma, Italy, 2022; Volume 3, pp. 1–415. ISBN 978-92-5-136639-4. [Google Scholar] [CrossRef]
- Calicioglu, O.; Flammini, A.; Bracco, S.; Bellù, L.; Sims, R. The future challenges of food and agriculture: An integrated analysis of trends and solutions. Sustainability 2019, 11, 222. [Google Scholar] [CrossRef]
- FAO. The State of the World’s Land and Water Resources for Food and Agriculture—Systems at Breaking Point, Syntesis Report 2021; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2021; p. 63. [Google Scholar] [CrossRef]
- Feng, T.; Xiong, R.; Huan, P. Productive use of natural resources in agriculture: The main policy lessons. Resour. Policy 2023, 85, 103793. [Google Scholar] [CrossRef]
- FAO. Land statistics and indicators 2000–2021. FAOSTAT Anal. Br. Ser. 2023, 71, 14. [Google Scholar] [CrossRef]
- FAO. AQUASTAT Dissemination Platform. Available online: https://data.apps.fao.org/aquastat/?lang=en (accessed on 18 December 2023).
- FAO. Greenhouse gas emissions from agrifood systems Global, regional and country trends, 2000–2020. FAOSTAT Anal. Br. Ser. 2022, 50, 1–12. [Google Scholar]
- Sing, J. Natural Resource Management for Sustainable Agriculture, 1st ed.; Assistant, J.S., Ed.; ANU Books: New Delhi, India, 2017; ISBN 9789382166511. [Google Scholar]
- Foley, J.A.; Ramankutty, N.; Brauman, K.A.; Cassidy, E.S.; Gerber, J.S.; Johnston, M.; Mueller, N.D.; O’Connell, C.; Ray, D.K.; West, P.C.; et al. Solutions for a cultivated planet. Nature 2011, 478, 337–342. [Google Scholar] [CrossRef] [PubMed]
- Sambo, P.; Nicoletto, C.; Giro, A.; Pii, Y.; Valentinuzzi, F.; Mimmo, T.; Lugli, P.; Orzes, G.; Mazzetto, F.; Astolfi, S.; et al. Hydroponic Solutions for Soilless Production Systems: Issues and Opportunities in a Smart Agriculture Perspective. Front. Plant Sci. 2019, 10, 923. [Google Scholar] [CrossRef] [PubMed]
- Fussy, A.; Papenbrock, J. An Overview of Soil and Soilless Cultivation Techniques—Chances, Challenges and the Neglected Question of Sustainability. Plants 2022, 11, 1153. [Google Scholar] [CrossRef] [PubMed]
- Benke, K.; Tomkins, B. Future food-production systems: Vertical farming and controlled-environment agriculture. Sustain. Sci. Pract. Policy 2017, 13, 13–26. [Google Scholar] [CrossRef]
- Sushma Devi, N.; Hatibarua, P.; Bijaya Devi, N.; Jamja, T.; Tagi, N.; Tabing, R. Urban Horticulture for Sustainable Food Production and Food Security. Eco. Env. Cons. 2022, 28, 324–335. [Google Scholar] [CrossRef]
- Orsini, F.; Pennisi, G.; Michelon, N.; Minelli, A.; Bazzocchi, G.; Sanyé-Mengual, E.; Gianquinto, G. Features and Functions of Multifunctional Urban Agriculture in the Global North: A Review. Front. Sustain. Food Syst. 2020, 4, 562513. [Google Scholar] [CrossRef]
- van Delden, S.H.; SharathKumar, M.; Butturini, M.; Graamans, L.J.A.A.; Heuvelink, E.; Kacira, M.; Kaiser, E.; Klamer, R.S.; Klerkx, L.; Kootstra, G.; et al. Current status and future challenges in implementing and upscaling vertical farming systems. Nat. Food 2021, 2, 944–956. [Google Scholar] [CrossRef]
- Orsini, F.; Kahane, R.; Nono-Womdim, R.; Gianquinto, G. Urban agriculture in the developing world: A review. Agron. Sustain. Dev. 2013, 33, 695–720. [Google Scholar] [CrossRef]
- Al-Kodmany, K. The vertical farm: A review of developments and implications for the vertical city. Buildings 2018, 8, 24. [Google Scholar] [CrossRef]
- Supraja, M.L. Opportunities and challenges of vertical farming. Int. J. Res. Trends Innov. 2022, 7, 1071–1074. [Google Scholar] [CrossRef]
- Van Gerrewey, T.; Boon, N.; Geelen, D. Vertical farming: The only way is up? Agronomy 2022, 12, 2. [Google Scholar] [CrossRef]
- Beacham, A.M.; Vickers, L.H.; Monaghan, J.M. Vertical farming: A summary of approaches to growing skywards. J. Hortic. Sci. Biotechnol. 2019, 94, 277–283. [Google Scholar] [CrossRef]
- Oh, S.; Lu, C. Vertical farming—Smart urban agriculture for enhancing resilience and sustainability in food security. J. Hortic. Sci. Biotechnol. 2023, 98, 133–140. [Google Scholar] [CrossRef]
- Kabir, M.S.N.; Reza, M.N.; Chowdhury, M.; Ali, M.; Samsuzzaman; Ali, M.R.; Lee, K.Y.; Chung, S. Technological Trends and Engineering Issues on Vertical Farms: A Review. Horticulturae 2023, 9, 1229. [Google Scholar] [CrossRef]
- Graamans, L.; Baeza, E.; van den Dobbelsteen, A.; Tsafaras, I.; Stanghellini, C. Plant factories versus greenhouses: Comparison of resource use efficiency. Agric. Syst. 2018, 160, 31–43. [Google Scholar] [CrossRef]
- Nikolaou, G.; Neocleous, D.; Katsoulas, N.; Kittas, C. Irrigation of Greenhouse Crops. Horticulturae 2019, 5, 7. [Google Scholar] [CrossRef]
- Avgoustaki, D.D.; Xydis, G. Plant factories in the water-food-energy Nexus era: A systematic bibliographical review. Food Secur. 2020, 12, 253–268. [Google Scholar] [CrossRef]
- Ghiat, I.; Mackey, H.R.; Al-Ansari, T. A Review of Evapotranspiration Measurement Models, Techniques and Methods for Open and Closed Agricultural Field Applications. Water 2021, 13, 2523. [Google Scholar] [CrossRef]
- Voogt, W.; Bar-Yosef, B. Water and Nutrient Management and Crops Response to Nutrient Solution Recycling in Soilless Growing Systems in Greenhouses, 2nd ed.; Elsevier B.V.: Amsterdam, The Netherlands, 2019; ISBN 9780444636966. [Google Scholar] [CrossRef]
- Heuvelink, E.; Bakker, M.; Stanghellini, C. Salinity effects on fruit yield in vegetable crops: A simulation study. Acta Hortic. 2003, 609, 133–140. [Google Scholar] [CrossRef]
- Stanghellini, C.; Kempkes, F.; Pardossi, A.; Incrocci, L. Closed Water Loop in Greenhouses: Effect of Water Quality and Value of Produce. Acta Hortic. 2005, 691, 233–242. [Google Scholar] [CrossRef]
- Giuffrida, F.; Lipari, V.; Leonardi, C. A simplified management of closed soilless cultivation systems. Acta Hortic. 2003, 614, 155–160. [Google Scholar] [CrossRef]
- Silberbush, M.; Ben-Asher, J. Simulation study of nutrient uptake by plants from soilless cultures as affected by salinity buildup and transpiration. Plant Soil 2001, 233, 59–69. [Google Scholar] [CrossRef]
- Sonneveld, C.; Voogt, W.; Spaans, L. A universal algorithm for calculation of nutrient solutions. Acta Hortic. 1999, 481, 331–339. [Google Scholar] [CrossRef]
- Carmassi, G.; Incrocci, L.; Maggini, R.; Malorgio, F.; Tognoni, F.; Pardossi, A. Modeling Salinity Build-Up in Recirculating Nutrient Solution Culture. J. Plant Nutr. 2005, 28, 431–445. [Google Scholar] [CrossRef]
- Carmassi, G.; Incrocci, L.; Malorgio, M.; Tognoni, F.; Pardossi, A. A simple model for salt accumulation in closed-loop hydroponics. Acta Hortic. 2003, 614, 149–154. [Google Scholar] [CrossRef]
- Carmassi, G.; Incrocci, L.; Maggini, R.; Malorgio, F.; Tognoni, F.; Pardossi, A. An aggregated model for water requirements of greenhouse tomato grown in closed rockwool culture with saline water. Agric. Water Manag. 2007, 88, 73–82. [Google Scholar] [CrossRef]
- Incrocci, L.; Massa, D.; Carmassi, G.; Pulizzi, R.; Maggini, R.; Pardossi, A.; Bibbiani, C. SIMULHYDRO, a simple tool for predicting water use and water use efficiency in tomato closed-loop soilless cultivations. Acta Hortic. 2008, 801 Pt 2, 1005–1011. [Google Scholar] [CrossRef]
- Son, J.-E.; Ahn, T.I.; Moon, T. Advances in nutrient management modelling and nutrient concentration prediction for soilless culture systems. In Advances in Horticultural Soilless Culture; Burleigh Dodds Science Publishing: London, UK, 2021; pp. 277–301. ISBN 9781003048206. [Google Scholar]
- Noumedem, J.A.K.; Djeussi, D.E.; Hritcu, L.; Mihasan, M.; Kuete, V. Lactuca sativa. In Medicinal Spices and Vegetables from Africa; Elsevier: Amsterdam, The Netherlands, 2017; pp. 437–449. [Google Scholar] [CrossRef]
- Shatilov, M.V.; Razin, A.F.; Ivanova, M.I. Analysis of the world lettuce market. IOP Conf. Ser. Earth Environ. Sci. 2019, 395, 012053. [Google Scholar] [CrossRef]
- Yang, X.; Gil, M.I.; Yang, Q.; Tomás-Barberán, F.A. Bioactive compounds in lettuce: Highlighting the benefits to human health and impacts of preharvest and postharvest practices. Compr. Rev. Food Sci. Food Saf. 2022, 21, 4–45. [Google Scholar] [CrossRef] [PubMed]
- FAO FAOSTAT. Crops and Livestock Products. Available online: https://www.fao.org/faostat/en/#data/QCL (accessed on 18 December 2023).
- Voutsinos, O.; Mastoraki, M.; Ntatsi, G.; Liakopoulos, G.; Savvas, D. Comparative Assessment of Hydroponic Lettuce Production Either under Artificial Lighting, or in a Mediterranean Greenhouse during Wintertime. Agriculture 2021, 11, 503. [Google Scholar] [CrossRef]
- Asseng, S.; Guarin, J.R.; Raman, M.; Monje, O.; Kiss, G.; Despommier, D.D.; Meggers, F.M.; Gauthier, P.P.G. Wheat yield potential in controlled-environment vertical farms. Proc. Natl. Acad. Sci. USA 2020, 117, 19131–19135. [Google Scholar] [CrossRef] [PubMed]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Walter, I.A.; Allen, R.G.; Elliott, R.; Jensen, M.E.; Itenfisu, D.; Mecham, B.; Howell, T.A.; Snyder, R.; Brown, P.; Echings, S.; et al. ASCE’s Standardized Reference Evapotranspiration Equation. In Proceedings of the Watershed Management and Operations Management 2000; American Society of Civil Engineers: Reston, VA, USA, 2001; pp. 1–11. [Google Scholar]
- Carmassi, G.; Maggini, R.; Incrocci, L. Modelling ion concentration in the culture solution of closed-loop hydroponics. Acta Hortic. 2004, 654, 251–256. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Martin Smith, S. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and drainage. Paper 56; FAO: Rome, Italy, 1998; ISBN 92-5-104219-5. [Google Scholar]
- Chapra, E.C.; Canale, R.P.; Valle Sotelo, J.C. Numerical Methods for Engineers, 5th ed.; McGraw-Hill Companies, Inc.: New York, NY, USA, 2006; ISBN 0-07-291873-X. [Google Scholar]
- Fylstra, D.; Lasdon, L.; Watson, J.; Waren, A. Design and Use of the Microsoft Excel Solver. Interfaces 1998, 28, 29–55. [Google Scholar] [CrossRef]
- Sonneveld, C. Effects of Salinity on Substrate Grown Vegetables and Ornamentals in Greenhouse Horticulture; Wageningen University: Wageningen, The Netherlands, 2004; ISBN 9058081907. [Google Scholar]
- Michael, P.R.; Johnston, D.E.; Moreno, W. A conversion guide: Solar irradiance and lux illuminance. J. Meas. Eng. 2020, 8, 153–166. [Google Scholar] [CrossRef]
- EU. European Commission Photovoltaic Geographical Information System (PVGIS). Solar Radiation. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/ (accessed on 18 December 2023).
- EU Meteostat Station Identifiers “Almeria Aeropuerto”. Available online: https://meteostat.net/en/station/08487?t=2023-05-05/2023-05-12 (accessed on 18 December 2023).
- Wang, S. Air speed profiles in a naturally ventilated greenhouse with a tomato crop. Agric. For. Meteorol. 1999, 96, 181–188. [Google Scholar] [CrossRef]
- AEMET (Agencia Estatal de Meteorología) Valores Climatológicos Normales, Almería Aeropuerto. Available online: https://www.aemet.es/es/serviciosclimaticos/datosclimatologicos/valoresclimatologicos?l=6325O&k=undefined (accessed on 18 December 2023).
- Franklin, J. Plant Growth Chamber Handbook; Langhans, R.W., Tibbits, T.W., Eds.; SR-99.; Cambridge University Press: Cambridge, UK; Iowa State University: Ames, IA, USA; Agriculture and Home Economics Experiment Station: Ames, IA, USA, 1997. [Google Scholar]
- Ahmed, H.A.; Yu-Xin, T.; Qi-Chang, Y. Optimal control of environmental conditions affecting lettuce plant growth in a controlled environment with artificial lighting: A review. South African J. Bot. 2020, 130, 75–89. [Google Scholar] [CrossRef]
- Pardossi, A.; Carmassi, G.; Diara, C.; Incrocci, L.; Maggini, R.; Massa, D. Fertigation and Substrate Management in Closed Soilless Culture; University of Pisa: Pisa, Italy, 2011; Volume 1. [Google Scholar]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, 1–24. [Google Scholar] [CrossRef]
- Hai, T.; Sharafati, A.; Mohammed, A.; Salih, S.Q.; Deo, R.C.; Al-Ansari, N.; Yaseen, Z.M. Global Solar Radiation Estimation and Climatic Variability Analysis Using Extreme Learning Machine Based Predictive Model. IEEE Access 2020, 8, 12026–12042. [Google Scholar] [CrossRef]
- Yang, J.M.; Yang, J.Y.; Liu, S.; Hoogenboom, G. An evaluation of the statistical methods for testing the performance of crop models with observed data. Agric. Syst. 2014, 127, 81–89. [Google Scholar] [CrossRef]
- Saxena, A.; Celaya, J.; Balaban, E.; Goebel, K.; Saha, B.; Saha, S.; Schwabacher, M. Metrics for evaluating performance of prognostic techniques. In Proceedings of the 2008 International Conference on Prognostics and Health Management, Denver, CO, USA, 6–9 October 2008. [Google Scholar] [CrossRef]
- Faraway, J.J. Linear Models with R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2004; ISBN 9781135437664. [Google Scholar]
- Barbosa, G.L.; Almeida Gadelha, F.D.; Kublik, N.; Proctor, A.; Reichelm, L.; Weissinger, E.; Wohlleb, G.M.; Halden, R.U. Comparison of land, water, and energy requirements of lettuce grown using hydroponic vs. Conventional agricultural methods. Int. J. Environ. Res. Public Health 2015, 12, 6879–6891. [Google Scholar] [CrossRef]
- Formisano, L.; Ciriello, M.; Cirillo, V.; Pannico, A.; El-Nakhel, C.; Cristofano, F.; Duri, L.G.; Giordano, M.; Rouphael, Y.; De Pascale, S. Divergent Leaf Morpho-Physiological and Anatomical Adaptations of Four Lettuce Cultivars in Response to Different Greenhouse Irradiance Levels in Early Summer Season. Plants 2021, 10, 1179. [Google Scholar] [CrossRef]
- Cristofano, F.; El-Nakhel, C.; Colla, G.; Cardarelli, M.; Pii, Y.; Lucini, L.; Rouphael, Y. Tracking the Biostimulatory Effect of Fractions from a Commercial Plant Protein Hydrolysate in Greenhouse-Grown Lettuce. Antioxidants 2023, 12, 107. [Google Scholar] [CrossRef]
- Carillo, P.; De Micco, V.; Ciriello, M.; Formisano, L.; El-Nakhel, C.; Giordano, M.; Colla, G.; Rouphael, Y. Morpho-Anatomical, Physiological, and Mineral Composition Responses Induced by a Vegetal-Based Biostimulant at Three Rates of Foliar Application in Greenhouse Lettuce. Plants 2022, 11, 2030. [Google Scholar] [CrossRef] [PubMed]
- Buturi, C.V.; Sabatino, L.; Mauro, R.P.; Navarro-León, E.; Blasco, B.; Leonardi, C.; Giuffrida, F. Iron Biofortification of Greenhouse Soilless Lettuce: An Effective Agronomic Tool to Improve the Dietary Mineral Intake. Agronomy 2022, 12, 1793. [Google Scholar] [CrossRef]
- Söylemez, S. The impact of different growth media and ammonium-nitrate ratio on yield and nitrate accumulation in lettuce (Lactuca sativa var. longifolia). Not. Bot. Horti Agrobot. Cluj-Napoca 2021, 49, 12540. [Google Scholar] [CrossRef]
- Lycoskoufis, I.; Kavga, A.; Koubouris, G.; Karamousantas, D. Ultraviolet Radiation Management in Greenhouse to Improve Red Lettuce Quality and Yield. Agriculture 2022, 12, 1620. [Google Scholar] [CrossRef]
- Hamidon, M.H.; Ahamed, T. Detection of Tip-Burn Stress on Lettuce Grown in an Indoor Environment Using Deep Learning Algorithms. Sensors 2022, 22, 7251. [Google Scholar] [CrossRef]
- Hernández, E.; Timmons, M.B.; Mattson, N.S. Quality, Yield, and Biomass Efficacy of Several Hydroponic Lettuce (Lactuca sativa L.) Cultivars in Response to High Pressure Sodium Lights or Light Emitting Diodes for Greenhouse Supplemental Lighting. Horticulturae 2020, 6, 7. [Google Scholar] [CrossRef]
- Li, Q.; Li, X.; Tang, B.; Gu, M. Growth responses and root characteristics of lettuce grown in Aeroponics, Hydroponics, and Substrate Culture. Horticulturae 2018, 4, 35. [Google Scholar] [CrossRef]
- Neumann, G.; Bott, S.; Ohler, M.A.; Mock, H.P.; Lippmann, R.; Grosch, R.; Smalla, K. Root exudation and root development of lettuce (lactuca sativa L. Cv. Tizian) as affected by different soils. Front. Microbiol. 2014, 5, 2. [Google Scholar] [CrossRef]
- Kerbiriou, P.J.; Stomph, T.J.; Van Der Putten, P.E.L.; Lammerts Van Bueren, E.T.; Struik, P.C. Shoot growth, root growth and resource capture under limiting water and N supply for two cultivars of lettuce (Lactuca sativa L.). Plant Soil 2013, 371, 281–297. [Google Scholar] [CrossRef]
- Gavhane, K.P.; Hasan, M.; Singh, D.K.; Kumar, S.N.; Sahoo, R.N.; Alam, W. Determination of optimal daily light integral (DLI) for indoor cultivation of iceberg lettuce in an indigenous vertical hydroponic system. Sci. Rep. 2023, 13, 10923. [Google Scholar] [CrossRef]
- Vetrano, F.; Moncada, A.; Miceli, A. Use of gibberellic acid to increase the salt tolerance of leaf lettuce and rocket grown in a floating system. Agronomy 2020, 10, 505. [Google Scholar] [CrossRef]
- Popkin, B.M.; D’Anci, K.E.; Rosenberg, I.H. Water, hydration, and health. Nutr. Rev. 2010, 68, 439–458. [Google Scholar] [CrossRef]
- Murray, J.J.; Basset, G.; Sandoya, G. Nutritional Benefits of Lettuce Consumed at Recommended Portion Sizes. EDIS 2021, 2021, 1–8. [Google Scholar] [CrossRef]
- Travieso, L.L.; Leon, A.P.; Logegaray, V.R.; Frezza, D.; Chiesa, A. Loose Leaf Lettuce Quality Grown in Two Production Systems. Eur. Sci. J. ESJ 2016, 12, 55. [Google Scholar] [CrossRef][Green Version]
- Gang, M.S.; Kim, H.J.; Kim, D.W. Estimation of Greenhouse Lettuce Growth Indices Based on a Two-Stage CNN Using RGB-D Images. Sensors 2022, 22, 5499. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, Z.F.R.; Alnuaimi, A.K.H.; Askri, A.; Tzortzakis, N. Evaluation of Lettuce (Lactuca sativa L.) Production under Hydroponic System: Nutrient Solution Derived from Fish Waste vs. Inorganic Nutrient Solution. Horticulturae 2021, 7, 292. [Google Scholar] [CrossRef]
- Savvas, D.; Giannothanasis, E.; Ntanasi, T.; Karavidas, I.; Ntatsi, G. State of the Art and New Technologies to Recycle the Fertigation Effluents in Closed Soilless Cropping Systems Aiming to Maximise Water and Nutrient Use Efficiency in Greenhouse Crops. Agronomy 2023, 14, 61. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).