Abstract
Hybrid modeling workflows combining machine learning with mechanistic process descriptions are becoming essential tools for bioprocess digitalization. In this study, a hybrid deep modeling method with state–space reduction was developed and showcased with a P. pastoris GS115 Mut+ strain expressing a single-chain antibody fragment (scFv). Deep feedforward neural networks (FFNN) with varying depths were connected in series with bioreactor macroscopic material balance equations. The hybrid model structure was trained with a deep learning technique based on the adaptive moment estimation method (ADAM), semidirect sensitivity equations and stochastic regularization. A state–space reduction method was investigated based on a principal component analysis (PCA) of the cumulative reacted amount. Data of nine fed-batch P. pastoris 50 L cultivations served to validate the method. Hybrid deep models were developed describing process dynamics as a function of critical process parameters (CPPs). The state–space reduction method succeeded to decrease the hybrid model complexity by 60% and to improve the predictive power by 18.5% in relation to the nonreduced version. An exploratory design space analysis showed that the optimization of the feed of methanol and of inorganic elements has the potential to increase the scFv endpoint titer by 30% and 80%, respectively, in relation to the reference condition.
1. Introduction
Many biomanufacturing companies are currently investing in digitalization tools such as big data analytics and digital twins [1]. Big data analytics applies artificial intelligence techniques on large collections of both structured and unstructured biological and process data. Such large volumes of heterogeneous data are processed with machine learning techniques such as artificial neural networks, deep learning, support vector machines, random forest and many others, to extract valuable process insights [2]. Digital twins (DT) rely on high-fidelity mathematical models with different levels of integration with the physical process. Fully fledged DT apply a mathematical model that receives information from the physical process in real time and also manipulates the process in real time [1,3]. In its simplest form, DT consist of a thoroughly validated mathematical model with historical data that are able to produce high-fidelity simulations of the physical process, thus allowing for conducting in silico experiments in replacement of the physical process [4].
Many authors are considering the combination of mechanistic models with machine learning in hybrid modeling workflows for bioprocess digitalization [5]. Hybrid modeling naturally pops up as a digitalization framework as it allows for integrating prior mechanistic knowledge with large volumes of process data in a straightforward way. Hybrid modeling is a well-established framework in process system engineering [6] and in bioprocessing [7]. It has covered a wide range of biological system applications for process measurement, monitoring, optimization and control, which are the basic building blocks of bioprocess DT [1].
The P. pastoris yeast has evolved to an industrial workhorse for the microbial production of recombinant proteins [8]. However, only a few studies have addressed hybrid modeling of P. pastoris cultures. Ferreira et al. [9] developed a simple hybrid model of P. pastoris GS115 (Mut+) based on a shallow feedforward neural network (FFNN) combined in series with macroscopic material balance equations. The shallow FFNN described the specific growth rate and specific product synthesis rate as a function of the reactor pH, temperature and volumetric methanol feeding rate. An iterative batch-to-batch control scheme was applied to optimize the methanol feeding, pH and temperature based on the hybrid model, resulting in a four-fold titer improvement after four optimization cycles. Brunner et al. developed a soft sensor based on a hybrid model that combined a carbon balance model (mechanistic) and a multilinear regression model (statistical) for the prediction of biomass concentration in real time [10]. The software sensor was able to adapt automatically between glycerol and methanol feeding. Pinto et al. [11] have recently applied a deep learning technique to a hybrid model of a P. pastoris process. FFNNs with 2–3 hidden layers were combined in series with material balance equations and trained with a deep learning technique, namely the adaptive moment estimation method (ADAM), semidirect sensitivity equations and stochastic regularization. The main outcome was an increase in the prediction accuracy by 18.4% and a decrease in the CPU training time by 43.4% in comparison to shallow hybrid modeling.
Previous P. pastoris hybrid modeling studies have considered only a few state variables due to the very simple culture medium employed. Indeed, P. pastoris is capable of growing in a chemical-defined media containing a carbon source (e.g., glycerol and/or methanol (Met)), a nitrogen source (ammonium (NH4)) and a few essential inorganic elements [12]. However, inorganic elements also play an important role in cell physiology. Magnesium (Mg), calcium (Ca), potassium (K), copper (Cu), strontium (Sr), iron (Fe), zinc (Zn), manganese (Mn) and chloride (Cl) were reported to be essential elements for yeast [13]. None of the previous hybrid modeling studies have analyzed the effect of inorganic element dynamics on recombinant protein production by P. pastoris. Metal ions serve as structural components of proteins and metalloenzymes and as structural elements of enzyme active sites [14]. Magnesium (Mg), Mn and Ca are cofactors of several enzymes present in yeast, such as ATPases [15,16], aspartases [17] and glycolytic enzymes [18]. Potassium (K) and Na are key elements in the regulation of electrochemical gradients in yeast [19,20]. The inclusion of Zn, Co and Mn in a P. pastoris medium was shown to affect the quality of the final product, namely the activity of a recombinant phospholipase C (PLC) [21].
In this work, a hybrid deep modeling framework was applied to describe the cultivation dynamics of a GS115 (Mut+) P. pastoris strain expressing a scFv. Cultivation data acquired in a pilot 50 L bioreactor in Basal Salts Media (BSM) (Invitrogen, Carlsbad, USA) under different conditions of methanol feeding, temperature and pH were analyzed. The BSM medium is probably the most frequently used medium for high-cell-density P. pastoris cultivation. It contains high concentrations of phosphorus (P), sulfur (S), Ca, Mg and K to support high cell density [22,23,24]. The precipitation of BSM salts, however, has been reported during BSM handling at a pH higher than 5.0 [25,26]. In this study, the inorganic elements were assayed during cultivation with inductively coupled plasma atomic emission spectroscopy (ICP-AES). A hybrid deep model was developed to describe process dynamics as a function of control inputs. A key difference from previous studies [11] is the inclusion of inorganic element dynamics in the state–space vector. Since the mechanisms underlying the biological kinetics of inorganic elements are not well understood, the hybrid mechanistic/FFNN approach was adopted.
2. Materials and Methods
2.1. Strain, Medium and Inoculum Preparation
A genetically engineered GS115 (Mut+) P. pastoris strain expressing a scFv was used in this study. The Basal Salts Media (BSM) was used during cell stocking, in cryogenic vials at −80 °C, and all cultivation steps (pre-inoculum, inoculum and bioreactor). The BSM solution was formulated and sterilized at 121 °C for 30 min containing 85% H3PO4, 26.70 mL/L; CaSO4.2H2O, 0.93 g/L; K2SO4, 18.20 g/L; MgSO4.7H2O, 14.90 g/L; KOH, 4.13 g/L; and glycerol, 40.00 g/L. A Pichia Trace Metal (PTM1) solution was formulated as follows: CuSO4.5H2O, 6.00 g/L; NaI, 0.08 g/L; MnSO4.H2O, 3.00 g/L; Na2MoO4.2H2O, 0.20 g/L; H3BO3, 0.02 g/L; CoCl2.6H2O, 0.50 g/L; ZnCl2, 20.00 g/L; FeSO4.7H2O, 65.00 g/L; H2SO4, 5.00 mL/L; and biotin, 0.20 g/L. The PTM1 solution was filter sterilized, using a 0.22 mm pore size filter, and added to the temperature-sterilized BSM solution at a volumetric ratio of 4.35 mL/L. The pH of the BSM solution was adjusted to pH 5.0 with 25% ammonium hydroxide. The pre-inoculum was composed of 40 mL of BSM (pH 5.0) and 1 mL of a cell stock. The pre-inoculum was incubated at 30 °C at 150 rpm for 3 days. The bioreactor inoculum consisted of 10 mL of the pre-inoculum and 750 mL of BSM (pH 5.0). It was incubated for 3 days at 30 °C and at 150 rpm.
2.2. Bioreactor Operation
A Lab Pilot Fermenter Type LP351, 50 L, with a 42 L working volume (Bioengineering, Wald, Switzerland) was used in all bioreactor experiments. The initial bioreactor volume was 15 L of BSM (pH 5.0). The aeration rate and overhead pressure were 1800 L.h−1 and 100 mbar, respectively, at the beginning of the operation. The cultivation started at a 300 rpm stirrer speed. The reactor was inoculated with 750 mL of the pre-inoculum. Then, the process underwent two distinct phases using two distinct substrates. The first phase was the glycerol batch/fed-batch (GBFB) phase. It started in the batch mode for approximately 30 h with an initial glycerol concentration of 40 g/L. Once the glycerol was nearly depleted, the glycerol fed-batch starts with an exponential feeding profile for approximately 12 h to increase cell density. The cell density reached at the end of the GBFB phase varied depending on the glycerol feeding program. The second phase started with methanol induction with the addition of 20 g/h to 100 g/h (depending on the experiment) of methanol for 5 h. A smooth transition between glycerol and methanol was applied to minimize the adaption time to methanol metabolization. It was then followed by a methanol fed-batch (MFB) phase with a feed program that varied in the experiments. The temperature and pH were controlled to different set points depending on the experiment. It was not possible to control temperatures below 23.6 °C due to a heat transfer limitation. The pH was controlled with the addition of ammonium hydroxide (25%). The dissolved oxygen (pO2) started at ~100% at the inoculation point and then decreased as the biomass grew. Once it reached 50% of saturation, a PID (Proportional-Integral-Derivative) controller started to manipulate the stirrer between 300 and 1000 rpm and then the pressure between 100 and 800 mbar in order to regulate pO2 to a constant 50% set point. Further details on the experimental protocol are provided elsewhere [9].
2.3. Analytical Techniques
Samples were withdrawn from the bioreactor at regular intervals for an off-line analysis at a frequency of 4–6 samples per day. The optical density was measured in a spectrophotometer at 600 nm (OD600) after an appropriate dilution of the broth, ensuring a value within the linear range (<0.6). For the determination of the wet cell weight per unit volume (gWCW/L), samples of the culture broth were taken in triplicate and centrifuged at 15,000 rpm for 10 min at 4 °C. The centrifuged cell pellets were weighed to determine the sample wet cell weight (WCW). The secreted scFv was assayed with an Enzyme-Linked Immunosorbent Assay (ELISA) according to the protocol described in [27]. The concentration of inorganic elements (P, K, Mg, S and Ca) in supernatant samples was assayed with inductively coupled plasma atomic emission spectroscopy (ICP-AES). The conditions of the ICP-AES system were the following: Argon with the flow of 15 L.min1, a temperature between 5700 and 10,000 °C, a pressure of 3 bar and a potency of the plasma equal to 1 kW.
2.4. Hybrid Deep Model with State-Space Reduction
Considering a perfectly mixed fed-batch bioreactor, the macroscopic material balance equations took the following state–space form:
with being a vector of state variables (concentrations in the liquid phase), being a vector of volumetric reaction rates, being the dilution rate, being the feed rate to the bioreactor, being the liquid volume inside the bioreactor and being a vector of the concentration in the feed stream to the bioreactor. The concentrations included in the state vector, , were those of the biomass (X), recombinant protein (scFv), methanol (Met), ammonium ion (NH4), Mg, K, Ca, P and S.
The vector of the cumulative reacted amount of each compound at a given time t, is defined as the time integral of the respective reaction rates as follows:
By combining Equations (1) and (2), may be estimated from measured data of concentrations and the culture volume (for simplicity, we assume negligible sampling and bleeding volume) as follows:
Using Equation (3), a transformed data matrix (with the same size as ) was computed for each fed-batch experiment with rows representing the process time and columns the cumulative reacted amount of compounds (X, scFv, Met, NH4, Mg, K, Ca, P and S). The matrices of all fed-batch experiments were stacked vertically in a single matrix and then normalized by dividing each column by the respective absolute maximum value, ,
with being the Hadamard division. The data matrix was decomposed in a matrix of scores, , and a matrix of coefficients, , with PCA using the alternating least-squares algorithm (MATLAB function “pca” with option ALS). This step was performed with the objective of data compression by choosing a number of principal components ,
A denormalized form of Equation (5) was obtained by multiplying with,
with ⊗ being the Hadamard multiplication.
Recognizing that the is obtained by the time integral of reaction rates (Equation (2)), then the compression of data according to Equation (6) with implicitly reduces the volumetric reaction rates, , to -linearly-independent reaction rates, ,
Equation (1) was finally transformed in a reduced state–space equation by replacing the volumetric reaction rates, , in Equation (1) by Equation (8) and then by multiplying each term by the pseudo-inverse of , resulting in the following reduced state–space model:
with,
The reduced state–space model is then completed with the linear measurement model,
Given that methanol feeding has a cumulative toxic effect in the metabolism of P. pastoris, an ODE that confers intracellular memory was added to the model,
with SH being the shock factor with the initial value SH(0) = 1 and being the rate of variation of the shock factor. The shock factor is thus an internal unmeasured state variable. A similar ODE has been proposed in (Lee and Ramirez, 1992).
The reaction rates are described with a FFNN with nh hidden layers as follows:
The input layer (Equation (12a)) receives the information of the reduced state–space vector, ; internal state, ; cultivation temperature, and (, , and are the absolute maximum of , , and , respectively). Each hidden layer computes a vector of outputs, from a vector of inputs, , which are the outputs of the preceding layer (Equation (12b)). The transfer function of hidden nodes, , was always the rectified linear unit ReLU(.). The output layer (Equation (12c)) computes the reaction rates in the reduced reaction space. The parameters are the node connection weights and are the bias weights. The resulting hybrid model structure with state–space reduction is represented in Figure 1.
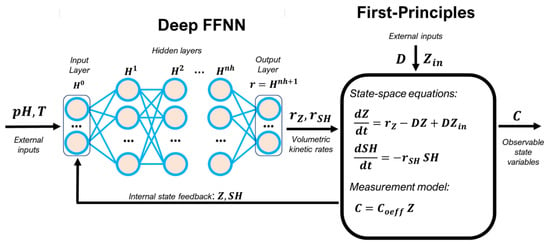
Figure 1.
Hybrid model structure with state–space reduction for the methanol fed-batch phase (MFB) of the P. pastoris GS115 (Mut+) fed-batch process. The kinetic rates are defined nonparametrically with a deep FFNN. Bioreactor dynamics are defined parametrically with macroscopic material balance equations in a perfectly mixed vessel. The observable state variables are the concentrations of = 9 compounds, C = [X, scFv, Met, NH4, Mg, K, Ca, P, S]T. The compressed internal state, , depends on the number of columns of the PCA coefficient matrix, The PCA coefficients were obtained with unsupervised learning using data of the cumulative reacted amount. The FFNN weights were trained with a deep learning method based on ADAM, stochastic regularization and semidirect sensitivity equations as described in [11].
All developed hybrid models were focused on the production MFB phase. The hybrid models were trained with the deep learning method proposed in [11] based on the ADAM method adapted to dynamic hybrid models. Briefly, the MFB phase data were portioned in a training and a testing data subset (more details in the Results section). The network weights were optimized on the training subset only (minimization of the weighted mean square error) using the ADAM algorithm and stochastic regularization. The objective function gradients were computed dynamically with the semidirect sensitivity equation method. For more details, the reader is referred to [11]. Two different metrics were adopted to compare the hybrid models. The weighted mean square error (WMSE) was computed as
with being the number of data points, being the observed concentration at time , being the predicted concentration at time and being the standard deviation of the measurement at time . The WMSE was minimized during the training and was also calculated for the test partition at the end of the training. The second metric was the Akaike Information Criterion with second-order bias correction (AICc),
The AICc was computed on the training partition only and is used to compare hybrid models of a different complexity (e.g., a different number of network parameters, ).
All of the code was developed in-house and implemented in MATLAB on a computer with Intel(R) Core(TM) i5-8265U CPU @ 1.60 GHz 1.80 GHz and 24 GB of RAM. The CPU time of the different tests performed was computed as the difference between the result of the “cputime” function in MATLAB. The source code and an example hybrid model implementation for the case study is accessible at https://github.com/sbegroup-nova/HYBMOD (accessed on 28 June 2023).
3. Results and Discussion
3.1. Cultivation Experiments
Nine 50 L fed-batch cultivations were performed with varying pH, temperature and feeding profiles of glycerol and methanol in order to analyze the effect of reactor operational parameters on process dynamics. The temperature and pH were always the same in the GBFB phase (30 °C and pH 5.0, respectively). In the MFB phase, the temperature level was 23.6 °C or 30 °C whereas the pH level was 4.0, 5.0, 6.5 or 7.0. Two experiments (A and E) were performed at baseline conditions (T = 30 °C and pH 5.0 according to Invitrogen guidelines). The overall results are summarized in Table 1. The final biomass concentration varied between 428.1 ± 3.8 and 598.1 ± 7.1 gWCW/L (40% variation) whereas the endpoint scFv titer had an almost ten-fold variation (between 5.9 ± 0.4 and 54.4 ± 1.3 mg/L). As discussed below, experiments A and F with the lowest and highest endpoint scFv titers were selected for testing while the remaining seven experiments (B, C, D, E, G, H and I) were selected for training the hybrid models. The product/biomass yield had a more than six-fold variation between 42 and 243.3 µg of scFv per unit of gWCW produced in the MFB phase. Experiment H, performed at 30 °C and pH 6.5, resulted in the highest scFv yield (243.3 µg of scFv per unit of gWCW produced). Experiment I was performed in similar conditions to experiment H except for the higher pH 7.0. This experiment delivered one of the lowest yields (45.7 µg of scFv per unit gWCW produced), denoting a very significant effect of the pH on the process kinetics.

Table 1.
Summary of 50 L fed-batch cultivation experiments performed and respective production yields. In the glycerol batch/fed-batch phase (GBFB), the glycerol feeding program varied but the temperature and pH were 30 °C and pH 5.0 in all cases. Temperature, pH and methanol feeding in the methanol fed-batch phase (MFB) varied from experiment to experiment.
3.2. Inorganic Element Dynamics
The dissolved concentration of inorganic elements Ca, Mg, K, S and P was assayed in the supernatant with ICP-AES during the MFB phase. Figure 2 shows the percentual variation of dissolved concentrations over time. These data show that in a typical BSM P. pastoris cultivation, run at 30 °C and pH 5.0 according to Invitrogen guidelines (experiments A and E), Ca and S tend to be in excess whereas K, P and Mg tend to deplete sooner. In general, Mg tends to deplete first as seen in experiments C, D, H and I. In [25], the precipitation of BSM salts at a pH higher than 5.0 was reported and the same was observed in the present study (Figure 2). The precipitation occurred in experiments H and I, which were performed at pH 6.5 and 7.0, respectively, during the MFB phase. The shift from pH 5.0 to 6.5 or 7.0 caused the severe precipitation of Mg and Ca salts as evidenced by the sudden variation of the respective dissolved concentrations, close to -100% in the case of Mg (e.g., complete depletion) and close to −80% in the case of Ca. The precipitation of other salts also occurred but not as severely. In experiments C and D, a pH shift from pH 5.0 to 7.0 occurred in the middle of the MFB phase (at 123.0 h and 125.0 h, respectively). This caused some precipitation of salts in both experiments. In the experiment that reached the highest biomass concentration (598.1 g-WCW.L−1, in experiment F), Mg and K depleted while P almost depleted. In the experiment that reached the lowest biomass concentration (428.1 g-WCW.L−1 in experiment I), the salt precipitation occurred early in the culture, caused by the pH shift to 7.0 at the methanol induction point. Overall, these data suggest a strong correlation between the pH, growth kinetics and salt precipitation. There seems to be a clear challenge to optimize the salt concentrations in a medium for high-cell-density P. pastoris. But even if the medium composition is optimized, e.g., by a statistical design of experiments, the salt concentrations will significantly decrease as cells grow over time. The salt dynamics may strongly affect the growth and protein expression kinetics in different phases of the process. Other factors such as the temperature and methanol feeding rate may also play an important role. Understanding the combined dynamic effects of all critical process parameters (CPPs) requires an in-depth data analysis using a suitable dynamic modeling framework as discussed next.
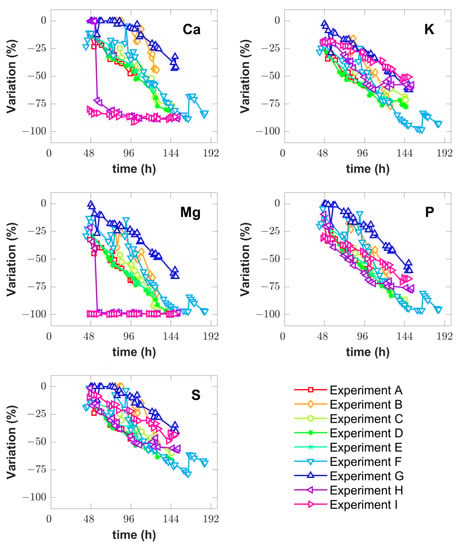
Figure 2.
Percentual variation of dissolved inorganic element concentrations (Ca, K, Mg, P and S) determined from ICP-AES measurements for each reactor experiment (A-I) (Table 1). The percentual variation of concentration was calculated as with being the concentration of element at cultivation time .
3.3. PCA of Cumulative Reacted Amount
The data analysis started with the computation of the cumulative reacted amount over time, , of the nine bioreactor compounds (X, scFv, Met, NH4, Ca, K, Mg, P and S) for each experiment (A-I, Table 1) using the previously described method. In the case of Met and NH4, the variation of concentrations in the liquid was assumed to be negligible in comparison to the cumulative amount metabolized by the cells. In the case of inorganic elements, it was not possible to distinguish between cellular uptake and precipitation/dissolution caused by the varying reactor conditions. The computed cumulative reacted amount thus aggregated both kinetic terms in the case of inorganic elements.
The IR data were normalized column wise by dividing with the maximum absolute value of each column. The normalized data were subject to PCA for a maximum number of principal components equal to eight . The data were partitioned into seven fed-batch experiments (B, C, D, E, G, H and I) for PCA and two experiments (A and F) for the validation. The validation experiments corresponded to the extreme low and high scFv endpoint titer experiments. The overall results are shown in Figure 3. The resulting 9 × 8 coefficient matrix (Equation (15)), with rows representing bioreactor compounds and columns representing the PCs, was used in the state–space reduction step described in the following section.
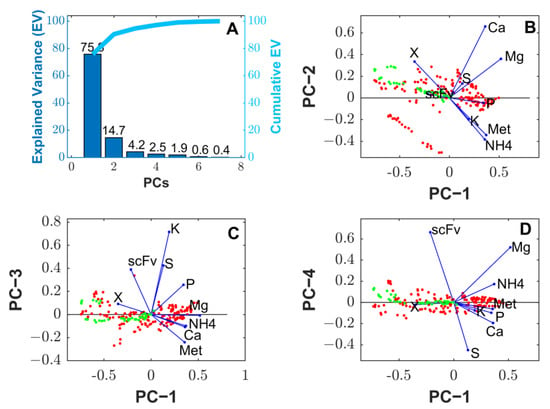
Figure 3.
PCA of normalized cumulative reacted amount data of X, Met, NH4, Ca, K, Mg, P and S for 9 fed-batch experiments. Each column was divided by the maximum absolute value of the reacted amount among the 9 fed-batch experiments. The PCA algorithm was the alternating least-squares (MATLAB function “pca” with option ALS). Red points are scores of training data. Green points are scores of validation data. Blue dots and blue lines are coefficients. (A): Explained variance over the number of principal components. (B): Scores and coefficients of principal component 2 over principal component 2. (C): Scores and coefficients of principal component 3 over principal component 1. (D): Scores and coefficients of principal component 4 over principal component 1.
Figure 3A shows that two to four principal components (PC) cumulatively explain 90.3%, 94.5% and 97.0% of the data variance. These results are evidence of strong linear dependencies between the biochemical transformations involving the nine bioreactor compounds. The PCA coefficients shown in Figure 3B (blue dots and blue lines) suggest a very strong correlation between the biomass production, methanol consumption, NH4 consumption and K consumption along the directions of PC-1 and PC-2, which together explain 90.3% of the data variance. PC-1 and PC-2 are mainly associated with cell growth metabolic processes (all other PCs have low biomass coefficients) with PC-2 showing a minor contribution to scFv synthesis (low scFv coefficient). The scFv synthesis is mainly explained with PC-1, PC-3 and PC-4. The scFv synthesis appears as positively correlated with cell growth along the direction of PC-1 (Figure 3B). However, in the biplots of PC-3 (4.2% explained variance, Figure 3C) and PC-4 (2.5% explained variance, Figure 3D), the coefficients of scFv and the biomass are large and negligible, respectively, suggesting cell growth dissociated product synthesis. The interpretation of the inorganic element coefficients is more difficult due to the occurrence of precipitation. The coefficients of PC-1 (75.6% explained variance) suggest that all inorganic elements are consumed for cell growth with S showing the least significant contribution. The elements Ca and Mg, which precipitated more severely, are orthogonal to X along the direction of PC-1 and PC-2 (Figure 3B), suggesting a low correlation with biomass growth. The S also appears orthogonal to X, also denoting a low correlation with biomass growth. Biomass growth seems to be controlled mainly by Met, NH4 and K availability and seems to be practically insensitive to Ca, Mg and S availability. As for the product synthesis, the main contributions are from PC-1 (75.6% explained variance) and PC-3 (4.2% explained variance). In the case of PC-1, the conclusions already taken for biomass growth hold for scFv synthesis. As for PC-3, the coefficients again show a low correlation with the Ca and Mg (direction of PC-3 in Figure 3C). On the other hand, scFv appears as positively correlated with K, S and P along the direction of PC-3, suggesting that the excessive consumption of these elements (e.g., lower reaction rates) is associated with a lower scFv synthesis rate. This interpretation is only qualitative as the different PCs collectively contribute to explain the data variance.
3.4. Hybrid Model Development
For a quantitative analysis of all critical process parameters (CPPs), hybrid models were developed to describe process dynamics using the previously described state–space reduction method. The PCA coefficient matrix obtained in the previous section was used to transform the concentration vector in a reduced Z state vector by applying the transformations.
Firstly, the effect of the state–space reduction on the hybrid model training and testing was investigated. Different hybrid models were developed by considering an increasing number of PCs, e.g., by taking an increasing number of columns of the matrix . The same data partitioning as for PCA was adopted, namely seven experiments were selected for training (B, C, D, E, G, H and I) and two experiments were selected for testing (A and F). The number of hidden layers was two with 10 nodes each, which were kept the same in all tests performed. The training method was also the same in all tests performed (ADAM with 1000 iterations and default hyperparameters, stochastic regularization with an 80% minibatch size and 20% weight dropout and semidirect sensitivity equations). The overall results are presented in Table 2. The final training error systematically decreased with the number of PCs. The lowest training error was achieved with the original unreduced state vector of concentrations. However, a clear minimum in the test error was obtained for 5–6 PCs, which corresponds to a reduction of 40% and 30% in the number of state variables (six and seven, respectively). The number of FFNN weights increased with the number of PCs but the AICc criterion failed to discriminate the model with the highest predictive power, which was the model with five PCs’ reduction.

Table 2.
Effect of state–space reduction on the hybrid modeling results. The number of principal components was increased from 1 to 8 in the state–space transformation defined by Equation (9b,c). Seven fed-batch experiments were selected for training (B, C, D, E, G, H and I) and two for testing (A and F). The training was performed with the ADAM algorithm with 1000 iterations and hyperparameters α = 0.001, β1 = 0.9, β2 = 0.999 and η = 1 × 10−7. Gradients were computed with the semidirect sensitivity equations. Stochastic regularization was applied with a weight dropout of 0.2 and minibatch size of 0.8. The training was repeated only once with random weight initialization from the uniform distribution between −0.01 and 0.01.
For both the unreduced and five PCs’ reduced hybrid models, the optimal size of the FFNN was further investigated. Several architectures were investigated with one to three hidden layers and with a varying number of nodes in the hidden layers. The same training/testing data partitioning and training methods were adopted. Table 3 shows the results for the hybrid model with the five PCs’ reduction. The best shallow hybrid structure had a single hidden layer with 13 nodes and 201 parameters. The training and testing errors were 0.50 and 1.10, respectively. The best deep structure had two hidden layers with 13 nodes each and 383 parameters. The final training error was the same as the shallow structure (0.50) but the test error was slightly lower (1.01). Nevertheless, given the lower model complexity reflected in the lower AICc value, the shallow structure with 13 hidden nodes was taken as the best hybrid model with the 5 PCs’ reduction. Table 4 presents the results for the unreduced hybrid model with varying FFNN sizes. The hybrid structure with two hidden layers (15 × 15) and 595 parameters stands out as the best model. It had a low training error (0.33), the lowest test error (1.35) and the lowest AICc value (−150).

Table 3.
Hybrid modeling results as a function of FFNN size for 5 principal components’ reduction (6 state variables). Seven fed-batch experiments were used to train the model (B, C, D, E, G, H and I) and two experiments were used for testing (A and F). The training was performed with the ADAM algorithm with 1000 iterations and hyperparameters α = 0.001, β1 = 0.9, β2 = 0.999 and η = 1 × 10−7. Gradients were computed with the semidirect sensitivity equations. Stochastic regularization was applied with a weight dropout of 0.2 and minibatch size of 0.8. The training was performed only once with random weight initialization from the uniform distribution between −0.01 and 0.01.

Table 4.
Hybrid modeling results as a function of FFNN size for the unreduced case (10 state variables). Seven fed-batch experiments were used to train the model (B, C, D, E, G, H and I) and two experiments were used for testing (A and F). The training was performed with the ADAM algorithm with 1000 iterations and hyperparameters α = 0.001, β1 = 0.9, β2 = 0.999 and η = 1 × 10−7. Gradients were computed with the semidirect sensitivity equations. Stochastic regularization was applied with a weight dropout of 0.2 and minibatch size of 0.8. The training was performed only once with random weight initialization from the uniform distribution between −0.01 and 0.01.
Comparing the best reduced model (with the five PCs’ reduction and a single hidden layer with 13 nodes, Table 3) and the best unreduced model (two hidden layers with 15 nodes each, Table 4), it becomes clear that the state–space reduction had a very positive impact in the hybrid model performance metrics. The model complexity was reduced by 66% partially due to the lower number of state variables, which was reflected in a lower number of FFNN inputs and outputs. Moreover, one hidden layer was removed comparatively to the best deep model. It may be argued that the PCA coefficients in Equation (8), act as a linear layer obtained using unsupervised learning (namely with PCA) downstream of the FFNN. Such structural differences resulted in a higher training error (51.5% higher) for the reduced shallow hybrid model but, more importantly, in a significantly lower testing error (18.5% lower). The AICc is not a good discrimination metric in this case because the training error is systematically lower for unreduced models; thus, unreduced structures are always favored The reduced hybrid model predictions and respective measured concentrations of the biomass, scFv and inorganic elements (Mg, K, Ca, P and S) are compared for the two test experiments (A and F) in Figure 4. The model was able to faithfully predict the state variables for the two extreme experiments with predictions always within or very close to measurement error bounds.
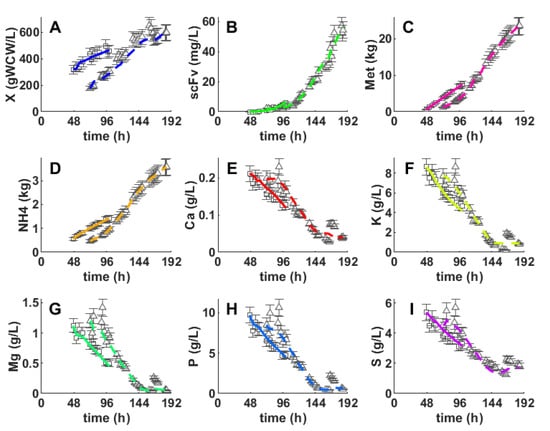
Figure 4.
Comparison between predictions of the hybrid model (5 × 13 × 5) with 5 state variables and experimental data of X, scFv, Met, NH3, Ca, K, Mg, P and S for the 2 fed-batch experiments (A and F). Squares and triangles are measurements of experiments A and F, respectively. Full lines and dashed lines are hybrid model predictions of experiments A and F, respectively. (A): Biomass. (B): Single-chain antibody fragment (scFv). (C): Cumulative methanol consumption (kg). (D): Cumulative NH4 consumption (kg). (E): Calcium (Ca, g/L). (F): Potassium (K, g/L). (G): Magnesium (Mg, g/L). (H): Phosphorus (P, g/L). (I): Sulfur (S, g/L).
3.5. Design Space Exploratory Analysis
Here, we illustrate how the hybrid model can be used as a DT prototype for dynamic design space exploration. The CPPs that affect recombinant protein production with methylotrophic P. pastoris are typically the pH, temperature and methanol feeding strategy [9,28,29,30,31]. In this study, the feeding of inorganic elements is also analyzed. The impact of CPPs on cell growth and scFv synthesis dynamics was characterized by process simulations using the best hybrid structure with the five PCs’ reduction and 13 hidden nodes developed in the previous section (Table 3 and Figure 4). A sensitivity analysis was performed taking, as a reference condition, experiment H, which delivered the highest scFv/biomass yield. Thus, the objective was to analyze the feasibility of increasing the scFv yield beyond the value obtained in experiment H by optimizing CPPs.
The optimal pH and temperature in the production phase depend on the nature and function of the expressed protein and on the genetic modification of the host cells. Figure 5 shows a sensitivity analysis of the scFv endpoint titer to the temperature and pH for the recombinant strain used in this study. The inner rectangle represents the domain of experience covered by the nine fed-bath experiments. These data suggest an optimal pH 5.75–6.75 and temperature 27.5–35 °C region corresponding to a higher endpoint scFv titer. These results are aligned with the data reported by Joseph et al. [32], obtained with a P. pastoris GS115 (Mut+) strain expressing recombinant thaumatin II. The authors consistently observed a higher viable cell density and higher secretion of protein at pH 6.0 compared to pH 5.0 (when the cells were grown at 30 °C) in different culture media. A low pH between 4.0 and 5.0 has been reported to decrease the proteolytic activity of proteases in a supernatant [28]. On the other hand, a high pH may counteract by increasing cellular viability, thereby reducing the cell lysis and the release of proteases [32]. A trade-off between both mechanisms must be evaluated on a case-by-case basis. Protein folding may also be severely affected by the temperature. Misfolded proteins can lead to a higher degradation rate in the cytosol and ultimately to a lower secretion rate. Joseph et al. [32] observed that protein levels were the highest at 30 °C compared to 20 and 25 °C at pH 6.0, thus the decrease in temperature did not improve the final titer. These results are in line with the optimal pH–temperature space identified in the present study. The identified optimal region encompasses experiment H (conducted at 30 °C and pH 6.5), which delivered the highest scFv/biomass yield of 243.3 µg/gWCW. Thus, it may be concluded that, for the strain used in the present study, the temperature and pH optimization has a low potential for further scFv titer improvement.
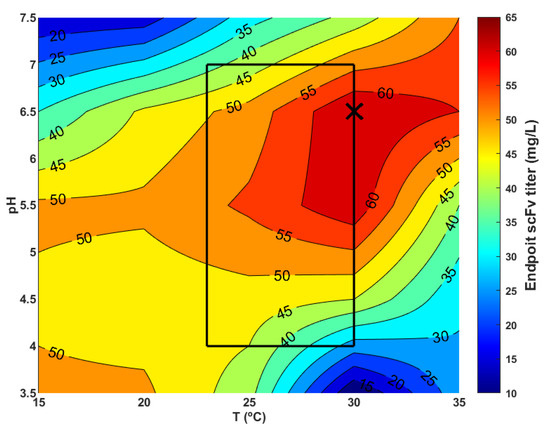
Figure 5.
Sensitivity analysis of scFv endpoint titer to temperature (15–35 °C) and pH (3.5–7.5). The methanol feeding strategy was that of experiment H (reference condition). Data were obtained with simulations of the hybrid shallow model with the 5 PCs’ reduction. The inner square represents the domain of experience. The cross-marker represents the temperature (30 °C) and pH (6.5) conditions of experiment H (reference condition).
The methanol feeding rate also plays a critical role in the P. pastoris GS115 Mut+ expression system. The protein expression is controlled by the very strong AOX1 promoter induced by methanol. Methanol also serves as a main carbon source for cell growth and protein expression. Overflow methanol metabolism may lead to the accumulation of reactive oxygen species and a pronounced oxidative stress response [30]. Protein expression kinetics in the Mut+ P. pastoris phenotype may vary considerably from strain to strain. It may be growth-coupled, negative growth-related and bell-shaped in relation to the specific growth rate profile [31]. The methanol feeding rate is typically used to control the specific growth rate and the associated specific protein expression rate. This control needs to be optimized on a case-by-case basis. Figure 6 shows a sensitivity analysis of the scFv endpoint titer to the methanol feeding strategy for the strain used in this study. Again, the most productive experiment (H) served as a reference condition. The pH varied between 3.5 and 7.5. The temperature was kept constant at 30 °C. The methanol feeding was decreased or increased in relation to the experiment H feeding program with a multiplying factor between 0.25 and 1.5. The overall results show that there is a significant potential for scFv endpoint titer improvement by increasing the methanol feeding rate. Specifically, the pH region between 5.5 and 6.5 combined with a 25% methanol feed rate increase (in relation to experiment H) has a scFv endpoint titer improvement potential of about 30%.
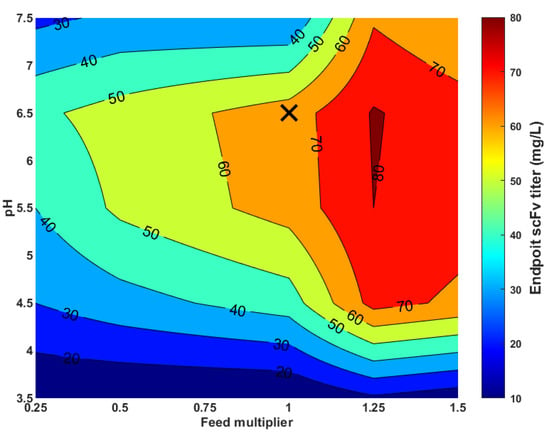
Figure 6.
Sensitivity analysis of scFv endpoint titer to pH (3.5–7.5) and methanol feeding program (0.25 to 1.5 multiplying factor in relation to the methanol feeding program applied to experiment H). The temperature was kept constant at 30 °C. The data were obtained with simulations of the hybrid shallow model with the 5 PCs’ reduction. The cross-marker represents the reference condition of experiment H.
The high concentration of salts in the BSM medium is required to supply inorganic elements at sufficient stoichiometric quantities to sustain a high cell density. An indication of this is the PC-1 coefficients (first column of Equation (15) and biplot of Figure 3B), showing that all inorganic elements have a significant contribution to the production of the biomass. However, a common problem is precipitation (Figure 2). The dilution of the BSM medium to one-quarter has been studied by Brady et al. [22] to mitigate the precipitation problem. The authors utilized a low-salt medium that did not reduce growth rates nor protein expression rates while avoiding medium precipitation. They observed no adverse effect on both glycerol and methanol growth kinetics. Later on, the dilution of BSM was shown to increase P. pastoris cellular viability and to reduce the cell death rate [33,34]. The reduction in the cell death rate decreases the accumulation of proteases in the supernatant and therefore the proteolytic attack on the secreted protein. Furthermore, the excess of trace metals was shown to decrease the expression of β-galactosidase by P. pastoris GS115 (Mut+) [14]. More recently, Joseph et al. [32] compared different media and concluded that BSM resulted in the highest total cell concentration (as measured by dry cell weight) concomitantly with the lowest viable cell concentration. The high concentrations of salts may cause high osmotic stress to the cells, resulting in a decrease in metabolic efficiency and cellular viability and in an increase in the cell death rate [34]. A higher cell death rate causes the release of proteolytic enzymes to the medium and a higher degradation of the expressed protein in the supernatant.
To test these hypotheses, a set of dynamic simulations were performed with the hybrid model with the five PCs’ reduction. The overall results are shown in Figure 7. Taking as a reference the best experiment (H) (methanol feeding program, 30 °C and pH 6.5), one simulation was performed with a reduction in inorganic element concentrations at the onset of the MFB phase to one-quarter. Another simulation was performed with controlled inorganic element concentrations to constant values corresponding to one-quarter of BSM concentrations throughout the complete MFB phase.
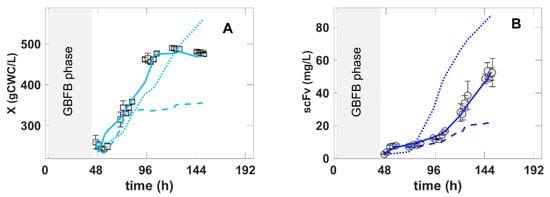
Figure 7.
In silico experiments obtained with simulations of the hybrid shallow model with the 5 PCs’ reduction based on experiment H control degrees of freedom. Symbols and error bars are measured data points of the reference condition (experiment H). Full lines are the hybrid model simulation of the reference condition (experiment H). Dashed lines are the hybrid model simulation of the reference condition with a one-quarter reduction in initial concentrations of inorganic elements at the onset of the MFB phase. Dotted lines are the hybrid model simulation of the reference condition with inorganic element concentrations controlled to constant values corresponding to one-quarter of BSM concentrations throughout the complete MFB phase. (A)—biomass concentration over time. (B)—scFv titer over time.
The simulation with the reduction to one-quarter of the initial salt concentrations showed no significant effect in the beginning of the MFB phase until approximately 72 h. This is in accordance with the experimental results reported in [22]. Since 72 h of cultivation, a severe cell growth limitation with inorganic elements was forecasted. The much lower cellular concentration resulted in a significant reduction in the scFv titer. This simulation suggests that a BSM/4 diluted medium is no longer able to sustain a high cell density.
The second simulation with inorganic element control to constant levels suggests a very significant increase in the scFv endpoint titer by 80% in relation to the reference condition and also an increase in the final biomass by approximately 15%. The cell growth rate decreased but the growth phase was extended to a longer period of time. The scFv specific productivity was boosted by keeping the salts at a constant and low concentration level. These results are in accordance with the experimental data reported in [29]. The authors developed a salt control system based on on-line conductivity monitoring in a P. pastoris process. The control of conductivity at 8 mS.cm−1 resulted in a 3.6-fold titer increase in relation to a standard BSM cultivation.
Overall, the design space analysis suggests that the control of inorganic salts in the MFB phase has the highest potential to further increase the scFv yield for the recombinant P. pastoris strain under study.
4. Conclusions
In this study, the dynamics of the main inorganic elements in P. pastoris GS115 (Mut+) cultures expressing a scFv were investigated. The ICP-AES data showed an excess of Ca and S over Mg, P and K in the BSM medium. In some cultures, Mg, P and K depleted completely, eventually limiting biomass growth and scFv expression. Precipitation occurred during the MFB phase at pH 6.5 and 7.0—more severely for Ca and Mg. A hybrid modeling framework with state–space reduction was applied for the data analysis and design space exploration. The state–space reduction framework succeeded to decrease the model complexity by 60% and to improve the predictive power by 18.5% in relation to a standard nonreduced hybrid model. The reduced hybrid model was able to correctly simulate the experiments performed including the test experiments. However, more data are required to strengthen the model validation before it can be considered for a process digital twin. An exploratory sensitivity analysis of process dynamics to CPPs was performed. It was concluded that a temperature of 30 °C and pH 6.5 are close to the optimal operating point. Interestingly, at these conditions, the culture suffered from severe salt precipitation, resulting in the highest scFv/biomass yield. The methanol feeding sensitivity analysis showed a significant 30% scFv endpoint titer improvement potential. The optimization of the inorganic element feeding showed the highest potential for further scFv endpoint titer improvement. Namely, the control of inorganic element concentration to one-quarter of the BSM during the MFB phase displayed an 80% scFv endpoint titer improvement potential.
Author Contributions
Conceptualization, R.O.; methodology, J.P., J.R.C.R. and R.O.; software, J.P. and R.S.C.; validation, J.R.C.R., R.S.C. and R.O.; formal analysis, J.P. and R.O.; investigation, J.P. and R.O.; resources, R.O.; data curation, J.P. and J.R.C.R.; writing—original draft preparation, J.P. and R.O.; writing—review and editing, J.P., J.R.C.R., R.S.C. and R.O.; supervision, R.O.; project administration, R.O.; funding acquisition, R.O. All authors have read and agreed to the published version of the manuscript.
Funding
This work received funding from the European Union’s Horizon 2020 research and innovation program under the grant agreement no. 870292 (BIOICEP).
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors acknowledge the support by the Associate Laboratory for Green Chemistry—LAQV, which is financed by national funds from FCT/MCTES (UIDB/50006/2020 and UIDP/50006/2020). JP acknowledges the PhD grant SFRD/BD14610472019, Fundação para a Ciência e Tecnologia (FCT). RSC acknowledges the contract CEECIND/01399/2017.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Udugama, I.A.; Öner, M.; Lopez, P.C.; Beenfeldt, C.; Bayer, C.; Huusom, J.K.; Gernaey, K.V.; Sin, G. Towards Digitalization in Bio-Manufacturing Operations: A Survey on Application of Big Data and Digital Twin Concepts in Denmark. Front. Chem. Eng. 2021, 3, 727152. [Google Scholar] [CrossRef]
- Yang, C.T.; Kristiani, E.; Leong, Y.K.; Chang, J.S. Big data and machine learning driven bioprocessing-Recent trends and critical analysis. Bioresour. Technol. 2023, 372, 128625. [Google Scholar] [CrossRef] [PubMed]
- Appl, C.; Moser, A.; Baganz, F.; Hass, V.C. Digital Twins for Bioprocess Control Strategy Development and Realisation. Digit. Twins Appl. Des. Optim. Bioprocesses 2021, 177, 63–94. [Google Scholar] [CrossRef]
- Lukowski, G.; Rauch, A.; Rosendahl, T. The Virtual Representation of the World Is Emerging. In Future Telco; Springer: Berlin/Heidelberg, Germany, 2019; pp. 165–173. [Google Scholar]
- Badr, S.; Sugiyama, H. A PSE perspective for the efficient production of monoclonal antibodies: Integration of process, cell, and product design aspects. Curr. Opin. Chem. Eng. 2020, 27, 121–128. [Google Scholar] [CrossRef]
- von Stosch, M.; Oliveira, R.; Peres, J.; de Azevedo, S.F. Hybrid semi-parametric modeling in process systems engineering: Past, present and future. Comput. Chem. Eng. 2014, 60, 86–101. [Google Scholar] [CrossRef]
- Agharafeie, R.; Oliveira, R.; Ramos, J.; Mendes, J. Application of Hybrid Neural Models to Bioprocesses: A Systematic Literature Review. Authorea Prepr. 2023. [Google Scholar] [CrossRef]
- De Brabander, P.; Uitterhaegen, E.; Delmulle, T.; De Winter, K.; Soetaert, W. Challenges and progress towards industrial recombinant protein production in yeasts: A review. Biotechnol. Adv. 2023, 64, 108121. [Google Scholar] [CrossRef]
- Ferreira, A.R.; Dias, J.M.L.; von Stosch, M.; Clemente, J.; Cunha, A.E.; Oliveira, R. Fast development of Pichia pastoris GS115 Mut(+) cultures employing batch-to-batch control and hybrid semi-parametric modeling. Bioprocess Biosyst. Eng. 2014, 37, 629–639. [Google Scholar] [CrossRef]
- Brunner, V.; Siegl, M.; Geier, D.; Becker, T. Biomass soft sensor for a Pichia pastoris fed-batch process based on phase detection and hybrid modeling. Biotechnol. Bioeng. 2020, 117, 2749–2759. [Google Scholar] [CrossRef]
- Pinto, J.; Mestre, M.; Ramos, J.; Costa, R.S.; Striedner, G.; Oliveira, R. A general deep hybrid model for bioreactor systems: Combining first principles with deep neural networks. Comput. Chem. Eng. 2022, 165, 107952. [Google Scholar] [CrossRef]
- Zhang, J.; Greasham, R. Chemically defined media for commercial fermentations. Appl. Microbiol. Biotechnol. 1999, 51, 407–421. [Google Scholar] [CrossRef]
- Spencer, J.F.T.; Spencer, D.M. Yeasts in Natural and Artificial Habitats; Springer: Berlin/Heidelberg, Germany, 1997; p. 381. [Google Scholar]
- Plantz, B.A.; Nickerson, K.; Kachman, S.D.; Schlegel, V.L. Evaluation of metals in a defined medium for Pichia pastoris expressing recombinant beta-galactosidase. Biotechnol. Prog. 2007, 23, 687–692. [Google Scholar] [CrossRef]
- Willsky, G.R. Characterization of the plasma-membrane Mg2+-ATPase from the yeast Saccharomyces cerevisiae. J. Biol. Chem. 1979, 254, 3326–3332. [Google Scholar] [CrossRef]
- Okorokov, L.A.; Lehle, L. Ca2+-ATPases of Saccharomyces cerevisiae: Diversity and possible role in protein sorting. Fems Microbiol. Lett. 1998, 162, 83–91. [Google Scholar] [CrossRef]
- Depue, R.H.; Moat, A.G. Factors affecting aspartase activity. J. Bacteriol. 1961, 82, 383–386. [Google Scholar] [CrossRef]
- Walker, G.M.; Maynard, A. Accumulation of magnesium ions during fermentative metabolism in Saccharomyces cerevisiae. J. Ind. Microbiol. Biotechnol. 1997, 18, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Arino, J.; Ramos, J.; Sychrova, H. Alkali Metal Cation Transport and Homeostasis in Yeasts. Microbiol. Mol. Biol. Rev. 2010, 74, 95–120. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Munoz, G.A.; Pena, A. In situ study of K+ transport into the vacuole of Saccharomyces cerevisiae. Yeast 2005, 22, 689–704. [Google Scholar] [CrossRef]
- Seo, K.H.; Rhee, J.I. High-level expression of recombinant phospholipase C from Bacillus cereus in Pichia pastoris and its characterization. Biotechnol. Lett. 2004, 26, 1475–1479. [Google Scholar] [CrossRef] [PubMed]
- Brady, C.P.; Shimp, R.L.; Miles, A.R.; Whitmore, M.; Stowers, A.W. High-level production and purification of P30P2MSP1(19), an important vaccine antigen for malaria, expressed in the methylotropic yeast Pichia pastoris. Protein Expr. Purif. 2001, 23, 468–475. [Google Scholar] [CrossRef] [PubMed]
- Cereghino, G.P.L.; Cereghino, J.L.; Ilgen, C.; Cregg, J.M. Production of recombinant proteins in fermenter cultures of the yeast Pichia pastoris. Curr. Opin. Biotechnol. 2002, 13, 329–332. [Google Scholar] [CrossRef] [PubMed]
- Damasceno, L.M.; Pla, I.; Chang, H.J.; Cohen, L.; Ritter, G.; Old, L.J.; Batt, C.A. An optimized fermentation process for high-level production of a single-chain Fv antibody fragment in Pichia pastoris. Protein Expr. Purif. 2004, 37, 18–26. [Google Scholar] [CrossRef]
- Cos, O.; Ramon, R.; Montesinos, J.L.; Valero, F. Operational strategies, monitoring and control of heterologous protein production in the methylotrophic yeast Pichia pastoris under different promoters: A review. Microb. Cell Factories 2006, 5, 17. [Google Scholar] [CrossRef] [PubMed]
- Ghosalkar, A.; Sahai, V.; Srivastava, A. Optimization of chemically defined medium for recombinant Pichia pastoris for biomass production. Bioresour. Technol. 2008, 99, 7906–7910. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.R.; Ataide, F.; von Stosch, M.; Dias, J.M.L.; Clemente, J.J.; Cunha, A.E.; Oliveira, R. Application of adaptive DO-stat feeding control to Pichia pastoris X33 cultures expressing a single chain antibody fragment (scFv). Bioprocess Biosyst. Eng. 2012, 35, 1603–1614. [Google Scholar] [CrossRef]
- Jahic, M.; Gustavsson, M.; Jansen, A.K.; Martinelle, M.; Enfors, S.O. Analysis and control of proteolysis of a fusion protein in Pichia pastoris fed-batch processes. J. Biotechnol. 2003, 102, 45–53. [Google Scholar] [CrossRef]
- Jahic, M.; Knoblechner, J.; Charoenrat, T.; Enfors, S.O.; Veide, A. Interfacing Pichia pastoris cultivation with expanded bed adsorption. Biotechnol. Bioeng. 2006, 93, 1040–1049. [Google Scholar] [CrossRef]
- Vanz, A.L.; Lunsdorf, H.; Adnan, A.; Nimtz, M.; Gurramkonda, C.; Khanna, N.; Rinas, U. Physiological response of Pichia pastoris GS115 to methanol-induced high level production of the Hepatitis B surface antigen: Catabolic adaptation, stress responses, and autophagic processes. Microb. Cell Factories 2012, 11, 103. [Google Scholar] [CrossRef]
- Looser, V.; Bruhlmann, B.; Bumbak, F.; Stenger, C.; Costa, M.; Camattari, A.; Fotiadis, D.; Kovar, K. Cultivation strategies to enhance productivity of Pichia pastoris: A review. Biotechnol. Adv. 2015, 33, 1177–1193. [Google Scholar] [CrossRef]
- Joseph, J.A.; Akkermans, S.; Van Impe, J.F.M. Effects of Temperature and pH on Recombinant Thaumatin II Production by Pichia pastoris. Foods 2022, 11, 1438. [Google Scholar] [CrossRef]
- Surribas, A.; Stahn, R.; Montesinos, J.L.; Enfors, S.O.; Valero, F.; Jahic, M. Production of a Rhizopus oryzae lipase from Pichia pastoris using alternative operational strategies. J. Biotechnol. 2007, 130, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.L.; Xue, C.; Wang, Y.; Yao, X.Q.; Liu, Z.M. Increasing the cell viability and heterologous protein expression of Pichia pastoris mutant deficient in PMR1 gene by culture condition optimization. Appl. Microbiol. Biotechnol. 2008, 81, 235–241. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).