Gallic Acid Reactive Extraction with and without 1-Octanol as Phase Modifier: Experimental and Modeling

Abstract

Gallic acid (GA) is a naturally occurring phenolic acid that can be found in the leaves, roots, flowers, or stems of a wide variety of plant species. It has a broad range of uses in the food and pharmaceutical industries. The objective of this research is to investigate the GA reactive extraction process employing dichloromethane and n-heptane as solvents, 1-octanol as a phase-modifier, and Amberlite LA-2 as an amine extractant dissolved in the organic phase. The separation yield and distribution coefficient data were discussed, along with the analysis of the extraction conditions and the extraction mechanism. Dichloromethane employed as the solvent, 80 g/L Amberlite LA2 used as the extractant, and 10% phase modifier were determined to be the ideal conditions for the reactive extraction onto a biphasic organic-aqueous system. Statistical regression and artificial neural networks (ANNs) established with the differential evolution (DE) algorithm were also used to model and optimize the process.

1. Introduction

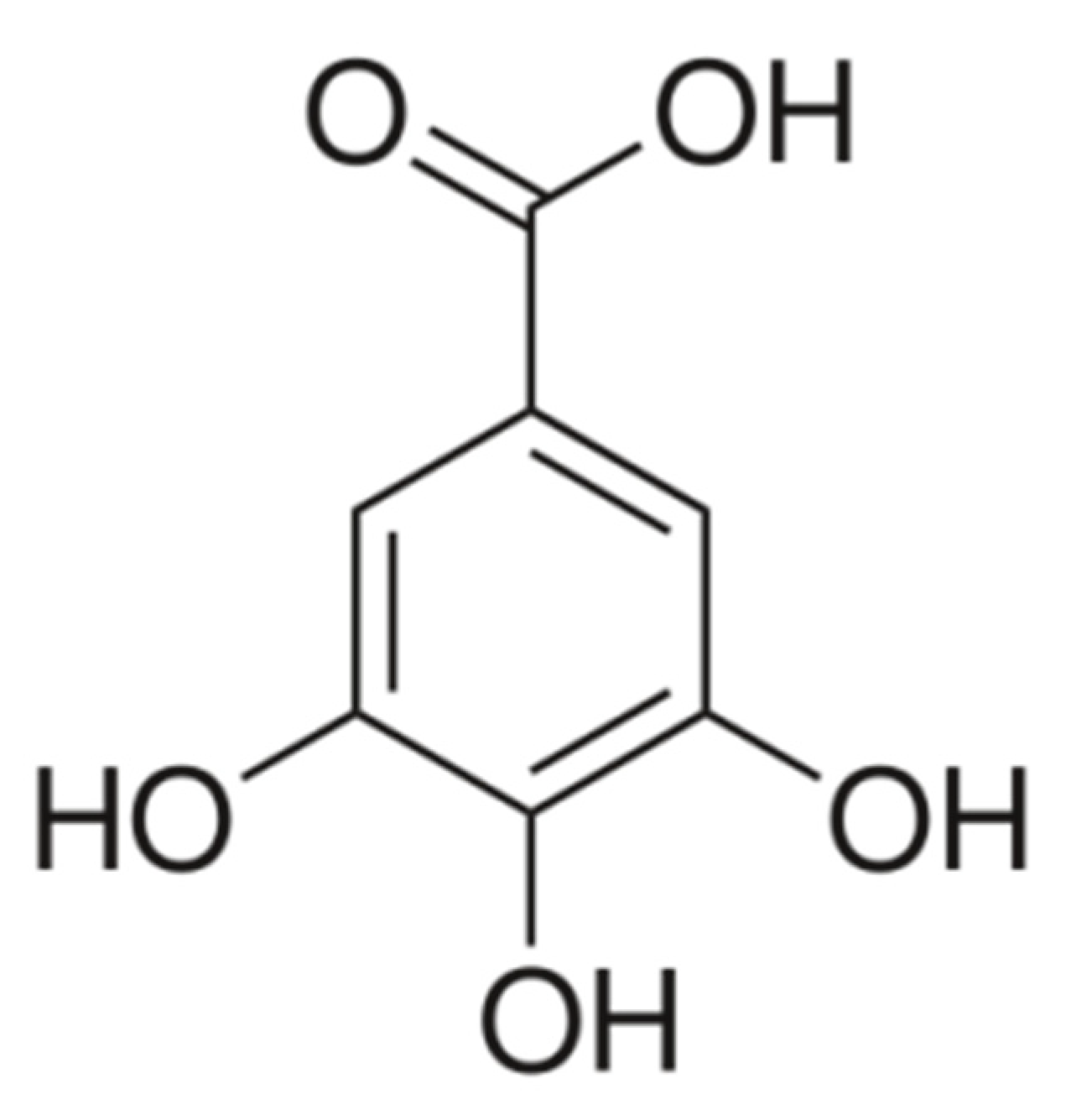
Gallic acid (3,4,5-trihydroxybenzoic acid, Figure 1) (GA) is a phenolic acid of natural origin, found in the leaves, roots, flowers, or stem of a large number of plant species (Bergia suffruticosa, Ceratonia siliqua, Tectonagrandis, and Casuarina equisetifolia) with numerous applications in the food and pharmaceutical industries [1].

GA is a white or pale-yellow crystalline compound, with the structural formula presented in Figure 1 and the main physicochemical properties in

Table 1. Main characteristics of gallic acid [2].

Characteristic	Value
Molar mass	170.12 g/mol (anhydrous)
Density	1.694 g/cm3
Solubility in water	1.19 g/100 mL (anhydrous, 20 °C)
Melting point	260 °C
Acidity constant	3.94 (COOH)
	8.45, 11.4, and 13 (phenolics OH)

.

From the pharmacological point of view, GA has antimicrobial, anti-inflammatory and antioxidant action [1,3]. In addition, GA inhibits the adhesion and development of microorganisms from the species Pseudomonas aeruginosa, Staphylococcus aureus, Streptococcus mutans, Chromobacterium violaceum, Listeria monocytogenes, and Shigella flexneri [4,5,6,7,8,9]. Moreover, it is able to exhibit degradative action on the cell wall of some Gram-negative microorganisms and an inhibitory effect on the activity of some enzymes (HIV-1 integrase, HIV-1 transcriptase, HCV serine protease, etc.) [10,11,12]. Additionally, a few studies present models for the use of GA and its derivatives in various diseases, including cancer [13]. The cytotoxic and antitumoral effect of GA results from modulating pro- and anti-oxidant activities [3].

Conventionally, GA can be obtained by acid hydrolysis of tannic acid. However, it implies high cost, low yield, low purity, and generation of toxic effluents. A more efficient process involves microbial hydrolysis of tannic acid (

Table 2. Production of gallic acid using tannase-producing microorganisms [14,15,16,17,18].

Microorganism	Process	Culture Media	GA Produced
B. subtilis AM1	Anaerobic batch fermentation, 30 °C, 48 h	FeSO4 × 7H2O, 0.01; NaNO3, 3; K2HPO4, 1; MgSO4 × 7H2O, 0.5; KCl, 0.5; and tannic acid 1%.	24.16 g/L
L. plantarum CIR1	Anaerobic batch fermentation, 30 °C, 48 h	FeSO4 × 7H2O, 0.01; NaNO3, 3; K2HPO4, 1; MgSO4 × 7H2O, 0.5; KCl, 0.5; and tannic acid 1%.	23.73 g/L
Sporidiobolus ruineniae A45.2	Aerobic batch fermentation, 1L stirred tank fermenter, 250 rpm, aeration rate of 0.2 vvm 30 °C for 48 h	3 g/L yeast extract, 3 g/L malt extract, 5 g/L peptone, 10 g/L glucose, 5 g/L tannic acid	11.2 g/L
Bacillus sphaericus	Batch fermentation, pH 6.0, 37 °C, 100 rpm, 48 h	2.0% tannic acid, 2.5% galactose, 0.25% ammonium chloride, and 0.1% MgSO4	90.8%
Rhizopus oryzae NRRL 21498, Aspergillus foetidus MTCC 3557	Modified solid-state fermentation, 30 °C and 80% relative humidity, pH 5	Powdered fruits of Terminalia chebula and powdered pod cover of Caesalpinia digyna	94.8%
Aspergillus fischeri MTCC 150	Batch fermentation 35 °C, pH: 4.0 to 3.5, agitation: 250 rpm	NH4NO3, 1.65 g/L, KNO3, 1.9 g/L, MgSO4 × 7H2O, 0.371.65 g/L, CaCl2 × 2H2O, 0.44 g/l, KH2PO4, 0.17 g/L, H3BO3, 6.2 mg/mL, MnSO4 × H2O, 16.9 mg/mL, ZnSO4 × 7H2O, 8.6 mg/mL, Na2MoO4 × 2H2O, 0.25 mg/mL, CuSO4 × 5H2O, 0.025 mg/mL, CoCl2 × 6H2O, 0.025 mg/mL, FeSO4 × 7H2O, 5.6 mg/mL, and Na2EDTA, 7.6 mg/mL, tannic acid 5.0 g/L	7.35 g GA/g biomass; 23% conversion obtained at 50 g/L tannic acid
Penicillium rolfsii (CCMB 714)	Submerged fermentation, 30 °C	10% tannic acid	21.51 g/L

) using tannase (tannin-acyl-hydrolase, EC 3.1. 1.20, an enzyme that catalyzes the breakdown of ester bonds in gallotannins) produced by fungal and bacterial strains.

Several studies have analyzed reactive extraction for the GA separation [19,20,21,22], showing its potential. Rewatkar et al. [19] obtained-under optimum conditions of 2.34 g/L GA, 65.65% v/v tri-n-butyl phosphate in hexanol, 19 °C, and pH 1.8-an extraction efficiency of 99.43% for gallic acid from an aqueous stream. Joshi et al. [20] obtained the following distributions coefficient of GA 1.94–27.57 for 2-octanone: 1.12–8.83 for lauryl alcohol, and 0.20–22.07 for n-heptane, increased values being obtained by adding 0.3652 mol/L TBP (tri-butyl phosphate) as an extractant. Pandey et al. [21,22] obtained the maximum GA extraction of 90.1%, at an initial acid concentration of 0.0588 mol/L, initial TOA concentration of 0.2762 mol/L, pH 2, and temperature of 25.0 °C. However, none of these studies have analyzed GA back extraction from organic solvents.

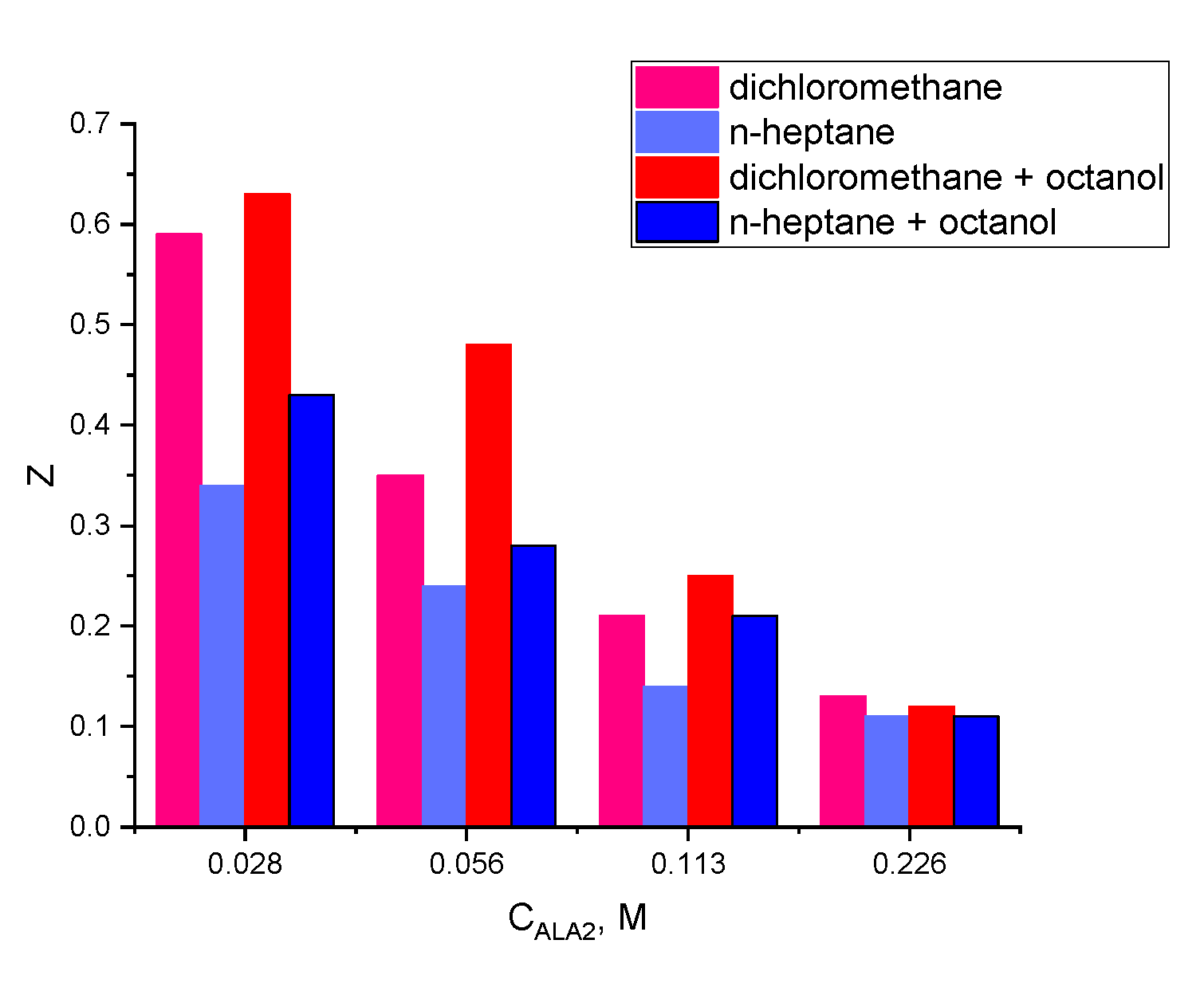
This study aims to provide a complete analysis (extraction, stripping, and optimization) of the GA reactive extraction process using Amberlite LA2 dissolved into two solvents with different dielectric constants: dichloromethane and n-heptane and a phase modifier (1-octanol). For reactive extraction of carboxylic acids during the intense mixture necessary for a good mass transfer, a third phase is formed—a stable emulsion very difficult to separate. The addition of a phase modifier, 1-octanol, prevents its formation, facilitating the organic and aqueous phase separation, and, it also increases the solvent polarity increasing the reactive extraction efficiency [23,24,25]. The results were discussed from the viewpoint of the extraction mechanism, separation yield and distribution coefficient, for different extraction conditions. Back extraction was successfully performed using NaOH solutions. In addition, the process was modeled and optimized using statistical regression and Artificial Neural Networks (ANNs) determined with the Differential Evolution (DE) algorithm. The objective is to rapidly identify the extraction efficiency without additional experiments and determine the optimal conditions that lead to maximum efficiency.

2. Materials and Methods

2.1. Chemicals

All chemicals, including gallic acid (98.0%), dichloromethane (99%), 1-octanol (99%), heptane (99%), sulfuric acid (95.0–98.0%), sodium hydroxide (>97%), lauryl tri-alkylmethylamine—Amberlite LA2 (99%), and acetonitrile (99.99%), were purchased by Sigma Aldrich (Burlington, VT, USA) and used as received without further processing.

2.2. Reactive Extraction Experiments

Reactive extraction and stripping experiments for GA separation were carried out using equal volumes of aqueous and organic phases (20 mL) in an extraction column with vibratory mixing (50 s⁻¹ frequency and 5 mm amplitude, the stirrer being maintained at the initial interface between the two phases), consisting in a glass column with a diameter of 36 mm and 250 mm height, provided with a thermostatic jacket that allowed temperature control: 25 ± 0.02 °C for all the reactive extraction experiments and 50 ± 0.02 °C for the back extraction. The reactive extraction experiments were performed using two solvents with different polarities: dichloromethane (dielectric constant 9.08 [26]) and n-heptane (dielectric constant 1.9 [26]). The first solvent, suitable for polar compounds, was chosen based on efficient reactive extraction obtained for other carboxylic acids (2-ketogluconic acid, formic acid, pseudomonic acid, acetic acid, etc. [23,24,25,27]), while the second one was chosen due to its green classification [28]. As a phase modifier, 1-octanol (dielectric constant 10.3 at 25 °C [26]) was added to the organic solution to increase the polarity of the solvent and to facilitate the phases separations (1-octanol prevents the formation of a third phase—a stable emulsion between the two phases). Solvent selection is an essential parameter since it influences the extraction efficiency and the design of a continuous extraction process and solvent regeneration cycle.

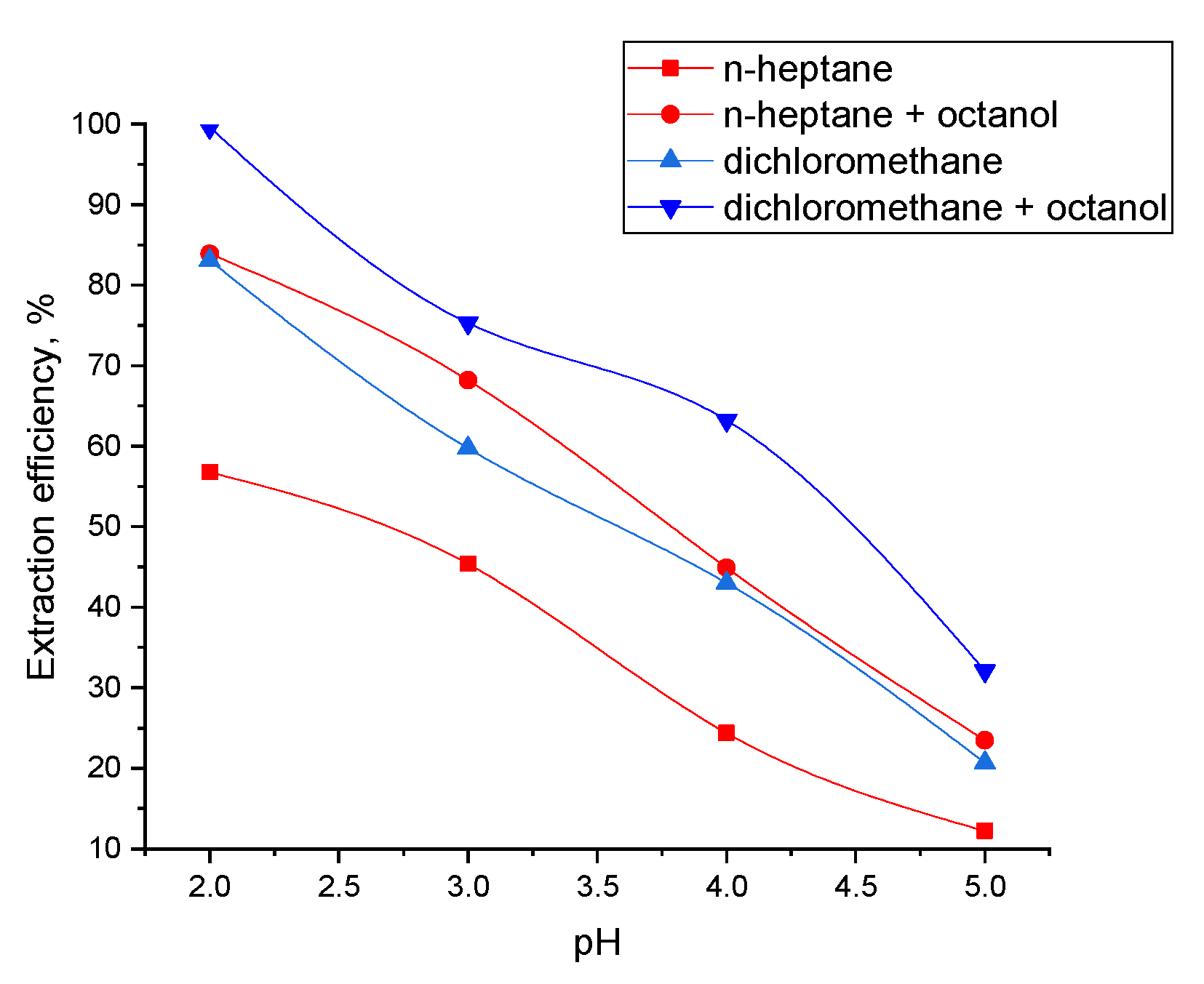
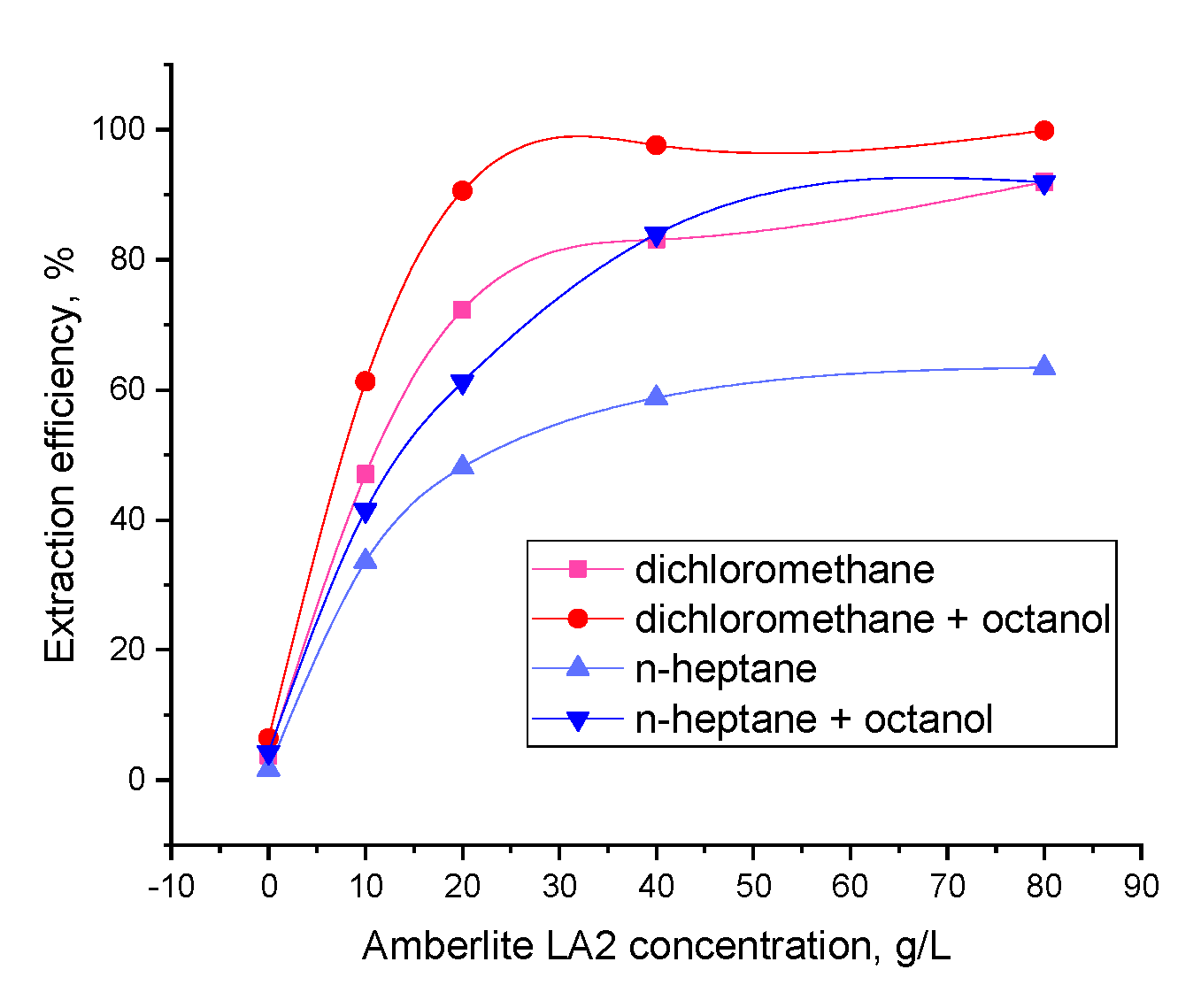
After the extraction and the stripping (each process having a duration of 1 min), phases were separated in a centrifugal separator at 4000 rpm. GA initial concentration in the aqueous phase was 5 g/L (2.29 × 10⁻² M), and the concentrations of the amine extractant, Amberlite LA-2, in the organic phase varied between 0 and 80 g/L (0.215 M). The pH value of the aqueous phase was between 2 and 5 for the extraction and 8 for the stripping experiments, modified using solutions of 3% sulfuric acid or 3% sodium hydroxide, by means of the indications of the digital pH meter (CONSORT C 836) (Turnhout, Belgium).

2.3. Analytical Procedures

The processes were analyzed on the basis of distribution coefficients and extraction efficiency, calculated using the mass balance based on the GA concentration in the aqueous phases measured by the high-performance liquid chromatography technique (HPLC) as described in the literature [19]. For this purpose, an HPLC system, UltiMate 3000 Dionex (Sunnyvale, CA, USA), provided with an Acclaim C18 (150 mm × 4.1 mm, 5 μm) column (Sunnyvale, CA, USA), 90% water, and 10% acetonitrile solution were used as mobile phase, with detection by UV absorbance at 264 nm wavelength, and the flow rate of 0.8 mL/min.

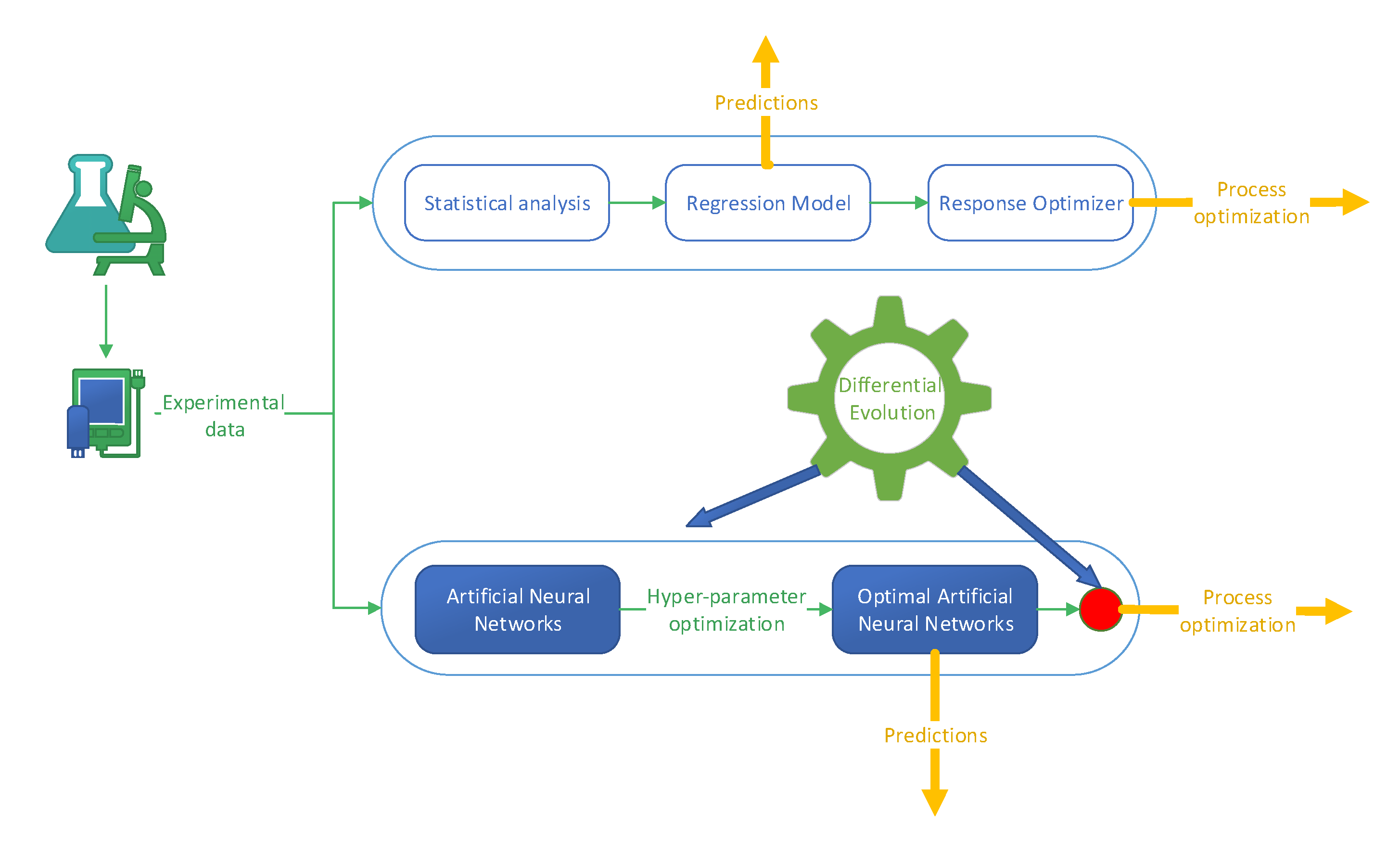
2.4. Modelling and Optimization

In order to model and optimize the considered process, two strategies were considered. One is based on the classical approaches that use statistical methods, and the other uses artificial intelligence techniques: ANNs and bio-inspired metaheuristics.

2.4.1. Statistic Approaches

The statistical analysis of the process was performed using Minitab (Coventry, UK), with a regression model with interactions through order 2 and terms through order 2, with a 95% confidence level for all intervals, and a forward selection strategy for parameter optimization. For process optimization, the Response Optimizer option was used.

2.4.2. Artificial Neural Networks and Differential Evolution

In this case, the process modeling was performed using ANNs. Although ANNs are relatively easy to use, their optimal configuration and hyper-parameters are a problem in themselves. Thus, a Keras sequential model was considered in this work, with an Adam optimizer and ReLU activation function for the hidden layers and a linear activation function for the output layer. Consequently, the training of the ANN is performed using the Keras framework. However, before training, an optimal architecture must be selected. This step is performed by DE, a population-based bio-inspired metaheuristic that showed a good capability to solve various problems from different areas. For example, in simple or different combinations, it was applied for: the prediction of polycyclic aromatic hydrocarbons formation in grilled meats [29] prediction of reactive extraction of pseudomonic acids [23], modeling the biogas production from anaerobic wastewater treatment plant [30], and optimization of biogas power plant feedstock [31].

Except for the determination of the ANN model architecture, in this work, DE is also applied to optimize the process. Since this step cannot be performed without a model, in this work, the ANN model was used in combination with DE.

Since DE is a population-based algorithm that uses vectors of real numbers, each of the two optimization problems is individually solved. In each case, a direct encoding transforms the problem into a structure that DE can work with. In the case of ANN optimization, the parameters considered are strictly related to the architecture: the number of hidden layers and neurons in each hidden layer. In the case of process optimization, the parameters considered are related to the process parameters: solvent, octanol addition, pH, and ALA-2 concentration.

Compared with the standard DE algorithm [32], the variant used in this work uses a self-adaptive procedure for the control parameters. This strategy is applied to eliminate the need for manually tuning the F and CR parameters that influence the algorithm’s performance. The F parameter controls the mutation rate of the individuals in the population. CR is the crossover rate that influences how the trial individuals are generated from the current and mutated population. Overall, the DE algorithm has fewer steps: initialization, mutation, crossover, and selection. In the initialization phase, the population is randomly generated using the limits of the considered problem. The limits are previously set for the ANN problem depending on how large a model is allowed. For process optimization, the limits are the ones used in the experimental phase. The mutation and the crossover phases are the ones responsible for generating new individuals. The mutation introduces changes in the individuals, and the crossover combines the characteristics of two parents to create children. Finally, in the selection phase, the best individuals are selected to participate in the next generation. The steps mutation, crossover, and selection are repeated until a stop criterion is reached (maximum number of generations).

The general schema of the workflow of the steps performed in this work is presented in Figure 2.

3. Results

3.1. Reactive Extraction

Reactive extraction is a separating technique that implies a chemical reaction between one or more components from a liquid mixture and a selective extractant dissolved in an organic solvent. The efficiency of the reactive extraction depends on the physical and chemical characteristics of the solute (hydrophobicity, acid-base properties), on properties of the extractant (reactivity, ability to form hydrophobic compounds with the solute) and on separation conditions (pH, mixing intensity, concentration level, etc.). Due to these conditions, the mechanism of interaction between solute and extractant, the optimal extraction conditions in correlation with the separation factors, and the extraction mechanism constitute the main study directions in reactive extraction.

3.1.1. Influence of Aqueous Phase pH on the Extraction Efficiency

The pH-value of aqueous solutions is an important parameter that influences the reactive extraction process, as it controls the form in which the acid is found in aqueous solutions: undissociated at pH value lower than pKa (3.94 for the carboxylic group), and dissociated at pH value superior to pKa. GA contains in his molecule a carboxylic group and three hydroxyl groups and the dissociation of these functional groups is represented in Figure 3:

However, due to polarizable hydroxyl from phenolic groups, GA can form hydrogen bonds, generating dimers [33].

Due to GA insolubility in both chosen solvents, the extraction is based on forming a complex between the extractant (Amberlite LA2) and the carboxylic group from the acid structure. The pH influence on the extraction efficiency (E, %—the ratio of GA concentration in the extracted phase and its initial concentration), depicted in Figure 4, suggest hydrogen bond formation between the un-dissociated acid and the extractant (for pH < pKa1, the acid dissociation in the aqueous phase can be considered negligible).

Adding 1-octanol increased the extraction efficiency for both solvents (

Table 3. The amplification factor values corresponding to 1-octanol addition (C_ALA2 = 40 g/L).

Solvent/pH	2	3	4	5
n-Heptane	1.47	1.50	1.84	1.92
Dichloromethane	1.19	1.26	1.47	1.55

), with a more significative influence at pH over 4. The organic phase consists either of two (diluent and extractant) or three components (diluent, extractant, and modifier). The extractant reacts with gallic acid, forming an amine–acid complex that is soluble only in the diluent (used primarily for decreasing extractant viscosity), solubility being improved by the modifier addition. The most important influence of 1-octanol is observed in the case of n-heptane, by improving its low transfer capabilities of the acid–amine complex in the organic phase.

The most important increase in the values of amplification factors has been reached for pH over 4, in the domain corresponding to the higher extent of carboxyl group dissociation.

3.1.2. Influence of Amine Concentration on the Extraction Efficiency

The reactive extraction of carboxylic acids, which are usually present in low concentrations in the fermentation broth, with an aminic extractant occurs, at equilibrium, at the organic-aqueous interface, with the formation of a strong hydrophobic compound. Solvation of this compound by the diluent is a critical factor in the extraction of most acids.

The experimental results regarding the influence of Amberlite LA2 concentration on the extraction efficiency are illustrated in Figure 5, for pH = 2 (pH value corresponding to the maximum extraction efficiency).

Physical extraction was found to be very poor in both used solvents. An increase in ALA2 concentration in the organic phase from 0 to 0.226 M, over the stoichiometric ratio (GA concentration was 2.935 × 10⁻² M), induces the continuous increase of the extraction degrees. These high extraction yield values suggest improved solvation by extractant molecules by increasing interfacial compounds hydrophobicity. Similar trends can be observed for other acid-extraction systems [23,24,25,27].

Adding 1-octanol improves the solvation power of the acid–amine complex, as shown by the amplification factors values presented in

Table 4. The amplification factors values corresponding to 1-octanol addition (pH = 2).

Solvent/A LA2 Concentration	10	20	40	80
n-Heptane	1.23	1.27	1.47	1.45
Dichloromethane	1.30	1.25	1.19	1.08

. In the case of the solvent with the lower polarity, the 1-octanol addition generates the lowest influence at low amine concentration in the organic phase. This proves that the modifier presence is more important for increased extractant quantities in the solvent, probably due to the formation of gallic acid dimers through intermolecular hydrogen bonds, resulting in carboxylic groups blocked and requiring higher amounts of extractant to make the interfacial reaction possible. The octanol provides a good solvation media for the interfacial product (acid–amine complex), but it can also form hydrogen bonds with gallic acid, due to the alcohol functional group. In the dichloromethane case, the highest influence can be observed at low amine concentrations, but the values are comparable with those obtained for n-heptane. At higher extractant concentrations in dichloromethane, the phase modifier influence is diminished, the extraction degree being high even in the absence of 1-octanol, due to increased solvent polarity.

3.1.3. Study of the Reactive Extraction Mechanism

To analyze the reactive extraction mechanism with and without 1-octanol as the phase modifier, the following interfacial equilibrium is considered (gallic acid is insoluble in n-heptane and in dichloromethane and Amberlite LA2 is insoluble in the aqueous phase). The purpose is to determine the extraction equilibrium constant (K_E) and the number of extractant molecules (n), using the law of mass action. As concluded from the pH influence, Amberlite LA2 extracts the non-dissociated form of GA when the pH < pK_a:

$$\mathrm{Gal}-{\mathrm{COOH}}_{\left(\mathrm{aq}\right)}+n{\mathrm{Q}}_{\left(\mathrm{o}\right)}\leftrightarrow \mathrm{Gal}-{\mathrm{COOHQn}}_{\left(\mathrm{o}\right)}$$

(1)

For this system, the distribution coefficient, D, is determined using Equation (2), the ratio of gallic acid concentration in the solvent phase and in the aqueous phase at equilibrium:

$$D=\frac{\left[\mathrm{Gal}-{\mathrm{COOH} \mathrm{Q}}_{\mathrm{n}\left(\mathrm{o}\right)}\right]}{\left[\mathrm{Gal}-{\mathrm{COOH}}_{\left(\mathrm{aq}\right)}\right]}$$

(2)

According to the interfacial reaction proposed, the equilibrium constant can be determined with Equation (3):

$$K_E=\frac{\left[\mathrm{Gal}-{\mathrm{COOH} \mathrm{Q}}_{\mathrm{n}\left(\mathrm{o}\right)}\right]}{\left[\overline{\mathrm{Gal}-{\mathrm{COOH}}_{\left(\mathrm{aq}\right)}}\right] {\left[{ \mathrm{Q}}_{\left(\mathrm{o}\right)}\right]}^n}\to \left[\mathrm{Gal}-{\mathrm{COOH} \mathrm{Q}}_{\mathrm{n}\left(\mathrm{o}\right)}\right]=K_E·\left[\overline{\mathrm{Gal}-{\mathrm{COOH}}_{\left(\mathrm{aq}\right)}}\right]·{\left[{\mathrm{Q}}_{\left(\mathrm{o}\right)}\right]}^{n }$$

(3)

The concentration of un-dissociated gallic acid in the aqueous solution is calculated through Equation (4), by using its total concentration, $\overline{\mathrm{Gal}-{\mathrm{COOH}}_{\text{aq}}}$ and Ka, the dissociation constant:

$$\left[\mathrm{Gal}-{\mathrm{COOH}}_{\left(aq\right)}\right]=\frac{\overline{[\mathrm{Gal}-{\mathrm{COOH}}_{\left(\mathrm{aq}\right)}}]}{1+\frac{K_a}{\left[H^{+}\right]}}$$

(4)

Using these three Equations (2)–(4) the equation for distribution coefficient D becomes:

$$D=K_E·\frac{{\left[{\mathrm{Q}}_{\left(\mathrm{o}\right)}\right]}^n}{1+\frac{K_a}{\left[H^{+}\right]}}$$

(5)

By applying the logarithm to relation Equation (5), the following equation (straight line) can be obtained:

$$\ln D+\ln \left(1+\frac{K_a}{\left[H^{+}\right]}\right)=\ln K_E+n\ln \left[{\mathrm{Q}}_{\left(\mathrm{o}\right)}\right]$$

(6)

Using the graphical representation of Equation (6), in Figure 6, it is possible to determine the number of Amberlite LA-2 molecules, n, which participate in the formation of the interfacial adduct (from the slope), and the value of the extraction constant, K_E, (from its intercept).

The results presented in

Table 5. Values of n and K_E for extraction systems with 1-octanol and Amberlite LA2.

Solvent	n	KE,
n-Heptane	1.86	56.56, L2/ mol2
Dichloromethane	1.18	358.31, L/mol
n-Heptane + octanol	1.08	82.43, L/mol
Dichloromethane + octanol	1.16	947.97, L/mol

, demonstrate that in the absence of the phase modifier, the reactive extraction occurs through the formation of an aminic adduct that contains two molecules of extractant for n-heptane, while for dichloromethane it occurs by forming an equimolecular complex between Amberlite LA2 and GA. The addition of 1-octanol changes the mechanism for the inert solvent n-heptane, for both solvents the interfacial complex containing one molecule of each reactant.

As can be observed from Table 5, the increase of organic phase polarity leads to the increase of the extraction constant K_E, thus suggesting the moving of the interfacial equilibrium towards the formation of extraction compounds. In order to confirm these results, the loading factor, Z, [Gal-COOH_(o)]/[Q_(o)] was calculated, the values being presented in Figure 7.

The decrease in the loading ratio, with Amberlite LA2 increasing concentration cumulated with values smaller than 0.5, confirms that only acid—extractant 1:1 (for dichloromethane with or without 1-octanol and n-heptane with 1-octanol) or 1:2 (for n-heptane)—complex is formed in the organic phase. The values of Z superiors to 0.5, obtained for dichloromethane at low Amberlite LA-2 concentrations (with or without the phase modifier) assume the formation of an acid: extractant complexes of 2:1 and 3:1 [22].

3.1.4. Study of Stripping Efficiency

Stripping is a necessary step for the recovery of GA from the interfacial complex, which can be attained by the reaction with NaOH that will convert the acid into its salt, regenerating the extractant in the same time. The results obtained for GA are presented in Figure 8.

The study was performed at an initial phase pH equal to 2, corresponding to the maximum efficiency of the reactive extraction process and different extractant concentrations. The maximum recovery yield was obtained at low amine concentrations in the organic phase corresponding to smaller equilibrium concentration of gallic acid in organic phase. The increase in temperature for the re-extraction at 50 °C facilitates the back extraction as the formation of the complex between gallic acid and Amberlite LA2 through hydrogen bonds is exothermic and decreases the system entropy. Increasing the system temperature diminishes the amount of gallic acid extracted, thus increasing the stripping efficiency.

3.2. Modelling and Optimization

3.2.1. Statistical Approaches

The regression model was determined based on the process parameters: solvent types (described by the dielectric constant), the octanol addition (0 if no octanol is added and 1 if octanol is added), pH, and ALA-2 concentration. The software used was MINITAB 17.1.0, and a forward selection was applied for parameter selection. The resulting model had an R² of 91.63% and an adjusted R² of 89.15%. The analysis of variance for the resulting model is presented in

Table 6. ANOVA analysis.

Source	DF	Adj_SS	Adj_MS	F-Value	p-Value
Regression	8	25,395.6	3174.45	36.94	0
pH	1	133.2	133.2	1.55	0.224
ALA_2	1	9175	9175.02	106.78	0
Solvent	1	1537.4	1537.36	17.89	0
Octanol	1	140.3	140.26	1.63	0.212
pH × pH	1	0.2	0.17	0	0.964
ALA_2 × ALA_2	1	6947.4	6947.38	80.86	0
pH × Octanol	1	209.7	209.69	2.44	0.13
ALA_2 × Octanol	1	828.8	828.79	9.65	0.004

, where DF indicates the degrees of freedom, Adj_SS is the adjusted sum of squares, Adj_MS is the measure of the adjusted mean of squares, and F-value indicates if the term is associated with the response. Finally, p-value is the probability that indicates the evidence against the null hypothesis.

The resulting models are indicated by Equations (7)–(10). The main explanation for the fact that there are four equations for the process is related to the fact that in the model, there are two categorical predictors: the solvent type and the octanol addition. Equation (7) corresponds to the case where the solvent used is n-heptane, and no octanol is added. Equation (8) corresponds to the case where n-heptane with octanol is used. Equation (9) corresponds to the case where the solvent used is dichloromethane, and Equation (10) describes the dichloromethane and octanol case.

$$Eff=42.6-18.2\times pH+2.558\times ALA\_2+0.1\times p{H}^2-0.02516\times ALA\_2^2$$

(7)

$$Eff=54.4-22.8\times pH+3.007\times ALA\_2+0.1\times p{H}^2-0.02516\times ALA\_2^2$$

(8)

$$Eff=55.7-18.2\times pH+2.558\times ALA\_2+0.1\times p{H}^2-0.02516\times ALA\_2^2$$

(9)

$$Eff=67.4-22.8\times pH+3.007\times ALA\_2+0.1\times p{H}^2-0.02516\times ALA\_2^2$$

(10)

The next step was determining the optimal conditions that lead to a maximization of efficiency. In MINITAB, this was performed using the Response Optimizer option. The solutions that resulted are presented in

Table 7. Optimization solutions obtained in MINITAB.

Solution	Solvent	Octanol	pH	ALA-2	Fit	Desirability
1	9.08	1	2.07477	80	100	1
2	1.9	1	2	59.7469	96.929	0.98891
3	9.08	0	2	50.8301	84.727	0.84183
4	9.08	1	3.5	59.7273	78.556	0.77792

, where Fit indicates the efficiency of the process, and Desirability is a measure that indicates the effectiveness of the response to the desired conditions.

3.2.2. Artificial Intelligence

In order to determine the optimal ANN model for the considered process, the DE algorithm in combination with the classical BackPropagation training technique optimized with Adam (a combination implemented in Python and using the Tensorflow library) was applied. As previously mentioned, two DE control parameters were included in a self-adaptive approach to eliminate the need for manual tuning. However, DE does not have only two parameters. It is also controlled by the number of individuals in the population and the number of generations. However, following the classical DE idea, these parameters are fixed through the run and, thus, can be easier to set up manually. Thus, based on a preliminary test series, the generations were set to 50 and the number of individuals to 25. These settings were used in all the optimization cases.

Regarding the ANN optimization problem, due to the direct encoding of the parameters, a set of limits were set to the ANN topology not to complicate the model too much. Thus, the maximum number of hidden layers was set to 5, with 50, 50, 30, 30, and 15 maximum number of neurons, respectively. After all the parameters were set, the experimental data were pre-processed (randomized, split into training and testing, and normalized) and fed to the DE procedure. Since the DE is a high stochastic algorithm, 10 runs were performed, and the best ANN was chosen from the pool of generated solutions based on the mean squared error (MSE) computed in the training phase. Due to the relatively low number of experimental points and the high number of hyper-parameters that need to be determined during the architecture determination and training, the best ANN determined—although it had a better performance than the regression models in a few cases—had an unacceptable low performance. This indicated that the ANN did not efficiently capture the process’s dynamic in all cases due to the low number of experimental data.

To solve this problem, the number of points was enlarged using a procedure that generates synthetic data based on actual data. First, the process’s dynamic was graphically determined for each type of solvent (with or without octanol), and intermediary points were obtained using the Digitizer tool from Origin. After that, the new extended dataset underwent the same procedure to determine the process model as in the original experimental data. The best model obtained had a single hidden layer with 50 neurons.

Table 8. Statistical indicators for the best ANN obtained.

	Training	Testing
Explained variance score	0.996	0.996
Mean absolute error	1.141	1.212
Mean squared error	2.552	2.794
Mean absolute percentage error	0.0401	0.032
Coefficient of determination	0.995	0.994

presents the main statistic indicators for this ANN model, which will be further referred as ANN (4:50:1).

A comparison between the experimental data, the statistical regression model’s predictions, and the ANN (4:50:1) model for a concentration of ALA-2 of 40 is presented in Figure 9. As observed, the regression model does not efficiently capture the efficiency dynamic and tends to be linear. On the other hand, the ANN predictions are closer to the experimental data. Moreover, there is a single ANN that models all the cases, and there is no need to change the relation based on the initial conditions. However, in terms of predicted values, especially at low pH, for n-heptane, the predicted values for the regression are far from the experimental data.

After that, the ANN model was applied for process optimization using the DE optimizer. The best results obtained are presented in

Table 9. Process optimization using DE with ANN (4:50:1).

Solvent	Octanol	pH	ALA-2	Fit
9.8	1	2.018	46.518	100.000
9.8	1	2.005	25.699	99.621
9.8	1	2.145	56.867	97.834
9.8	1	2.310	42.744	93.193
9.8	1	2.310	28.929	92.596
9.8	1	2.409	56.697	90.889
1.9	1	2.047	67.956	89.606
9.8	1	2.477	56.784	89.105
9.8	1	2.477	44.331	88.840
9.8	1	2.537	32.539	86.787
9.8	1	2.560	37.518	86.524
9.8	1	2.560	35.597	86.397
9.8	0	2.060	39.118	83.427
1.9	1	2.253	47.333	82.726
9.8	0	2.129	35.986	80.973
1.9	1	2.643	78.369	78.558
1.9	1	2.495	52.322	78.328
9.8	0	2.060	31.291	77.855
1.9	1	2.344	37.328	75.971
9.8	1	3.285	68.010	74.854
9.8	0	2.129	52.254	74.464
9.8	1	3.467	53.442	73.858
9.8	0	2.060	24.065	70.132
1.9	0	2.000	80.000	63.486
1.9	0	2.000	76.601	63.481
1.9	0	2.040	77.793	63.003
1.9	0	2.000	66.550	61.763

.

As it can be observed, the DE algorithm provided various solutions for each combination of solvents with or without octanol.

4. Conclusions

This article reports a comprehensive study on gallic acid separation including: reactive extraction, stripping, and modeling. The optimum conditions for the reactive extraction onto a biphasic organic-aqueous system were: pH of aqueous phase 2, dichloromethane used as solvent, 80 g/L Amberlite LA2 used as extractant, and 10% phase modifier (1-octanol). The extraction mechanism analysis confirmed the formation of complexes involving hydrogen bonds between 1 molecule of GA and 1 of extractant, for dichloromethane (with or without 1-octanol) and n-heptane with 10% 1-octanol, and 1:2 (acid:extractant) complexes for n-heptane. The organic phase is regenerated at a high temperature (323 K) with sodium hydroxide, allowing its simultaneous regeneration. Moreover, the process was modeled and optimized with statistical approaches and artificial intelligence tools (ANNs and DE). The results indicated that an effective model process could be further used to generate predictions and eliminate the need for additional experimental work.