Abstract
The present work aims to develop a mathematical model, based on Gompertz equations and ANNs to predict the concentration of four solvent compounds (isobutanol, ethyl acetate, amyl alcohol and n-propanol) produced by the yeasts S. cerevisiae, Safale S04, using only the fermentation temperature as input data. A beer wort was made, daily samples were taken and analysed by GC-FID. The database was grouped into five datasets of fermentation at different setpoint temperatures (15.0, 16.5, 18.0, 19.0 and 21.0 °C). With these data, the Gompertz models were parameterized, and new virtual datasets were used to train the ANNs. The coefficient of determination (R2) and p-value were used to compare the results. The ANNs, trained with the virtual data generated with the Gompertz functions, were the models with the highest R2 values (0.939 to 0.996), showing that the proposed methodology constitutes a useful tool to improve the quality (flavour and aroma) of beers through temperature control.
1. Introduction
Beer is a complex beverage that contains more than 450 different compounds, including higher alcohols, esters, acids and aldehydes, which have a great impact on aroma and flavour characteristics. This impact could be positive or negative depending on the beer style and also on the concentration of these compounds. Therefore, it is interesting to develop mathematical models that help predict its concentration.
In general, when brewers refer to the compounds found in a beer, it is not common to do so by their names but by the characteristics they produce; thus, they are known as “organoleptic descriptors”, which can refer to a compound, several of them or even mouthfeel, flavours and aromas. One of these descriptors is solvents, which are described as: “similar to acetone or lacquer thinner aromas” [1]. According to different authors, some of the compounds that can be found in beers and possess these characteristics are the higher alcohols n-propanol, isobutanol, amyl alcohols and ester ethyl acetate [2,3].
According to Loviso et al., higher alcohols are formed from the anabolism or catabolism of different amino acids (Ehrlich’s pathway); the esters, on the other hand, are formed by enzymatic reactions of organic acids and alcohols. In other words, both are related and are generally produced by yeast metabolism [4,5]. The authors clarify that part of the reactions involved in the formation of these alcohols are not yet fully understood. The factors that affect its formation are wort composition, carbohydrates, nitrogen sources and temperature, although it should not be forgotten that the predominant factor is the genetics of the yeast strain. Yeasts S. cerevisiae (ale) produce higher amounts of higher alcohols than S. pastorianus (lager).
These solvents are desirable at certain levels as they add complexity to the flavours and aromas. However, if these compounds exceed certain limits, they could become major quality failures. Considering this, the obvious question would be: how much solvent is desirable? This question does not have a clear answer, but it will be the brewmaster with his experience who decides how much the optimal amount is. Thus, it is important to understand which are the variables that influence the concentration of solvents, but at the same time which are the ones that brewmasters can manipulate practically. As far as the authors know, there are no fermentation control systems that use temperature as a control variable to estimate these solvents, despite the important impact they have on the organoleptic quality of the final product.
Considering that brewers try to standardize their recipes and brewing methods, the temperature is practically the only variable that allows exercising control over the fermentation process. For this reason, the mathematical model must consider the temperature as the main input value and the solvent concentration as an output.
Due to the sigmoidal behaviour of the compound concentration growth curves, these can be modelled using Gompertz functions [6]. However, each temperature and each compound will be represented by a unique function, which makes the practical applicability of the model for different working temperature ranges difficult. ANNs have proven to be powerful tools in the modelling of different parameters in beers, prediction of compound concentration, classification of beers, pattern recognition in noses and electronic tongues, among other uses [7,8,9,10,11,12]. The use of neural networks has the advantage that once trained is possible to estimate all the possible values that can befall.
The objective of this work is to provide specific models to predict the final concentration of four solvent compounds: isobutanol, ethyl acetate, propanol and amyl alcohol, using only temperature and timestamp readings as control variables.
2. Materials and Methods
2.1. Wort Production, Fermentation Process and Data Acquisition
The brewed base style was a British Strong Bitter, category BJCP 11C. Fermentation was carried out in a 25 L stainless-steel conical fermenter, double-walled for cooling and a heater plate for heating (BSGI NZ Ltd, Auckland, New Zealand). Wort produced was a 100% barley malt (5.53 kg): 90.3% Pale Ale malt (Finest Pale Ale Golden Promise) (Thomas Fawcett, Castleford, West Yorkshire, UK), 9% caramel malt (Crystal Light) (Castle Malting, Beloeil, Wallonia, Belgium) and 0.7% dark malt (Dark Crystal 250-300 EBC) (Thomas Fawcett, Castleford, United Kingdom) in late addition. Mashing was a single-step infusion (66 °C) for 120 min. During boiling, four East Kent Goldings hop additions (135 g) were made: 26% min 60, 22% min 90, 22% min 110, 30% min 120. Water was purified with a reverse osmosis filter, later all batches used the specific target water profile: Ca+2 75 ppm, Mg+2 7 ppm, Na+2 20 ppm, Cl−2 50 ppm, SO4−2 120 ppm, HCO3− 0 ppm. S. cerevisiae commercial yeast strain Safale S-04 (Fermentis, Marcq-en-Barœul, Hauts-de-France, France) was used for main fermentation; 11.5 g following direct pitch E2UTM directive recommended by Fermentis [13] at 20–21 °C. The main analytical characteristics of the wort were: OG 1.054, EBC 16, IBU 35, BU:GU 0.68, ABV 5.4% (est).
Five fermentations (dataset from 1 to 5) of 10 days each were carried out at different target temperatures: 15.0 °C, 16.5 °C, 18.0 °C, 19.0 °C, 21.0 °C. Samples were taken daily (every 24 h) for 10 days for chromatographic analysis. For the quantification of the four compounds, three replicates of each sample were analysed, resulting in thirty experimental data per fermentation temperature for each compound.
Beers were not filtered, neither was any type of clarifier added.
Tilt™ hydrometer—thermometer (Tilt, Santa Rosa, CA, USA) was installed to provide temperature and density real-time data. These data were sent through a Raspberry Pi 3B+ (Raspberry Pi Foundation, Cambridge, UK) using the Tilt™ Pi V2 Buster App to a ThingSpeak™ channel (MathWorks, Natick, MA, USA). Tilt accurate for temperature is ±0.5 °C.
2.2. Sample Description and Experimental Data and Analysis of Solvents Using GC-FID
This method was extensively described by Loira et al. [14]. Each day samples were taken in triplicate and analysed with a gas chromatograph coupled with a flame ionisation detector (GC-FID). Samples were injected after filtration through 0.45 μm cellulose methyl ester membrane filters (Labbox, Madrid, Spain). The equipment was the Agilent Technologies 6850 gas chromatograph (Palo Alto, CA, USA). The injection temperature was 250 °C and the detector temperature was 300 °C. The column used was a DB-624 capillary column (60 m × 250 μm × 1.40 μm) (stationary phase 6% cyanopropyl phenyl, 94% polydimethylsiloxane). The column temperature ramp was 40 °C during the first five minutes, then a linear increase of 10 °C per minute until 250 °C. This temperature was maintained for 5 minutes. The total runtime of each sample was 40 min. The carrier gas used was hydrogen with a flow rate in the column of 2.2 L·min−1 and 100 μL of internal standard (4-methyl-2-pentanol, 500 mg/L) (Fluka Chemie GmbH, Buchs, Switzerland) was added to 1 mL test samples. This method is a variant of one recommended by the International Organisation of Vine and Wine (OIV) for the analysis of higher alcohols. The detection limit was 0.1 mg/L. The volatile compounds analysed were previously calibrated with five-point calibration curves (R2): 1-propanol (0.999), ethyl acetate (0.999), isobutanol (0.999), 2-methyl-1-butanol (0.999), and 3-methyl-1-butanol/isoamyl alcohol (0.999).
2.3. Mathematical Fitting Models: Gompertz Functions and ANNs
For curve fitting, ANNs training and data analysis Matlab® R2021a (MathWorks, Natick, MA, USA) was used.
To fit the experimental data obtained, Gompertz functions (Equation (1)) were used as described by Sunita et al., Zwietering et al. and more recently by Benucci et al. [15,16,17]. In equation 1, y [mg L−1] is compound concentration, t [h] is time, a [mg L−1], b (dimensionless) and c [h−1] are mathematical parameters to describe the sigmoidal growth curve.
From the Gompertz mathematical parameters a, b, c can be estimated and the values A, kg, λ can be calculated (Equations (2)–(4)), which has the advantage of having a practical biological interpretation as described by Zwietering et al.; A [mgL−1] is an asymptote, representing the upper value of the compound concentration when time tends to infinity; kg [mg L−1 h−1] represents the specific max growth rate; finally, λ [h] represents the lag time from zero to the moment when the exponential growth begins, i.e., the intercept on the abscissa axis of the tangent that passes through the inflexion point on an exponential curve, as explained in detail by Singh et al. [16].
Once the adjustment parameters of the model were obtained for each compound and each temperature, the Gompertz functions were used to generate a database larger than the original one; the object was to train the neural network and thus obtain robust results. A matrix with 140,625 × 4 values was generated with this porpoise.
Four models were developed using ANNs. The inputs were temperature and timepoints in all cases. The outputs were n-propanol, ethyl acetate, amyl alcohol and isobutanol. The training algorithm was Bayesian Regularization with ten neurons in the hidden layer for n-propanol, ethyl acetate and amyl alcohol and five for isobutanol since this algorithm works well on small datasets [2] (Figure 1). Random data division (70% training and 30% testing) was used. The means squared error (MSE) and root means square error (RMSE) algorithms were used for performance purposes.
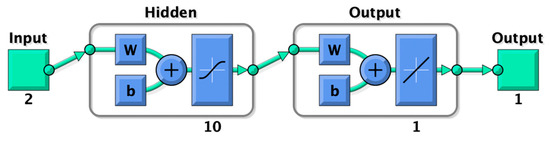
Figure 1.
Diagram of the two-layer feedforward ANNs with a tan-sigmoid function in the hidden layer and a linear transfer function in the output layer. Ten neurons were used for amyl alcohol, ethyl acetate and n-propanol and five for isobutanol.
2.4. Statistical Analysis
Raw data were compared using F-test, p-value (p < 0.05) and R2-value, with the simulated data from the Gompertz functions and AANs results to assess the performance of the functions.
3. Results and Discussion
To examine the effects of different temperatures in the solvent’s concentrations, five experiments were carried out in five datasets (1, 2, 3, 4, 5) which correspond to the setpoint temperatures (15.0, 16.5, 18.0, 19.0, and 21.0 °C), respectively. Despite setting the system at those temperatures, the sensor measurements (°C) varied over time. In this work, all the calculations were performed with these measured values. Measured statistical data is given in Table 1.

Table 1.
Temperature data registered by Tilt sensor. All values are given in °C.
Each model was fitted to each dataset with Gompertz functions, the estimated mathematical parameters are given in Table 2. From the Gompertz parameters a, b and c, the values of A, kg, and λ have been calculated, which correspond to the amplitude (maximum value), the maximum growth rate and the lag time of the compounds. These values are given in Table 2. This information is useful for understanding and predicting the lag phase of yeast and its relationship with the generation of the studied compounds.

Table 2.
Estimated mathematical parameters for Gompertz functions for n-propanol, ethyl acetate, amyl alcohol and isobutanol, for different temperatures. A is the asymptote; kg represents the specific maximum growth rate; λ is the lag time. Data in parentheses represent 95% of confidence limits.
The use of Gompertz functions to model similar compounds has been done before in other works such as Membré and Tholozan [6] although with other microorganisms, or Benucci et al. [17] for different compounds but similar purposes.
The results obtained have been represented in Figure 2, Figure 3, Figure 4 and Figure 5. The experimental values are shown, in addition to the means and standard deviation for each experimental dataset.
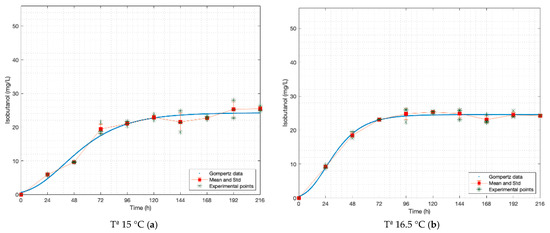
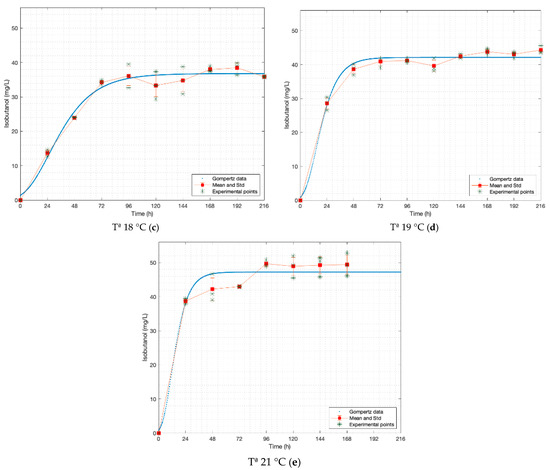
Figure 2.
Gompertz graphs of predicted values for isobutanol. (a) Dataset 15 °C; (b) dataset 16.5 °C; (c) dataset 18 °C; (d) dataset 19 °C; (e) dataset 21 °C. Blue lines represent the Gompertz function. Asterisk for experimental raw data. Squares and red lines represent the means and standard deviations.
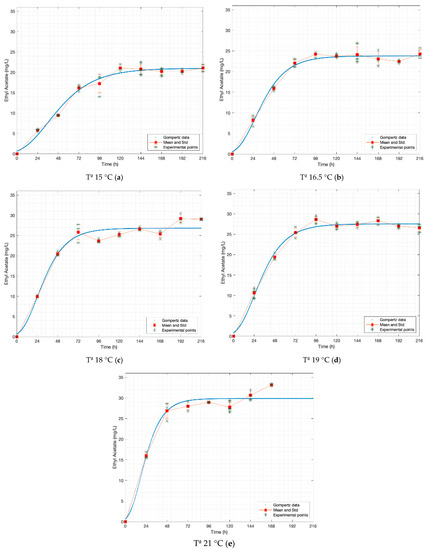
Figure 3.
Gompertz graphs of predicted values for ethyl acetate. (a) Dataset 15 °C; (b) dataset 16.5 °C; (c) dataset 18 °C; (d) dataset 19 °C; (e) dataset 21 °C. Blue lines represent the Gompertz function. Asterisk represents experimental raw data. Squares and red lines represent the means and standard deviations.
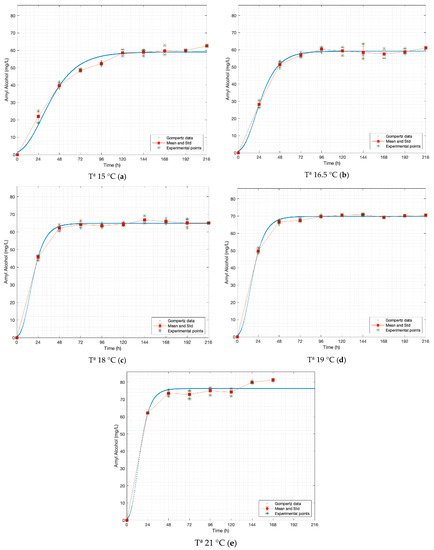
Figure 4.
Gompertz graphs of predicted values for amyl alcohol. (a) Dataset 15 °C; (b) dataset 16.5 °C; (c) dataset 18 °C; (d) dataset 19 °C; (e) dataset 21 °C. Blue lines represent the Gompertz function. Asterisk represents experimental raw data. Squares and red lines represent the means and standard deviations.
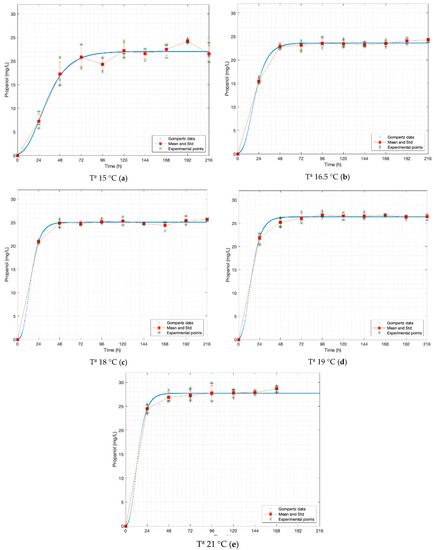
Figure 5.
Gompertz graphs of predicted values for propanol. (a) Dataset 15 °C; (b) dataset 16.5 °C; (c) dataset 18 °C; (d) dataset 19 °C; (e) dataset 21 °C. Blue lines represent the Gompertz function. Asterisk represents experimental raw data. Squares and red lines represent the means and standard deviations.
The maximum concentration values of the compounds (A) are consistent with those reported in previous works at similar temperatures such as Pires et al., although that work focuses on lagers [3]. Pires report 8–32 [mg L−1] for ethyl acetate, 50–70 [mg L−1] for amyl alcohol, 4–17 [mg L−1] for n-propanol and 4–57 [mg L−1] for isobutanol. In contrast, Canonico et al. report similar values for n-propanol 28.09 [mg L−1] and isobutanol 27.54 [mg L−1] but demonstrate lower values for amyl alcohols 7.28 [mg L−1] and ethyl acetate 7.42 [mg L−1] [18]. It is important to mention that this work is based on the use of Safale US 05, an S. cerevisiae strain that Fermentis reports as “neutral”, which may explain this difference. García et al. report a concentration of 30 [mg L−1] at 19 °C and 25 [mg L−1] at 16 °C for propanol; and 19 [mg L−1] at 19 °C and 16 [mg L−1] at 16 °C for isobutanol; but with a strain of S. carlsbersgensis (S. pastorianus) [19]. It should be noted that in the bibliography different concentrations of the studied compounds can be found. Most of these studies do not specify the composition of the worts or the yeast strains used. Without this information, it is difficult to accurately compare the results obtained, due to, as it is known, the differences in the composition of sugars and nitrogen present directly affect the concentration of higher alcohols [5] and thus that of esters [4].
Regarding λ, the standard deviation for the n-propanol values at different temperatures is 1.69 [h], ethyl acetate is 1.04 [h], amyl alcohol is 1.09 [h], and isobutanol is 2.33 [h]; thus, isobutanol is the compound at which temperature exerts the greatest influence on the speed at which the exponential growth phase begins.
Regarding ethyl acetate (Figure 3), Stewart reported similar values for three different strains of S. cerevisiae (20.6, 36.2, 25.6 [mg L−1], at 20 °C) [19]. García et al. worked with a strain of S. pastorianus and found comparable but lower values (18.0 [mg L−1] at 19 °C and 16.0 [mg L−1] at 16 °C) [20].
Riverol and Cooney reported that the rate constants of ethyl acetate do not change concerning temperature [21], which differs from the present work and that reported by Loviso et al. and García et al. [4,20]. Riverol et al. did not specify which yeast they modelled, but fermentation temperatures were between 10 °C and 15 °C which suggests that it was a strain of S. pastorianus.
In the cases of propanol and isobutanol, the odour thresholds are not exceeded at any of the temperatures, while in amyl alcohol it is close to the lower limit when fermented at 15.0 °C and it exceeds from 18.0 °C. For ethyl acetate, various values of odour thresholds are found in the literature, 3 [mg L−1] according to Stewart, 21 [mg L−1] according to De Francesco et al. and 30 [mg L−1] according to Olaniran et al. [22,23,24]. The values obtained in this work are within or very close to these ranges (20.99–29.95 [mg L−1]), thus we can say it is perceived in the aroma, even though its intensity varies.
Table 3 shows that all models fit the data reasonably, which is demonstrated by the values close to one of all R2-values calculated from Gompertz functions. n-propanol (at 15 °C) is the only function with an R2-value less than 0.95.

Table 3.
Statistical comparison for Gompertz and ANNs functions vs RAW data. The F and p statistics are the result of the analysis of variance.
The analysis of variance, for the same fermentation time and temperature, from the Gompertz equation for each case indicates that there are no significant differences between the experimental and estimated data. The statistical comparison with raw data is given in Table 3. Among F-values, the highest ones are those from 21 °C (its p-values are the lowest). Due to this higher temperature, the experimental data corresponding to the first 24 h of fermentation is close to the value of the asymptote A.
Using a simulated dataset from the twenty Gompertz functions (five fermentation temperatures for four compounds) developed, a data mesh was generated with Matlab ndgrid function (Figure 6), with all possible values of temperature and time between the minimum (14.4 °C) and maximum (20.6 °C) values reported by the temperature sensor, and between a time of 0 to 9 days. With this meshing, the neural network has been trained.
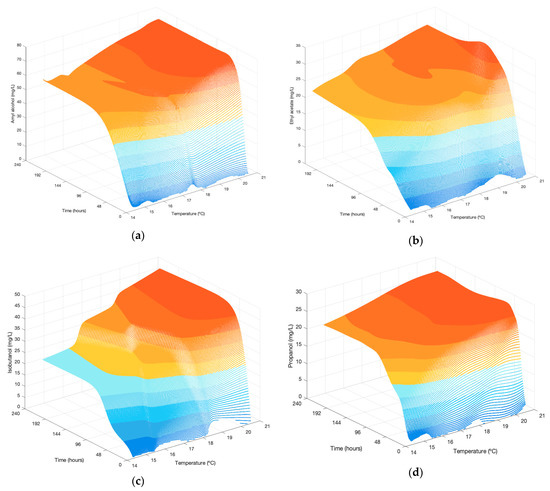
Figure 6.
Scatter graphs of predicted values by ANNs: (a) amyl alcohol; (b) ethyl acetate; (c) isobutanol; (d) n-propanol.
Amyl alcohol, ethyl acetate and n-propanol ANNs were generated with ten neurons in the hidden layer, isobutanol with five neurons. The results have been represented in Figure 6, where isobutanol is the compound on which the temperature exerts the greatest influence, n-propanol and amyl alcohol are the fastest to reach high values with mean kg values of 1.142 and 2.324 [mg L−1 h−1] respectively.
The result of the data obtained from the simulation carried out with the neural network is compared with the raw data, the R2 values are similar to those obtained in the Gompertz functions, most being slightly lower except for ethyl acetate in datasets 4 and 5 and amyl alcohol in dataset 1, which are slightly higher (Table 2).
The p-values are higher in 14 of the 20 ANNs results compared to those of the Gompertz functions. In the case of dataset 5, the values are considerably higher (on average 70.4% higher), which would indicate that in this case, the ANNs model has significantly better quality than the Gompertz one, even though they were developed with data simulated by these functions.
With the data presented, all the ANN models fit well considering that they are small datasets, which is precisely one of the advantages provided by the Bayesian regularization algorithm. In addition, Gonzalez et al [25] comments that an indicator of a good model without overfitting occurs when the validation correlation coefficient is close to the training correlation coefficient and the MSE of the training stage must be lower than the other phases. The first condition cannot be verified because the Bayesian regularization algorithm does not present a validation phase, while the second condition is fulfilled. All these values are shown in Table 4. In the worst case scenario for MSE overall values (0.32 in isobutanol), the RMSE is 0.57 [mg L−1], which considering the ranges of A according to temperature (24.27–47.24 [mg L−1]), represents an error between 2.3 and 1.2%. For ethyl acetate, the error represents for overall values (MSE 0.016) an RMSE of 0.13 [mg L−1], considering the ranges according to temperature (20.99–29.85 [mg L−1]), represents an error between 0.6 and 0.4%, if we compare these values with the results of Riverol (1%) we can verify the benefits of the model [21].

Table 4.
Statistical data for ANNs models.
It can be seen in Figure 6 that the initial values of the ANNs (t = 0) are not zero, as understood in the experimental results. This is a consequence of the use of the Gompertz functions, which due to the mathematical nature of the parameter b (Equation (1)) makes the behaviour of the starting point a relative value, as a percentage of the asymptote A, and does not pass through the point (0,0) [26].
4. Conclusions
To the best of our knowledge, this is the first work to model and predict the concentration of solvents (isobutanol, n-propanol, ethyl acetate and amyl alcohols) produced by the commercial ale yeast S. cerevisiae Safale S04 from the perspective of temperature as the only input value.
This work has shown that Gompertz functions could be a high-precision data source for ANNs. High R2 values (0.939 to 0.9962), the precision of the ANNs and the simple way to implement these models make them a useful tool to improve the quality (flavour and aroma) of beers through temperature control.
Author Contributions
Conceptualization, V.M.A., B.D.I. and E.C.C.H., methodology, software, validation, formal analysis, investigation, V.M.A., resources, visualization, writing—original draft preparation, V.M.A., B.D.I. and E.C.C.H., funding acquisition, data curation V.M.A.; writing—review and editing, V.M.A., B.D.I. and E.C.C.H.; supervision, B.D.I. and E.C.C.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Secretaría de Educación Superior, Ciencia, Tecnología e Innovación de la República de Ecuador: ARSEQ-BEC-005319-2016.
Data Availability Statement
V.M.A. can be contacted for access to data.
Acknowledgments
The main author wishes to thank the Department of Food Science and Technology of the Universidad Politécnica de Madrid (UPM) for their technical support with gas chromatography analysis.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Beer Faults. Available online: https://dev.bjcp.org/education-training/education-resources/beer-faults/ (accessed on 25 August 2021).
- Viejo, C.G.; Fuentes, S.; Torrico, D.D.; Godbole, A.; Dunshea, F.R. Chemical characterization of aromas in beer and their effect on consumers liking. Food Chem. 2019, 293, 479–485. [Google Scholar] [CrossRef]
- Pires, E.J.; Teixeira, J.A.; Branyik, T.; Vicente, A.A. Yeast: The soul of beer’s aroma-a review of flavour-active esters and higher alcohols produced by the brewing yeast. Appl. Microbiol. Biotechnol. 2014, 98, 1937–1949. [Google Scholar] [CrossRef] [Green Version]
- Loviso, C.L.; Libkind, D. Synthesis and regulation of flavor compounds derived from brewing yeast: Esters. Rev. Argent. Microbiol. 2018, 50, 436–446. [Google Scholar] [CrossRef]
- Loviso, C.L.; Libkind, D. Synthesis and regulation of flavor compounds derived from brewing yeast: Fusel alcohols. Rev. Argent. Microbiol. 2019. [Google Scholar] [CrossRef]
- Membré, J.M.; Tholozan, J.L. Modeling growth and off-flavours production of spoiled beer bacteria, Pectinatus frisingensis. J. Appl. Bacteriol. 1994, 77, 456–460. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1365-2672.1994.tb03449.x (accessed on 10 September 2021). [CrossRef]
- Zhang, Y.; Jia, S.; Zhang, W. Predicting acetic acid content in the final beer using neural networks and support vector machine. J. Inst. Brew. 2012, 118, 361–367. [Google Scholar] [CrossRef]
- Trelea, I.C.; Titica, M.; Landaud, S.; Latrille, E.; Corrieu, G.; Cheruy, A. Predictive modelling of brewing fermentation: From knowledge-based to black-box models. Math. Comput. Simul. 2001, 56, 405–424. [Google Scholar] [CrossRef]
- Shi, Y.; Gong, F.; Wang, M.; Liv, J.; Wu, Y.; Men, H. A deep feature mining method of electronic nose sensor data for identifying beer olfactory information. J. Food Eng. 2019, 263, 437–445. [Google Scholar] [CrossRef]
- Siadat, M.; Losson, E.; Ghasemi-Varnamkhasti, M.; Mohtasebi, S.S. Application of Electronic Nose to Beer Recognition Using Supervised Artificial Neural Networks; IEEE: New York, NY, USA, 2014; p. 645. [Google Scholar]
- Sanchez, C.; Lozano, J.; Pedro Santos, J.; Azabal, A.; Ruiz-Valdepenas, S. Discrimination of aromas in beer with electronic nose. In Proceedings of the 2018 12th Spanish Conference on Electron. Devices (Cde), Salamanca, Spain, 14–16 November, 2018; Mateos, J.G.T., Ed.; IEEE: New York, NY, USA, 2018. [Google Scholar]
- Viejo, C.G.; Fuentes, S.; Godbole, A.; Widdicombe, B.; Unnithan, R.R. Development of a low-cost e-nose to assess aroma profiles: An artificial intelligence application to assess beer quality. Sens. Actuator B Chem. 2020, 308, 127688. [Google Scholar] [CrossRef]
- Brewing with E2U™: No More Rehydration Needed. Available online: https://fermentis.com/en/knowledge-center/expert-insights/beer/brewing-easy-2-use/ (accessed on 1 September 2021).
- Loira, I.; Vejarano, R.; Morata, A.; Ricardo-da-Silva, J.M.; Laureano, O.; González, M.C.; Suárez-Lepe, J.A. Effect of Saccharomyces strains on the quality of red wines aged on lees. Food Chem. 2013, 139, 1044–1051. Available online: https://www.sciencedirect.com/science/article/pii/S0308814613000423 (accessed on 10 September 2021). [CrossRef]
- Zwietering, M.H.; Jongenburger, I.; Rombouts, F.M.; Van’t Riet, K.J. Modeling of the Bacterial Growth Curve. Appl. Environ. Microbiol. 1990, 56, 1875–1881. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.; Singh, K.N.; Mandjiny, S.; Holmes, L. Modeling the Growth of Lactococcus lactis NCIM 2114 under Differently Aerated and Agitated Conditions in Broth Medium. Fermentation 2015, 1, 86. [Google Scholar] [CrossRef]
- Benucci, I.; Cecchi, T.; Lombardelli, C.; Maresca, D.; Mauriello, G.; Esti, M. Novel microencapsulated yeast for the primary fermentation of green beer: Kinetic behavior, volatiles and sensory profile. Food Chem. 2021, 340, 127900. [Google Scholar] [CrossRef]
- Canonico, L.; Ciani, E.; Galli, E.; Comitini, F.; Ciani, M. Evolution of Aromatic Profile of Torulaspora delbrueckii Mixed Fermentation at Microbrewery Plant. Fermentation 2020, 6, 7. Available online: https://explore.openaire.eu/search/publication?articleId=dedup_wf_001::158f64d9bee437bd2369d2594d11e338 (accessed on 8 September 2021). [CrossRef] [Green Version]
- Garcia, A.I.; Garcia, L.A.; Diaz, M. Fusel Alcohols Production in Beer Fermentation Processes. Process. Biochem 1994, 29, 303–309. [Google Scholar] [CrossRef]
- Garcia, A.I.; Garcia, L.A.; Diaz, M. Prediction of ester production in industrial beer fermentation. Enzym. Microb. Technol. 1994, 16, 66–71. [Google Scholar] [CrossRef]
- Riverol, C.; Cooney, J. Estimation of the ester formation during beer fermentation using neural networks. J. Food Eng. 2007, 82, 585–588. [Google Scholar] [CrossRef]
- Stewart, G. The Production of Secondary Metabolites with Flavour Potential during Brewing and Distilling Wort Fermentations. Fermentation 2017, 3, 63. Available online: https://search.proquest.com/docview/2124628708 (accessed on 11 September 2021). [CrossRef] [Green Version]
- De Francesco, G.; Marconi, O.; Sileoni, V.; Freeman, G.; Lee, E.G.; Floridi, S.; Perretti, G. Influence of the dealcoholisation by osmotic distillation on the sensory properties of different beer types. J. Food Sci. Technol.-Mysore 2020, 58, 1488–1498. [Google Scholar] [CrossRef] [PubMed]
- Olaniran, A.O.; Hiralal, L.; Mokoena, M.P.; Pillay, B. Flavour-active volatile compounds in beer: Production, regulation and control. J. Inst. Brew. 2017, 123, 13–23. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez Viejo, C.; Torrico, D.D.; Dunshea, F.R.; Fuentes, S. Development of Artificial Neural Network Models to Assess Beer Acceptability Based on Sensory Properties Using a Robotic Pourer: A Comparative Model Approach to Achieve an Artificial Intelligence System. Beverages 2019, 5, 33. Available online: https://explore.openaire.eu/search/publication?articleId=dedup_wf_001::0efb80f70f10e64e85f2ec0ba398dbd7 (accessed on 15 August 2021). [CrossRef] [Green Version]
- Tjorve, K.M.C.; Tjorve, E. The use of Gompertz models in growth analyses, and new Gompertz-model approach: An addition to the Unified-Richards family. PLoS ONE 2017, 12, e0178691. Available online: https://www.ncbi.nlm.nih.gov/pubmed/28582419 (accessed on 1 August 2021). [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).