Comparative Evaluation of Ensemble Machine Learning Models for Methane Production from Anaerobic Digestion
Abstract
:1. Introduction
2. Materials and Methods
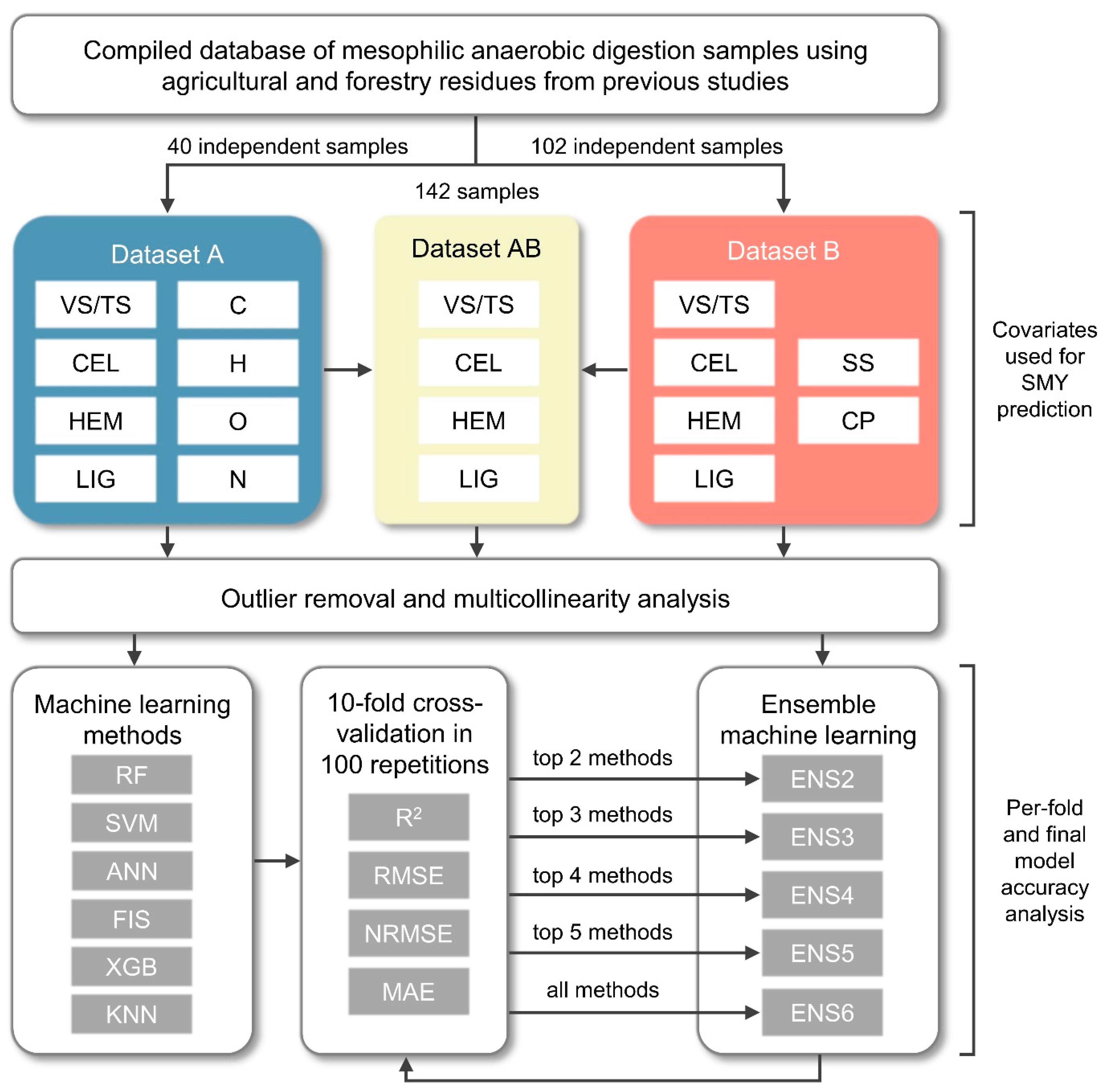
2.1. Input Sample Data Collection and Statistical Preprocessing
2.2. Comparative Evaluation Process of Ensemble Machine Learning Models for Predicting SMY
2.2.1. Ensemble Construction Process and Input Data Preprocessing
2.2.2. Individual Machine Learning Methods Used for Constructing Ensemble Models
2.3. Accuracy Assessment of Predicted SMY Values
3. Results and Discussion
3.1. Correlation Analysis of Three Datasets Used for SMY Prediction
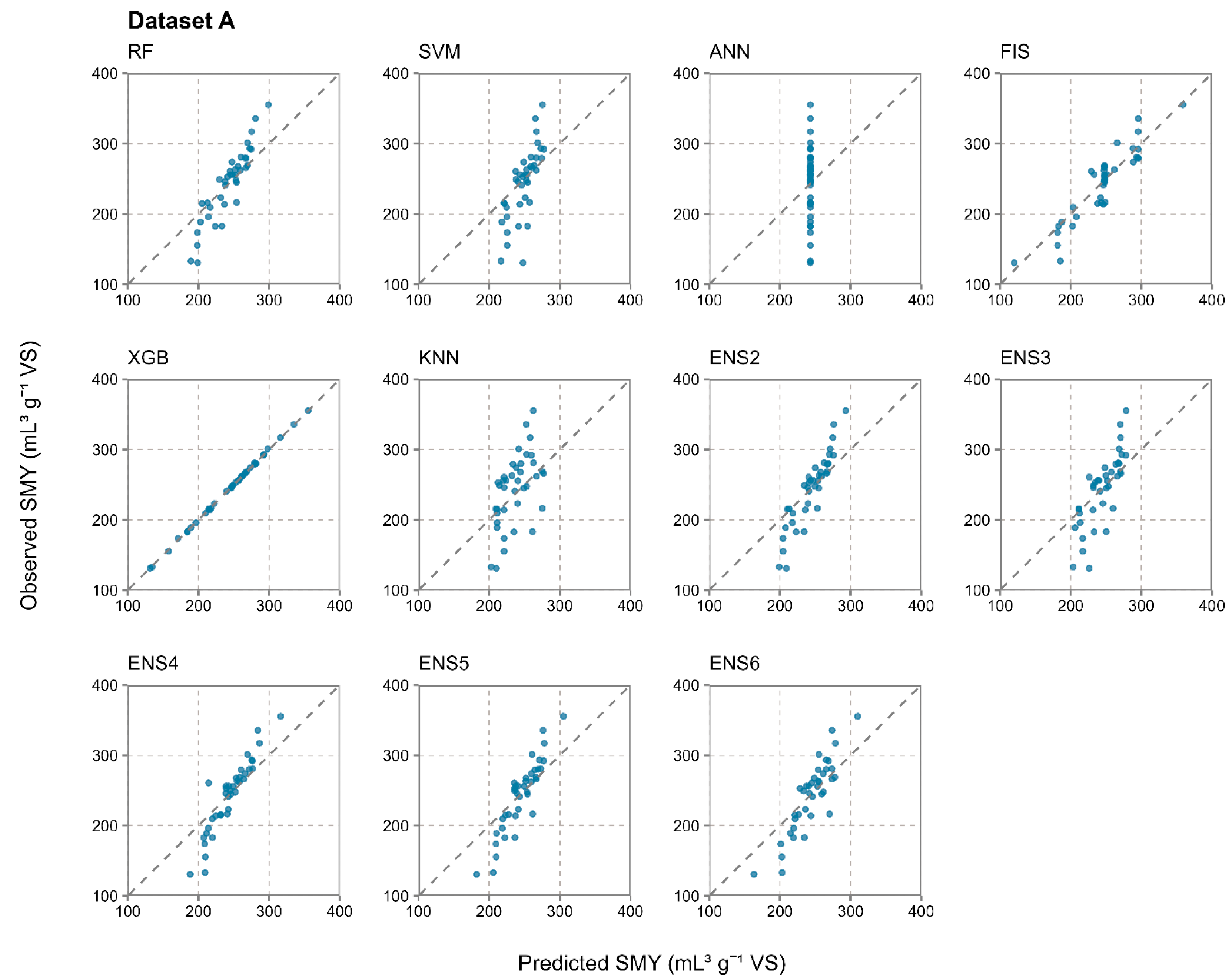
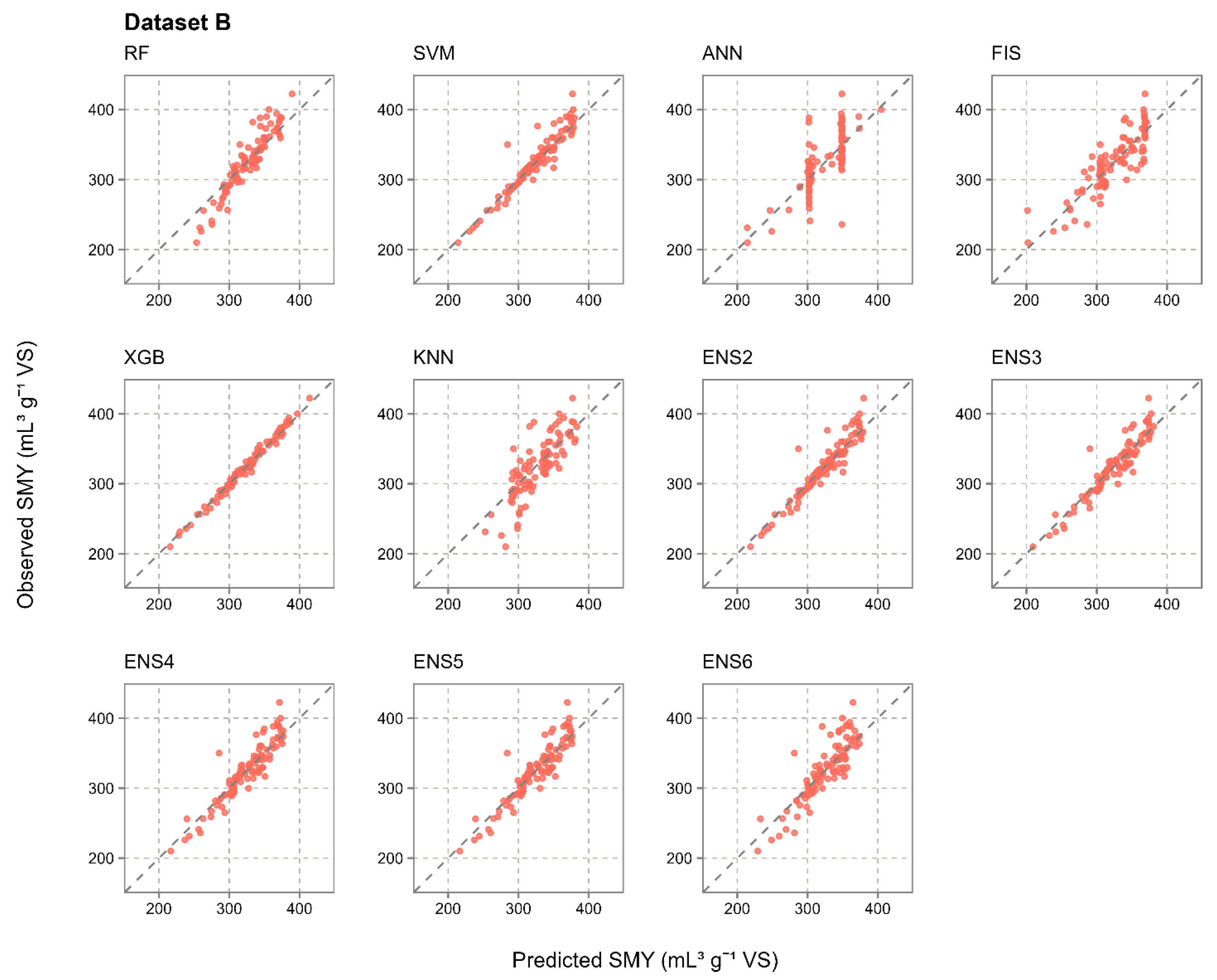
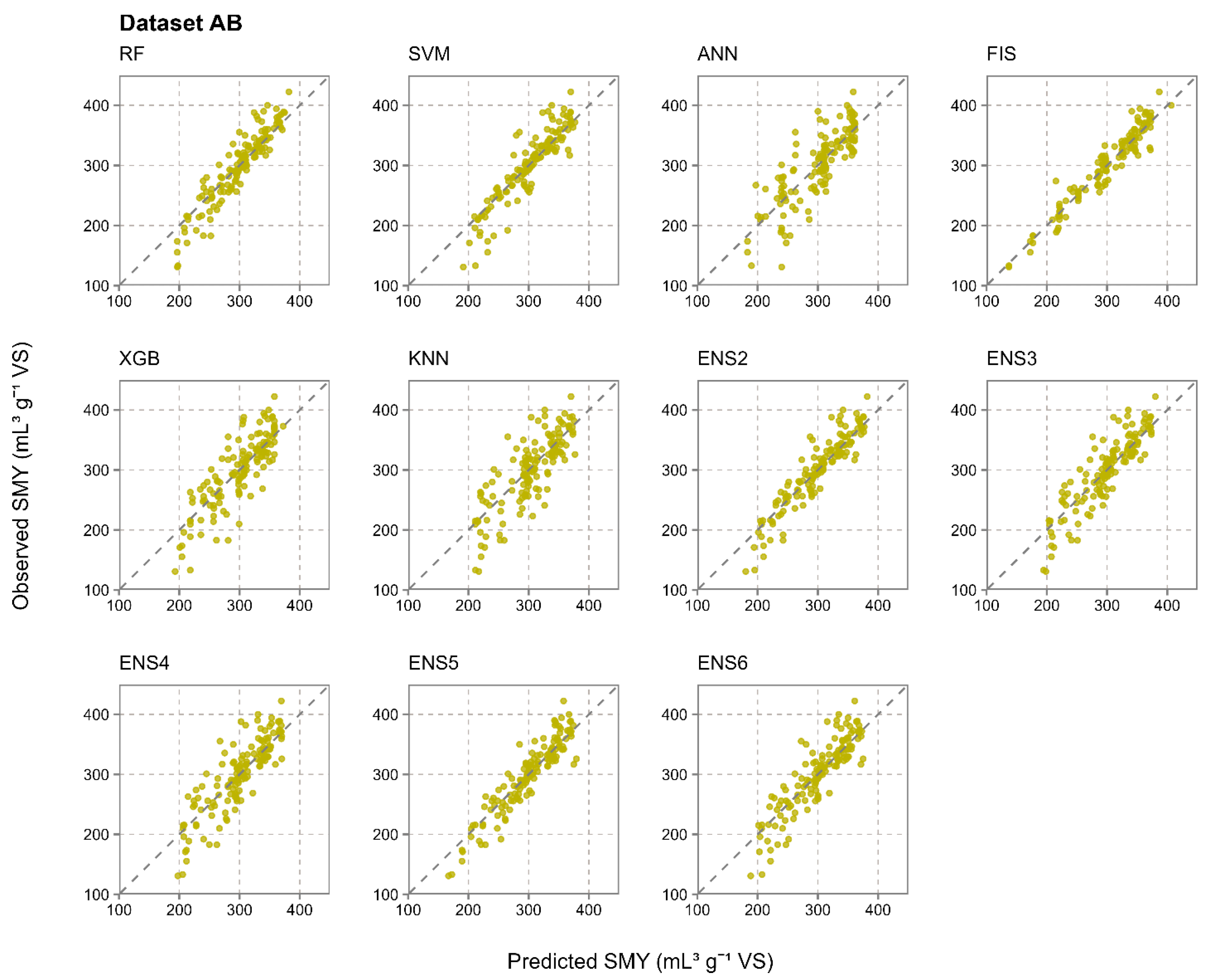
3.2. Prediction Accuracy of Evaluated Individual and Ensemble Machine Learning Models
3.3. Comparison of Ensemble Prediction Approach to Individual Methods and Study Limitations
4. Conclusions
- The ensemble machine learning approach could not consistently outperform the most accurate individual machine learning method in all datasets. The ensemble approach was optimal according to all four statistical metrics, R2, RMSE, NRMSE, and MAE, only for dataset AB, which consisted of the most samples and the least covariates out of the three used datasets.
- The results from a total of 1000 iterations in 10-fold cross-validation in 100 repetitions strongly suggest that ensemble models were much more resistant to the randomness in the training and test data properties during the data split, achieving a much more stable prediction accuracy than the individual methods. The coefficients of variation for RMSE from the most accurate ensemble and individual models were notably lower for the ensemble approach, with 0.393 for RF and 0.031 for ENS4 in dataset A, 0.272 for SVM and 0.026 for ENS5 in dataset B, and 0.217 for SVM and 0.021 for ENS5 in dataset AB. In dataset A, which had 40 samples, RF was the most accurate individual prediction method and achieved R2 values in the range of 0.001–0.999 across 1000 iterations due to the randomness in the data split, for which the ensemble approach was much more resistant.
- Out of the five evaluated ensemble model constructions per dataset, which ranged from two to six used individual machine learning methods, ENS4 was optimal for SMY prediction from dataset A, while ENS5 was optimal for datasets B and AB. The optimal ensemble constructions generally benefited from a higher number of individual methods included, as well as from their diversity in terms of prediction principles, including decision trees, support vector machines, fuzzy inference systems, and instance-based learning. ANN was the only model which was not applied in any optimal ensemble model, struggling with input data complexity and a restricted number of input samples likely due to computational complexity and overfitting.
- A large discrepancy between accuracy assessment metrics from cross-validation and final model fitting was observed for the same models, with the final model fitting results generally indicating higher prediction accuracy and being prone to overfitting. Cross-validation was preferred for determining prediction accuracy and the ranking of machine learning methods in this study since these accuracy metrics represent the ability of machine learning models to accurately predict SMY using new, unseen data. Since the reporting of prediction accuracy based on final model fitting and the single split-sample approach is highly prone to randomness, the adoption of a cross-validation in multiple repetitions is proposed as a standard in future studies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Dataset | Machine Learning Method | Optimal Hyperparameters |
|---|---|---|
| A | RF | mtry = 2, splitrule = “extratrees”, min.node.size = 5 |
| SVM | sigma = 0.102, C = 0.5 | |
| ANN | size = 1, decay = 0 | |
| FIS | num.labels = 5, max.iter = 10 | |
| XGB | nrounds = 50, max_depth = 3, eta = 0.3, gamma = 0, colsample_bytree = 0.6, subsample = 1 | |
| KNN | k = 7 | |
| B | RF | mtry = 3, splitrule = “extratrees”, min.node.size = 5 |
| SVM | sigma = 0.395, C = 2 | |
| ANN | size = 3, decay = 0.1 | |
| FIS | num.labels = 5, max.iter = 10 | |
| XGB | nrounds = 50, max_depth = 3, eta = 0.3, gamma = 0, colsample_bytree = 0.8, subsample = 1 | |
| KNN | k = 5 | |
| AB | RF | mtry = 2, splitrule = “extratrees”, min.node.size = 5 |
| SVM | sigma = 0.637, C = 1 | |
| ANN | size = 3, decay = 0.1 | |
| FIS | num.labels = 13, max.iter = 10 | |
| XGB | nrounds = 50, max_depth = 1, eta = 0.3, gamma = 0, colsample_bytree = 0.8, subsample = 1 | |
| KNN | k = 7 |
References
- Andrade Cruz, I.; Chuenchart, W.; Long, F.; Surendra, K.C.; Renata Santos Andrade, L.; Bilal, M.; Liu, H.; Tavares Figueiredo, R.; Khanal, S.K.; Fernando Romanholo Ferreira, L. Application of Machine Learning in Anaerobic Digestion: Perspectives and Challenges. Bioresour. Technol. 2022, 345, 126433. [Google Scholar] [CrossRef]
- Ling, J.Y.X.; Chan, Y.J.; Chen, J.W.; Chong, D.J.S.; Tan, A.L.L.; Arumugasamy, S.K.; Lau, P.L. Machine Learning Methods for the Modelling and Optimisation of Biogas Production from Anaerobic Digestion: A Review. Environ. Sci. Pollut. Res. 2024, 31, 19085–19104. [Google Scholar] [CrossRef]
- Enitan, A.M.; Adeyemo, J.; Swalaha, F.M.; Kumari, S.; Bux, F. Optimization of Biogas Generation Using Anaerobic Digestion Models and Computational Intelligence Approaches. Rev. Chem. Eng. 2017, 33, 309–335. [Google Scholar] [CrossRef]
- Khan, M.; Chuenchart, W.; Surendra, K.C.; Kumar Khanal, S. Applications of Artificial Intelligence in Anaerobic Co-Digestion: Recent Advances and Prospects. Bioresour. Technol. 2023, 370, 128501. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Zhang, L.; Hou, J.; Zhang, Z.; Liu, H.; You, S.; Sik Ok, Y.; Li, W. Review of Explainable Machine Learning for Anaerobic Digestion. Bioresour. Technol. 2023, 369, 128468. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Peng, X.; Xia, A.; Shah, A.A.; Yan, H.; Huang, Y.; Zhu, X.; Zhu, X.; Liao, Q. Comparison of Machine Learning Methods for Predicting the Methane Production from Anaerobic Digestion of Lignocellulosic Biomass. Energy 2023, 263, 125883. [Google Scholar] [CrossRef]
- Song, C.; Zhang, Z.; Wang, X.; Hu, X.; Chen, C.; Liu, G. Machine Learning-Aided Unveiling the Relationship between Chemical Pretreatment and Methane Production of Lignocellulosic Waste. Waste Manag. 2024, 187, 235–243. [Google Scholar] [CrossRef]
- Cavaiola, M.; Tuju, P.E.; Ferrari, F.; Casciaro, G.; Mazzino, A. Ensemble Machine Learning Greatly Improves ERA5 Skills for Wind Energy Applications. Energy AI 2023, 13, 100269. [Google Scholar] [CrossRef]
- Kesriklioğlu, E.; Oktay, E.; Karaaslan, A. Predicting Total Household Energy Expenditures Using Ensemble Learning Methods. Energy 2023, 276, 127581. [Google Scholar] [CrossRef]
- Khan, P.W.; Byun, Y.C.; Jeong, O.-R. A Stacking Ensemble Classifier-Based Machine Learning Model for Classifying Pollution Sources on Photovoltaic Panels. Sci. Rep. 2023, 13, 10256. [Google Scholar] [CrossRef]
- Brandt, P.; Beyer, F.; Borrmann, P.; Möller, M.; Gerighausen, H. Ensemble Learning-Based Crop Yield Estimation: A Scalable Approach for Supporting Agricultural Statistics. GIScience Remote Sens. 2024, 61, 2367808. [Google Scholar] [CrossRef]
- Mahdizadeh Gharakhanlou, N.; Perez, L. From Data to Harvest: Leveraging Ensemble Machine Learning for Enhanced Crop Yield Predictions across Canada amidst Climate Change. Sci. Total Environ. 2024, 951, 175764. [Google Scholar] [CrossRef]
- Kovačić, Đ.; Radočaj, D.; Jurišić, M. Ensemble Machine Learning Prediction of Anaerobic Co-Digestion of Manure and Thermally Pretreated Harvest Residues. Bioresour. Technol. 2024, 402, 130793. [Google Scholar] [CrossRef]
- Sun, J.; Xu, Y.; Nairat, S.; Zhou, J.; He, Z. Prediction of Biogas Production in Anaerobic Digestion of a Full-Scale Wastewater Treatment Plant Using Ensembled Machine Learning Models. Water Environ. Res. 2023, 95, e10893. [Google Scholar] [CrossRef] [PubMed]
- Mohammed, A.; Kora, R. A Comprehensive Review on Ensemble Deep Learning: Opportunities and Challenges. J. King Saud Univ.-Comput. Inf. Sci. 2023, 35, 757–774. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, F.; Hao, N.; Wang, T.; Cao, N.; Wang, X. The Combined Machine Learning Model SMOTER-GA-RF for Methane Yield Prediction during Anaerobic Digestion of Straw Lignocellulose Based on Random Forest Regression. J. Clean. Prod. 2024, 466, 142909. [Google Scholar] [CrossRef]
- Yildirim, O.; Ozkaya, B. Prediction of Biogas Production of Industrial Scale Anaerobic Digestion Plant by Machine Learning Algorithms. Chemosphere 2023, 335, 138976. [Google Scholar] [CrossRef] [PubMed]
- Ganaie, M.A.; Hu, M.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble Deep Learning: A Review. Eng. Appl. Artif. Intell. 2022, 115, 105151. [Google Scholar] [CrossRef]
- R Foundation for Statistical Computing. R Core Team R: A Language and Environment for Statistical Computing. Vienna, Austria. Available online: https://www.R-project.org/ (accessed on 14 October 2024).
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Benesty, M.; et al. Caret: Classification and Regression Training. Available online: https://CRAN.R-project.org/package=caret (accessed on 30 November 2024).
- Deane-Mayer, Z.A.; Knowles, J.E. Caretensemble: Ensembles of Caret Models. Available online: https://cran.r-project.org/web/packages/caretEnsemble/index.html (accessed on 30 November 2024).
- Wright, M.N.; Wager, S.; Probst, P. Ranger: A Fast Implementation of Random Forests. Available online: https://cran.r-project.org/web/packages/ranger/index.html (accessed on 14 October 2024).
- Karatzoglou, A.; Smola, A.; Hornik, K.; Maniscalco, M.A.; Teo, C.H. Kernlab: Kernel-Based Machine Learning Lab. Available online: https://cran.r-project.org/web/packages/kernlab/index.html (accessed on 14 October 2024).
- Ripley, B.; Venables, W. Nnet: Feed-Forward Neural Networks and Multinomial Log-Linear Models. Available online: https://cran.r-project.org/web/packages/nnet/index.html (accessed on 14 October 2024).
- Riza, L.S.; Bergmeir, C.; Herrera, F.; Benitez, J.M. Frbs: Fuzzy Rule-Based Systems for Classification and Regression Tasks. Available online: https://cran.r-project.org/web/packages/frbs/index.html (accessed on 14 October 2024).
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. Xgboost: Extreme Gradient Boosting. Available online: https://cran.r-project.org/web/packages/xgboost/index.html (accessed on 14 October 2024).
- Genuer, R.; Poggi, J.-M. Random Forests. In Random Forests with R; Genuer, R., Poggi, J.-M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 33–55. ISBN 978-3-030-56485-8. [Google Scholar]
- Sagi, O.; Rokach, L. Approximating XGBoost with an Interpretable Decision Tree. Inf. Sci. 2021, 572, 522–542. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining; Association for Computing Machinery: San Francisco, CA, USA, 13 August, 2016; pp. 785–794. [Google Scholar]
- Pisner, D.A.; Schnyer, D.M. Chapter 6—Support Vector Machine. In Machine Learning; Mechelli, A., Vieira, S., Eds.; Academic Press: Cambridge, MA, USA, 2020; pp. 101–121. ISBN 978-0-12-815739-8. [Google Scholar]
- Ding, X.; Liu, J.; Yang, F.; Cao, J. Random Radial Basis Function Kernel-Based Support Vector Machine. J. Frankl. Inst. 2021, 358, 10121–10140. [Google Scholar] [CrossRef]
- Katal, A.; Singh, N. Artificial Neural Network: Models, Applications, and Challenges. In Innovative Trends in Computational Intelligence; Tomar, R., Hina, M.D., Zitouni, R., Ramdane-Cherif, A., Eds.; EAI/Springer Innovations in Communication and Computing; Springer International Publishing: Cham, Switzerland, 2022; pp. 235–257. ISBN 978-3-030-78284-9. [Google Scholar]
- Jallal, M.A.; González-Vidal, A.; Skarmeta, A.F.; Chabaa, S.; Zeroual, A. A Hybrid Neuro-Fuzzy Inference System-Based Algorithm for Time Series Forecasting Applied to Energy Consumption Prediction. Appl. Energy 2020, 268, 114977. [Google Scholar] [CrossRef]
- Zhang, Z. Introduction to Machine Learning: K-Nearest Neighbors. Ann. Transl. Med. 2016, 4, 218. [Google Scholar] [CrossRef] [PubMed]
- Halder, R.K.; Uddin, M.N.; Uddin, M.A.; Aryal, S.; Khraisat, A. Enhancing K-Nearest Neighbor Algorithm: A Comprehensive Review and Performance Analysis of Modifications. J. Big Data 2024, 11, 113. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-Mean-Square Error (RMSE) or Mean Absolute Error (MAE): When to Use Them or Not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Sonwai, A.; Pholchan, P.; Tippayawong, N. Machine Learning Approach for Determining and Optimizing Influential Factors of Biogas Production from Lignocellulosic Biomass. Bioresour. Technol. 2023, 383, 129235. [Google Scholar] [CrossRef] [PubMed]
- Song, C.; Cai, F.; Yang, S.; Wang, L.; Liu, G.; Chen, C. Machine Learning-Based Prediction of Methane Production from Lignocellulosic Wastes. Bioresour. Technol. 2024, 393, 129953. [Google Scholar] [CrossRef]
- Wang, Y.; Huntington, T.; Scown, C.D. Tree-Based Automated Machine Learning to Predict Biogas Production for Anaerobic Co-Digestion of Organic Waste. ACS Sustain. Chem. Eng. 2021, 9, 12990–13000. [Google Scholar] [CrossRef]
- Jeong, K.; Abbas, A.; Shin, J.; Son, M.; Kim, Y.M.; Cho, K.H. Prediction of Biogas Production in Anaerobic Co-Digestion of Organic Wastes Using Deep Learning Models. Water Res. 2021, 205, 117697. [Google Scholar] [CrossRef]
- Tryhuba, I.; Tryhuba, A.; Hutsol, T.; Cieszewska, A.; Andrushkiv, O.; Glowacki, S.; Bryś, A.; Slobodian, S.; Tulej, W.; Sojak, M. Prediction of Biogas Production Volumes from Household Organic Waste Based on Machine Learning. Energies 2024, 17, 1786. [Google Scholar] [CrossRef]
- Chowdhury, M.S. Comparison of Accuracy and Reliability of Random Forest, Support Vector Machine, Artificial Neural Network and Maximum Likelihood Method in Land Use/Cover Classification of Urban Setting. Environ. Chall. 2024, 14, 100800. [Google Scholar] [CrossRef]
- You, H.; Ma, Z.; Tang, Y.; Wang, Y.; Yan, J.; Ni, M.; Cen, K.; Huang, Q. Comparison of ANN (MLP), ANFIS, SVM, and RF Models for the Online Classification of Heating Value of Burning Municipal Solid Waste in Circulating Fluidized Bed Incinerators. Waste Manag. 2017, 68, 186–197. [Google Scholar] [CrossRef] [PubMed]
- Bates, S.; Hastie, T.; Tibshirani, R. Cross-Validation: What Does It Estimate and How Well Does It Do It? J. Am. Stat. Assoc. 2024, 119, 1434–1445. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Overfitting, Model Tuning, and Evaluation of Prediction Performance. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Montesinos López, O.A., Montesinos López, A., Crossa, J., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 109–139. ISBN 978-3-030-89010-0. [Google Scholar]
- Ma, Z.; Wang, R.; Song, G.; Zhang, K.; Zhao, Z.; Wang, J. Interpretable Ensemble Prediction for Anaerobic Digestion Performance of Hydrothermal Carbonization Wastewater. Sci. Total Environ. 2024, 908, 168279. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhao, Y.; Feng, Y.; Yu, Y.; Li, Y.; Li, J.; Ren, Z.; Chen, S.; Feng, L.; Pan, J.; et al. Novel Intelligent System Based on Automated Machine Learning for Multiobjective Prediction and Early Warning Guidance of Biogas Performance in Industrial-Scale Garage Dry Fermentation. ACS EST Eng. 2024, 4, 139–152. [Google Scholar] [CrossRef]


| Machine Learning Type | Machine Learning Algorithm | Abbreviation | Tuning Hyperparameters | R Library | Reference |
|---|---|---|---|---|---|
| Decision trees | Random forest | RF | mtry, splitrule, min.node.size | ranger | [22] |
| Support vector machines | Support vector regression with radial basis function kernel | SVM | sigma, C | kernlab | [23] |
| Neural networks | Artificial neural network | ANN | size, decay | nnet | [24] |
| Fuzzy inference system | Hybrid fuzzy inference system | FIS | num.labels, max.iter | frbs | [25] |
| Decision trees | Extreme gradient boosting | XGB | nrounds, max_depth, eta, gamma, colsample_bytree, min_child_weight, subsample | xgboost | [26] |
| Instance-based learning | K-nearest neighbors | KNN | k | base R | [19] |
| Dataset | Prediction Method | Cross-Validation | Final Model Fit | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | NRMSE | MAE | R2 | RMSE | NRMSE | MAE | ||
| Dataset A | RF | 0.458 | 44.44 | 0.183 | 36.70 | 0.855 | 27.59 | 0.113 | 21.12 |
| SVM | 0.405 | 46.32 | 0.190 | 38.50 | 0.567 | 39.34 | 0.162 | 27.89 | |
| ANN | 0.358 | 52.28 | 0.215 | 42.93 | N/A | 50.04 | 0.206 | 39.43 | |
| FIS | 0.451 | 48.50 | 0.199 | 39.61 | 0.849 | 19.72 | 0.081 | 15.29 | |
| XGB | 0.421 | 52.83 | 0.217 | 42.49 | 1.000 | 1.17 | 0.005 | 0.93 | |
| KNN | 0.379 | 46.41 | 0.191 | 39.74 | 0.311 | 42.57 | 0.175 | 34.36 | |
| ENS2 | 0.100 | 47.52 | 0.195 | 36.32 | 0.845 | 29.76 | 0.122 | 22.04 | |
| ENS3 | 0.117 | 47.06 | 0.194 | 36.48 | 0.628 | 35.24 | 0.145 | 25.83 | |
| ENS4 | 0.173 | 45.55 | 0.187 | 33.99 | 0.869 | 26.97 | 0.111 | 20.57 | |
| ENS5 | 0.143 | 46.37 | 0.191 | 35.47 | 0.838 | 29.33 | 0.121 | 22.89 | |
| ENS6 | 0.157 | 45.99 | 0.189 | 35.35 | 0.780 | 29.09 | 0.120 | 23.65 | |
| Dataset B | RF | 0.508 | 30.99 | 0.095 | 23.04 | 0.883 | 17.35 | 0.071 | 12.62 |
| SVM | 0.549 | 28.71 | 0.088 | 21.89 | 0.903 | 13.46 | 0.055 | 8.63 | |
| ANN | 0.392 | 37.07 | 0.114 | 28.37 | 0.580 | 27.22 | 0.112 | 19.38 | |
| FIS | 0.504 | 31.20 | 0.096 | 24.02 | 0.730 | 21.81 | 0.090 | 16.93 | |
| XGB | 0.405 | 34.51 | 0.106 | 26.97 | 0.988 | 4.84 | 0.020 | 3.77 | |
| KNN | 0.476 | 31.60 | 0.097 | 24.41 | 0.659 | 25.04 | 0.103 | 18.88 | |
| ENS2 | 0.492 | 29.87 | 0.092 | 21.98 | 0.900 | 13.77 | 0.057 | 9.33 | |
| ENS3 | 0.519 | 29.05 | 0.089 | 21.24 | 0.885 | 14.47 | 0.060 | 10.29 | |
| ENS4 | 0.519 | 29.06 | 0.089 | 21.50 | 0.864 | 15.88 | 0.065 | 11.56 | |
| ENS5 | 0.527 | 28.80 | 0.088 | 21.12 | 0.855 | 16.26 | 0.067 | 11.86 | |
| ENS6 | 0.516 | 29.15 | 0.089 | 21.35 | 0.754 | 21.33 | 0.088 | 15.39 | |
| Dataset AB | RF | 0.585 | 39.29 | 0.131 | 29.34 | 0.870 | 23.69 | 0.097 | 17.45 |
| SVM | 0.602 | 38.71 | 0.129 | 29.05 | 0.837 | 25.41 | 0.104 | 17.19 | |
| ANN | 0.501 | 43.88 | 0.146 | 34.18 | 0.678 | 33.73 | 0.139 | 25.62 | |
| FIS | 0.552 | 42.33 | 0.141 | 32.97 | 0.925 | 16.33 | 0.067 | 12.04 | |
| XGB | 0.524 | 41.92 | 0.140 | 31.74 | 0.708 | 32.49 | 0.134 | 24.03 | |
| KNN | 0.567 | 40.08 | 0.133 | 30.65 | 0.655 | 35.14 | 0.145 | 26.83 | |
| ENS2 | 0.565 | 39.17 | 0.130 | 28.69 | 0.862 | 22.81 | 0.094 | 16.40 | |
| ENS3 | 0.560 | 39.40 | 0.131 | 28.98 | 0.787 | 27.89 | 0.115 | 20.83 | |
| ENS4 | 0.568 | 39.05 | 0.130 | 28.92 | 0.730 | 31.17 | 0.128 | 23.23 | |
| ENS5 | 0.610 | 37.08 | 0.123 | 27.33 | 0.868 | 22.41 | 0.092 | 16.98 | |
| ENS6 | 0.591 | 37.97 | 0.126 | 28.17 | 0.784 | 28.04 | 0.115 | 20.46 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radočaj, D.; Jurišić, M. Comparative Evaluation of Ensemble Machine Learning Models for Methane Production from Anaerobic Digestion. Fermentation 2025, 11, 130. https://doi.org/10.3390/fermentation11030130
Radočaj D, Jurišić M. Comparative Evaluation of Ensemble Machine Learning Models for Methane Production from Anaerobic Digestion. Fermentation. 2025; 11(3):130. https://doi.org/10.3390/fermentation11030130
Chicago/Turabian StyleRadočaj, Dorijan, and Mladen Jurišić. 2025. "Comparative Evaluation of Ensemble Machine Learning Models for Methane Production from Anaerobic Digestion" Fermentation 11, no. 3: 130. https://doi.org/10.3390/fermentation11030130
APA StyleRadočaj, D., & Jurišić, M. (2025). Comparative Evaluation of Ensemble Machine Learning Models for Methane Production from Anaerobic Digestion. Fermentation, 11(3), 130. https://doi.org/10.3390/fermentation11030130









