Ab Initio Study of Optical Properties of Hybrid Films Based on Bilayer Graphene and Single-Walled Carbon Nanotubes
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
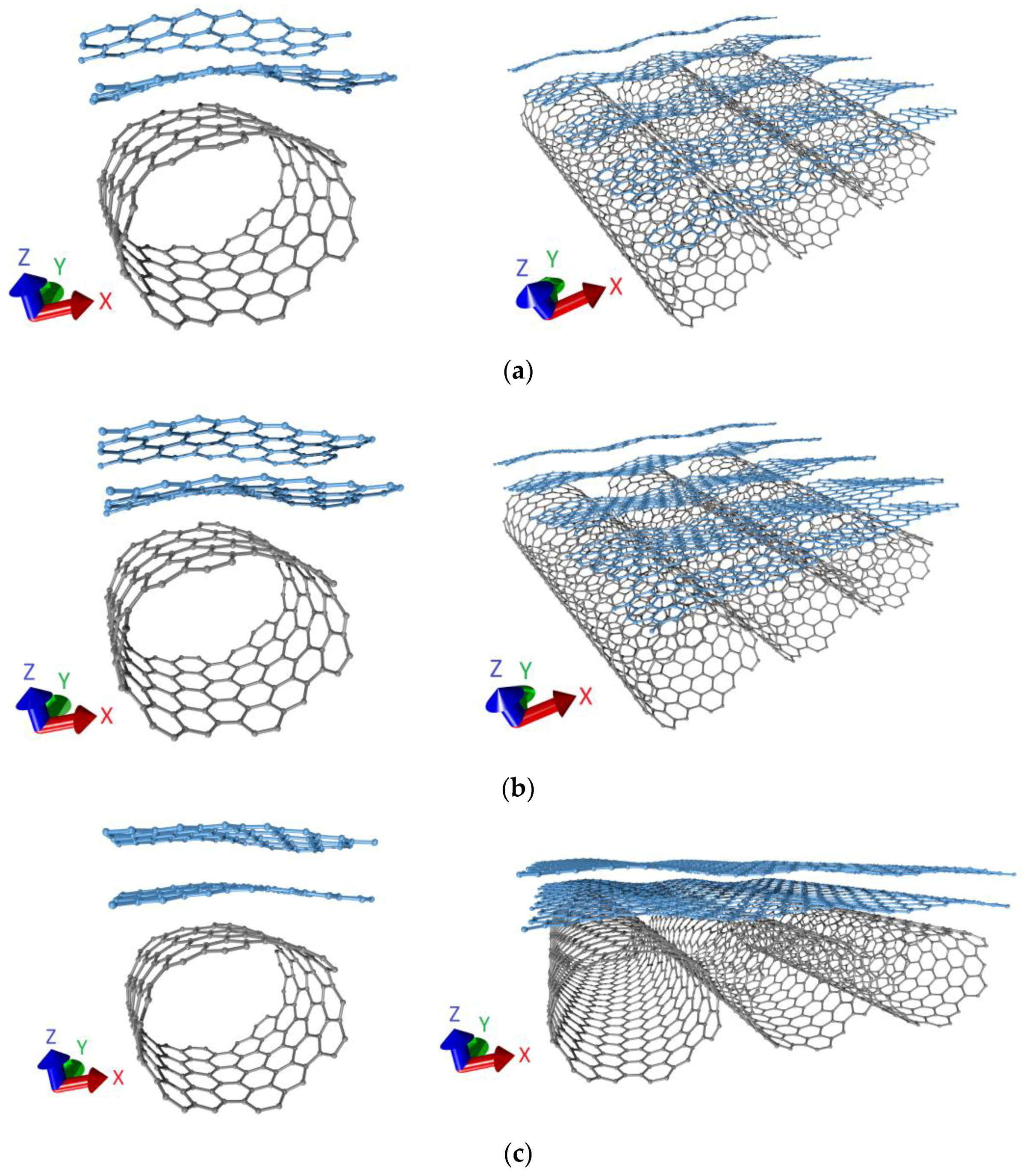
3.1. Atomic Structure of Supercells of Graphene-SWCNT (12,6) Hybrid
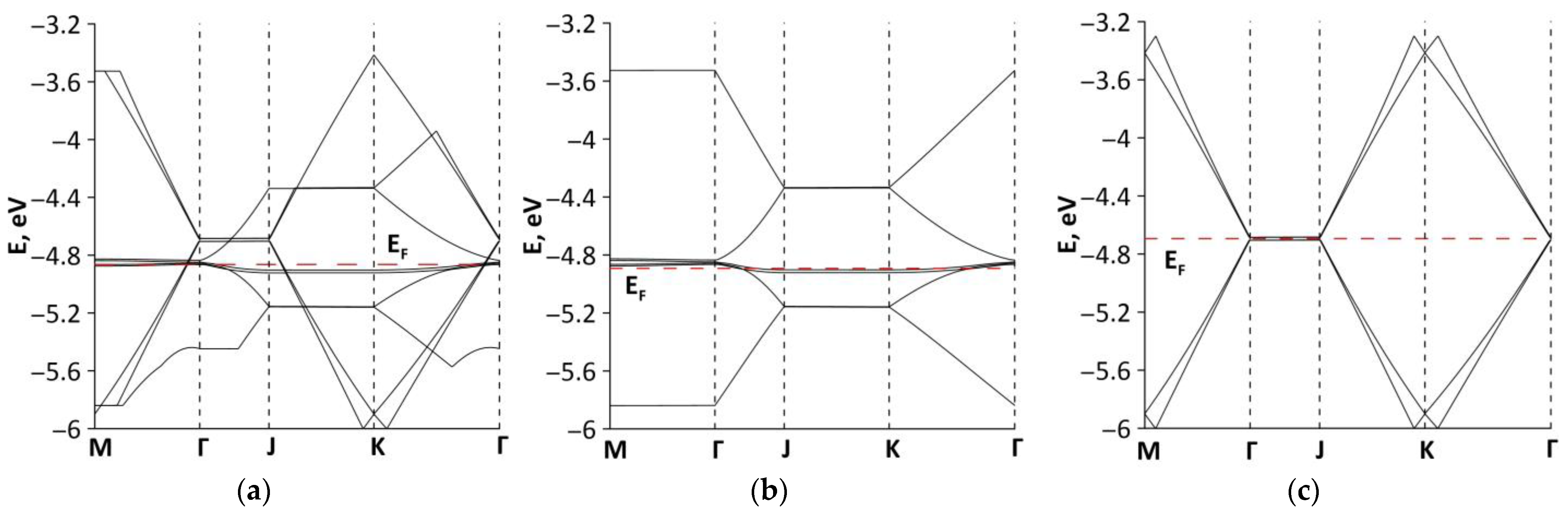
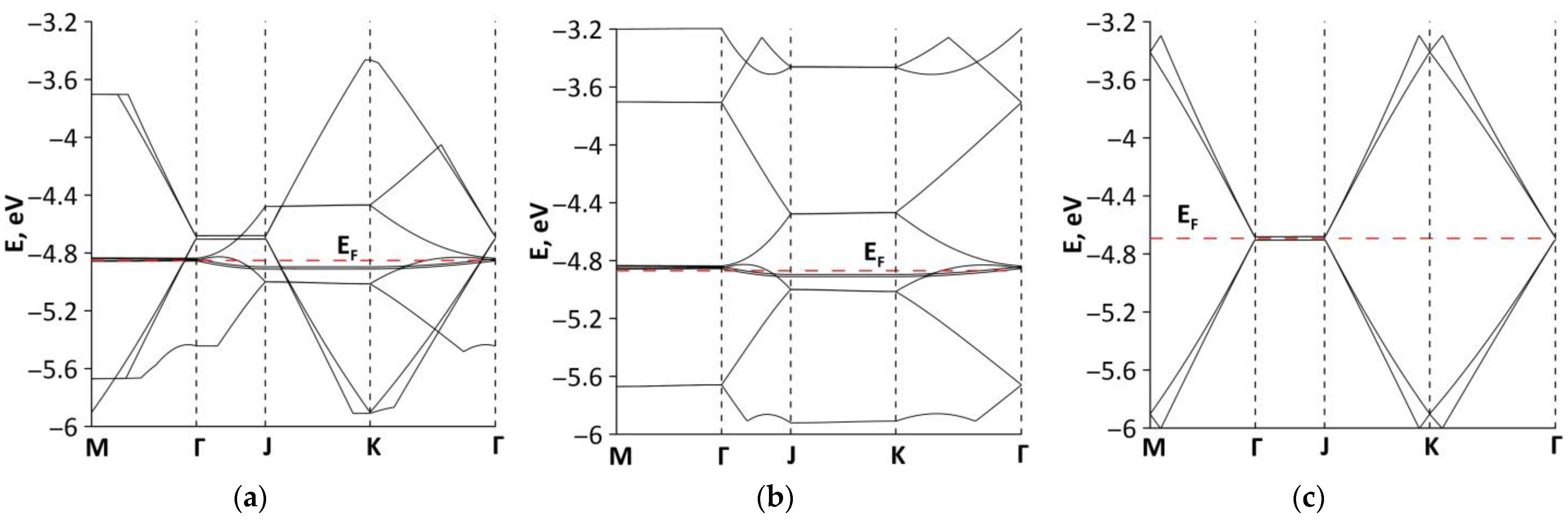
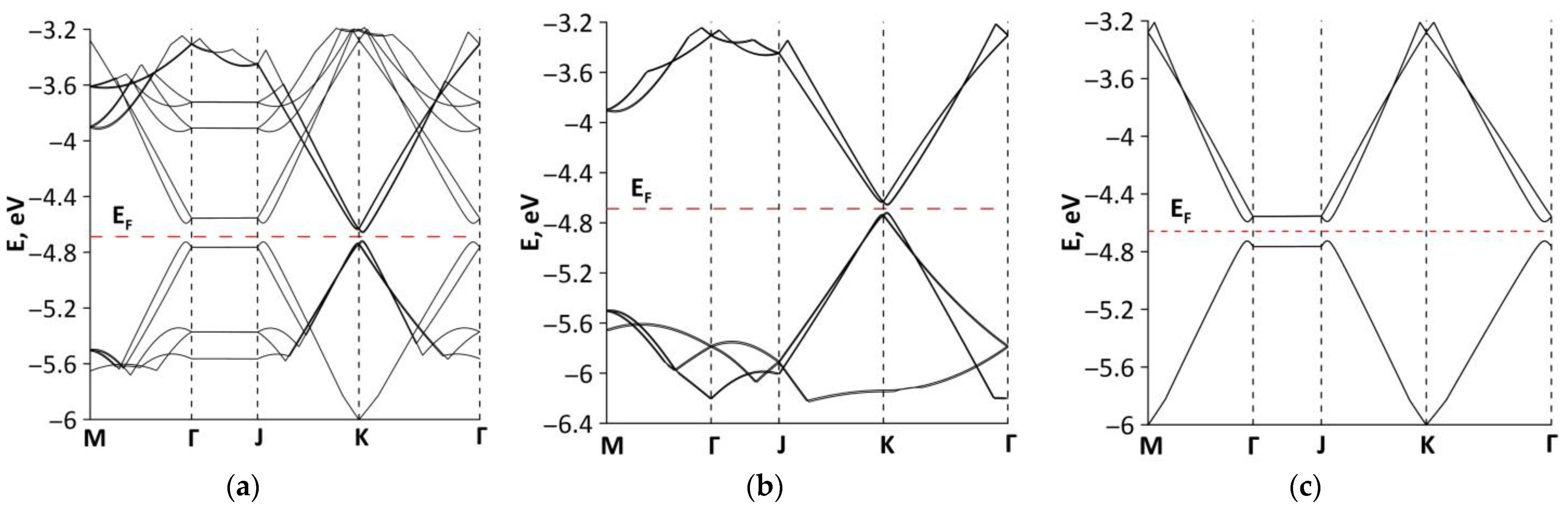
3.2. Electronic Structure of Graphene-SWCNT (12,6) Hybrid Films
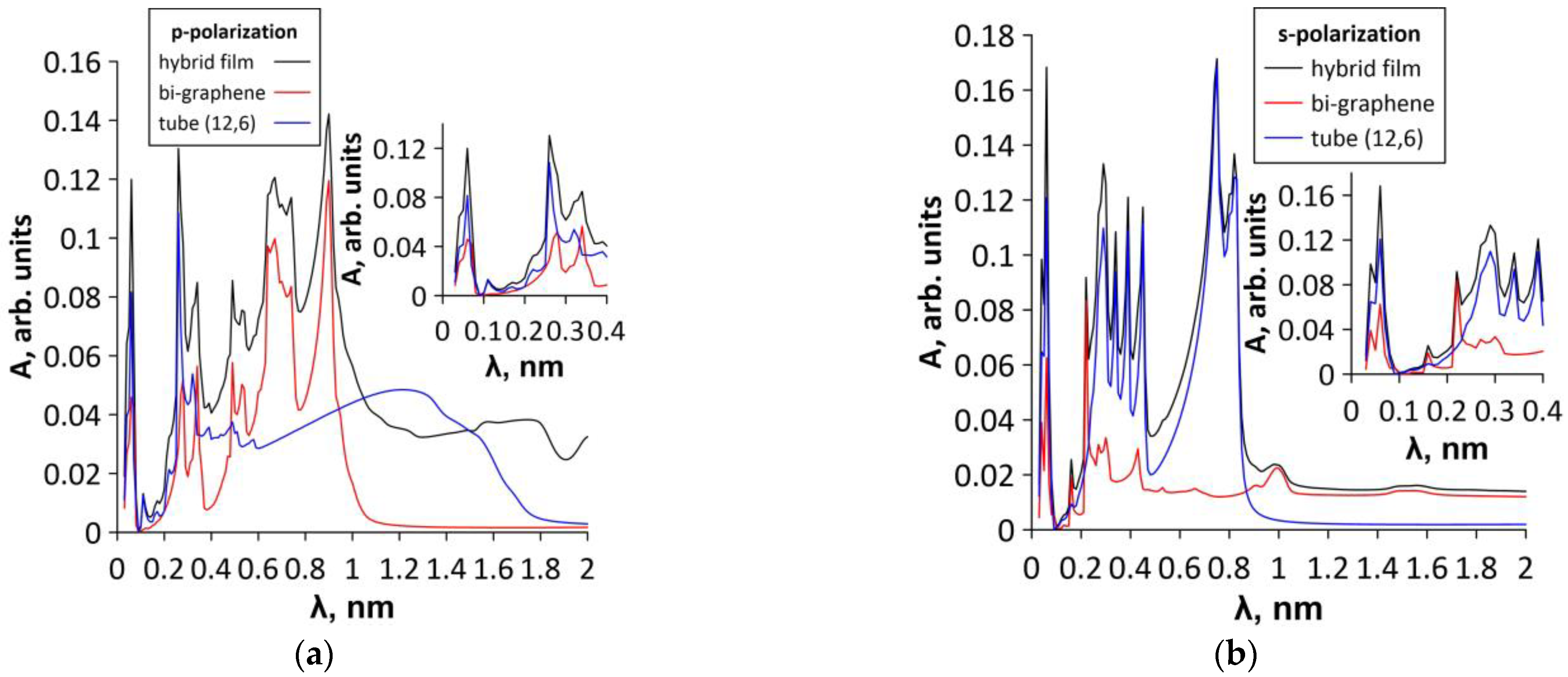
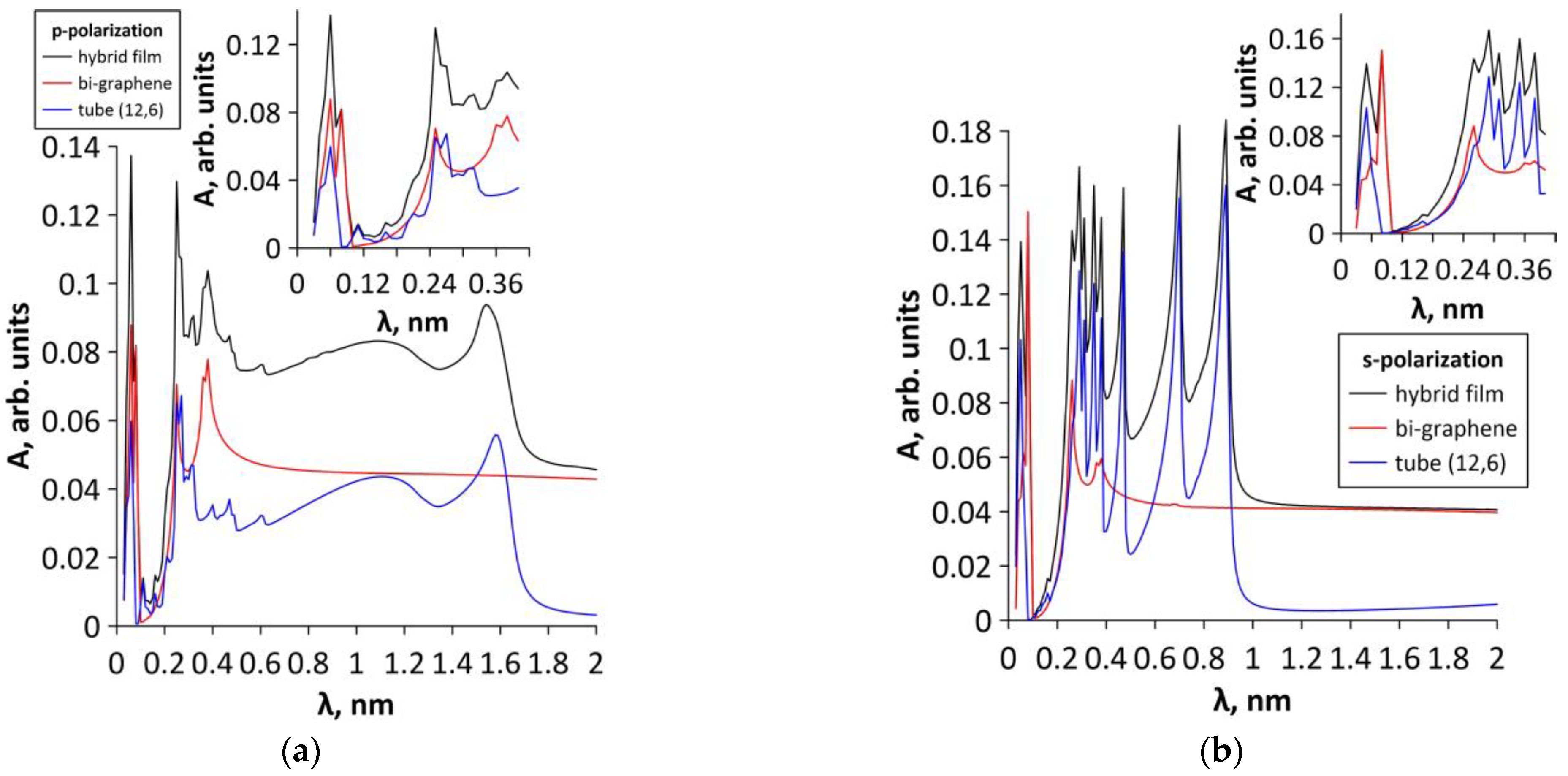
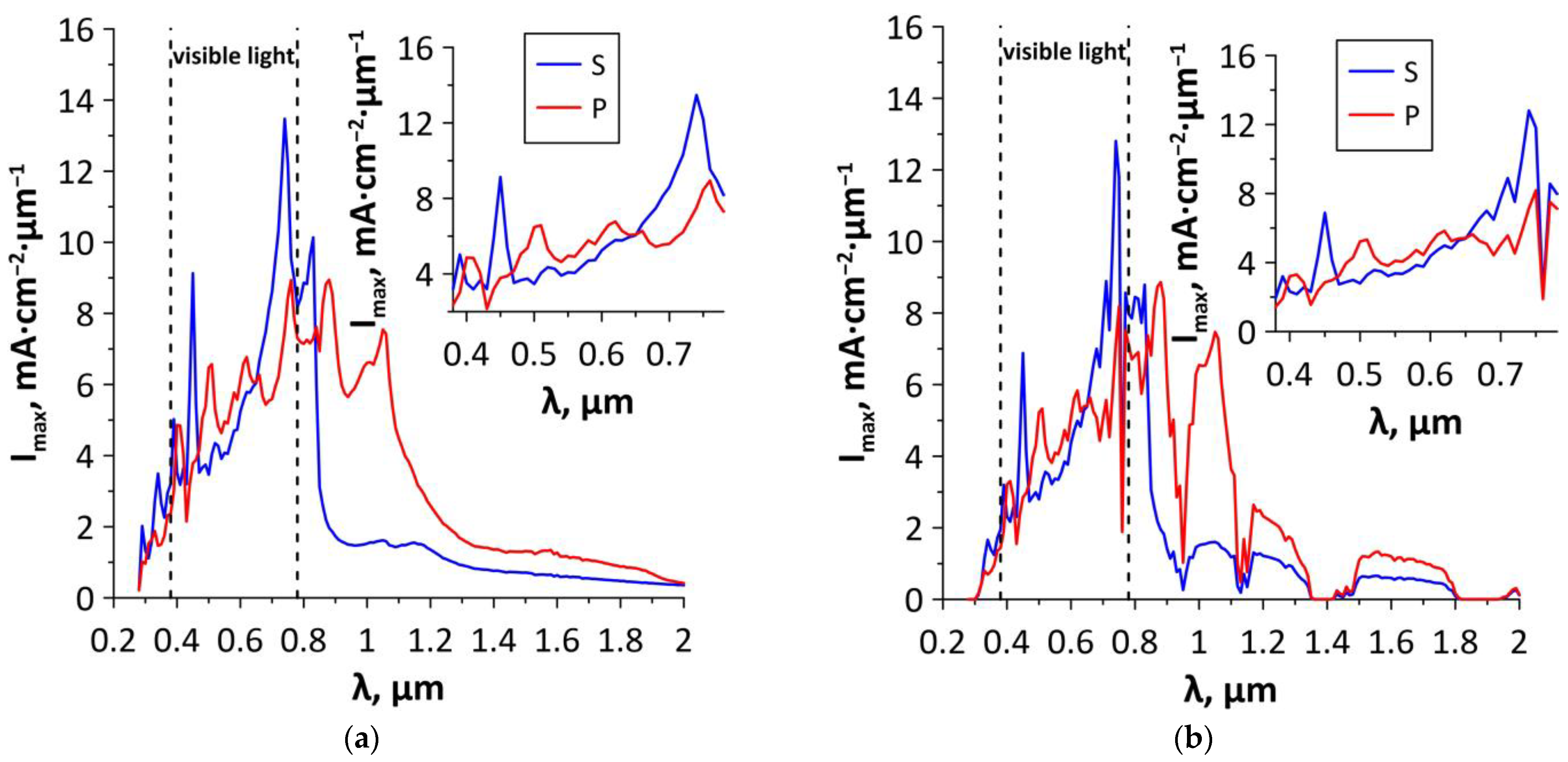
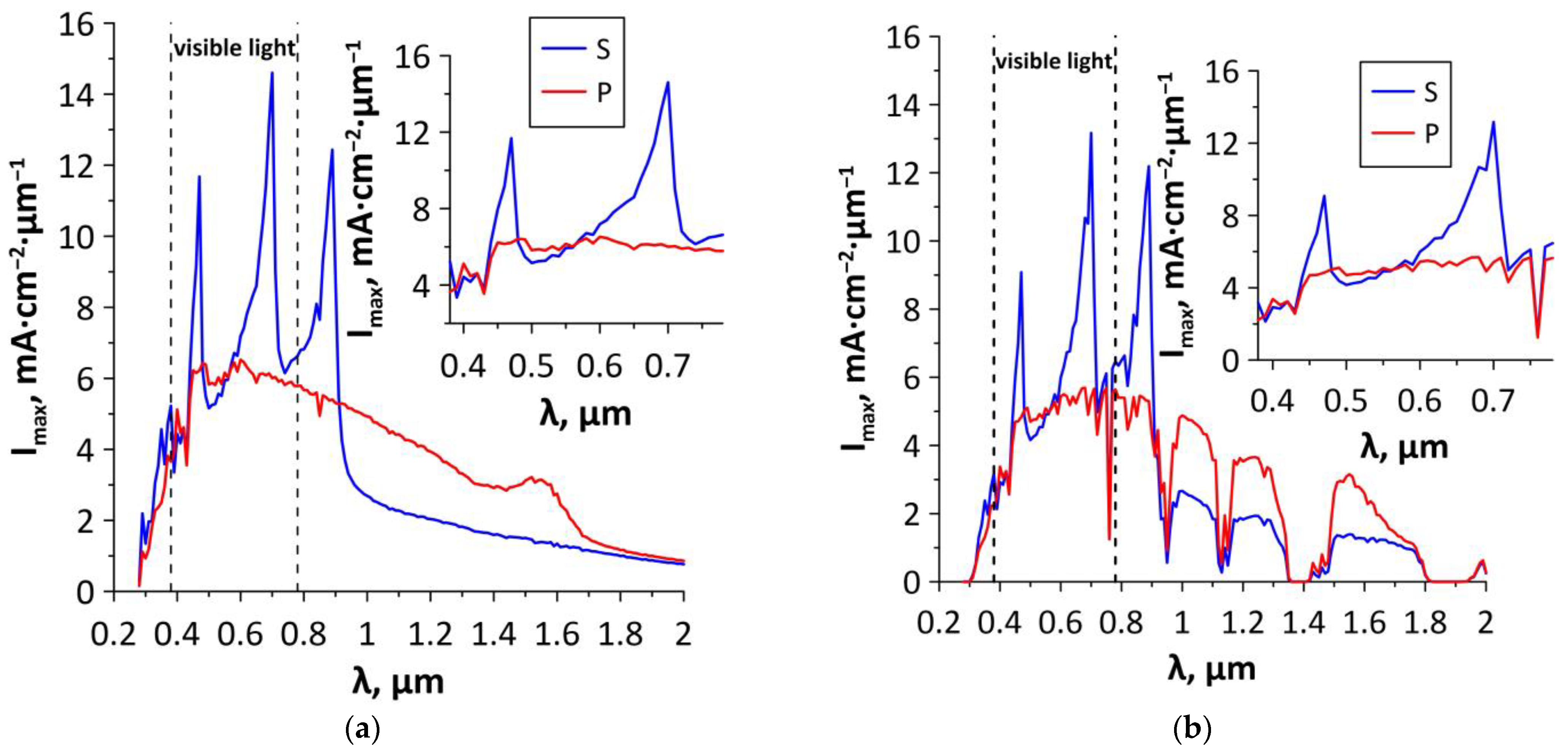
3.3. Optical and Optoelectronic Properties of Graphene-SWCNT (12,6) Hybrid Films
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, F.; Yang, K.; Liu, G.; Chen, Y.; Wang, M.; Li, S.; Li, R. Recent advances on graphene: Synthesis, properties and applications. Compos. Part A Appl. Sci. Manuf. 2022, 160, 107051. [Google Scholar] [CrossRef]
- Rathinavel, S.; Priyadharshini, K.; Panda, D. A review on carbon nanotube: An overview of synthesis, properties, functionalization, characterization, and the application. Mater. Sci. Eng. B. 2021, 268, 115095. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, H.; Zhang, H.; Maruyama, S.; Lin, L. The Roadmap of Graphene: From Fundamental Research to Broad Applications. Adv. Funct. Mater. 2022, 32, 2208378. [Google Scholar] [CrossRef]
- Venkataraman, A.; Amadi, E.V.; Chen, Y.; Papadopoulos, C. Carbon Nanotube Assembly and Integration for Applications. Nanoscale Res. Lett. 2019, 14, 220. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.D.; Kysar, J.W.; Hone, J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef] [PubMed]
- Stankovich, S.; Dikin, D.A.; Piner, R.D.; Kohlhaas, K.A.; Kleinhammes, A.; Jia, Y.; Wu, Y.; Nguyen, S.T.; Ruoff, R.S. Synthesis of Graphene-Based Nanosheets via Chemical Reduction of Exfoliated Graphite Oxide. Carbon 2007, 45, 1558–1565. [Google Scholar] [CrossRef]
- Wilhite, P.; Vyas, A.A.; Tan, J.; Tan, J.; Yamada, T.; Wang, P.; Park, J.; Yang, C.Y. Metal–nanocarbon contacts. Semicond. Sci. Technol. 2014, 29, 054006. [Google Scholar] [CrossRef]
- Du, W.; Ahmed, Z.; Wang, Q.; Yu, C.; Feng, Z.; Li, G.; Zhang, M.; Zhou, C.; Senegor, R.; Yang, C.Y. Structures, properties, and applications of CNT-graphene heterostructures. 2D Mater. 2019, 6, 042005. [Google Scholar] [CrossRef]
- Fan, W.; Longsheng, Z.; Tianxi, L. Graphene-Carbon Nanotube Hybrids for Energy and Environmental Applications, 1st ed.; Springer: Singapore, 2017; pp. 21–51. [Google Scholar]
- Lv, R.; Cruz-Silva, E.; Terrones, M. Building Complex Hybrid Carbon Architectures by Covalent Interconnections: Graphene-Nanotube Hybrids and More. ACS Nano 2014, 8, 4061–4069. [Google Scholar] [CrossRef]
- Li, Y.G.; Zhou, W.; Wang, H.L.; Xie, L.M.; Liang, Y.Y.; Wei, F.; Idrobo, J.C.; Pennycook, S.J.; Dai, H.J. An Oxygen Reduction Electrocatalyst Based on Carbon Nanotube-Graphene Complexes. Nat. Nanotechnol. 2012, 7, 394–400. [Google Scholar] [CrossRef]
- Kim, S.H.; Song, W.; Jung, M.W.; Kang, M.A.; Kim, K.; Chang, S.J.; Lee, S.S.; Lim, J.; Hwang, J.; Myung, S.; et al. Carbon nanotube and graphene hybrid thin film for transparent electrodes and field effect transistors. Adv. Mater. 2014, 26, 4247–4252. [Google Scholar] [CrossRef]
- Shi, E.; Li, H.; Yang, L.; Hou, J.; Li, Y.; Li, L.; Cao, A.; Fang, Y. Carbon nanotube network embroidered graphene films for monolithic all-carbon electronics. Adv. Mater. 2015, 27, 682–688. [Google Scholar] [CrossRef] [PubMed]
- Kholmanov, I.N.; Magnuson, C.W.; Piner, R.; Kim, J.Y.; Aliev, A.E.; Tan, C.; Kim, T.Y.; Zakhidov, A.A.; Sberveglieri, G.; Baughman, R.H.; et al. Optical, electrical, and electromechanical properties of hybrid graphene/carbon nanotube films. Adv. Mater. 2015, 27, 3053–3059. [Google Scholar] [CrossRef]
- Etesami, M.; Nguyen, M.T.; Yonezawa, T.; Tuantranont, A.; Somwangthanaroj, A.; Kheawhom, S. 3D carbon nanotubes-graphene hybrids for energy conversion and storage applications. Chem. Eng. J. 2022, 446, 137190. [Google Scholar] [CrossRef]
- Zang, X.; Jiang, Y.; Sanghadasa, M.; Lin, L. Chemical vapor deposition of 3D graphene/carbon nanotubes networks for hybrid supercapacitors. Sens. Actuator A Phys. 2020, 304, 111886. [Google Scholar] [CrossRef]
- Yuan, G.-J.; Xie, J.-F.; Li, H.-H.; Shan, B.; Zhang, X.-X.; Liu, J.; Li, L.; Tian, Y.-Z. Thermally Reduced Graphene Oxide/Carbon Nanotube Composite Films for Thermal Packaging Applications. Materials 2020, 13, 317. [Google Scholar] [CrossRef] [PubMed]
- Advincula, P.A.; Beckham, J.L.; Choi, C.H.; Chen, W.; Han, Y.; Kosynkin, D.V.; Lathem, A.; Mayoral, A.; Yacaman, M.J.; Tour, J.M. Tunable Hybridized Morphologies Obtained through Flash Joule Heating of Carbon Nanotubes. ACS Nano 2023, 17, 2506–2516. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.Y.; Ai, Q.Q.; Mao, L.N.; Guo, J.X.; Gong, T.X.; Lin, Y.; Wu, G.T.; Huang, W.; Zhang, X.S. Hybrid strategy of graphene/carbon nanotube hierarchical networks for highly sensitive, flexible wearable strain sensors. Sci. Rep. 2021, 11, 21006. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Sun, J.; You, Q.; Li, K.; Zhu, M.; Deng, T. A Micro Broadband Photodetector Based on Single Wall Carbon Nanotubes-Graphene Heterojunction. J. Light. Technol. 2022, 40, 149–155. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; You, Q.; Sun, J.; Li, K.; Hong, H.; Kong, L.; Zhu, M.; Deng, T.; Liu, Z. A broadband 3D microtubular photodetector based on a single wall carbon nanotube–graphene heterojunction. Nanoscale 2023, 15, 1402–1411. [Google Scholar] [CrossRef]
- Alamri, M.; Liu, B.; Berrie, C.L.; Walsh, M.; Wu, J.Z. Probing the role of CNTs in Pt nanoparticle/CNT/graphene nanohybrids H2 sensors. Nano Express 2022, 3, 035004. [Google Scholar] [CrossRef]
- Zhao, W.; Ghaznavi, A.; Gao, Y.; Wu, M.; Xu, J. Synthesis of a Functionalized Carbon Nanotube Graphene Composite Enabling pH-Responsive Electrochemical Sensing for Biomedical Applications. ACS Appl. Electron. Mater. 2023, 5, 1224–1233. [Google Scholar] [CrossRef]
- Ho, Y.H.; Chiu, Y.H.; Lu, J.M.; Lin, M.F. Low-energy electronic structures of nanotube–Graphene hybrid carbon systems. Phys. E 2010, 42, 744–747. [Google Scholar] [CrossRef]
- Cook, B.G.; French, W.R.; Varga, K. Electron transport properties of CNT–graphene contacts. Appl. Phys. Lett. 2012, 101, 153501. [Google Scholar] [CrossRef]
- Akhukov, M.A.; Yuan, S.; Fasolino, A.; Katsnelson, M.I. Electronic, magnetic and transport properties of graphene ribbons terminated by nanotubes. New J. Phys. 2012, 14, 123012. [Google Scholar] [CrossRef]
- Ivanovskaya, V.V.; Zobelli, A.; Wagner, P.; Heggie, M.I.; Briddon, P.R.; Rayson, M.J.; Ewels, C.P. Low-Energy Termination of Graphene Edges via the Formation of Narrow Nanotube. Phys. Rev. Lett. 2011, 107, 065502. [Google Scholar] [CrossRef]
- Artyukh, A.A.; Chernozatonskii, L.A.; Sorokin, P.B. Mechanical and electronic properties of carbon nanotube–graphene compounds. Phys. Status Solidi B 2010, 247, 2927. [Google Scholar] [CrossRef]
- Slepchenkov, M.M.; Glukhova, O.E. Mechanical and Electroconductive Properties of Mono- and Bilayer Graphene–Carbon Nanotube Films. Coatings 2019, 9, 74. [Google Scholar] [CrossRef]
- Slepchenkov, M.M.; Mitrofanov, V.V.; Nefedov, I.S.; Glukhova, O.E. Electrical and Photovoltaic Properties of Layered Composite Films of Covalently Bonded Graphene and Single-Walled Carbon Nanotubes. Coatings 2020, 10, 324. [Google Scholar] [CrossRef]
- Elstner, M.; Seifert, G. Density functional tight binding. Phil. Trans. R. Soc. A 2014, 372, 20120483. [Google Scholar] [CrossRef]
- DFTB+ Density Functional based Tight Binding (and More). Available online: https://dftbplus.org/ (accessed on 12 May 2022).
- Mulliken, R.S. Electronic Population Analysis on LCAO–MO Molecular Wave Functions I. J. Chem. Phys. 1955, 23, 1833. [Google Scholar] [CrossRef]
- Marder, M. Condensed Matter Physics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2010; pp. 623–631. [Google Scholar]
- Calderín, L.; Karasiev, V.V.; Trickey, S.B. Kubo-Greenwood electrical conductivity formulation and implementation for projector augmented wave datasets. Comput. Phys. Commun. 2017, 221, 118–142. [Google Scholar] [CrossRef]
- Pedersen, T.G.; Pedersen, K.; Kriestensen, T.B. Optical matrix elements in tight-binding calculations. Phys. Rev. B 2001, 63, 201101(R). [Google Scholar] [CrossRef]
- Allen, P.B. Electron transport. In Conceptual Foundations of Materials, 2nd ed.; Louie, S.G., Cohen, M.L., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2006; Volume 2, pp. 172–175. [Google Scholar]
- Glukhova, O.E.; Nefedov, I.S.; Shalin, A.S.; Slepchenkov, M.M. New 2D graphene hybrid composites as an effective base element of optical nanodevices. Beilstein J. Nanotechnol. 2018, 9, 1321–1327. [Google Scholar] [CrossRef] [PubMed]
- Kuang, J.; Dai, Z.; Liu, L.; Yang, Z.; Jinc, M.; Zhang, Z. Synergistic effects from graphene and carbon nanotubes endow ordered hierarchical structure foams with a combination of compressibility, super-elasticity and stability and potential application as pressure sensors. Nanoscale 2015, 7, 9252–9260. [Google Scholar] [CrossRef]
- Slepchenkov, M.M.; Barkov, P.V.; Glukhova, O.E. Hybrid Films Based on Bilayer Graphene and Single-Walled Carbon Nanotubes: Simulation of Atomic Structure and Study of Electrically Conductive Properties. Nanomaterials 2021, 11, 1934. [Google Scholar] [CrossRef]
- Zhang, S.; Kang, L.; Wang, X.; Tong, L.; Yang, L.; Wang, Z.; Qi, K.; Deng, S.; Li, Q.; Bai, X.; et al. Arrays of horizontal carbon nanotubes of controlled chirality grown using designed catalysts. Nature 2017, 543, 234–238. [Google Scholar] [CrossRef]
- Liu, B.; Wu, F.; Gui, H.; Zheng, M.; Zhou, C. Chirality-Controlled Synthesis and Applications of Single-Wall Carbon Nanotubes. ACS Nano 2017, 11, 31–53. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory (NREL). Available online: https://www.nrel.gov/ (accessed on 15 September 2022).


| Solar Spectrum AM0 | |||
|---|---|---|---|
| The Integral Value of the Photocurrent for the Entire Solar Radiation Spectrum, mA/cm2 | Maximum Photocurrent at a Wavelength of 550 nm, mA cm−2 μm−1 | Integral Value of the Photocurrent for the Visible Spectrum 380–780 nm, mA/cm2 | |
| 12_6_ver_1_s | 3.80 | 3.42 | 2.29 |
| 12_6_ver_1_p | 5.24 | 5.23 | 2.47 |
| 12_6_ver_2_s | 4.34 | 4.08 | 2.46 |
| 12_6_ver_2_p | 5.86 | 4.96 | 2.22 |
| 12_6_ver_3_s | 6.07 | 5.95 | 2.33 |
| 12_6_ver_3_p | 6.40 | 6.16 | 2.86 |
| Solar Spectrum AM1.5 | |||
| 12_6_ver_1_s | 2.98 | 2.83 | 1.84 |
| 12_6_ver_1_p | 4.09 | 4.33 | 2.02 |
| 12_6_ver_2_s | 3.38 | 3.37 | 2.00 |
| 12_6_ver_2_p | 4.56 | 4.10 | 1.80 |
| 12_6_ver_3_s | 4.67 | 4.91 | 2.34 |
| 12_6_ver_3_p | 4.75 | 5.09 | 1.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slepchenkov, M.M.; Barkov, P.V.; Kolosov, D.A.; Glukhova, O.E. Ab Initio Study of Optical Properties of Hybrid Films Based on Bilayer Graphene and Single-Walled Carbon Nanotubes. C 2023, 9, 51. https://doi.org/10.3390/c9020051
Slepchenkov MM, Barkov PV, Kolosov DA, Glukhova OE. Ab Initio Study of Optical Properties of Hybrid Films Based on Bilayer Graphene and Single-Walled Carbon Nanotubes. C. 2023; 9(2):51. https://doi.org/10.3390/c9020051
Chicago/Turabian StyleSlepchenkov, Michael M., Pavel V. Barkov, Dmitry A. Kolosov, and Olga E. Glukhova. 2023. "Ab Initio Study of Optical Properties of Hybrid Films Based on Bilayer Graphene and Single-Walled Carbon Nanotubes" C 9, no. 2: 51. https://doi.org/10.3390/c9020051
APA StyleSlepchenkov, M. M., Barkov, P. V., Kolosov, D. A., & Glukhova, O. E. (2023). Ab Initio Study of Optical Properties of Hybrid Films Based on Bilayer Graphene and Single-Walled Carbon Nanotubes. C, 9(2), 51. https://doi.org/10.3390/c9020051







