Hands-On Quantum Sensing with NV− Centers in Diamonds
Abstract
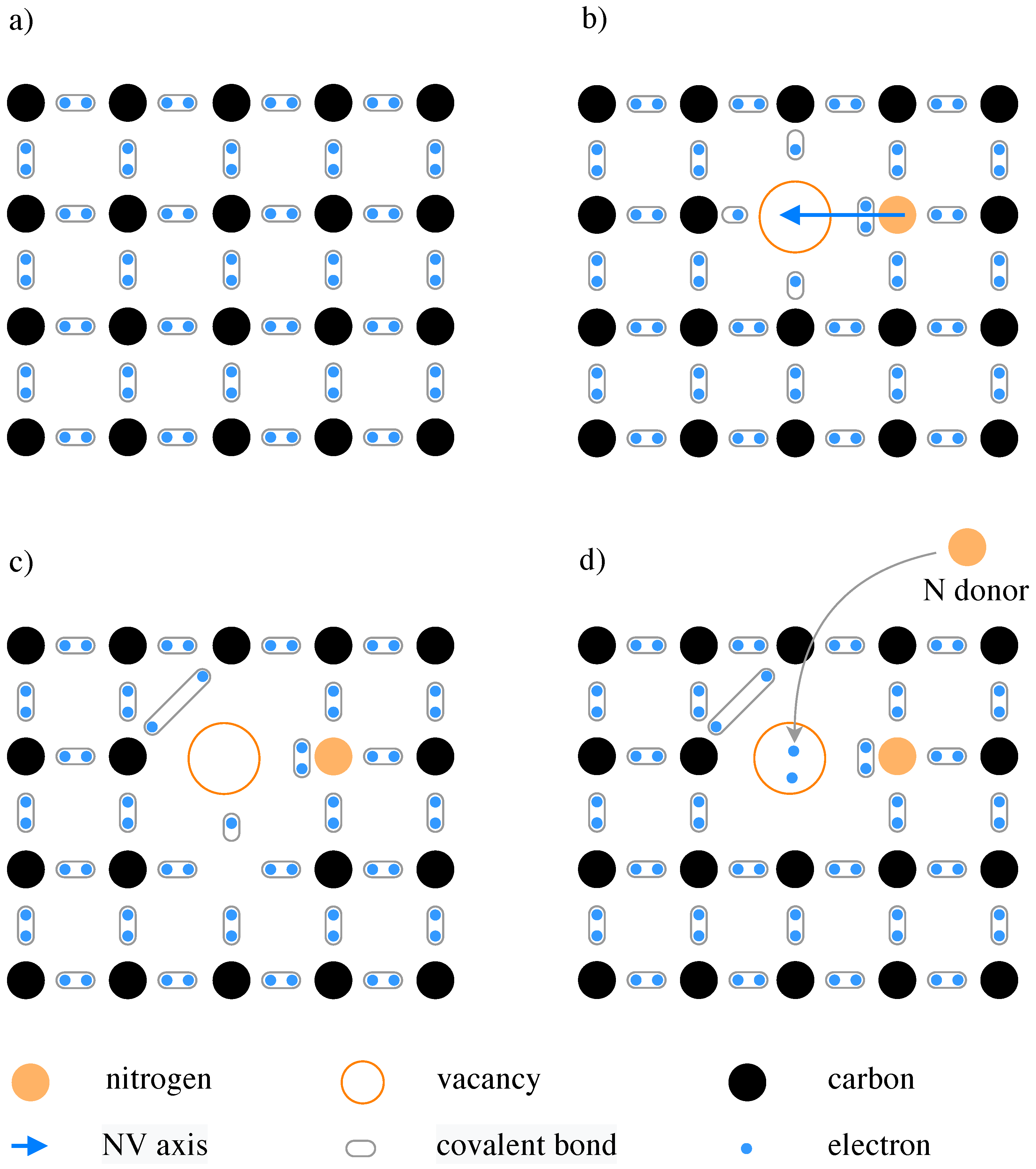
1. Introduction
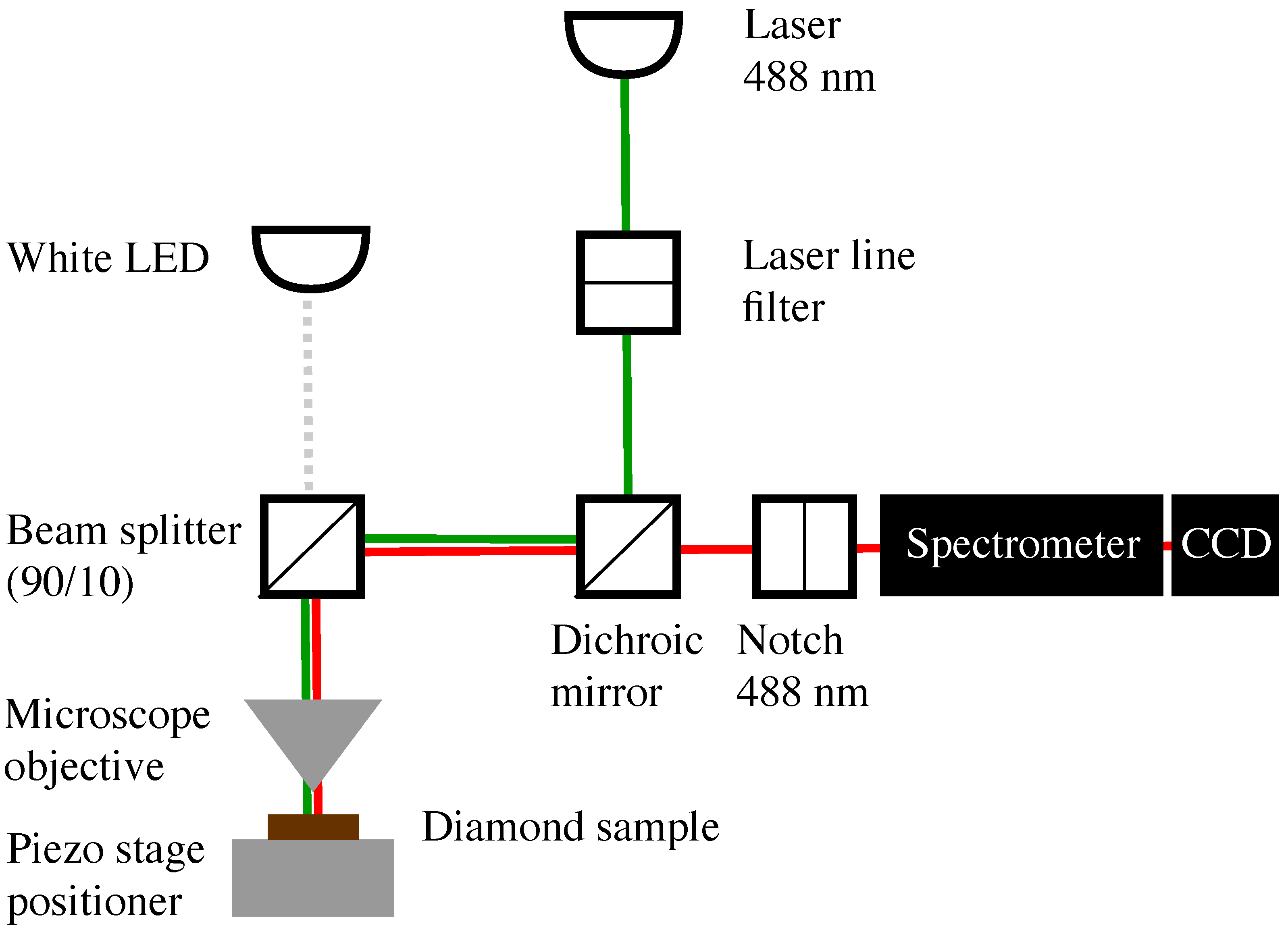
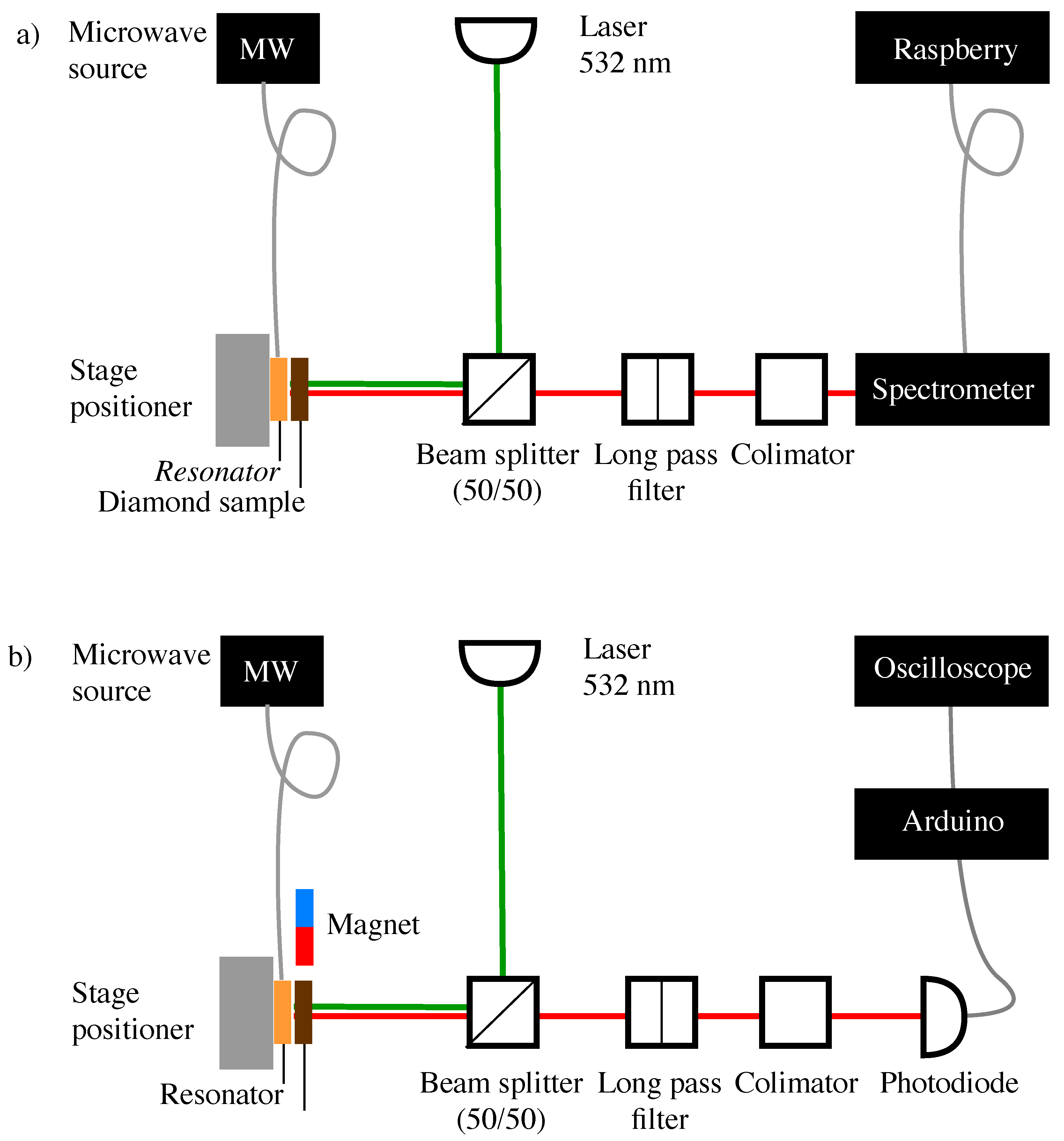
2. Materials and Methods
3. Results and Discussion
3.1. Optical Characterization
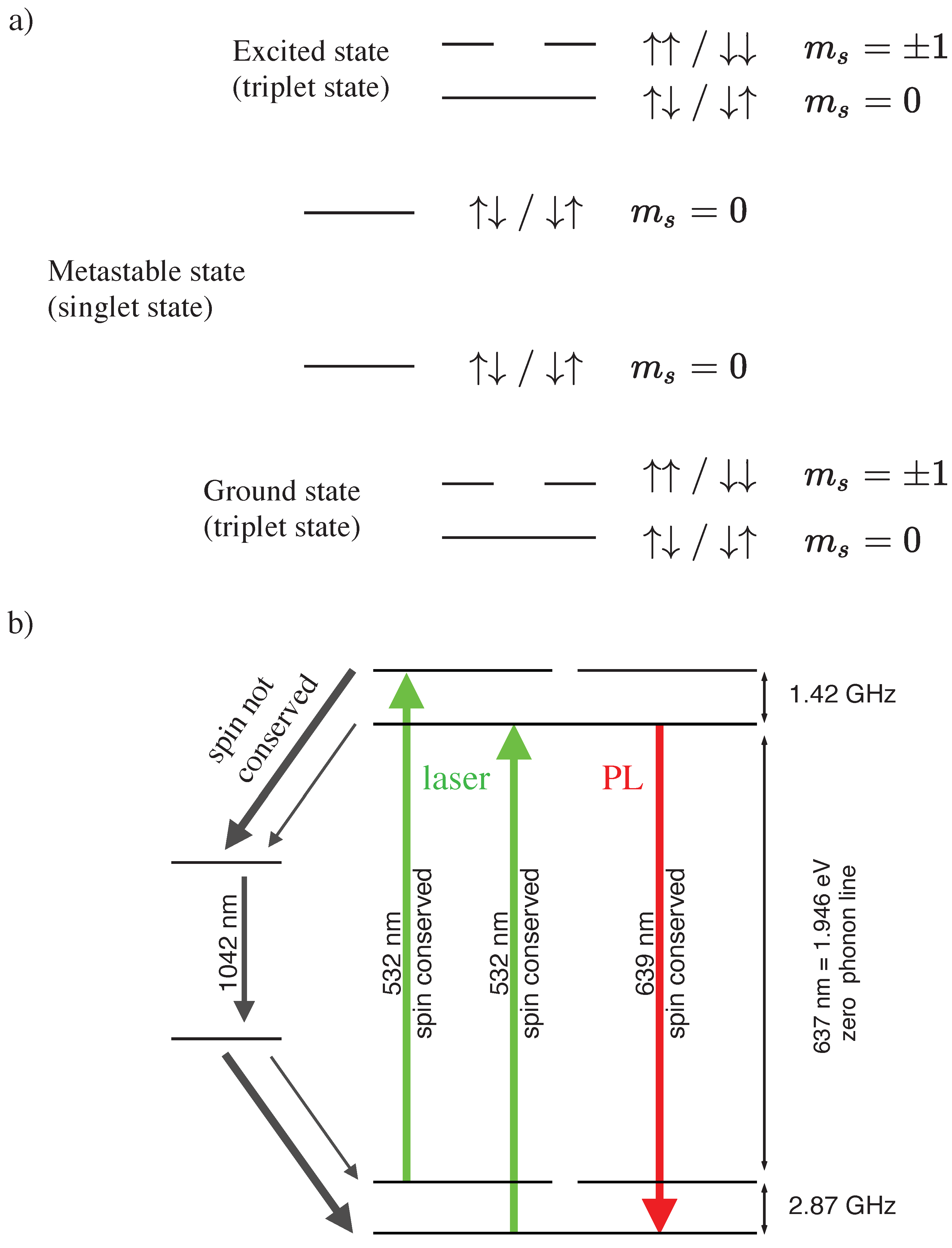
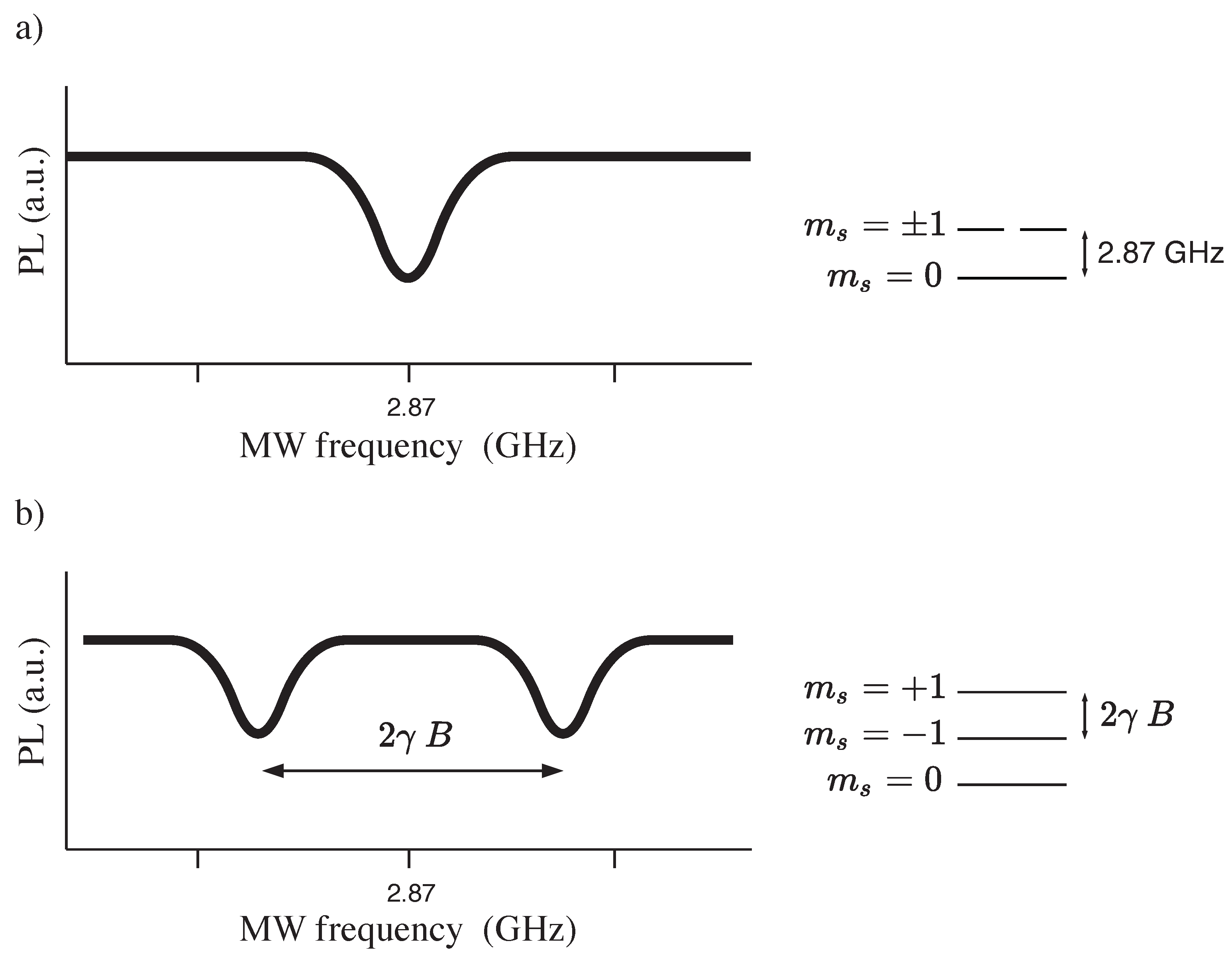
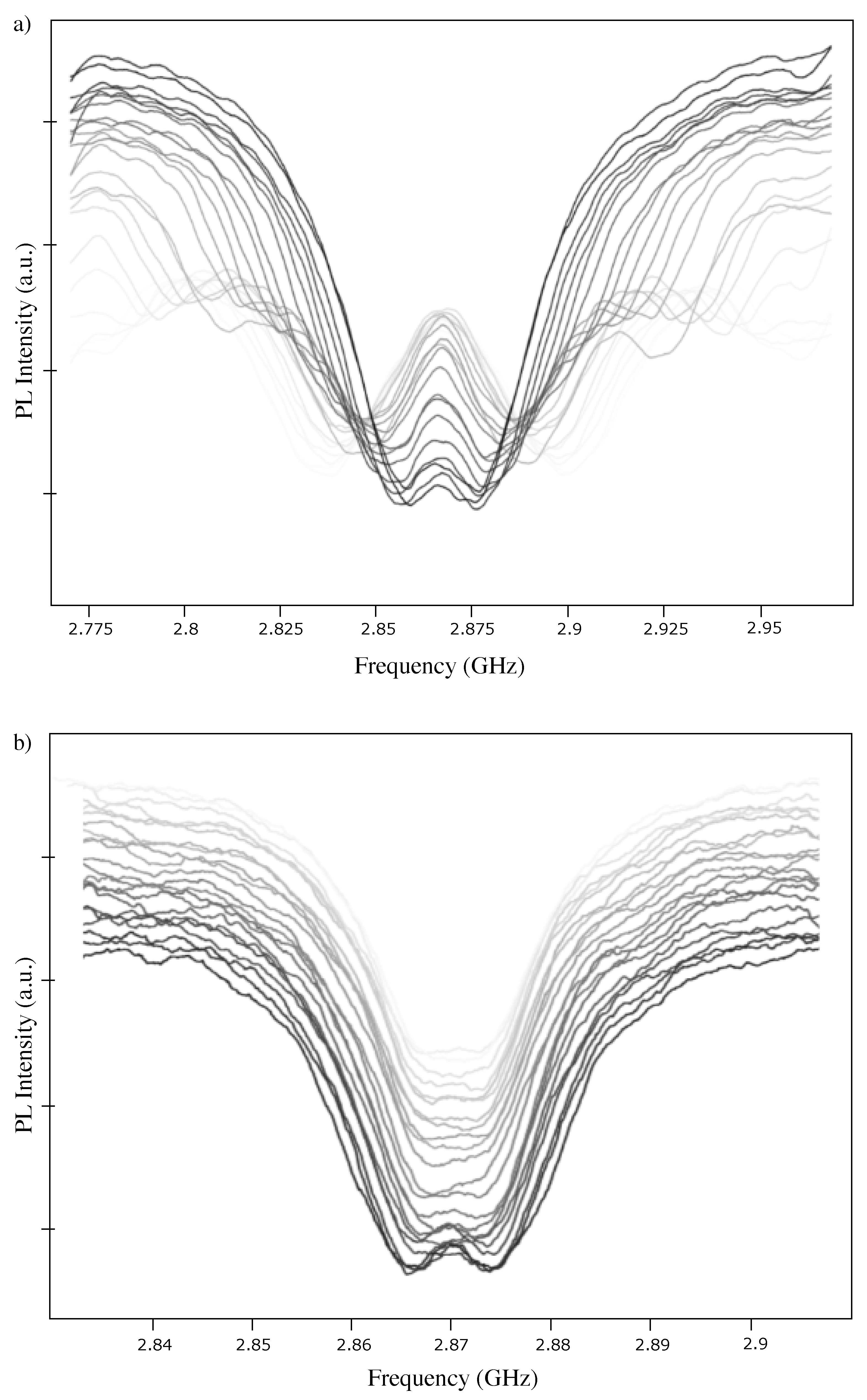
3.2. Optically Detected Magnetic Resonance (ODMR)
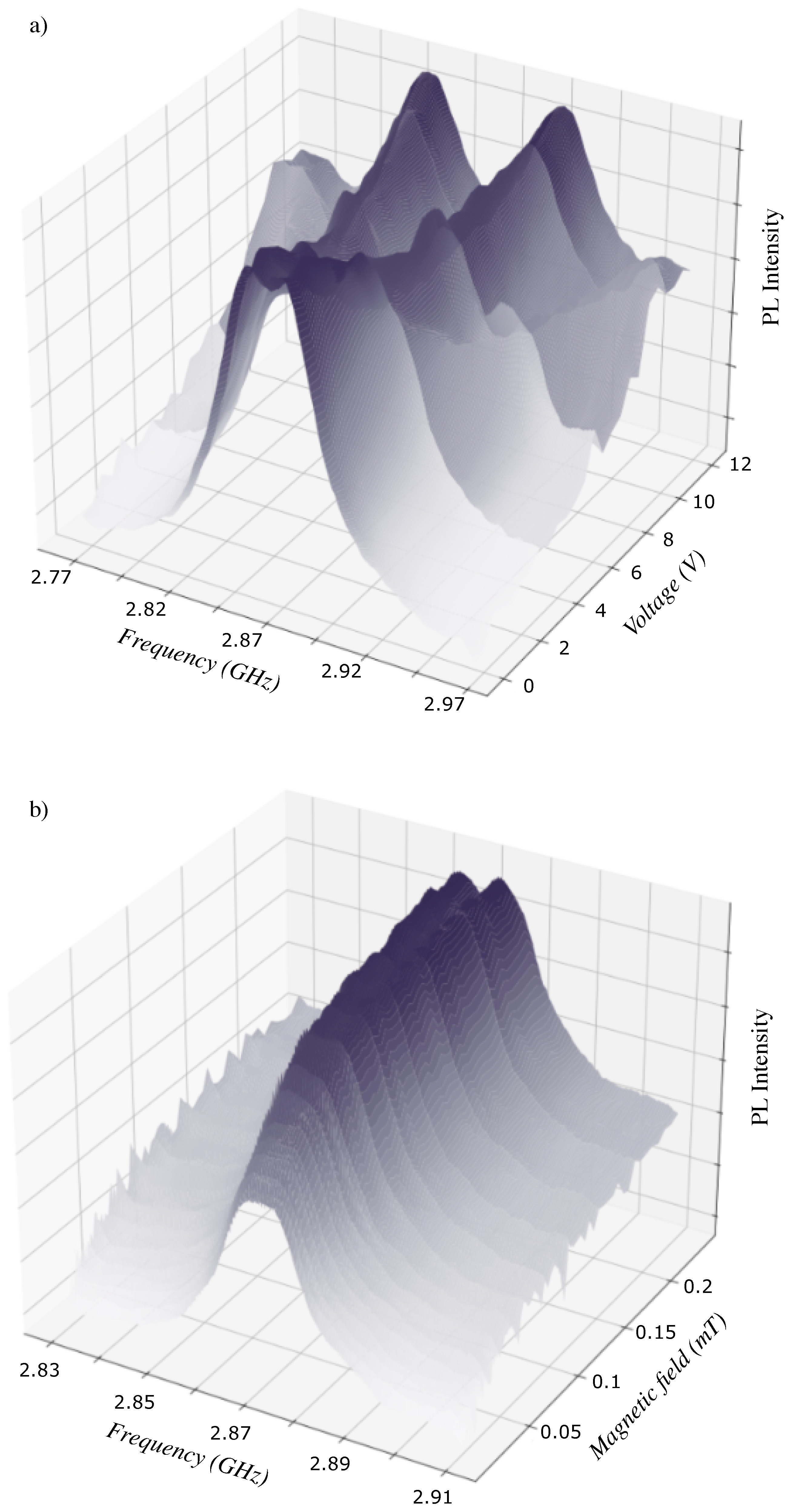
3.3. Photoluminescence Intensity in Proportion to the Applied Microwave Frequency
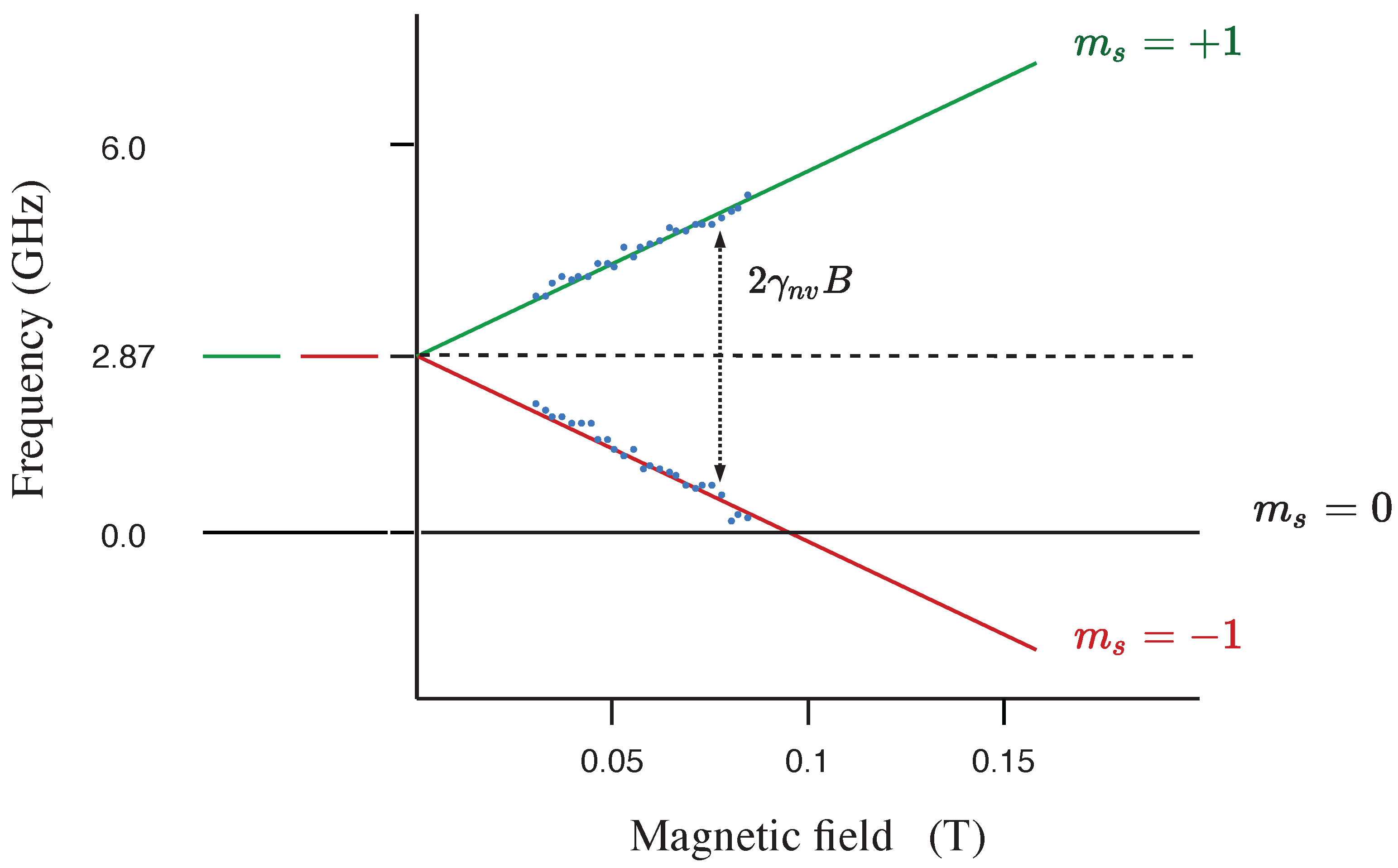
3.4. PL under an External Magnetic Field
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
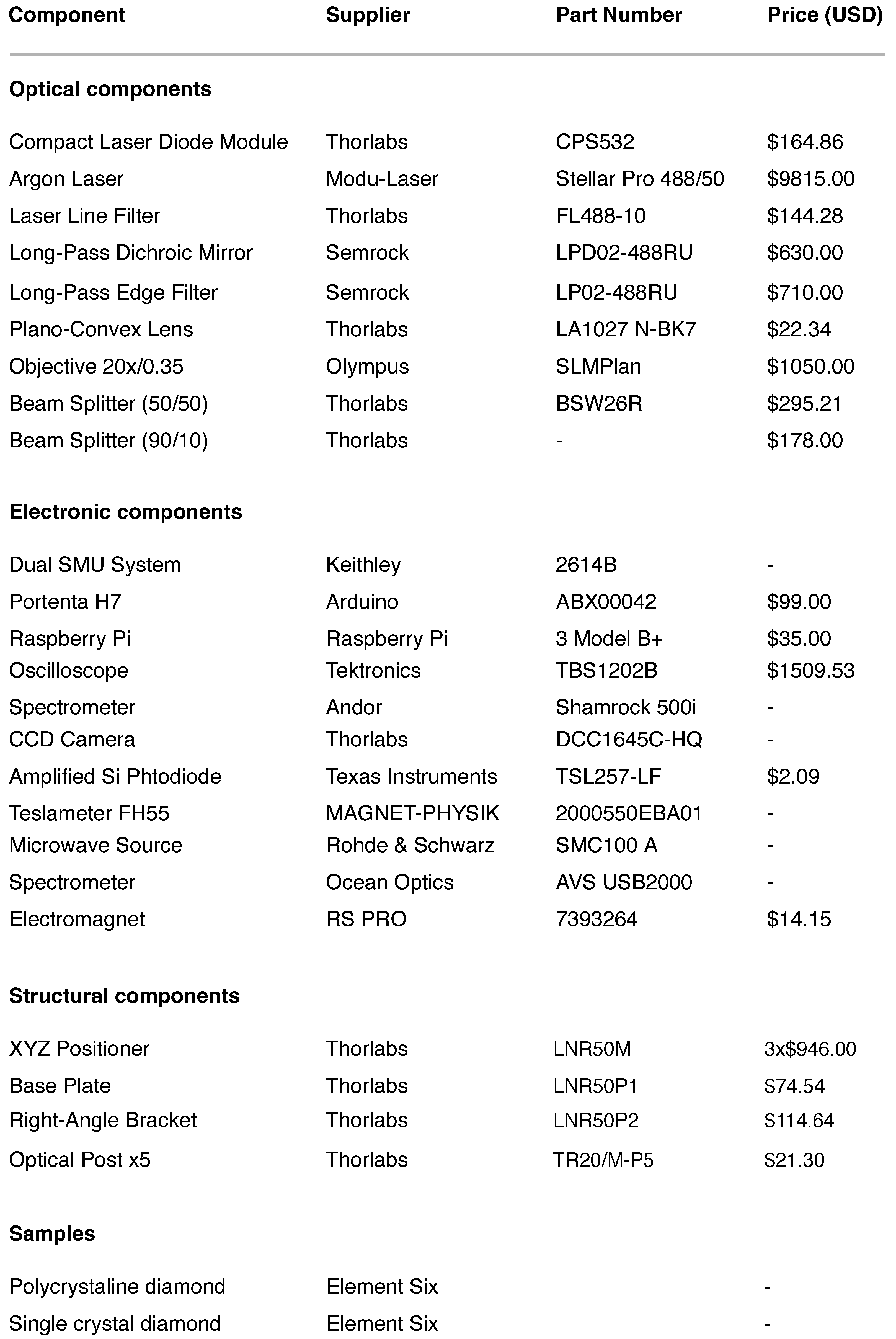
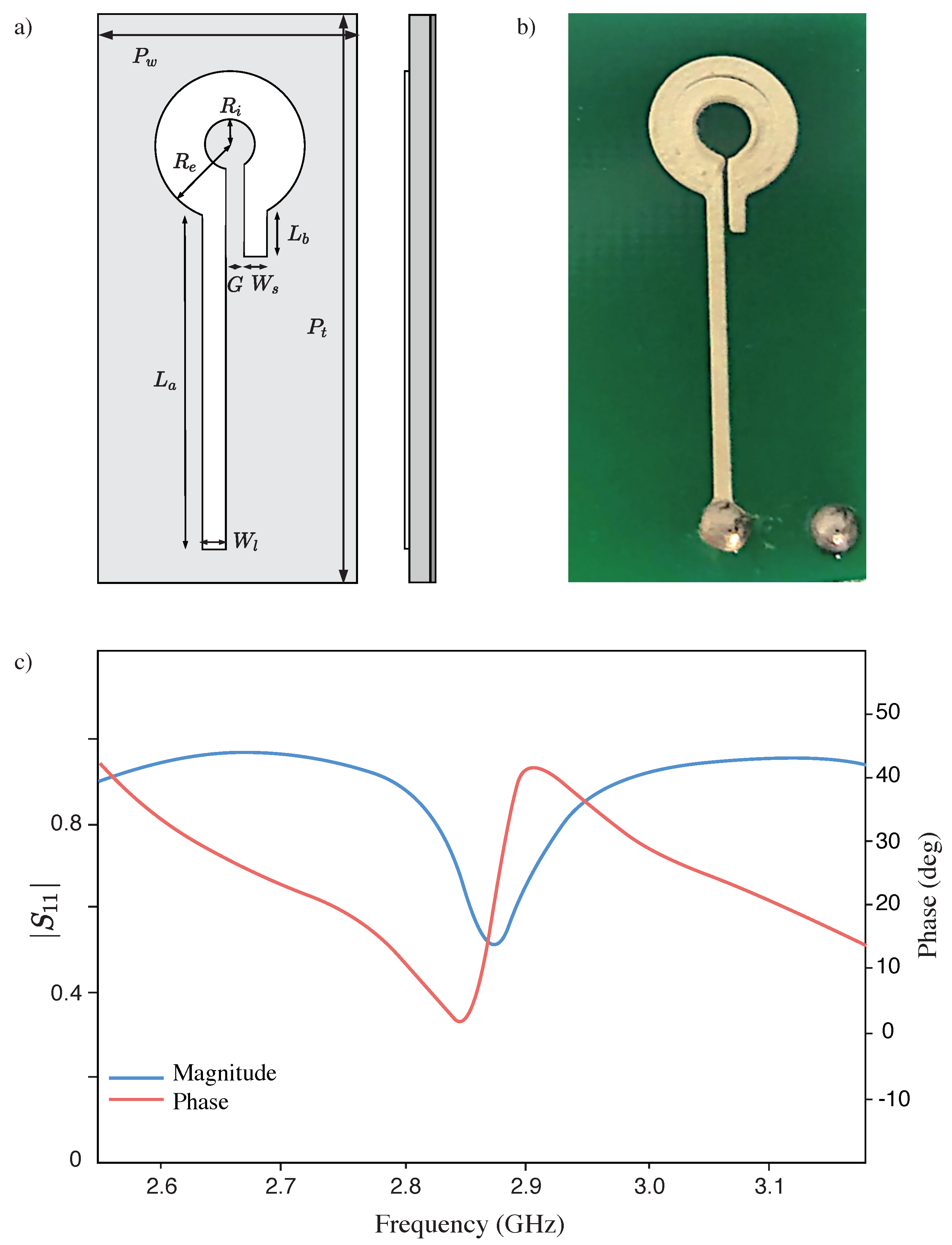
Appendix A. Component Detail
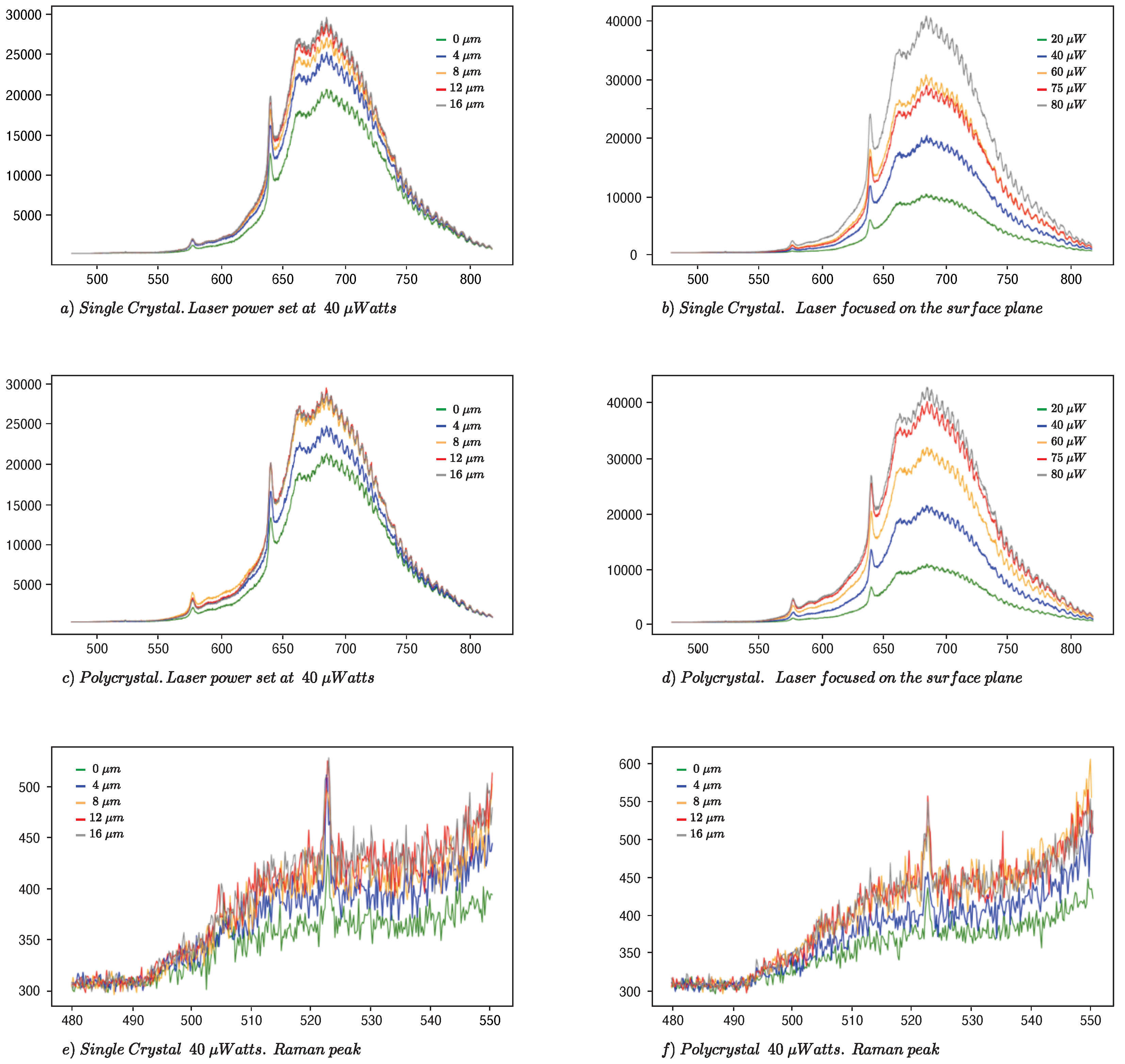
Appendix B. Characterization Details

References
- Doherty, M.W.; Manson, N.B.; Delaney, P.; Jelezko, F.; Wrachtrup, J.; Hollenberg, L.C. The nitrogen-vacancy colour centre in diamond. Phys. Rep. 2013, 528, 1–45. [Google Scholar] [CrossRef]
- Taylor, J.M.; Cappellaro, P.; Childress, L.; Jiang, L.; Budker, D.; Hemmer, P.R. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 2008, 4, 810–816. [Google Scholar] [CrossRef]
- Dang, H.B.; Maloof, A.C.; Romalis, M.V. Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer. Appl. Phys. Lett. 2010, 97, 151110. [Google Scholar] [CrossRef]
- Drung, D.; Assmann, C.; Beyer, J.; Kirste, A.; Peters, M.; Ruede, F.; Schurig, T. Highly Sensitive and Easy-to-Use SQUID Sensors. IEEE Trans. Appl. Supercond. 2007, 17, 699–704. [Google Scholar] [CrossRef]
- Todaro, M.; Sileo, L.; Vittorio, M. Magnetic Field Sensors Based on Microelectromechanical Systems (MEMS) Technology. Magn. Sens. 2012. [Google Scholar] [CrossRef]
- Degen, C.; Poggio, M.; Mamin, H.; Rettner, C.; Rugar, D. Nanoscale magnetic resonance imaging. Proc. Natl. Acad. Sci. USA 2009, 106, 1313–1317. [Google Scholar] [CrossRef]
- Amir Borna, T.R.C. Non-Invasive Functional-Brain-Imaging with an OPM-based Magnetoencephalography System; Technical report; Sandia National Laboratories: Albuquerque, NM, USA, 2020. [Google Scholar]
- Khaneja, N. SQUID Magnetometers, Josephson Junctions, Confinement and BCS Theory of Superconductivity. In Magnetometers; Curilef, S., Ed.; IntechOpen: Rijeka, Croatia, 2019; Chapter 5. [Google Scholar] [CrossRef]
- Tierney, T.; Holmes, N.; Mellor, S. Optically pumped magnetometers: From quantum origins to multi-channel magnetoencephalography. NeuroImage 2019, 199, 598–608. [Google Scholar] [CrossRef]
- Degen, C.; Reinhard, F.; Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 2017, 89, 035002. [Google Scholar] [CrossRef]
- Maze, J.; Stanwix, P.; Hodges, J.; Hong, S.; Taylor, J.; Cappellaro. Nanoscale magnetic sensing with an individual electronic spin in diamond. Nature 2008, 455, 644–647. [Google Scholar] [CrossRef]
- Hall, L.; Beart, G.; Thomas, E.; Simpson, D.; Mcguinness. High spatial and temporal resolution wide-field imaging of neuron activity using quantum NV-diamond. Sci. Rep. 2012, 2, 401. [Google Scholar] [CrossRef]
- Wolf, T.; Neumann, P.; Nakamura, K.; Sumiya, H.; Ohshima, T.; Isoya, J.; Wrachtrup, J. Subpicotesla Diamond Magnetometry. Phys. Rev. X 2015, 5, 041001. [Google Scholar] [CrossRef]
- Mitchell, M.W.; Alvarez, S.P. Quantum limits to the energy resolution of magnetic field sensors. Rev. Mod. Phys. 2020, 92, 21001. [Google Scholar] [CrossRef]
- Marcus, W.; Doherty, N.B.M. The Nitrogen-Vacancy Colour Centre in Diamond; Technical report; School of Physics, University of Melbourne: Melbourne, VIC, Australia, 2013. [Google Scholar]
- Wikipedia Contributors. Molecular symmetry Wikipedia, The Free Encyclopedia. 2022. Available online: https://en.wikipedia.org/w/index.php?title=Element_Six&oldid=1118487397 (accessed on 23 May 2022).
- Humphreys, J.; Liu, Q.; Humphreys, J.; Erne, R. A Course in Group Theory; Oxford Graduate Texts in Mathematics, Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Ferrari, A.M.; D’Amore, M.; El-Kelany, K.E.; Gentile, F.S.; Dovesi, R. The NV0 defects in diamond: A quantum mechanical characterization through its vibrational and Electron Paramagnetic Resonance spectroscopies. J. Phys. Chem. Solids 2022, 160, 110304. [Google Scholar] [CrossRef]
- Gali, A. Theory of the neutral nitrogen-vacancy center in diamond and its application to the realization of a qubit. Phys. Rev. B 2009, 79, 235210. [Google Scholar] [CrossRef]
- Kasper Jensen, P.K. Magnetometry with Nitrogen-Vacancy Centers in Diamond; Technical report; Niels Bohr Institute, University of Copenhagen: Copenhagen, Denmark, 2017. [Google Scholar]
- van Oort, E.; Glasbeek, M. Cross-relaxation dynamics of optically excited NV centers in diamond. Phys. Rev. B 1989, 40, 6509–6517. [Google Scholar] [CrossRef]
- Alkahtani, M.; Hemmer, P. Charge Stability of Nitrogen-Vacancy Color Center in Organic Nanodiamonds. Opt. Mater. Express 2020, 10. [Google Scholar] [CrossRef]
- Gaebel, T.; Domhan, M.; Wittmann, C. Photochromism in single nitrogen-vacancy defect in diamond. Appl. Phys. 2006, 455, 243–246. [Google Scholar] [CrossRef]
- Choi, S.; Jain, M.; Louie, S. Mechanism for optical initialization of spin in NV center in diamond. Phys. Rev. B 2012, 86, 041202. [Google Scholar] [CrossRef]
- Rogers, L.J.; Armstrong1, S.; Sellars, M.L.; Manson, N.B. New Infrared Emission of the NV Centre in Diamond: Zeeman and Uniaxial Stress Studies; Technical report; Laser Physics Center, Australian National University: Canberra, Australia, 2008. [Google Scholar]
- Robledo, L.; Bernien, H.; van Weperen, I.; Hanson, R. Control and Coherence of the Optical Transition of Single Nitrogen Vacancy Centers in Diamond. Phys. Rev. Lett. 2010, 105, 177403. [Google Scholar] [CrossRef]
- Subedi, S.D.; Fedorov, V.V.; Peppers, J.; Martyshkin, D.V.; Mirov, S.B.; Shao, L.; Loncar, M. Laser spectroscopic characterization of negatively charged nitrogen-vacancy (NV−) centers in diamond. Opt. Mater. Express 2019, 9, 2076–2087. [Google Scholar] [CrossRef]
- Neumann, P.; Kolesov, R.; Jacques, V.; Beck, J. Excited-state spectroscopy of single NV defects in diamond using optically detected magnetic resonance. New J. Phys. 2009, 11, 013017. [Google Scholar] [CrossRef]
- Element Six. Synthetic Diamond and Tungsten Carbide Experts. 2022.
- Vavilov, V.S. The properties of natural and synthetic diamond. Physics-Uspekhi 1993, 36, 1083–1084. [Google Scholar] [CrossRef]
- Jelezko, F.; Wrachtrup, J. Single Defect Centres in Diamond: A Review; Technical report; DPhysikalisches Institut, Universität Stuttgart: Stuttgart, Germany, 2006. [Google Scholar]
- Childress, L.; Dutt, M.G.; Taylor, J.M.; Zibrov, A.S.; Jelezko, F. Coherent Dynamics of Coupled Electron and Nuclear Spin Qubits in Diamond. Science 2006, 314, 281–285. [Google Scholar] [CrossRef]
- Trofimov, S.D.; Tarelkin, S.A.; Bolshedvorskii, S.V. Spatially controlled fabrication of single NV centers in IIa HPHT diamond. Opt. Mater. Express 2020, 10, 198–207. [Google Scholar] [CrossRef]
- Man Zhao, Q.L. Antenna for Microwave Manipulation of NV Colour Centres; Technical report; The Institution of Engineering and Technology: London, UK, 2020. [Google Scholar]
- Eisuke Abe, K.S. Tutorial: Magnetic Resonance with Nitrogen-Vacancy Centers in Diamond Microwave Engineering, Materials Science, and Magnetometry; Technical report; Spintronics Research Center, Keio University: Tokyo, Japan, 2018. [Google Scholar]
- Voltera v-one PCB Printer. 2022. Available online: https://www.voltera.io/store/v-one (accessed on 24 July 2022).
- Maria Simanovskaia, K.J. Sidebands in Optically Detected Magnetic Resonance Signals of Nitrogen Vacancy Centers in Diamond; Technical report; Department of Physics, University of California: Berkeley, CA, USA, 2013. [Google Scholar]
- Harrison, J.; Sellars, M.; Manson, N. Optical spin polarisation of the N-V centre in diamond. J. Lumin. 2004, 107, 245–248. [Google Scholar] [CrossRef]
- Rogers, L.; Jahnke, K.; Metsch, M.; Sipahigil, A.; Binder, J.; Teraji. All-Optical Initialization, Readout, and Coherent Preparation of Single Silicon-Vacancy Spins in Diamond. Phys. Rev. Lett. 2014, 113, 263602. [Google Scholar] [CrossRef]
- Magnetic Field Strength Meter Gauss-/Teslameter FH 55. 2022. Available online: https://www.magnet-physik.de/upload/31925018-FH-55-e-3157.pdf (accessed on 24 July 2022).
- Gilkes, K.; Prawer, S.; Nugent, K.; Robertson, J.; Sands, H.; Lifshitz, Y.; Shi, X. Direct quantitative detection of the sp3 bonding in diamond-like carbon films using ultraviolet and visible Raman spectroscopy. J. Appl. Phys. 2000, 87, 7283–7289. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez Toural, J.L.; Marzoa, V.; Bernardo-Gavito, R.; Pau, J.L.; Granados, D. Hands-On Quantum Sensing with NV− Centers in Diamonds. C 2023, 9, 16. https://doi.org/10.3390/c9010016
Sánchez Toural JL, Marzoa V, Bernardo-Gavito R, Pau JL, Granados D. Hands-On Quantum Sensing with NV− Centers in Diamonds. C. 2023; 9(1):16. https://doi.org/10.3390/c9010016
Chicago/Turabian StyleSánchez Toural, J. L., V. Marzoa, R. Bernardo-Gavito, J. L. Pau, and D. Granados. 2023. "Hands-On Quantum Sensing with NV− Centers in Diamonds" C 9, no. 1: 16. https://doi.org/10.3390/c9010016
APA StyleSánchez Toural, J. L., Marzoa, V., Bernardo-Gavito, R., Pau, J. L., & Granados, D. (2023). Hands-On Quantum Sensing with NV− Centers in Diamonds. C, 9(1), 16. https://doi.org/10.3390/c9010016






