Abstract
Benzenoid hydrocarbons have regular structures, attracting the opportunity to test the structural descriptors of their series. In the present study, we compared information entropy, Wiener indices, topological efficiencies, topological roundness, and symmetries of oligoacenes, phenacenes, and helicenes. We found and discussed the mismatches between the descriptors and the symmetry of benzenoids. Among the studied series, helicenes demonstrate the parity effect when the information entropy and topological roundness form saw-like functions depending on the number of the member, odd or even. According to our quantum chemical calculations, this parity effect has no consequences for such molecular properties as molecular polarizability and frontier molecular orbital energies. Further, we demonstrated that the changes in the structural descriptors upon the chemical reactions of benzenoids could be used for the numerical description of chemical processes. Interestingly, the view of the information entropy reaction profile is similar to the energy profiles of chemical reactions. Herewith, the intermediate chemical compounds have higher information entropy values compared with the initial and final compounds, which reminisce the activation barrier.
1. Introduction
Polycyclic aromatic hydrocarbons (PAHs) are a wide class of carbon-rich compounds widespread in natural media such as heavy oil fractions [1,2,3], coal [4,5,6], products of incomplete fuel combustion [7,8], astrophysical environments [6,9,10,11,12], etc. Molecules of typical polycyclic aromatic hydrocarbons are constructed only with the condensed benzene rings [13]. Oligoacenes, phenacenes, and helicenes represent benzenoid hydrocarbons with regular structures (Figure 1). The structural, molecular, chemical, and physical properties of benzenoids strongly depend on the condensation pattern [13,14,15,16,17,18,19,20,21,22,23,24]; therefore, their properties are usually studied contextually with the chemical structure. For example, the mean polarizability of phenacenes increases linearly with the growth of the molecular size, whereas oligoacenes show quadratic growth [20,22]. A ‘kinked’ condensation pattern is more preferable thermodynamically than a linear one [23,24], i.e., phenacenes are more stable compounds than oligoacenes, according to the total energy criterion.

Figure 1.
Benzenoid PAHs under study: addition patterns (left) and chemical models of the isomers with four benzene rings (right). Note that oligoacene and phenacene molecules are planar, whereas helicenes are not.
Our studies focus on fullerenes and nanostructures composed with fullerene building blocks [25,26,27,28,29,30,31,32,33,34,35,36]. Such nanostructures possess tunable topology, and we succeeded in rationalizing their properties using structural descriptors: distances [25,26,27], cage volumes [28,29,32], topological roundness [30,31,32], Wiener index [30,31,32], and information entropy [31,33,34,35,36]. For example, topological roundness well correlates with the stability of isomeric isolated-pentagon-rule fullerenes [30], whereas mean polarizability correlates with the geometric estimates rather than the topological ones in the case of endofullerenes [29] and multicage fullerene derivatives [25,26,27].
Studying the relations, we found that the calculated indices are valuable in their own right, especially when the correlations between the structural descriptor and the geometric or chemical parameters are characteristic for the considered class of molecular objects [31]. In this case, the numerical estimates could be used for the automated classification of the chemical objects [37]. The latter seems important for designing databases, digital twins of molecular objects, and related computational tasks.
Previously, we have found parity effects in the triad ‘rotational symmetry number–information entropy–extreme topological roundness’ for zigzag-shaped nano-aggregates (C60)n that makes them computationally distinguishable from linear (C60)n [31]. In continuation of this work, we perform a comparative study of oligoacenes, phenacenes, and helicenes. These benzenoid PAHs have regular carbon skeletons, which could be topologically represented as six-ring chains. Additionally, we exemplify the applicability of our approach to other benzenoid hydrocarbons composed with the benzene rings without condensation.
2. Computational Details
We treat the title PAH molecules under the two complement approaches below. The first one, information theoretic, focuses on atom types, and the second one, topological, deals with chemical bonds. Herewith, we apply both approaches to the molecules, omitting the hydrogen atoms (this omission is conventional [38,39,40]).
2.1. Information Entropy Calculations
According to the approach [40,41,42,43,44], we represent the carbon skeleton of the molecule as the set of N1 atoms of the first type, N2 atoms of the second type, and Nn atoms of the n-th type, where n is the number of atom types and Σ Nj is the total number of carbon atoms in the molecule. Information entropy (h) of the PAH molecule is introduced as a sum of the logarithms of the weights of each atom type (Nj/Σ Nj):
Note that:
Discriminating atoms by atom types is based on their positions in the molecular graph. The details of calculating information entropies of molecular graphs can be found in previous works [40,41,42,43,44]. In general, information entropy characterizes the structural complexity of the chemical object represented as the subsets of atoms. The information entropy of carbon skeletons depends on the number of the constituting atoms and symmetry (the factors increasing and reducing the h values, respectively).
The following designation of partitions is used in our works: (number of atom types) × (number of atoms within the type). The application of the approach to the title molecules is explained in Section 3.2.
2.2. Calculations of Topologial Descriptors
Previously, we have found important links between the topology and the geometry of several stable chemical systems, including all-carbon molecules (fullerenes). For example, the combined role of topological roundness and geometrical sphericity have been reported to favor the stability of the isolated pentagon isomers of the C84 fullerene [30]. Adopting a topological view, one may also rank the molecules in terms of their inherent topological compactness by computing the most celebrated graph descriptor, the Wiener index, whose role in selecting stable molecules has also been established in several numerical tests with noticeable results [45,46,47]. Here, we just mention the non-trivial case of the C66 fullerene, another all-carbon molecule, whose isomers have non-isolated pentagons. The combined effect of topological compactness and roundness immediately indicates the C66 (C2v) molecule as the best candidate among the series of 4478 C66 isomers for producing stable Sc2@C66 endo clusters (this result agrees with the experiment) [48]. This elegant and fast computational method is worth applying to the benzenoid PAHs.
Chemical graphs for oligoacene O(N) and phenacene P(N) lattices with N carbon atoms are built starting from the translationally invariant unit cells UO and UP shown in Figure 2. The lattices correspond to chemical graphs with N nodes.
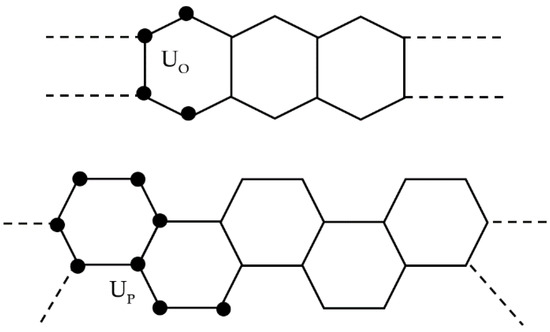
Figure 2.
Oligoacenes (top) and phenacenes (bottom) described as linear 1D graphs: carbon atoms correspond to the graph nodes. Nodes forming the unit cells are shown as circles. The selected unit cells are capable to build the lattices by translations only.
UO and UP contain, respectively, four and eight sites (circles) with maximum valence (degree) equal to δ = 3. For large N, the PAHs form 1D lattices (polymers) by adding an increasing number L of the unit cells along the horizontal axis. Hence, the number of atoms is N = 4L for oligoacenes and N = 8L for phenacenes. Due to the peculiar selection of the unit cells (Figure 2), the number of edges (chemical bonds) denoted by B is B = 5N/4 − 2 in both cases.
The Wiener index W(N) [49] is defined as the half-sum of all dij chemical distances in the graph with where M(N) is the graph diameter (the longest distance in the graph connecting a pair of atoms):
In Equation (3), wi designates the contributions to W(N) from vertex (atom) i. The nodes most compactly embedded in the graphs are, by definition, the topologically most stable vertices having the lowest wi values. We therefore indicate with and for introducing related invariants efficient in comparing graphs of similar structure and size. The term ‘similar’ should be considered here as an acceptable approximation, because the structures under study all consist of benzenoid rings arranged in chains (1D lattices). The two graph descriptors are the topological efficiency ρ and extreme topological efficiency ρE (or topological roundness):
whose ability to detect stable chemical systems has been extensively tested and compared with ab initio techniques [30,48,50,51], even for selected PAH molecules [52].
The intimate connection between the topology and the chemical structure is made more evident when the strong influence on W(N) exerted by the dimensionality D of the chemical system is considered. Original conjecture [53] holds in all tested cases so far and shows the key influence of system dimensionality D on graph connectivity in the large N limit:
Chemically, for large N we scale in D = 1 from molecules to polymers, s = 3 and:
Rational coefficients a, b, c, and d specify a given graph (see Section 3.3). Cubic closed forms for the Wiener index for polymers were originally proposed in the 1980 seminal article [54], but the general link with D (Equations (6) and (7)) was discovered only in 2010 [53,55].
For D = 1, our investigations show some other dimensionality-related properties, namely the asymptotic limits for the topological efficiency indices:
Even more intriguing is the asymptotic equivalence in 1D of the topological efficiency ρ and the ration between the Wiener index W of the open graph and its counterpart WC computed for the same periodically closed graph:
Additional features of our topological approach, including the role of graph dimensionality in determining W, is presented in [56].
2.3. Auxiliary Quantum Chemical Calculations
Trying to find the correspondence between the regularities in structural and molecular properties, we performed the auxiliary quantum chemical computations of helicenes. We did not scrutinize a wide set of properties, focusing on those which are the most sensitive to the changes in the chemical structure: mean polarizability (α) and energies of highest occupied and lowest unoccupied orbitals (EHOMO and ELUMO).
The quantum chemical computations were performed with two density functional theory methods. The first one—PBE/3ζ (program PRIRODA [57,58])—was chosen due to our good experience of its use for studying carbon-rich molecules; it reliably describes the mean polarizabilities, structural, and thermochemical properties of PAHs [20,21,22]). Unfortunately, we found (see Section 4.1) that this method provided negative values for ELUMO, which indicated an instability of the molecules and corresponded to the case with an ambiguous interpretation [59]. Therefore, based on the previous relevant studies [60,61,62], we recalculated the orbital energies with the ωB97X-D3/6-311G(d,p) method (GAUSSIAN program package [63]). The use of the latter DFT method corrected the situation and the ELUMO values became positive.
The quantum chemical study of helicenes was performed using standard computational protocols [58,63]. All structures were optimized without the restrictions on symmetry. The calculated hessians associated with the molecules contained no imaginary frequency that proved the correspondence of the found structures to the minima of potential energy surfaces. Mean polarizabilities were calculated in terms of the finite field approach [20,21,22]. Cartesian coordinates of the optimized molecular geometries can be found in Supplementary Materials.
Note that quantum chemical calculations corresponded to the helicene molecules, whereas only carbon skeletons were treated in the topological and information entropy calculations.
3. Results
3.1. Symmetry Trends in the Series of Regular Benzenoid PAHs
We analyzed the geometries of the benzenoid molecules previously optimized with relevant DFT methods [20,21,22,23,24]. It is important that the exact optimized geometries differ depending on the used method, but the symmetries are reproduced by different quantum chemical methods. All the molecules under study are symmetric. In the oligoacene and helicene series, the symmetry remains constant, being, respectively, D2h and C2 for all members. This means that all oligoacene and helicene molecules have the rotational symmetry numbers (σ) equal to four and two, respectively.
In the case of the phenacene series, there is a symmetry alternation: the odd members are C2v-symmetry molecules as the even ones have a lower symmetry, viz. C2. This alternation is not decisive for the rotational symmetry number: σ(C2v) = σ(C2) = 2.
Note that we assign symmetry point groups D2h, C2, C2v, and C2 to all members of the oligoacene, helicene and odd and even phenacenes with one reservation that symmetry reduction may take place in the case of the higher members of these series (e.g., due to the Jahn–Teller effect [64]).
3.2. Information Entropy in the Series of Regular Benzenoid PAHs
We omit hydrogen atoms in the benzenoid molecules and treat carbon skeletons. The examples of their dividing over atom types are shown in Figure 3, where we intentionally dissect odd and even members from the studied benzenoid series (because we are looking for differences between them).
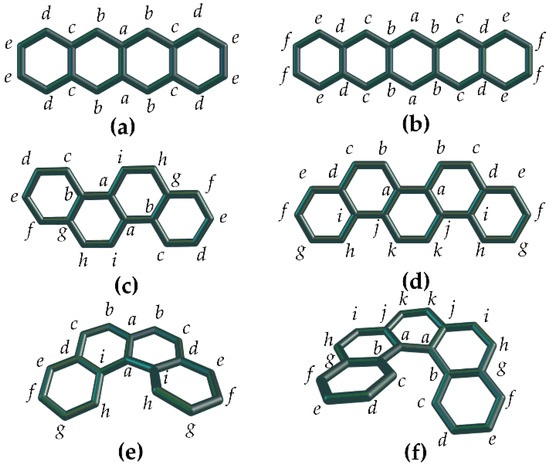
Figure 3.
Partition of the exemplifying benzenoid molecules over atom types (designated with italic Latin letters): tetracene (a), pentacene (b), chrysene (c), benzochrysene (d), [4]helicene (e), and [5]helicene (f). Herewith, compounds (a,c,e) are even members of the corresponding series; (b,d,f) are odd members.
Note that the numbers of the carbon atoms (N) and the benzene rings (R) in the studied PAH molecules are connected with the simple relation: N = 4R + 2. The chemical structure is regularly changed with the molecular size within each hydrocarbon series, so we can obtain analytical expressions between N (or R) and information entropies (Table 1). These expressions are deduced from the definition (Equation (1)) after simplifications that account for the partition patterns of the molecules. The corresponding plots are shown in Figure 4.

Table 1.
Analytical expressions for partitions and information entropies of the studied benzenoids.
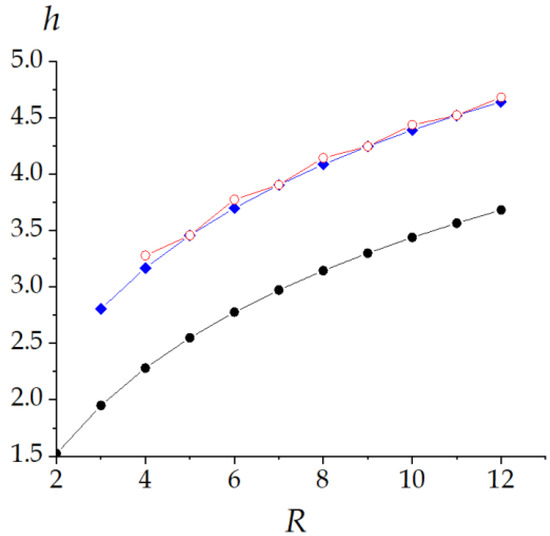
Figure 4.
Dependence of information entropy (h) on the molecular size. Black, blue, and red colors correspond to oligoacenes, phenacenes, and helicenes, respectively.
Expectedly, the h values increase with the molecular size in each benzenoid series (Figure 4). In the case of the isomers (the molecules with the same N), the lowest h values correspond to the oligoacene molecules having much higher symmetry than their counterparts. This agrees with the general trend of lower information entropy for more symmetric molecular species [33]. There are no other worth-mentioning features for dependence h = f(N) of oligoacenes. This trend is quite common (Figure 4).
A more complicated situation is observed in the case of the phenacenes and helicenes. In spite of the symmetry alternations C2v–C2 for odd–even members, the partitions of odd and even phenacenes coincide (Figure 4).
As mentioned above, all helicene molecules have a C2 symmetry. However, the partitions differ for even and odd members of the series. This is due to the way the symmetry axis is placed in the molecule. We illustrate it in the example of the first members of the helicene family (Figure 5). In the case of the even helicene, we distinguish one ‘central’ carbon–carbon bond lying on the C2 symmetry axis. Thus, the two carbon atoms are inequivalent and make up two different atom types. The remaining atoms of this molecule are divided over the atom types populated with two items. Odd helicenes are more homogeneous in the aspect of partition. For their molecules, the C2 symmetry axis passes through the middles of two central bonds, so that all atoms of the molecule are grouped in twos. This more homogeneous partition leads to lower information entropy values. The difference in the partition of odd and even members explains the saw-like plot h = f(N) for the helicene series.
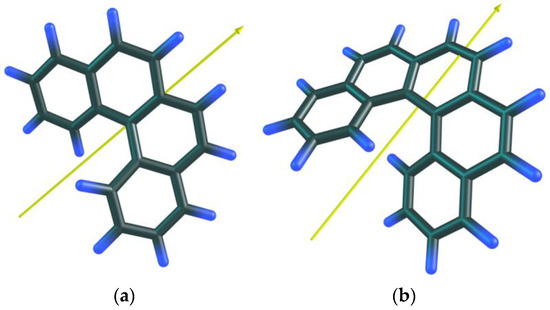
Figure 5.
The [4]helicene (a) and [5]helicene (b) molecules with the C2 symmetry axes.
Since the partitions of odd helicenes and phenacenes coincide, they have equal h values, being indistinguishable in terms of information entropy only.
3.3. Topological Indices in the Series of Regular Benzenoid PAHs
Table 2 shows the characteristic topological invariants for the title chemical systems. It is noteworthy that all distance-based invariants are represented as closed forms, with helicenes showing the invariant , whose value is sensible to the parity of the number of six-rings present in the molecule. This parity dependence is mathematically expressed with k coefficient in the corresponding polynomials. As these coefficients are constant, their contributions to the resulting invariant values become smaller with increasing molecular size. In other words, parity effect is smoothed when N → ∞.

Table 2.
Analytical expressions for topological invariants of the studied benzenoids.
3.3.1. Topological Stability in Terms of Molecular Compactness
The present topological calculations of the Wiener index for the selected benzenoid series show that helicenes have lower W values. Hence, they keep more compact structures than their isomers from other series (Figure 6). This is consistent with the geometrical size of the molecules that decreases from oligoacenes to helicenes. Curve (c) of Figure 6 provides clear evidence of the fact that, over a certain size (N ≈ 26 that corresponds to six benzene rings in the molecule), the helicene mesh has a more compact structure. The remaining curves of Figure 6 (a,b) show that the oligoacene and phenacene series behave very closely in terms of compactness W(N).

Figure 6.
Wiener index cubic polynomials for oligoacenes (a), phenacenes (b), and helicenes (c) as functions of the size (N).
3.3.2. Topological Stability of Helicenes in Terms of Molecular Roundness
Topological simulations allow a deeper view into the helicene structure. The plot of the topological roundness versus the molecular size of helicenes is shown in Figure 7. The plot has local minima corresponding to the odd members of the series. This is consistent with the information entropy calculations. Thus, both indices show parity alternations.

Figure 7.
Topological roundness (a) and topological efficiency (b) in the helicene series.
The selection of peculiar sizes for helicenes is a typical topological phenomenon arising from the topological long-distance connectivity of the helicene pattern and has been reported in the literature for structures with D = 2 such as the graphene ribbons and the 1-pentagon nanocone [65].
3.4. Toward the Use of Strucutral Descriptors for Chemical Reaction Series of PAHs
In this section, we demonstrate the applicability of our approach to other benzenoids, e.g., having non-condensed benzene rings. For this purpose, we have studied a series of the related PAH molecules, which are intermediates of the hexaphenylbenzene conversion to hexa-peri-benzocoronene via a stepwise Scholl reaction (Table 3 and Figure 8). These compounds have been previously studied experimentally and theoretically [66,67]. The mentioned reaction series is accompanied with the planarization of the benzenoid substrate and the increasing number of the condensed benzene rings.

Table 3.
Partitions and information entropies of the benzenoid molecules of Figure 8.
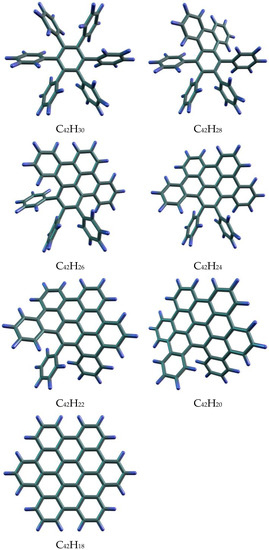
Figure 8.
Initial, intermediate, and final benzenoids of the hexaphenylbenzene conversion to hexa-peri-coronene.
The partitions of the molecules and the calculated information entropies are shown in Table 3. The information entropies of the initial benzenoid and the product of its condensation are equal, whereas the h values of the intermediate products are higher (Figure 9). We can propose the analogy between this case and the potential energy plot that connects the initial and final states of the reaction system. In both cases, the system should overcome the barrier. In the case of the energy reaction profiles, we call it the activation barrier. In the present work, we similarly consider the information entropy barrier. It could be associated with the necessity of some structural disorder when a molecular system converts from one stable state to another. In the aspect of the information theory, it means that moving the system from one informationally stable state to another, its information capacity must be temporarily increased. Note that, previously, we found similar barriers on the information entropy plots for the dendrimer molecules with incomplete shells, which are intermediates between the ‘closed-shell’ dendrimers [68].

Figure 9.
The information entropy changes upon the stepwise conversion of hexaphenylbenzene to hexa-peri-coronene.
We observe a completely different picture in the case of the topological invariants for the structures associated with the hexaphenylbenzene → … → hexa-peri-benzocoronene conversion (Table 4). As found, W and ρ are better suitable for discriminating molecules in this series. The descriptors are minimal for the most compact structure C42H18 (the product of the reaction). Thus, all considered topological descriptors decrease upon the successive Scholl reactions of hexaphenylbenzene; this decrease is linear (Figure 10). No extremal points are found on the way from C42H30 to C42H18. The linear dependence reflects the regular stitching between the benzene rings forming the planar graphene-like structure. As a consequence, the descriptors correlate with the hydrogen contents in this PAH series as each additional bond is formed due to the elimination of two hydrogen atoms.

Table 4.
Topological invariants of the benzenoid molecules shown in Figure 8.

Figure 10.
Linear correlation between the Wiener index and the topological efficiency for the benzenoids formed upon the stepwise conversion of hexaphenylbenzene to hexa-peri-coronene.
4. Discussion
4.1. Relevance of Parity Effects to Molecular Properties
We continue the series of works on the reliability of structural descriptors applied to carbon-rich molecules. Our interest in topological and information theoretic indices is due to their digital application rather than their physicochemical one. In this regard, the indices are expected to facilitate navigating chemical space and to reduce central processing unit time.
In the present work, we found the unusual behavior of size-dependences of information entropy (h) and Wiener-based topological indices (ρ and ρE) for helicenes, viz. the alternation for odd and even members of the series. Herewith, in the case of oligoacehenes and phenacenes, no parity effects are observed, and functions h = f(N), ρ = f(N), and ρE = f(N) monotonously ascend. The variance between the indices and the symmetry estimates should be highlighted. Indeed, all helicene molecules have the same symmetry (C2), but the corresponding functions ρ = f(N) and ρE = f(N) manifest parity effects. At the same time, the symmetries of the phenacenes alternate (C2v versus C2), which is not reflected by the structural descriptors. Possibly, the difference in the symmetries is too small to be caught by the indices. In addition, the effects on the topological structure caused by the closure of the benzenoid chains will be further investigated.
On the other hand, the indices are a more precise descriptive tool compared with the symmetry point group of the molecule, because they consider the inequivalent atoms (h) or bonds (W, ρ, and ρE). A deep and more fundamental question remains outside the scope of this work: when should the symmetry estimates correlate with the structural descriptors and when should they not? We formulate this question, because previously we have found good correlations between rotational symmetry numbers, information entropy, and topological roundness within the fullerene oligomers family [31].
Another question we formulate: if we observe the alternation in the structural descriptors, should we expect a similar behavior for any measurable/computable properties of the compounds? We have calculated their mean polarizabilities and frontier orbital energies with the PBE/3ζ and ωB97X-D3/6-311G(d,p) methods (Figure 11). As follows from the illustration, there are no odd–even alternations of the suggested properties depending on the number of the compound in the series. Previously, we have not found such correlations in the case of the fullerene compounds (C60)n [31]. Hence, it seems that the mentioned correlations are not mandatory.

Figure 11.
Size dependences for the frontier molecular orbital energies (a,b) and mean polarizability (c). The EHOMO and ELUMO values have been computed with the PBE/3ζ and ωB97X-D3/6-311G(d,p) methods (red and blue circles, respectively). The mean polarizabilities are obtained with PBE/3ζ. Numerical data associated with the plot can be found in the Supplementary information.
We will try to continue the search for the link between the parity effects in the structural descriptors and the molecular parameters. Here, we note that the first ones are mathematical constructs aimed to facilitate the perception and digital description of the chemical structures. The found correlations between the chemical structure (molecular size or number of homologs in the series) and the structural descriptors (topological roundness or information entropy) may or may not have the consequences in the realm of the measurable molecular properties. The last sentence is our conjecture that requires more cases to be confirmed.
4.2. Information Entropy and Reaction Path
The other finding to be discussed is that the conversion of the nonplanar hexaphenylbenzene into hexa-peri-benzocoronene is accompanied with the increase in the information entropy for the intermediate benzenoid structures and further going down (Figure 9). The picture is very reminiscent of the sections of the potential energy surfaces (PES), where the energy maximum between the reactants and products correspond to the transition state. Note that, in the present study, we deal with the intermediate molecules not the transition states. Additionally, PESs are continual functions, whereas information entropy vs. reaction coordinate path correspond to the discrete one. Nevertheless, the similarity of PES plots and information entropy path is striking. This is the second time we meet such a plot (see also [68]) and we will develop the concept of information entropy path.
In the case of the studied topological indices, there are no such analogies. The indices monotonously increase, indicating that the molecular system (hexaphenylbenzene) goes to a more bonded state (hexa-peri-benzocoronene) (Table 4). We think that the last finding could be interesting for the numerical description of the chemical structures and their reactions, focusing on the structural descriptors instead of the energies or thermodynamic parameters (see, e.g., [69,70]).
5. Conclusions
We have studied the dependences of a number of structural descriptors on the molecular size for benzenoid hydrocarbons: oligoacenes, phenacenes, and helicenes. The most interesting results have been obtained for the helicene series demonstrating a parity effect, viz. saw-like dependences of the information entropy/roundness on the number of the homolog in the series. We have found no correlations of this ‘structural’ parity with the selected molecular parameters (mean polarizabilities and HOMO/LUMO energies). In the cases of phenacenes and helicenes, there is a mismatch between the structural descriptors and the symmetry. The symmetries of the molecules in the phenacene series alternate depending on the homolog number, but the information entropy does not catch the alternation, because the partitions of the odd and even homologs of the set coincide; vice versa, the symmetry remains the same for all compounds of the helicenes series, but the structural diversity and, consequently, the information entropy and topological indices differ for the odd and even homologs’ structural diversity.
The changes in the structural descriptors upon the reactions of benzenoinds have been studied. In the case of the information entropy, the plot reminisces the energy profiles of chemical reactions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/c8030042/s1. Data associated with Figure 11: cartesian coordinates of helicenes obtained with the DFT methods.
Author Contributions
Conceptualization, D.S.S. and O.O.; methodology, D.S.S. and O.O.; validation, O.O., A.A.T., and I.S.S.; investigation, D.S.S., O.O., A.A.T., and I.S.S.; writing—original draft preparation, D.S.S. and O.O.; writing—review and editing, D.S.S. and O.O.; visualization, D.S.S. and I.S.S.; funding acquisition, D.S.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, project “Information entropy of chemical reactions: A novel methodology for digital organic chemistry”, grant number 22-13-20095.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Marr, L.C.; Kirchstetter, T.W.; Harley, R.A.; Miguel, A.H.; Hering, S.V.; Hammond, S.K. Characterization of polycyclic aromatic hydrocarbons in motor vehicle fuels and exhaust emissions. Environ. Sci. Technol. 1999, 33, 3091–3099. [Google Scholar] [CrossRef]
- De Souza, C.V.; Correa, S.M. Polycyclic aromatic hydrocarbons in diesel emission, diesel fuel and lubricant oil. Fuel 2016, 185, 925–931. [Google Scholar] [CrossRef]
- Dolomatov, M.Y.; Burangulov, D.Z.; Dolomatova, M.M.; Osipenko, D.F.; Zaporin, V.P.; Tukhbatullina, A.A.; Akhmetov, A.F.; Sabirov, D.S. Low-sulphur vacuum gasoil of western siberia oil: The impact of its structural and chemical features on the properties of the produced needle coke. C—J. Carbon Res. 2022, 8, 19. [Google Scholar] [CrossRef]
- Achtena, C.; Hofmann, T. Native polycyclic aromatic hydrocarbons (PAH) in coals—A hardly recognized source of environmental contamination. Sci. Total Environ. 2009, 407, 2461–2473. [Google Scholar] [CrossRef]
- Wang, R.; Liu, G.; Zhang, J.; Chou, C.-L.; Liu, J. Abundances of polycyclic aromatic hydrocarbons (PAHs) in 14 Chinese and American coals and their relation to coal rank and weathering. Energy Fuels 2010, 24, 6061–6066. [Google Scholar] [CrossRef]
- Cataldo, F.; García-Hernández, D.A.; Manchado, A. Far- and mid-infrared spectroscopy of complex organic matter of astrochemical interest: Coal, heavy petroleum fractions and asphaltenes. MNRAS Mon. Not. R. Astron. Soc. 2013, 429, 3025–3039. [Google Scholar] [CrossRef]
- Mastral, A.M.; Callen, M.S. A review on polycyclic aromatic hydrocarbon (PAH) emissions from energy generation. Environ. Sci. Technol. 2000, 34, 3051–3057. [Google Scholar] [CrossRef]
- Du, W.; Wang, J.; Zhuo, S.; Zhong, Q.; Wang, W.; Chen, Y.; Wang, Z.; Mao, K.; Shen, G.; Tao, S. Emissions of particulate PAHs from solid fuel combustion in indoor cookstoves. Sci. Total Environ. 2021, 771, 145411. [Google Scholar] [CrossRef]
- Snow, T.; Le Page, V.; Keheyan, Y.; Bierbaum, V.M. The interstellar chemistry of PAH cations. Nature 1998, 391, 259–260. [Google Scholar] [CrossRef]
- Ehrenfreund, P.; Ruiterkamp, R.; Peeters, Z.; Foing, B.; Salama, F.; Martins, Z. The ORGANICS experiment on BIOPAN V: UV and space exposure of aromatic compounds. Planet. Space Sci. 2007, 55, 383–400. [Google Scholar] [CrossRef]
- Bauschlicher, C.W., Jr.; Peeters, E.; Allamandola, L.J. The Infrared Spectra of Very Large, Compact, Highly Symmetric, Polycyclic Aromatic Hydrocarbons (PAHs). ApJ Astrophys. J. Lett. 2008, 678, 316–327. [Google Scholar] [CrossRef]
- Ai-Haimoud, Y.; Perez, L.M.; Maddalena, R.J.; Roshi, D.A. Search for polycyclic aromatic hydrocarbons in the Perseus molecular cloud with the Green Bank Telescope. MNRAS Mon. Not. R. Astron. Soc. 2015, 447, 315–324. [Google Scholar] [CrossRef]
- Slayden, S.W.; Liebman, J.F. The energetics of aromatic hydrocarbons: An experimental thermochemical perspective. Chem. Rev. 2001, 101, 1541–1566. [Google Scholar] [CrossRef] [PubMed]
- Anthony, J.E. The larger acenes: Versatile organic semiconductors. Angew. Chem. Int. Ed. 2008, 47, 452–483. [Google Scholar] [CrossRef] [PubMed]
- Malloci, G.; Cappellini, G.; Mulas, G.; Mattoni, A. Electronic and optical properties of families of polycyclic aromatic hydrocarbons: A systematic (time-dependent) density functional theory study. Chem. Phys. 2011, 384, 19–27. [Google Scholar] [CrossRef]
- Portella, G.; Poater, J.; Bofill, J.M.; Alemany, P.; Sola, M. Local aromaticity of [n]acenes, [n]phenacenes, and [n]helicenes (n = 1−9). J. Org. Chem. 2005, 70, 2509–2521. [Google Scholar] [CrossRef]
- Zhang, X.; Xin, J.; Ding, F. The edges of graphene. Nanoscale 2013, 5, 2556–2569. [Google Scholar] [CrossRef]
- Pauncz, R.; Berencz, F. The diamagnetic anisotropy of four-ring condensed aromatic hydrocarbons. Acta Phys. Hung. 1952, 2, 183–193. [Google Scholar] [CrossRef]
- Jones, L.; Lin, L. An in silico study on the isomers of pentacene: The case for air-stable and alternative C22H14 acenes for organic electronics. J. Phys. Chem. A 2017, 121, 2804–2813. [Google Scholar] [CrossRef]
- Sabirov, D.S. A correlation between the mean polarizability of the “kinked” polycyclic aromatic hydrocarbons and the number of H…H bond critical points predicted by Atoms-in-Molecules theory. Comput. Theor. Chem. 2014, 1030, 81–86. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Garipova, R.R.; Cataldo, F. Polarizability of isomeric and related interstellar compounds in the aspect of their abundance. Mol. Astrophys. 2018, 12, 10–19. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Tukhbatullina, A.A.; Shepelevich, I.S. Polarzability in astrochemical studies of complex carbon-based compounds. ACS Earth Space Chem. 2022, 6, 1–17. [Google Scholar] [CrossRef]
- Pino-Rios, R.; Báez-Grez, R.; Solà, M. Acenes and phenacenes in their lowest-lying triplet states. Does kinked remain more stable than straight? Phys. Chem. Chem. Phys. 2021, 23, 13574–13582. [Google Scholar] [CrossRef] [PubMed]
- Poater, J.; Visser, R.; Sola, M.; Bickelhaupt, F.M. Polycyclic benzenoids: Why kinked is more stable than straight. J. Org. Chem. 2007, 72, 1134–1142. [Google Scholar] [CrossRef] [PubMed]
- Pankratyev, E.Y.; Tukhbatullina, A.A.; Sabirov, D.S. Dipole polarizability, structure, and stability of [2+2]-linked fullerene nanostructures (C60) n (n ≤ 7). Physica E 2017, 86, 237–242. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Terentyev, A.O.; Bulgakov, R.G. Polarizability of fullerene [2+2]-dimers: A DFT study. Phys. Chem. Chem. Phys. 2014, 16, 14594–14600. [Google Scholar] [CrossRef]
- Tukhbatullina, A.A.; Shepelevich, I.S.; Sabirov, D.S. Exaltation of polarizability as a common property of fullerene dimers with diverse intercage bridges. Fuller. Nanotub. Carbon Nanostruct. 2018, 26, 661–666. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Garipova, R.R. The increase in the fullerene cage volume upon its chemical functionalization. Fuller. Nanotub. Carbon Nanostruct. 2019, 27, 702–709. [Google Scholar] [CrossRef]
- Zakirova, A.D.; Sabirov, D.S. Volume of the fullerene cages of endofullerenes and hydrogenated endofullerenes with encapsulated atoms of noble gases and nonadditivity of their polarizability. Russ. J. Phys. Chem. 2020, 94, 963–971. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Ori, O.; László, I. Isomers of the C84 fullerene: A theoretical consideration within energetic, structural, and topological approaches. Fuller. Nanotub. Carbon Nanostruct. 2018, 26, 100–110. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Ori, O.; Tukhbatullina, A.A.; Shepelevich, I.S. Covalently bonded fullerene nano-aggregates (C60)n: Digitalizing their energy-topology-symmetry. Symmetry 2021, 13, 1899. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Ori, O. Skeletal rearrangements of the C240 Fullerene: Efficient topological descriptors for monitoring Stone–Wales transformations. Mathematics 2020, 8, 968. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Ōsawa, E. Information entropy of fullerenes. J. Chem. Inf. Model. 2015, 55, 1574–1576. [Google Scholar] [CrossRef] [PubMed]
- Sabirov, D.S.; Terentyev, A.O.; Sokolov, V.I. Activation energies and information entropies of helium penetration through fullerene walls. Insights into the formation of endofullerenes nX@C60/70 (n = 1 and 2) from the information entropy approach. RSC Adv. 2016, 6, 72230–72237. [Google Scholar] [CrossRef]
- Sabirov, D.S. Information entropy of interstellar and circumstellar carbon-containing molecules: Molecular size against structural complexity. Comput. Theor. Chem. 2016, 1097, 83–91. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Garipova, R.R.; Kinzyabaeva, Z.S. Fullerene–1,4-dioxane adducts: A DFT study of the structural features and molecular properties. Fuller. Nanotub. Carbon Nanostruct. 2020, 28, 154–159. [Google Scholar] [CrossRef]
- Sabirov, D.; Koledina, K. Classification of isentropic molecules in terms of Shannon entropy. EPJ Web Conf. 2020, 244, 01016. [Google Scholar] [CrossRef]
- Bertz, S.H. Complexity of synthetic reactions. The use of complexity indices to evaluate reactions, transforms and disconnections. New J. Chem. 2003, 27, 860–869. [Google Scholar] [CrossRef]
- Böttcher, T. An additive definition of molecular complexity. J. Chem. Inf. Model. 2016, 56, 462–470. [Google Scholar] [CrossRef]
- Bonchev, D. Kolmogorov’s information, Shannon’s entropy, and topological complexity of molecules. Bulgar. Chem. Commun. 1995, 28, 567–582. Available online: https://www.researchgate.net/publication/255992446 (accessed on 21 August 2022).
- Barigye, S.J.; Marrero-Ponce, Y.; Pérez-Giménez, F.; Bonchev, D. Trends in information theory-based chemical structure codification. Mol. Divers. 2014, 18, 673–686. [Google Scholar] [CrossRef]
- Basak, S.C.; Gute, B.D.; Grunwald, G.D. Use of topostructural, topochemical, and geometric parameters in the prediction of vapor pressure: A hierarchical QSAR approach. J. Chem. Inf. Comput. Sci. 1997, 37, 651–655. [Google Scholar] [CrossRef]
- Sabirov, D. Information entropy changes in chemical reactions. Comput. Theor. Chem. 2018, 1123, 169–179. [Google Scholar] [CrossRef]
- Sabirov, D.S. Information entropy of mixing molecules and its application to molecular ensembles and chemical reactions. Comput. Theor. Chem. 2020, 1187, 112933. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef] [PubMed]
- Smolenskii, E.A. The Wiener distance matrix for acyclic compounds and polymers. J. Chem. Inf. Comput. Sci. 2004, 44, 522–528. [Google Scholar] [CrossRef]
- Nikolić, S.; Trinajstić, N.; Mihalić, Z. The Wiener index: Development and applications. Croat. Chem. Acta 1995, 68, 105–129. [Google Scholar]
- Vukicevic, D.; Cataldo, F.; Ori, O.; Graovac, A. Topological efficiency of C66 fullerene. Chem. Phys. Lett. 2011, 501, 442–445. [Google Scholar] [CrossRef]
- Iranmanesh, A.; Ashrafi, A.R.; Graovac, A.; Cataldo, F.; Ori, O. Wiener index role in topological modeling of hexagonal systems-from fullerenes to graphene. In Distance in Molecular Graphs-Applications; Gutman, I., Furtula, B., Eds.; University Kragujevac: Kragujevac, Serbia, 2012; pp. 135–155. [Google Scholar]
- Ori, O.; Cataldo, F.; Graovac, A. Topological ranking of C28 fullerenes reactivity. Fuller. Nanotub. Carbon Nanostruct. 2009, 17, 308–323. [Google Scholar] [CrossRef]
- Koorepazan-Moftakhar, F.; Ashrafi, A.R.; Ori, O.; Putz, M.V. Sphericality of some classes of fullerenes measured by topology. In Fullerenes: Chemistry, Natural Sources and Technological Applications; Ellis, S.B., Ed.; Nova Science Publishers, Inc.: New York, NY, USA, 2014; pp. 285–304. [Google Scholar]
- Putz, M.V.; Ori, O.; Cataldo, F.; Putz, A.M. Parabolic reactivity “coloring” molecular topology: Application to carcinogenic PAHs. Curr. Org. Chem. 2013, 17, 2816–2830. [Google Scholar] [CrossRef]
- Cataldo, F.; Ori, O.; Iglesias-Groth, S. Topological lattice descriptors of graphene sheets with fullerene-like nanostructures. Mol. Simul. 2010, 36, 341–353. [Google Scholar] [CrossRef]
- Bonchev, D.; Mekenyan, O. A topological approach to the calculation of the π–electron energy and energy gap of infinite conjugated polymers. Z. Nat. A 1980, 35, 739–747. [Google Scholar] [CrossRef]
- Ori, O.; Cataldo, F.; Vukicevic, D.; Graovac, A. Wiener way to dimensionality. Iran. J. Math. Chem. 2010, 1, 5–15. [Google Scholar] [CrossRef]
- Ori, O.; Cataldo, F.; Putz, M.V.; Kaatz, F.; Bultheel, A. Cooperative topological accumulation of vacancies in honeycomb lattices. Fuller. Nanotub. Carbon Nanostruct. 2016, 24, 353–362. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Laikov, D.N.; Ustynyuk, Y.A. PRIRODA-04: A quantum-chemical program suite. New possibilities in the study of molecular systems with the application of parallel computing. Russ. Chem. Bull. 2005, 54, 820–826. [Google Scholar] [CrossRef]
- Cárdenas, C.; Ayers, P.; De Proft, F.; Tozer, D.J.; Geerlings, P. Should negative electron affinities be used for evaluating the chemical hardness? Phys. Chem. Chem. Phys. 2011, 13, 2285–2293. [Google Scholar] [CrossRef]
- Wannere, C.S.; Sattelmeyer, K.W.; Schaefer, H.F., III; von Ragué Schleyer, P. Aromaticity: The alternating C–C bond length structures of [14]-, [18]-, and [22]annulene. Angew. Chem. Int. Ed. 2004, 43, 4200–4206. [Google Scholar] [CrossRef]
- Szczepanik, D.W.; Solà, M.; Andrzejak, M.; Pawełek, B.; Dominikowska, J.; Kukułka, M.; Dyduch, K.; Krygowski, T.M.; Szatylowicz, H. The role of the long-range exchange corrections in the description of electron delocalization in aromatic species. J. Comput. Chem. 2017, 38, 1640–1654. [Google Scholar] [CrossRef]
- Torrent-Sucarrat, M.; Navarro, S.; Cossío, F.P.; Anglada, J.M.; Luis, J.M. Relevance of the DFT method to study expanded porphyrins with different topologies. J. Comput. Chem. 2017, 38, 2819–2828. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Fox, D.J. Gaussian 09; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Tampieri, F.; Barbon, A.; Tommasini, M. Analysis of the Jahn–Teller effect in coronene and corannulene ions and its effect in EPR spectroscopy. Chem. Phys. Impact 2021, 2, 100012. [Google Scholar] [CrossRef]
- Bultheel, A.; Ori, O. Topological modeling of 1-pentagon carbon nanocones–topological efficiency and magic sizes. Fuller. Nanotub. Carbon Nanostruct. 2018, 26, 291–302. [Google Scholar] [CrossRef]
- Rempala, P.; Kroulik, J.; King, B.T. A Slippery Slope: Mechanistic analysis of the intramolecular Scholl reaction of hexaphenylbenzene. J. Am. Chem. Soc. 2004, 126, 15002–15003. [Google Scholar] [CrossRef] [PubMed]
- Lukmanov, T.I.; Shepelevich, I.S.; Sabirov, D.S. Polarizability of polycyclic aromatic hydrocarbon compounds from the intermediate stages of the oxidative condensation of hexaphenylbenzene into hexa-peri-hexabenzocoronene. Vestn. Bashkir. Univ. 2022, 27, 98–101. [Google Scholar] [CrossRef]
- Sabirov, D.; Tukhbatullina, A.; Shepelevich, I. Information entropy of regular dendrimer aggregates and irregular intermediate structures. Liquids 2021, 1, 2. [Google Scholar] [CrossRef]
- Balasubramanian, K. Symmetry and combinatorial concepts for cyclopolyarenes, nanotubes and 2D-sheets: Enumerations, isomers, structures spectra & properties. Symmetry 2021, 14, 34. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Shepelevich, I.S. Information entropy in chemistry: An overview. Entropy 2021, 23, 1240. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).