Crystallization Kinetics of Poly(lactic acid)–Graphene Nanoscroll Nanocomposites: Role of Tubular, Planar, and Scrolled Carbon Nanoparticles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of PLA-GNS Polymer Nanocomposite
2.3. Differential Scanning Calorimeter (DSC)
2.4. Nanoindentation
3. Results and Discussion
3.1. Isothermal Crystallization Studies
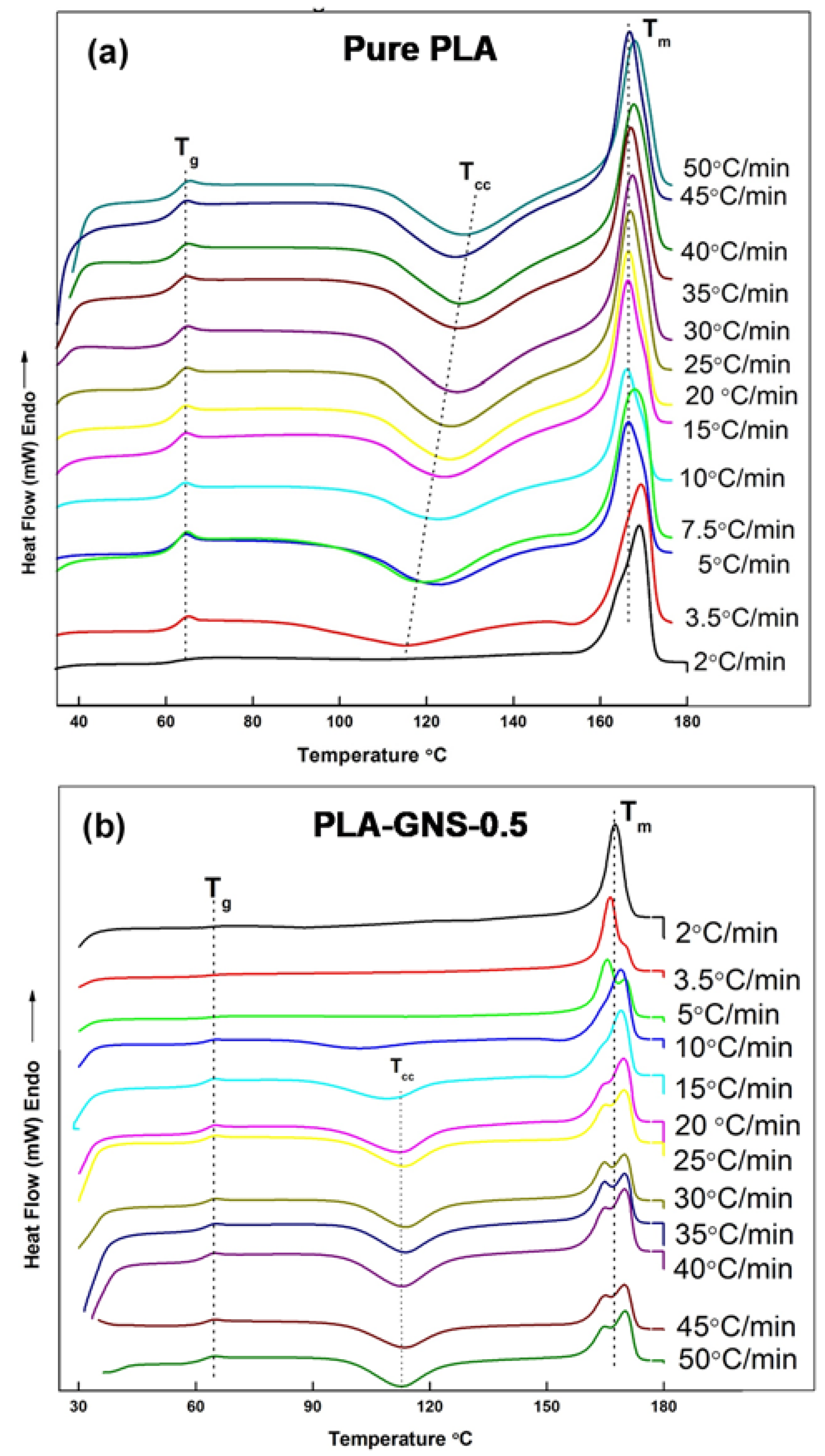
3.2. Non-Isothermal Crystallization Studies
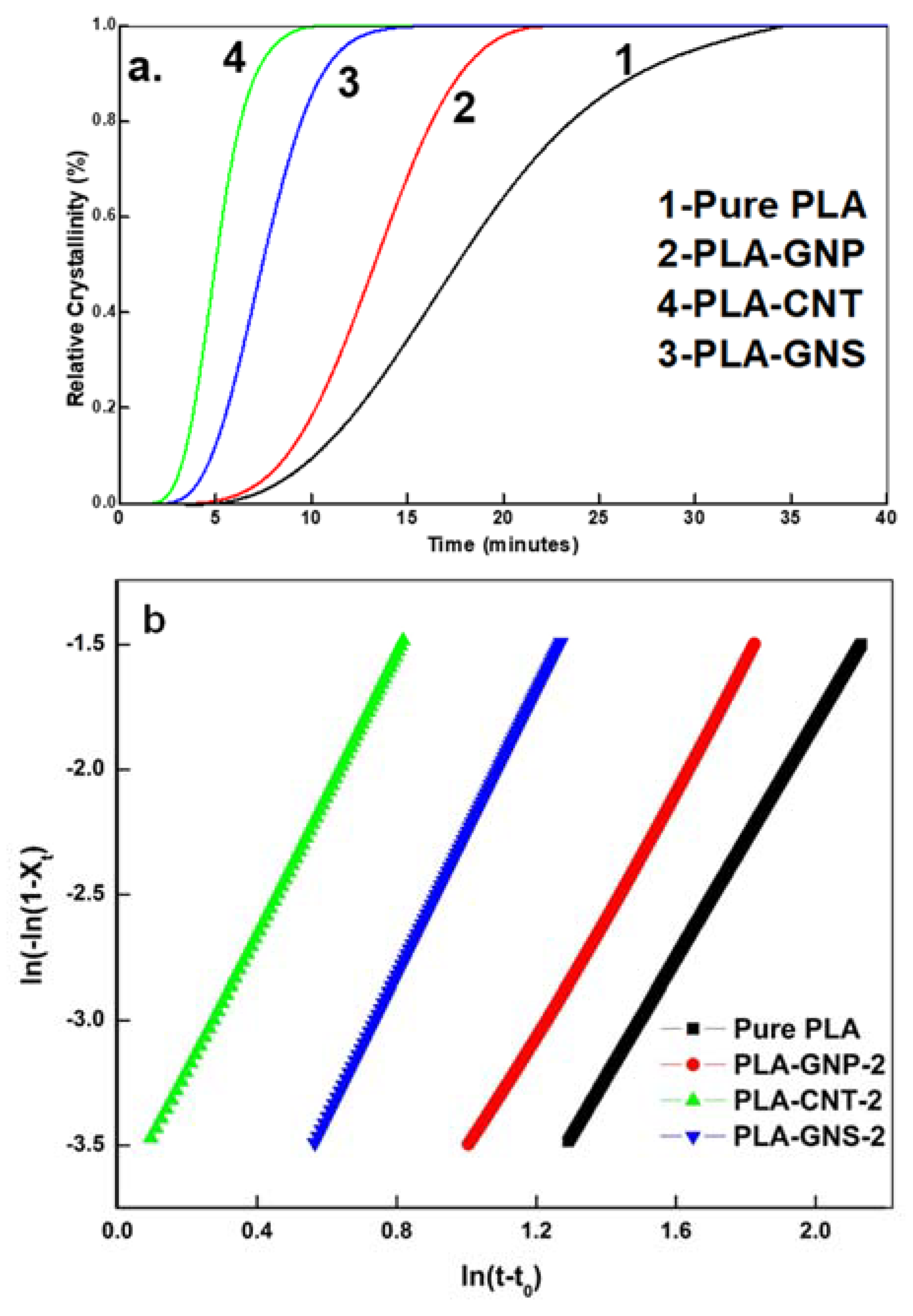
3.3. Comparative Analysis of PLA-GNS, PLA-CNT, PLA-GNP
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Murariu, M.; Dubois, P. PLA composites: From production to properties. Adv. Drug Deliv. Rev. 2016, 107, 17–46. [Google Scholar] [CrossRef]
- Feng, Y.; Ma, P.; Xu, P.; Wang, R.; Dong, W.; Chen, M.; Joziasse, C. The crystallization behavior of poly(lactic acid) with different types of nucleating agents. Int. J. Biol. Macromol. 2018, 106, 955–962. [Google Scholar] [CrossRef]
- Farah, S.; Anderson, D.G.; Langer, R. Physical and Mechanical Properties of PLA, and Their Functions in Widespread Applications—A Comprehensive Review. Adv. Drug. Deliv. Rev. 2016, 107, 367–392. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hamad, K.; Kaseem, M.; Yang, H.W.; Deri, F.; Ko, Y.G. Properties and medical applications of poly(lactic acid): A review. Express Polym. Lett. 2015, 9, 435–455. [Google Scholar] [CrossRef]
- Wachirahuttapong, S.; Thongpin, C.; Sombatsompop, N. Effect of PCL and compatibility contents on the morphology, crystallization and mechanical properties of PLA/PCL blends. Energy Procedia 2016, 89, 198–206. [Google Scholar] [CrossRef] [Green Version]
- Saeidlou, S.; Huneault, M.A.; Li, H.; Park, C.B. Poly(lactic acid) crystallization. Prog. Polym. Sci. 2012, 37, 1657–1677. [Google Scholar] [CrossRef]
- Li, H.; Huneault, M.A. Effect of nucleation and plasticization on the crystallization of poly(lactic acid). Polymer 2007, 48, 6855–6866. [Google Scholar] [CrossRef] [Green Version]
- Nampoothiri, K.M.; Nair, N.R.; John, R.P. An overview of the recent developments in polylactide (PLA) research. Bioresour. Technol. 2010, 101, 8493–8501. [Google Scholar] [CrossRef]
- Castro-Aguirre, E.; Iniguez-Franco, F.; Samsudin, H.; Fang, X.; Auras, R. Poly(lactic acid)—Mass production, processing, industrial applications, and end of life. Adv. Drug Deliv. Rev. 2016, 107, 333–366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, B.; Xu, Z.; Gao, C. Mass production of graphene nanoscrolls and their application in high rate performance supercapacitors. Nanoscale 2016, 8, 1413–1420. [Google Scholar] [CrossRef]
- Dhar, P.; Gaur, S.S.; Kumar, A.; Katiyar, V. Cellulose nanocrystal templated graphene nanoscrolls for high performance supercapacitors and hydrogen storage: An experimental and molecular simulation study. Sci. Rep. 2018, 8, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Zheng, B.N.; Gao, C. Preparation of graphene nanoscrolls/poly(aniline) composites and their use in high performance super capacitors. New Carbon Mater. 2016, 31, 315–320. [Google Scholar] [CrossRef]
- Xu, Z.; Zheng, B.; Chen, J.; Gao, C. Highly efficient synthesis of neat graphene nanoscrolls from graphene oxide by well-controlled lyophilization. Chem. Mater. 2014, 26, 6811–6818. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, B.; Yang, Z.; Zhang, P.; Zheng, Z.; Ren, W.; Yan, X. Facile preparation of large-scale graphene nanoscrolls from graphene oxide sheets by cold quenching in liquid nitrogen. Carbon 2014, 79, 470–477. [Google Scholar] [CrossRef]
- Gao, Y.; Chen, X.; Xu, H.; Zou, Y.; Gu, R.; Xu, M.; Jen, A.K.Y.; Chen, H. Highly efficient fabrication of nanoscrolls from functionalized graphene oxide by Langmuir Blodgett method. Carbon 2010, 48, 4475–4482. [Google Scholar] [CrossRef]
- Li, H.; Papadakis, R.; Jafri, S.H.M.; Thersleff, T.; Michler, J.; Ottosson, H.; Leifer, K. Superior adhesion of graphene nanoscrolls. Commun. Phys. 2018, 1, 44. [Google Scholar] [CrossRef]
- Chen, X.; Li, L.; Sun, X.; Kia, H.G.; Peng, H. A novel synthesis of graphene nanoscrolls with tunable dimension at a large scale. Nanotechnology 2012, 23, 055603. [Google Scholar] [CrossRef]
- Liu, M.; Zhao, Q.; Wang, Y.; Zhang, C.; Mo, Z.; Cao, S. Melting behaviors, isothermal and non-isothermal crystallization kinetics of nylon 1212. Polymer 2003, 44, 2537–2545. [Google Scholar] [CrossRef]
- Ajala, O.; Werther, C.; Nikaeen, P.; Singh, R.P.; Depan, D. Influence of graphene nanoscrolls on the crystallization behavior and nano-mechanical properties of poly(lactic acid). Polym. Adv. Technol. 2019, 30, 1825–1835. [Google Scholar] [CrossRef]
- Bianchi, O.; Oliveira, R.V.B.; Fiorio, R.; Martins, J.D.N.; Zattera, A.J.; Canto, L.B. Assessment of Avrami, Ozawa and Avrami–Ozawa equations for determination of EVA crosslinking kinetics from DSC measurements. Polym. Test. 2008, 27, 722–729. [Google Scholar] [CrossRef]
- Jiang, X.L.; Luo, S.J.; Sun, K.; Chen, X.D. Effect of nucleating agents on crystallization kinetics of PET. Express Polym. Lett. 2007, 1, 245–251. [Google Scholar] [CrossRef]
- Wu, D.; Cheng, Y.; Feng, S.; Yao, Z.; Zhang, M. Crystallization behavior of polylactide/graphene composites. Ind. Eng. Chem. Res. 2013, 52, 6731–6739. [Google Scholar] [CrossRef]
- Lorenzo, A.T.; Arnal, M.L.; Albuerne, J.; Müller, A.J. DSC isothermal polymer crystallization kinetics measurements and the use of the Avrami equation to fit the data: Guidelines to avoid common problems. Polym. Test. 2007, 26, 222–231. [Google Scholar] [CrossRef]
- Barrau, S.; Vanmansart, C.; Moreau, M.; Addad, A.; Stoclet, G.; Lefebvre, J.M.; Seguela, R. Crystallization behavior of carbon nanotube-polylactide nanocomposites. Macromolecules 2011, 44, 6496–6502. [Google Scholar] [CrossRef]
- Kummara, S.; Tashiro, K.; Monma, T.; Horita, K. Isotope Effect on the Melt–Isothermal Crystallization of Polyoxymethylene D/H Random Copolymers and D/H Blend Samples. Macromolecules 2015, 48, 8070–8081. [Google Scholar] [CrossRef]
- Sperling, L.H. Introduction to Physical Polymer Science, 4th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Kawai, T.; Rahman, N.; Matsuba, G.; Nishida, K.; Kanaya, T.; Nakano, M.; Okamoto, H.; Kawada, J.; Usuki, A.; Honma, N.; et al. Crystallization and melting behavior of poly(L-lactic acid). Macromolecules 2007, 40, 9463–9469. [Google Scholar] [CrossRef]
- Wang, H.; Qiu, Z. Crystallization behaviors of biodegradable poly(L-lactic acid)/graphene oxide nanocomposites from the amorphous state. Thermochim. Acta 2011, 526, 229–236. [Google Scholar] [CrossRef]
- Xu, Z.; Niu, Y.; Yang, L.; Xie, W.; Li, H.; Gan, Z.; Wang, Z. Morphology, rheology and crystallization behavior of polylactide composites prepared through addition of five-armed star polylactide grafted multiwalled carbon nanotubes. Polymer 2010, 51, 730–737. [Google Scholar] [CrossRef]
- Xu, J.Z.; Chen, T.; Yang, C.L.; Li, Z.M.; Mao, Y.M.; Zeng, B.Q.; Hsiao, B.S. Isothermal crystallization of poly(L-lactide) induced by graphene nanosheets and carbon nanotubes: A comparative study. Macromolecules 2010, 43, 5000–5008. [Google Scholar] [CrossRef]
- Li, L.; Li, C.Y.; Ni, C. Polymer crystallization-driven, periodic patterning on carbon nanotubes. J. Am. Chem. Soc. 2006, 128, 1692–1699. [Google Scholar] [CrossRef]
- Xin, S.; Li, Y.; Zhao, H.; Bian, Y.; Li, W.; Han, C.; Dong, Q.; Ning, Z.; Dong, L. Confinement crystallization of poly(lactide) induced by mutiwalled carbon nanotubes and graphene nanosheets. J. Therm. Anal. Calor. 2015, 122, 379–391. [Google Scholar] [CrossRef]
- Zafeiropoulos, N.E.; Baillie, C.A.; Matthews, F.L. A study of transcrystallinity and its effect on the interface in flax fiber reinforced composite materials. Composite A Appl. Sci. Manufact. 2015, 32, 525–543. [Google Scholar] [CrossRef]
- He, Y.; Chen, W.F.; Yu, W.B.; Ouyang, G.; Yang, G.W. Anomalous interface adhesion of graphene membranes. Sci. Rep. 2013, 3, 2660. [Google Scholar] [CrossRef] [PubMed]
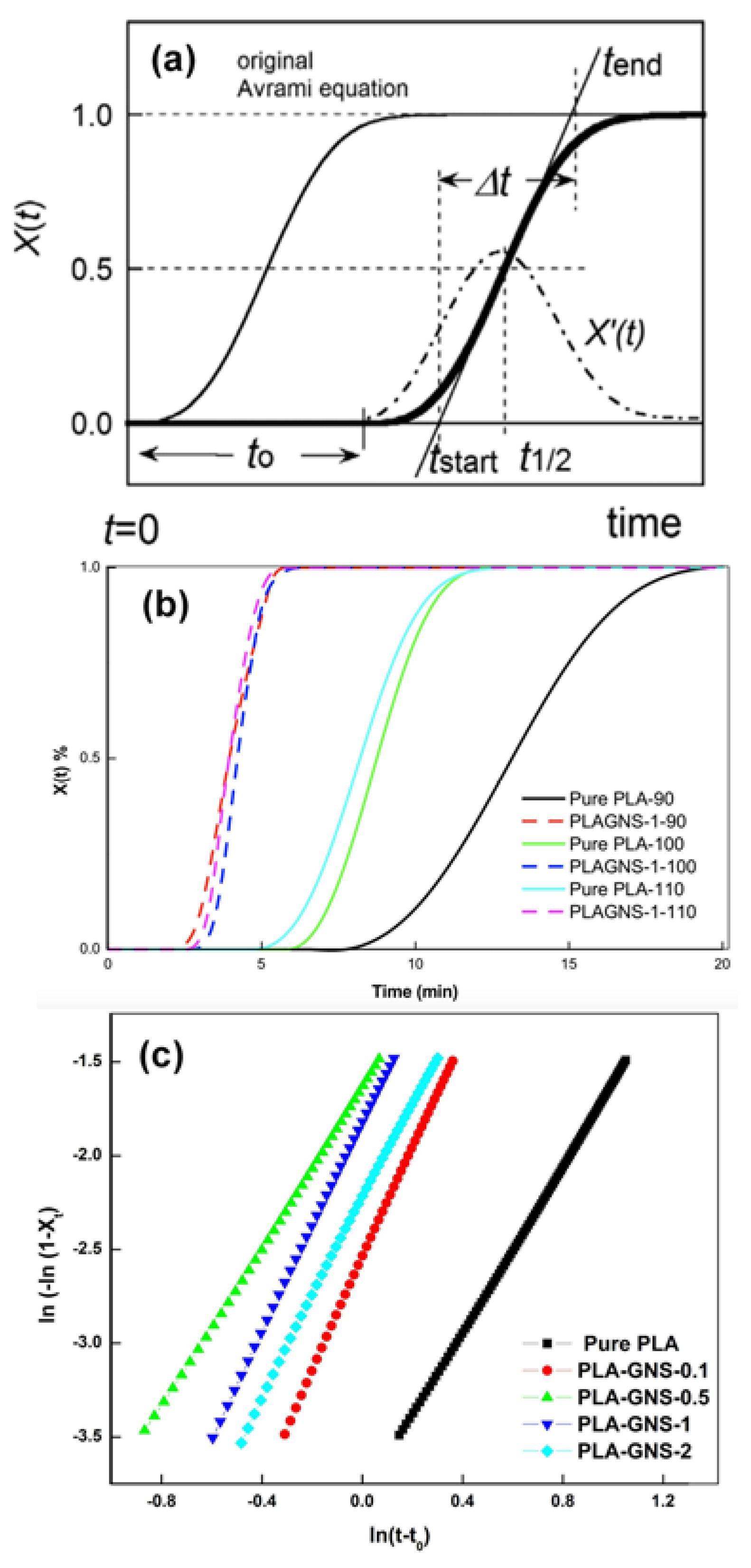

| Samples | Tc (°C) | Xc (%) | t0 (min) | t1/2 (obs) (min) | t1/2 (calc) (min) | n | k (min−n) | |
|---|---|---|---|---|---|---|---|---|
| Pure PLA | 90 | 38.0 | 40.8 | 4.06 | 17.58 | 17.65 | 2.37 | 1.44 × 10−3 |
| 100 | 33.8 | 41.7 | 1.83 | 6.46 | 6.59 | 2.22 | 2.16 × 10−2 | |
| 110 | 33.3 | 36.0 | 1.70 | 6.34 | 6.49 | 2.18 | 2.29 × 10−2 | |
| PLA-GNS-0.1 | 90 | 47.2 | 50.7 | 2.21 | 7.06 | 7.10 | 2.35 | 1.66 × 10−2 |
| 100 | 39.6 | 42.5 | 1.35 | 3.52 | 3.44 | 2.96 | 7.84 × 10−2 | |
| 110 | 34.4 | 36.9 | 1.70 | 3.00 | 2.95 | 2.65 | 1.63 × 10−1 | |
| PLA-GNS-0.5 | 90 | 56.6 | 60.7 | 1.49 | 6.78 | 6.64 | 2.51 | 1.14 × 10−2 |
| 100 | 34.3 | 36.8 | 1.03 | 2.81 | 2.85 | 2.13 | 1.94 × 10−1 | |
| 110 | 38.5 | 41.4 | 1.03 | 2.60 | 2.52 | 2.76 | 2.32 × 10−1 | |
| PLA-GNS-1 | 90 | 51.1 | 54.9 | 1.68 | 6.80 | 6.51 | 3.64 | 2.25 × 10−3 |
| 100 | 42.1 | 45.2 | 1.35 | 3.10 | 3.03 | 2.79 | 1.62 × 10−1 | |
| 110 | 34.3 | 36.8 | 1.17 | 2.43 | 2.39 | 2.73 | 3.99 × 10−1 | |
| PLA-GNS-2 | 90 | 50.1 | 53.8 | 2.09 | 7.47 | 7.38 | 2.84 | 6.12 × 10−3 |
| 100 | 41.4 | 44.5 | 1.37 | 3.56 | 3.42 | 2.59 | 1.07 × 10−1 | |
| 110 | 33.6 | 36.0 | 1.24 | 2.24 | 2.28 | 2.24 | 6.37 × 10−1 |
| Sample | ϕ (°C min−1) | Tg (°C) | Tm1 (°C) | Tm2 (°C) | Tcc (°C) | ΔHf (J g−1) | ΔHc (J g−1) | Xc (%) |
|---|---|---|---|---|---|---|---|---|
| Pure PLA | 2 | 62.7 | 168.9 | - | 30.7 | 33.02 | ||
| 3.5 | 62.7 | 169.3 | - | 115.2 | 35.7 | −16.5 | 20.58 | |
| 5 | 62.3 | 167.9 | - | 119.3 | 40.2 | −31.7 | 9.15 | |
| 7.5 | 62.2 | 166.5 | - | 123.6 | 30.2 | −29.3 | 0.98 | |
| 10 | 61.8 | 166.1 | - | 123.0 | 24.0 | −21.2 | 2.99 | |
| 15 | 61.9 | 166.4 | - | 124.3 | 29.6 | −29.6 | −0.09 | |
| 20 | 61.9 | 166.5 | - | 125.5 | 31.4 | −32.1 | −0.72 | |
| 25 | 62.4 | 166.9 | - | 125.9 | 33.2 | −30.8 | 2.58 | |
| 30 | 61.5 | 166.7 | - | 126.6 | 33.1 | −32.5 | 0.63 | |
| 35 | 62.2 | 167.4 | - | 127.1 | 35.4 | −33.7 | 1.81 | |
| 40 | 62.0 | 167.0 | - | 127.4 | 32.5 | −31.0 | 1.61 | |
| 45 | 62.6 | 167.6 | - | 128.0 | 30.3 | −32.8 | −2.78 | |
| 50 | 62.6 | 168.0 | - | 128.4 | 29.7 | −24.3 | 5.77 | |
| PLA-GNS-0.1 | 2 | 62.9 | 167.6 | - | - | 45.3 | - | 48.61 |
| 3.5 | 63.7 | 166.2 | - | - | 33.2 | - | 35.62 | |
| 5 | 62.6 | 165.1 | 169.9 | - | 29.3 | - | 31.52 | |
| 7.5 | 62.4 | 168.9 | - | 105.4 | 40.8 | −11.8 | 31.17 | |
| 10 | 61.9 | 168.3 | - | 101.0 | 37.1 | −9.9 | 29.23 | |
| 15 | 62.2 | 165.3 | 169.1 | 115.4 | 32.5 | −30.2 | 2.52 | |
| 20 | 62.1 | 165.0 | 169.5 | 117.0 | 34.5 | −33.0 | 1.63 | |
| 25 | 62.3 | 165.1 | 169.6 | 116.4 | 33.4 | −35.9 | −2.75 | |
| 30 | 61.8 | 164.6 | 169.8 | 114.1 | 29.5 | −30.7 | −1.29 | |
| 35 | 62.0 | 164.3 | 169.9 | 113.9 | 31.3 | −32.7 | −1.49 | |
| 40 | 63.0 | 164.8 | 170.3 | 114.4 | 30.6 | −30.9 | −0.27 | |
| 45 | 62.9 | 165.8 | 170.3 | 117.3 | 36.6 | −41.2 | −4.98 | |
| 50 | 61.9 | 165.1 | 170.2 | 114.8 | 34.5 | −37.4 | −3.14 | |
| PLA-GNS-0.5 | 2 | 63.6 | 167.3 | - | - | 39.9 | - | 42.87 |
| 3.5 | 62.7 | 166.0 | - | - | 32.2 | - | 34.58 | |
| 5 | 63.5 | 165.4 | 170.0 | - | 32.6 | - | 35.00 | |
| 10 | 62.7 | 168.9 | - | 101.9 | 39.5 | −10.3 | 31.38 | |
| 15 | 62.4 | 168.9 | - | 108.9 | 35.7 | −24.1 | 12.52 | |
| 20 | 62.4 | 164.5 | 169.6 | 112.2 | 38.4 | −32.1 | 6.74 | |
| 25 | 62.3 | 164.9 | 169.8 | 113.5 | 32.0 | −30.7 | 1.41 | |
| 30 | 62.3 | 164.7 | 169.8 | 113.7 | 28.8 | −29.9 | −1.20 | |
| 35 | 62.5 | 164.7 | 170.0 | 113.7 | 30.1 | −29.1 | 1.14 | |
| 40 | 62.5 | 164.8 | 169.8 | 113.0 | 37.8 | −36.7 | 1.17 | |
| 45 | 62.8 | 164.8 | 169.8 | 113.5 | 27.0 | −26.0 | 1.05 | |
| 50 | 62.6 | 164.6 | 170.1 | 112.8 | 29.6 | −26.0 | 3.89 | |
| PLA-GNS-1 | 2 | 62.4 | 166.1 | - | - | 33.5 | - | 36.02 |
| 3.5 | 62.2 | 165.5 | - | - | 36.0 | - | 38.71 | |
| 5 | 63.5 | 164.8 | 169.8 | - | 23.5 | - | 25.25 | |
| 7.5 | 61.0 | 163.6 | 169.0 | - | 31.2 | −3.0 | 30.29 | |
| 10 | 62.4 | 164.3 | 169.2 | 111.3 | 35.0 | −23.5 | 12.37 | |
| 15 | 61.4 | 163.4 | 168.5 | 111.1 | 33.5 | −13.8 | 21.20 | |
| 20 | 62.7 | 164.2 | 170.0 | 111.6 | 31.6 | −25.9 | 6.06 | |
| 25 | 62.3 | 164.2 | 169.6 | 113.4 | 29.2 | −23.2 | 6.46 | |
| 30 | 62.6 | 165.0 | 170.3 | 111.9 | 48.0 | −47.0 | 1.07 | |
| 35 | 62.4 | 164.6 | 170.3 | 113.8 | 35.1 | −37.3 | −2.33 | |
| 40 | 62.7 | 165.0 | 170.4 | 114.7 | 29.9 | −29.5 | 0.45 | |
| 45 | 62.8 | 165.0 | 170.3 | 115.2 | 36.1 | −37.1 | −1.11 | |
| 50 | 62.5 | 163.9 | 170.0 | 112.6 | 36.9 | −38.2 | −1.39 | |
| PLA-GNS-2 | 2 | 64.4 | 166.9 | - | - | 33.2 | - | 35.70 |
| 3.5 | 63.0 | 165.3 | 169.8 | - | 28.2 | - | 30.31 | |
| 5 | 62.9 | 165.0 | 170.1 | - | 31.4 | - | 33.77 | |
| 7.5 | 62.0 | 164.6 | 169.4 | - | 24.5 | −2.1 | 24.07 | |
| 10 | 62.3 | - | 168.6 | 105.8 | 35.5 | −15.4 | 21.55 | |
| 15 | 62.3 | - | 169.2 | 109.5 | 37.2 | −22.6 | 15.66 | |
| 20 | 61.9 | - | 169.7 | 110.4 | 36.6 | −30.6 | 6.42 | |
| 25 | 62.1 | 163.8 | 169.8 | 112.0 | 32.0 | −27.8 | 4.49 | |
| 30 | 62.1 | 163.8 | 169.8 | 110.8 | 25.9 | −23.9 | 2.14 | |
| 35 | 62.3 | 164.7 | 170.3 | 113.9 | 45.1 | −41.4 | 3.89 | |
| 40 | 61.7 | 162.8 | 169.3 | 109.0 | 22.7 | −19.8 | 3.18 | |
| 45 | 62.6 | 163.3 | 169.8 | 110.5 | 27.8 | −27.0 | 0.86 | |
| 50 | 62.6 | 163.5 | 170.4 | 109.7 | 38.7 | −35.7 | 3.16 |
| ϕ (°C min−1) | Sample | n | k | R2 | t1/2 |
|---|---|---|---|---|---|
| 2 | Pure PLA | 1.81 | 1.54 × 10−3 | 0.9999 | 30.25 |
| PLA-GNS-0.1 | 3.76 | 5.19 × 10−3 | 1 | 28.82 | |
| PLA-GNS-0.5 | 4.32 | 2.56 × 10−3 | 0.9998 | 29.2 | |
| PLA-GNS-1 | 3.46 | 4.00 × 10−3 | 1 | 30.32 | |
| PLA-GNS-2 | 2.72 | 8.30 × 10−3 | 0.9935 | 30.6 | |
| 3.5 | Pure PLA | 2.79 | 5.37 × 10−2 | 0.999 | 23.05 |
| PLA-GNS-0.1 | 4.04 | 7.23 × 10−3 | 1 | 17.77 | |
| PLA-GNS-0.5 | 3.56 | 1.02 × 10−1 | 1 | 17.97 | |
| PLA-GNS-1 | 3.45 | 8.32 × 10−2 | 0.9999 | 18.42 | |
| PLA-GNS-2 | 3.47 | 6.99 × 10−2 | 1 | 18.42 | |
| 5 | Pure PLA | 1.24 | 7.07 × 10−2 | 0.9985 | 15.73 |
| PLA-GNS-0.1 | 3.1 | 8.70 × 10−1 | 0.9999 | 13.33 | |
| PLA-GNS-0.5 | 2.94 | 2.40 × 10−1 | 0.9931 | 14.32 | |
| PLA-GNS-1 | 4.4 | 9.30 × 10−2 | 0.998 | 13.78 | |
| PLA-GNS-2 | 4.11 | 3.55 × 10−1 | 0.9996 | 13.32 | |
| 7.5 | Pure PLA | 1.55 | 1.85 × 10−1 | 0.9975 | 12.73 |
| PLA-GNS-0.1 | 2.63 | 6.43 × 10−2 | 0.9999 | 10.62 | |
| PLA-GNS-0.5 | 2.14 | 3.87 × 10−1 | 1 | 10.07 | |
| PLA-GNS-1 | 2.89 | 7.29 × 10−2 | 0.9981 | 9.72 | |
| PLA-GNS-2 | 2.97 | 8.52 × 10−2 | 0.9994 | 9.6 | |
| 10 | Pure PLA | 2.34 | 3.08 × 100 | 0.9983 | 11.5 |
| PLA-GNS-0.1 | 2.74 | 8.97 × 100 | 1 | 8.33 | |
| PLA-GNS-0.5 | 2.79 | 1.12 × 101 | 0.9997 | 8.25 | |
| PLA-GNS-1 | 2.52 | 6.81 × 100 | 0.9977 | 8.57 | |
| PLA-GNS-2 | 2.57 | 1.09 × 101 | 0.9991 | 8.55 |
| Scheme | Parameters | PLA-GNS | PLA-CNT | PLA-GNP |
|---|---|---|---|---|
| 2.84 | 2.76 | 2.46 | ||
| (min−n) | 6.12 × 10−3 | 2.34 × 10−2 | 2.43 × 10−3 | |
| R2 | 1 | 0.9998 | 0.9989 | |
| t0 (minutes) | 5.4 | 3.4 | 9.2 | |
| t1/2 (minutes) | 7.5 | 5 | 13.3 | |
| ΔHf (J g−1) | 51.3433 | 50.9566 | 48.3337 | |
| Xc (%) | 55.149 | 54.733 | 51.916 | |
| Tm (°C) | 168.35 | 168.35 | 167.97 | |
| Tg (°C) | 66.13 | 64.4 | 65.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ajala, O.; Werther, C.; Mahmudzade, R.; Nikaeen, P.; Depan, D. Crystallization Kinetics of Poly(lactic acid)–Graphene Nanoscroll Nanocomposites: Role of Tubular, Planar, and Scrolled Carbon Nanoparticles. C 2021, 7, 75. https://doi.org/10.3390/c7040075
Ajala O, Werther C, Mahmudzade R, Nikaeen P, Depan D. Crystallization Kinetics of Poly(lactic acid)–Graphene Nanoscroll Nanocomposites: Role of Tubular, Planar, and Scrolled Carbon Nanoparticles. C. 2021; 7(4):75. https://doi.org/10.3390/c7040075
Chicago/Turabian StyleAjala, Oluwakemi, Caroline Werther, Rauf Mahmudzade, Peyman Nikaeen, and Dilip Depan. 2021. "Crystallization Kinetics of Poly(lactic acid)–Graphene Nanoscroll Nanocomposites: Role of Tubular, Planar, and Scrolled Carbon Nanoparticles" C 7, no. 4: 75. https://doi.org/10.3390/c7040075
APA StyleAjala, O., Werther, C., Mahmudzade, R., Nikaeen, P., & Depan, D. (2021). Crystallization Kinetics of Poly(lactic acid)–Graphene Nanoscroll Nanocomposites: Role of Tubular, Planar, and Scrolled Carbon Nanoparticles. C, 7(4), 75. https://doi.org/10.3390/c7040075







