Effects of the Stacking Faults on the Electrical Resistance of Highly Ordered Graphite Bulk Samples
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Resistance before and after Contacting the Edge of a Graphite Sample
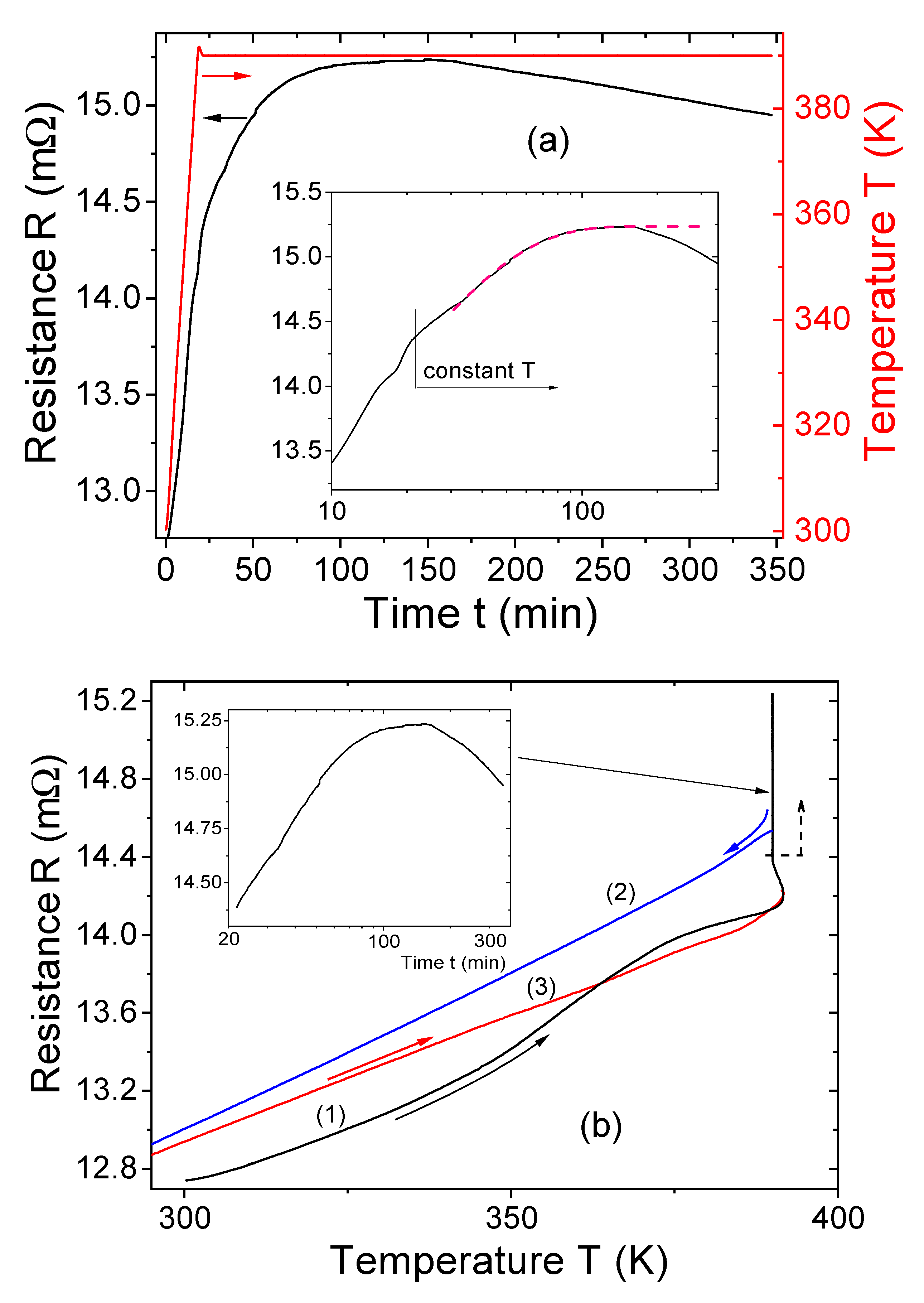
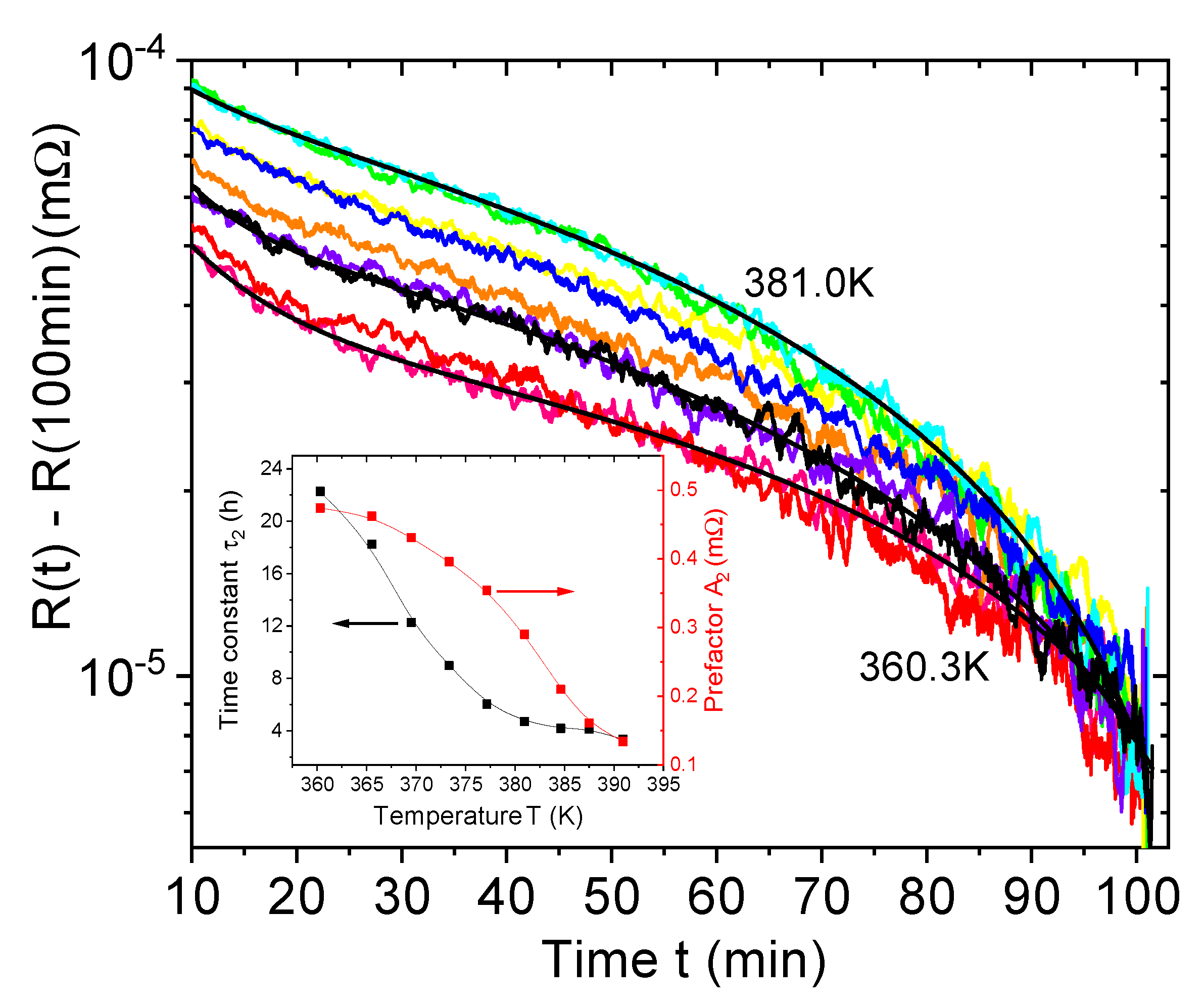
3.2. High-Temperature Annealing Effects on the Resistance
3.3. Influence of Air Atmosphere: Recovery of the Resistance
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| XRD | X-ray diffraction |
| TEM | transmission electron microscopy |
| HOPG | highly oriented pyrolytic graphite |
| AC LR700 | Alternating Current Linear Research 700 |
| 2D | two dimensional |
References
- Kelly, B.T. Physics of Graphite; Applied Science Publishers: London, UK, 1981. [Google Scholar]
- Esquinazi, P. (Ed.) Basic Physics of Functionalized Graphite; Springer Series in Materials Science 244; Springer International Publishing AG: Cham, Switzerland, 2016. [Google Scholar]
- Celzard, A.; Marêché, J.; Payot, F.; Furdin, G. Electrical conductivity of carbonaceous powders. Carbon 2002, 40, 2801–2815. [Google Scholar] [CrossRef]
- Pérez-Rodríguez, S.; Torres, D.; Lázaro, M. Effect of oxygen and structural properties on the electrical conductivity of powders of nanostructured carbon materials. Powder Technol. 2018, 340, 380–388. [Google Scholar] [CrossRef]
- González, J.C.; Muñoz, M.; García, N.; Barzola-Quiquia, J.; Spoddig, D.; Schindler, K.; Esquinazi, P. Sample-Size Effects in the Magnetoresistance of Graphite. Phys. Rev. Lett. 2007, 99, 216601. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, K.S.; Gangulin, N. Large Anisotropy of the Electrical Conductivity of Graphite. Nature 1939, 144, 667. [Google Scholar] [CrossRef]
- Barzola-Quiquia, J.; Yao, J.L.; Rödiger, P.; Schindler, K.; Esquinazi, P. Sample size effects on the transport properties of mesoscopic graphite samples. Phys. Status Sol. (A) 2008, 205, 2924–2933. [Google Scholar] [CrossRef]
- García, N.; Esquinazi, P.; Barzola-Quiquia, J.; Dusari, S. Evidence for semiconducting behavior with a narrow band gap of Bernal graphite. New J. Phys. 2012, 14, 053015. [Google Scholar] [CrossRef]
- Precker, C.E.; Esquinazi, P.D.; Champi, A.; Barzola-Quiquia, J.; Zoraghi, M.; Muiños-Landin, S.; Setzer, A.; Böhlmann, W.; Spemann, D.; Meijer, J.; et al. Identification of a possible superconducting transition above room temperature in natural graphite crystals. New J. Phys. 2016, 18, 113041. [Google Scholar] [CrossRef]
- Kuwabara, M.; Clarke, D.R.; Smith, A.A. Anomalous superperiodicity in scanning tunnelling microscope images in graphite. Appl. Phys. Lett. 1990, 56, 2396. [Google Scholar] [CrossRef]
- Miller, D.L.; Kubista, K.D.; Rutter, G.M.; Ruan, M.; de Heer, W.A.; First, P.N.; Stroscio, J.A. Structural analysis of multilayer graphene via atomic moiré interferometry. Phys. Rev. B 2010, 81, 125427. [Google Scholar] [CrossRef]
- Flores, M.; Cisternas, E.; Correa, J.; Vargas, P. Moiré patterns on STM images of graphite induced by rotations of surface and subsurface layer. Chem. Phys. 2013, 423, 49–54. [Google Scholar] [CrossRef]
- Brihuega, I.; Mallet, P.; González-Herrero, H.; de Laissardière, G.T.; Ugeda, M.M.; Magaud, L.; Gómez-Rodríguez, J.M.; Ynduráin, F.; Veuillen, J.Y. Unraveling the Intrinsic and Robust Nature of van Hove Singularities in Twisted Bilayer Graphene by Scanning Tunneling Microscopy and Theoretical Analysis. Phys. Rev. Lett. 2012, 109, 196802. [Google Scholar] [CrossRef] [PubMed]
- Esquinazi, P.; Heikkilä, T.T.; Lysogoskiy, Y.V.; Tayurskii, D.A.; Volovik, G.E. On the superconductivity of graphite interfaces. JETP Lett. 2014, 100, 336–339. [Google Scholar] [CrossRef]
- Volovik, G.E. Graphite, Graphene, and the Flat Band Superconductivity. JETP Lett. 2018, 107, 516–517. [Google Scholar] [CrossRef]
- Kopnin, N.B.; Heikkilä, T.T. Carbon-Based Superconductors: Towards High-Tc Superconductivity; CRC Press: Boca Raton, FL, USA, 2015; Chapter 9; pp. 231–263. [Google Scholar] [CrossRef]
- Kopnin, N.B.; Ijäs, M.; Harju, A.; Heikkilä, T.T. High-temperature surface superconductivity in rhombohedral graphite. Phys. Rev. B 2013, 87, 140503. [Google Scholar] [CrossRef]
- Muñoz, W.A.; Covaci, L.; Peeters, F. Tight-binding description of intrinsic superconducting correlations in multilayer graphene. Phys. Rev. B 2013, 87, 134509. [Google Scholar] [CrossRef]
- Precker, C.E.; Barzola-Quiquia, J.; Esquinazi, P.D.; Stiller, M.; Chan, M.K.; Jaime, M.; Zhang, Z.; Grundmann, M. Record-Breaking Magnetoresistance at the Edge of a Microflake of Natural Graphite. Adv. Eng. Mater. 2019, 21, 1970039. [Google Scholar] [CrossRef]
- Zoraghi, M.; Barzola-Quiquia, J.; Stiller, M.; Esquinazi, P.D.; Estrela-Lopis, I. Influence of interfaces on the transport properties of graphite revealed by nanometer thickness reduction. Carbon 2018, 139, 1074–1084. [Google Scholar] [CrossRef]
- Kopnin, N.B.; Heikkilä, T.T.; Volovik, G.E. High-temperature surface superconductivity in topological flat-band systems. Phys. Rev. B 2011, 83, 220503. [Google Scholar] [CrossRef]
- Ballestar, A.; Barzola-Quiquia, J.; Scheike, T.; Esquinazi, P. Evidence of Josephson-coupled superconducting regions at the interfaces of highly oriented pyrolytic graphite. New J. Phys. 2013, 15, 023024. [Google Scholar] [CrossRef]
- Ballestar, A.; Esquinazi, P.; Böhlmann, W. Granular superconductivity below 5 K in SPI-II pyrolytic graphite. Phys. Rev. B 2015, 91, 014502. [Google Scholar] [CrossRef]
- Stiller, M.; Esquinazi, P.D.; Barzola-Quiquia, J.; Precker, C.E. Local Magnetic Measurements of Trapped Flux through a Permanent Current Path in Graphite. J. Low Temp. Phys. 2018, 191, 105–121. [Google Scholar] [CrossRef]
- Henck, H.; Avila, J.; Ben Aziza, Z.; Pierucci, D.; Baima, J.; Pamuk, B.; Chaste, J.; Utt, D.; Bartos, M.; Nogajewski, K.; et al. Flat electronic bands in long sequences of rhombohedral-stacked graphene. Phys. Rev. B 2018, 97, 245421. [Google Scholar] [CrossRef]
- Esquinazi, P.D.; Lysogorskiy, Y. Experimental Evidence for the Existence of Interfaces in Graphite and Their Relation to the Observed Metallic and Superconducting Behavior; Esquinazi, P., Ed.; Springer Series in Materials Science 244; Springer International Publishing AG: Cham, Switzerland, 2016; Chapter 7; pp. 145–179. [Google Scholar] [CrossRef]
- Esquinazi, P.D.; Precker, C.E.; Stiller, M.; Cordeiro, T.R.S.; Barzola-Quiquia, J.; Setzer, A.; Böhlmann, W. Evidence for room temperature superconductivity at graphite interfaces. Quantum Stud. Math. Found. 2017. [Google Scholar] [CrossRef]
- Lin, Q.; Li, T.; Liu, Z.; Song, Y.; He, L.; Hu, Z.; Guo, Q.; Ye, H. High-resolution TEM observations of isolated rhombohedral crystallites in graphite blocks. Carbon 2012, 50, 2369–2371. [Google Scholar] [CrossRef]
- Spemann, D.; Esquinazi, P. Evidence for Magnetic Order in Graphite from Magnetization and Transport Measurements; Esquinazi, P., Ed.; Springer Series in Materials Science 244; Springer International Publishing AG: Cham, Switzerland, 2016; pp. 45–76. [Google Scholar] [CrossRef]
- Steinmann, R. About Continuous Flow Cryostats. Available online: http://as-specialdevices.com/index.php/fr/news-and-announcements (accessed on 24 July 2020).
- Zoraghi, M.; Barzola-Quiquia, J.; Stiller, M.; Setzer, A.; Esquinazi, P.; Kloess, G.; Muenster, T.; Lühmann, T.; Estrela-Lopis, I. Influence of rhombohedral stacking order in the electrical resistance of bulk and mesoscopic graphite. Phys. Rev. B 2017, 95, 045308. [Google Scholar] [CrossRef]
- Scheike, T.; Esquinazi, P.; Setzer, A.; Böhlmann, W. Granular superconductivity at room temperature in bulk highly oriented pyrolytic graphite samples. Carbon 2013, 59, 140–149. [Google Scholar] [CrossRef]
- Semenenko, B.; Esquinazi, P. Diamagnetism of Bulk Graphite Revised. Magnetochemistry 2018, 4, 52. [Google Scholar] [CrossRef]
- Levesque, P.L.; Sabri, S.S.; Aguirre, C.M.; Guillemette, J.; Siaj, M.; Desjardins, P.; Szkopek, T.; Martel, R. Probing charge transfer at surfaces using graphene transistors. Nano Lett. 2011. [Google Scholar] [CrossRef]
- Xu, H.; Chen, Y.; Zhang, J.; Zhang, H. Investigating the mechanism of hysteresis effect in graphene electrical field device fabricated on SiO2 substrates using raman spectroscopy. Small 2012. [Google Scholar] [CrossRef]
- Pinto, H.; Jones, R.; Goss, J.P.; Briddon, P.R. Mechanisms of doping graphene. Phys. Status Sol. (A) 2010. [Google Scholar] [CrossRef]
- Zahab, A.; Spina, L.; Poncharal, P.; Marlière, C. Water-vapor effect on the electrical conductivity of a single-walled carbon nanotube mat. Phys. Rev. B Condens. Matter Mater. Phys. 2000. [Google Scholar] [CrossRef]
- Kong, J.; Franklin, N.R.; Zhou, C.; Chapline, M.G.; Peng, S.; Cho, K.; Dai, H. Nanotube molecular wires as chemical sensors. Science 2000. [Google Scholar] [CrossRef] [PubMed]

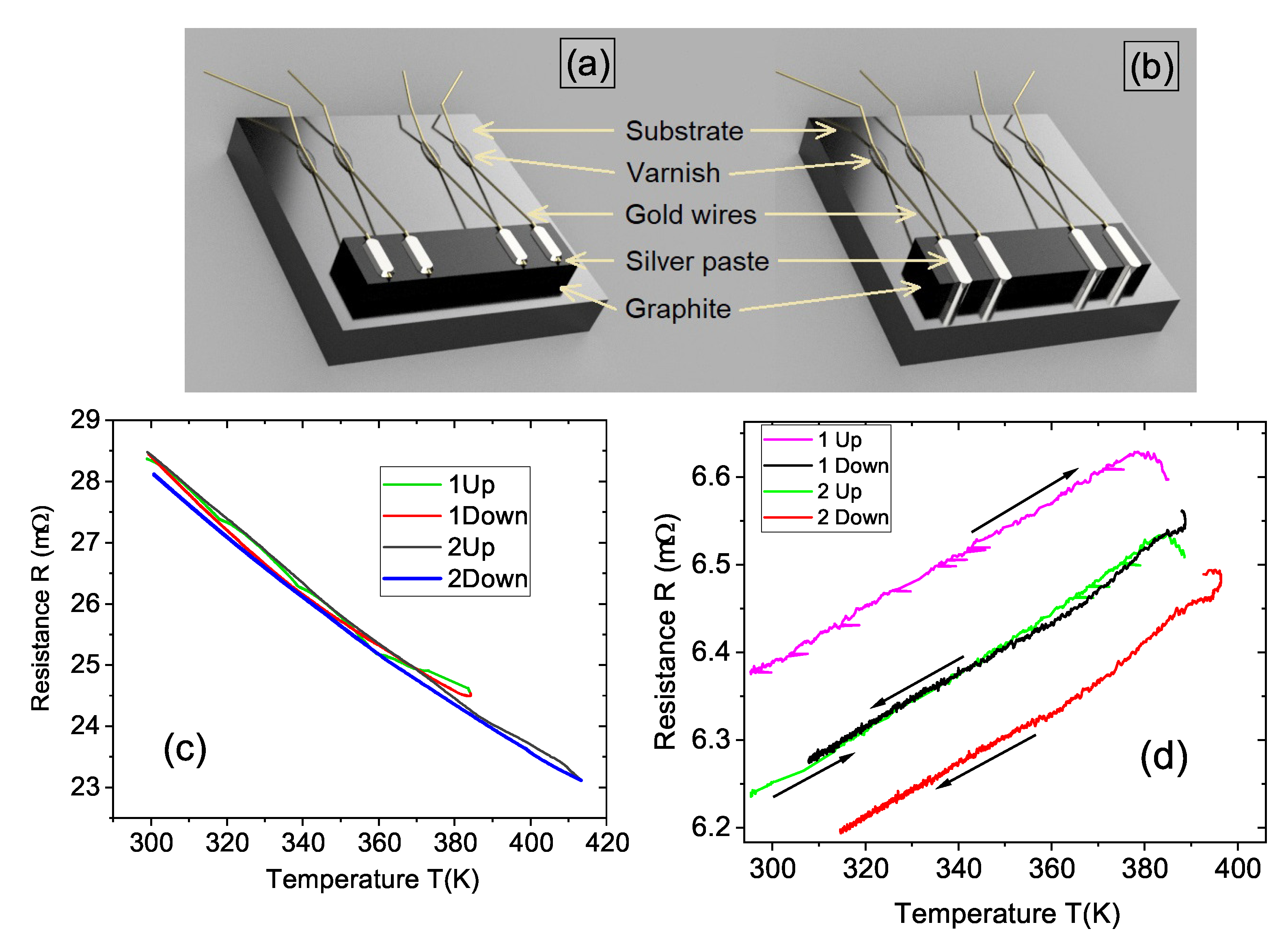

| Sample | Origin | Dimensions (mm) |
|---|---|---|
| #1 | HOPG-Advanced Ceramics | 4.63 × 1.3 × 0.47 |
| #2 | Natural Graphite-Sri Lanka | 3.2 × 0.5 × 0.14 |
| #3 | HOPG-Advanced Ceramics | 4.4 × 1.28 × 0.35 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hentrich, A.; Esquinazi, P.D. Effects of the Stacking Faults on the Electrical Resistance of Highly Ordered Graphite Bulk Samples. C 2020, 6, 49. https://doi.org/10.3390/c6030049
Hentrich A, Esquinazi PD. Effects of the Stacking Faults on the Electrical Resistance of Highly Ordered Graphite Bulk Samples. C. 2020; 6(3):49. https://doi.org/10.3390/c6030049
Chicago/Turabian StyleHentrich, Andreas, and Pablo D. Esquinazi. 2020. "Effects of the Stacking Faults on the Electrical Resistance of Highly Ordered Graphite Bulk Samples" C 6, no. 3: 49. https://doi.org/10.3390/c6030049
APA StyleHentrich, A., & Esquinazi, P. D. (2020). Effects of the Stacking Faults on the Electrical Resistance of Highly Ordered Graphite Bulk Samples. C, 6(3), 49. https://doi.org/10.3390/c6030049






