CUBIT: Capacitive qUantum BIT
Abstract
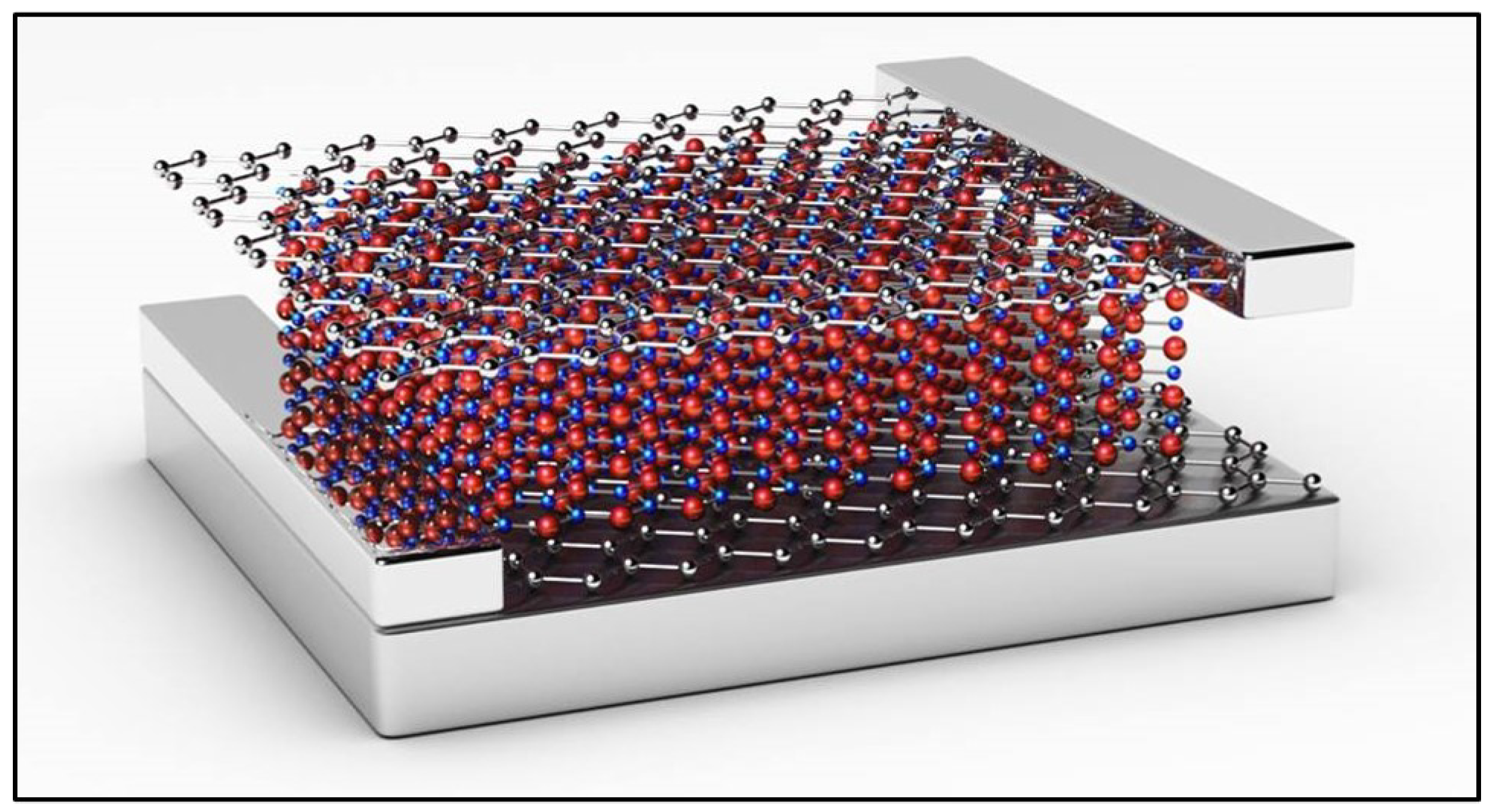
1. Introduction
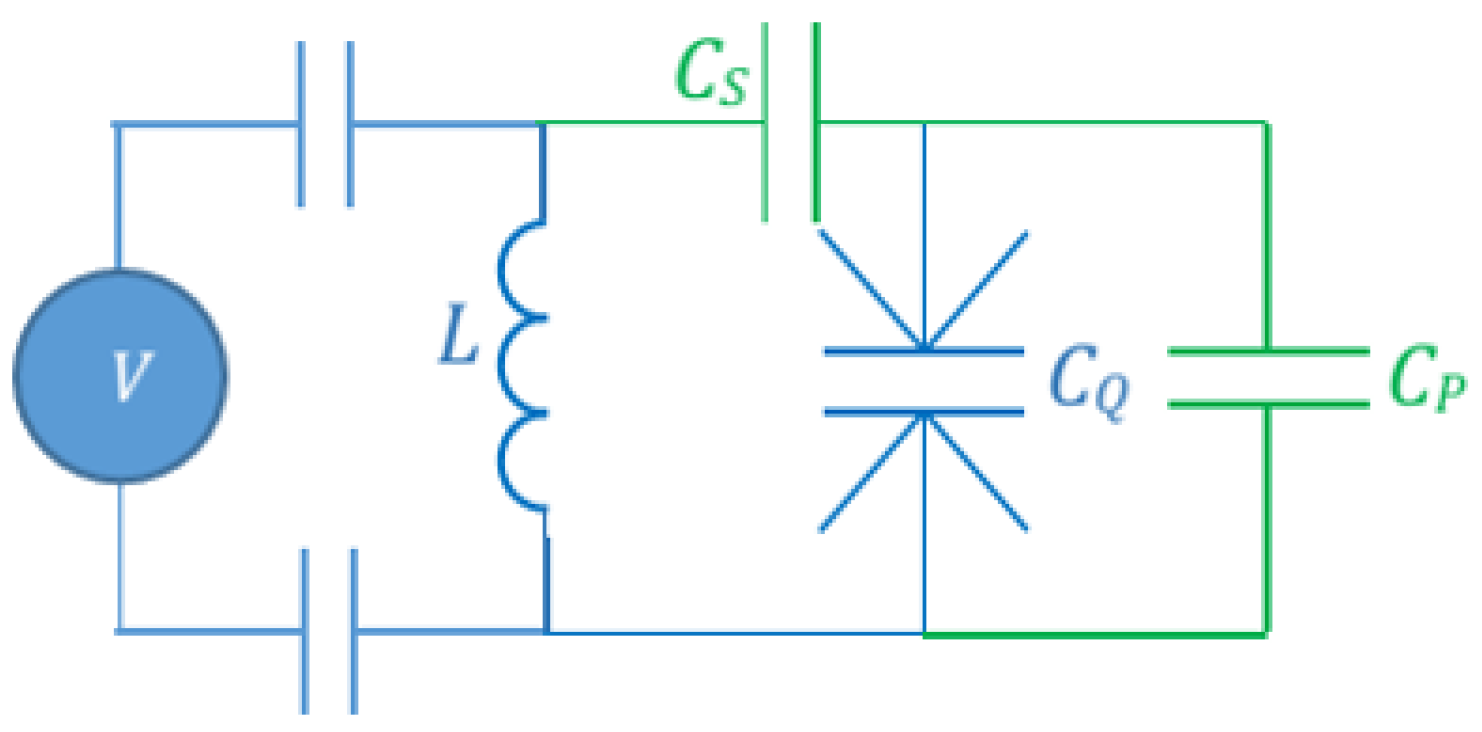
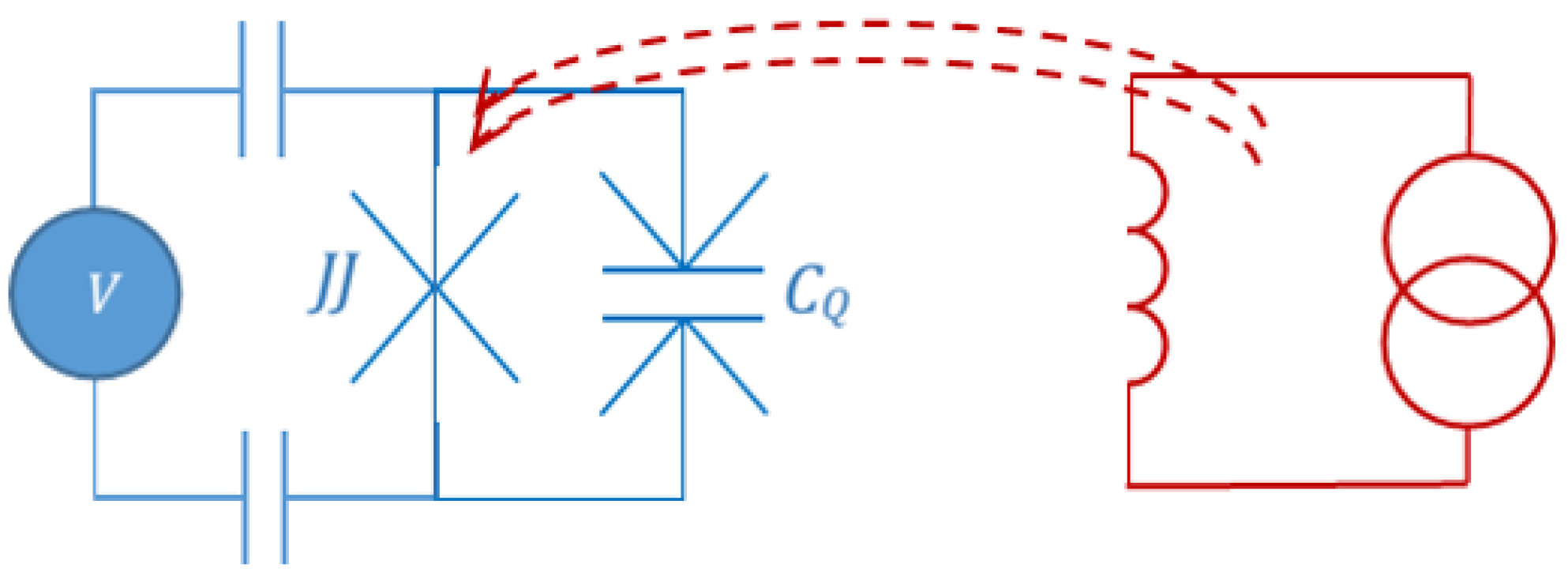
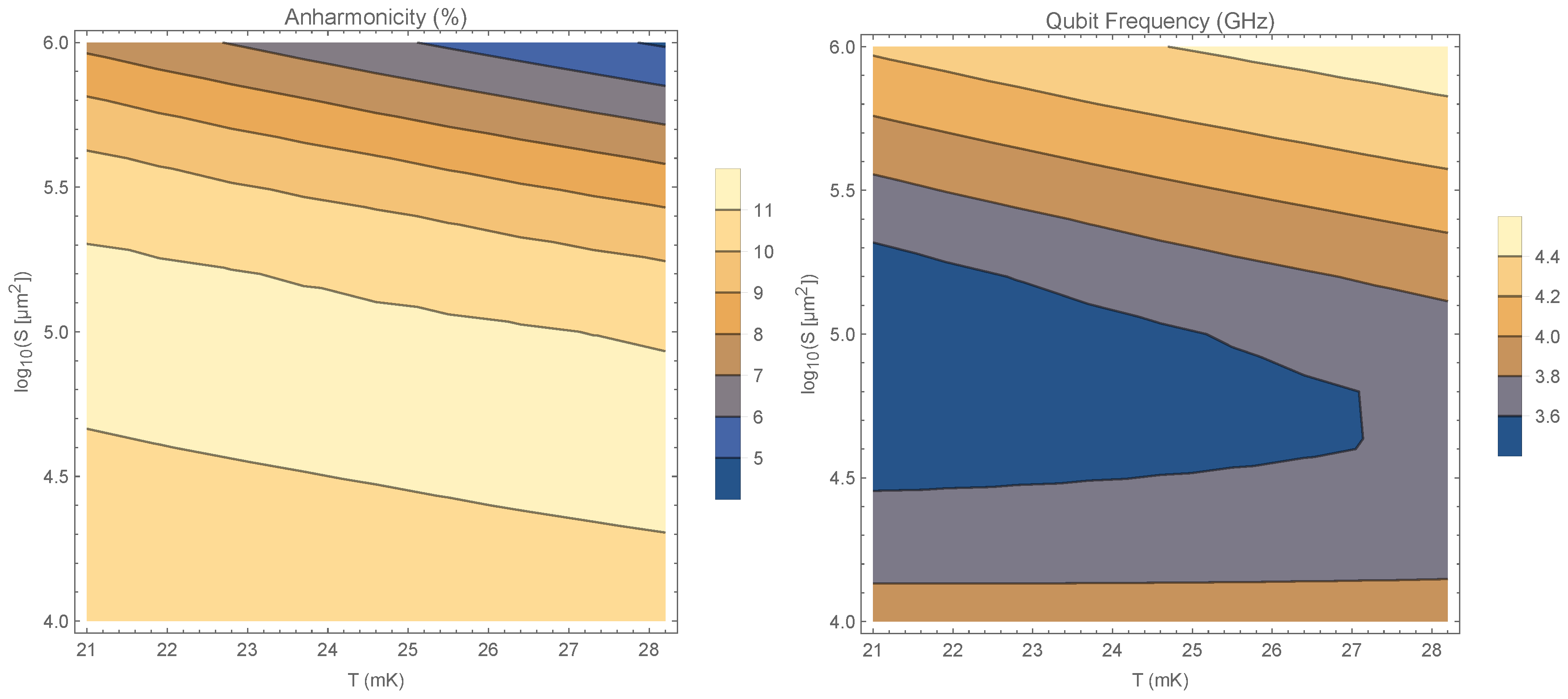
2. Results
3. Practical Considerations
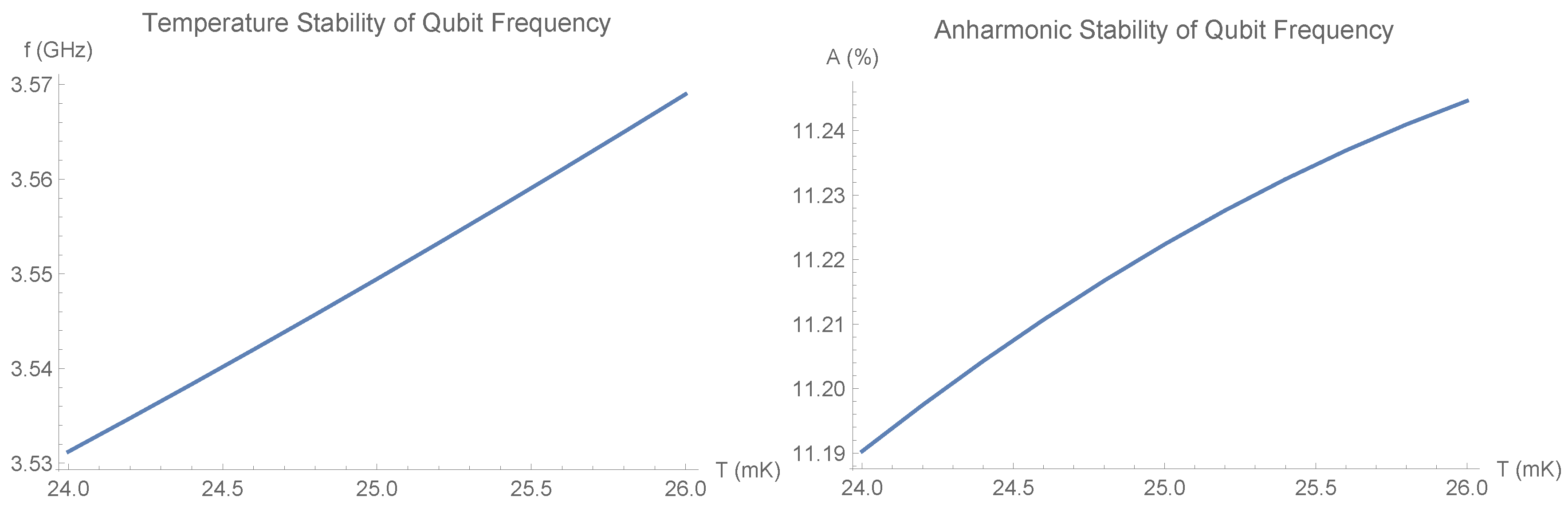
3.1. Potential Puddles
3.2. Zero-Point Fluctuations
3.3. Decoherence and Dephasing
3.4. Parametric Amplifiers
4. Conclusions & Future Work
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Xia, J.; Chen, F.; Li, J.; Tao, N. Measurement of the quantum capacitance of graphene. Nat. Nanotechnol. 2009, 4, 505–509. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Ma, F.; Liang, W.; Sun, M. Electrical properties and applications of graphene, hexagonal boron nitride (h-BN), and graphene/h-BN heterostructures. Mater. Phys. Today 2017, 2, 6–34. [Google Scholar] [CrossRef]
- Mikhailov, S.A. Graphene-based voltage-tunable coherent terahertz emitter. Phys. Rev. B 2013, 87, 115405. [Google Scholar] [CrossRef]
- Khorasani, S.; Koottandavida, A. Nonlinear graphene quantum capacitors for electro-optics. npj 2D Mat. Appl. 2017, 1, 7. [Google Scholar] [CrossRef]
- Humble, T.S.; Thapliyal, H.; Muñoz-Coreas, E.; Mohiyaddin, F.A.; Bennink, R.S. Quantum computing circuits and devices. arXiv 2018, arXiv:1804.10648. [Google Scholar]
- Wendin, G. Quantum information processing with superconducting circuits: A review. Rep. Prog. Phys. 2017, 80, 106001. [Google Scholar] [CrossRef] [PubMed]
- Job, J.; Lidar, D. Test-driving 1000 qubits. Quantum Sci. Technol. 2018, 3, 030501. [Google Scholar] [CrossRef]
- Krinner, S.; Storz, S.; Kurpiers, P.; Magnard, P.; Heinsoo, J.; Keller, R.; Lütolf, J.; Eichler, C.; Wallraff, A. Engineering cryogenic setups for 100-qubit scale superconducting circuit systems. arxiv, 2018; arXiv:1806.07862. [Google Scholar]
- Acín, A.; Bloch, I.; Buhrman, H.; Calarco, T.; Eichler, C.; Eisert, J.; Esteve, D.; Gisin, N.; Glaser, S.J.; Jelezko, F.; et al. The European Quantum Technologies Roadmap. arxiv, 2017; arXiv:1712.03773. [Google Scholar]
- Wu, H.; Qian, Y.; Du, Z.; Zhu, R.; Kan, E.; Deng, K. Prediction of another semimetallic silicene allotrope with Dirac fermions. Phys. Lett. A 2017, 381, 3754–3759. [Google Scholar] [CrossRef]
- Acun, A.; Zhang, L.; Bampoulis, P.; Farmanbar, M.; van Houselt, A.; Rudenko, A.N.; Lingenfelder, M.; Brocks, G.; Poelsema, B.; Katsnelson, M.I. Germanene: The germanium analogue of graphene. J. Phys. Condens. Matter 2015, 27, 443002. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Deng, S.; Liu, Z.; Liu, Z. The rare two-dimensional materials with Dirac cones. Nat. Sci. Rev. 2015, 2, 22. [Google Scholar] [CrossRef]
- Balendhran, S.; Walia, S.; Nili, H.; Sriram, S.; Bhaskaran, M. Elemental analogues of Graphene: Silicene, Germanene, Stanene, and Phosphorene. Small 2014, 11, 640–652. [Google Scholar] [CrossRef] [PubMed]
- Vlassiouk, I.V.; Stehle, Y.; Pudasaini, P.R.; Unocic, R.R.; Rack, P.D.; Baddorf, A.P.; Ivanov, I.N.; Lavrik, N.V.; List, F.; Gupta, N.; et al. Evolutionary selection growth of two-dimensional materials on polycrystalline substrates. Nat. Mater. 2018, 17, 318–322. [Google Scholar] [CrossRef] [PubMed]
- Di Bernardo, A.; Millo, O.; Barbone, M.; Alpern, H.; Kalcheim, Y.; Sassi, U.; Ott, A.K.; De Fazio, D.; Yoon, D.; Amado, M.; et al. p-Wave triggered superconductivity in single-layer graphene on an electron-doped oxide superconductor. Nat. Commun. 2017, 8, 14024. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Fatemi, V.; Fang, S.; Watanabe, K.; Taniguchi, T.; Kaxiras, E.; Jarillo-Herrero, P. Unconventional superconductivity in magic-angle graphene superlattices. Nature 2018, 556, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Khorasani, S. Tunable spontaneous emission from layered graphene/dielectric tunnel junctions. IEEE J. Quantum Electron. 2014, 50, 307–313. [Google Scholar] [CrossRef]
- Ranjan, V.; Zihlmann, S.; Makk, P.; Watanabe, K.; Taniguchi, T.; Schönenberger, C. Contactless microwave characterization of encapsulated graphene p-n junctions. Phys. Rev. Appl. 2017, 7, 054015. [Google Scholar] [CrossRef]
- Freitag, N.M.; Reisch, T.; Chizhova, L.A.; Nemes-Incze, P.; Holl, C.; Woods, C.R.; Gorbachev, R.V.; Cao, Y.; Geim, A.K.; Novoselov, K.S.; et al. Large tunable valley splitting in edge-free graphene quantum dots on boron nitride. Nat. Nanotechnol. 2018, 13, 392–397. [Google Scholar] [CrossRef] [PubMed]
- Dröscher, S.; Roulleau, P.; Molitor, F.; Studerus, P.; Stampfer, C.; Ensslin, K.; Ihn, T. Quantum capacitance and density of states of graphene. Appl. Phys. Lett. 2010, 96, 152104. [Google Scholar] [CrossRef]
- Fang, T.; Konar, A.; Xing, H.; Jena, D. Carrier statistics and quantum capacitance of graphene sheets and ribbons. Appl. Phys. Lett. 2007, 91, 092109. [Google Scholar] [CrossRef]
- Koch, J.; Yu, T.M.; Gambetta, J.; Houck, A.A.; Schuster, D.I.; Majer, J.; Blais, A.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 2007, 76, 042319. [Google Scholar] [CrossRef]
- Khorasani, S. New basis functions for wave equation. Sci. Iran. 2016, 23, 2928–2933. [Google Scholar] [CrossRef]
- Groszkowski, P.; Di Paolo, A.; Grimsmo, A.L.; Blais, A.; Schuster, D.I.; Houck, A.A.; Koch, J. Coherence properties of the 0-π qubit. New J. Phys. 2018, 20, 043053. [Google Scholar] [CrossRef]
- Hardal, A.Ü.C.; Aslan, N.; Wilson, C.M.; Müstecaplıoǧlu, Ö.E. Quantum heat engine with coupled superconducting resonators. Phys. Rev. E 2017, 96, 062120. [Google Scholar] [CrossRef] [PubMed]
- Altintas, F.; Hardal, A.Ü.C.; Müstecaplıoǧlu, Ö.E. Rabi model as a quantum coherent heat engine: From quantum biology to superconducting circuits. Phys. Rev. A 2015, 91, 023816. [Google Scholar] [CrossRef]
- Allen, E.H.; Altintas, F.; Hardal, A.Ü.C.; Müstecaplıoǧlu, Ö. Quantum Otto Engine. U.S. Patent 9,909,460, 6 March 2018. [Google Scholar]
- Khorasani, S. Solution of cross-Kerr interaction combined with parametric amplification. arxiv, 2018; arXiv:1804.07053. [Google Scholar]

| S () | Design (GHz) | T (mK) | (fF) | Actual (GHz) | A (%) |
|---|---|---|---|---|---|
| 1 | 2.5 | 25 | − | 2.29 | 3.9 |
| 1 | 5 | 25 | − | 4.41 | 6.04 |
| 1 | 10 | 25 | − | 8.31 | 8.26 |
| S ( ) | Design (GHz) | T (mK) | (fF) | Actual (GHz) | A (%) |
|---|---|---|---|---|---|
| 1 | 2.5 | 25 | 100 | 2.39 | 0.44 |
| 1 | 5 | 25 | 100 | 4.77 | 0.76 |
| 1 | 10 | 25 | 1000 | 8.71 | 5.67 |
| S () | Design (GHz) | T (mK) | (fF) | Actual (GHz) | A (%) |
|---|---|---|---|---|---|
| 0.1 | 10 | 25 | − | 6.42 | 11.2 |
| 0.1 | 15 | 25 | − | 11.1 | 9.02 |
| 0.1 | 20 | 25 | − | 11.5 | 11.1 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khorasani, S. CUBIT: Capacitive qUantum BIT. C 2018, 4, 39. https://doi.org/10.3390/c4030039
Khorasani S. CUBIT: Capacitive qUantum BIT. C. 2018; 4(3):39. https://doi.org/10.3390/c4030039
Chicago/Turabian StyleKhorasani, Sina. 2018. "CUBIT: Capacitive qUantum BIT" C 4, no. 3: 39. https://doi.org/10.3390/c4030039
APA StyleKhorasani, S. (2018). CUBIT: Capacitive qUantum BIT. C, 4(3), 39. https://doi.org/10.3390/c4030039





