An Atomistic Carbide-Derived Carbon Model Generated Using ReaxFF-Based Quenched Molecular Dynamics
Abstract
1. Introduction
2. Computational Details
2.1. Quenched Molecular Dynamics Simulations
2.2. Grand Canonical Monte Carlo Simulations
3. Experimental Methods
3.1. CDC Synthesis and Annealing
3.2. Gas Sorption and Porosimetry
3.3. Ex Situ X-Ray Total Scattering
3.4. Abberation Corrected Scanning Transmission Electron Microscopy
4. Results and Discussion
4.1. Imaging and Spectroscopy of CDC Structures
4.2. QMD-Generated CDC Structures
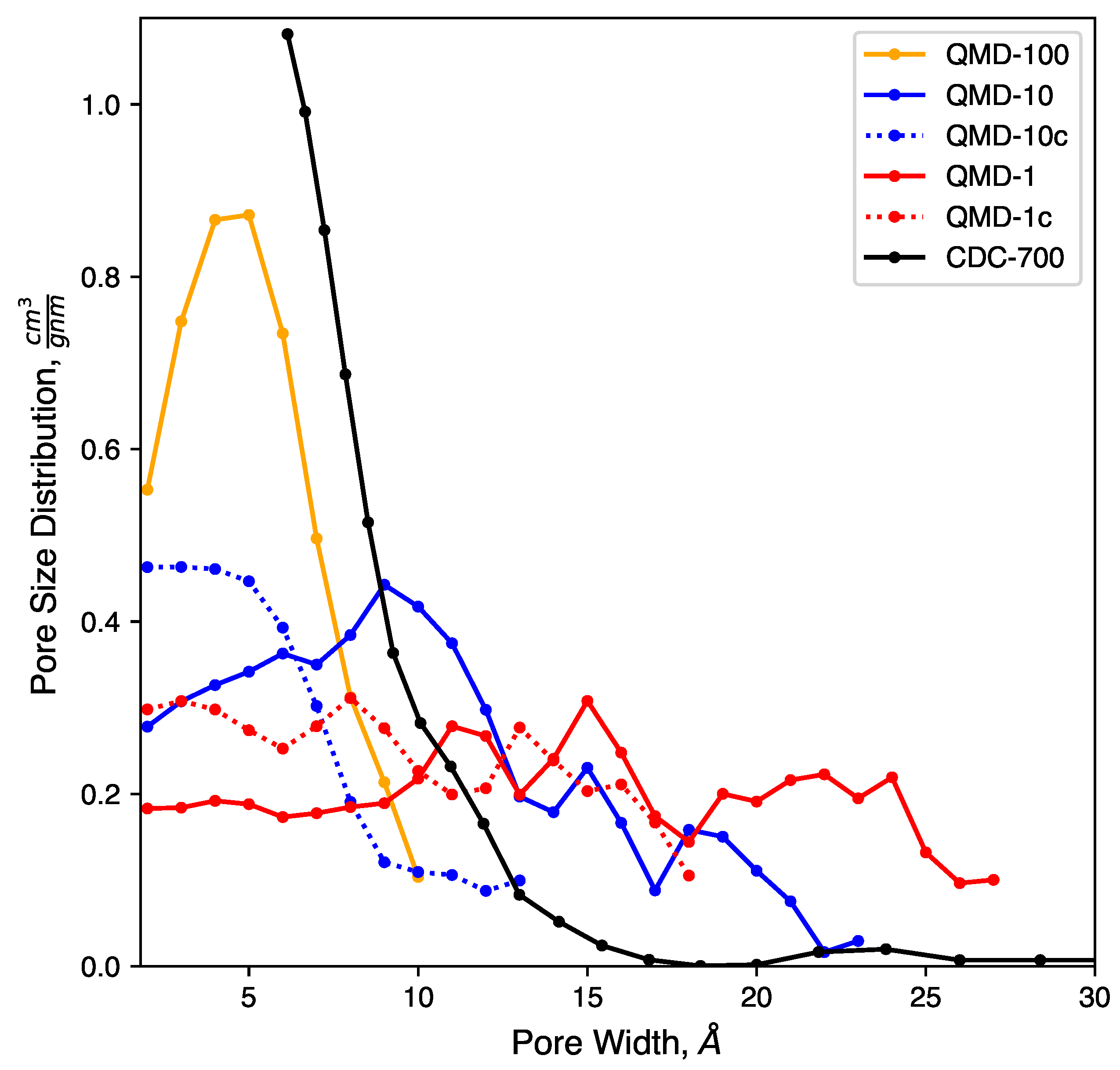
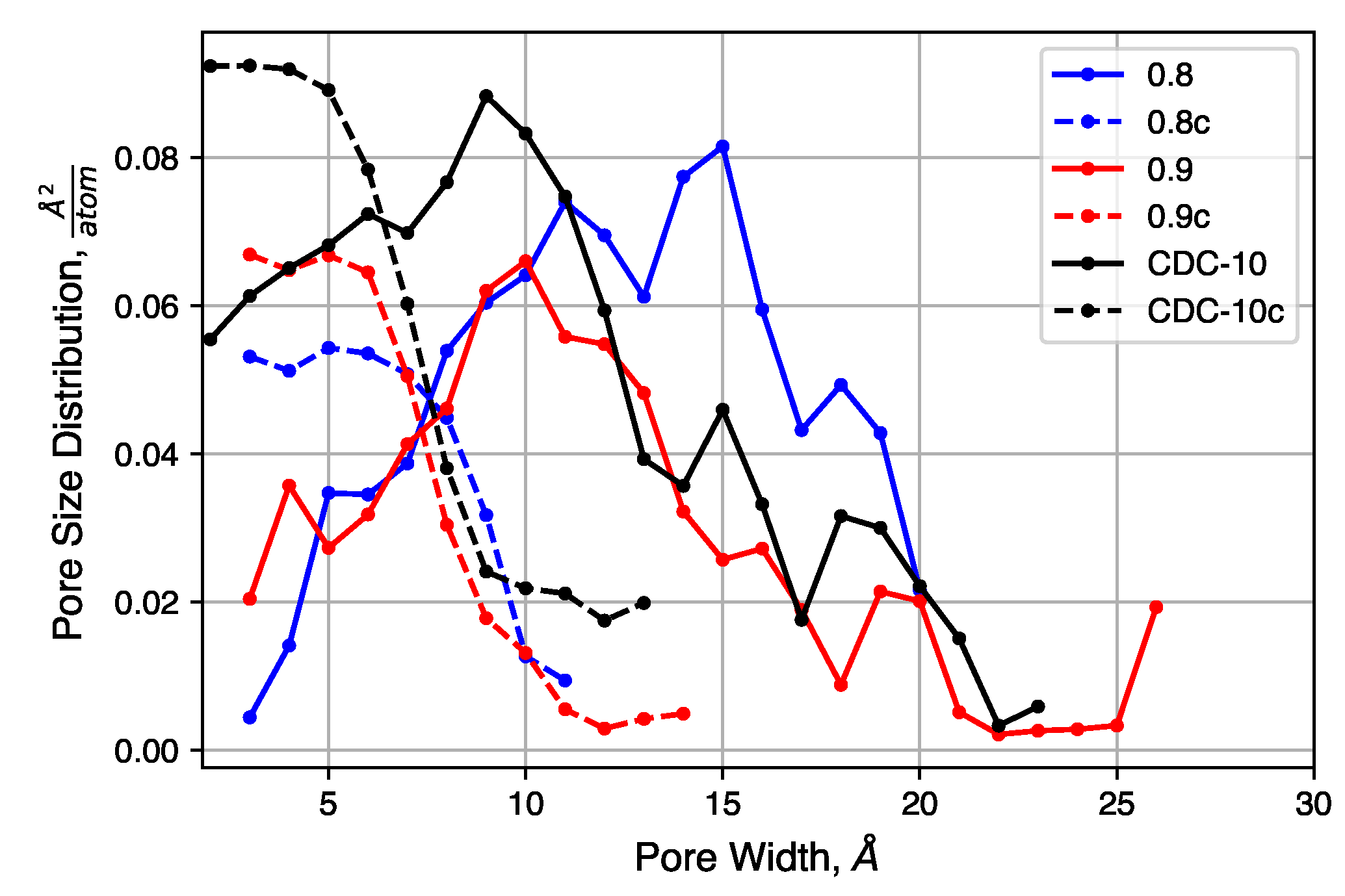
4.2.1. Pore Size Distribution
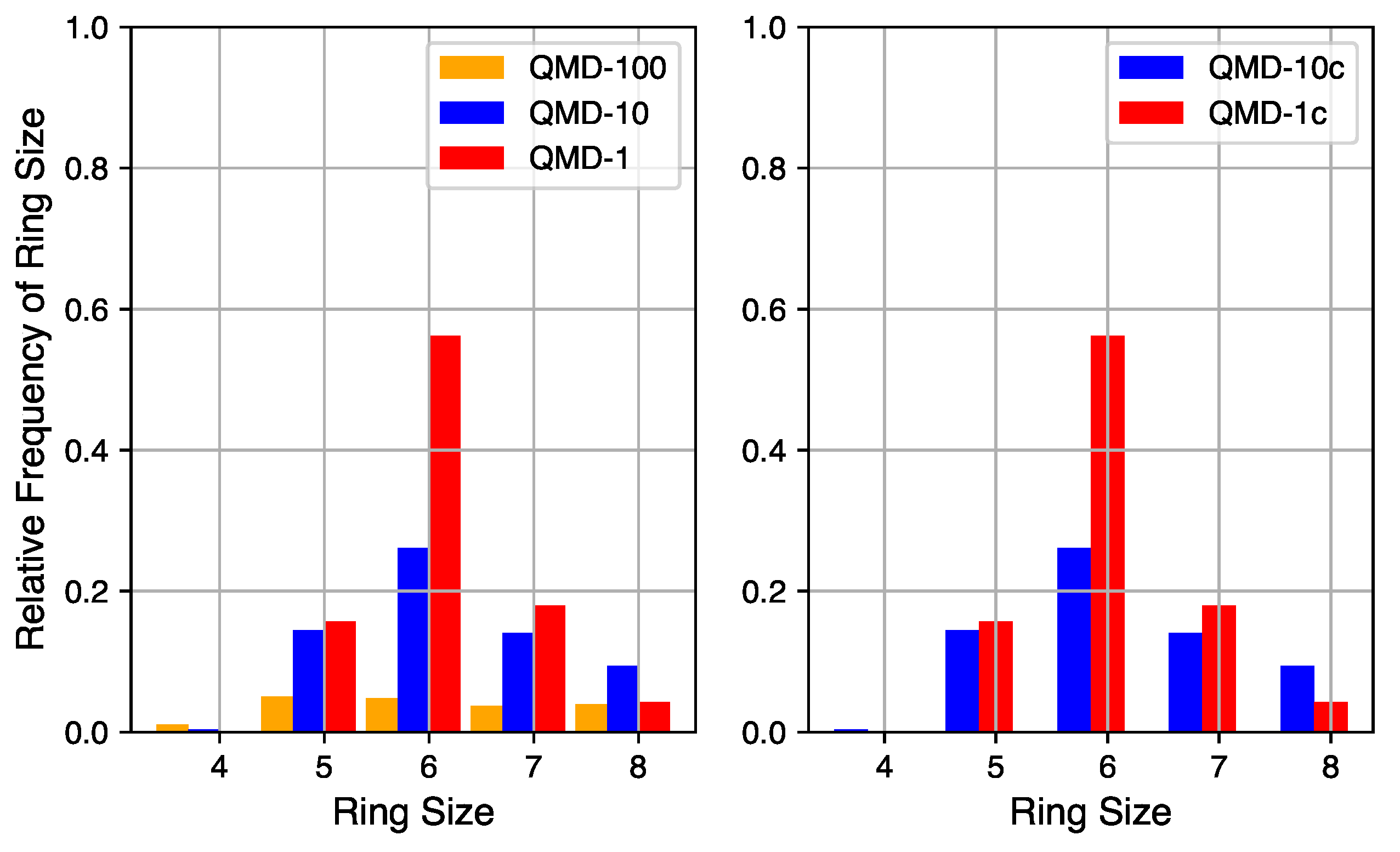
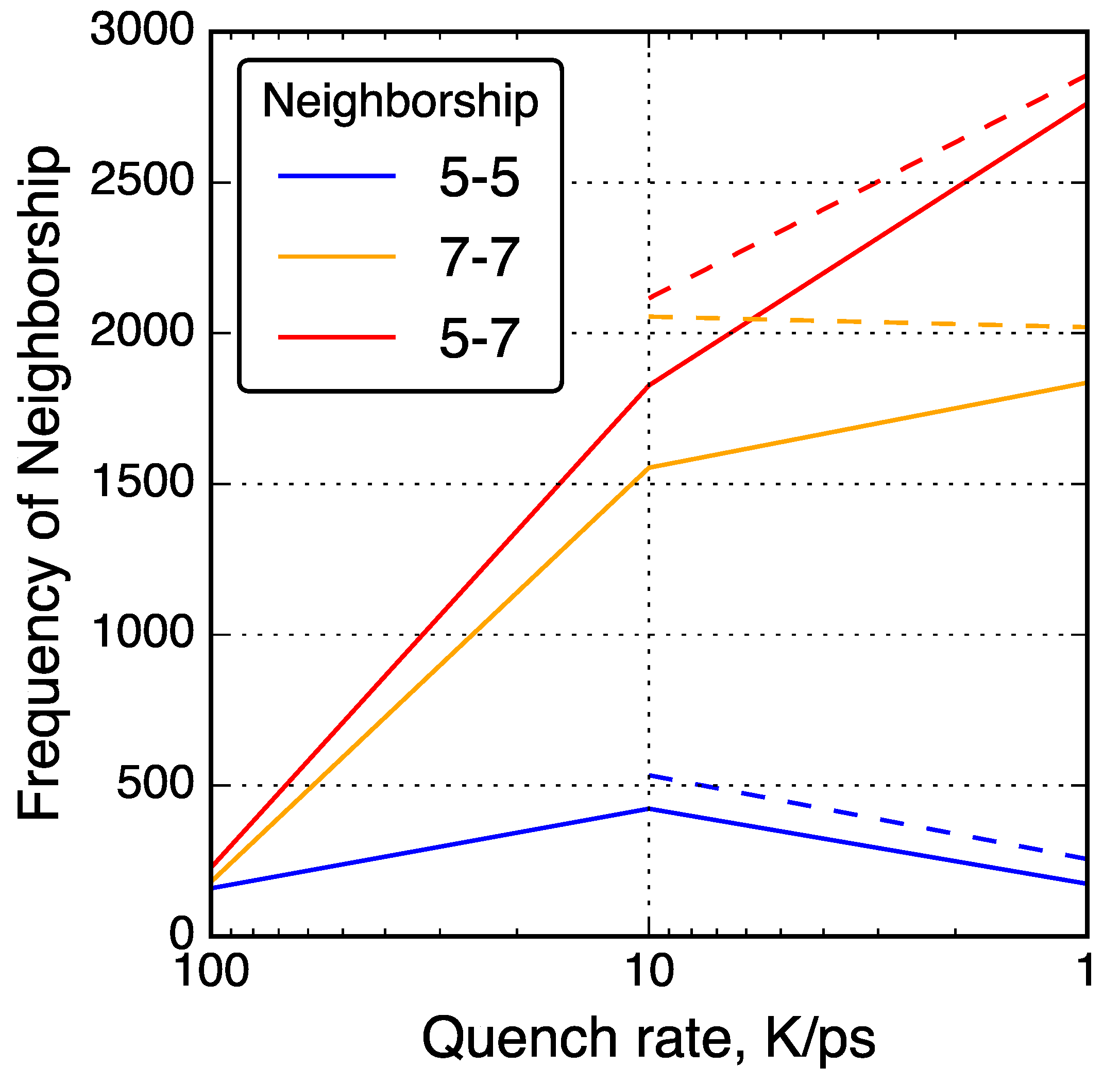
4.2.2. Ring Size Distributions
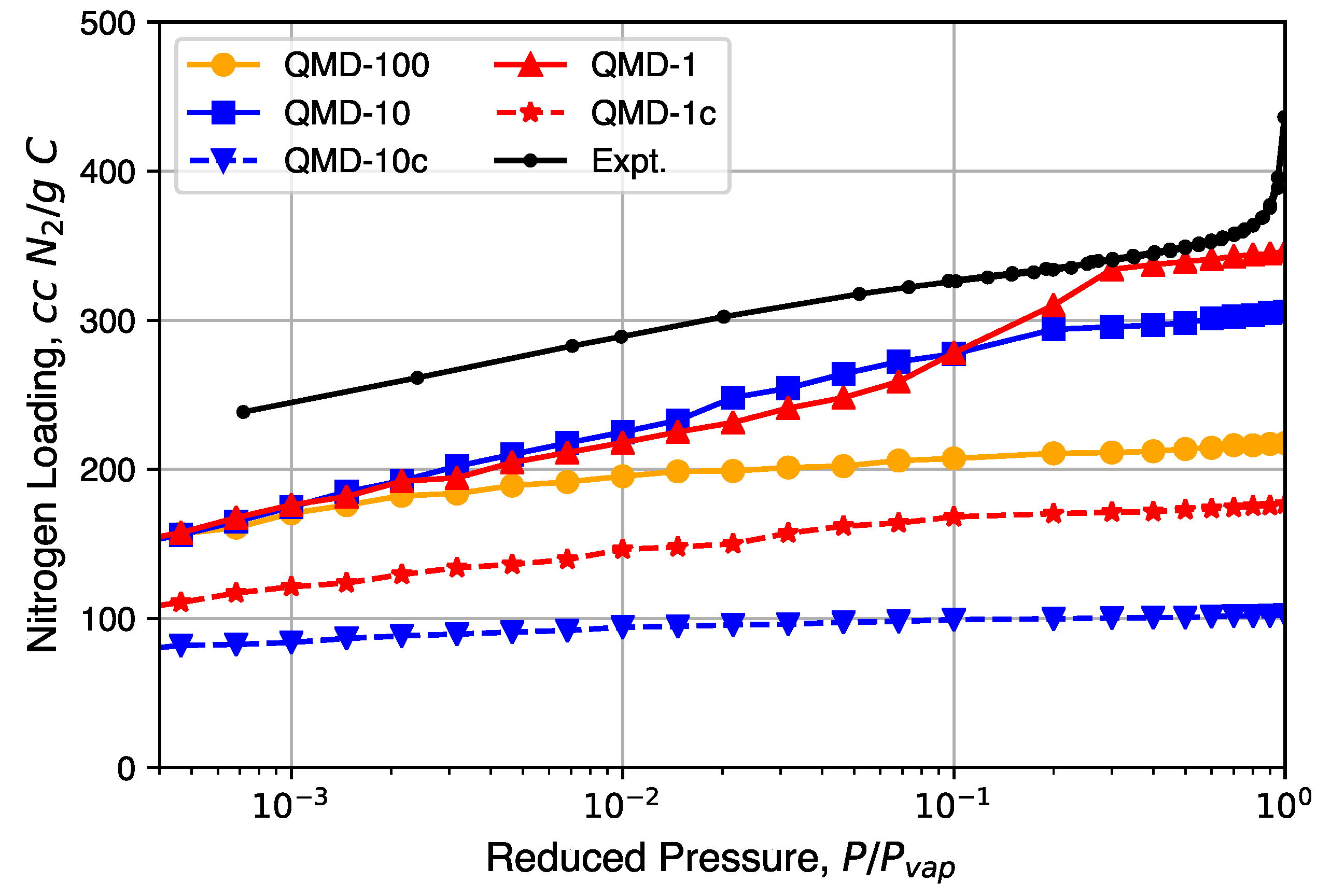
4.3. Sorptive Loading
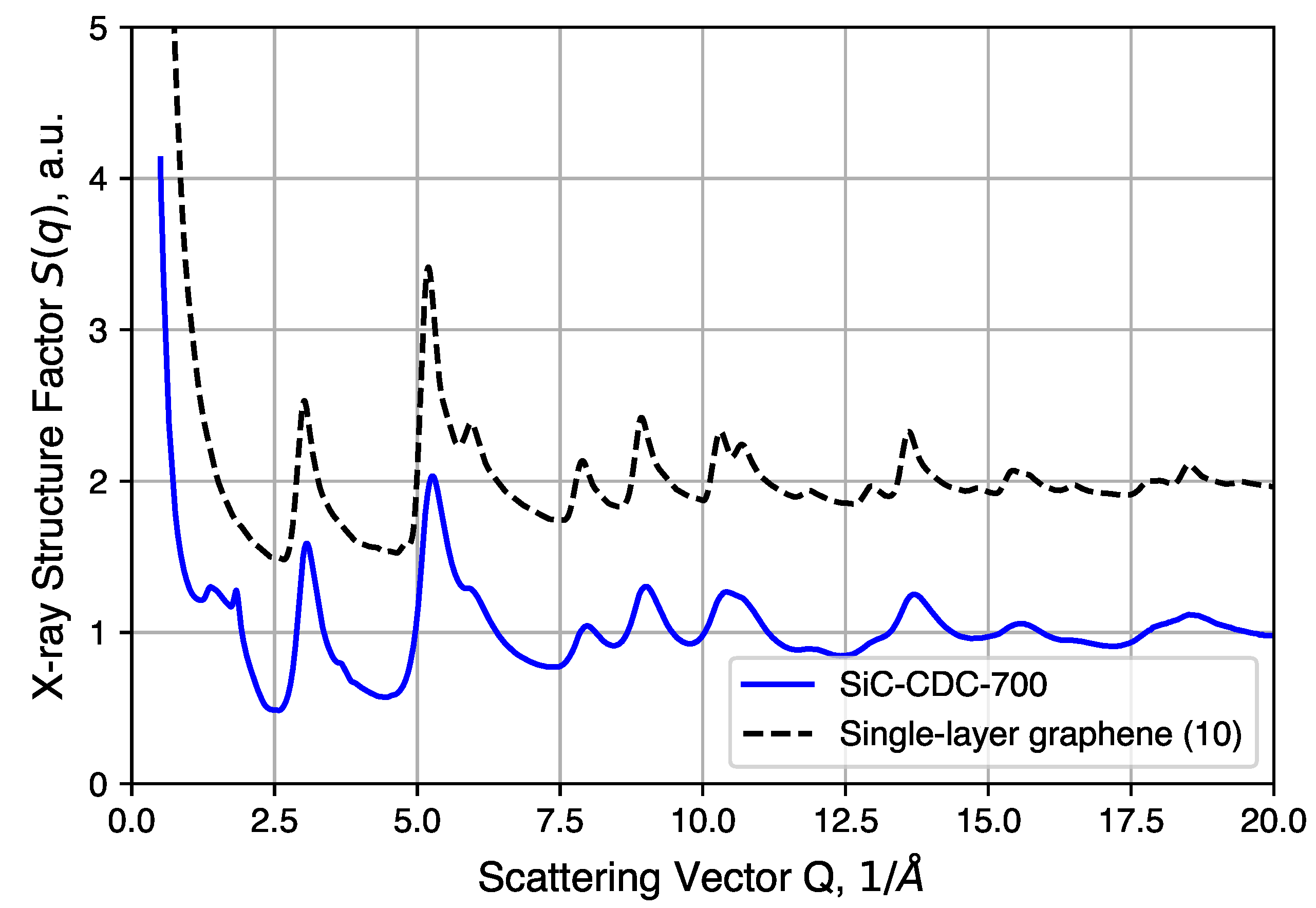
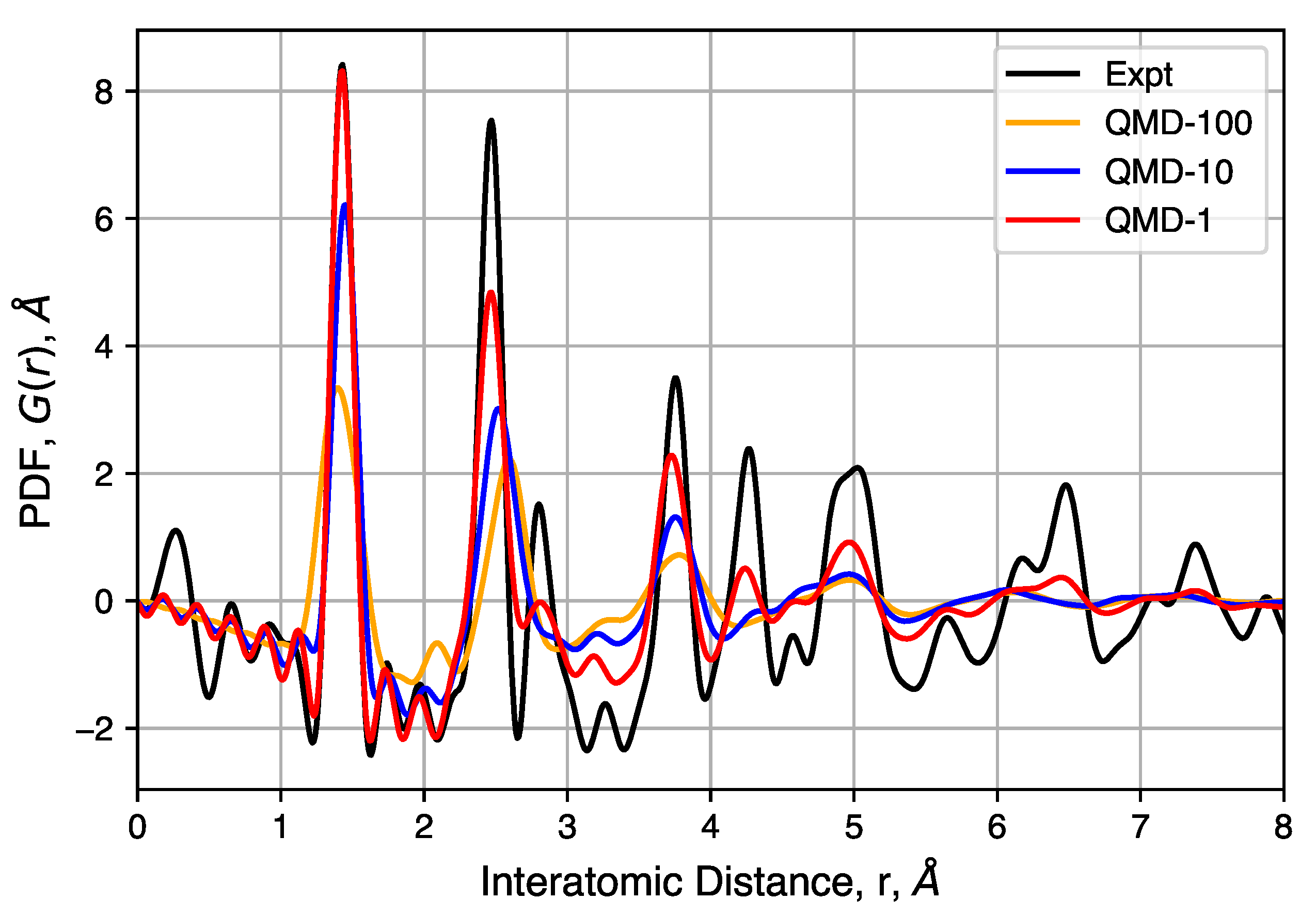
4.4. X-Ray Total Scattering
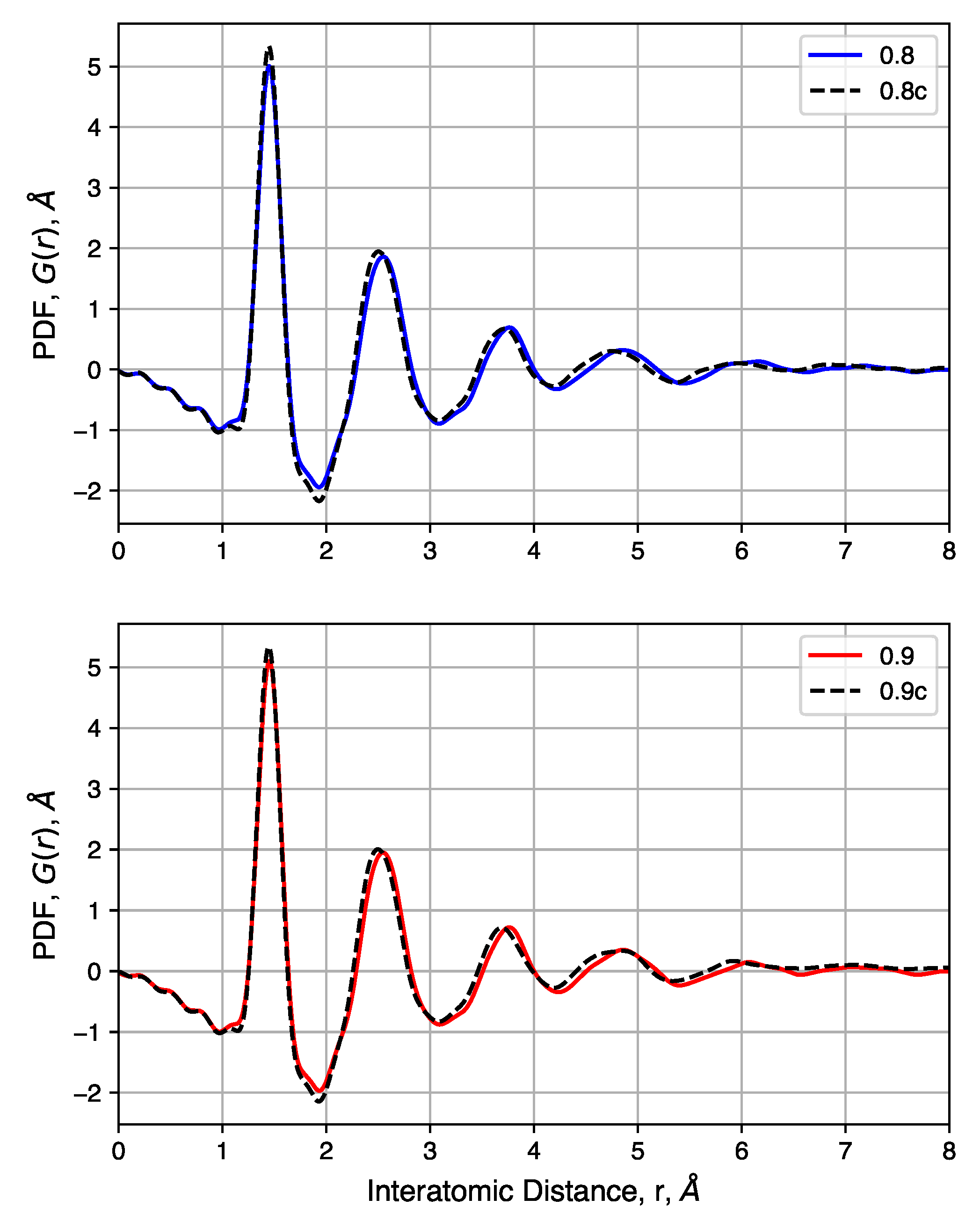
4.5. Effects of Initial Density
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Presser, V.; Heon, M.; Gogotsi, Y. Carbide-Derived Carbons—From Porous Networks to Nanotubes and Graphene. Adv. Funct. Mater. 2011, 21, 810–833. [Google Scholar] [CrossRef]
- Dash, R.; Chmiola, J.; Yushin, G.; Gogotsi, Y.; Laudisio, G.; Singer, J.; Fischer, J.; Kucheyev, S.O. Titanium carbide derived nanoporous carbon for energy-related applications. Carbon 2006, 44, 2489–2497. [Google Scholar] [CrossRef]
- Jänes, A.; Thomberg, T.; Kurig, H.; Lust, E. Nanoscale fine-tuning of porosity of carbide-derived carbon prepared from molybdenum carbide. Carbon 2009, 47, 23–29. [Google Scholar] [CrossRef]
- Hoffman, E.N.; Yushin, G.; El-Raghy, T.; Gogotsi, Y.; Barsoum, M.W. Micro and mesoporosity of carbon derived from ternary and binary metal carbides. Microporous Mesoporous Mater. 2008, 112, 526–532. [Google Scholar] [CrossRef]
- Gogotsi, Y.; Nikitin, A.; Ye, H.; Zhou, W.; Fischer, J.E.; Yi, B.; Foley, H.C.; Barsoum, M.W. Nanoporous carbide-derived carbon with tunable pore size. Nat. Mater. 2003, 2, 591–594. [Google Scholar] [CrossRef] [PubMed]
- Laudisio, G.; Dash, R.K.; Singer, J.P.; Yushin, G.; Gogotsi, Y.; Fischer, J.E. Carbide-derived carbons: A comparative study of porosity based on small-angle scattering and adsorption isotherms. Langmuir 2006, 22, 8945–8950. [Google Scholar] [CrossRef] [PubMed]
- Osswald, S.; Chmiola, J.; Gogotsi, Y. Structural evolution of carbide-derived carbons upon vacuum annealing. Carbon 2012, 50, 4880–4886. [Google Scholar] [CrossRef]
- Nič, M.; Jirát, J.; Košata, B.; Jenkins, A.; McNaught, A. IUPAC Compendium of Chemical Terminology; IUPAC: Research Triagle Park, NC, USA, 2009. [Google Scholar]
- Chmiola, J.; Yushin, G.; Gogotsi, Y.; Portet, C.; Simon, P.; Taberna, P.L. Anomalous increase in carbon capacitance at pore sizes less than 1 nanometer. Science 2006, 313, 1760–1763. [Google Scholar] [CrossRef] [PubMed]
- Chmiola, J.; Yushin, G.; Dash, R.; Gogotsi, Y. Effect of pore size and surface area of carbide derived carbons on specific capacitance. J. Power Sources 2006, 158, 765–772. [Google Scholar] [CrossRef]
- Chmiola, J.; Largeot, C.; Taberna, P.L.; Simon, P.; Gogotsi, Y. Monolithic Carbide-Derived Carbon Films for Micro-Supercapacitors. Science 2010, 328, 480–483. [Google Scholar] [CrossRef] [PubMed]
- Lin, R.; Huang, P.; Ségalini, J.; Largeot, C.; Taberna, P.L.; Chmiola, J.; Gogotsi, Y.; Simon, P. Solvent effect on the ion adsorption from ionic liquid electrolyte into sub-nanometer carbon pores. Electrochim. Acta 2009, 54, 7025–7032. [Google Scholar] [CrossRef]
- Nguyen, T.X.; Bae, J.S.S.; Bhatia, S.K. Characterization and adsorption modeling of silicon carbide-derived carbons. Langmuir 2009, 25, 2121–2132. [Google Scholar] [CrossRef] [PubMed]
- Presser, V.; McDonough, J.; Yeon, S.H.; Gogotsi, Y. Effect of pore size on carbon dioxide sorption by carbide derived carbon. Energy Environ. Sci. 2011, 4, 3059. [Google Scholar] [CrossRef]
- Vakifahmetoglu, C.; Presser, V.; Yeon, S.H.; Colombo, P.; Gogotsi, Y. Enhanced hydrogen and methane gas storage of silicon oxycarbide derived carbon. Microporous Mesoporous Mater. 2011, 144, 105–112. [Google Scholar] [CrossRef]
- Yushin, G.; Hoffman, E.N.; Barsoum, M.W.; Gogotsi, Y.; Howell, C.A.; Sandeman, S.R.; Phillips, G.J.; Lloyd, A.W.; Mikhalovsky, S.V. Mesoporous carbide-derived carbon with porosity tuned for efficient adsorption of cytokines. Biomaterials 2006, 27, 5755–5762. [Google Scholar] [CrossRef] [PubMed]
- Yachamaneni, S.; Yushin, G.; Yeon, S.H.; Gogotsi, Y.; Howell, C.; Sandeman, S.; Phillips, G.; Mikhalovsky, S. Mesoporous carbide-derived carbon for cytokine removal from blood plasma. Biomaterials 2010, 31, 4789–4794. [Google Scholar] [CrossRef] [PubMed]
- Portet, C.; Taberna, P.L.; Simon, P.; Flahaut, E.; Laberty-Robert, C. High power density electrodes for Carbon supercapacitor applications. Electrochim. Acta 2005, 50, 4174–4181. [Google Scholar] [CrossRef]
- Gogotsi, Y.; Presser, V. Carbon Nanomaterials, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Simon, P.; Gogotsi, Y. Capacitive Energy Storage in Nanostructured Carbon—Electrolyte Systems. Acc. Chem. Res. 2013, 46, 1094–1103. [Google Scholar] [CrossRef] [PubMed]
- Vora, P.M.; Gopu, P.; Rosario-Canales, M.; Pérez, C.R.; Gogotsi, Y.; Santiago-Avilés, J.J.; Kikkawa, J.M. Correlating magnetotransport and diamagnetism of sp2-bonded carbon networks through the metal-insulator transition. Phys. Rev. B 2011, 84, 155114. [Google Scholar] [CrossRef]
- Pak, A.J.; Paek, E.; Hwang, G.S. Tailoring the performance of graphene-based supercapacitors using topological defects: A theoretical assessment. Carbon 2014, 68, 734–741. [Google Scholar] [CrossRef]
- Xing, L.; Vatamanu, J.; Borodin, O.; Bedrov, D. On the atomistic nature of capacitance enhancement generated by ionic liquid electrolyte confined in subnanometer pores. J. Phys. Chem. Lett. 2013, 4, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Faber, K.; Badaczewski, F.; Oschatz, M.; Mondin, G.; Nickel, W.; Kaskel, S.; Smarsly, B.M. In-depth investigation of the carbon microstructure of silicon carbide-derived carbons by wide-angle X-ray scattering. J. Phys. Chem. C 2014, 118, 15705–15715. [Google Scholar] [CrossRef]
- Zhan, C.; Neal, J.N.; Wu, J.; Jiang, D.E. Quantum Effects on the Capacitance of Graphene-Based Electrodes. J. Phys. Chem. C 2015, 119, 22297–22303. [Google Scholar] [CrossRef]
- Portet, C.; Kazachkin, D.; Osswald, S.; Gogotsi, Y.; Borguet, E. Impact of synthesis conditions on surface chemistry and structure of carbide-derived carbons. Thermochim. Acta 2010, 497, 137–142. [Google Scholar] [CrossRef]
- Dyatkin, B.; Mamontov, E.; Cook, K.M.; Gogotsi, Y. Capacitance, charge dynamics, and electrolyte-surface interactions in functionalized carbide-derived carbon electrodes. Prog. Nat. Sci. Mater. Int. 2015, 25, 631–641. [Google Scholar] [CrossRef]
- Ewert, J.K.; Weingarth, D.; Denner, C.; Friedrich, M.; Zeiger, M.; Schreiber, A.; Jäckel, N.; Presser, V.; Kempe, R. Enhanced capacitance of nitrogen-doped hierarchically porous carbide-derived carbon in matched ionic liquids. J. Mater. Chem. A 2015, 3, 18906–18912. [Google Scholar] [CrossRef]
- Pinkert, K.; Oschatz, M.; Borchardt, L.; Klose, M.; Zier, M.; Nickel, W.; Giebeler, L.; Oswald, S.; Kaskel, S.; Eckert, J. Role of Surface Functional Groups in Ordered Mesoporous Carbide-Derived Carbon/Ionic Liquid Electrolyte Double-Layer Capacitor Interfaces. ACS Appl. Mater. Interfaces 2014, 6, 2922–2928. [Google Scholar] [CrossRef] [PubMed]
- Gor, G.Y.; Thommes, M.; Cychosz, K.A.; Neimark, A.V. Quenched solid density functional theory method for characterization of mesoporous carbons by nitrogen adsorption. Carbon 2012, 50, 1583–1590. [Google Scholar] [CrossRef]
- Kurig, H.; Russina, M.; Tallo, I.; Siebenbürger, M.; Romann, T.; Lust, E. The suitability of infinite slit-shaped pore model to describe the pores in highly porous carbon materials. Carbon 2016, 100, 617–624. [Google Scholar] [CrossRef]
- Kondrat, S.; Kornyshev, A.A. Pressing a spring: What does it take to maximize the energy storage in nanoporous supercapacitors? Nanoscale Horiz. 2016, 1, 45–52. [Google Scholar] [CrossRef]
- Pak, A.J.; Hwang, G.S. Molecular Insights into the Complex Relationship between Capacitance and Pore Morphology in Nanoporous Carbon-based Supercapacitors. ACS Appl. Mater. Interfaces 2016, 8, 34659–34667. [Google Scholar] [CrossRef] [PubMed]
- Striolo, A.; Chialvo, A.A.; Cummings, P.T.; Gubbins, K.E. Water Adsorption in Carbon-Slit Nanopores. Langmuir 2003, 19, 8583–8591. [Google Scholar] [CrossRef]
- Wang, Q.; Johnson, J.K. Molecular simulation of hydrogen adsorption in single-walled carbon nanotubes and idealized carbon slit pores. J. Chem. Phys. 1999, 110, 577–586. [Google Scholar] [CrossRef]
- Cracknell, R.F.; Nicholson, D.; Quirke, N. A grand canonical Monte Carlo study of Lennard-Jones mixtures in slit shaped pores. Mol. Phys. 1993, 80, 885–897. [Google Scholar] [CrossRef]
- He, Y.; Huang, J.; Sumpter, B.G.; Kornyshev, A.A.; Qiao, R. Dynamic Charge Storage in Ionic Liquids-filled Nanopores: Insight from a Computational Cyclic Voltammetry Study. J. Phys. Chem. Lett. 2015, 6, 22–30. [Google Scholar] [CrossRef] [PubMed]
- Kondrat, S.; Wu, P.; Qiao, R.; Kornyshev, A.A. Accelerating charging dynamics in subnanometre pores. Nat. Mater. 2014, 13, 387–393. [Google Scholar] [CrossRef] [PubMed]
- Miyahara, M.; Gubbins, K.E. Freezing/melting phenomena for Lennard-Jones methane in slit pores: A Monte Carlo study. J. Chem. Phys. 1997, 106, 2865–2880. [Google Scholar] [CrossRef]
- Feng, G.; Qiao, R.; Huang, J.; Dai, S.; Sumpter, B.G.; Meunier, V. The importance of ion size and electrode curvature on electrical double layers in ionic liquids. Phys. Chem. Chem. Phys. 2011, 13, 1152–1161. [Google Scholar] [CrossRef] [PubMed]
- Wood, B.C.; Ogitsu, T.; Otani, M.; Biener, J. First-Principles-Inspired Design Strategies for Graphene-Based Supercapacitor Electrodes. J. Phys. Chem. C 2014, 118, 4–15. [Google Scholar] [CrossRef]
- Palmer, J.C.; Moore, J.D.; Brennan, J.K.; Gubbins, K.E. Simulating local adsorption isotherms in structurally complex porous materials: A direct assessment of the slit pore model. J. Phys. Chem. Lett. 2011, 2, 165–169. [Google Scholar] [CrossRef]
- Bandaru, P.; Yamada, H.; Narayanan, R.; Hoefer, M. Charge transfer and storage in nanostructures. Mater. Sci. Eng. R Rep. 2015, 96, 1–69. [Google Scholar] [CrossRef]
- McGreevy, R.L.; Pusztai, L. Reverse Monte Carlo Simulation: A New Technique for the Determination of Disordered Structures. Mol. Simul. 1988, 1, 359–367. [Google Scholar] [CrossRef]
- Duane, S.; Kennedy, A.; Pendleton, B.J.; Roweth, D. Hybrid Monte Carlo. Phys. Lett. B 1987, 195, 216–222. [Google Scholar] [CrossRef]
- Pikunic, J.; Clinard, C.; Cohaut, N.; Gubbins, K.E.; Guet, J.M.; Pellenq, R.J.M.; Rannou, I.; Rouzaud, J.N. Structural Modeling of Porous Carbons: Constrained Reverse Monte Carlo Method. Langmuir 2003, 19, 8565–8582. [Google Scholar] [CrossRef]
- Zetterström, P.; Urbonaite, S.; Lindberg, F.; Delaplane, R.G.; Leis, J.; Svensson, G. Reverse Monte Carlo studies of nanoporous carbon from TiC. J. Phys. Condens. Matter 2005, 17, 3509–3524. [Google Scholar] [CrossRef]
- Palmer, J.C.; Brennan, J.K.; Hurley, M.; Balboa, A.; Gubbins, K.E. Detailed structural models for activated carbons from molecular simulation. Carbon 2009, 47, 2904–2913. [Google Scholar] [CrossRef]
- Farmahini, A.H.; Opletal, G.; Bhatia, S.K. Structural Modelling of Silicon Carbide-Derived Nanoporous Carbon by Hybrid Reverse Monte Carlo Simulation. J. Phys. Chem. C 2013, 117, 14081–14094. [Google Scholar] [CrossRef]
- Jedlovszky, P.; Bakó, I.; Pálinkás, G.; Radnai, T.; Soper, A.K. Investigation of the uniqueness of the reverse Monte Carlo method: Studies on liquid water. J. Chem. Phys. 1996, 105, 245–254. [Google Scholar] [CrossRef]
- Soper, A. Empirical potential Monte Carlo simulation of fluid structure. Chem. Phys. 1996, 202, 295–306. [Google Scholar] [CrossRef]
- Palmer, J.C.; Gubbins, K.E. Atomistic models for disordered nanoporous carbons using reactive force fields. Microporous Mesoporous Mater. 2012, 154, 24–37. [Google Scholar] [CrossRef]
- Shi, Y. A mimetic porous carbon model by quench molecular dynamics simulation. J. Chem. Phys. 2008, 128, 234707. [Google Scholar]
- Powles, R.; Marks, N.; Lau, D. Self-assembly of 2-bonded carbon nanostructures from amorphous precursors. Phys. Rev. B 2009, 79, 1–11. [Google Scholar] [CrossRef]
- Palmer, J.C.; Llobet, A.; Yeon, S.H.H.; Fischer, J.E.; Shi, Y.; Gogotsi, Y.; Gubbins, K.E. Modeling the structural evolution of carbide-derived carbons using quenched molecular dynamics. Carbon 2010, 48, 1116–1123. [Google Scholar] [CrossRef]
- Garofalini, S.H. Molecular dynamics simulation of the frequency spectrum of amorphous silica. J. Chem. Phys. 1982, 76, 3189. [Google Scholar] [CrossRef]
- Gelb, L.D.; Gubbins, K.E. Pore Size Distributions in Porous Glasses: A Computer Simulation Study. Langmuir 1999, 15, 305–308. [Google Scholar] [CrossRef]
- Litton, D.A.; Garofalini, S.H. Modeling of hydrophilic wafer bonding by molecular dynamics simulations. J. Appl. Phys. 2001, 89, 6013–6023. [Google Scholar] [CrossRef]
- Kluge, M.D.; Ray, J.R.; Rahman, A. Amorphous-silicon formation by rapid quenching: A molecular-dynamics study. Phys. Rev. B 1987, 36, 4234–4237. [Google Scholar] [CrossRef]
- Ding, K.; Andersen, H.C. Molecular-dynamics simulation of amorphous germanium. Phys. Rev. B 1986, 34, 6987–6991. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Marks, N.A. Generalizing the environment-dependent interaction potential for carbon. Phys. Rev. B 2000, 63, 035401. [Google Scholar] [CrossRef]
- Tersoff, J. Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys. Rev. B 1989, 39, 5566–5568. [Google Scholar] [CrossRef]
- Mi, X.; Shi, Y. Topological defects in nanoporous carbon. Carbon 2013, 60, 202–214. [Google Scholar] [CrossRef]
- De Tomas, C.; Suarez-Martinez, I.; Vallejos-Burgos, F.; López, M.J.; Kaneko, K.; Marks, N.A. Structural prediction of graphitization and porosity in carbide-derived carbons. Carbon 2017, 119, 1–9. [Google Scholar] [CrossRef]
- Schweizer, S.; Meissner, R.; Amkreutz, M.; Thiel, K.; Schiffels, P.; Landwehr, J.; Etzold, B.J.; Hill, J.R. Molecular Modeling of Microporous Structures of Carbide-Derived Carbon Based Supercapacitors. J. Phys. Chem. C 2017, 121, 7221–7231. [Google Scholar] [CrossRef]
- De Tomas, C.; Suarez-Martinez, I.; Marks, N.A. Graphitization of amorphous carbons: A comparative study of interatomic potentials. Carbon 2016, 109, 681–693. [Google Scholar] [CrossRef]
- Welz, S.; McNallan, M.J.; Gogotsi, Y. Carbon structures in silicon carbide derived carbon. J. Mater. Process. Technol. 2006, 179, 11–22. [Google Scholar] [CrossRef]
- Van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A Reactive Force Field for Hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Srinivasan, S.G.; van Duin, A.C.T.; Ganesh, P. Development of a ReaxFF Potential for Carbon Condensed Phases and Its Application to the Thermal Fragmentation of a Large Fullerene. J. Phys. Chem. A 2015, 119, 571–580. [Google Scholar] [CrossRef] [PubMed]
- Ranganathan, R.; Rokkam, S.; Desai, T.; Keblinski, P. Generation of amorphous carbon models using liquid quench method: A reactive molecular dynamics study. Carbon 2017, 113, 87–99. [Google Scholar] [CrossRef]
- Aktulga, H.M.; Fogarty, J.C.; Pandit, S.A.; Grama, A.Y. Parallel reactive molecular dynamics: Numerical methods and algorithmic techniques. Parallel Comput. 2012, 38, 245–259. [Google Scholar] [CrossRef]
- Chenoweth, K.; van Duin, A.C.T.; Goddard, W.A. ReaxFF Reactive Force Field for Molecular Dynamics Simulations of Hydrocarbon Oxidation. J. Phys. Chem. A 2008, 112, 1040–1053. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Chenoweth, K.; van Duin, A.C.T.; Dasgupta, S.; Goddard, W.A., III. Initiation Mechanisms and Kinetics of Pyrolysis and Combustion of JP-10 Hydrocarbon Jet Fuel. J. Phys. Chem. A 2009, 113, 1740–1746. [Google Scholar] [CrossRef] [PubMed]
- Castro-Marcano, F.; Kamat, A.M.; Russo, M.F.; van Duin, A.C.T.; Mathews, J.P. Combustion of an Illinois No. 6 coal char simulated using an atomistic char representation and the ReaxFF reactive force field. Combust. Flame 2012, 159, 1272–1285. [Google Scholar] [CrossRef]
- Bundy, F. Pressure-temperature phase diagram of elemental carbon. Phys. A Stat. Mech. Appl. 1989, 156, 169–178. [Google Scholar]
- Bundy, F.; Bassett, W.; Weathers, M.; Hemley, R.; Mao, H.; Goncharov, A. The pressure-temperature phase and transformation diagram for carbon. updated through 1994. Carbon 1996, 34, 141–153. [Google Scholar] [CrossRef]
- Shinoda, W.; Shiga, M.; Mikami, M. Rapid estimation of elastic constants by molecular dynamics simulation under constant stress. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 69, 16–18. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Tsai, W.Y.; Gao, P.C.; Daffos, B.; Taberna, P.L.; Perez, C.R.; Gogotsi, Y.; Favier, F.; Simon, P. Ordered mesoporous silicon carbide-derived carbon for high-power supercapacitors. Electrochem. Commun. 2013, 34, 109–112. [Google Scholar] [CrossRef]
- Dyatkin, B.; Gogotsi, Y. Effects of structural disorder and surface chemistry on electric conductivity and capacitance of porous carbon electrodes. Faraday Discuss. 2014, 172, 139–162. [Google Scholar] [CrossRef] [PubMed]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Caguiat, J.N.; Kirk, D.W.; Jia, C.Q. Uncertainties in characterization of nanoporous carbons using density functional theory-based gas physisorption. Carbon 2014, 72, 47–56. [Google Scholar] [CrossRef]
- Hammersley, A.P.; Svensson, S.O.; Hanfland, M.; Fitch, A.N.; Hausermann, D. Two-dimensional detector software: From real detector to idealised image or two-theta scan. High Press. Res. 1996, 14, 235–248. [Google Scholar] [CrossRef]
- Qiu, X.; Thompson, J.W.; Billinge, S.J.L. PDFgetX2: A GUI-driven program to obtain the pair distribution function from X-ray powder diffraction data. J. Appl. Crystallogr. 2004, 37, 678. [Google Scholar] [CrossRef]
- Chupas, P.J.; Qiu, X.; Hanson, J.C.; Lee, P.L.; Grey, C.P.; Billinge, S.J.L. Rapid-acquisition pair distribution function (RA-PDF) analysis. J. Appl. Crystallogr. 2003, 36, 1342–1347. [Google Scholar] [CrossRef]
- Farrow, C.L.; Juhas, P.; Liu, J.W.; Bryndin, D.; Božin, E.S.; Bloch, J.; Proffen, T.; Billinge, S.J.L. PDFfit2 and PDFgui: computer programs for studying nanostructure in crystals. J. Phys. Condens. Matter 2007, 19, 335219. [Google Scholar] [CrossRef] [PubMed]
- Krivanek, O.L.; Chisholm, M.F.; Nicolosi, V.; Pennycook, T.J.; Corbin, G.J.; Dellby, N.; Murfitt, M.F.; Own, C.S.; Szilagyi, Z.S.; Oxley, M.P.; et al. Atom-by-atom structural and chemical analysis by annular dark-field electron microscopy. Nature 2010, 464, 571–574. [Google Scholar] [CrossRef] [PubMed]
- Voyles, P.M.; Muller, D.A.; Grazul, J.L.; Citrin, P.H.; Gossmann, H.J.L. Atomic-scale imaging of individual dopant atoms and clusters in highly n-type bulk Si. Nature 2002, 416, 826–829. [Google Scholar] [CrossRef] [PubMed]
- Gelb, L.D.; Gubbins, K.E. Characterization of Porous Glasses: Simulation Models, Adsorption Isotherms, and the Brunauer-Emmett-Teller Analysis Method. Langmuir 1998, 14, 2097–2111. [Google Scholar] [CrossRef]
- Stone, A.J.; Wales, D.J. Theoretical studies of icosahedral C60 and some related species. Chem. Phys. Lett. 1986, 128, 501–503. [Google Scholar] [CrossRef]
- Meyer, J.C.; Kisielowski, C.; Erni, R.; Rossell, M.D.; Crommie, M.F.; Zettl, A. Direct imaging of lattice atoms and topological defects in graphene membranes. Nano Lett. 2008, 8, 3582–3586. [Google Scholar] [CrossRef] [PubMed]
- Proffen, T.; Neder, R.B. DISCUS: A program for diffuse scattering and defect-structure simulation. J. Appl. Crystallogr. 1997, 30, 171–175. [Google Scholar] [CrossRef]
- Petkov, R.G.; Difrancesco, S.J.L.V. Local structure of nanoporous carbons. Philos. Mag. B 1999, 79, 1519–1530. [Google Scholar] [CrossRef]
- Forse, A.C.; Merlet, C.; Allan, P.K.; Humphreys, E.K.; Griffin, J.M.; Aslan, M.; Zeiger, M.; Presser, V.; Gogotsi, Y.; Grey, C.P. New Insights into the Structure of Nanoporous Carbons from NMR, Raman, and Pair Distribution Function Analysis. Chem. Mater. 2015, 27, 6848–6857. [Google Scholar] [CrossRef]


| Sample | Q, Kps | , nm | L, nm | , gcm | Compression |
|---|---|---|---|---|---|
| QMD-100 | 100 | 0.50 | 7.488 | 0.950 | No |
| QMD-10 | 10 | 0.97 | 7.488 | 0.950 | No |
| QMD-10c | 10 | 0.56 | 6.489 | 1.467 | Yes |
| QMD-1 | 1 | 1.40 | 7.488 | 0.950 | No |
| QMD-1c | 1 | 0.91 | 6.733 | 1.311 | Yes |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thompson, M.W.; Dyatkin, B.; Wang, H.-W.; Turner, C.H.; Sang, X.; Unocic, R.R.; Iacovella, C.R.; Gogotsi, Y.; Van Duin, A.C.T.; Cummings, P.T. An Atomistic Carbide-Derived Carbon Model Generated Using ReaxFF-Based Quenched Molecular Dynamics. C 2017, 3, 32. https://doi.org/10.3390/c3040032
Thompson MW, Dyatkin B, Wang H-W, Turner CH, Sang X, Unocic RR, Iacovella CR, Gogotsi Y, Van Duin ACT, Cummings PT. An Atomistic Carbide-Derived Carbon Model Generated Using ReaxFF-Based Quenched Molecular Dynamics. C. 2017; 3(4):32. https://doi.org/10.3390/c3040032
Chicago/Turabian StyleThompson, Matthew W., Boris Dyatkin, Hsiu-Wen Wang, C. Heath Turner, Xiahan Sang, Raymond R. Unocic, Christopher R. Iacovella, Yury Gogotsi, Adri C. T. Van Duin, and Peter T. Cummings. 2017. "An Atomistic Carbide-Derived Carbon Model Generated Using ReaxFF-Based Quenched Molecular Dynamics" C 3, no. 4: 32. https://doi.org/10.3390/c3040032
APA StyleThompson, M. W., Dyatkin, B., Wang, H.-W., Turner, C. H., Sang, X., Unocic, R. R., Iacovella, C. R., Gogotsi, Y., Van Duin, A. C. T., & Cummings, P. T. (2017). An Atomistic Carbide-Derived Carbon Model Generated Using ReaxFF-Based Quenched Molecular Dynamics. C, 3(4), 32. https://doi.org/10.3390/c3040032








