How to Detect Low-Energy Isomers of Fullerenes Using Clar Covers

Abstract

We demonstrate that the energetic stability of carbon (5,6)-fullerene isomers can, to a large extent, be inferred from two topological invariants: the Kekulé count K and the Clar count C. Although neither invariant alone exhibits a strong correlation with the total electronic energy at equilibrium geometry, the application of a min–max principle (maximizing C while minimizing K) proves effective in identifying the lowest-energy subset of ${\mathrm{C}}_n$ isomers for $n=$ 50–100. This finding substantially reduces the complexity of determining the most stable isomer among larger fullerenes.

1. Introduction

The molecular structure of a carbon (5,6)-fullerene ${\mathrm{C}}_n$ consists of 12 pentagons and $\frac{n}{2}-10$ hexagons, fused over the surface of a locally-deformed ellipsoid [1,2,3,4]. This characterization gives rise to a huge number of isomers of ${\mathrm{C}}_n$ [5,6], which grow approximately as $n^9$ [7,8], yielding 271 isomers of ${\mathrm{C}}_{50}$, 1812 isomers of ${\mathrm{C}}_{60}$, 8149 isomers of ${\mathrm{C}}_{70}$, 31,924 isomers of ${\mathrm{C}}_{80}$, 99,918 isomers of ${\mathrm{C}}_{90}$, and 285,914 isomers of ${\mathrm{C}}_{100}$ [5]. Quantum chemical identification and characterization of the lowest-energy isomer for each ${\mathrm{C}}_n$ family require substantial computational resources, particularly for large values of n [9,10,11,12,13,14,15,16,17,18,19]. This task could be substantially simplified if an efficient strategy was available for the identification of low-energy isomers of ${\mathrm{C}}_n$, which allows a substantial reduction in the set of isomers for which quantum chemical calculations must be performed. Various strategies have been identified in this context [1,3,9,20,21,22,23,24,25], involving purely topological indices [26,27,28,29,30,31,32,33,34] as well as mixed topological–geometrical descriptors [35,36,37,38]. Despite considerable progress, none of these strategies can be deemed as entirely successful, allowing predictions of the energetic stability of fullerene cages within a few kcal/mol. The existing literature on the topic is overwhelming and consists of thousands of papers reporting various types of quantum chemical computations and applications of diversified physical and graph-theoretical fullerene invariants. For a thorough discussion of other approaches, the reader is referred to numerous reviews on the topic [6,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55] and to extensive introductions in our two recent papers [56,57].

In our recent publications [56,57], we have reported various topological invariants of carbon (5,6)-fullerenes ${\mathrm{C}}_n$ with $n=20–70$, including a complete list of the Kekulé counts K, the Clar counts C, and the Clar numbers $Cl$ for all possible isomers of these fullerenes. The topological invariants were efficiently determined [58,59,60] as the corresponding Zhang–Zhang (ZZ) polynomials [61,62,63,64,65,66,67] directly from the adjacency matrix defining each fullerene isomer. None of these quantities displayed significant correlations with the quantum chemical energies and hence could not be used on their own for determination of the energetic stability of isomers for a given ${\mathrm{C}}_n$. However, it was observed that the plot of C vs. K has a special structure that permits the location of the low-energy isomers of each fullerene. For the fullerenes ${\mathrm{C}}_n$ with $n=52–70$, the lowest-energy isomers were always located at the left upper edge of the C vs. K distribution graph, with the minimum-energy isomer having the tendency to be located in the upper part of this subset of points [57]. There remained a question of whether this observation can be generalized to larger fullerenes. A positive answer to this question could substantially reduce the effort required to identify the set of isomers that need to be explicitly considered when finding the lowest-energy isomer for larger fullerenes, where the total number of isomers is too large to allow systematic analyses of all conceivable isomers using quantum chemical calculations. To test this hypothesis, in the current short paper, we extend the previous study to larger fullerenes, explicitly considering all the (5,6)-isomers of ${\mathrm{C}}_{80}$, ${\mathrm{C}}_{90}$, and ${\mathrm{C}}_{100}$. The resulting correlations between the total energy E, the Kekulé count K, and the Clar count C are presented in the next sections together with the previously obtained data for ${\mathrm{C}}_{50}$, ${\mathrm{C}}_{60}$, and ${\mathrm{C}}_{70}$, allowing us to analyze the trends with a growing value of n.

2. Computational Details

The thermodynamic stability of the isomers of ${\mathrm{C}}_{50}$, ${\mathrm{C}}_{60}$, ${\mathrm{C}}_{70}$, ${\mathrm{C}}_{80}$, ${\mathrm{C}}_{90}$, and ${\mathrm{C}}_{100}$ is assessed by computing their total density functional tight-binding (DFTB) energies at the equilibrium geometry of each isomer. We use third-order DFTB [68,69] together with the 3OB Slater–Koster parameter file for carbon without any dispersion correction [70]. The calculations for ${\mathrm{C}}_{80}$, ${\mathrm{C}}_{90}$, and ${\mathrm{C}}_{100}$ are performed using the DFTB+ program [71] with the $1\times {10}^{-12}$ convergence criterion for the self-consistent charges and the force convergence criterion of $1\times {10}^{-5}$. The electronic temperature was set to $T=0.0001$ K to avoid convergence problems for isomers with small HOMO-LUMO gaps. Note that DFTB has been successfully used for similar types of calculations several times before [10,11,56,57,72], giving good correlation with the corresponding DFT results for the isomers of ${\mathrm{C}}_{60}$ [9].

The topological invariants (K and C) were computed in the form of the ZZ polynomial using the program ZZPolyCalc [58,60,73]. The ring-spiral pentagon lists for the fullerene isomers of ${\mathrm{C}}_{80}$, ${\mathrm{C}}_{90}$, and ${\mathrm{C}}_{100}$ were taken from the database included in the FULLERENE program [2] (Version 4.5). The initial geometries of the isomers were generated using the adjacency matrix eigenvector (AME) method [1]. These structures were subsequently optimized using a force-field approach [74], extended to account for the third bond type and additional dihedral angles (activated using the ‘iopt = 3’ flag in the FULLERENE program). In instances when this procedure failed to generate a meaningful converged geometry, the process was repeated using Tutte embedding (3D-TE) [75] instead of AME and optimized using the ‘iopt = 2’ flag in the FULLERENE code. In a few rare cases, where this procedure also led to a fullerene structure with unreasonable bond lengths, the FULLERENE molecular mechanics procedure was repeated with ‘iopt = 3’, ‘iopt = 4’, and ‘iopt = 5’ based on variations in the force field of Wu et al. [74].

3. Results

We begin our presentation of results by showing the correlations between the total DFTB energies of all isomers of the fullerenes ${\mathrm{C}}_{50}$, ${\mathrm{C}}_{60}$, ${\mathrm{C}}_{70}$, ${\mathrm{C}}_{80}$, ${\mathrm{C}}_{90}$, and ${\mathrm{C}}_{100}$ and the corresponding topological invariants (Kekulé count K and Clar count C). As noted earlier for the fullerenes ${\mathrm{C}}_n$ with $n=52–70$, none of these quantities (neither K nor C) displayed significant correlations with the quantum chemical energies. We now extend this observation to larger fullerenes. Figure 1 shows a scatter plot, in which each point $(x,y)=({log}_{10}K,E^{\mathrm{DFTB}}/n)$ represents a single isomer of ${\mathrm{C}}_n$. Figure 1 is divided into six panels, each corresponding to a different size of fullerenes ${\mathrm{C}}_n$. Each of these panels shows a similar distribution of dots, suggesting a mild anticorrelation between ${log}_{10}K$ and $E^{\mathrm{DFTB}}/n$. Interestingly, the isomers with the largest value of K correspond to high-energy structures. This observation runs counter to typical resonance stability arguments well-accepted in organic chemists’ analyses of planar aromatic structures. The non-planarity of fullerenes does not seem to have a pronounced effect in this observation: The highest-energy isomer maximizes the Kekulé count K, both for the largest structure analyzed (${\mathrm{C}}_{100}$, small curvature) and the smallest structure analyzed (${\mathrm{C}}_{50}$, large curvature). Simultaneously, the most stable isomer corresponds to an intermediate value of K in each family of fullerenes. These observations show the Kekulé count K to be a mediocre predictor of fullerene stability, extending the results reported earlier for ${\mathrm{C}}_{60}$ [9,76,77,78], ${\mathrm{C}}_{20}$–${\mathrm{C}}_{50}$ [56], and ${\mathrm{C}}_{52}$–${\mathrm{C}}_{70}$ [57].

Figure 2 shows similar scatter plots with the Kekulé count K replaced with the Clar count C (We recall here briefly that the Kekulé count K of some benzenoid $\mathbf{B}$ is the number of distinct resonance structures that can be constructed for $\mathbf{B}$ using single and double bonds, while the Clar count C is the number of (generalized) resonance structures that can be constructed for $\mathbf{B}$ using single and double bonds, as well as aromatic Clar sextets). The $(x,y)=({log}_{10}C,E^{\mathrm{DFTB}}/n)$ distributions in each of the panels of Figure 2 have similar irregular and somewhat ellipsoidal shapes, providing no correlation between ${log}_{10}C$ and $E^{\mathrm{DFTB}}/n$. For some families of fullerenes, the isomer with the largest value of C corresponds to the lowest DFTB energy; for others, it corresponds to the intermediate or even the highest energy values. The situation is probably best illustrated by ${\mathrm{C}}_{50}$, where the four isomers with the largest C comprise both the highest and the lowest-energy structures. It seems that the Clar count C alone cannot be a useful predictor of fullerene stability in close analogy to the Kekulé count K discussed above, extending the observations reported earlier for ${\mathrm{C}}_{20}$–${\mathrm{C}}_{50}$ [56] and ${\mathrm{C}}_{52}$–${\mathrm{C}}_{70}$ [57].

The key discovery of our previous publication [57] was the observation of a unique correlation in the scatter plots relating the Clar count C with the Kekulé count K. Namely, we demonstrated that such distributions for ${\mathrm{C}}_n$ ($n=52–70$) form a slanted wedge with the most stable isomers grouping near the left edge of the wedge. This observation could be rephrased more formally by saying that the most stable isomers maximize the Clar count C while minimizing the Kekulé count K. In the parlance of multi-objective optimization, they are located in the vicinity of the Pareto front of the optimization problem $min\left(-C,K\right)$ [79]. This regularity can prove useful by providing a tool for discriminating a subgroup of low-energy isomers in each family of fullerenes, provided that a similar observation can be extended to larger fullerenes, for which methodical quantum chemical investigations of all possible isomers are characterized by prohibitive numerical cost.

The main objective of the current study is to extend this analysis to larger fullerenes. Figure 3 shows scatter plots where each dot, with coordinates $(x,y)=({log}_{10}K,{log}_{10}C)$, represents a single isomer of six families of fullerenes: ${\mathrm{C}}_{50}$, ${\mathrm{C}}_{60}$, ${\mathrm{C}}_{70}$, ${\mathrm{C}}_{80}$, ${\mathrm{C}}_{90}$, and ${\mathrm{C}}_{100}$. The 1% of structures (or more; details in the caption of Figure 3) corresponding to the lowest-energy isomers in each family are depicted as red circles, while the remaining structures are depicted as (somewhat smaller) black circles. Additionally, the lowest-energy structure in each panel is depicted in blue. It is clear from Figure 3 that the lowest-energy portion of isomers is in each case located at the left edge of the wedge-like distribution, confirming the observation made earlier for ${\mathrm{C}}_n$ with $n=52–70$ [57]. The generality of this observation has far-reaching consequences: It allows us to reduce the problem of identifying the most stable isomer in a given family of fullerenes ${\mathrm{C}}_n$ to those located at the left edge of the distributions analogous to those shown in Figure 3. Note that obtaining such distributions using the ZZPolyCalc program version 19.0.117 [60] reported by us recently and freely distributed via GitHub 3.15.12 [73] does not require quantum chemical calculations and is extremely efficient with a computational time within 1 s per isomer.

A drawback of this screening technique needs to be mentioned: Not all isomers located on the left edge of the distributions shown in Figure 3 correspond to low-energy structures. Therefore, the screening technique will substantially reduce (to a few percentage points of the original size) the subfamily of isomers for which quantum chemical calculations must be performed in order to identify the most stable isomer, but it most probably will not single out a handful of isomers that contain the most stable structure. Another technical difficulty is designing an appropriate numerical parameter allowing us to locate isomers at the Pareto front and in its vicinity (i.e., close to the left edge of the distribution wedge) for each ${\mathrm{C}}_n$ family. A simple descriptor, $C/K$, is not always effective here. When all isomers of ${\mathrm{C}}_{90}$ and ${\mathrm{C}}_{100}$ are sorted by their falling $C/K$ ratio, the lowest-energy structure lies within the top 0.3% and 2.0%, respectively, of the two distributions. However, for ${\mathrm{C}}_{80}$, the lowest-energy structure is contained within the bottom 0.3% of the $C/K$ distribution because the lowest-energy structure is located at—nomen est omen—the thin edge of the wedge, belonging simultaneously to the left and to the right edge. An appropriate descriptor correctly resolving these nuances and identifying structures located close to the Pareto front remains to be discovered.

It is instructive to briefly discuss the location of the lowest- and highest-energy structures in the wedge-like distributions. Figure 4 provides such a detailed plot for ${\mathrm{C}}_{100}$: The 20 lowest-energy structures are depicted in red and the 20 highest-energy structures are depicted in blue. Additionally, we have labeled the three highest- and the three lowest-energy isomers. Three important observations arise.

1.

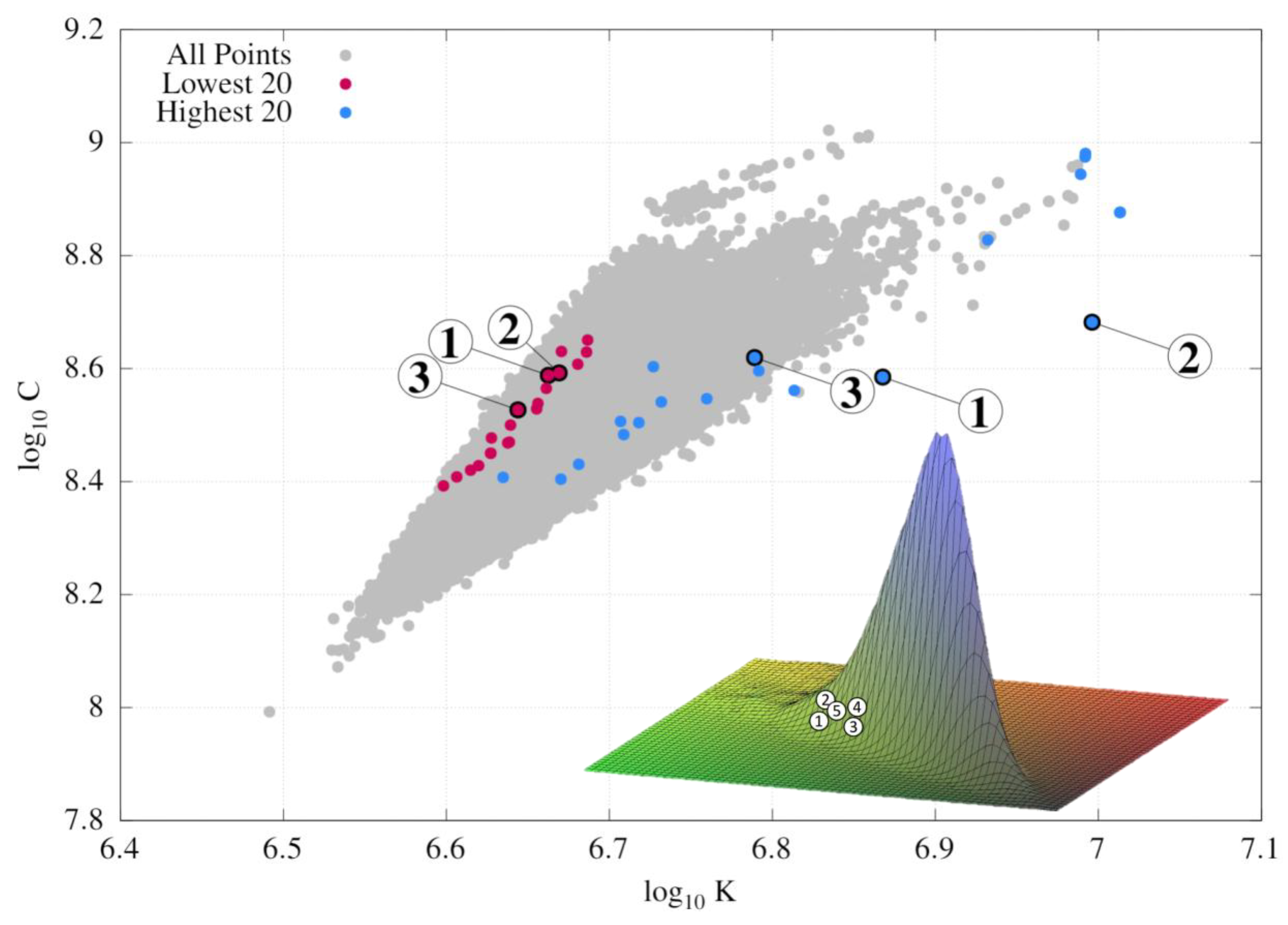
The lowest-energy structures are indeed distributed close to the left edge of the wedge, in contrast to the highest-energy structures, which are closer to the right edge.

2.

These maximal and minimal points are not located directly on the edge, but only in its vicinity, showing that the C vs. K distribution can be treated only as an approximate descriptor of the thermodynamic stability of fullerene isomers.

3.

The 2D visualization of the wedge in Figure 4 lacks information about the distribution density, leading to an incorrect impression that the low-energy structures are located in the midst of the distribution, rather than on its edge. In reality, both edges of the distribution are flat and account for a small number of points; the majority are located along the bisector of the wedge, with the right edge growing more steeply than the left edge. This behavior is clearest from the 3D visualization of the distribution shown as an inset in Figure 4, where the locations of the five lowest-energy isomers are depicted by numbers. This 3D visualization of the distribution was created by representing each isomer as a 2D Gaussian peak of unit volume located at $({log}_{10}K,{log}_{10}C)$; the whole distribution is a union of such peaks.

4. Conclusions

We show that for ${\mathrm{C}}_{50}$, ${\mathrm{C}}_{60}$, ${\mathrm{C}}_{70}$, ${\mathrm{C}}_{80}$, ${\mathrm{C}}_{90}$, and ${\mathrm{C}}_{100}$, the two topological invariants, the Kekulé K and the Clar counts C, can be jointly used to identify the lowest-energy isomers of carbon fullerenes. The $({log}_{10}K,{log}_{10}C)$ distribution of all isomers of a given fullerene ${\mathrm{C}}_n$ forms a wedge-shaped pattern, with the most stable isomers situated along its left boundary. This insight allows us to significantly reduce the number of candidates that must be analyzed through explicit quantum–chemical calculations. The main observation of this paper is that low-energy isomers of carbon fullerenes tend to maximize their Clar count C while simultaneously minimizing their Kekulé count K.