Fracture Mechanics of Tetragraphene: Effects of Structural Variations and Loading Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Mechanical Properties of Tetragraphene Using DFT
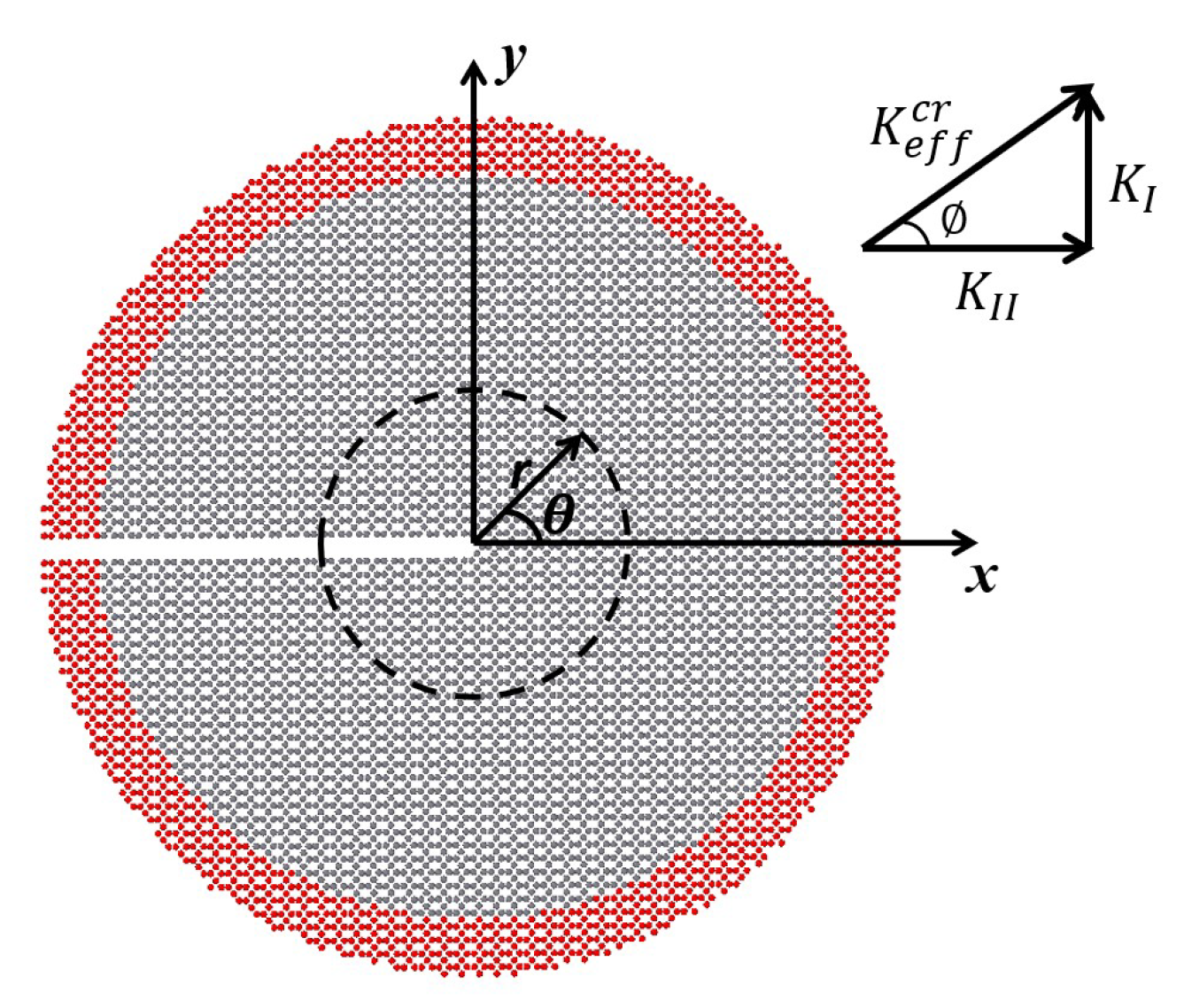
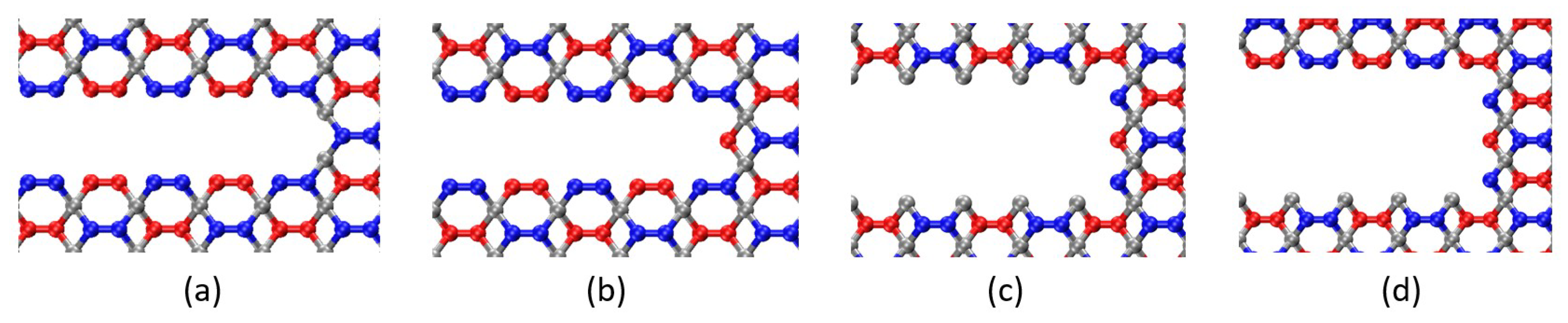
2.2. Fracture Properties of Tetragraphene
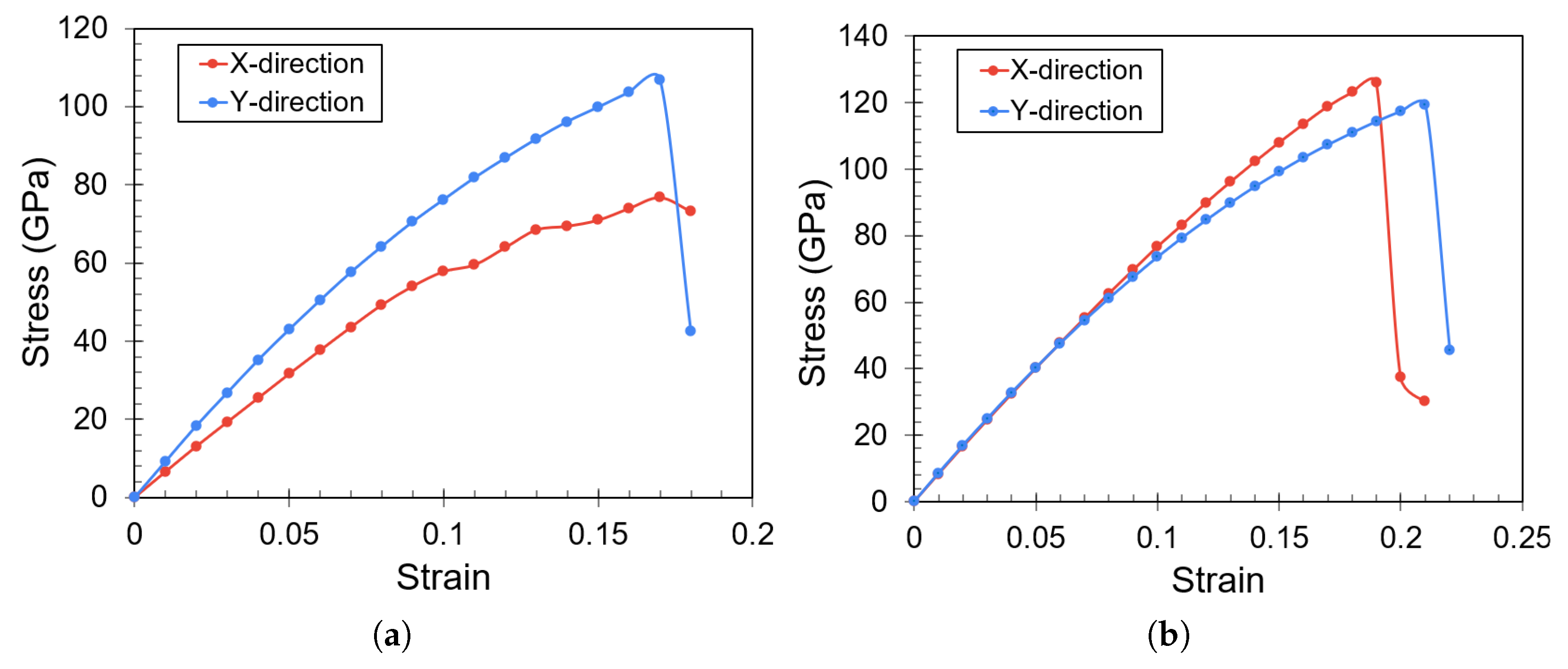
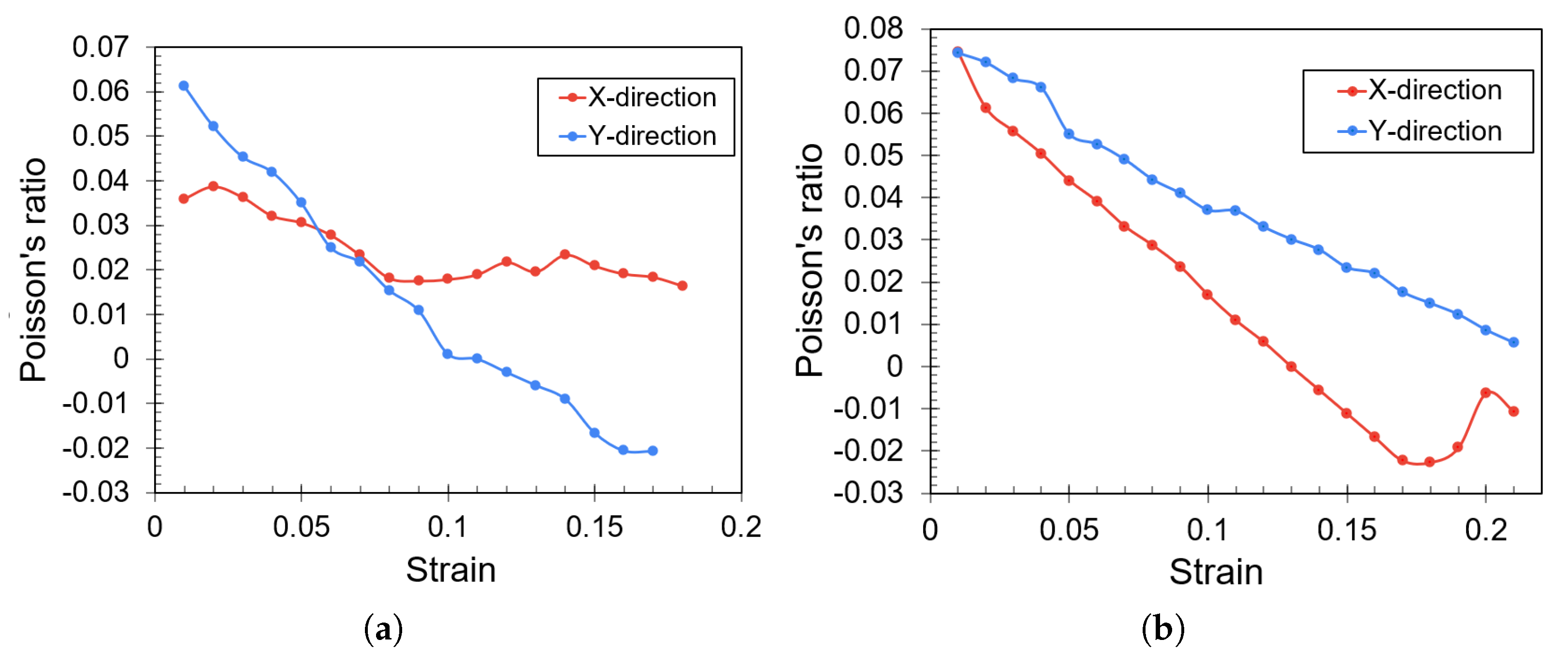
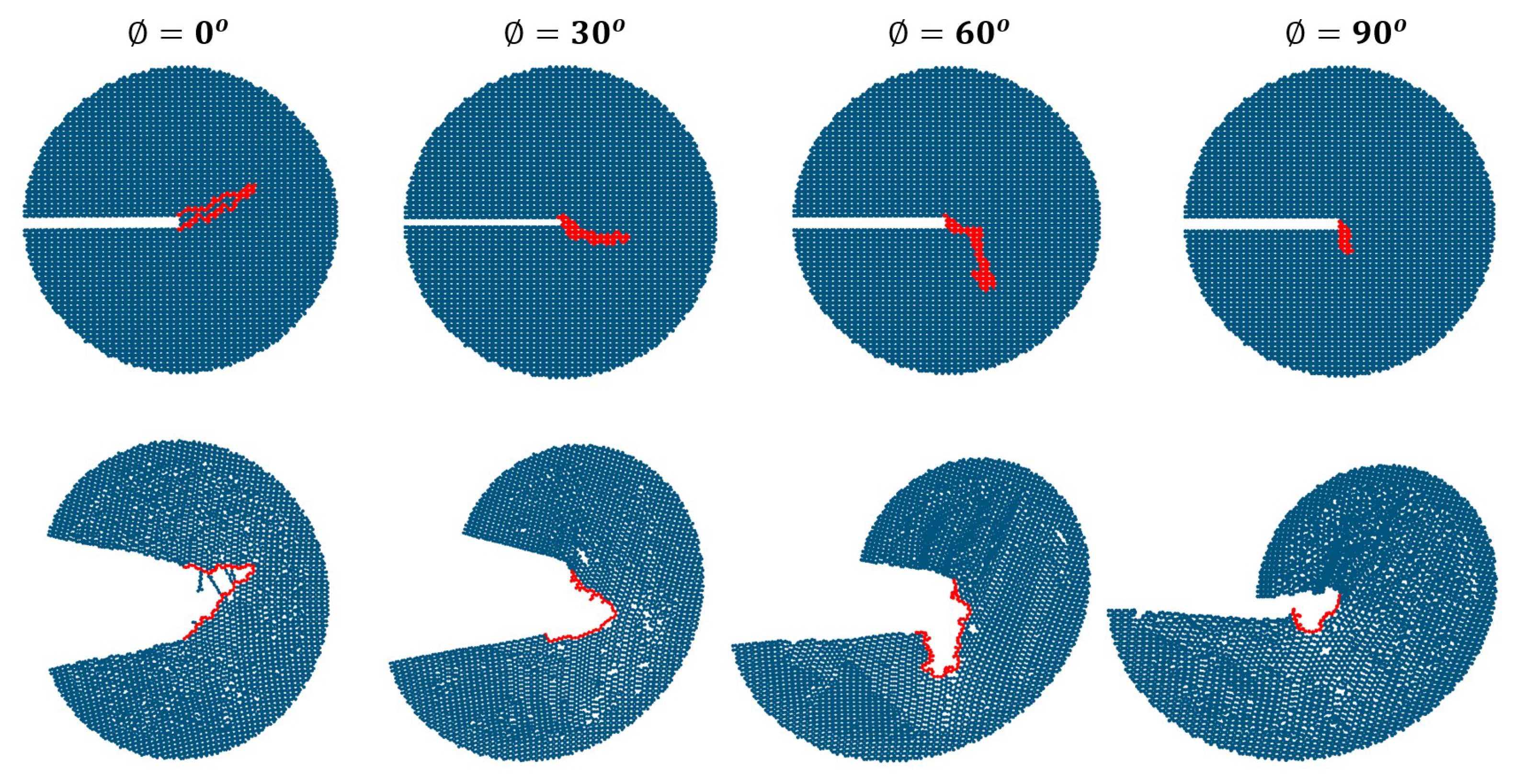
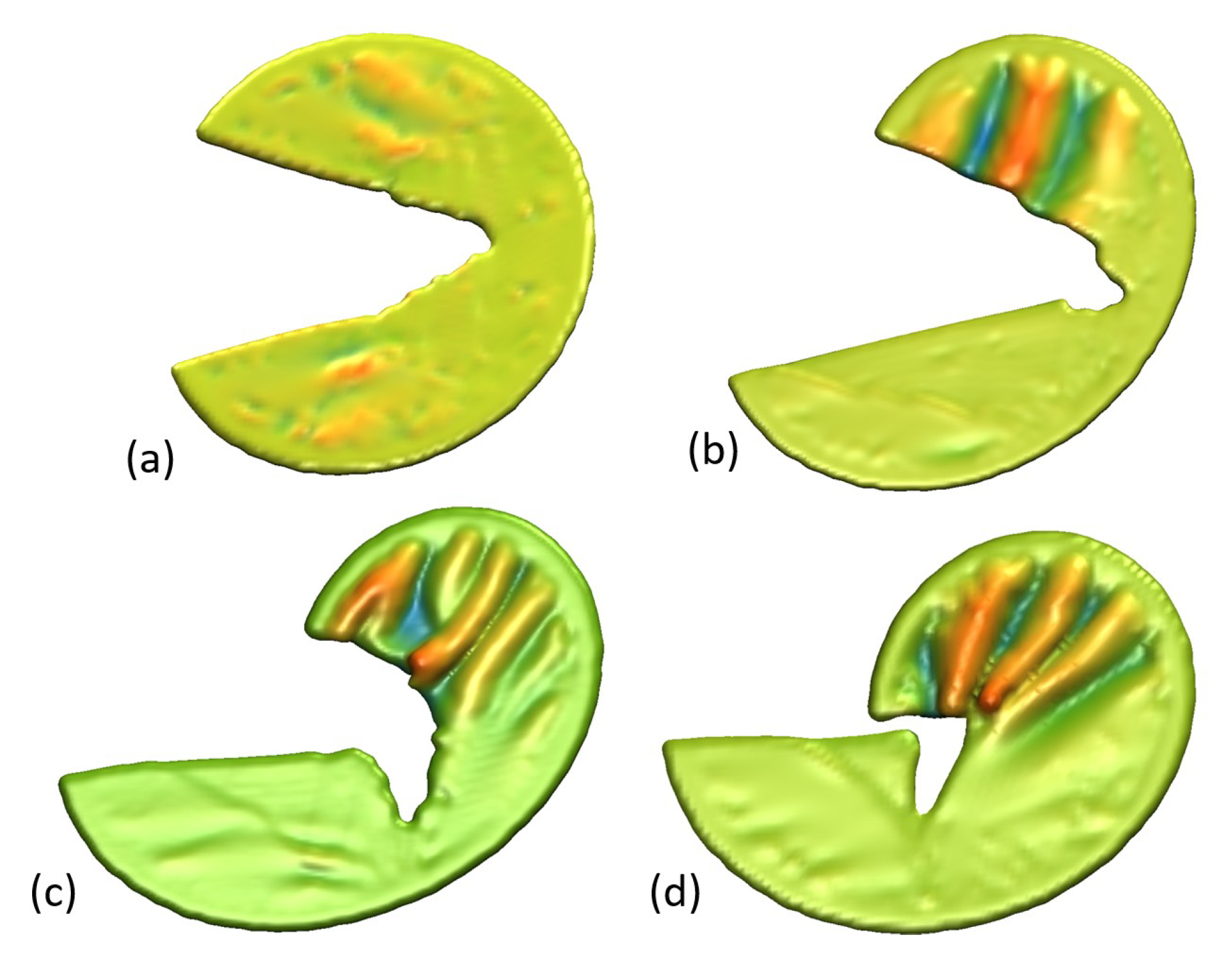
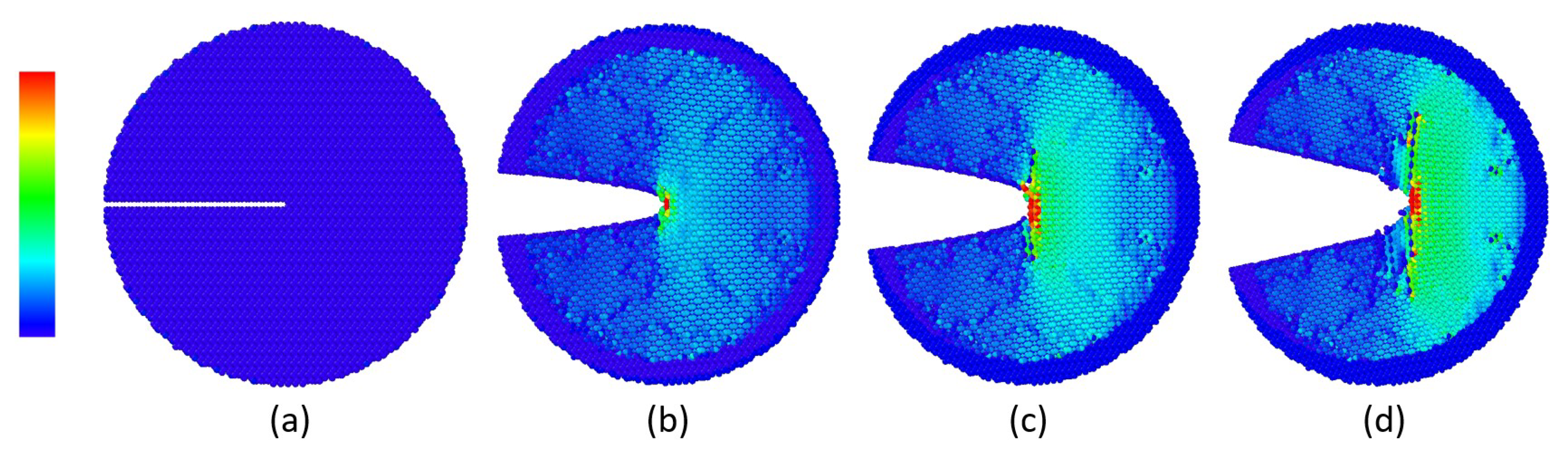
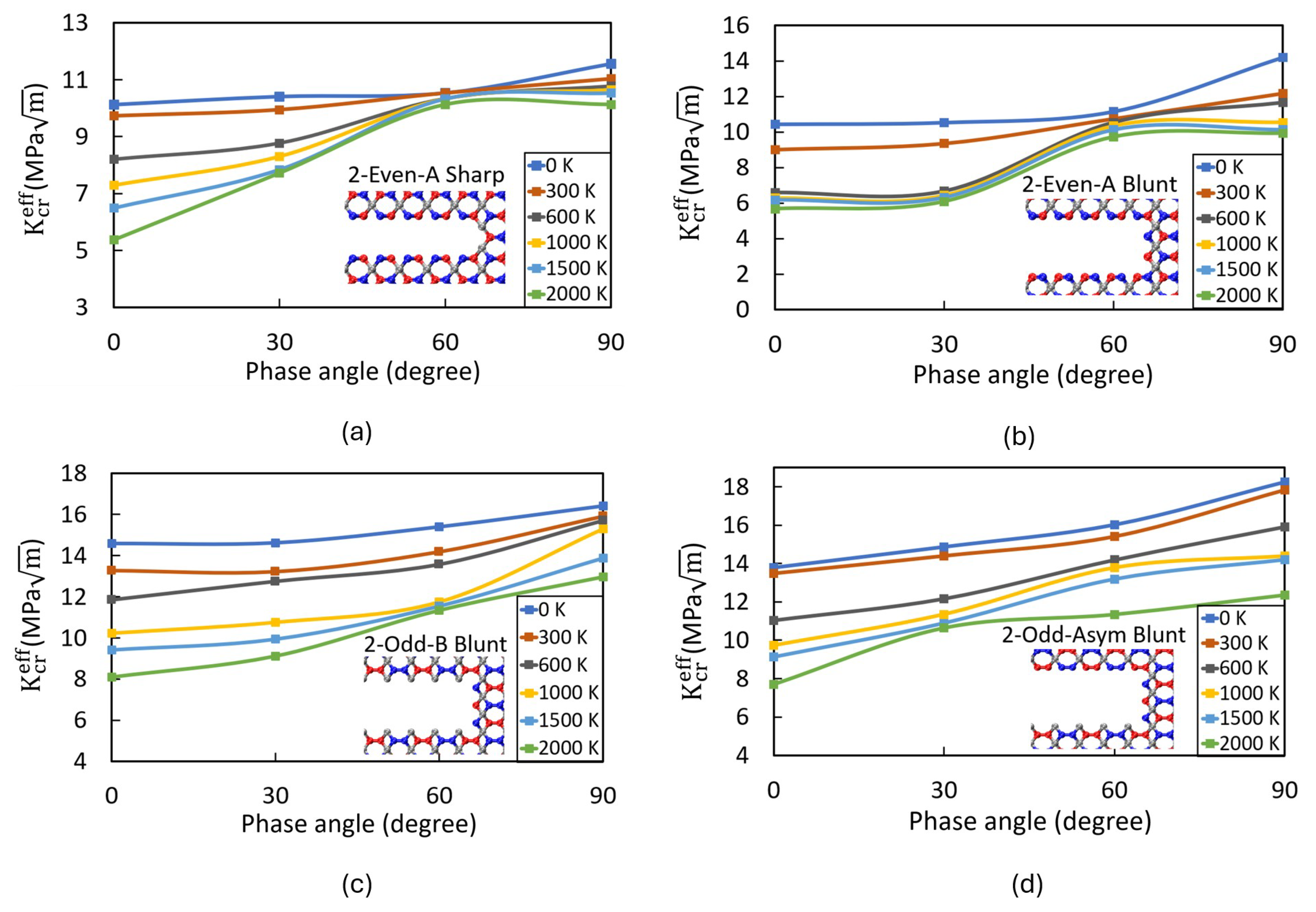
3. Results
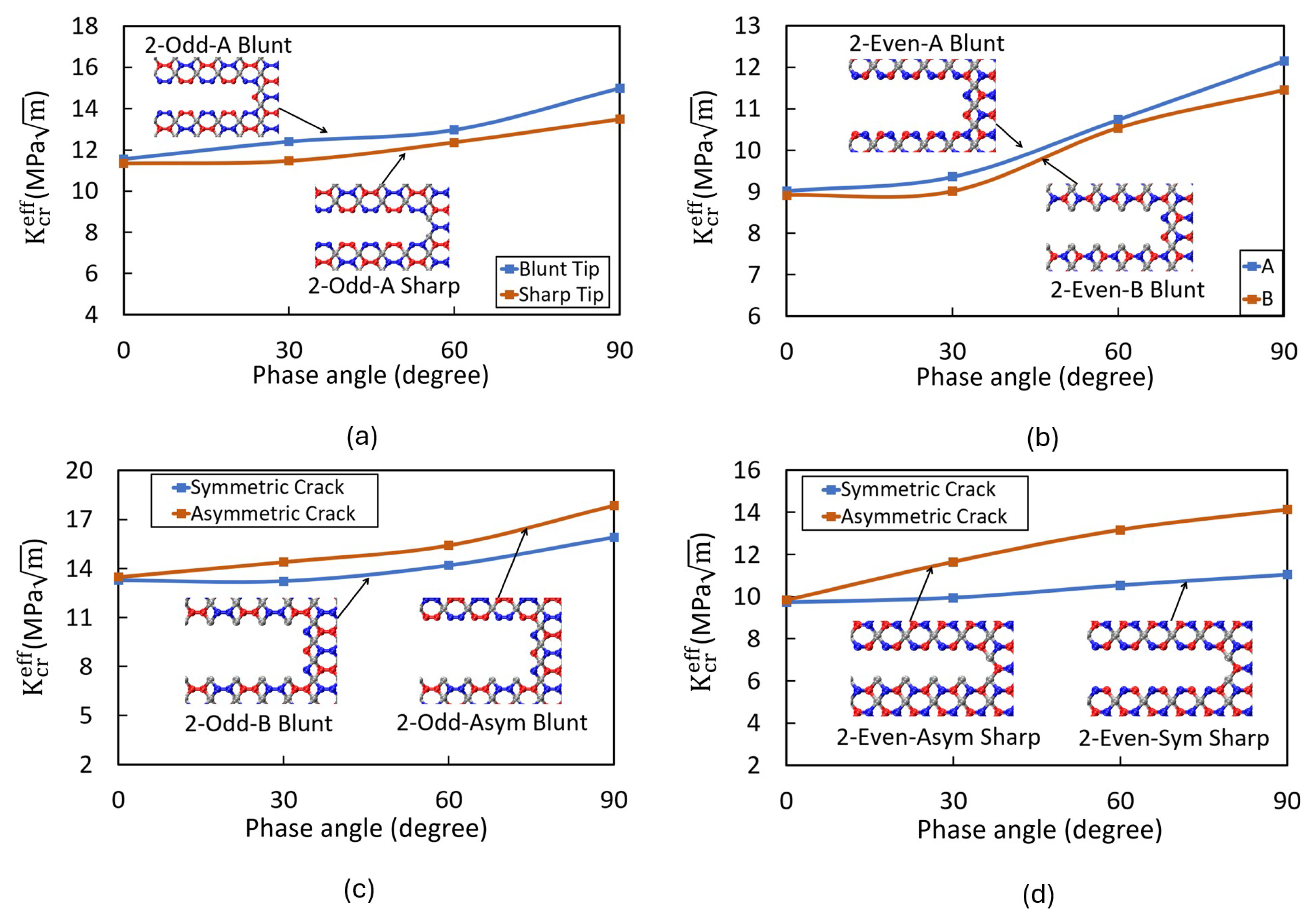
Impact of Crack Tip and Edge Structure on Critical SIF
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pumera, M. Electrochemistry of graphene: New horizons for sensing and energy storage. Chem. Rec. 2009, 9, 211–223. [Google Scholar] [CrossRef] [PubMed]
- Elapolu, M.S.; Tabarraei, A.; Wang, X.; Spearot, D.E. Fracture mechanics of multi-layer molybdenum disulfide. Eng. Fract. Mech. 2019, 212, 1–12. [Google Scholar] [CrossRef]
- Leedahl, B.; Abooalizadeh, Z.; LeBlanc, K.; Moewes, A. Tunability of room-temperature ferromagnetism in spintronic semiconductors through nonmagnetic atoms. Phys. Rev. B 2017, 96, 045202. [Google Scholar] [CrossRef]
- Izadi, S.; Jabari, K.; Izadi, M.; Hamedani, K.H.; Ghaffari, A. Identification and Diagnosis of Dynamic and Static Misalignment in Induction Motor Using Unscented Kalman Filter. In Proceedings of the 2021 13th Iranian Conference on Electrical Engineering and Computer Science (ICEESC), Tehran, Iran, 18–20 May 2021; pp. 155–160. [Google Scholar]
- Partoens, B.; Peeters, F. From graphene to graphite: Electronic structure around the K point. Phys. Rev. B 2006, 74, 075404. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Wei, Q.; Yang, G.; Peng, X. Auxetic tetrahex carbon with ultrahigh strength and a direct band gap. Phys. Rev. Appl. 2020, 13, 034065. [Google Scholar] [CrossRef]
- Xu, M.; Tabarraei, A.; Paci, J.T.; Oswald, J.; Belytschko, T. A coupled quantum/continuum mechanics study of graphene fracture. Int. J. Fract. 2012, 173, 163–173. [Google Scholar] [CrossRef]
- Zhang, B.; Mei, L.; Xiao, H. Nanofracture in graphene under complex mechanical stresses. Appl. Phys. Lett. 2012, 101, 121915. [Google Scholar] [CrossRef]
- Elapolu, M.S.; Tabarraei, A. Mechanical and fracture properties of polycrystalline graphene with hydrogenated grain boundaries. J. Phys. Chem. C 2021, 125, 11147–11158. [Google Scholar] [CrossRef]
- Elapolu, M.S.; Tabarraei, A. Stress Corrosion Cracking of Graphene. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Virtual, 16–19 November 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; Volume 84607, p. V012T12A030. [Google Scholar]
- Paci, J.T.; Xu, M.; Tabarraei, A.; Oswald, J.; Belytschko, T. Coupled quantum and continuum mechanics for the study of graphene fracture. In Abstracts of Papers of the American Chemical Society; American Chemical Society: Washington, DC, USA, 2012; Volume 244. [Google Scholar]
- Brandão, W.H.; Aguiar, A.L.; Fonseca, A.F.; Galvão, D.; De Sousa, J. Mechanical properties of tetragraphene single-layer: A molecular dynamics study. Mech. Mater. 2023, 176, 104503. [Google Scholar] [CrossRef]
- De Vasconcelos, F.M.; Souza Filho, A.G.; Meunier, V.; Girão, E.C. Electronic properties of tetragraphene nanoribbons. Phys. Rev. Mater. 2019, 3, 066002. [Google Scholar] [CrossRef]
- Kilic, M.E.; Lee, K.R. Tuning the electronic, mechanical, thermal, and optical properties of tetrahexcarbon via hydrogenation. Carbon 2020, 161, 71–82. [Google Scholar] [CrossRef]
- Esmaeili, A.; Kuhzadmohammadi, A.; Safarabadi, M. Notch stress intensity factor analysis for orthotropic media with a constrained range of anisotropic behavior. Theor. Appl. Fract. Mech. 2025, 136, 104835. [Google Scholar] [CrossRef]
- Esmaeili, A.; Kuhzadmohammadi, A.; Safarabadi, M. An Analytical Approach for the Near-Tip Field Around V-Notch in Orthotropic Materials. Fatigue Fract. Eng. Mater. Struct. 2025, 48, 487–501. [Google Scholar] [CrossRef]
- Behseresht, S.; Mehdizadeh, M. Stress intensity factor interaction between two semi-elliptical cracks in thin-walled cylinder. In Proceedings of the 28th Annual International Conference of Iranian Society of Mechanical Engineers—ISME 2020, Tehran, Iran, 27–29 May 2020; pp. 27–29. [Google Scholar]
- Rahmanidehkordi, A.; Ghasemi, A.H. Traffic Density Control for Heterogeneous Highway Systems with Input Constraints. IEEE Control Syst. Lett. 2024, 8, 2787–2792. [Google Scholar] [CrossRef]
- Nagashima, T.; Omoto, Y.; Tani, S. Stress intensity factor analysis of interface cracks using X-FEM. Int. J. Numer. Methods Eng. 2003, 56, 1151–1173. [Google Scholar] [CrossRef]
- Huang, R.; Wu, L.; He, Q.; Li, J. Stress intensity factor analysis and the stability of overhanging rock. Rock Mech. Rock Eng. 2017, 50, 2135–2142. [Google Scholar] [CrossRef]
- Garcia-Manrique, J.; Camas, D.; Lopez-Crespo, P.; Gonzalez-Herrera, A. Stress intensity factor analysis of through thickness effects. Int. J. Fatigue 2013, 46, 58–66. [Google Scholar] [CrossRef]
- Kilic, M.E.; Lee, K.R. First-principles study of fluorinated tetrahexcarbon: Stable configurations, thermal, mechanical, and electronic properties. J. Phys. Chem. C 2020, 124, 8225–8235. [Google Scholar] [CrossRef]
- de Vasconcelos, F.M.; Souza Filho, A.G.; Meunier, V.; Girão, E.C. Electronic and structural properties of tetragraphenes. Carbon 2020, 167, 403–413. [Google Scholar] [CrossRef]
- Kilic, M.E.; Lee, K.R. Tetrahex carbides: Two-dimensional group-IV materials for nanoelectronics and photocatalytic water splitting. Carbon 2021, 174, 368–381. [Google Scholar] [CrossRef]
- Rad, M.T.; Foroutan, M. Wettability of Tetrahexcarbon: MD, DFT, and AIMD Approaches. Langmuir 2023, 39, 8279–8296. [Google Scholar] [CrossRef] [PubMed]
- Peng, X.; Wei, Q.; Yang, G. Enhanced carrier mobility in anisotropic two-dimensional tetrahex-carbon through strain engineering. Carbon 2020, 165, 37–44. [Google Scholar] [CrossRef]
- Ram, B.; Mizuseki, H. Tetrahexcarbon: A two-dimensional allotrope of carbon. Carbon 2018, 137, 266–273. [Google Scholar] [CrossRef]
- Ordejón, P.; Artacho, E.; Soler, J.M. Self-consistent order-N density-functional calculations for very large systems. Phys. Rev. B 1996, 53, R10441. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993. [Google Scholar] [CrossRef]
- Kleinman, L.; Bylander, D. Efficacious form for model pseudopotentials. Phys. Rev. Lett. 1982, 48, 1425. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Erhart, P.; Albe, K. Analytical potential for atomistic simulations of silicon, carbon, and silicon carbide. Phys. Rev. B 2005, 71, 035211. [Google Scholar] [CrossRef]
- Lai, S.; Setiyawati, I.; Yen, T.; Tang, Y. Studying lowest energy structures of carbon clusters by bond-order empirical potentials. Theor. Chem. Acc. 2017, 136, 20. [Google Scholar] [CrossRef]
- Ajori, S.; Eftekharfar, A. Mechanical properties and fracture analysis of defective penta-graphene under temperature variation: Insight from molecular dynamics. Diam. Relat. Mater. 2022, 124, 108956. [Google Scholar] [CrossRef]
- Winczewski, S.; Rybicki, J. Anisotropic mechanical behavior and auxeticity of penta-graphene: Molecular statics/molecular dynamics studies. Carbon 2019, 146, 572–587. [Google Scholar] [CrossRef]
- Tu, W.; Wang, K.; Qin, L.; Sun, Z.; Chen, J. Intrinsic mechanical properties and fracture mechanism of monolayer penta-graphene investigated by nanoindentation: A molecular dynamics study. Comput. Mater. Sci. 2019, 169, 109145. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Brighenti, R. Buckling of cracked thin-plates under tension or compression. Thin-Walled Struct. 2005, 43, 209–224. [Google Scholar] [CrossRef]
- Yan, J.H.; Sutton, M.A.; Deng, X.; Cheng, C.S. Mixed-mode fracture of ductile thin-sheet materials under combined in-plane and out-of-plane loading. Int. J. Fract. 2007, 144, 297–321. [Google Scholar] [CrossRef]
- Wang, X.; Tabarraei, A.; Spearot, D.E. Fracture mechanics of monolayer molybdenum disulfide. Nanotechnology 2015, 26, 175703. [Google Scholar] [CrossRef]
- Tabarraei, A.; Wang, X. A molecular dynamics study of nanofracture in monolayer boron nitride. Mater. Sci. Eng. A 2015, 641, 225–230. [Google Scholar] [CrossRef]
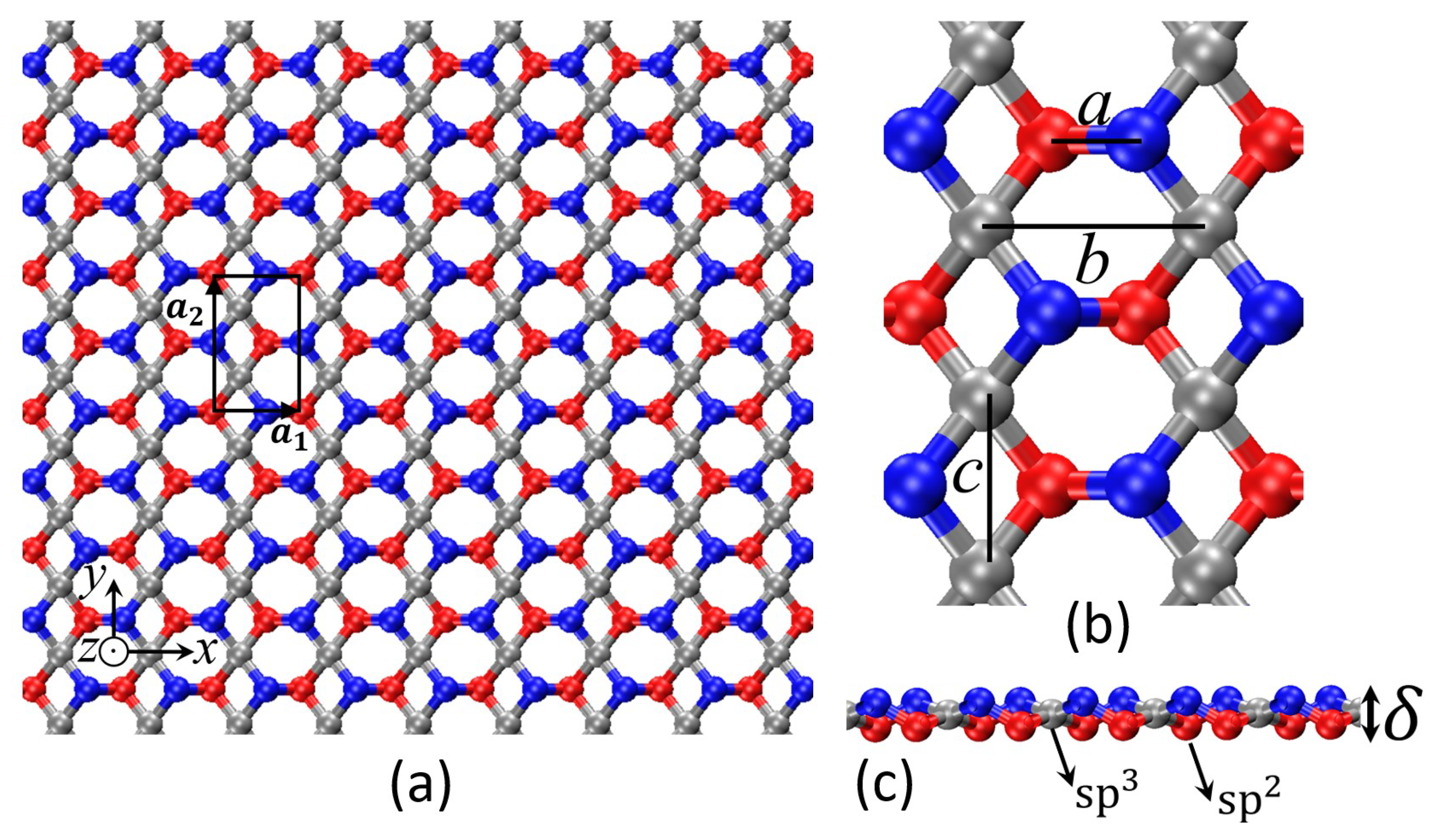
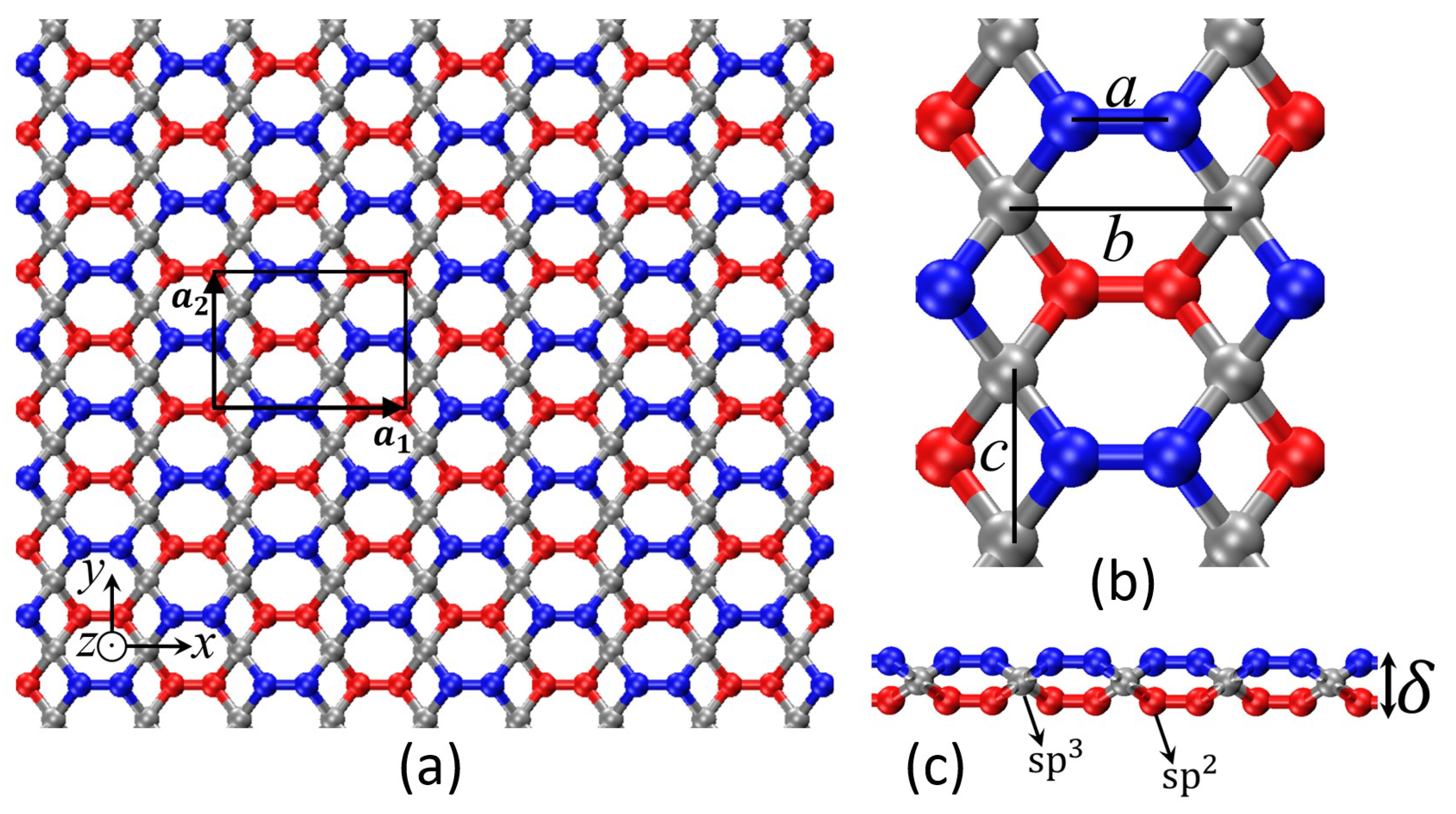

| Structural Parameters (Å) | a | b | c | |
|---|---|---|---|---|
| 2-even | 1.41 | 3.06 | 2.37 | 0.72 |
| 2-odd | 1.35 | 3.06 | 2.27 | 1.18 |
| Unit Cell Dimensions (Å) | ||
|---|---|---|
| 2-even | 3.057 | 4.734 |
| 2-odd | 6.110 | 4.535 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haddadi, E.; Tabarraei, A. Fracture Mechanics of Tetragraphene: Effects of Structural Variations and Loading Conditions. C 2025, 11, 40. https://doi.org/10.3390/c11030040
Haddadi E, Tabarraei A. Fracture Mechanics of Tetragraphene: Effects of Structural Variations and Loading Conditions. C. 2025; 11(3):40. https://doi.org/10.3390/c11030040
Chicago/Turabian StyleHaddadi, Elnaz, and Alireza Tabarraei. 2025. "Fracture Mechanics of Tetragraphene: Effects of Structural Variations and Loading Conditions" C 11, no. 3: 40. https://doi.org/10.3390/c11030040
APA StyleHaddadi, E., & Tabarraei, A. (2025). Fracture Mechanics of Tetragraphene: Effects of Structural Variations and Loading Conditions. C, 11(3), 40. https://doi.org/10.3390/c11030040





