Innovative X-Ray Absorption Technology for Improved Monitoring of the Degradation and Oxidation of Granular Activated Carbon Filters Used in Hospital Water Treatment Systems
Abstract
1. Introduction
2. Materials and Methods
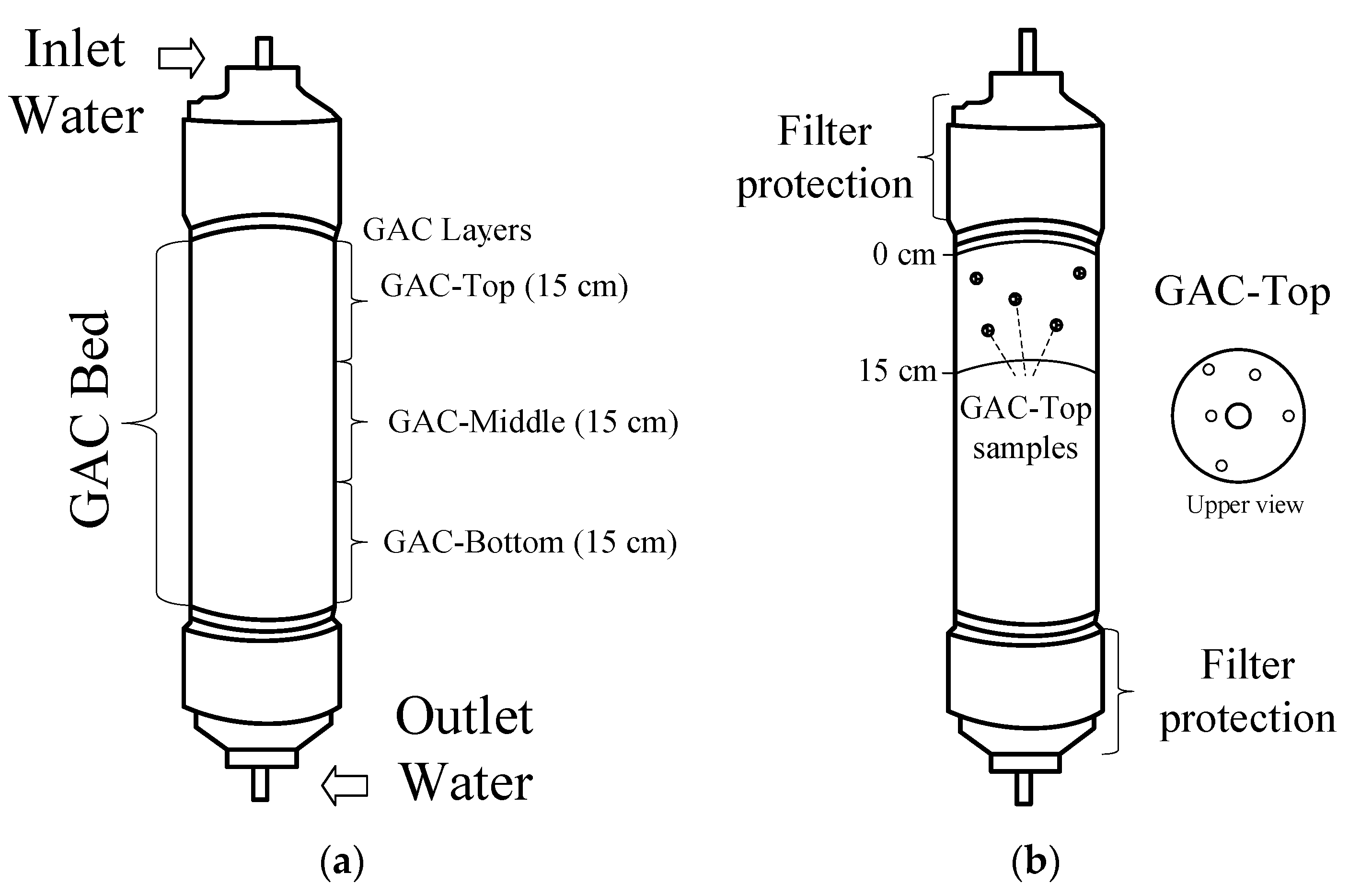
2.1. GAC Samples and Sampling Method
2.2. Sample Preparation
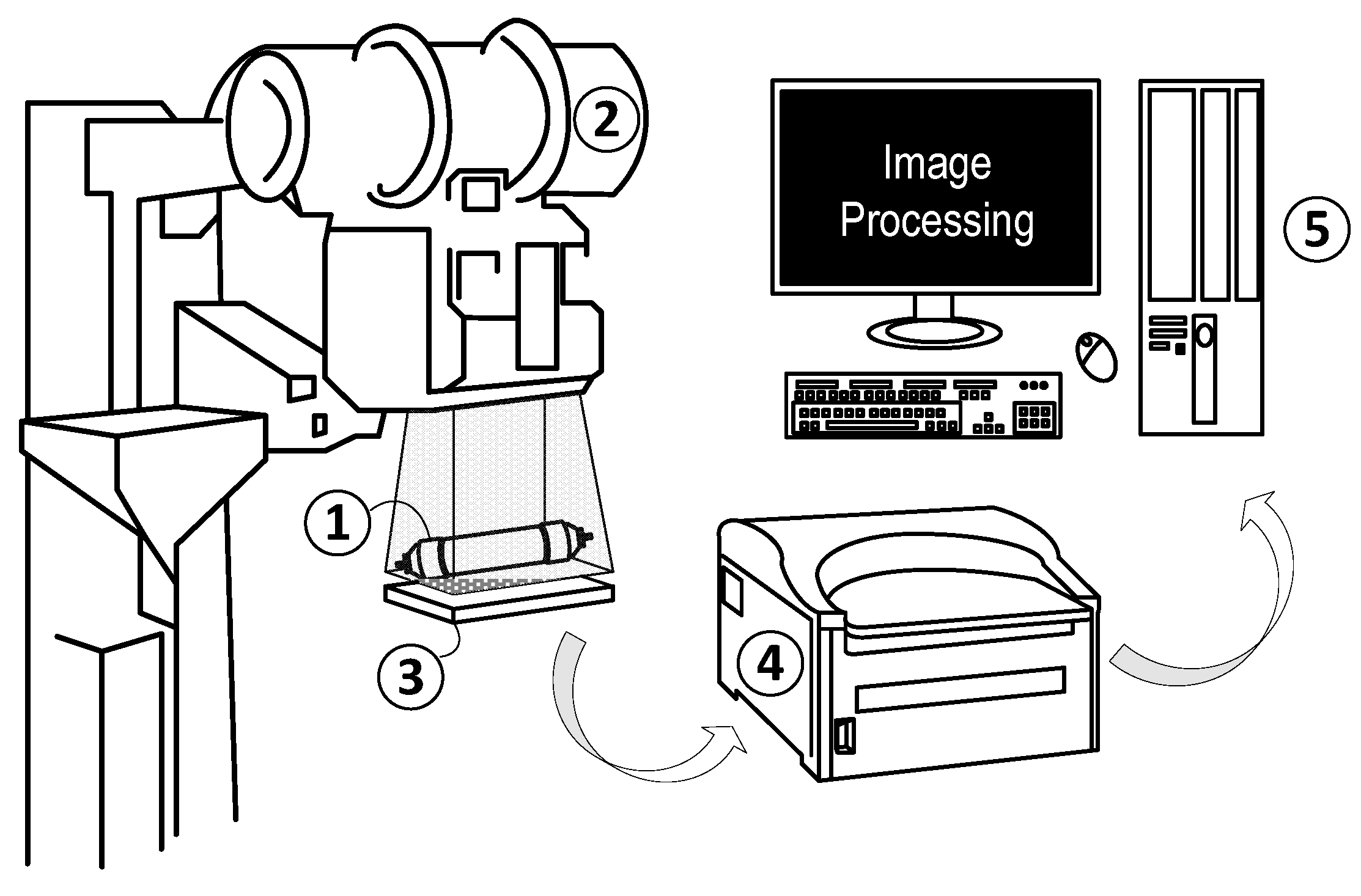
2.3. XRA Experiments
2.3.1. XRA Method 1
2.3.2. XRA Method 2 (New Method)
2.4. Breakthrough Curves for Free Chlorine Removal
3. Theory and Calculation
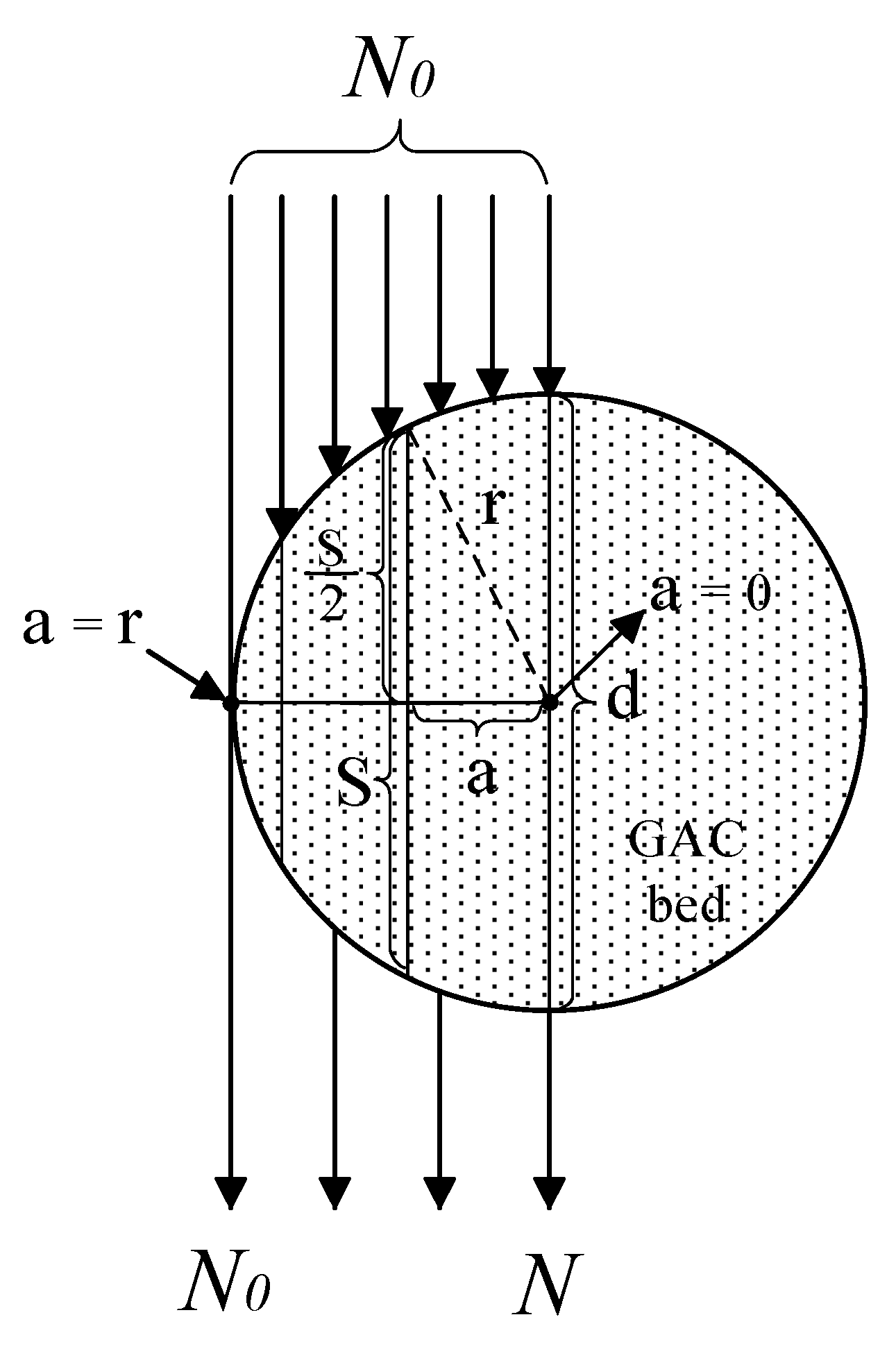
3.1. XRA Method 2: Relationship Between Grey-Scale Intensity (GSI), Linear Absorption Coefficient (), Radius (), and Apothem () for a Cylindrical GAC Filter
3.2. Parameters for the Breakthrough Curves for Free Chlorine Removal
4. Results and Discussion
4.1. XRF Analysis
4.2. Elemental Analysis (EA) Results
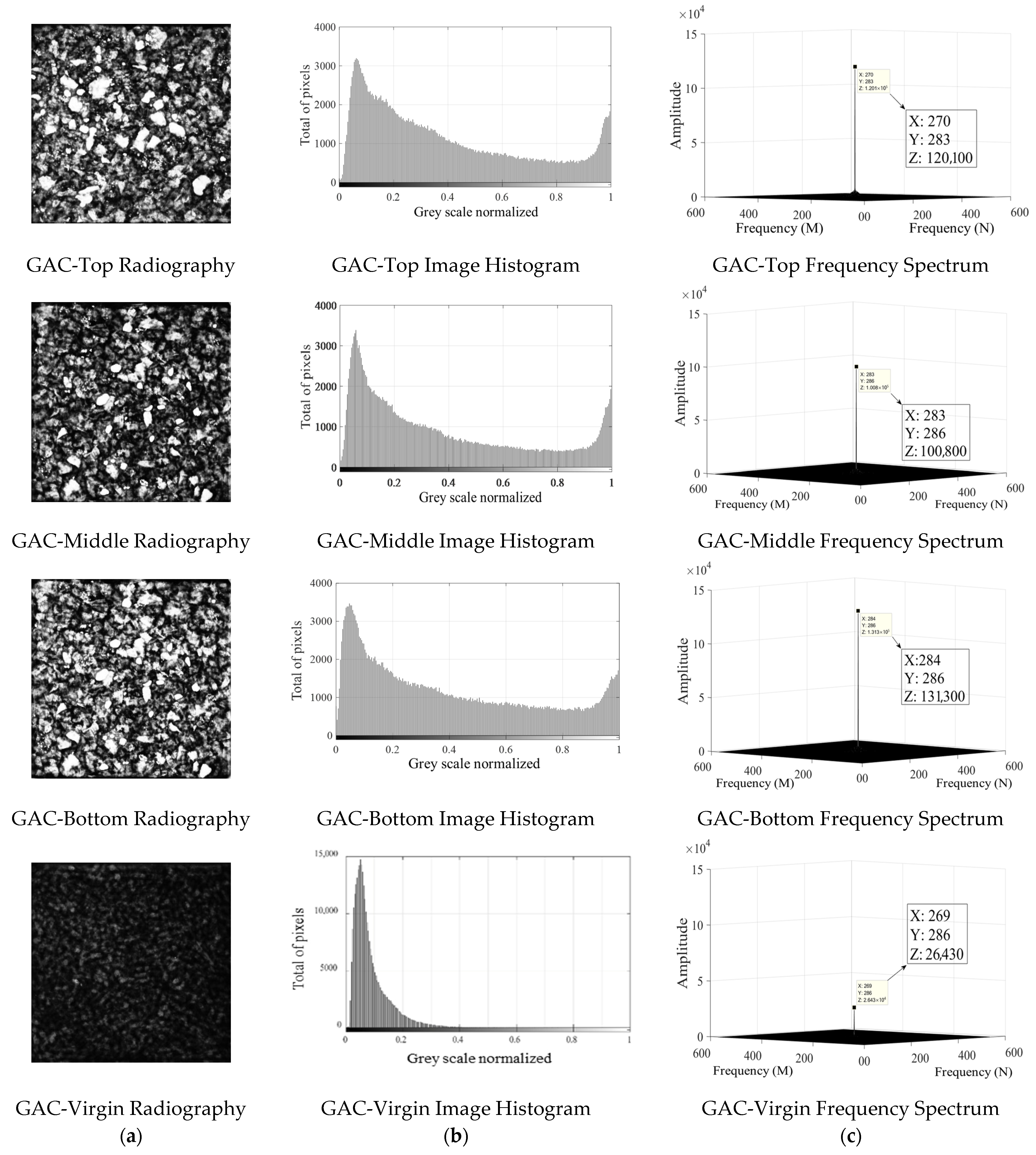
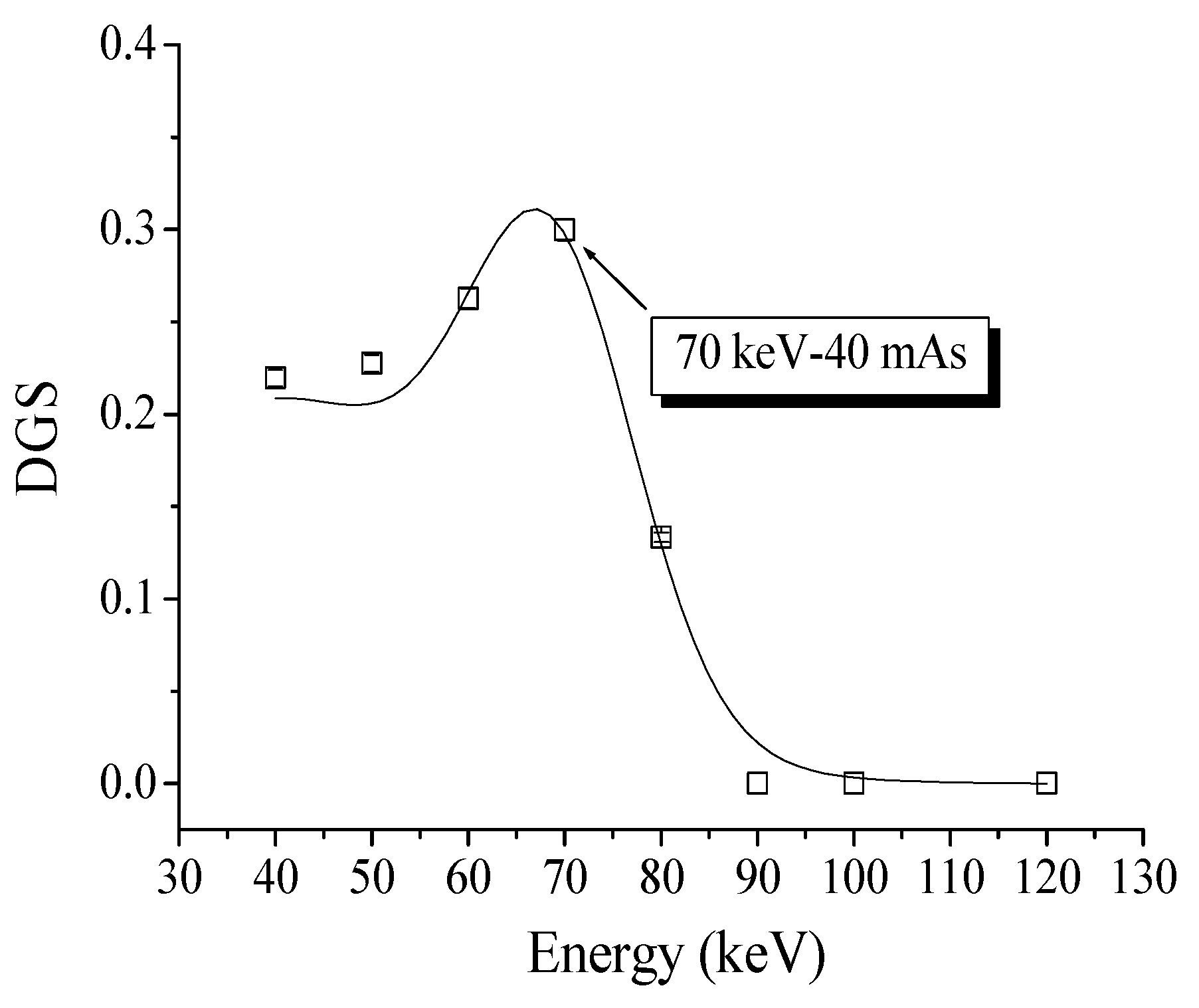
4.3. XRA Method 1
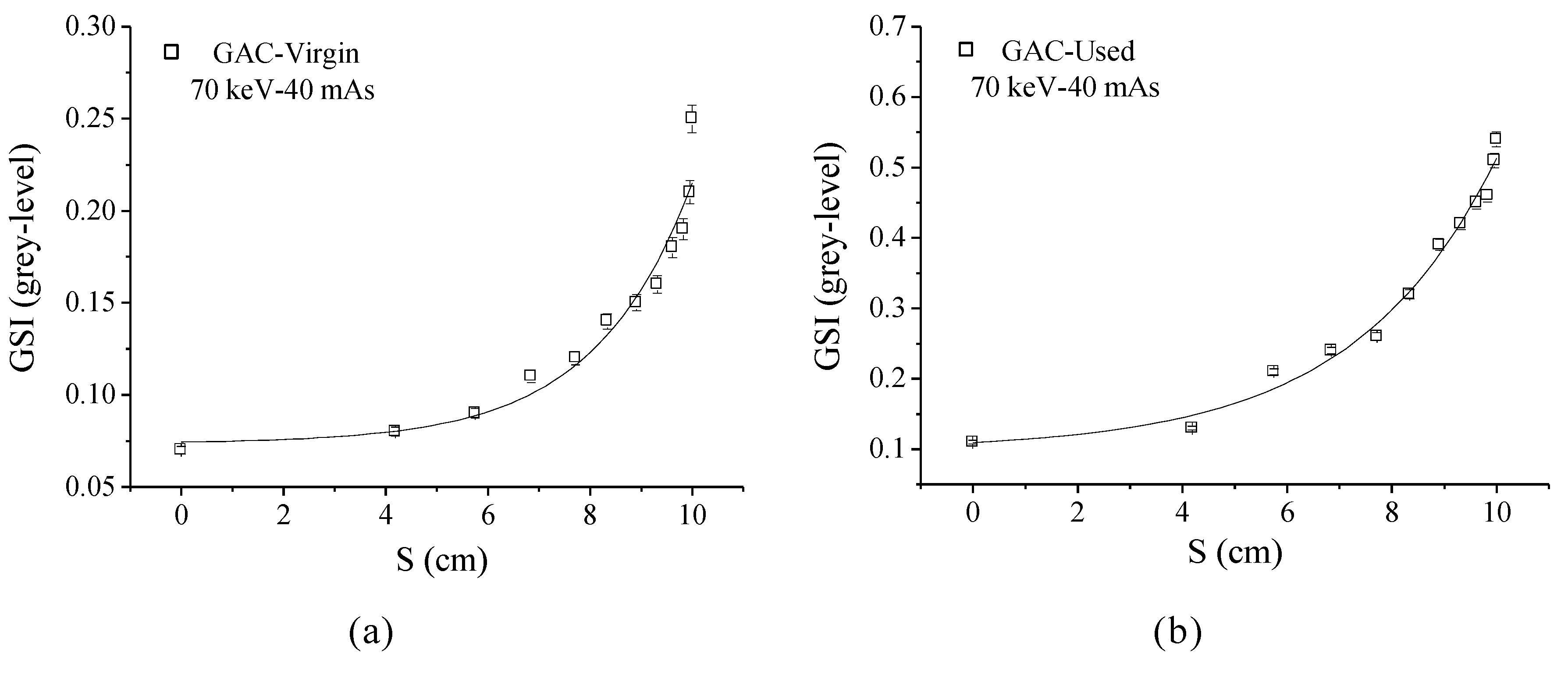
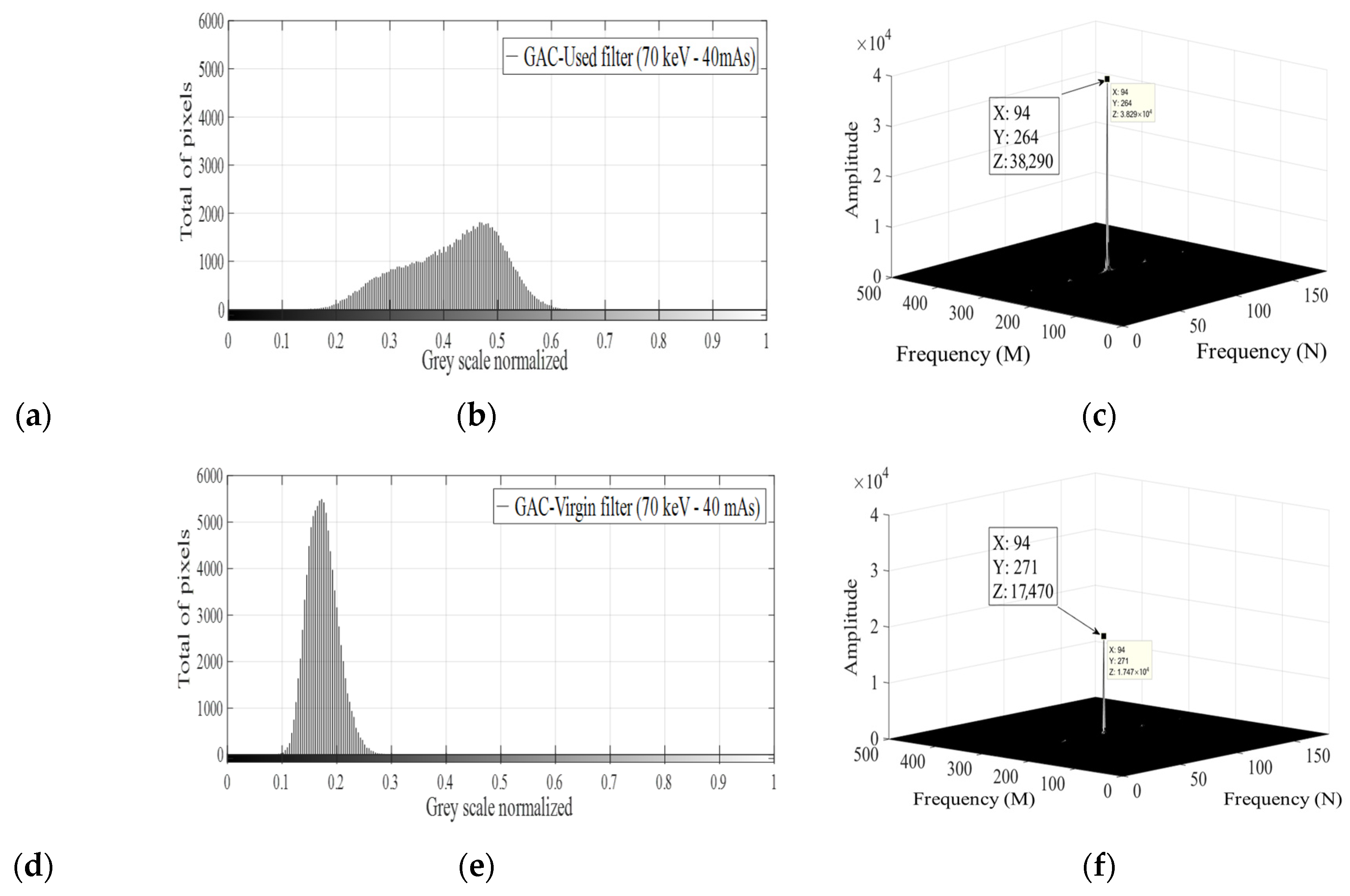
4.4. XRA Method 2
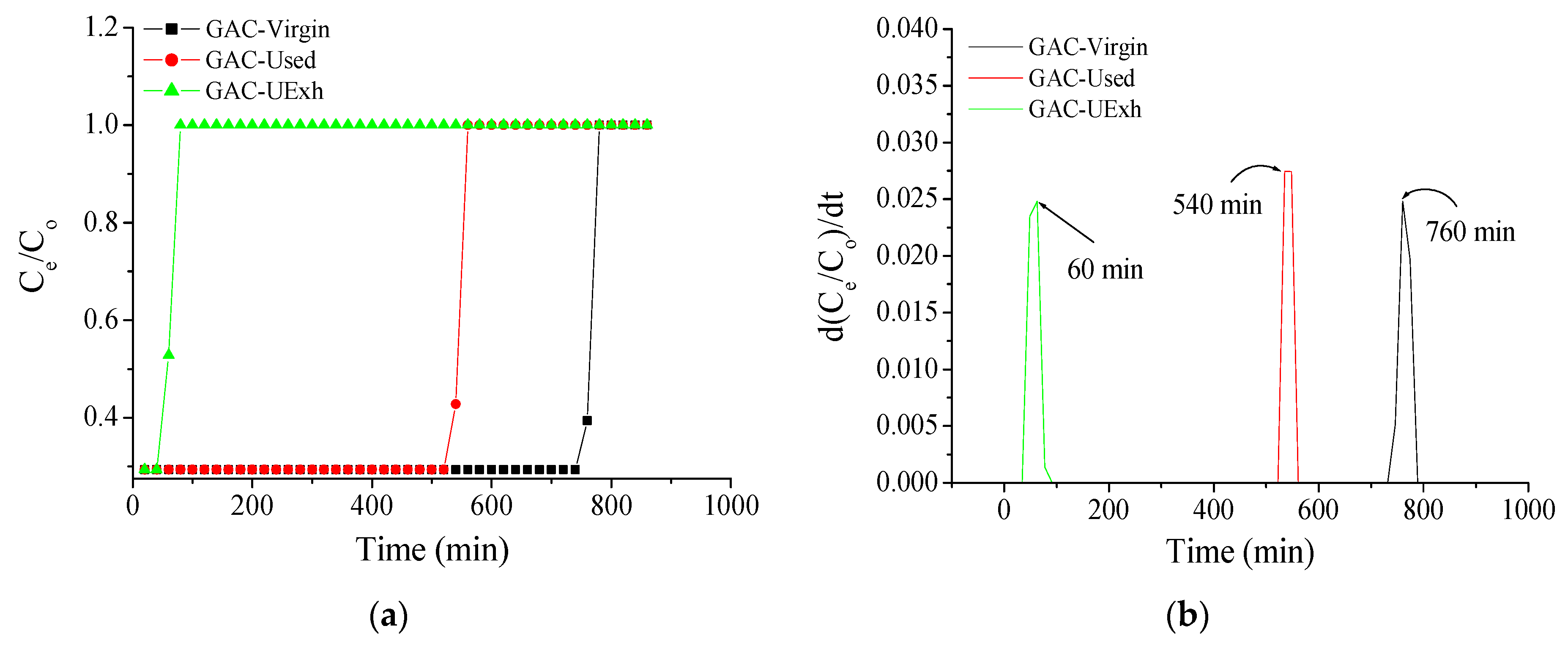
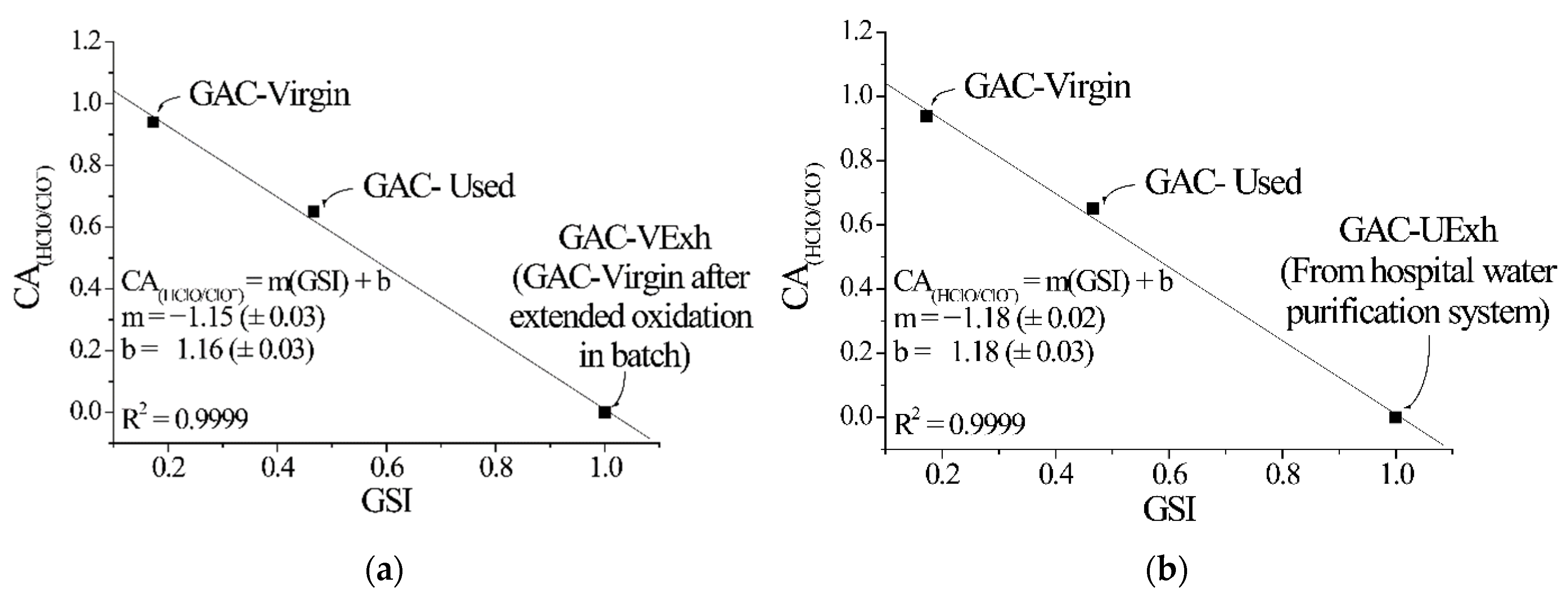
4.5. Relation Between XRA Method 2 and the GAC Free Chlorine Removal Capacity
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bansal, R.C.; Goyal, M. Activated Carbon Adsorption; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Hsieh, C.-T.; Teng, H. Influence of mesopore volume and adsorbate size on adsorption capacities of activated carbons in aqueous solutions. Carbon 2000, 38, 863–869. [Google Scholar] [CrossRef]
- Ying, W. Proceedings of the 44th Purdue Industrial Waste Conference, West Lafayette, IN, USA, 9–11 May 1989; Lewis Publishers: Chelsea, MI, USA, 1989. [Google Scholar]
- DeSilva, F.J. Activated Carbon Filtration; Water Quality Products: Arlington Heights, IL, USA, 2000; p. 16. [Google Scholar]
- Tran, H.N.; You, S.J.; Hosseini-Bandegharaei, A.; Chao, H.P. Mistakes and inconsistencies regarding adsorption of contaminants from aqueous solutions: A critical review. Water Res. 2017, 120, 88–116. [Google Scholar] [CrossRef]
- Lim, M.; Delehomme, C.; Capece, J. Removal of Residual Chlorine from Drinking-Water by Solar Radiation (UV) and Activated Carbon Filtration; Intelligentsia International, Inc.: LaBelle, FL, USA, 2008. [Google Scholar]
- Magee, V. The application of granular active carbon for dechlorination of water supplies. In Proceedings of the Society of Water Treatment Examination, Chorleywood, UK, 12–14 June 1956. [Google Scholar]
- Abdul-Ahad, M.Y. Design Criteria of an Activated Carbon Bed for Dechlorination of Water. Iraqi J. Chem. Pet. Eng. 2008, 9, 41–49. [Google Scholar] [CrossRef]
- Adachi, A.; Kimata, S.; Noguchi, M.; Okano, T. Decomposition of monochloramine from water with rice bran. J. Health Sci. 2002, 48, 126–129. [Google Scholar] [CrossRef][Green Version]
- Soice, N.P.; Pellegrino, J.; Kavanagh, J.; Riley, R.L. Oxidative degradation of polyamide reverse osmosis membranes: Studies of molecular model compounds and selected membranes. J. Appl. Polym. Sci. 2003, 90, 1173–1184. [Google Scholar] [CrossRef]
- Adachi, A.; Okano, T. Generation of cyanide ion by the reaction of hexamine and losartan potassium with sodium hypochlorite. J. Health Sci. 2008, 54, 581–583. [Google Scholar] [CrossRef][Green Version]
- Puente Torres, J.; Crespo Sariol, H.; Yperman, J.; Brito Sauvanell, Á.; Carleer, R.; Navarro Campa, J. A novel X-ray radiography approach for the characterization of granular activated carbons used in the rum production. J. Anal. Sci. Technol. 2018, 9, 1–15. [Google Scholar] [CrossRef]
- Puente Torres, J.; Crespo Sariol, H.; Yperman, J.; Adriaensens, P.; Carleer, R.; Peacok, T.M.; Brito Sauvanell, Á.; Thijssen, E.; Reggers, G.; Haeldermans, T.; et al. X-ray absorption as an alternative method to determine the exhausting degree of activated carbon layers in water treatment system for medical services. Talanta 2019, 205, 120058. [Google Scholar] [CrossRef] [PubMed]
- Puente Torres, J.; Crespo Sariol, H.; Mariño Peacok, T.; Brito Sauvanell, Á.; Cuyvers, G.; Reggers, G.; Samyn, P.; Vandamme, D.; Yperman, J.; Adriaensens, P.; et al. Chemical Regeneration of Activated Carbon Used in A Water Treatment System for Medical Services. Adv. Environ. Eng. Res. 2023, 4, 1–28. [Google Scholar] [CrossRef]
- Puente Torres, J.; Crespo Sariol, H.; Mariño Peacok, T.; Yperman, J.; Adriaensens, P.; Carleer, R.; Brito Sauvanell, Á. X-Ray absorption (XRA): A new Technique for the characterization of Granular Activated Carbons. Materials 2021, 14, 91. [Google Scholar] [CrossRef] [PubMed]
- D 2867-04; ASTM, Standard Test Methods for Moisture in Activated Carbon. ASTM International: West Conshohocken, PA, USA, 2011.
- Johns, H.E.; Cunningham, J.R. The Physics of Radiology; Charles C. Thomas: Springfield, IL, USA, 1983. [Google Scholar]
- Hossain, S.; Cook, D.; Chow, C.W.K.; Hewa, G.A. Development of an optical method to monitor nitrification in drinking water. Sensors 2021, 21, 7525. [Google Scholar] [CrossRef] [PubMed]
- Danial, L.H. Current Technology of Chlorine Analysis for Water and Wastewater; Technical Information Series-Booklet No. 17; Hach Company: Loveland, CO, USA, 1995. [Google Scholar]
- Mariño Peacok, T.; Crespo Sariol, H.; Sánchez Roca, Á.; Puente Torres, J.; Gryglewicz, G.; Yperman, J. Efficiency evaluation of thermally and chemically regenerated activated carbons used in a water cleaning system by acoustic emission analysis. J. Porous Mater. 2021, 28, 451–469. [Google Scholar] [CrossRef]
- Turlapati, V.Y.; Kumar, S.; Singh, R.K.; Sharma, M. Analysis of micropore size distribution using Dubinin’s theory of volume filling-Effect of particle size on pore characterization of organic-rich Indian shales. J. Nat. Gas Sci. Eng. 2022, 106, 104746. [Google Scholar] [CrossRef]
- Harp, D.L.; Hach, C.C. Current Technology of Chlorine Analysis for Water and Wastewater; Technical Information Series-Booklet No. 22; Hach Company: Loveland, CO, USA, 2003. [Google Scholar]

| (a) | ||||||||
| N | SD | C | SD | H | SD | O | SD | |
| GAC-Virgin | 0.44 | 0.01 | 93.54 | 0.62 | 0.81 | 0.07 | 2.22 | 0.57 |
| GAC-Bottom | 0.57 | 0.02 | 76.41 | 0.46 | 2.14 | 0.07 | 17.89 | 0.41 |
| GAC-Middle | 0.54 | 0.01 | 75.92 | 0.74 | 2.23 | 0.11 | 18.31 | 0.76 |
| GAC-Top | 0.56 | 0.02 | 76.63 | 0.01 | 1.04 | 0.02 | 18.78 | 0.25 |
| (b) | ||||||||
| N | SD | C | SD | H | SD | O | SD | |
| GAC-VExh | 0.46 | 0.03 | 86.44 | 0.03 | 0.91 | 0.01 | 9.21 | 0.04 |
| 50 keV | 60 keV | 70 keV | 80 keV | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 5.00 | 0.00 | 0.11 | 0.07 | 0.12 | 0.13 | 0.11 | 0.07 | 0.10 | 0.07 |
| 4.54 | 4.19 | 0.15 | 0.09 | 0.25 | 0.15 | 0.13 | 0.08 | 0.11 | 0.07 |
| 4.09 | 5.75 | 0.19 | 0.10 | 0.28 | 0.17 | 0.21 | 0.09 | 0.13 | 0.07 |
| 3.64 | 6.85 | 0.25 | 0.10 | 0.34 | 0.17 | 0.24 | 0.11 | 0.15 | 0.08 |
| 3.18 | 7.72 | 0.34 | 0.11 | 0.35 | 0.19 | 0.26 | 0.12 | 0.16 | 0.08 |
| 2.73 | 8.34 | 0.35 | 0.13 | 0.35 | 0.21 | 0.32 | 0.14 | 0.19 | 0.08 |
| 2.27 | 8.91 | 0.40 | 0.13 | 0.37 | 0.21 | 0.39 | 0.15 | 0.20 | 0.08 |
| 1.82 | 9.32 | 0.41 | 0.15 | 0.39 | 0.21 | 0.42 | 0.16 | 0.21 | 0.08 |
| 1.36 | 9.62 | 0.42 | 0.12 | 0.41 | 0.22 | 0.45 | 0.18 | 0.22 | 0.08 |
| 0.91 | 9.83 | 0.43 | 0.15 | 0.42 | 0.25 | 0.46 | 0.19 | 0.23 | 0.08 |
| 0.45 | 9.96 | 0.52 | 0.12 | 0.44 | 0.27 | 0.51 | 0.21 | 0.25 | 0.10 |
| 0.00 | 10.0 | 0.53 | 0.18 | 0.57 | 0.33 | 0.54 | 0.25 | 0.32 | 0.12 |
| 50 keV-40 mAs | |||||
| Evaluated Parameter | GSI0 | e(GSI0) | m | e(m) | R2 |
| 0.160 | 0.008 | −0.010 | 0.002 | 0.86 | |
| 0.550 | 0.006 | −0.080 | 0.002 | 0.98 | |
| 60 keV-40 mAs | |||||
| Evaluated Parameter | GSI0 | e(GSI0) | m | e(m) | R2 |
| 0.290 | 0.009 | −0.030 | 0.003 | 0.95 | |
| 0.510 | 0.020 | −0.060 | 0.008 | 0.93 | |
| 70 keV-40 mAs | |||||
| Evaluated Parameter | GSI0 | e(GSI0) | m | e(m) | R2 |
| 0.230 | 0.004 | −0.030 | 0.001 | 0.99 | |
| 0.560 | 0.001 | −0.080 | 0.003 | 0.99 | |
| 80 keV-40 mAs | |||||
| Evaluated Parameter | GSI0 | e(GSI0) | m | e(m) | R2 |
| 0.090 | 0.004 | −0.007 | 0.001 | 0.79 | |
| 0.280 | 0.008 | −0.040 | 0.003 | 0.97 | |
| Evaluated Parameter | GSI0 | e(GSI0) | m | e(m) | t | e(t) | R2 |
|---|---|---|---|---|---|---|---|
| 7 · | 1 | 7 · | 1 | 2.0 | 0.99 | ||
| 1 · | 1 | 1 · | 5 | 3.0 | 3 | 0.99 |
| GAC-Sample | ||
|---|---|---|
| GAC-Virgin | 522.0 | 1.00 |
| GAC-Used | 338.0 | 0.65 |
| GAC-UExh | 30.52 | 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puente Torres, J.; Crespo Sariol, H.; Mariño Peacok, T.; Haeldermans, T.; Reggers, G.; Yperman, J.; Adriaensens, P.; Carleer, R.; Vandamme, D. Innovative X-Ray Absorption Technology for Improved Monitoring of the Degradation and Oxidation of Granular Activated Carbon Filters Used in Hospital Water Treatment Systems. C 2025, 11, 30. https://doi.org/10.3390/c11020030
Puente Torres J, Crespo Sariol H, Mariño Peacok T, Haeldermans T, Reggers G, Yperman J, Adriaensens P, Carleer R, Vandamme D. Innovative X-Ray Absorption Technology for Improved Monitoring of the Degradation and Oxidation of Granular Activated Carbon Filters Used in Hospital Water Treatment Systems. C. 2025; 11(2):30. https://doi.org/10.3390/c11020030
Chicago/Turabian StylePuente Torres, Jeamichel, Harold Crespo Sariol, Thayset Mariño Peacok, Tom Haeldermans, Guy Reggers, Jan Yperman, Peter Adriaensens, Robert Carleer, and Dries Vandamme. 2025. "Innovative X-Ray Absorption Technology for Improved Monitoring of the Degradation and Oxidation of Granular Activated Carbon Filters Used in Hospital Water Treatment Systems" C 11, no. 2: 30. https://doi.org/10.3390/c11020030
APA StylePuente Torres, J., Crespo Sariol, H., Mariño Peacok, T., Haeldermans, T., Reggers, G., Yperman, J., Adriaensens, P., Carleer, R., & Vandamme, D. (2025). Innovative X-Ray Absorption Technology for Improved Monitoring of the Degradation and Oxidation of Granular Activated Carbon Filters Used in Hospital Water Treatment Systems. C, 11(2), 30. https://doi.org/10.3390/c11020030








