Nonlocal-Strain-Gradient-Based Anisotropic Elastic Shell Model for Vibrational Analysis of Single-Walled Carbon Nanotubes
Abstract
1. Introduction
2. Sanders–Koiter Shell Theory for SWCNTs
3. Nonlocal-Strain-Gradient-Based Anisotropic Elastic Shell Model
4. Force and Moment Resultants
5. Equations of Motion
6. Solution Method
7. Numerical Results
7.1. Validation of the Anisotropic Elastic Shell Model
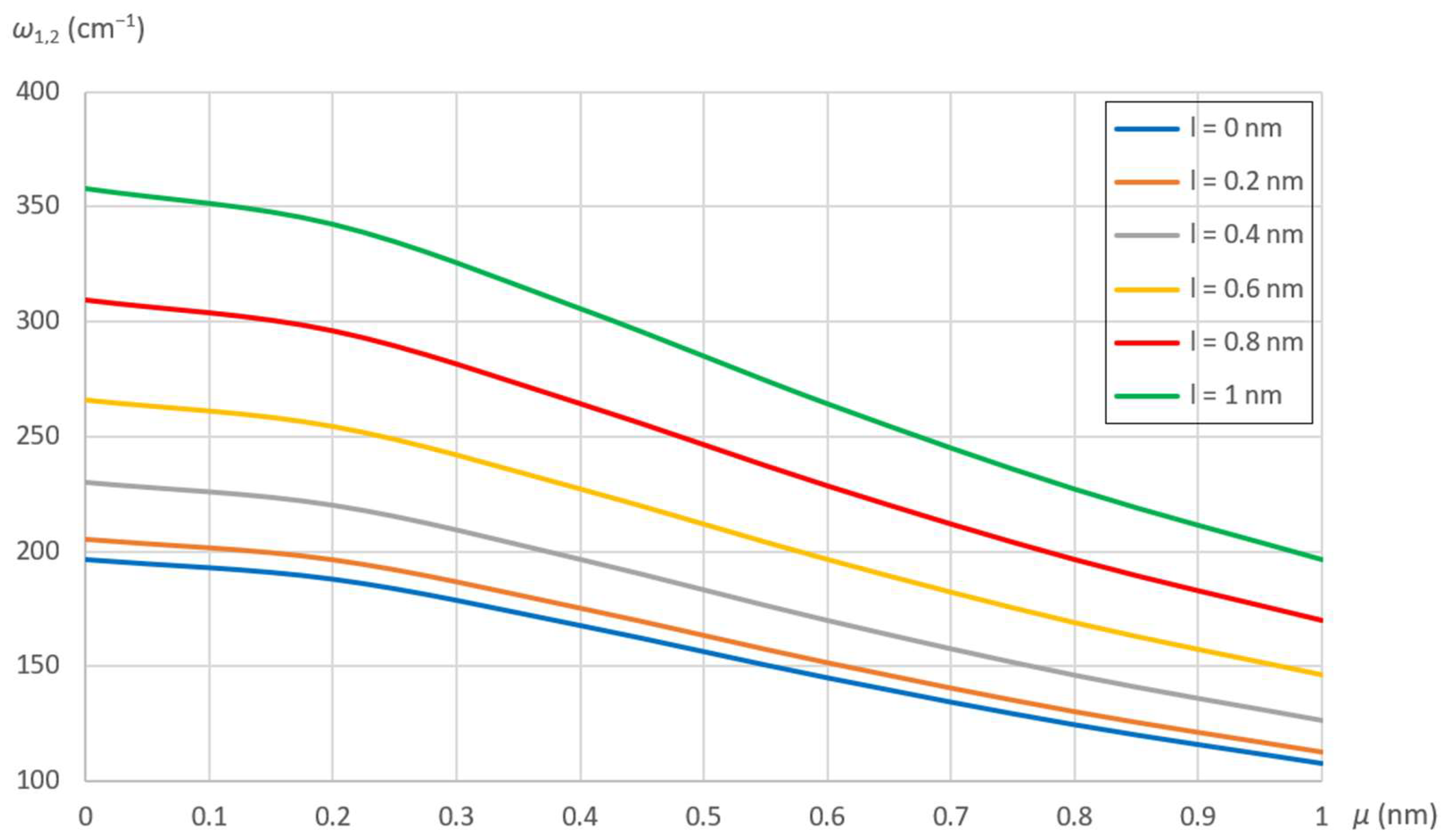
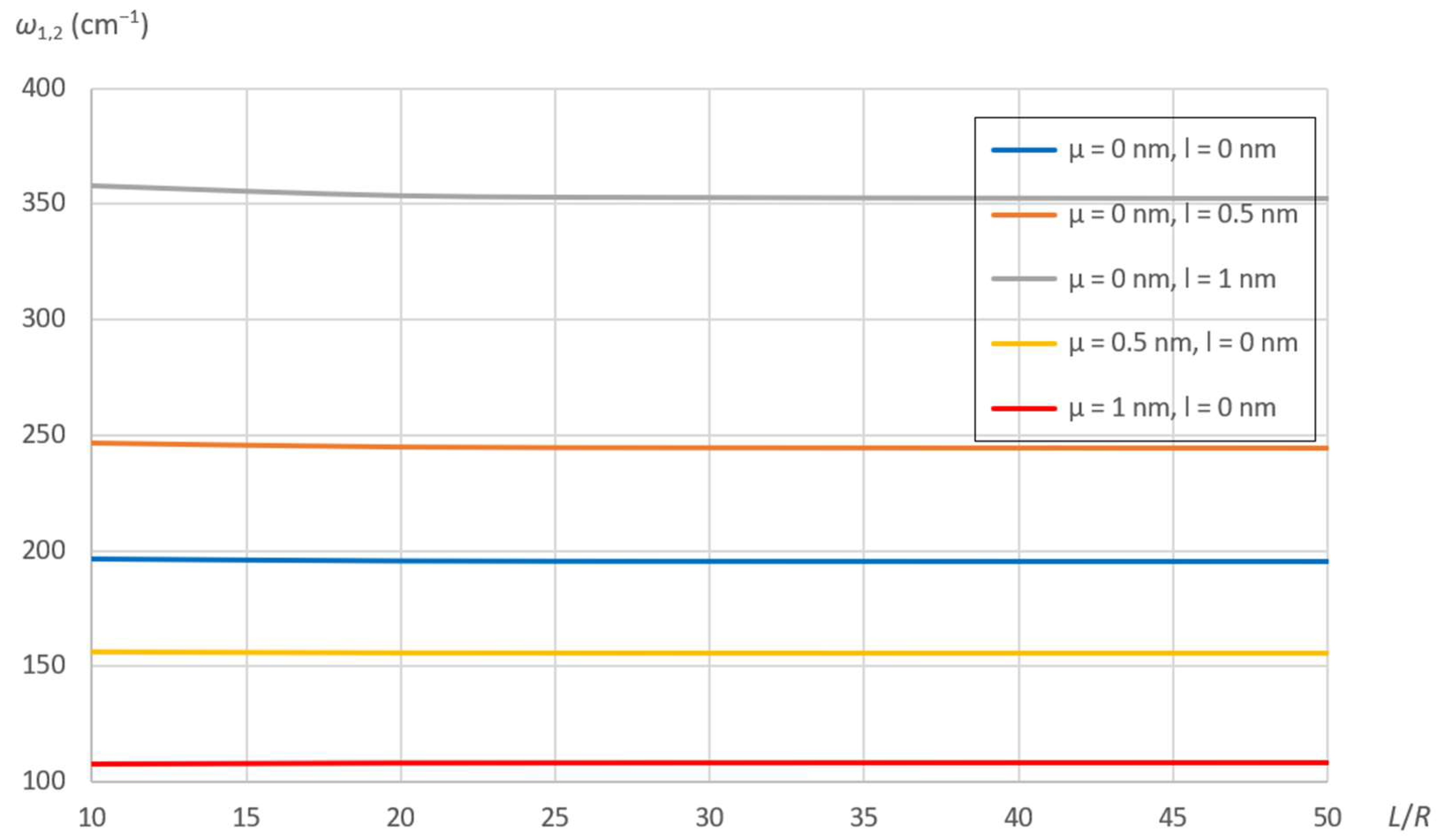
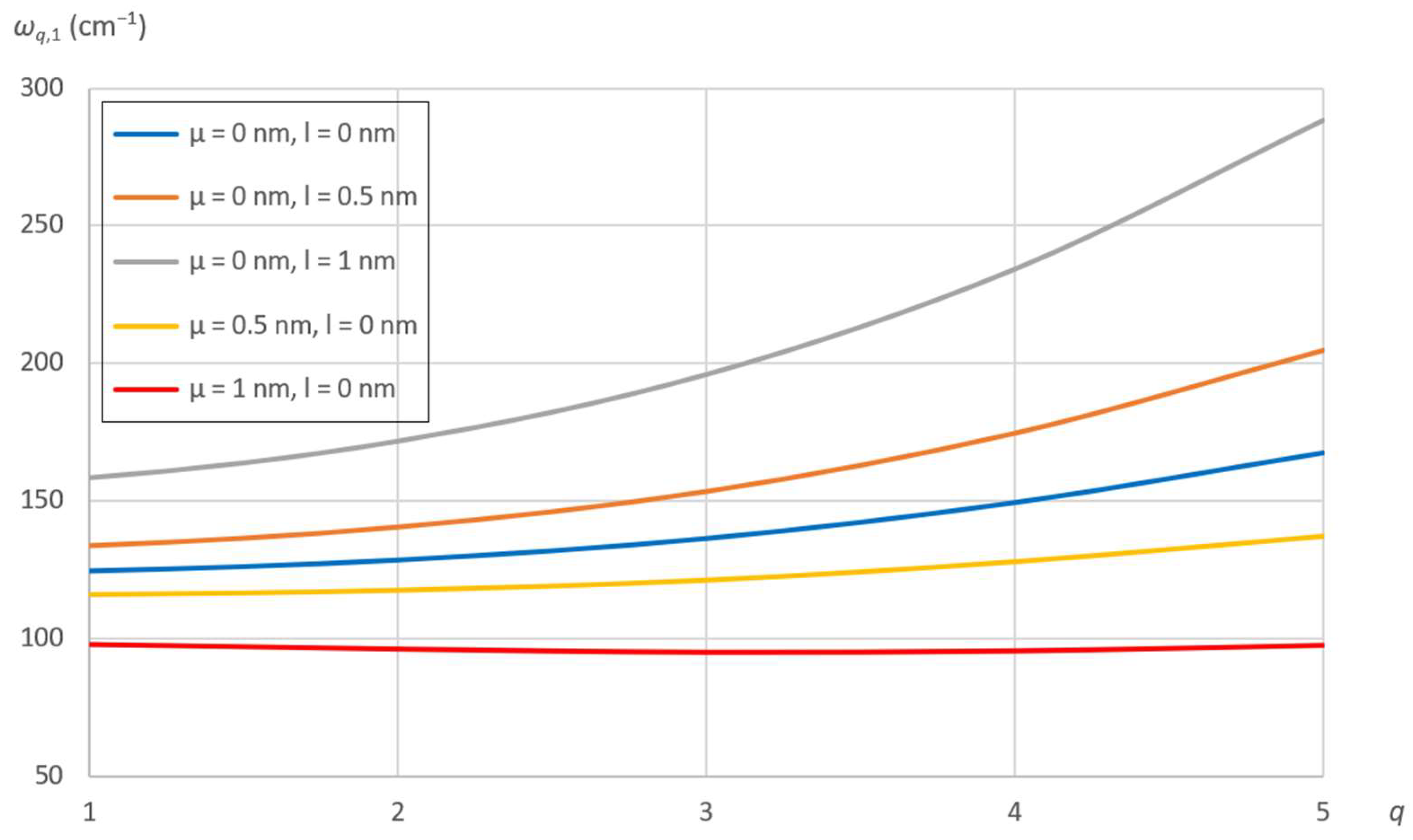
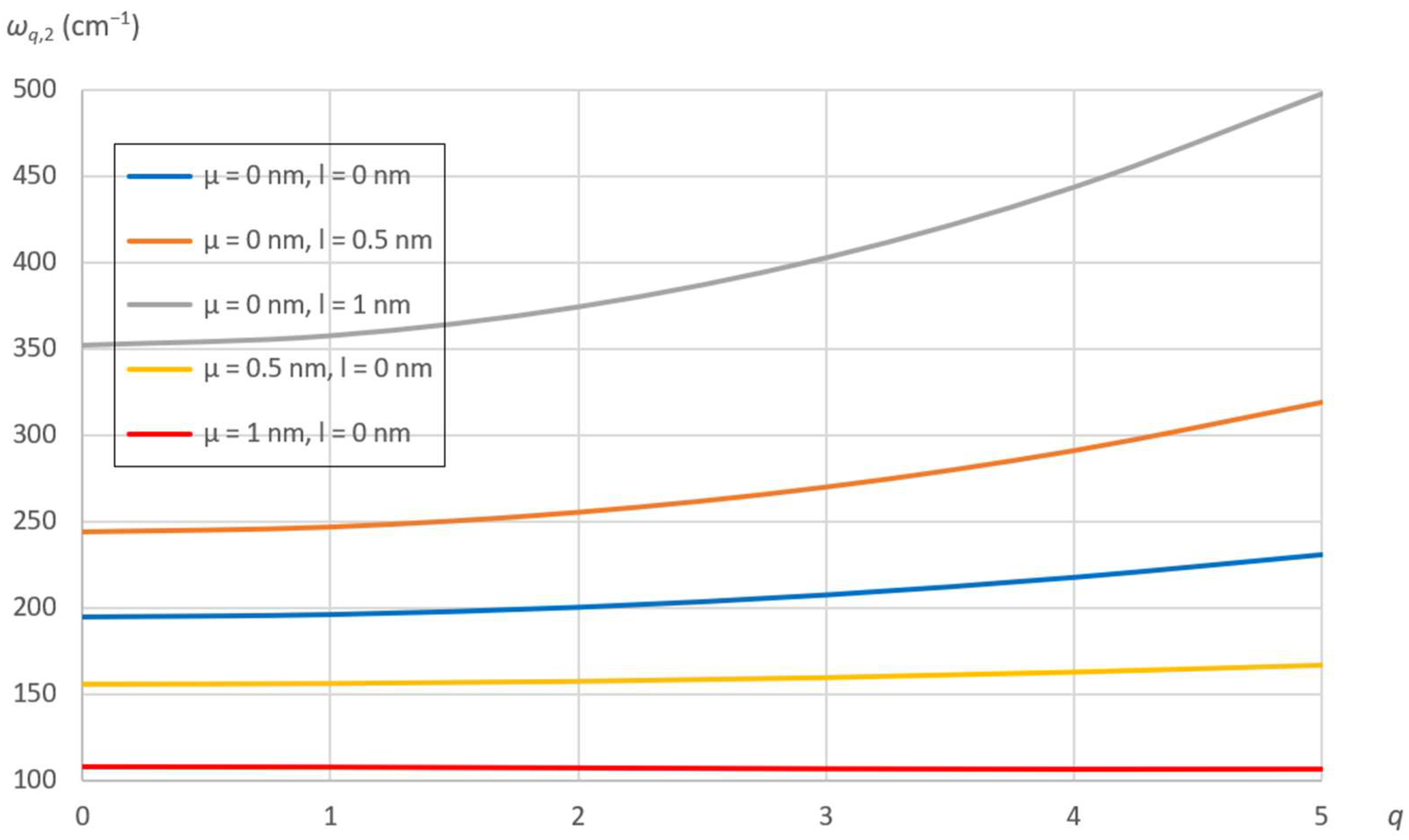
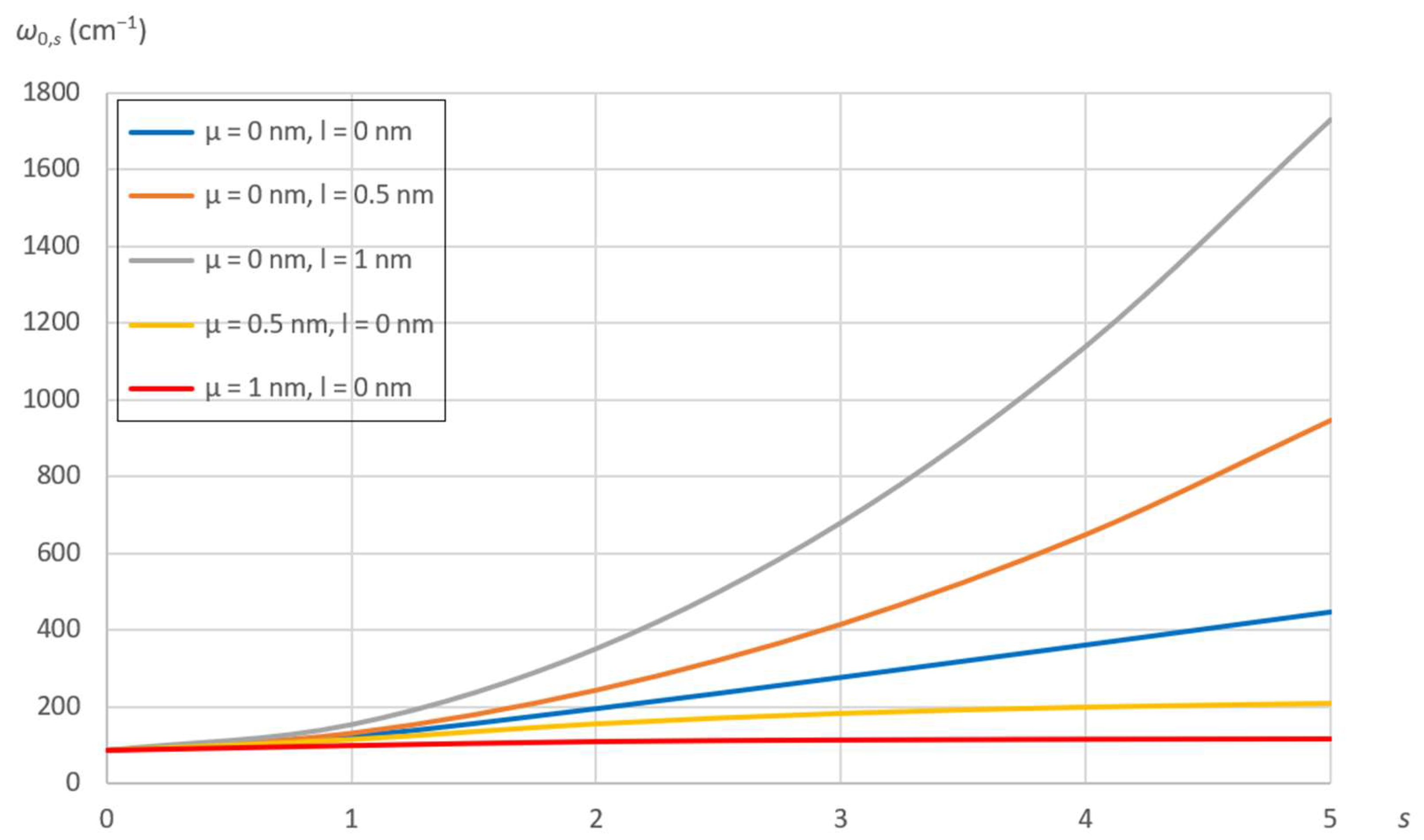
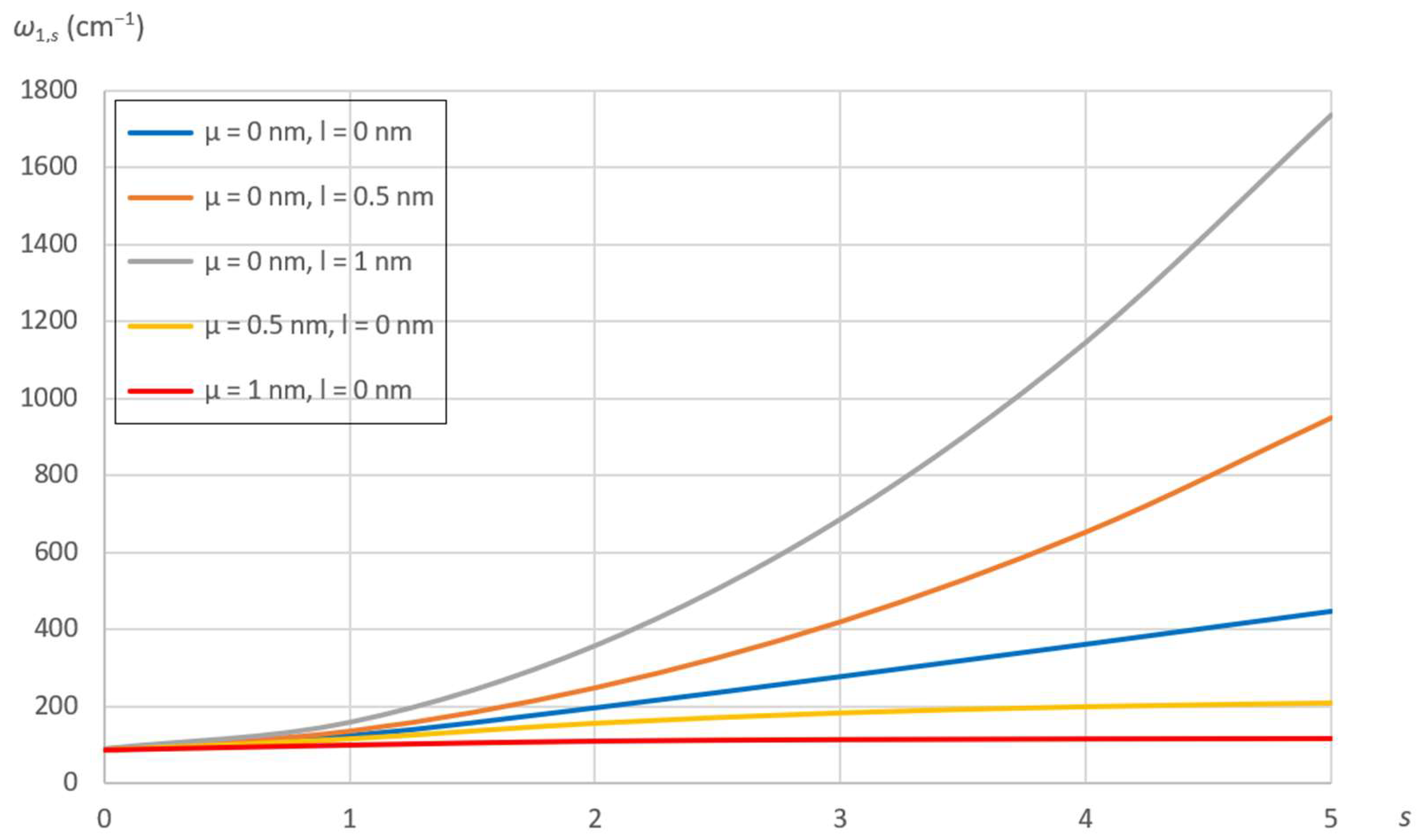
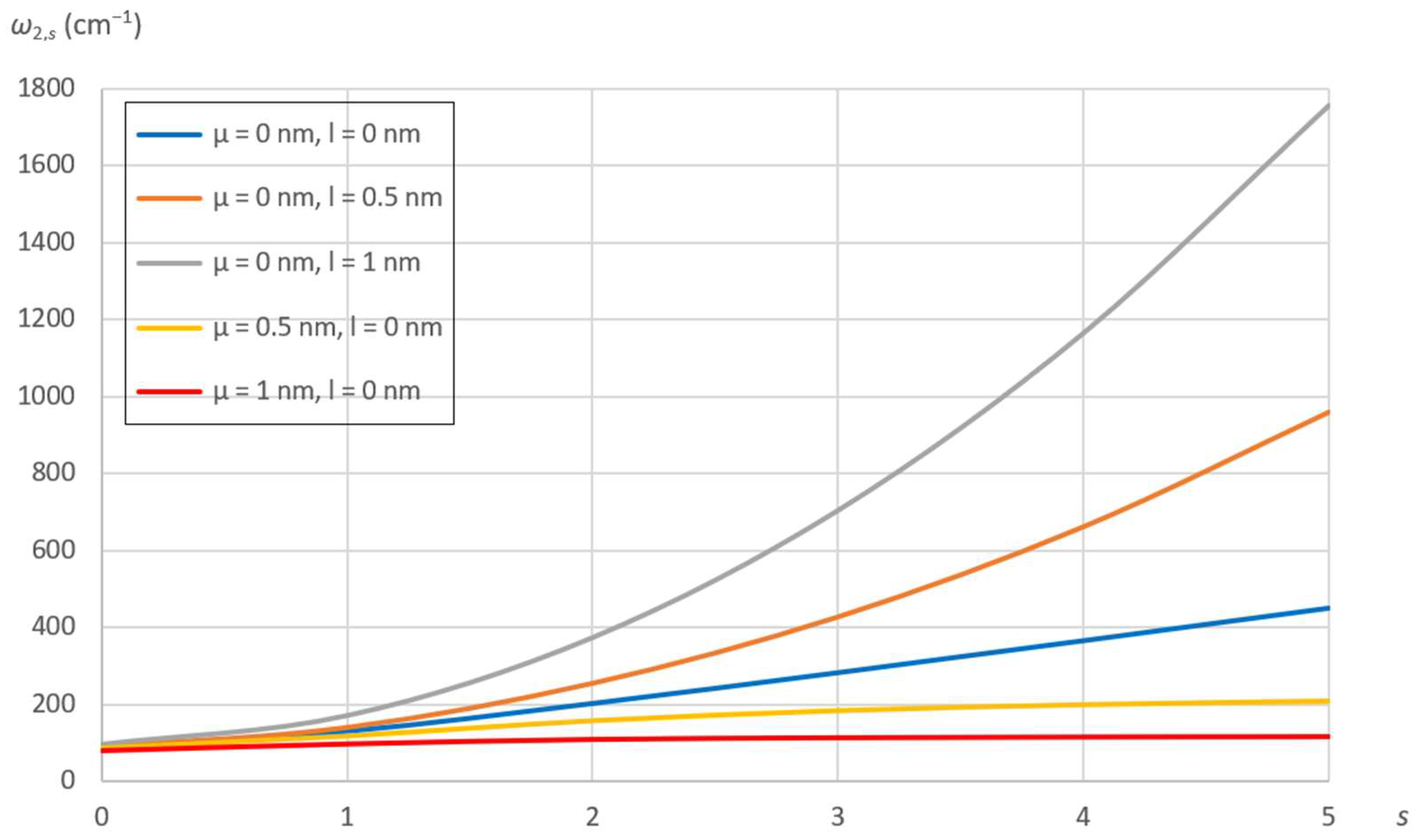
7.2. Effects of Nonlocal and Material Parameters
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Chang, T.; Geng, J.; Guo, X. Prediction of chirality-and size-dependent elastic properties of single-walled carbon nanotubes via a molecular mechanics model. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 462, 2523–2540. [Google Scholar] [CrossRef]
- Chang, T. A molecular based anisotropic shell model for single-walled carbon nanotubes. J. Mech. Phys. Solids 2010, 58, 1422–1433. [Google Scholar] [CrossRef]
- Ghavanloo, E.; Fazelzadeh, S.A. Vibration characteristics of single-walled carbon nanotubes based on an anisotropic elastic shell model including chirality effect. Appl. Math. Model. 2012, 36, 4988–5000. [Google Scholar] [CrossRef]
- Strozzi, M.; Elishakoff, I.; Bochicchio, M.; Cocconcelli, M.; Rubini, R.; Radi, E. A Comparison of Shell Theories for Vibration Analysis of Single-Walled Carbon Nanotubes Based on an Anisotropic Elastic Shell Model. Nanomaterials 2023, 13, 1390. [Google Scholar] [CrossRef] [PubMed]
- Eringen, A.C. Linear theory of nonlocal elasticity and dispersion of plane waves. Int. J. Eng. Sci. 1972, 10, 425–435. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Fazelzadeh, S.A.; Ghavanloo, E. Nonlocal anisotropic elastic shell model for vibrations of single-walled carbon nanotubes with arbitrary chirality. Compos. Struct. 2012, 94, 1016–1022. [Google Scholar] [CrossRef]
- Mindlin, R.D. Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 1964, 16, 51–78. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Eshel, N.N. On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Gutkin, M.Y.; Aifantis, E.C. Dislocations in the theory of gradient elasticity. Scr. Mater. 1999, 40, 559–566. [Google Scholar] [CrossRef]
- Askes, H.; Aifantis, E.C. Gradient elasticity and flexural wave dispersion in carbon nanotubes. Phys. Rev. B 2009, 80, 195412. [Google Scholar] [CrossRef]
- Aifantis, E.C. Update on a class of gradient theories. Mech. Mater. 2003, 35, 259–280. [Google Scholar] [CrossRef]
- Lim, C.W.; Zhang, G.; Reddy, J.N. A higher-order nonlocal elasticity and strain gradient theory and its applications in the wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Li, L.; Li, X.; Hu, Y. Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 102, 77–92. [Google Scholar] [CrossRef]
- Li, X.; Li, L.; Hu, Y.; Ding, Z.; Deng, W. Bending, buckling and vibration of axially functionally graded beams based on nonlocal strain gradient theory. Compos. Struct. 2017, 165, 250–265. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 107, 77–97. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; Marotti de Sciarra, F. Free vibrations of elastic beams by modified nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 133, 99–108. [Google Scholar] [CrossRef]
- Thai, H.T.; Vo, T.P.; Nguyen, T.K.; Kim, S.E. A review of continuum mechanics models for size-dependent analysis of beams and plates. Compos. Struct. 2017, 177, 196–219. [Google Scholar] [CrossRef]
- Roudbari, M.A.; Jorshari, T.D.; Lü, C.; Ansari, R.; Kouzani, A.Z.; Amabili, M. A review of size-dependent continuum mechanics models for micro- and nano-structures. Thin-Walled Struct. 2022, 170, 108562. [Google Scholar] [CrossRef]
- Hosseini, M.; Hadi, A.; Malekshahi, A.; Shishesaz, M. A review of size-dependent elasticity for nanostructures. J. Comput. Appl. Mech. 2018, 49, 197–211. [Google Scholar]
- Mehralian, F.; Beni, Y.T.; Zeverdejani, M.K. Nonlocal strain gradient theory calibration using molecular dynamics simulation based on small scale vibration of nanotubes. Phys. B Condens. Matter 2017, 514, 61–69. [Google Scholar] [CrossRef]
- Ru, C.Q. Chirality-Dependent Mechanical Behavior of Carbon Nanotubes Based on an Anisotropic Elastic Shell Model. Math. Mech. Solids 2009, 14, 88–101. [Google Scholar] [CrossRef]
- Chang, T.; Geng, J.; Guo, X. Chirality- and size-dependent elastic properties of single-walled carbon nanotubes. Appl. Phys. Lett. 2005, 87, 251929. [Google Scholar] [CrossRef]
- Yakobson, B.I.; Brabec, C.J.; Bernholc, J. Nanomechanics of Carbon Tubes: Instabilities beyond Linear Response. Phys. Rev. Lett. 1996, 76, 2511–2514. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.S.; Bosco, F.G.; Batra, R.C. Wall thickness and elastic moduli of single-walled carbon nanotubes from frequencies of axial, torsional and inextensional modes of vibration. Comput. Mater. Sci. 2010, 47, 1049–1059. [Google Scholar] [CrossRef]
- Cheng, H.C.; Liu, Y.L.; Wu, C.; Chen, W.H. On radial breathing vibration of carbon nanotubes. Comput. Methods Appl. Mech. Eng. 2010, 199, 2820–2827. [Google Scholar] [CrossRef]
- Gupta, S.; Bosco, F.G.; Batra, R.C. Breakdown of structural models for vibrations of single-wall zigzag carbon nanotubes. J. Appl. Phys. 2009, 106, 063527. [Google Scholar] [CrossRef]
- Duan, W.H.; Wang, C.M.; Zhang, Y.Y. Calibration of nonlocal scaling effect parameter for free vibration of carbon nanotubes by molecular dynamics simulations. J. Appl. Phys. 2007, 101, 024305. [Google Scholar] [CrossRef]
- Ansari, R.; Ajori, S.; Arash, B. Vibrations of single and double-walled carbon nanotubes with layerwise boundary conditions: A molecular dynamics study. Curr. Appl. Phys. 2012, 12, 707–711. [Google Scholar] [CrossRef]
- Leissa, A.W. Vibrations of Shells; Government Printing Office: Washington, DC, USA, 1973.
- Yamaki, N. Elastic Stability of Circular Cylindrical Shells; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Ventsel, E. Thin Plates and Shells. Theory, Analysis and Applications; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Soedel, W. Vibrations of Shells and Plates, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Calladine, C. Theory of Shell Structures; Cambridge University Press: New York, NY, USA, 1983. [Google Scholar]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar]
- Strozzi, M.; Smirnov, V.V.; Pellicano, F.; Kovaleva, M. Nonlocal anisotropic elastic shell model for vibrations of double-walled carbon nanotubes under nonlinear van der Waals interaction forces. Int. J. Non-Linear Mech. 2022, 146, 104172. [Google Scholar] [CrossRef]
- Avramov, K.V. Nonlinear vibrations characteristics of single-walled carbon nanotubes by nonlocal elastic shell model. Int. J. Non-Linear Mech. 2018, 107, 149–160. [Google Scholar] [CrossRef]
- Yang, J.; Ke, L.L.; Kitipornchai, S. Nonlinear free vibration of single-walled carbon nanotubes using nonlocal Timoshenko beam theory. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 42, 1727–1735. [Google Scholar] [CrossRef]
- Strozzi, M.; Smirnov, V.V.; Manevitch, L.I.; Pellicano, F. Nonlinear normal modes, resonances and energy exchange in single-walled carbon nanotubes. Int. J. Non-Linear Mech. 2020, 120, 103398. [Google Scholar] [CrossRef]
- Fang, B.; Zhen, Y.X.; Zhang, C.P.; Tang, Y. Nonlinear vibration analysis of double-walled carbon nanotubes based on nonlocal elasticity theory. Appl. Math. Model. 2013, 37, 1096–1107. [Google Scholar] [CrossRef]
- Soltani, P.; Farshidianfar, A. Periodic solution for nonlinear vibration of a fluid-conveying carbon nanotube based on the nonlocal continuum theory by energy balance method. Appl. Math. Model. 2012, 36, 3712–3724. [Google Scholar] [CrossRef]
- Strozzi, M.; Pellicano, F. Nonlinear Resonance Interaction between Conjugate Circumferential Flexural Modes in Single-Walled Carbon Nanotubes. Shock. Vib. 2019, 2019, 3241698. [Google Scholar] [CrossRef]
- Avramov, K.V.; Kabylbekova, B.; Seitkazenova, K.; Myrzaliyev, D.S.; Pecherskiy, V.N. Nonlocal anisotropic shell model of linear vibrations of multi-walled carbon nanotubes. J. Mech. Eng. 2020, 23, 14–26. [Google Scholar] [CrossRef]
- Strozzi, M.; Smirnov, V.V.; Manevitch, L.I.; Pellicano, F. Nonlinear vibrations and energy exchange of single-walled carbon nanotubes. Radial breathing modes. Compos. Struct. 2018, 184, 613–632. [Google Scholar] [CrossRef]
- Mikhasev, G.; Radi, E.; Misnik, V. Modeling pull-in instability of CNT nanotweezers under electrostatic and van der Waals attractions based on the nonlocal theory of elasticity. Int. J. Eng. Sci. 2024, 195, 104012. [Google Scholar] [CrossRef]
- Mikhasev, G.; Radi, E.; Misnik, V. Pull-in instability analysis of a nanocantilever based on the two-phase nonlocal theory of elasticity. J. Appl. Comput. Mech. 2022, 8, 1456–1466. [Google Scholar]




| Carbon–carbon bond length, a (nm) | 0.142 |
| Carbon–carbon bond elongation, Kρ (nN/nm) | 742 |
| Carbon–carbon bond angle variance, Kθ (nN·nm) | 1.42 |
| Equivalent thickness, h (nm) | 0.0665 |
| Equivalent mass density, ρ (kg/m3) | 11,700 |
| SWCNT radius, R (nm) | 1.34 |
| Natural Frequency, ωRBM (cm−1) | Difference (%) | ||
|---|---|---|---|
| Chirality Indices (n, m) | Anisotropic Elasticity Model (Sanders’s Shell Theory) | Molecular Dynamics Simulation [25] | |
| (10, 0) | 294.310 | 290.810 | 1.20 |
| (6, 6) | 284.460 | 278.450 | 2.16 |
| (12, 0) | 245.868 | 242.576 | 1.36 |
| (7, 7) | 244.074 | 239.020 | 2.11 |
| (8, 8) | 213.709 | 209.323 | 2.10 |
| (14, 0) | 211.067 | 207.980 | 1.48 |
| (16, 0) | 184.870 | 181.960 | 1.60 |
| (10, 10) | 171.104 | 167.644 | 2.06 |
| (18, 0) | 164.443 | 161.773 | 1.65 |
| (20, 0) | 148.073 | 145.577 | 1.71 |
| (12, 12) | 142.650 | 139.778 | 2.05 |
| (25, 0) | 118.551 | 116.439 | 1.81 |
| (15, 15) | 114.161 | 111.878 | 2.04 |
| (30, 0) | 98.835 | 97.013 | 1.88 |
| (18, 18) | 95.153 | 93.253 | 2.04 |
| (33, 0) | 89.865 | 87.507 | 2.69 |
| (20, 20) | 85.645 | 83.935 | 2.04 |
| Natural Frequency, ωRBM (cm−1) | Difference (%) | ||
|---|---|---|---|
| Chirality Indices (n, m) | Isotropic Elasticity Model (Sanders’s Shell Theory) | Molecular Dynamics Simulation [25] | |
| (10, 0) | 299.083 | 290.810 | 2.84 |
| (6, 6) | 288.075 | 278.450 | 3.46 |
| (12, 0) | 249.447 | 242.576 | 2.83 |
| (7, 7) | 246.812 | 239.020 | 3.26 |
| (8, 8) | 215.923 | 209.323 | 3.15 |
| (14, 0) | 213.955 | 207.980 | 2.87 |
| (16, 0) | 187.002 | 181.960 | 2.77 |
| (10, 10) | 172.925 | 167.644 | 3.15 |
| (18, 0) | 166.287 | 161.773 | 2.79 |
| (20, 0) | 149.741 | 145.577 | 2.86 |
| (12, 12) | 144.037 | 139.778 | 3.05 |
| (25, 0) | 119.753 | 116.439 | 2.85 |
| (15, 15) | 115.183 | 111.878 | 2.95 |
| (30, 0) | 99.772 | 97.013 | 2.84 |
| (18, 18) | 96.003 | 93.253 | 2.95 |
| (33, 0) | 90.665 | 87.507 | 3.61 |
| (20, 20) | 86.396 | 83.935 | 2.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strozzi, M.; Elishakoff, I.E.; Bochicchio, M.; Cocconcelli, M.; Rubini, R.; Radi, E. Nonlocal-Strain-Gradient-Based Anisotropic Elastic Shell Model for Vibrational Analysis of Single-Walled Carbon Nanotubes. C 2024, 10, 24. https://doi.org/10.3390/c10010024
Strozzi M, Elishakoff IE, Bochicchio M, Cocconcelli M, Rubini R, Radi E. Nonlocal-Strain-Gradient-Based Anisotropic Elastic Shell Model for Vibrational Analysis of Single-Walled Carbon Nanotubes. C. 2024; 10(1):24. https://doi.org/10.3390/c10010024
Chicago/Turabian StyleStrozzi, Matteo, Isaac E. Elishakoff, Michele Bochicchio, Marco Cocconcelli, Riccardo Rubini, and Enrico Radi. 2024. "Nonlocal-Strain-Gradient-Based Anisotropic Elastic Shell Model for Vibrational Analysis of Single-Walled Carbon Nanotubes" C 10, no. 1: 24. https://doi.org/10.3390/c10010024
APA StyleStrozzi, M., Elishakoff, I. E., Bochicchio, M., Cocconcelli, M., Rubini, R., & Radi, E. (2024). Nonlocal-Strain-Gradient-Based Anisotropic Elastic Shell Model for Vibrational Analysis of Single-Walled Carbon Nanotubes. C, 10(1), 24. https://doi.org/10.3390/c10010024