Abstract
During this research, aerodynamic shape optimization is conducted on the Ahmed body with the drag coefficient as the objective function and the ramp shape as the design variable, while aero-structural optimization is conducted on NACA 0012 to reduce the drag coefficient for the aerodynamic performance with the shape as the design variable while reducing structural mass with the thickness of the panels as the design variables. This is accomplished through a gradient-based optimization process and coupled finite element and computational fluid dynamics (CFD) solvers under fluid–structure interaction (FSI). In this study, DAFoam (Discrete Adjoint with OpenFOAM for High-fidelity Multidisciplinary Design Optimization) and TACS (Toolkit for the Analysis of Composite Structures) are integrated to optimize the aero-structural design of an airfoil concurrently under the FSI condition, with TACS and DAFoam as coupled structural and CFD solvers integrated with a gradient-based adjoint optimization solver. One-way coupling between the fluid and structural solvers for the aero-structural interaction is adopted by using Mphys, a package that standardizes high-fidelity multiphysics problems in OpenMDAO. At the end of the paper, we compare and discuss our findings in the context of existing research, specifically highlighting previous results on the aerodynamic and aero-structural optimization of wind turbine blades.
1. Introduction
In the work of Triet et al. [1], ANSYS Fluent R16.0 was used to conduct analyses to determine the velocity and pressure distribution on the wing surface. Additionally, the varying relative velocities were used to derive the drag and lift coefficients. It was noted that the actual outcomes agreed with the predicted outcomes. In addition to wind tunnel testing, CFD analysis can be used to compute lift and drag forces. Under various angles of attack and with a Reynolds number of , a 2D subsonic flow analysis was conducted by Patel et al. [2] for the NACA 0012 airfoil. The results of the analysis and simulation coincide. As an alternative to experimental approaches, the analyses demonstrated they were accurate.
In the study of Kumar et al. [3], the NACA 23024 airfoil was subjected to CFD analysis using the Ansys Fluent solver. The turbulence models employed in the analysis were the Standard K-Epsilon, the Spalart Allmaras, and the K-omega SST. There was a good agreement between the findings of the study and the experimental wind, according to assessments made at that point. Göv and Korkmaz [4] conducted an analysis to examine the flow separation of the airfoils NACA 4412 and S809. Various values of the angle of attack were used to compare the aerodynamic performance of these two airfoil profiles. The performance parameters were flow separation, moment coefficient (CM), lift coefficient (CL), drag coefficient (CD), and flow separation. In another work of Göv et al. [5], in order to attain optimal performance at various angles of attack, the wing profile was modified throughout the flight. Based on the NACA 4412 airfoil, a two-dimensional CFD analysis was employed in the study. By altering the NACA 4412 profile, two distinct wing profiles were created, and the aerodynamic performances of these two profiles were assessed in comparison with the initial NACA 4412 profile to attain higher aerodynamic performance at various angles of attack during flight. These analyses looked at the attachment loss performance metrics, lift coefficient, and drag coefficient.
Engineers have long struggled with the computational resources and time needed to solve complex problems, particularly when it comes to optimization problems that involve numerous simulations. Design optimization has been a significant challenge in this regard. When an optimization problem involves many variables, it directly impacts the computational time required to find a solution. Consequently, substantial computational resources are necessary to solve such design optimization problems. Thus, there is a need to represent the geometry of the problem with a minimal number of design variables, as the number of design variables directly affects the optimization process in aerodynamic shape optimization problems. This has prompted researchers to search for efficient parameterization methods. According to Wu and Samareh [6], the choice of parameterization significantly impacts the overall optimization process. Balu and Selvakumar [7] also found that parameterization schemes based on polynomials have a substantial influence on the final optimized design. Sobieczky [8] developed the PARSEC parameterization scheme specifically for airfoils, allowing for the expression of a wide range of airfoil shapes without a baseline shape, making it particularly suitable for airfoil optimization.
Gradient-based techniques are widely used in aerodynamic design optimization. The dependence of an objective function on design variables can be established by applying the adjoint method. The literature indicates that adjoint techniques outperform similar approaches. Among the approaches are finite differences, complex sensitivity analysis, and direct sensitivity analysis [9]. They are a versatile method and are available in two main forms: discrete and continuous. There are numerous reference models available for studying the flow in the automotive sector [10]. Each reference includes specific geometric models that study the surrounding fluid behavior under specific constraints. Understanding basic action forms facilitates comprehension of what happens when more complicated shapes are used [11]. The two most used reference models are SAE and Ahmed [12]. By varying the rear slant angle in increments of 50, Ahmed et al. [13] examined the time-averaged wake formation surrounding the Ahmed body at a Reynolds number of .
On the other hand, the analysis produced no data regarding the flow parameters surrounding the Ahmed body that are unsteady.
The external aerodynamics of the Ahmed body were investigated by Bayraktar et al. [14] for rear slant angles of 0 degrees, 12.5 degrees, and 25 degrees. The primary focus was determining the wind-averaged drag coefficients and monitoring the impact of Reynolds number variation on the lift and drag coefficients. The pressure and forces, which are subsequently used to compute the drag coefficients, were measured using a 10-inch water column equipped with an electronic scanning module and a force balancing system. Experiments were conducted by Spohn and Gillieron [15] to study the flow properties of the Ahmed body at a slant angle of 25 degrees and a Reynolds number of . The electrolyte precipitation method was used in the experiment at both the Ahmed body’s front and back, inside a closed water tunnel. By using the Coanda effect to design a generic SUV, Singh et al. [16] developed and executed the curved boat tail arrangement without the AFC device. This caused the airflow under and over the SUV to take a curved path, which resulted in the blowing of air in the immediate wake region. They looked at how it affected several aerodynamic characteristics and found that it significantly reduced drag by 8.013 percent and increased the average pressure in the wake zone.
CFD computations and wind tunnel tests were carried out on the Ahmed body using two rear slant angle configurations by Gabriel et al. [11]. Both the Fluent and the Reynold Stress Model were used to carry out the simulation. The meshing tool SPIDER was used to create the mesh. With an unstructured volume mesh and four prism layers around the body, it contained a total of 7.7 million cells. This kind of meshing technique is frequently used since it would take too long to construct a structured grid around actual vehicle shapes, which would make it impossible for engineers to work within the stringent deadlines set by vehicle design cycles. The CFD computation produced values for the lift and drag coefficients of 0.387 and 0.295 for the 25° angle, respectively, but the wind tunnel experiment yielded values of 0.345 and 0.299 for the same angle. The CFD computation produced values for the lift and drag coefficients of 0.387 and 0.295 for the 25° angle, respectively, but the wind tunnel experiment yielded values of 0.345 and 0.299 for the same angle. In comparison to the pressure measurement performed by Lienhart et al. [12], the RSM model displayed an overestimation of the pressure coefficient over the slant angle.
Three shape parameters were used by Han [9] to optimize the aerodynamic shape of the Ahmed body: the ramp angle, the boat tail angle, and the backlight angle. A technique for optimization was combined with the CFD solver for the k-ε turbulence model. In this work, the design variables were used to develop an analytical approximation function for the objective function. With these optimal parameter values, the CFD simulation was executed again, and new data were added to the objective function. This procedure was carried out repeatedly until the minimal drag parameters were achieved. After optimization, the best rear body angles were found to be 9.2 degrees for the ramp, 18.9 degrees for the boat tail, and 17.8 degrees for the backlight. The results of the experiment indicated that the values of 9–14 ramp angles, 15–22 boat tail angles, and 15–18 backlight angles corresponded to the least drag values. The modified geometry resulted in a drag coefficient of 0.110, down from 0.209 for a square back. Nevertheless, complicated geometries cannot be parameterized using the method employed in this study.
In the literature, the use of Genetic Algorithms for global aerodynamic shape optimization is frequently recommended [17,18,19]. These algorithms are robust and accurate, making them suitable for achieving optimal designs. Panel methods, as suggested by Hess [20] and Katz and Plotkin [21], are commonly employed for solving incompressible potential flows. These methods are advantageous as they provide reasonably accurate results without requiring excessive computational resources. Panel methods are often utilized in the early stages of aircraft design to obtain initial predictions of aerodynamic forces while conserving computational resources. Aero-structural optimization enhances wind turbine or aircraft efficiency by concurrently optimizing aerodynamics and structure. Sequential aero-structural optimization, though computationally efficient, might miss synergistic design enhancements. Altering structural aspects can influence aerodynamics and vice versa, difficult to capture through sequential optimization. This iterative approach can prolong the design cycle and consume significant computational resources.
In contrast, high-fidelity concurrent optimization optimizes both aerodynamic and structural facets simultaneously using accurate models, yielding more optimal designs by considering the interplay between these disciplines. Techniques like computational fluid dynamics (CFD) for aerodynamics and finite element analysis (FEA) for structures provide precise real-world behavior representation, enhancing the optimization process. Multidisciplinary design optimization (MDO) integrates advanced tools like CFD and computational structural mechanics (CSM) to boost design confidence, demanding intricate grid models. MDO encompasses sizing, topology, and shape optimization, vital for achieving an efficient structural layout. The choice of shape parameterization significantly affects the optimization problem. MDO is crucial for enhancing airfoil performance and efficiency by integrating aerodynamics, structures, and manufacturing. Among MDO methods, the discrete adjoint method stands out for its efficiency and accuracy. This paper explores its application in airfoil MDO, coupling flow and structural solvers under two-way fluid–structure interaction conditions. The discrete adjoint method efficiently computes sensitivities, providing a systematic way to optimize airfoil shape considering multiple objectives and constraints.
The multidisciplinary design optimization process using the discrete adjoint method involves geometric parameterization of the airfoil, aerodynamic and structural analyses, coupling of CFD and structural solvers for FSI, sensitivity analysis, and optimization based on obtained sensitivities to find the optimal airfoil shape maximizing performance objectives while meeting constraints. The discrete adjoint method offers key advantages in airfoil multidisciplinary design optimization. It provides precise shape gradients, enhancing convergence efficiency and reducing design iterations. Moreover, it enables optimization of multiple objectives and constraints simultaneously, resulting in superior airfoil designs. Employing this method in airfoil design, integrating aerodynamics and structural analyses through FSI coupling, facilitates finding optimal shapes that maximize performance while adhering to design constraints. The accurate sensitivity analysis of the discrete adjoint method is vital for achieving efficient and precise airfoil shape optimization. In airfoil design, the discrete adjoint method couples aerodynamic and structural solvers, enabling comprehensive two-way FSI and MDO for shape and internal structure optimization. Aerodynamic analysis employs CFD techniques to compute the flow field, while structural analysis determines deformation and stresses. The adjoint equations, derived from governing fluid and solid mechanics equations, yield sensitivities for aerodynamic and structural responses to shape variations.
Our team focuses on concurrent multidisciplinary design optimization (MDO) of wind turbine blades using aerodynamic and structural optimization. We employ DAFoam for aerodynamics and TACS for structural analysis [22], coupled through Mphys in OpenMDAO [23], streamlining the design process. Our objective is to achieve wind turbine blade designs that blend aerodynamic efficiency and structural integrity, advancing wind energy by enhancing turbine performance and reliability. The study starts with the aerodynamic shape optimization of the Ahmed body, a simplified version of a car body, with the ramp shape as the design variable and drag coefficient as the objective function. Then, the aero-structural optimization of NACA 0012 airfoil is enumerated, followed by the discussion of previous results on the wind turbine optimization obtained by our team.
2. Methodology
2.1. Aero-Structural Optimization Framework
High-fidelity solvers can provide better accuracy and a more comprehensive model specification in aero-structural design optimization, although requiring more computing resources and effort to implement than low-fidelity solvers [24]. Gradient-based optimization strategies, such the use of adjoint-based derivative calculations, are needed to manage the high-dimensional and high-fidelity optimization formulations in a tractable numerical issue. To address multidisciplinary design optimization concerns in engineering systems, the OpenMDAO framework has been extended to include many aero-structural, hydro-structural, aerothermal, aero-propulsive, and aeroelastic MDO issues [25].
The gradient-based optimization utilizing the analytic derivatives feature of the OpenMDAO high-performance computing platform, which is built on Python, is its primary purpose. The implementation described in this paper is based on a two-way fluid–structure interaction (FSI) in the OpenMDAO framework, which couples the Toolkit for the Analysis of Composite Structures (TACS) [25] with MPhys [25] and the discrete adjoint with OpenFOAM for High-fidelity Multidisciplinary Design Optimization (DAFoam) [26]. Together, the structural and aerodynamic systems produce loads; the structural group takes these loads as input and produces structural displacements, while the aerodynamics group receives a mesh as input and produces aerodynamic loads as an output. Numerous studies have explored this method’s possible applications in the optimization of aircraft aerodynamics and aero-structural design, garnering a great deal of prior research attention [27,28,29]. The MACH [30] is a collection of closely related sub-modules that enable geometry parametrization and deformation, coupled aero-structural analysis, and effective derivatives assessment in an optimization environment, according to the Extended Design Structure Matrix (XDSM) schematic [31] in Figure 1.
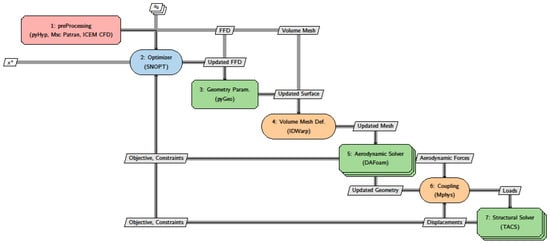
Figure 1.
MACH optimization framework’s XDSM diagram.
The optimization process is performed using the OpenMDAO framework, which is based on Mach-aero [25]. Preprocessing includes the development of the aerodynamic mesh in pyHyp [23] and the structural mesh in MSC Patran 2019. The geometry parametrization package, pyGeo [32], uses the Non-Uniform Rational B-Splines (NURBS) scheme and the Free-Form Deformation (FFD) approach to modify the geometry. Via the mesh deformation module IDwarp [23], surface node displacements are sent from the updated geometry to the volume mesh. Using the FD Jacobian methodology and Krylov method, the aerodynamic solver DAFoam performs [26] the discrete adjoint for high-fidelity multidisciplinary design optimization. The aero-structural coupling is created using the OpenMDAO/Mphys framework [25], and the load and displacement transfer is computed using FUNtoFEM [25]. In this work, the structural solution Toolkit for the Analysis of Composite Structures (TACS) [33], which can handle both linear and nonlinear geometric structural difficulties, was used. PyOptSparse [34] manages the data flow between the optimizer and the solvers as well as the formulation of the optimization problem. Steady-state turbulent flow is simulated using OpenFOAM’s SimpleFoam solver.
2.2. Discrete Adjoint Derivatives’ Formulation
In our case, the drag coefficient acts as the objective function , and represents the vector of design variables. The complete derivatives may be computed fast using the adjoint technique. The discrete approach is based on the assumption that the governing equations can be discretized by the primal solver and that the discrete residual equations , where represents the residual vector, are satisfied by the design variable vector and the state variable vector As a result, the relevant functions rely on the state and design variables: In the following derivations, is considered as a scalar for the purpose of generality, even if there could be several functions of interest. It will become evident later on that the solution of an additional adjoint system is necessary for each new function. The chain rule is used to obtain the entire derivative .
The estimation of the partial derivatives and is very easy as no implicit computations are required. Nonetheless, the implicit determination of the total derivative matrix via the residual equations = 0 makes its computation costly. We can find the derivative by using the chain rule on R. Using this knowledge, we may verify that the governing equations remain valid. Consequently, , the total of the derivatives, must equal zero.
Equation (1)’s formula for is changed to Equation (2), yielding the following outcome:
By utilizing the transpose of the state Jacobian matrix as the right-hand side, we may solve the adjoint equation.
After solving the adjoint vector equation, represented by , we may obtain the total derivative by substituting the adjoint vector into Equation (3). This exchange produces the desired result.
To save processing costs, the adjoint equations only need to be solved once for each function of interest because the design variable is not stated directly in Equation (4). Because of this, the computational cost is not affected by the amount of design variables, but rather scales proportionately with the number of interesting functions.
When there are several design considerations but only a few key functions, the adjoint methodology, a method for resolving design challenges in aeronautical engineering, provides benefits. To put the discrete adjoint into practice, four key steps need to be finished: calculating the partial derivatives, solving the adjoint equations, and carrying out the following important actions:
- (1)
- Evaluating the transpose of the partial derivatives and .
- (2)
- Solving the linear Equation (4) to determine the adjoint vector .
- (3)
- Computing the partial derivatives and through a computational process.
- (4)
- Utilizing Equation (5) to calculate the total derivative .
These four procedures can be applied to any set of discrete partial differential equations (PDEs) without assuming a specific form for the residual function .
2.3. Integration of Aerodynamics and Structural Mechanics
The state variables from the finite element method (FEM) and computational fluid dynamics (CFD) must be integrated and solved concurrently to use the adjoint formulation previously stated. On the other hand, this approach increases the memory need and produces a bigger Jacobian matrix. To tackle this issue, we employ a unique technique known as block Gauss-Seidel to solve the aero-structural adjoint in a connected manner. The method is demonstrated in the example below.
The abbreviations CFD and FEM, which stand for computational fluid dynamics and finite element method, respectively, represent the residual and state variables in these solvers. DAFoam is used to address the adjoint issue in a CFD.
DAFoam makes use of automated differentiation in the Jacobian-free adjoint approach, which computes matrix-vector products and partial derivatives. This strategy is explained in the study that was carried out by Kenway and colleagues [35]. DAFoam uses the generalized minimum residual (GMRES) iterative linear equation solver from the PETSc package to solve the adjoint problem [36]. DAFoam uses the incomplete lower and upper (ILU) factorization technique with a single level of fill-in for local preconditioning and a layered strategy utilizing the additive Schwartz method for global preconditioning. The preconditioner matrix is produced by estimating the residuals and their linearization to enhance convergence [37].
This matrix is only generated once, in the first-time step, and is then utilized again in the adjoint equation. As constructing takes up around 30% of the adjoint runtime, this leads to a considerable decrease in adjoint runtime. TACS is used to solve the adjoint equation for the finite element method (FEM) component.
Automatic differentiation is used to compute the vector multiplication of the matrix’s non-diagonal elements rather than directly producing the matrix itself. The modular use of MPhys and OpenMDAO allowed for a flexible design of the aero-structural system. To perform the multiplication of the state Jacobian matrix with a specific vector and to generate output that is dependent on input, the elements displayed in Figure 1 were required. The adjoint total derivative computation was combined by OpenMADO using the MAUD method [38].
2.4. RANS-Based Turbulent Simulation
A three-dimensional steady incompressible flow is described using the Navier–Stokes equations for the conservation of mass and momentum.
These equations are represented by the numbers 1 and 2, where u stands for velocity, p for pressure, d for density, v for dynamic viscosity. The turbulence model used is the Spalart–Allmaras model [39], which converges well, is easy to use, and is dependable. The initial values for k, ε, νt, ω, and ṽ are 0.015 m2/s2, 0.14 m2/s3, 4.5 × 10−5 m2/s, 100 s−1, and 4.5 × 10−5 m2/s, respectively. The inlet velocity of the fluid is 52.08 m/s, and the angle of attack is 10 degrees.
2.5. Multidisciplinary Design Optimization of NACA 0012
In multidisciplinary design optimization, the NACA 0012 airfoil is chosen as the base geometry. The aerodynamic mesh is crafted using pyHyp [23], generating 9576 mesh cells for accurate analysis as shown in Figure 2.
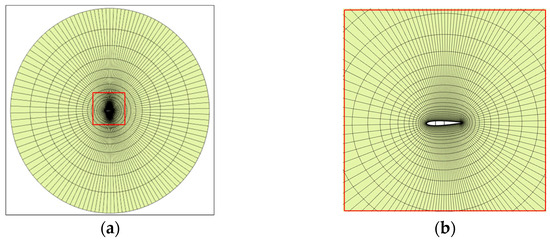
Figure 2.
Meshes: (a) Aerodynamic mesh and structural mesh (inside the aerodynamic mesh); (b) detail view with marked red square.
The Allmaras model is used for both the NACA 0012 airfoil and Ahmed body optimization in order to reduce the computational cost instead of other expensive turbulence models mentioned in the form of citations. As to the solver, the DASimpleFoam is opted for both cases, which is the discrete form of SimpleFoam solver. As for the aerodynamic mesh of the NACA 0012 airfoil, the surface mesh is generated first with python code and then the open-source mesh generation tool, pyHyp, is used to extrude the surface mesh with a march distance of 20 m at a growth ratio of 1.2 with an initial expansion layer of 0.00003 m for three specific layer numbers. And as for the structural mesh of the NACA 0012 airfoil, the mesh is generated based on commercial software, MSC Patran 2019, based on CQUAD hexahedral shell elements with a size of 5 mm.
The structural analysis involves a finite element mesh created using MSC Patran, focusing on spar caps and the main shear web for robust analysis. The mesh provides the necessary discretization and fidelity for accurate evaluation of airfoil performance and structural response. The structural mesh employs CQUAD hexahedral shell elements, ensuring accurate representation of airfoil structural behavior as shown in Figure 3b. It incorporates spar caps and the main shear web, crucial for load distribution and structural integrity.
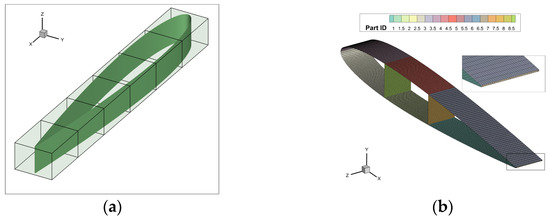
Figure 3.
(a) FFD points, intersection of lines representing an FFD point; (b) structural mesh (each patch with different color represents a structural design variable).
In the multidisciplinary design optimization of airfoils, the discrete adjoint method is an efficient and accurate technique for achieving optimal designs. This approach considers the interplay between aerodynamics and structures, aiming to minimize mass and maximize torque. Structural optimization focuses on reducing the weight of the airfoil while maintaining its structural integrity. On the other hand, aerodynamic optimization aims to enhance performance by maximizing the torque generated by the airfoil. By concurrently optimizing for these objectives, the discrete adjoint method enables engineers to find the optimal balance between weight reduction and torque maximization, leading to superior airfoil designs.
In the multidisciplinary design optimization of airfoils using the discrete adjoint method, a comprehensive set of design variables is considered. These variables include local shapes, comprising 28 individual design variables, along with one angle of attack. Additionally, the control points of Free-Form Deformation (FFD) are utilized to construct the design variables for the aerodynamic optimization process. This design variable configuration is depicted in Figure 3a. The optimization process involves separate optimizations for both the airfoil shape and the angle of attack, allowing for a thorough exploration of the design space and enabling the identification of the optimal configurations for each parameter.
In addition to the aerodynamic design variables, the structural design variables were incorporated into the optimization process. The structural mesh of the airfoil was modified by introducing two shear webs and three chordwise sections, creating distinct upper and lower parts. Each of these structural panels was assigned a separate design variable. This can be visualized in Figure 3b, where the airfoil is divided into eight panels, each representing a specific design variable. By utilizing the Toolkit for the Analysis of Composite Structures (TACS), the optimizer has the capability to manipulate the thickness of each panel independently, resulting in a total of eight design variables that can be adjusted during the optimization process.
The combination of aerodynamic and structural meshes enables comprehensive analysis for multidisciplinary design optimization, providing essential discretization and fidelity for precise evaluation. The wing material is aluminum, with mechanical properties detailed in Table 1.

Table 1.
Mechanical properties.
Attention is carefully given to balancing aerodynamic performance and weight reduction during the optimization, ensuring compliance with performance and structural constraints. This integrated approach recognizes the importance of structural and aerodynamic improvements in enhancing overall turbine efficiency. By comprehensively considering both aspects, engineers can create airfoils that are structurally robust and aerodynamically efficient, resulting in decreased drag and reduced fatigue loads. MDO facilitates systematic exploration of design options through integrated aerodynamic and structural analyses using computational tools like computational fluid dynamics (CFD) and finite element analysis (FEA). This approach aims to improve both structural integrity and aerodynamic efficiency by considering mass, drag coefficient, and aeroelastic response, ultimately enhancing overall aerodynamic and structural performance.
Multidisciplinary design optimization (MDO) enhances wind turbine blade performance by considering both structural and aerodynamic aspects. The current quasi-3D approach for airfoil optimization is applied in wind turbine blade design, aiming to improve overall performance by optimizing mass and drag coefficients, as shown in Table 2.

Table 2.
The specifications of aero-structural optimization.
In the design optimization of airfoils using the discrete adjoint method, various constraints are considered to ensure the aerodynamic and structural integrity of the design. For aerodynamic optimization, constraints such as volume, thickness, leading edge (LE) and trailing edge (TE) shapes, as well as lift requirements, are considered. These constraints ensure that the airfoil design meets the desired performance objectives while maintaining geometric and aerodynamic feasibility. On the other hand, for structural optimization, constraints such as yield stress, minimum thickness, and maximum thickness are considered to ensure the structural integrity and safety of the airfoil design. These constraints guarantee that the airfoil can withstand the expected loads and stresses without exceeding material limitations. By incorporating these constraints into the optimization process, the multidisciplinary design optimization of airfoils using the discrete adjoint method ensures a balanced and robust design solution that meets both aerodynamic and structural requirements.
Verification and Validation
Three distinct mesh levels, L0, L1, and L2, have been taken into consideration in a comprehensive analysis of mesh convergence. Table 3 presents the specifics of these levels. The investigation was conducted using a fluid input velocity of 52.08 m/s and an angle of attack of 10 degrees. A 1.2 growth ratio was used during the development of the hyperbolic expansion layer. To keep the y+ value near to 1, the beginning cell height from the turbine surface was also set at 0.00003 m. Here, the superscript “cross” denotes that the distance has been normalized with respect to that axis, and y+ represents a dimensionless distance along that axis from the wall to the first mesh node.

Table 3.
Mesh convergence by comparing the torque result from simulation against experimental value.
According to Table 3, the torque errors for the three mesh L0-, L1-, and L2-based CFD simulations are 7.01 percent, 29.24 percent, and 32.35 percent, respectively, when compared to the Ladson experimental value. To obtain better results, the L0 mesh is utilized in our optimization.
As shown in Figure 4, the comparison of the Cp value of all levels of mesh represents considerable well-matched values with the Cp data from Ladson experiments.
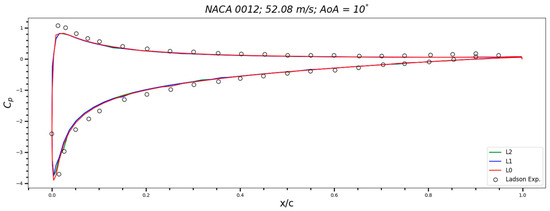
Figure 4.
Comparison of the pressure coefficients (Cp) from three levels of mesh and Ladson experimental data.
2.6. High-Fidelity Shape Optimization of Ahmed Body
With increasing concerns about the unsustainability of burning fossil fuels, environmental degradation, and rising energy prices, automobile manufacturers are introducing more fuel-efficient vehicles to the market. One of the main factors affecting fuel consumption is aerodynamic drag, which accounts for over half of the engine power at highway speeds. The pressure drags, which are influenced by vehicle geometry, are caused by the separation of the boundary layer from the rear trailing end of the vehicle, resulting in the formation of a wake region behind it. The location of this separation determines the size of the wake region and, consequently, the value of the aerodynamic drag coefficient, which measures the resistance of an object in a fluid environment. Lower drag coefficients indicate more efficient cars. However, reducing drag too much can reduce downforce, increase lift, decrease road traction, and raise the risk of accidents. There are various ways to optimize a car’s aerodynamics and decrease its drag coefficient, such as removing aftermarket accessories like roof racks, mud flaps, spoilers, and radio antennas. Wheel covers, partial grille blocks, properly designed under trays, fender skirts, and modified front bumpers can also be utilized. These drag-reducing methods are categorized as either active or passive control methods. Passive methods, like vortex generators, involve modifying the vehicle’s geometry. Active control methods, on the other hand, use actuators that require power, typically derived from the vehicle’s engine. Active methods employ movable walls, circular holes, or slots distributed over the vehicle’s surface to control airflow. While active control methods such as suction and blowing exist in theory, their practical feasibility and optimization are yet to be determined. The Ahmed body [13], a bluff body with simplified car-like geometry, is commonly used as a model due to its simplicity and relevance. To reduce computational costs, a symmetry plane is introduced to simulate half of the model.
We focus on optimizing the aerodynamic shape of the Ahmed body. Specifically, we select the configuration with a ramp angle of 25° and 1.21 million cells as our baseline case while the wind velocity is 40 m/s. In this case, we only took half of the baseline geometry to make a symmetric case. And the mesh is as shown in Figure 5. The Ansys mesh generator is used with a mesh size of 0.2 m along with a face mesh size of 0.005 m on the Ahmed surface, while the expansion layer number is 10 with a 1.2 growth rate starting at the first layer height of 0.00001 m.
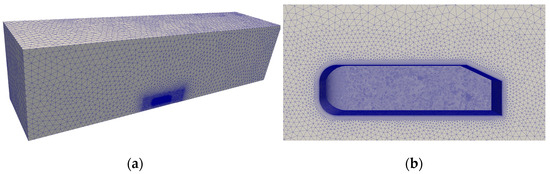
Figure 5.
Ahmed body mesh: (a) symmetric domain; (b) expansion layer from the view of symmetry side.
The velocity streamlines of the flow over the Ahmed body of the chosen slant angle at the velocity of 40 m/s are shown in Figure 6. When considering the Ahmed body with a slant angle of 25 degrees and a wind speed of 40 m/s, the visualization of velocity streamlines provides valuable insights into the flow behavior around the body. The velocity streamlines illustrate the paths followed by fluid particles as they move around the body. At the given slant angle and wind speed, the velocity streamlines over the Ahmed body reveal important flow features. As the approaching airflow encounters the body, it divides into two primary streams: one flows over the upper surface of the body, while the other flows underneath. These two streams converge at the rear of the body, forming a region of recirculating flow or a wake.

Figure 6.
Velocity streamline over the Ahmed body.
The streamlines over the top surface of the Ahmed body typically exhibit a faster airflow, especially on the leading edge, where the flow accelerates. As the flow progresses along the body’s surface, it gradually slows down due to increasing pressure and separation of the boundary layer. The streamlines follow the contour of the body, curving over the upper surface, and eventually converge near the rear end. On the bottom surface of the Ahmed body, the streamlines show a similar behavior, but with slower velocities compared to the top surface. This is primarily due to the longer path length and increased friction with the surface. The increased friction on the lower surface is due to the existence of lower vortices using Wall-Resolved Large Eddy Simulation (LES) [40,41]. These lower vortices occur along either side of the lower surface due to an increase in pressure from boundary layer growth along the underside of the body. The region of recirculating flow or wake behind the Ahmed body can also be observed through the velocity streamlines. The streamlines in this region loop back towards the rear end of the body, indicating the presence of vortices and a complex flow pattern. The size and shape of the wake can provide insights into the aerodynamic characteristics of the body and its drag-inducing features.
Next, we proceed to optimize the aerodynamic shape by considering the 9 × 10 Free-Form Deformation (FFD) points located just above the ramp surface as shown in Figure 7, where the FFD points in the area interested are marked in red, with the fixed points in black. The positions of the other FFD points, including those on the top edge of the ramp, are kept fixed. The movement of the FFD points is restricted to vertical directions, allowing for adjustments in the surface shape of the ramp. This approach enables us to refine the aerodynamic characteristics of the design while maintaining the overall structure of the ramp.
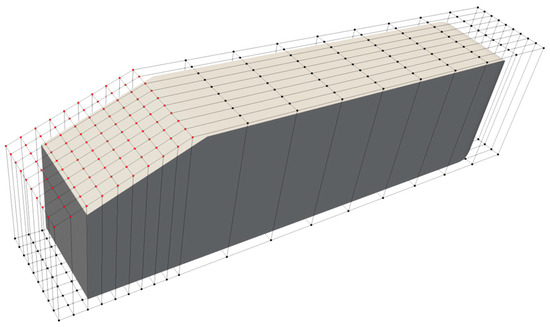
Figure 7.
FFD points for the optimization.
3. Results and Discussion
3.1. NACA 0012
Figure 8 illustrates the implementation of one-way static fluid structural interaction in the multidisciplinary design optimization (MDO) process. The load transfer from the aerodynamic to structural solvers is facilitated using Mphys. For the simplicity and clarity of presentation of the optimization method proposed, we neglected the effects of other non-aerodynamic forces, which are nonnegligible when it comes to the optimization of wind turbine blades as well as aircraft wings. The optimization is made based on a solution in parallel using separate criteria for the shape of the airfoil with low aerodynamic drag as an objective function, which is not affected by the structural properties, and adjusting the internal geometry of the structure using other criteria for its selection.
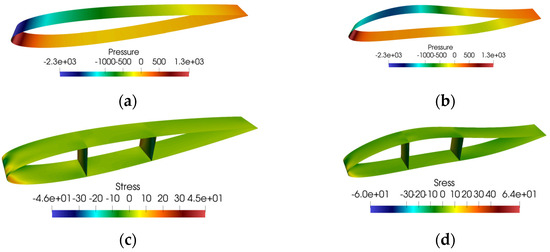
Figure 8.
Pressure and stress color map before and after the optimization: (a) pressure color map before the optimization; (b) pressure color map after the optimization; (c) stress color map before the optimization; (d) stress color map after the optimization.
The confirmation of load transfer can be obtained by referring to Figure 8, where it can be observed that the aerodynamic shape and structural shape exhibit an identical configuration. This correspondence between the two shapes provides evidence for the effective transfer of loads between the aerodynamic and structural domains. Such alignment supports the integration of aerodynamic and structural analyses in the multidisciplinary design optimization process, ensuring that changes in the airfoil shape appropriately influence both the aerodynamic performance and structural integrity. By optimizing the external shape of the airfoil as indicated by the adjoint solver, an attempt is made to obtain the lightest possible internal structure that meets the given criteria of not exceeding the allowable stresses due to the aerodynamic load. This is achieved in successive iterations from shape modification to structure adjustment. And there is no strong coupling between aerodynamic forces and structure in this case without bidirectional coupling between aerodynamics and structure. The airfoil shape is defined by the aerodynamics followed by the mandatory match of the structure.
The aerodynamic optimization stage leverages the capabilities of the discrete adjoint method to determine the optimal shape of the airfoil. By considering the sensitivities of the aerodynamic responses with respect to shape variations, the discrete adjoint method efficiently converges towards an improved airfoil geometry. This leads to enhanced aerodynamic performance, as evidenced by the variations in the objective function, drag coefficient, depicted in Figure 9 with the reduction of 12.5%. The initial mass of the airfoil structure, considered during the structural optimization phase, is recorded as 1.618 kg. Following the mass optimization procedure, a final mass value of 1.455 kg is attained, indicating a reduction in mass during the optimization process. Furthermore, the multidisciplinary nature of the design optimization process allows for the consideration of both aerodynamics and structural aspects. While the focus is primarily on optimizing the aerodynamic performance of the airfoil, structural optimization is also incorporated to ensure that the final design adheres to necessary structural constraints. The initial mass of the airfoil structure is initially determined to be 1.618 kg. However, as optimization progresses, a dedicated mass optimization phase is employed to reduce the mass of the structure. This results in a final mass value of 1.455 kg, reflecting the successful achievement of a lighter airfoil structure without compromising its structural integrity.
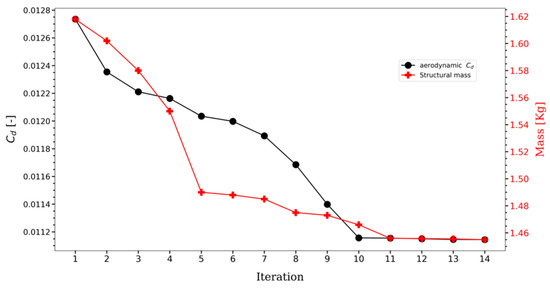
Figure 9.
Optimization of the airfoil.
Figure 10 illustrates the outcomes of the aerodynamic optimization, showcasing the variance in the pressure coefficient (Cp) before and after the optimization process.
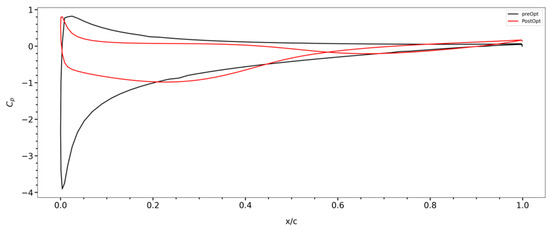
Figure 10.
Pressure coefficient before and after the optimization.
3.2. Ahmed Body
Before and after the optimization process for the Ahmed body, changes in pressure and velocity contours can provide valuable insights into the effectiveness of the modifications made to the aerodynamic shape. Before optimization, the pressure and velocity contours over the Ahmed body may exhibit certain characteristics. The pressure contours highlight areas of high and low pressure, indicating regions of compression and expansion in the airflow. Typically, a high-pressure region is observed on the front face of the body, where the approaching airflow encounters resistance and slows down. The velocity contours reveal the distribution of flow velocities over the body. Higher velocities are typically observed on the top surface of the body, especially near the leading edge, where the flow accelerates due to the body’s shape. The velocity gradually decreases as the flow encounters resistance and experiences boundary layer separation along the body’s surface. The velocity contours can help identify areas of flow separation, recirculation, or regions with low velocities.
The pressure and velocity change before and after the optimization around the surface of the Ahmed body are depicted in Figure 11.
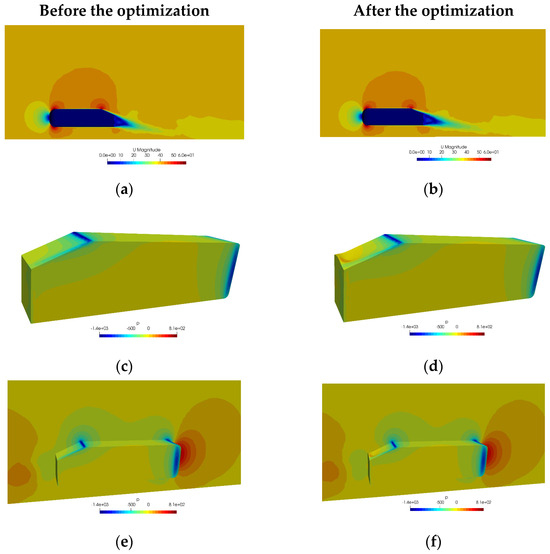
Figure 11.
(a) Velocity contour on the symmetry plane before the optimization; (b) velocity contour on the symmetry plane after the optimization; (c) pressure contour on the Ahmed body before the optimization; (d) pressure contour on the Ahmed body after the optimization; (e) pressure contour on the symmetry plane as well as the Ahmed body before the optimization; (f) pressure contour on the symmetry plane as well as the Ahmed body after the optimization.
After the shape optimization of the Ahmed body, the design of the ramp underwent changes while the remaining portions of the body remained unchanged as shown in Figure 12. This targeted modification was aimed at improving the aerodynamic performance of the vehicle by specifically adjusting the shape of the ramp. The optimization process focused on altering the shape of the ramp to enhance the flow characteristics and minimize drag. By manipulating the Free-Form Deformation (FFD) points associated with the ramp, the surface shape of the ramp was modified, allowing for a more favorable airflow interaction. The shape optimization of the ramp involved adjusting the position of the FFD points along the vertical axis, allowing for upward and downward movement. This enabled the optimization algorithm to refine the curvature and contour of the ramp surface, influencing the airflow patterns and pressure distribution. The changes in the ramp shape resulting from the optimization process aimed to reduce flow separation, improve attachment of the boundary layer, and minimize the formation of vortices and turbulence.
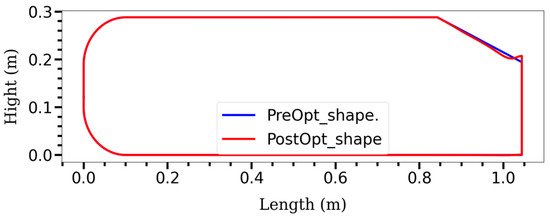
Figure 12.
Cross-sectional shape changes of the Ahmed body ramp through the optimization.
By optimizing the ramp shape, the goal was to streamline the flow, reduce drag, and potentially enhance the overall aerodynamic efficiency of the Ahmed body. While the rest of the body remained unchanged, the modifications made to the ramp shape could have a significant impact on the overall flow behavior and performance. The optimized ramp shape aimed to improve the flow transition from the front to the rear of the body, reducing drag-inducing features and enhancing the vehicle’s aerodynamic characteristics. In our case, we aim to reduce the drag coefficient and obtained the result shown in Figure 13.
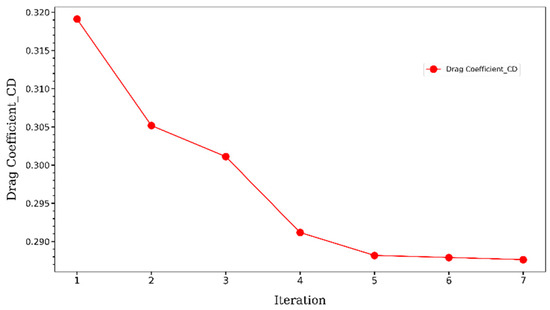
Figure 13.
Drag coefficient change during the optimization.
During the optimization process of the Ahmed body, it took five iterations for the optimization algorithm to converge to a final solution. This convergence indicates that the algorithm reached a stable and satisfactory outcome in terms of the desired optimization objectives. Throughout the iterations, the optimization algorithm made successive adjustments to the shape of the ramp, targeting improvements in the body’s aerodynamic performance. The algorithm analyzed the flow behavior, pressure distribution, and drag coefficient to guide the modifications made to the ramp shape. The primary objective of the optimization process was to reduce the drag coefficient of the Ahmed body, as this parameter quantifies the resistance encountered by the body in the fluid environment. Initially, the drag coefficient was measured at 0.319 before the optimization process began while the experimental value is 0.299 according to the experiment conducted by W. Meile et al. [42]. Therefore, the error is around 6.7% compared to the experimental value.
After the five iterations, the optimization algorithm successfully decreased the drag coefficient to 0.287. This reduction indicates a 10% improvement in the aerodynamic efficiency of the body. A lower drag coefficient implies reduced resistance to the airflow, leading to enhanced performance and potentially improved fuel efficiency for the Ahmed body. By achieving a 10% optimization in the drag coefficient, the optimization process demonstrated its effectiveness in refining the aerodynamic characteristics of the body. The convergence of the optimization algorithm and the resulting decrease in the drag coefficient indicate successful modifications to the shape of the ramp and improvements in the airflow interaction around the Ahmed body.
3.3. Three-Dimensional Static MDO for a Wind Turbine Blade
Apart from the high-fidelity aerodynamic shape optimization of the Ahmed body and aero-structural optimization of the NACA airfoils, our team has been making efforts to optimize wind turbine blades both in terms of aerodynamic shape [43] and aero-structural optimizations [29]. The open-source program DAFoam [43] is used throughout the process of optimization the high-fidelity aerodynamic design that was previously discussed, which incorporates pyOptSparse [34] and pyGeo [44] for optimization, along with OpenFOAM as the fluid solver. The program makes use of the adjoint approach, a quick way to calculate derivatives, which makes it possible to apply gradient-based optimization to systems with a lot of design variables. The commercial nonlinear optimizer SNOPT [45] was utilized to manage the several design variables and the complex nature of the design process.
The NREL Phase VI design, which was created especially for verifying applicable CFD studies, is the foundation of the optimization process. The Unsteady Aerodynamic Experiment (UAE), conducted in the NASA-Ames wind tunnel, is thoroughly evaluated by the NREL Phase VI experiment. Based on the S809 airfoil, the experiment employs a two-bladed rotor with a diameter of 10.058 m [46]. The initial configuration is depicted in Figure 14.
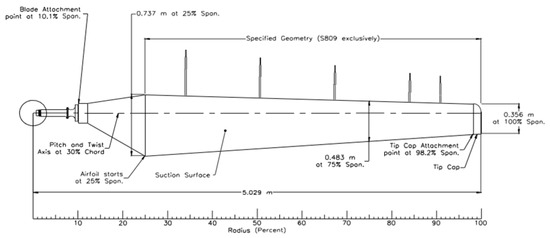
Figure 14.
Baseline geometry [46].
Table 4 presents the categorization of optimization algorithms, and the optimization process is carried out accordingly using the following schemes: Optimization Scheme S1 focuses on pitch optimization, where the pitch angle serves as the sole design variable. Optimization Scheme S2 involves shape and twist optimization, employing 120 shapes in the y direction and 6 twist angles as design variables, resulting in a total of 126 variables.

Table 4.
Optimization schemes.
Optimization Scheme S3 combines shape and chord optimization, utilizing 120 shapes in the y direction and 2 chord lengths as design variables, resulting in a total of 122 variables. Optimization Scheme S4 incorporates shape and dihedral optimization, employing 120 shapes in the y direction and 6 dihedrals in the y direction as design variables, resulting in a total of 126 variables. Optimization Scheme S5 encompasses twist, chord, and dihedral optimization, utilizing 6 twist angles, 2 chord lengths, and 6 dihedrals in the y direction as design variables, resulting in a total of 14 variables.
As shown in Figure 15, the optimization results of wind turbine blades are based on six schemes, S1 (pitch angle optimization), S2 (combination of shape and twist angle optimization), S3 (combination of shape and chord length optimization), S4 (combination of shape and dihedral optimization), S5 (combination of twist angle, chord length, and dihedral optimization), and S6 (aero-structural optimization in terms of shape and mass of the wind turbine blades), where the S1, S2, S3, S4, and S5 optimizations are published in the work [43] and S6 optimization is published in the work [29]. We quote the published results here to demonstrate that the method has been extended successfully for fully 3D MDO for wind turbine blades and we are working towards dynamic MDO based on the two-way FSI, shell structure model, and VLES turbulence model.
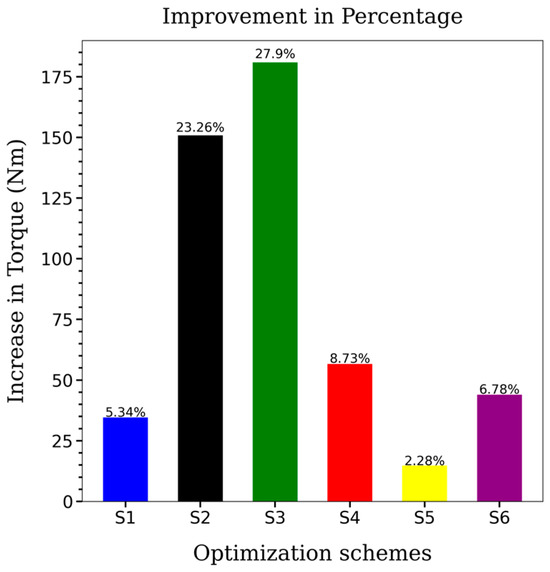
Figure 15.
Optimization results of wind turbine blades.
4. Conclusions
In conclusion, this study demonstrates the effectiveness and versatility of high-fidelity aerodynamic and aero-structural optimization techniques across different aerodynamic bodies. The initial optimization of the Ahmed body validated our computational methodologies, ensuring their reliability for more complex applications. The core focus on the NACA 0012 airfoil revealed significant improvements in both aerodynamic performance and structural integrity, showcasing the potential of integrated optimization approaches in achieving balanced and efficient designs.
Furthermore, the comparison with previous studies on wind turbine blade optimization highlights the broader applicability of these methods, affirming their relevance to various aerodynamic challenges. The findings indicate that advanced optimization strategies can lead to substantial performance gains while maintaining or enhancing structural robustness. This work lays a solid foundation for future research, suggesting that these techniques can be adapted and extended to other aerodynamic and aero-structural optimization problems, ultimately contributing to the development of more efficient and resilient aerodynamic designs.
Author Contributions
Conceptualization, S.B. and E.Y.K.N.; Methodology, S.B. and Y.Z.; Software, S.B. and T.Z.; Validation, Y.Z.; Formal analysis, E.S. and T.Z.; Investigation, S.B., A.B., E.S. and T.K.; Resources, A.B., Y.Z., T.Z., E.Y.K.N. and T.K.; Data curation, A.B., Y.Z. and T.K.; Writing—review & editing, A.B., T.Z. and E.Y.K.N.; Visualization, E.S. and T.K.; Supervision, E.Y.K.N.; Project administration, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This study is funded by Nazarbayev University through FDCR grant No. 20122022FD4126.
Data Availability Statement
Data are available upon request to the first author (shaheidula.batai@nu.edu.kz).
Acknowledgments
The authors would like to thank Nazarbayev University for the financial support for this work through FDCR grant No. 20122022FD4126.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Nguyen, M.T.; Nguyen Ngoc, V.; Pham Manh, T. Aerodynamic Analysis of Aircraft Wing. VNU J. Sci. Math. Phys. 2015, 31, 68–75. [Google Scholar]
- Patel, K.S.; Patel, S.B.; Patel, U.B.; Ahuja, A.P. CFD Analysis of an Aerofoil. Int. J. Eng. Res. 2014, 3, 154–158. [Google Scholar] [CrossRef]
- Anil Kumar, B.S.; Ramalingaiah Manjunath, S.; Ganganna, R. Computational Investigation of Flow Separation over NACA 23024 Airfoil at 6 Million Free Stream Reynolds Number Using k-Epsilon Turbulence Model. Mater. Today Proc. 2018, 5, 12632–12640. [Google Scholar] [CrossRef]
- Göv, İ.; Korkmaz, Ü. Comparison of Aerodynamic Performance of NACA 4412 and S809 Airfoil Profile. In Proceedings of the International Mechanical Engineering and Technologies Conference, Istanbul, Turkey, 17–18 May 2016; pp. 183–188. [Google Scholar]
- Doğru, M.H.; Göv, İ.; Korkmaz, Ü. Uçuş Esnasında Değiştirilebilir Kanat Profili Kullanarak NACA 4412′nin Aerodinamik Performansının Artırılması. Gazi Üniversitesi Mühendislik-Mimar. Fakültesi Derg. 2019, 34, 1109–1126. [Google Scholar] [CrossRef]
- Wu, H.-Y.; Yang, S.; Liu, F.; Tsai, H.-M. Comparisons of Three Geometric Representations of Airfoils for Aerodynamic Optimization. In Proceedings of the 16th AIAA Computational Fluid Dynamics Conference, Orlando, FL, USA, 23–26 June 2003; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2003. [Google Scholar] [CrossRef]
- Ulaganathan, S.; Balu, R. Optimum Hierarchical Bezier Parameterisation of Arbitrary Curves and Surfaces. In Proceedings of the 11th Annual AeSI CFD Symposium, Bangalore, India, 11–12 August 2022; Indian Institute of Science: Bangalore, India, 2009; pp. 46–48. [Google Scholar]
- Sobieczky, H. Parametric Airfoils and Wings; Springer: Berlin/Heidelberg, Germany, 1999; pp. 71–87. [Google Scholar] [CrossRef]
- Han, T.; Hammond, D.C.; Sagi, C.J. Optimization of bluff body for minimum drag in ground proximity. AIAA J. 1992, 30, 882–889. [Google Scholar] [CrossRef]
- Morelli, A. A New Aerodynamic Approach to Advanced Automobile Basic Shapes; SAE: Warrendale, PA, USA, 2000. [Google Scholar] [CrossRef]
- Gabriel, A.; Drage, P.; Lindbichler, G.; Hörmann, T.; Brenn, G.; Meile, W. Efficient Use of Computational Fluid Dynamics for the Aerodynamic Development Process in the Automotive Industry. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Toulouse, France, 16–19 May 2022; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2008. [Google Scholar] [CrossRef]
- Lienhart, H.; Stoots, C.; Becker, S. Flow and Turbulence Structures in the Wake of a Simplified Car Model (Ahmed Modell). In New Results in Numerical and Experimental Fluid Mechanics III; Springer: Berlin/Heidelberg, Germany, 2002; pp. 323–330. [Google Scholar] [CrossRef]
- Ahmed, S.R.; Ramm, G.; Faltin, G. Some Salient Features of The Time-Averaged Ground Vehicle Wake; SAE: Warrendale, PA, USA, 1984. [Google Scholar] [CrossRef]
- Bayraktar, I.; Landman, D.; Baysal, O. Experimental and Computational Investigation of Ahmed Body for Ground Vehicle Aerodynamics; SAE: Warrendale, PA, USA, 2001. [Google Scholar] [CrossRef]
- Spohn, A.; Gilliéron, P. Flow Separations Generated by a Simplified Geometry of an Automotive Vehicle; Kluwer Academic: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Singh, S.; Zunaid, M.; Ansari, N.A.; Bahirani, S.; Dhall, S.; Kumar, S. Numerical Study of the Generic Sports Utility Vehicle Design with a Drag Reduction Add-On Device. J. Comput. Eng. 2014, 2014, 785294. [Google Scholar] [CrossRef][Green Version]
- Quagliarella, D.; Cioppa, A.D. Genetic algorithms applied to the aerodynamic design of transonic airfoils. J. Aircr. 1995, 32, 889–891. [Google Scholar] [CrossRef]
- Wang, J.F.; Periaux, J.; Sefrioui, M. Parallel evolutionary algorithms for optimization problems in aerospace engineering. J. Comput. Appl. Math. 2002, 149, 155–169. [Google Scholar] [CrossRef]
- Marco, N.; Lanteri, S. A two-level parallelization strategy for Genetic Algorithms applied to optimum shape design. Parallel. Comput. 2000, 26, 377–397. [Google Scholar] [CrossRef]
- Hess, J.L. Panel Methods in Computational Fluid Dynamics. Annu. Rev. Fluid Mech. 1990, 22, 255–274. [Google Scholar] [CrossRef]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics: From Wing Theory to Panel Methods, 12th ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Kennedy, G.J.; Martins, J.R.R.A. A parallel finite-element framework for large-scale gradient-based design optimization of high-performance structures. Finite Elem. Anal. Des. 2014, 87, 56–73. [Google Scholar] [CrossRef]
- Secco, N.R.; Kenway, G.K.W.; He, P.; Mader, C.; Martins, J.R.R.A. Efficient Mesh Generation and Deformation for Aerodynamic Shape Optimization. AIAA J. 2021, 59, 1151–1168. [Google Scholar] [CrossRef]
- EL-Seesy, A.I.; Hassan, H. Investigation of the effect of adding graphene oxide, graphene nanoplatelet, and multiwalled carbon nanotube additives with n-butanol-Jatropha methyl ester on a diesel engine performance. Renew. Energy 2019, 132, 558–574. [Google Scholar] [CrossRef]
- Gray, J.S.; Hwang, J.T.; Martins, J.R.R.A.; Moore, K.T.; Naylor, B.A. OpenMDAO: An open-source framework for multidisciplinary design, analysis, and optimization. Struct. Multidiscip. Optim. 2019, 59, 1075–1104. [Google Scholar] [CrossRef]
- He, P.; Mader, C.A.; Martins, J.R.R.A.; Maki, K.J. DAFoam: An Open-Source Adjoint Framework for Multidisciplinary Design Optimization with OpenFOAM. AIAA J. 2020, 58, 1304–1319. [Google Scholar] [CrossRef]
- Sgueglia, A.; Schmollgruber, P.; Bartoli, N.; Benard, E.; Morlier, J.; Jasa, J.; Martins, J.R.R.A.; Hwang, J.T.; Gray, J.S. Multidisciplinary Design Optimization Framework with Coupled Derivative Computation for Hybrid Aircraft. J. Aircr. 2020, 57, 715–729. [Google Scholar] [CrossRef]
- Bons, N.P.; Martins, J.R.R.A.; Odaguil, F.I.K.; Cuco, A.P.C. Aerostructural Wing Optimization of a Regional Jet Considering Mission Fuel Burn. ASME Open J. Eng. 2022, 1, 011046. [Google Scholar] [CrossRef]
- Batay, S.; Baidullayeva, A.; Zhao, Y.; Wei, D.; Baigarina, A.; Sarsenov, E.; Shabdan, Y. Aerostructural Design Optimization of Wind Turbine Blades. Processes 2023, 12, 22. [Google Scholar] [CrossRef]
- Martins, J.R.R.A.; Marriage, C.; Tedford, N. pyMDO. ACM Trans. Math. Softw. 2009, 36, 1–25. [Google Scholar] [CrossRef]
- Lambe, A.B.; Martins, J.R.R.A. Extensions to the design structure matrix for the description of multidisciplinary design, analysis, and optimization processes. Struct. Multidiscip. Optim. 2012, 46, 273–284. [Google Scholar] [CrossRef]
- Hajdik, H.M.; Yildirim, A.; Wu, E.; Brelje, B.J.; Seraj, S.; Mangano, M.; Anibal, J.L.; Jonsson, E.; Adler, E.J.; Mader, C.A.; et al. pyGeo: A geometry package for multidisciplinary design optimization. J. Open Source Softw. 2023, 8, 5319. [Google Scholar] [CrossRef]
- Boopathy, K.; Kennedy, G.J. Parallel Finite Element Framework for Rotorcraft Multibody Dynamics and Discrete Adjoint Sensitivities. AIAA J. 2019, 57, 3159–3172. [Google Scholar] [CrossRef]
- Wu, E.; Kenway, G.; Mader, C.A.; Jasa, J.; Martins, J.R.R.A. pyOptSparse: A Python framework for large-scale constrained nonlinear optimization of sparse systems. J. Open Source Softw. 2020, 5, 2564. [Google Scholar] [CrossRef]
- Kenway, G.K.W.; Mader, C.A.; He, P.; Martins, J.R.R.A. Effective adjoint approaches for computational fluid dynamics. Prog. Aerosp. Sci. 2019, 110, 100542. [Google Scholar] [CrossRef]
- Balay, S.; Abhyankar, S.; Adams, M.; Brown, J.; Brune, P.; Buschelman, K.; Dalcin, L.; Dener, A.; Eijkhout, V.; Gropp, W.; et al. PETSc Users Manual; Revision 3.10; Argonne National Laboratory: Lemont, IL USA, 2018. [Google Scholar] [CrossRef]
- He, P.; Mader, C.A.; Martins, J.R.R.A.; Maki, K.J. An aerodynamic design optimization framework using a discrete adjoint approach with OpenFOAM. Comput. Fluids 2018, 168, 285–303. [Google Scholar] [CrossRef]
- Martins, J.R.R.A.; Hwang, J.T. Review and Unification of Methods for Computing Derivatives of Multidisciplinary Computational Models. AIAA J. 2013, 51, 2582–2599. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1992. [Google Scholar] [CrossRef]
- Krajnović, S. Large eddy simulation of flows around ground vehicles and other bluff bodies. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2009, 367, 2917–2930. [Google Scholar] [CrossRef] [PubMed]
- Krajnović, S.; Davidson, L. Flow Around a Simplified Car, Part 1: Large Eddy Simulation. J. Fluids Eng. 2005, 127, 907–918. [Google Scholar] [CrossRef]
- Walter, M.; Günter, B.; Aaron, R.; Bernhard, L.; Anton, F.; Penerbit, A.B. Experiments and numerical simulations on the aerodynamics of the Ahmed body. CFD Lett. 2011, 3, 32–39. [Google Scholar]
- Batay, S.; Kamalov, B.; Zhangaskanov, D.; Zhao, Y.; Wei, D.; Zhou, T.; Su, X. Adjoint-Based High-Fidelity Concurrent Aerodynamic Design Optimization of Wind Turbine. Fluids 2023, 8, 85. [Google Scholar] [CrossRef]
- Kenway, G.; Kennedy, G.; Martins, J. A CAD-Free Approach to High-Fidelity Aerostructural Optimization. In Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference, Fort Worth, TX, USA, 13–15 September 2010; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2010. [Google Scholar]
- Gill, P.; Murray, W.; Saunders, M. SNOPT: An SQP algorithm for large-scale constrained optimization. SIAM J. Optim. 2002, 12, 979–1006. [Google Scholar] [CrossRef]
- Hand, M.; Simms, D.; Fingersh, L.; Jager, D.; Cotrell, J.; Schreck, S.; Larwood, S. Unsteady Aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns; National Renewable Energy Laboratory: Golden, CO, USA, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
