Abstract
Stochastic equations of the hydrodynamic theory of plasma are presented in relation to strong external fields. It is shown that the use of these stochastic equations makes it possible to obtain new theoretical solutions for plasma as a result of its heating in a strong external electric field. Theoretical solutions for the conductivity of turbulent plasma when heated in an external electric field of 100 V/cm are considered. Calculated values for the electron drift velocity, electron mobility, electron collision frequency, and the Coulomb logarithm in the region of strong electric fields are obtained. Here we consider experiments on turbulent heating of hydrogen plasma in the range of electric field strength of 100 < E < 1000. The calculated dependences of plasma conductivity are in satisfactory agreement with experimental data for heating plasma in a strong electric field. It is shown that the plasma turbulence in the region of strong electric fields E ~1000 V/cm is close to 100%. For the first time, it is confirmed that the derived dependences for collision frequency, drift velocity, and other values include the degree of turbulence of plasma, which makes it possible to correctly describe experimental data for heating plasma even with strong electric fields. In addition, it was determined that the scatter of experimental data may be associated with the variability of the function in the expression for the heat flux density. For the first time, it is shown theoretically that the experimentally determined fact of the possibility of the existence of an approximate constancy of plasma conductivity in the region E = 100–1000 V/cm can occur with an error of ~30%. The results show significant advantages of the stochastic hydrodynamic plasma theory over other methods that are not yet able to satisfactorily as well as qualitatively and quantitatively predict long-known experimental data while taking into account the degree of turbulence.
1. Introduction
The stochastic equations of the hydrodynamic theory of plasma are presented in relation to strong external fields. The system of stochastic plasma equations is used for calculating the heating of turbulent hydrogen plasma in strong external electric fields. The problem of finding equations for solving the turbulence [1,2,3,4] is an important theoretical problem. The phenomenon of turbulence was tried to be solved using different ideas: (1) using the theory of attractors [5,6,7,8,9,10,11]; (2) on the basis of chaos theory [12,13]; (3) on the basis of the physics of nonlinear phenomena [14,15]; (4) on the basis of statistic theory [16,17,18,19,20,21,22,23,24]; (5) the theory of solitons [1]; (6) a quasi-periodic process [25,26,27,28]; (7) using the theory of self-organization [29,30]. Attempts to find solutions to this problem by numerical methods were made using DNS [31,32,33,34,35,36,37,38,39,40,41,42,43,44,45], LES, and RANS codes [46,47,48,49,50,51].
The processes of heating plasma by an electric field are connected with the turbulence in plasma [52,53,54,55,56,57,58,59,60,61,62,63]. The statistical theory of plasma physics [64,65,66,67,68,69,70] is used for describing these processes. But these processes can be determined using the theory of stochastic equations and equivalent measures [71,72,73]. In [74,75,76,77,78,79,80], the possibility of calculating critical Reynolds numbers was shown for isothermal flows [81,82,83,84,85,86] and for non-isothermal flows [87,88,89,90]. The profiles of averaged velocity and temperature were also determined in [91,92,93].The friction coefficients and heat transfer coefficients were obtained in [84,85]. Also, the second-order correlations were presented in [91,93,94,95,96,97,98]. The correlation dimension of the attractor in the boundary layer was calculated in [99,100]. The equation for the spectral function was shown in [101,102,103,104,105,106]. For non-isothermal flows, the Reynolds analogy was obtained in [104]. Then the formulas for friction coefficients on the wall of a flat plate and in a round tube during a laminar–turbulent transition [107,108] were derived.
2. Definition of Equivalence of Measures between Deterministic and Random Motions
It should be noted that the problem of transition from laminar to turbulent flow was discussed in [71,72,73,74,81,82,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108]. As a result, fluid and gas flows around a cylinder, as well as in the boundary layer on a sphere, on a flat plate, in a pipe, and in a jet, were studied on the basis of stochastic theory. It is also known that a statistical apparatus developed for a continuous medium [32,33,34,35] is used for the hydrodynamic description of the turbulent plasma motion [32,33,34,35]. Here, on the basis of stochastic equations and equivalence relations of measures [71,72,73] developed for the continuum, the new results for turbulent plasma motion are presented. The correlator DN,M was derived in [71,72,73,74,99,100,101,102,103,104]; see also [105,108] as the definition of equivalence of measures between laminar (deterministic) and turbulent (random) motions. The application of the correlator DN,M for solving equations for mass, motion, and energy leads to sets of stochastic equations for four space–time areas: (1) the onset of generation (subscript 1, 0, or 1); (2) the generation (subscript 1, 1); (3) the diffusion (subscript 1, 1, 1) and (4) the dissipation of the turbulent fields. In the critical point for the parameter and for each of four space–time regions of the correlator. The correlator [72,73,74,75,100,101,102,103,104,105] for the pair (M,N) = (1,0) gives the following equations , here“d” is the full differential. Then the correlator for the pair (M,N) = (1,1), gives the following equations: , . Here Φ is the substantial quantity {mass (density ρ), momentum (ρU), and energy (E)}. Here is the deterministic component (subscript cost) having the zero stochastic component of measure, is the stochastic component (subscript st), is the lifetime of , L = 2π/k, and k is the wave number. The subscripts “cr” or “c” refer to the critical point r (xcr, τcr) or rc. The critical point is the space–time point of the onset of the interaction between the deterministic and random motions, which leads to the turbulence. It is important to emphasize that one of the main differences between statistical and stochastic theory is the number of regions inspace–time. The statistic theory envelops only three space–time areas: (2) the generation; (3) the diffusion; and (4) the dissipation of turbulent fields [16,17,18,19,20,21,22,23,24].
3. Stochastic Equations for Plasma
In accordance with [71,72,73,83,84,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,104,105,106,107,108], the stochastic equations were obtained without external and internal forces. These forces are taken into account for the stochastic plasma equations in accordance with [52,53,54,55,56,57,58]:
α is the component of plasma (particles of class α, electron–ion liquid). The forces resulting from the action of normal stresses (pressure) and tangential stresses are written as and, then, it is possible to write that
Here, i, j, l = 1, 2, 3, the coefficients μ and are the dynamic and second viscosities, respectively. The values ui, uj, ul,xi, xj, xl are the velocities and coordinates corresponding to i, j, l. The Kronecker delta is δij = 1 for i = j, and δij = 0 for i ≠ j. is the sum of k external forces acting on particles of class «α» in the «i» direction. = , k = 1, 2, …, n; i = 1, 2, 3. For an electromagnetic field = .
In addition, are the internal (intercomponent or interphase) forces caused by the interaction of liquid components with each other. In the case of a heterogeneous mixture, these are the interphase forces; in the case of plasma, these are the forces caused by the collision of particles of various kinds with each other (subscript int): [53,54,55,56,57,65,69]. The force of relative friction, depending on the relative velocity of electrons and ions is and the thermal force: . Here , are the reduced particle mass, the effective temperature, and the collision frequency. The equation for the energy per unit volume of the plasma grade α components ( are the mass and concentration of particles).
Here . In addition, the work caused by the collision of particles of different sorts with each other is determined by the dependence [52,53,54,55,56,64,68]. The work of relative friction forces depending on the relative velocity of electrons and ions is . The work of the thermal force is [52,53,54,55,56,64,68]. The work of external forces acting on particles of class «α» in the «i» direction is = , is the braking radiation power per unit volume, is the particle energy. The written equations are defined as instantaneous provided that the hypothesis of plasma continuity is observed. At the same time, the direct consideration of equation for the collision frequencies of particles of the same grade and different grades among themselves determines, as is known, the limits of the hypothesis of continuity and the dualism when describing the motion of charged particles in plasma as a multicomponent fluid. This important aspect seems substantial for writing down the stochastic equations of conservation of plasma motion in an external electromagnetic field.
4. Equivalent Measures and Excitation of Plasma Turbulence by an Electric Field
In accordance with [72,73,74,75,100,101,102,103,104,105,106,107,108,109], for space–time area (1) of the onset of generation for a pair , the set of Equations (1)–(3) can be written as follows (see also [105,108]):
For the case under consideration, the expression for the stress tensor of the flow of electrons and ions is determined as well as the expression for the relative friction force between electrons and ions and the equations for thermal forces for each plasma component (electrons and ions [53,54,55,56,57]).
- (a)
- The stress tensor for the flow of electrons and ions [53,54,55,56,57,65,69]
- (b)
- The friction forces [53,54,55,56,57,65,69]:
- (c)
The thermal forces [53,54,55,56,57] are
The external forces are , where e is the elementary charge of electron, Z is the element number, and is the concentration of negative and positive particles. Here is the electron collision frequency, is the plasma frequency of electron oscillations taking into account the thermal motion , the thermal velocity of electrons is , is the termal energy and Coulomb logarithm is , ; [109,110,111,112,113,114,115,116,117,118].
- (d)
- For the energy equation, respectively, the work caused by the collision of particles of different sorts is and
The work caused by the external forces is
The equation for the heat flux is . For the flow electrons , δ [52,53,54,55,56,64,68]. The equation for the braking radiation power [J/(cm3)] [52,53,54,55,56,117].
It should be noted here that the speed of sound in plasma, as is known, is determined by the formula . Now it is possible to obtain theoretical equations for the critical value of external electrical field substituting the received expressions into the set of equations for the region of onset of turbulence. Here .
5. Plasma Conductivity
In accordance with the last set of Equation (15), for the electron flow with it can be written that
In the case of a plane directional motion Te = T0Tue = u0exp(−iwt + kr); ne = n0exp(−iwt + knr); and d(q)/dx = −3.16(n/mνe)Te2k2T, we have a parabolic equation, and for , the last equation can be written as
Let us consider two cases when: (1) the wave numbers
, so ;
Substituting the expression , we obtain:
Considering that and .
Here, are the electron thermal speed and electron drift speed
Here = 8.85*10−12 (C2/(N*m2)).
Let us introduce the notation
The third term is
Further, the value determined by Equation (24) is not taken into account due to Equation (17).
Thus, the first relation is obtained from the second equation of set (15)
Then, from the first equation of set , we obtain the following relations ( is the electron termal energy):
; is taking in accordance with [102] for the region of generation of turbulence:
Then, and, finally, + = .
Also, from the first equation of set , it is possible to obtain the following relations
Then, using Equation (27), it is possible to obtain the following relations:
It is easy to see that when , the stochastic energy equals to the thermal energy; then, and . For the wave number, we obtain
In Equations (17)–(29), . Here, 3; = /ωpe; ;;.
The value of critical electrical strength [67,68,69,70] may be obtained from Equation (17) as
Then, in according to Ohm’s law γ = j/E given that j = en in the general case, the conductivity is
Let us estimate an effect of on the electron conductivity. From data [119]: Te = 100 Ev, n = 1018, .
Therefore, this value is neglected further for the conditions of hydrogen plasma [118].
6. Comparison of Calculation Results with Experiments
Here, we present below the calculations for conductivity in plasma and for the value of the critical electrical field using the theory of stochastic equations and equivalence of measure. In Table 1, Table 2, Table 3 and Table 4, the results of the calculation are presented for the energy of electrons with densities n = 1018 m−3 and Te = 100–10,000 eV; is taken in accordance with Equation (27). For calculating the drift speed of electrons, we used Equations (28) and (29), for the wave number, Equation (25); for , Equations (17)–(26); and for conductivity, Equation (33) are used. Table 3 and Table 4 show the results of calculations according to the initial data indicated above in the tables and the sequence of calculations according to points (1)–(9).The presented algorithm for calculating the electronic conductivity for hydrogen-plasma experiments is based on the theoretical solution of stochastic equations for turbulent plasma.

Table 1.
.

Table 2.
.

Table 3.
Results of calculation of the electronic conductivity for data [118]: n = 1018 [m−3]; ; Te = 100 Ev(160−19 J) ; rd = ᶹpe/ωpe; rs = 0.18*10−9 [m]; ᶹpe = 4.193*106 [m/c], .

Table 4.
Results of calculation of the electronic conductivity for data [118]: n = 1018 [m−3]; ; Te = 10,000 Ev(160−19 J); rd = ᶹpe/ωpe; rs = 0.18 × 10−11 [m]; ᶹpe = 4.193 × 107 [m/c], .
- (1)
- (2)
- − = 1.967106 [m/c]
- (3)
- = 7.74; = /ωpe = 3.506*10−5; rd/rs = 41.52*104; ()3 = 1040.9439.69 = 3.272105 [c−1]
- (4)
- ;
- (5)
- ; ;
- (6)
- = 3.67 + 76.176 − 76.176 [B/m]
- (7)
- = 9669.56 [V/m]
- (8)
- + = 11,044.19 [V/m] = [110.44] [V/cm]
- (9)
- [1/(Om*m)]
In CGSE 9 * 109 = 0.26 * 1012 [c−1]
- (1)
- (2)
- − = 107 [m/c]=
- (3)
- = /ωpe = 1.996*10−4; rd/rs = 4.149*108;()3 = = 2.7489431852103 [c−1]
- (4)
- ;
- (5)
- ; ;
- (6)
- = |0.187 + + * 1.018 = 1033.87 [B/m]
- (7)
- = 66,050.8 [V/m]
- (8)
- + 66,050.8 = 67,084.6703 [V/m] = [671.72] [V/cm]
- (9)
- [1/(Om*m)]
In CGSE 9 * 109 = 0.24 * 1012 [c−1]
7. Discussion
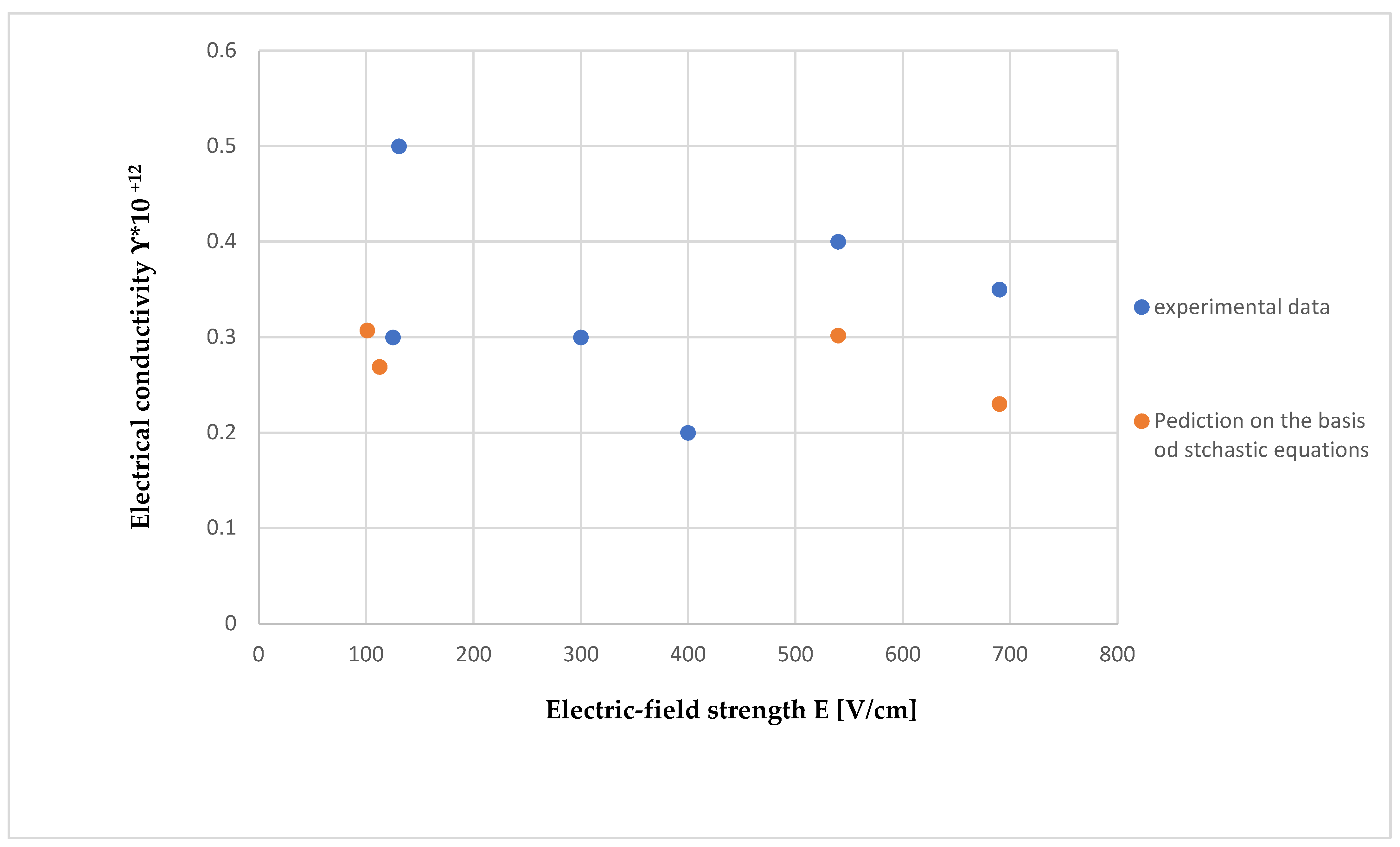
The authors of [118] showed the results for strong electric fields E from 100 to 700 V/cm. As can be seen, the predicted results presented in Figure 1 are consistent with experimental data [118] for this electric field region.
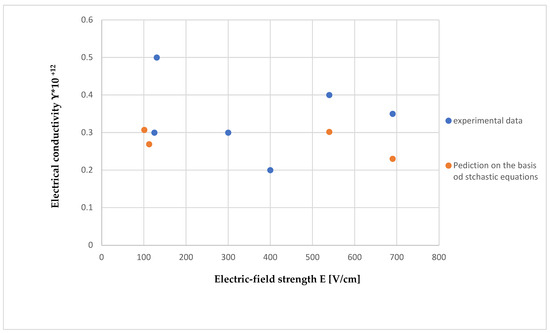
Figure 1.
Plasma conductivity as a function of electric-field strength for hydrogen according to data [118].
Also, the presented results of calculations based on the stochastic equations confirm that there is an electric-field region with approximately constant conductivity of ~30%. That is, in the equivalence region, there is a distribution corresponding to the experimentally determined in [118] for 100 < E < 700 V/cm.
This is the second region with approximately constant conductivity. This region was first experimentally determined in [118]. In this study, the measurements were carried out in a wide range of electric-field strength of 0.5 < E < 700 V/cm, while, in the region of 0.5 < E < 90 V/cm, there were only three measurements. Nevertheless, the authors of [118] confirmed the presence of a region with a constant conductivity in the range of 0.2 < E < 20 V/cm with a subsequent decrease in conductivity down to the voltage E = 100, which was first determined in [119].
The conductivity and current of a non-turbulent plasma are determined by well-known ratios: ; , ; the formula for the conductivity is = . The mobility of electrons is = . The known formula for the collision frequency includes . The calculations show that the value of the thermal velocity in the case of the plasma turbulence gives no correct magnitudes of electrical conductivity of the turbulent plasma. Thus, it is important to calculate the effective collision frequency . The solutions of stochastic equations enabled us to derive the formula for the drift velocity (see Equation (24)) . Then it is possible writing ; , ; here, the mobility of electrons is = and the formula for the conductivity is = . It is easy to see that, now, the drift velocity of a turbulent plasma depends also on the intensity of plasma turbulence, its temperature (thermal energy), and the scale of turbulence of the turbulent plasma flow, instead of only on the frequency of collisions of electrons . New Formulas (29) and (30) may be converted into Equation (33) for a classical neutral plasma with Langrumov inhomogeneity. The calculations of each of the motion components depending on the external field are presented as . Here is the value of the electric-field strength corresponding to the force of relative friction dependent on the relative velocity of electrons and ions . is the value of the electric field strength, corresponding to the gas pressure of telectrons and ions. Here is the value of the electric field strength corresponding to the voltage tensor caused by the viscosity of the flow of electrons and plasma ions. The value of is the electric-field strength corresponding to the thermal force, and is the electric-field strength corresponding to the heat flow. Table 3 and Table 4 show that . The obtained Formulas (17)–(33) for the Coulomb logarithm, the wave number (turbulence scale), the collision frequency, the current, and the drift velocity enable us to achieve agreement between the predicted and experimental data for the conductivity j of turbulent plasma in a strong electric field of 100 < E < 1000 V/cm. The development of the theory for calculating plasma heating was undertaken in [120,121,122,123,124,125,126,127,128].
It should be noted that, for the data of the experiments [118], no calculations with using the theory of ion-sound instability are known in the literature. Nevertheless, even if there are results of prediction using the theory of ion–sound instability, it only means that there are currently several theoretical tools, one of which is presented in this article and represents the stochastic theory of turbulent plasma.
It should also be noted that, usually, the Boltzmann equation with the Fokker–Planck collision term takes into consideration only a dynamical frictional force coming from the many-body collisions through the Coulomb force [128]. In [129], the electron transport under the effect of two kinds of friction in an electron–deuteron plasma was discussed. Equations (31) and (32) present new formulas for the value of the critical electric field strength. We also mention data from [130,131,132].
8. Conclusions
The obtained results show that the stochastic turbulence theory based on stochastic differential equations and equivalence of measures between deterministic and random fields is valid also for the turbulent plasma during heating by the strong electric field {Equations (1)–(15)}. It is shown that, after the onset of plasma turbulence, the existing experimental data have a certain spread of ~30% for a strong electric field of 100 < E < 1000 V/cm; see data in [118] and Figure 1. The energy balance was discussed for the plasma with the temperature Te~10,000 Ev in the region of the external strong electric field of 100 < E < 1000 V/cm. It is theoretically shown that the energy of the external electric field compensates also the energy costs due to heat flux E3 and the total shear-stress tensor of the plasma particles E2, which are the functions of the collision integral, instead of only the energy costs due to the forces between the particles E1. Thus, the plasma becomes more turbulent with constant conductivity, and a plateau is formed even in the region of the external strong electric field of 100 < E < 1000 V/cm. It is theoretically determined that, starting from a voltage of about 100 V/cm, the plateau exists, and the energy of the deterministic field continues to pass mainly only into a random turbulent field.
In addition, on the basis of stochastic equations for the experimental values of electron density and temperature, the plasma current, and conductivity, we theoretically determined also the drift velocity, collision frequency, Coulomb interval, and the wave number (turbulence scale). Besides, we determined theoretically the level of turbulence of plasma for electrical field E = 100 V/cm and for electric field E = 700 V/cm.
As a result, the correct application of stochastic theory in the range of 100–1000 V/cm was confirmed. It should be noted that both the development of stochastic theory for plasma and the theoretical tool is proposed for the calculation of turbulent heating by the strong electric field in the range of 100 < E < 1000 V/cm. Stochastic theory for plasma processes can apparently lead to the development of tools for the numerical methodology [102,106,107] of direct theoretical–numerical simulation.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The author declares no conflict of interest.
References
- Sreenivasan, K.R. Fractals and multifractals in fluid turbulence. Ann. Rev. Fluid Mech. 1991, 23, 539–600. [Google Scholar] [CrossRef]
- Ladyzhenskaya, O.A. On a dynamical system generated by Navier–Stokes equations. J. Sov. Math. 1975, 3, 458–479. [Google Scholar] [CrossRef]
- Vishik, M.I.; Komech, A.I. Kolmogorov equations corresponding to a two-dimensional stochastic Navier–Stokes system. Tr. Mosk. Mat. Obs. 1983, 46, 3–43. [Google Scholar]
- Samarskii, A.A.; Mazhukin, V.I.; Matus, P.P.; Mikhailik, I.A. Z/2 conservative schemes for the Korteweg–de Vries equations. Dokl. Akad. Nauk. 1997, 357, 458–461. [Google Scholar]
- Ruelle, D.; Takens, F. On the nature of turbulence. Commun. Math. Phys. 1971, 20, 167–192. [Google Scholar] [CrossRef]
- Packard, N.H.; Crutchfield, J.P.; Farmer, J.D.; Shaw, R.S. Geometry from a time series. Phys. Rev. Lett. 1980, 45, 712–715. [Google Scholar] [CrossRef]
- Malraison, B.; Berge, P.; Dubois, M. Dimension of strange attractors: An experimental determination for the chaotic regime of two convective systems. J. Phys. Lett. 1983, 44, L897–L902. [Google Scholar] [CrossRef]
- Procaccia, I.; Grassberger, P. Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 1983, 28, 2591–2593. [Google Scholar]
- Constantin, P.; Foais, C.; Temam, R. On dimensions of the attractors in two-dimensional turbulence. Phys. D 1988, 30, 284–296. [Google Scholar] [CrossRef]
- Grassberger, P.; Procaccia, I. Dimensions and entropies of strange attractors from a fluctuating dynamics approach. Phys. D Nonlinear Phenom. 1984, 13, 34–54. [Google Scholar] [CrossRef]
- Kozlov, V.V.; Rabinovich, M.I.; Ramazanov, M.P.; Reiman, A.M.; Sushchik, M.M. Correlation dimension of the flow and spatial development of dynamic chaos in the boundary layer. JETP Lett. 1987, 13, 987. [Google Scholar]
- Haller, G. Chaos near Resonance; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar] [CrossRef]
- Brandstater, A.; Swift, J.; Swinney, H.L.; Wolf, A.; Farmer, D.J.; Jen, E.; Crutchfield, P.J. Low-dimensional chaos in hydrodynamic system. Phys. Rev. Lett. 1983, 51, 1442–1446. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Feigenbaum, M. The transition to aperiodic behavior in turbulent sets. Commun. Math. Phys. 1980, 77, 65–86. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Mathematical models of turbulent motion of an incompressible viscous fluid. Usp. Mat. Nauk. 2004, 59, 5–10. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. About the entropy per time unit as a metric invariant of automorphisms. Dokl. Akad. Nauk SSSR 1958, 124, 754–755. [Google Scholar]
- Taylor, G.A. Statistical theory of turbulence. Proc. R. Soc. Lond. A 1935, 151, 421–444. [Google Scholar] [CrossRef]
- Hinze, J.O. Turbulence, 2nd ed.; McGraw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Schlichting, H. Boundary-Layer Theory, 6th ed.; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Dmitrenko, A.V. Fundamentals of heat and mass transfer and hydrodynamics of single-phase and two-phase media. In Criterial Integral Statistical Methods and Direct Numerical Simulation; Galleya Print: Moscow, Russia, 2008; 254p, Available online: http://search.rsl.ru/ru/catalog/record/6633402 (accessed on 10 April 2024).
- Dmitrenko, A.V. Heat and mass transfer in combustion chamber using a second-moment turbulence closure including an influence coefficient of the density fluctuation in film cooling conditions. In Proceedings of the 34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA Paper 98-3444, Cleveland, OH, USA, 13–15 July 1998. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Nonselfsimilarity of a boundary-layer flow of a high-temperature gas in a Laval nozzle. Aviats. Tekh. 1993, 1, 39–42. [Google Scholar]
- Monin, A.S.; Yaglom, A.M. Statistical Fluid Mechanics; MIT Press: Cambridge, MA, USA, 1971. [Google Scholar]
- Landau, L.D. Toward the problem of turbulence. Dokl. Akad. Nauk SSSR 1944, 44, 339–342. [Google Scholar]
- Landau, L.D.; Lifshits, E.F. Fluid Mechanics; Perg. Press Oxford: London, UK, 1959. [Google Scholar]
- Kolmogorov, A.N. Dissipation of energy in locally isotropic turbulence. Dokl. Akad. Nauk SSSR 1941, 32, 16–18. [Google Scholar]
- Kolmogorov, A.N. A new metric invariant of transitive dynamic sets and automorphisms of the Lebesgue spaces. Dokl. Akad. Nauk SSSR 1958, 119, 861–864. [Google Scholar]
- Klimontovich, Y.L. Problems of the statistical theory of open sets: Criteria of the relative degree of the ordering of states in the self-organization processes. Usp. Fiz. Nauk. 1989, 158, 59–91. [Google Scholar] [CrossRef]
- Struminskii, V.V. Origination of turbulence. Dokl. Akad. Nauk SSSR 1989, 307, 564–567. [Google Scholar]
- Mayer, C.S.J.; von Terzi, D.A.; Fasel, H.F. Direct numerical simulation of investigation of complete transition to turbulence via oblique breakdown at Mach 3. J. Fluid Mech. 2011, 674, 5–42. [Google Scholar] [CrossRef]
- Ma, Y.; Zu, J. The simulation of canopy fabric air permeability’s influence on the round parachute during the landing process. In Proceedings of the 2015 International Industrial Informatics and Computer Engineering, Xi’an, China, 10–11 January 2015; pp. 2156–2159. [Google Scholar]
- Content, C.; Houdeville, R. Application of the g-R laminar-turbulent transition model in Navier-Stokes computations. In Proceedings of the AIAA 40 Fluid Dynamics, Chicago, IL, USA, 28 June 2010. [Google Scholar]
- Orzag, S.A.; Kells, L.C. Transition to turbulence in plane Poiseuille and plane Couette flow. J. Fluid Mech. 1980, 96, 159–205. [Google Scholar] [CrossRef]
- Goldstein, M.E. Effect of free-stream turbulence on boundary layer transition. Philos. Trans. R. Soc. A 2014, 372, 20130354. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 102, 16–42. [Google Scholar] [CrossRef]
- Visbal, M.R.; Gaitonde, D.V. On the use of high-order finite-difference schemes on curvilinear and deforming meshes. J. Comput. Phys. V 2002, 181, 155–185. [Google Scholar] [CrossRef]
- Mardsen, O.; Bogey, C.; Bailly, C. High-order curvilinear simulations of flows around non-cartesian bodies. J. Comput. Acoust. V 2005, 13, 731–748. [Google Scholar]
- Tam, C.K.W.; Ju, H. Numerical simulation of the generation of airfoil tones at a moderate Reynolds number. In Proceedings of the 12th AIAA/CEAS Aeroacoustics Conference, Cambridge, MA, USA, 8–10 May 2006; 23p. [Google Scholar]
- Yee, H.C.; Sandham, N.D.; Djomehri, M.J. Low dissipation high order shock-capturing methods using characteristic-based filters. J. Comput. Phys. 1999, 150, 199–238. [Google Scholar] [CrossRef]
- Desquenes, G.; Terracol, M.; Sagaut, P. Numerical investigation of the tone noise mechanism over laminar airfoils. J. Fluid Mech. 2007, 591, 155–182. [Google Scholar] [CrossRef]
- Chuvakhov, P.V.; Fedorov, A.V.; Obraz, A.O. Numerical simulation of turbulent spots generated by unstable wave packets in a hypersonic boundary layer. Comput. Fluids 2018, 162, 26–38. [Google Scholar] [CrossRef]
- Salwen, H.; Cotton, F.W.; Grosch, C.E. Linear stability of Poiseuille flow in a circular pipe. J. Fluid Mech. 1980, 98, 273–284. [Google Scholar] [CrossRef]
- Priymak, V.G. Splitting dynamics of coherent structures in a transitional round-pipe flow. Dokl. Phys. 2013, 58, 457–465. [Google Scholar] [CrossRef]
- Newton, P.K. The fate of random initial vorticity distributions for two-dimensional Euler equations on a sphere. J. Fluid Mech. 2016, 786, 1–4. [Google Scholar] [CrossRef]
- Tutt, B.; Charles, R.; Roland, S.; Noetscher, G. Development of parachute simulation techniques in LS-DYNA. In Proceedings of the 11th International LS-DYNA Users Conference, Detroit, MI, USA, 9–11 May 2017; pp. 19–25. [Google Scholar]
- Dmitrenko, A.V. Calculation of the boundary layer of a two-phase medium. High Temp. 2002, 40, 706–715. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Heat and mass transfer and friction in injection to a supersonic region of the Laval nozzle. Heat Transf. Res. 2000, 31, 338–399. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Film cooling in nozzles with large geometric expansion using method of integral relation and second moment closure model for turbulence. In Proceedings of the 33th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, AIAA Paper 97-2911. Seattle, WA, USA, 6–9 July 1997. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Computational investigations of a turbulent thermal boundary layer in the presence of external flow pulsations. In Proceedings of the 11th Conference on Young Scientists, Moscow, Russia, 10 November 1986; Part 2. Physicotechnical Institute: Moscow, Russia, 1986; pp. 48–52, Deposited at VINITI 08.08.86, No. 5698-B8. [Google Scholar]
- Dmitrenko, A.V. Calculation of pressure pulsations for a turbulent heterogeneous medium. Dokl. Phys. 2007, 52, 384–387. [Google Scholar] [CrossRef]
- Dodin, I.Y. Quasilinear theory for inhomogeneous plasma. J. Plasma Phys. 2022, 88, 905880407. [Google Scholar] [CrossRef]
- Joglekar, A.S.; Thomas, A.G.R. Unsupervised discovery of nonlinear plasma physics using differentiable kinetic simulations. J. Plasma Phys. 2022, 88, 905880608. [Google Scholar] [CrossRef]
- Rogister, A.; Oberman, C. On the kinetic theory of stable and weakly unstable plasma. Part 1. J. Plasma Phys. 1968, 2, 33. [Google Scholar] [CrossRef]
- Rogister, A.; Oberman, C. On the kinetic theory of stable and weakly unstable plasma. Part 2. J. Plasma Phys. 1969, 3, 119. [Google Scholar] [CrossRef]
- Besse, N.; Elskens, Y.; Escande, D.F.; Bertrand, P. Validity of quasilinear theory: Refutations and new numerical confirmation. Plasma Phys. Control. Fusion 2011, 53, 025012. [Google Scholar] [CrossRef]
- Chernyshov, A.; Karelsky, K.V.; Petrosyan, A.S. Three-dimensional modeling of compressible magnetohydrodynamic turbulence in the local interstellar medium. Astrophys. J. 2008, 686, 1137. [Google Scholar] [CrossRef]
- Miesch, M.S.; Matthaeus, W.H.; Brandenburg, A.; Petrosyan, A.; Pouquet, A.; Cambon, C.; Jenko, F.; Uzdensky, D.; Stone, J.; Tobias, S.; et al. Large-Eddy Simulations of Magnetohydrodynamic Turbulence in Heliophysics and Astrophysics. Space Sci. Rev. 2015, 194, 97. [Google Scholar] [CrossRef]
- Petrosyan, A.; Balogh, A.; Goldstein, M.L.; Léorat, J.; Marsch, E.; Petrovay, K.; Roberts, B.; von Steiger, R.; Vial, J.C. Turbulence in the Solar Atmosphere and Solar Wind. Space Sci. Rev. 2010, 156, 135–238. [Google Scholar] [CrossRef]
- Petrosyan, A.; Galperin, B.; Larsen, S.E.; Lewis, S.R.; Määttänen, A.; Read, P.L.; Renno, N.; Rogberg, L.P.H.T.; Savijärvi, H.; Siili, T.; et al. The Martian Atmospheric Boundary Layer. Rev. Geophys. 2011, 49, RG3005. [Google Scholar] [CrossRef]
- Chernyshov, A.A.; Karelsky, K.V.; Petrosyan, A.S. Subgrid-scale modeling for the study of compressible magnetohydrodynamic turbulence in space plasmas. Phys. Usp. 2014, 57, 421–452. [Google Scholar] [CrossRef]
- Smolyakov, A.; Zintel, T.; Couedel, L.; Sydorenko, D.; Umnov, A.; Sorokina, E.; Marusov, N. Anomalous Electron Transport in One-Dimensional ElectronCyclotron Drift Turbulence. Plasma Phys. Rep. 2020, 46, 408–418. [Google Scholar] [CrossRef]
- Benyahia, A.; Castillon, L.; Houdeville, R. Prediction of separation-induced transition on high lift low pressure turbine blade. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, Canada, 6–10 June 2011; ASME: The American Society of Mechanical Engineers: New York, NY, USA, 2011; pp. 1835–1846. [Google Scholar]
- Artsimovich, L.A.; Sagdeev, R.G. Plasma Physics for Physicists; Atomizdat Publisher: Moscow, Russia, 1979; p. 318. (In Russian) [Google Scholar]
- Hansen, J.-P.; McDonald, I.R. Theory of Simple Liquids; Elsevier: London, UK, 2006; 416p. [Google Scholar]
- Freidberg, J. Plasma Physics and Fusion Energy; Cambridge University Press: Cambridge, UK, 2007; p. 666. ISBN 139780521851077. [Google Scholar]
- Bittencourt, J.A. Fundamentals of Plasma Physics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2004; p. 378. [Google Scholar]
- Tsytovich, V.N. Theory of Turbulent Plasma, 1st ed.; Springer: New York, NY, USA, 1977; p. 535. ISBN 978-0-306-10894-5. [Google Scholar]
- Golant, V.E.; Zhilinsky, A.P.; Sakharov, I.E. Fundamentals of Plasma Physics; John Wiley & Sons: Hoboken, NJ, USA, 1980; 405p. [Google Scholar]
- Tsytovich, V.N. Development of the concepts of plasma turbulence. Phys. Usp. 1973, 15, 632–650. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Equivalence of measures and stochastic equations for turbulent flows. Dokl. Phys. 2013, 58, 228–235. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Regular Coupling between Deterministic (Laminar) and Random (Turbulent) Motions-Equivalence of Measures. Sci. Discov. Diploma 2013. [Google Scholar]
- Dmitrenko, A.V. Theory of Equivalent Measures and Sets with Repeating Denumerable Fractal Elements. In Stochastic Thermodynamics and Turbulence Determinacy–Randomness Correlator; Galleya-Print: Moscow, Russia, 2013; Available online: https://search.rsl.ru/ru/record/01006633402 (accessed on 10 April 2024). (In Russian)
- Mataoui, A.; Schiestel, R.; Salem, A. Study of the oscillatory regime of a turbulent plane jet impinging in a rectangular cavity. Appl. Math. Model. 2003, 27, 89–114. [Google Scholar] [CrossRef]
- Saiyed, N.H.; Mikkelsen, K.L.; Bridges, J.E. Acoustics and thrust of quiet separate-fow high-bypass-ratio nozzles. AIAA J. 2003, 41, 372–378. [Google Scholar] [CrossRef]
- Alkislar, M.B.; Krothapalli, A.; Choutapalli, I.; Lourenco, L. Structure of supersonic twin jets. AIAA J. 2005, 43, 2309–2318. [Google Scholar] [CrossRef]
- Kompenhans, J.; Arnott, A.; Agos, A.; Gilliot, A.; Monnier, J.C. Application of PIV for the investigation of high speed fow felds. In West East High Speed Flow Field; Artes Gráfcas Torres, S.A.: Barcelona, Spain, 2002; pp. 39–52. [Google Scholar]
- Knob, M.; Safarik, P.; Uruba, V. The efect of the side walls on a two-dimensional impinging jet. In Proceedings of the 16th International Symposium on Transport Phenomena, Prague, Czech, 29 August–3 September 2005; Available online: http://fuids.fs.cvut.cz/akce/konference/istp_2005/full/168.pdf (accessed on 10 April 2024).
- Suzuki, T.; Colonius, T. Instability waves in a subsonic round jet detected using a near-feld phased microphone array. J. Fluid Mech. 2006, 565, 197–226. [Google Scholar] [CrossRef]
- Kopiev, V.F.; Zaitsev, M.Y.; Chernyshev, S.A.; Ostrikov, N.N. Vortex ring input in subsonic jet noise. Int. J. Aeroacoust 2007, 6, 375–405. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Some analytical results of the theory of equivalence measures and stochastic theory of turbulence for nonisothermal flows. Adv. Stud. Theor. Phys. 2014, 8, 1101–1111. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Determination of critical Reynolds numbers for non-isothermal flows using stochastic theory of turbulence and equivalent measures. Heat Transf. Res. 2016, 47, 41–48. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. The theory of equivalence measures and stochastic theory of turbulence for non-isothermal flow on the flat plate. Int. J. Fluid Mech. Res. 2016, 43, 182–187. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Analytical estimation of velocity and temperature fields in a circular tube on the basis of stochastic equations and equivalence of measures. J. Eng. Phys. Thermophys. 2015, 88, 1569–1576. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. An estimation of turbulent vector fields, spectral and correlation functions depending on initial turbulence based on stochastic equations. The Landau fractal equation. Int. Fluid Mech. Res. 2016, 43, 82–91. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Stochastic equations for continuum and determination of hydraulic drag coefficients for smooth flat plate and smooth round tube with taking into account intensity and scale of turbulent flow. Contin. Mech. Thermodyn. 2017, 29, 1–9. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Analytical determination of the heat transfer coefficient for gas, liquid and liquidmetal flows in the tube based on stochastic equations and equivalence of measures for continuum. Contin. Mech. Thermodyn. 2017, 29, 1197–1205. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Determination of the coefficients of heat transfer and friction in supercritical-pressure nuclear reactors with account of the intensity and scale of flow turbulence on the basis of the theory of stochastic equations and equivalence of measures. J. Eng. Phys. Thermophys. 2017, 90, 1288–1294. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Analytical estimates of critical Taylor number for motion between rotating coaxial cylinders based ontheory of stochastic equations and equivalence of measures. Fluids 2021, 6, 306. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Results of investigations of non-isothermal turbulent flows based on stochastic equations of the continuum and equivalence of measures. IOP Conf. Ser. J. Phys. Conf. Ser. 2018, 1009, 012017. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. The stochastic theory of the turbulence. IOP Conf. Ser. Mater. Sci. Eng. 2018, 468, 012021. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Determination of the correlation dimension of an attractor in a pipe based on the theory of stochastic equations and equivalence of measures. J. Phys. Conf. Ser. 2019, 1250, 012001. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. The construction of the portrait of the correlation dimension of an attractor in the boundary layer of Earth’s atmosphere. J. Phys. Conf. Ser. 2019, 1337, 012006. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. The correlation dimension of an attractor determined on the base of the theory of equivalence of measures and stochastic equations for continuum. Contin. Mech. Therm. 2020, 32, 63–74. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. The possibility of using low-potential heat based on the organicRankine cycle and determination of hydraulic characteristics of industrial units based on the theory of stochastic equations. JP J. Heat Mass Transfer. 2020, 21, 125–132. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. The theoretical solution for the Reynolds analogy based on the stochastic theory of turbulence. JP J. Heat Mass Transfer. 2019, 18, 463–476. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Reynolds Analogy Based on the Theory of Stochastic Equations and Equivalence of Measures. J. Eng. Phys. Thermophy. 2021, 94, 186–193. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Formation of the turbulence spectrum in the inertial interval on the basis of the theory of stochastic equations and equivalence of measures. J. Eng. Phys. Thermophys. 2020, 93, 122–127. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. The Spectrum of the turbulence based on theory of stochastic equations and equivalence of measures. J. Phys. Conf. Ser. 2020, 1705, 012021. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Theoretical solutions for spectral function of the turbulent medium based on the stochastic equations and equivalence of measures. Contin. Mech. Thermod. 2021, 33, 603–610. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Some aspects of the formation of the spectrum of atmospheric turbulence. JP J. Heat Mass Transf. 2020, 19, 201–208. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Uncertainty relation in turbulent shear flow based on stochastic equations of the continuum and the equivalence of measures. Contin. Mech. Thermod. 2020, 32, 161–171. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Determination of critical Reynolds number in the jet based on the theory of stochastic equations and equivalence of measures. J. Phys. Conf. Ser. 2020, 1705, 012015. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. An estimation of the velocity profile for the laminar-turbulent transition in the plane jet on the basis of the theory of stochastic equations and equivalence of measures. Adv. Aerodyn. 2022, 4, 40. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Determination of Critical Reynolds Number for the Flow Near a Rotating Disk on the Basis of the Theory of Stochastic Equations and Equivalence of Measures. Fluids 2021, 6, 5. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Theoretical calculation of laminar–turbulent transition in the round tube on the basis of stochastic theory of turbulence and equivalence of measures. Contin. Mech Thermodyn. 2022, 34, 1375–1392. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Prediction of laminar–turbulent transition on flat plate on the basis of stochastic theory of turbulence and equivalence of measures. Contin. Mech. Thermodyn. 2022, 34, 601–615. [Google Scholar] [CrossRef]
- Dmitrenko, A.V. Theoretical Estimates of the Critical Reynolds Number in the Flow around the Sphere on the Basis of Theory of Stochastic Equations and Equivalence of Measures. Fluids 2023, 8, 81. [Google Scholar] [CrossRef]
- Ivlev, A.; Lowen, H.; Morfill, G.; Royall, C.P. Complex Plasmas and Colloidal Dispersions: Particle-Resolved Studies of Classical Liquids and Solids; Series in Soft Condensed Matter; World Scientific: Singapore, 2012; Volume 5. [Google Scholar]
- Belashov, V.Y.; Vladimirov, S.V. Solitary Waves in Dispersive Complex Media. Theory Simulation Applications; Springer: Berlin/Heidelberg, Germany, 2005; 292p. [Google Scholar]
- Dudoladov, S.O.; Larionov, N.V. The condition for application of the Crocco integral in the mathematical description of a laser welding plasma plume. St. Petersburg Polytech. Univ. J. Phys. Math. 2021, 14, 60–75. [Google Scholar]
- Wesson, J. Tokamaks, 4th ed.; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Stejner, M.; Salewski, M.; Korsholm, S.B.; Bindslev, H.; Delabie, E.; Leipold, F.; Meo, F.; Michelsen, P.K.; Moseev, D.; Nielsen, S.K.; et al. Measurements of ion temperature and plasma hydrogenic composition by collective Thomson scattering in neutral beam heated discharges at TEXTOR. Plasma Phys. Control. Fusion 2013, 55, 085002. [Google Scholar] [CrossRef]
- Valinurov, M.A.; Gavrikov, A.V.; Liziakin, G.D.; Oiler, A.P.; Timirkhanov, R.A. Plasma Potential Fluctuations in a Reflex Discharge with Thermionic Cathode. Plasma Phys. Rep. 2023, 49, 649. [Google Scholar] [CrossRef]
- Akishev Yu, S.; Alekseeva, T.; Karalnik, V.; Petryakov, A. Phenomenology of High-Current Discharge in N2 and He at Medium Pressures between Two Electrodes of Rail Geometry. Plasma Phys. Rep. 2023, 49, 549. [Google Scholar] [CrossRef]
- Schweitzer, F. Brownian Agents and Active Particles: Collective Dynamics in the Natural and Social Sciences; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Longair Malcolm, S. High Energy Astrophysics; Cambridge University Press: Cambridge, UK, 1994; pp. xv–xvi. [Google Scholar] [CrossRef]
- Hamberger, S.M.; Friedman, M. Electrical conductivity of a highly turbulent plasma. Phys. Rev. Lett. 1968, 21, 674–676. [Google Scholar] [CrossRef]
- Fanchenko, S.D.; Demidov, A.; Elagin, N.I.; Ryutov, D.D. Anomalous Resistance and Microwave Radiation from a Plasma in a Strong Electric Field. Sov. Phys. JETP 1964, 19, 337. [Google Scholar]
- Zavoiski, E.K.; Rydakov, L.I. Turbulent plasma heating. Sov. At. Energy 1967, 23, 1171–1186. [Google Scholar] [CrossRef]
- Braginskii, V.B.; Manukin, Z. Ponderomotive Effects of Electromagnetic Radiation. Sov. Phys. JETP 1967, 25, 653. [Google Scholar]
- Shapiro, V.E. Ponderomotive Effects of Electromagnetic Radiation. Sov. Phys.-Tech. Phys. 1969, 28, 301. [Google Scholar]
- Burdakov, A.V.; Arzhannikov, A.V.; Astrelin, V.T.; Ivanov, I.A.; Ivantsivsky, M.V.; Koidan, V.S.; Mekler, K.I.; Polosatkin, S.V.; Postupaev, V.V.; Rovenskikh, A.F.; et al. Fast heating of ions in GOL-3 multiple mirror trap. In Proceedings of the 31th European Physical Society Conference on Plasma Physics, London, UK, 28 June–2 July 2004. [Google Scholar]
- Bobylev, A.V.; Bychenkov VYu Potapenko, I.F. Numerical and analytical study of the electron heating by plasma. Plasma Waves 2017. [Google Scholar] [CrossRef]
- Astrelin, V.T.; Burdakov, A.V.; Kozlinskaya, T.V. Numerical Simulation of Plasma Dynamics in a Nonuniform Magnetic Field. J. App. Mech. Technol. 2006, 47, 27–35. [Google Scholar] [CrossRef]
- Sun, X.; Yang, M.; Chai, S.; Li, H. Fluid Simulation of the Plasma Characteristics in an Inductively Coupled Plasma Source with Planar and Cylindrical Coils. Plasma Phys. Rep. 2023, 49, 491–501. [Google Scholar] [CrossRef]
- Fedotova, M.A.; Klimchakova, D.A.; Petrosyan, A.S. Wave Processes in Plasma Astrophysics. Plasma Phys. Rep. 2023, 49, 303–350. Available online: https://link.springer.com/content/pdf/10.1134/S1063780X22601900.pdf?pdf=core (accessed on 10 April 2024).
- Dreicer, H. Electron and Ion Runaway in a Fully Ionized Gas. I Phys. Rev. 1959, 115, 238. [Google Scholar] [CrossRef]
- Nagata, M. Electron Transport under the Influence of Two Kinds of Friction in an Electron-Deuteron Plasma. J. Mod. Phys. 2020, 11, 1111108. [Google Scholar] [CrossRef]
- Shao, Z.Q. Global structure stability of Riemann solutions for linearly degenerate hyperbolic conservation laws under small BV perturbations of the initial data. Nonlinear Anal. Real World Appl. 2010, 11, 3791–3808. [Google Scholar] [CrossRef]
- Flamarion, M.V.; Gao, T.; Ribeiro, R., Jr. An investigation of the flow structure beneath solitary waves with constant vorticity on a conducting fluid under normal electric fields. Phys. Fluids 2023, 35, 037118. [Google Scholar] [CrossRef]
- Ghany, H.A. Exact Solutions for Stochastic Generalized Hirota-Satsuma Coupled KdV Equations. Chin. J. Phys. 2011, 49, 926–940. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).