Abstract
Stratified Taylor–Couette flow (STCF) undergoes transient growth. Recent studies have shown that there exists transient amplification in the linear regime of counter-rotating STCF. The kinetic budget of the optimal transient perturbation is analysed numerically to simulate the interaction of the shear production (SP), buoyancy flux (BP), and other energy components that contributes to the total optimal transient kinetic energy. These contributions affect the total energy by influencing the perturbation to extract kinetic energy (KE) from the mean flow. The decay of the amplification factor resulted from the positive amplification of both BP and SP, while the growth is attributed to the negative and positive amplification of BP and SP, respectively. The optimal SP is positively amplified, implying that there is the possibility of constant linear growth. These findings agree with the linear growth rate for increasing values of Grashof number.
1. Introduction
The Taylor–Couette system consists of a thin layer of a viscous fluid confined between two vertical rotating coaxial cylinders. The stability conditions for co-rotating cylinders was first examined by [1]. Counter-rotating Taylor–Couette flow refers to the flow of a fluid confined between two coaxial and independently rotating cylinders in opposite directions. Stratified Taylor–Couette flow (STCF) introduces an additional layer of complexity by incorporating density variations in the fluid. Stratification refers to the presence of density gradients in the fluid, which can occur due to variations in temperature, salinity, or other properties. The buoyancy effect, resulting from the density differences caused by stratification, introduces a new dimension to the dynamics of STCF. It interacts with the rotational forces, and its impact on the stability of the flow has been the subject of considerable research interest [2,3,4,5,6,7,8,9,10]. Understanding the dynamics of stratified Taylor–Couette flow holds relevance in many practical applications, including geophysics, oceanography, and industrial processes in the oil and gas sector. The combination of the horizontal angular shear induced by the cylinders and buoyancy effects due to density stratification gives rise to intriguing patterns, transitions, and stability regimes. In recent years, numerous studies have been conducted to better understand the underlying mechanisms and characteristics of this flow regime [11,12]. This flow configuration has been extensively studied for decades and in recent times, primarily in the absence of stratification [13,14,15,16,17]. Conversely, in the presence of stratification, the flow becomes more complex with more degrees of freedom [18,19].
Although linear stability analysis predicts plane Couette and pipe Poiseuille flows to be stable, they exhibit turbulence in practical scenarios for sufficiently large Reynolds numbers, as indicated by [20,21,22], and recent studies [23,24]. For plane Poiseuille flow, an instability is predicted to occur beyond a Reynolds number around 5772; in practice, the critical Reynolds number is found to be around 2300.
The inconsistency in these results is attributed to the non-normality of the linearised Navier–Stokes operator, leading to transient growth in the linear regime and triggering the transition from laminar to turbulent flow [25,26,27].
A recent work by Godwin et al. [28] focused specifically on the short-time instability of STCF. To explore the short-time instability of STCF, the authors conducted a detailed numerical investigation employing transient growth analysis techniques. The authors analysed the transient stability of STCF by considering small perturbations to the base flow. By systematically varying the Grashof number for various model configurations, they were able to quantify the influence of these parameters on the transient instability characteristics. The study sheds light on the transient instability induced by buoyancy in counter-rotating STCF within the bounds of the linear regime considered, but it does not capture the physical mechanism that triggers the transient bifurcation phenomena at Grashof number Gr ≈ . As in [28], the critical value is the value of Gr when the amplification factor reaches a local minimum.
There is a preference to considering these ubiquitous flows within the modal analysis framework, but this analysis predicts linear stability for all values of the Reynolds number R, which is contrary to experimental observations.
Transient growth exists when the eigenvectors of the system are non-normal. To investigate transient growth, non-modal analysis is necessary, and this is the reason that a study based on non-modal analysis is presented here. Additionally, Couette flow is asymptotically stable according to linear theory, and since non-modal analysis determines the largest possible growth of a perturbation in a finite time interval, also called optimal growth, it is hoped that non-modal analysis will bridge the gap between theory and experiment. The initial disturbance yielding optimal growth is called an optimal initial condition, and in our study, we have also allowed for thermal disturbances. The latter ones can be removed in a limiting process, allowing therefore the possibility of connection between linear and nonlinear regimes.
The primary goal of this study is to explore the physical processes responsible for triggering a transient bifurcation with specific objectives outlined as follows: developing a linear model for STCF and conducting a numerical evaluation using the Chebyshev collocation method, determining the least stable eigenvalue for each configuration, identifying the maximum amplification factor and optimal perturbation for the least stable mode, and ultimately deriving and evaluating the energy budget quantities associated with the optimal perturbation. This paper primarily focuses on the last objective, as the other aspects have already been satisfactorily addressed in previous work [28].
Since non-modal analysis is a relatively new method of analysis, it is used here as an important tool to predict instabilities. Nowadays, it is understood that a perturbation in a shear flow can experience significant transient energy growth. This growth is responsible for the initial linear amplification of disturbances and is mainly responsible for the appearance of a subcritical transition to turbulence. Non-modal effects can therefore explain the discrepancy between the observed experimental results in incompressible shear flows and the theoretically predicted critical Reynolds number for a linear instability in wall-bounded shear flows. We therefore need to use non-modal analysis to gain further insight into the linear stability of Couette flow.
It is reported that as Gr increases, the maximum amplification factor initially decays before it eventually starts growing after reaching a critical value . Assuming other parameters of the model are kept constant, the value changes as a function of different speed ratios of the cylinders. The observed decay/growth pattern of is attributed to the interplay between the induced shear and buoyancy. In this study, the mechanism that triggers this observed pattern is investigated.
In Section 1, a brief overview of the investigated problem is presented. Section 2 focuses on deriving, linearising, and numerically discretising the governing equations of the STCF model. The discussion of optimal transient budget quantities is covered in Section 3 with detailed derivations provided in Appendix A. Section 4 delves into a comprehensive analysis of the investigation’s results. Finally, Section 5 summarises the conclusions drawn from this study.
2. Mathematical Model
In this study, we consider an incompressible fluid between two concentric rotating heated vertical cylinders of infinite height. The inner cylinder has radius , rotates with an angular velocity of and is held at the temperature , where is the ambient temperature and is the temperature difference between the two cylinders. The outer cylinder has radius , rotates with an angular velocity of and is held at the temperature . We assume that the density varies linearly with the temperature such that
where is the coefficient of thermal expansion. We assume that the dynamic viscosity of the fluid and thermal conductivity are constant, whilst we define as the kinematic viscosity. We notice we can write where .
The presence of temperature gradients with the rotating concentric cylinders induces complex flow patterns and thermal effects. The variation in the density, due to the temperature gradients, induces various buoyancy-driven flow regimes. The equations are nondimensionalised using (bold here denotes a vector)
where , , , and are the dimensionless velocity, temperature, spatial coordinate, time and pressure, with . By defining we can express the dimensionless inner and outer radii as and , respectively. By dropping the accents for convenience, the resulting dimensionless equations become
where is the unit vector in the vertical axial direction, and the Grashof number, Prandtl number and relative density are given by
The dimensionless boundary conditions are given as
where is the unit vector in the azimuthal direction, and the inner and outer Reynolds numbers are given by
Due to the cylindrical boundaries, we perform our calculations in cylindrical polar coordinates. The steady base state velocity takes the form
In order to have a constant pressure gradient in the axial direction, we impose the zero mass flux constraint, namely
The well-known analytical base state solution to this problem is given by
where the constants A, B and C are given by
and
Now, we consider small perturbations to the base state in the form
where is assumed to be a small constant, is the base state pressure, not presented here for convenience, and is the perturbation to the velocity. Substituting Equation (12) into the dimensionless Equations (2)–(4) and linearising in , we obtain
To perform a stability analysis on this system, we seek perturbations of the form
where and are the azimuthal and axial wavenumbers, respectively. Substituting these expansions into the linearized Equations (13)–(15) and simplifying yields
where , and
By letting , we can write Equations (16)–(20) as
where
and
By assuming a solution of the form
we transform the initial value problem to a generalized eigenvalue problem:
The scalar eigenvalue is complex and defines the temporal stability of the flow. That is, if the real part of is negative, the flow is stable and the amplitude of the perturbations will decay in time. Conversely, if the real part of is positive, the flow is unstable and the amplitude of the perturbation will grow asymptotically in time. Further more, in order to define the boundary conditions, we assume that the perturbation of the velocity and temperature of the fluid motion must vanish at the walls:
In other words, we impose a homogeneous boundary condition for the velocity and temperature perturbations at the respective walls of the cylinders.
3. Perturbation Energy Budget
The asymptotic stability approach employed in perturbation analysis can effectively capture the length and time scales of unstable modes [29,30]. However, this method lacks an intuitive physical interpretation of the internal processes driving the instability. To gain a deeper understanding of the physical underpinnings of the instability, it is advantageous to adopt a more intuitive approach [25,31,32,33]. Exploring the processes influencing the kinetic energy distribution of perturbations can provide valuable insights [34,35,36].
The presence of kinetic energy in thermal stratified shear flow significantly impacts the perturbation’s decay or growth process [35,37]. The perturbation process is characterized by the conservation or transformation of energy across different states. For perturbations to grow, an energy exchange must occur. In the case of shear flow, perturbations grow by accessing kinetic energy. Investigating the quantities of energy sources interacting to form perturbation kinetic energy allows for a further understanding of the nature of induced instability—whether it is induced by shear or buoyancy—due to transient growing modes.
To calculate the kinetic energy of the optimal perturbation, we multiply the linearized Equations (A1)–(A4) by the complex conjugate of the optimal perturbation and evaluate the average over the entire domain in azimuthal and axial coordinating directions. Using the singular value decomposition method we computed the largest (negative) eigenvalues of Equation (25). The associated eigenvectors to these eigenvalues are the optimal perturbations. One notes that eigenvalues remain negative as this problem is predicted to be linearly stable even though full nonlinear simulations and experiments show this problem to be unstable. This process yields the following energy budget equation:
where KE is the kinetic energy of the perturbation, SP is the shear production, BP is the buoyancy production, EF is the energy flux, CKEV is the convergence of kinetic energy of the optimal perturbation due to viscosity and VD is the viscosity dissipation. All of these terms are defined in Appendix A.
4. Results and Discussion
Before discussing our results, it is important to acknowledge that in mixed convection flow, shear instability can manifest when there are relatively moving shear layers of fluid. The perturbations that arise from this instability may experience damping due to a stable stratification because the perturbation’s energy must be expended to counteract the force of gravity induced by the stratification. Consequently, the growth rate of these perturbations will decrease, and the instability will be suppressed if the stratification is sufficiently strong. These intricate processes are elucidated through the examination of the energy budget quantities within the framework of optimal transient perturbations particularly in relation to the amplification factor.
The kinetic budget quantities of the optimal growth perturbation are numerical investigated for different stratified STCF configurations. In Table 1, the parameter values for the four different configurations are given. Furthermore, the critical value for each configuration is also included.

Table 1.
This table displays the 4 configurations examined in [28]. Here, ratio refers to .
The analysis is carried out over a range of Grashof number values along with the following values: Pr = 68, = 0.067 and = 0.881, with values of and given in Table 1. These values are chosen to allow a comparison of the current results with those in the literature and correspond to the experimental values in [38]. The results obtained for the above parameter values are illustrative of the results we obtained from a larger number of numerical simulations. To obtain sufficiently accurate results, 128 Chebyshev nodes were used to compute the energy quantities.
The least stable modes for each configuration are first identified. The energy quantities are computed using the optimal disturbances as inputs for each of the selected Gr values. These values are chosen for illustrative purposes to show how the energy quantities oscillate between the cylinders depending on the value of Gr. For a more detailed discussion on how the amplification factor depends on Gr, please see Figure 4 of [28].
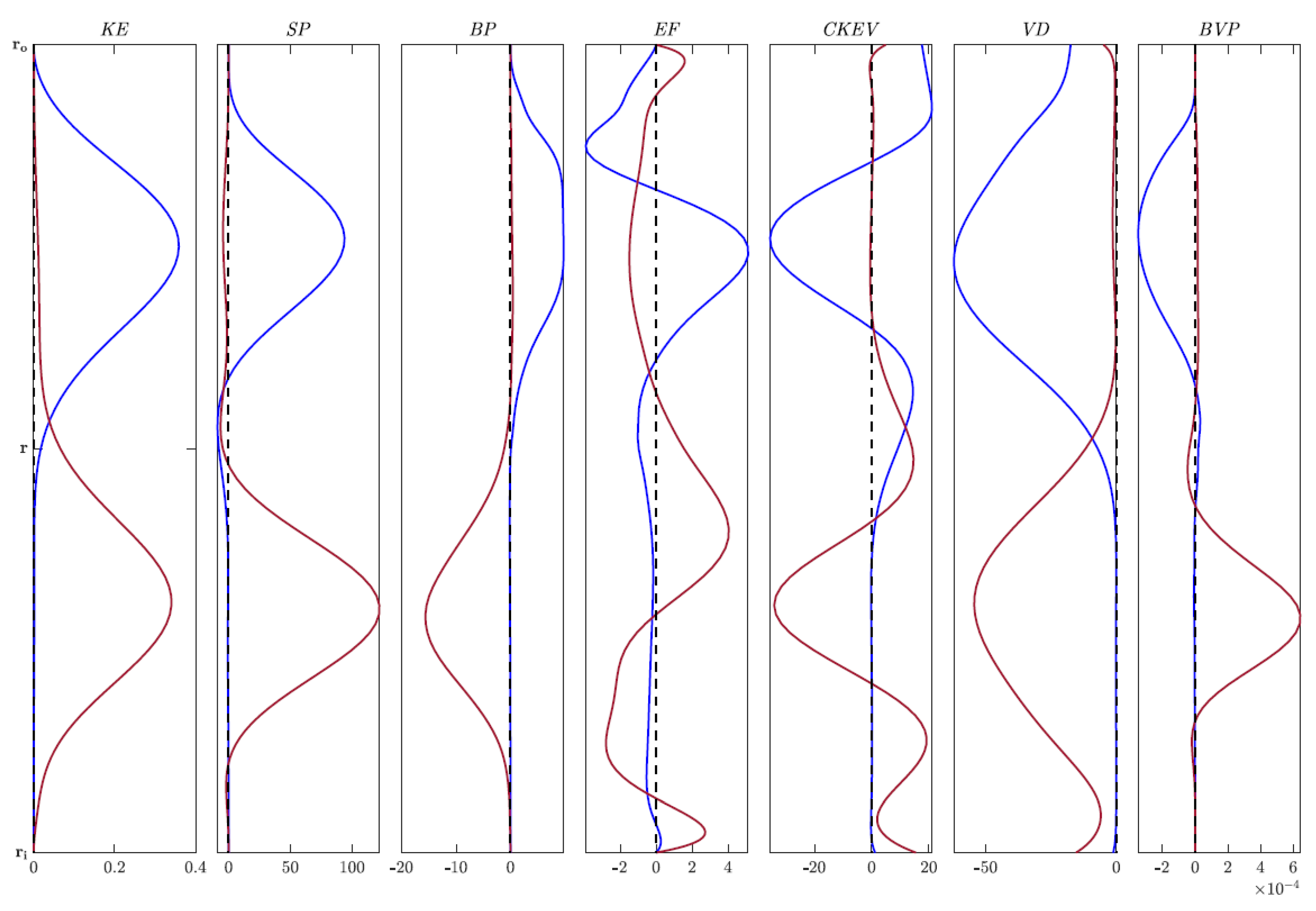
Figure 1 illustrates the energy quantities for the configuration for two values of Gr, namely Gr = 2500 (blue) and Gr = 3500 (red). The curves are presented at the time when the amplification factor is optimal.
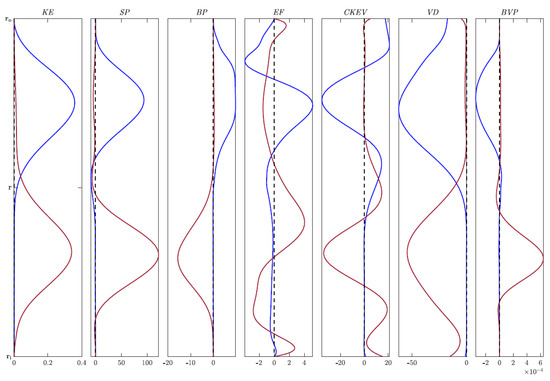
Figure 1.
The optimal perturbation energy (temperature) budget quantities for the configuration ; see Table 1. The blue curve corresponds to Gr = 2500, whilst the red curve corresponds to Gr = 3500. The curves are presented at the time when the amplification factor is optimal.
In Figure 1, the blue curve corresponds to Gr < whilst the red curve corresponds to Gr > . All of the blue curves in Figure 1 show peaks concentrated around the outer cylinder, whilst the red curves show peaks concentrated around the inner cylinder. Notice that the peaks of BVP are at least times smaller than the peaks of the other six quantities. When BP is positive, buoyancy causes the warmer, less dense fluid to rise, while the cold dense fluid sinks. We found that configurations , and produced very similar results to those of .
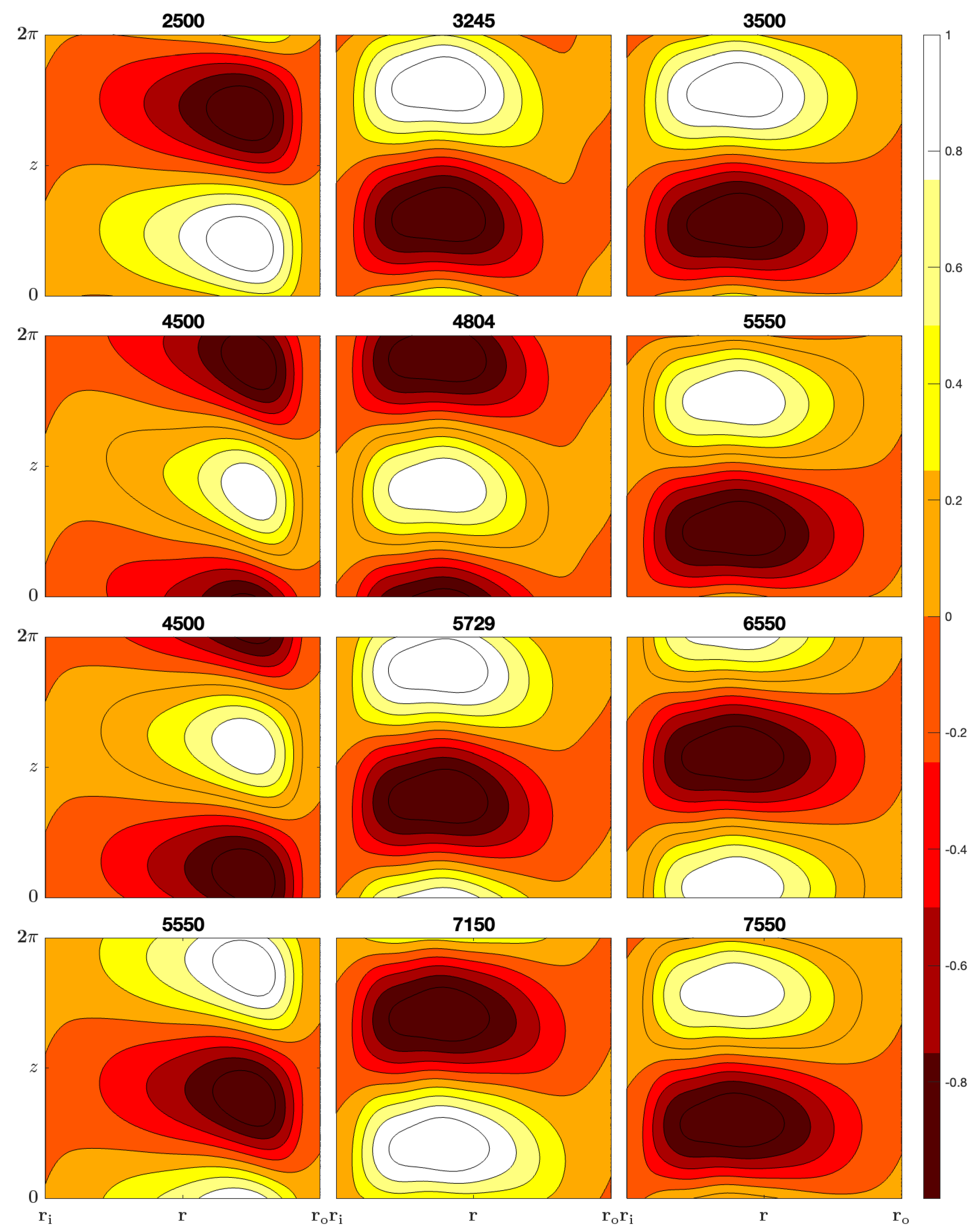
In Figure 2, we illustrate contour plots in the r–z plane of the perturbations to the base state temperature at the optimal wavenumber for . The values of Gr above each contour plot in the left column correspond to values of Gr less than , the middle column corresponds to values of Gr within 5% of , whilst the right column corresponds to values of Gr greater than . The rows from top to bottom correspond to the configurations –.
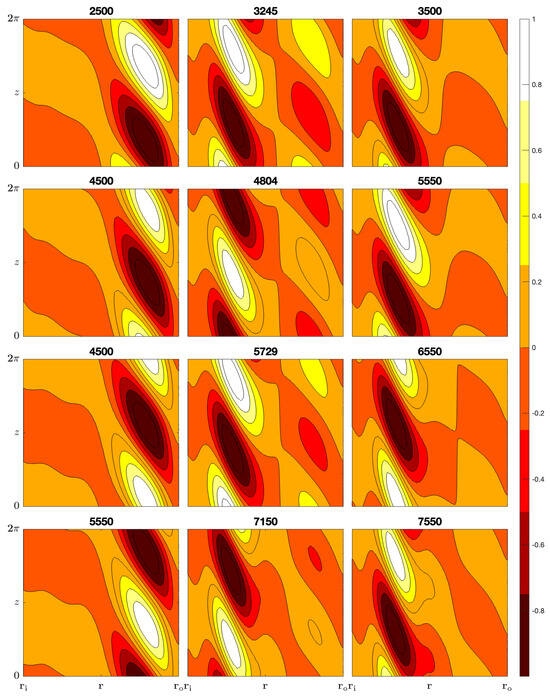
Figure 2.
Contours of the perturbations to the base state temperature of the optimal perturbation in the r–z plane for . Configurations , , , and are organized in rows from top to bottom, for selected Gr values, as indicated above each contour plot.
The left column in Figure 2 shows that the extrema in the perturbed temperature occurs towards the outer cylinder for values of Gr < . Conversely, the right column in Figure 2 shows that the extrema in the perturbed temperature occurs towards the inner cylinder for values of Gr > . The perturbations to the angular and vertical velocity were very similar to that of the temperature comtour plots and thus are not presented here. These results are consistent with the energy budget quantities shown in Figure 1.
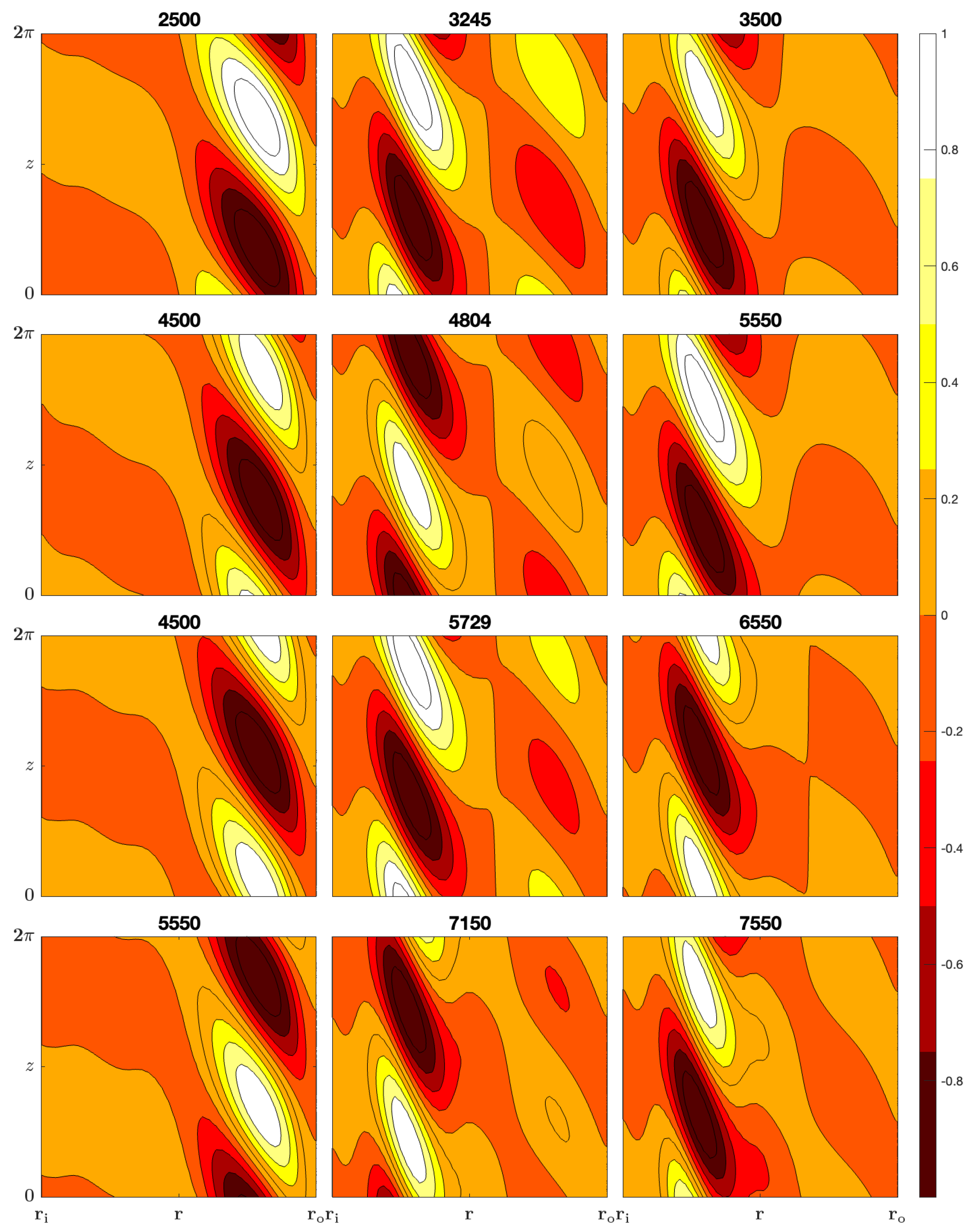
In Figure 3, we illustrate contour plots in the plane of the perturbations to the base state radial velocity at the optimal wavenumber for . The values of Gr above each contour plot in the left column correspond to values of Gr less than , the middle column corresponds to values of Gr within 5% of , whilst the right column corresponds to values of Gr greater than . The rows from top to bottom correspond to the configurations –.
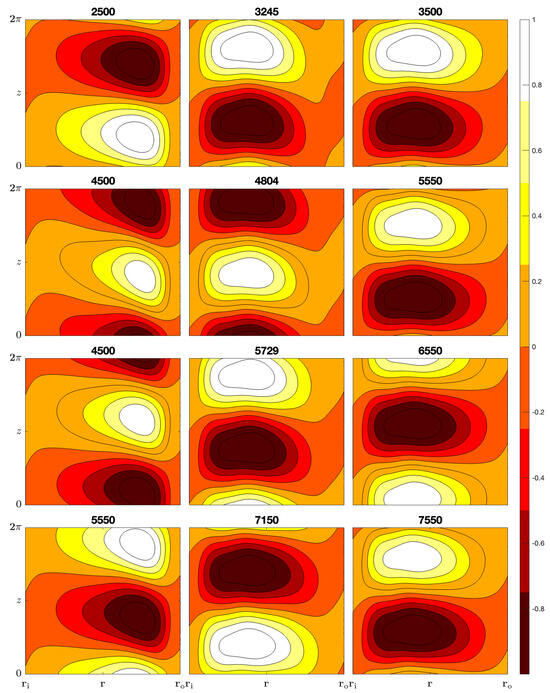
Figure 3.
Contours of the perturbations to the base state radial velocity of the optimal perturbation in the r–z plane for . Configurations , , , and are organized in rows from top to bottom, for selected Gr values, as indicated above each contour plot.
The left column in Figure 3 shows that the extrema in the perturbed radial velocity occurs towards the outer cylinder for values of Gr < . Conversely, the right column in Figure 3 shows that the extrema in the perturbed radial velocity occurs towards the inner cylinder for values of Gr > . Again, these results are consistent with the energy budget quantities shown in Figure 1. We notice that there are alternating convective rolls arranged vertically above each other, which is consistent with the vortices which appear as secondary states in the Taylor–Couette flow.
5. Conclusions
In this study, we have revisited the stratified Taylor–Couette flow via the non-modal stability analysis the singular value decomposition method and via computing the largest negative eigenvalues of Equation (25). Sequentially we used the energy budget equation to perform our calculations. Our results are presented for values of the Grashof number less than, around, and greater than the critical Grashof number, where the critical Grashof number has been defined as the value which minimises the optimal amplification factor. We found that when Gr < , then the perturbations to the base state flow are focused around the outer wall; conversely, when Gr > , then the perturbations to the base state flow are focused around the inner wall.
The complex dynamics of mixed convection flow with a particular focus on shear instability and its manifestation in the presence of stratified conditions were investigated with a systematic numerical investigation of kinetic budget quantities for optimal growth perturbations in various stratified configurations of Taylor–Couette flow. The key findings shed light on the interplay of different energy components and their effects on the transient growth.
Our results reveal distinct behaviours of energy quantities before, around, and beyond the turning point in the amplification factor. Prior to the turning point, the values of SP and BF near the outer cylinder wall induce significant kinetic energy KE peaks. This positive amplification of BF indicates a buoyant fluid rise, while the negative amplification suggests shear-induced instability opposing gravity. Around the turning point, the kinetic energy distribution exhibits peaks either towards the outer or inner cylinder, emphasizing the transient nature of the amplification process. Beyond the turning point, the energy quantities show similar amplification peaks with SP and BF near the inner cylinder wall causing significant KE peaks.
Our analysis also highlighted the role of buoyancy and shear drag in triggering short-time and long-time instability. We found that the disparity between BF and SP values significantly influences the nature of amplification with a sufficiently high shear production leading to the decay of short-time amplification. This long-time behavior is captured by an asymptotic analysis of the eigenvalue. Contrary to initial assumptions, the study argues that shear drag, rather than buoyancy, is the primary trigger for short-time instability.
The perturbation functions change shape even for small Gr increments as shown in Figure 2 and Figure 3 due to the proximity of the optimal amplification factor. Small changes indicate the change of stability and the possibility of existence of nonlinear solutions. Sometimes shifted to the inner wall and sometimes to the outer wall the flow meanders as it rearranges itself for effective mass transport. This work is slightly distinctive to modal analysis where the eigenvalues indicate the critical mode(s) and indicates an alternative transfer to nonlinearity.
Furthermore, our findings have shown that the viscous processes CKEV and VD disperse energy without contributing to the overall KE, while dissipative terms VD lead to the decay of KE. Viscosity acts as an energy sink, gradually diminishing the velocity at the boundary and influencing the perturbation’s configuration to extract KE from the background mean flow.
In summary, our analysis provides insight into the intricate processes governing mixed convection flow with shear instability, emphasizing the role of buoyancy, shear drag, and viscosity in shaping the flow dynamics. These findings contribute to a deeper understanding of the underlying mechanisms in complex fluid systems.
Author Contributions
Conceptualization, L.E.G.; methodology, L.E.G. and S.C.G.; software, L.E.G.; validation, L.E.G. and S.C.G.; formal analysis, L.E.G. and S.C.G.; investigation, L.E.G. and S.C.G.; resources, L.E.G. and S.C.G.; writing—original draft preparation, L.E.G.; writing—review and editing, L.E.G., P.M.J.T., T.A. and S.C.G.; supervision, P.M.J.T. and S.C.G.; project administration, P.M.J.T. and S.C.G.; funding acquisition, L.E.G. and S.C.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by RISE Horizon 2020 ATM2BT, Atomistic to Molecular Turbulence, Grant No. 824022, PTDF ED/PHD/GLE/826/16 scholarship and DTI EPSRC grant, Aston University sponsorship.
Data Availability Statement
The Matlab sources codes used to generate the data in this study can be made available upon request.
Acknowledgments
We would like to thank Samesa Igirigi and Hart Abarasi for many fruitful discussions.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Derivations of Optimal Perturbation Energy Budget Equation
The linearised version of the Navier-Stokes equations about the base state is given by
If we multiply each of the first three equations by the associated velocity component and then take the sum of these equations we can obtain
Now, we integrate over the axial and azimuthal directions and assume periodic boundary conditions in both those directions to give
where denotes the average given by . If we multiply Equation (A4) by and average as before, we obtain
Now, the conservation of mass equation is given by
If we multiply Equation (A6) by , integrate over the axial and azimuthal directions, and then add this equation to Equation (A5), we obtain
where the terms are defined as follows:
where the kinetic energy of the perturbation is KE, the shear production is SP, the buoyancy production is BP, the energy flux is EF, CKEV is the convergence of kinetic energy of the optimal perturbation due to viscosity, VD is the viscosity dissipation, and BVP is the buoyancy variance.
References
- Taylor, G.I. VIII. Stability of a viscous liquid contained between two rotating cylinders. Philos. Trans. R. Soc. A 1923, 223, 289–343. [Google Scholar]
- Lopez, J.M.; Lopez, J.M.; Marques, F. Stably stratified Taylor–Couette flows. Philos. Trans. R. Soc. A 2023, 381, 20220115. [Google Scholar] [CrossRef] [PubMed]
- Lopez, J.; Marques, F. Three-dimensional instabilities in a discretely heated annular flow: Onset of spatio-temporal complexity via defect dynamics. Phys. Fluids 2014, 26, 064102. [Google Scholar] [CrossRef]
- Lopez, J.; Marques, F.; Avila, M. The Boussinesq approximation in rapidly rotating flows. J. Fluid Mech. 2013, 737, 56–77. [Google Scholar] [CrossRef]
- Caton, F.; Janiaud, B.; Hopfinger, E. Stability and bifurcations in stratified Taylor–Couette flow. J. Fluid Mech. 2000, 419, 93–124. [Google Scholar] [CrossRef]
- Molemaker, M.; McWilliams, J.; Yavneh, I. Instability and equilibration of centrifugally stable stratified Taylor-Couette flow. Phys. Rev. Lett. 2001, 86, 5270. [Google Scholar] [CrossRef]
- Caton, F.; Janiaud, B.; Hopfinger, E. Primary and secondary Hopf bifurcations in stratified Taylor-Couette flow. Phys. Rev. Lett. 1999, 82, 4647. [Google Scholar] [CrossRef]
- Hua, B.; Le Gentil, S.; Orlandi, P. First transitions in circular Couette flow with axial stratification. Phys. Fluids 1997, 9, 365–375. [Google Scholar] [CrossRef][Green Version]
- Hua, B.; Moore, D.; Le Gentil, S. Inertial nonlinear equilibration of equatorial flows. J. Fluid Mech. 1997, 331, 345–371. [Google Scholar] [CrossRef]
- Thorpe, S. The stability of stratified Couette flow. In Notes on 1966 Summer School on Geophysical Fluid Dynamics; Woods Hole Oceanographic Institution: Falmouth, MA, USA, 1966; pp. 80–107. [Google Scholar]
- Bengana, Y.; Tuckerman, L. Spirals and ribbons in counter-rotating Taylor-Couette flow: Frequencies from mean flows and heteroclinic orbits. Phys. Rev. Fluids 2019, 4, 044402. [Google Scholar] [CrossRef]
- Obaidullah, K.; Baig, M.; Sanghi, S. Counter-rotating Taylor-Couette flows with radial temperature gradient. Int. J. Heat Fluid Flow 2022, 95, 108980. [Google Scholar] [CrossRef]
- Hamede, M.; Merbold, S.; Egbers, C. Experimental investigation of turbulent counter-rotating Taylor-Couette flows for radius ratio η = 0.1. J. Fluid Mech. 2023, 964, A36. [Google Scholar] [CrossRef]
- Wang, B.; Ayats, R.; Deguchi, K.; Mellibovsky, F.; Meseguer, A. Self-sustainment of coherent structures in counter-rotating Taylor–Couette flow. J. Fluid Mech. 2022, 951, A21. [Google Scholar] [CrossRef]
- Avila, K.; Hof, B. Second-Order Phase Transition in Counter-Rotating Taylor-Couette Flow Experiment. Entropy 2021, 23, 58. [Google Scholar] [CrossRef]
- Huisman, S.; Lohse, D.; Sun, C. Statistics of turbulent fluctuations in counter-rotating Taylor-Couette flows. Phys. Rev. E 2013, 88, 063001. [Google Scholar] [CrossRef] [PubMed]
- Coles, D. Transition in circular Couette flow. J. Fluid Mech. 1965, 21, 385–425. [Google Scholar] [CrossRef]
- Boubnov, B.; Gledzer, E.; Hopfinger, E. Stratified circular Couette flow: Instability and flow regimes. J. Fluid Mech. 1995, 292, 333–358. [Google Scholar] [CrossRef]
- Boubnov, B.; Gledzer, E.; Hopfinger, E.; Orlandi, P. Layer formation and transitions in stratified circular Couette flow. Dyn. Atmos. Ocean. 1996, 23, 139–153. [Google Scholar] [CrossRef]
- Romanov, V.A. Stability of plane-parallel Couette flow. Funct. Anal. Its Appl 1973, 7, 137–146. [Google Scholar] [CrossRef]
- Davey, A. On the Stability of Plane Couette flow to Infinitesimal Disturbances. J. Fluid Mech. 1973, 57, 369–380. [Google Scholar] [CrossRef]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability. J. Fluid Mech. 1981, 124, 529–533. [Google Scholar] [CrossRef]
- Sano, M.; Tamai, K. A universal transition to turbulence in channel flow. Nat. Phys. 2016, 12, 249–253. [Google Scholar] [CrossRef]
- Eckhardt, B. Transition to Turbulence in Shear Flows. Physica A 2018, 504, 121–129. [Google Scholar] [CrossRef]
- Trefethen, L.N.; Trefethen, A.E.; Reddy, S.C.; Driscoll, T.A. Hydrodynamic stability without eigenvalues. Science 1993, 261, 578–584. [Google Scholar] [CrossRef] [PubMed]
- Andersson, P.; Berggren, M.; Henningson, D.S. Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 1999, 11, 134–150. [Google Scholar] [CrossRef]
- Kreilos, T.; Khapko, T.; Schlatter, P.; Duguet, Y.; Henningson, D.S.; Eckhardt, B. Bypass transition and spot nucleation in boundary layers. Phys. Rev. Fluids 2016, 1, 043602. [Google Scholar] [CrossRef]
- Godwin, L.; Trevelyan, P.M.J.; Akinaga, T.; Generalis, S. Transient Dynamics in Counter-Rotating Stratified Taylor–Couette Flow. Mathematics 2023, 11, 3250. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Stuart, J.T. On the non-linear mechanics of wave disturbances in stable and unstable parallel flows Part 1. The basic behaviour in plane Poiseuille flow J. Fluid Mech. 1960, 9, 353–370. [Google Scholar]
- Schmid, P.J.; Brandt, L. Analysis of Fluid Systems: Stability, Receptivity, Sensitivity: Lecture notes from the FLOW-NORDITA Summer School on Advanced Instability Methods for Complex Flows, Stockholm, Sweden, 2013. Appl. Mech. Rev. 2014, 66, 024803. [Google Scholar] [CrossRef]
- Meseguer, A. Energy transient growth in the Taylor-Couette problem. Phys. Fluids 2002, 14, 1655–1660. [Google Scholar] [CrossRef]
- Reddy, S.C.; Henningson, D.S. Energy growth in viscous channel flows. J. Fluid Mech. 1993, 252, 209–238. [Google Scholar] [CrossRef]
- Dandoy, V.; Park, J.; Augustson, K.; Astoul, A.; Mathis, S. How tidal waves interact with convective vortices in rapidly rotating planets and stars. Astron. Astrophys. 2023, 673, A6. [Google Scholar] [CrossRef]
- Lian, Q.; Smyth, W.; Liu, Z. Numerical Computation of Instabilities and Internal Waves from In Situ Measurements via the Viscous Taylor–Goldstein Problem. J. Atmos. Ocean. Tech. 2020, 37, 759–776. [Google Scholar] [CrossRef]
- Lin, S.P. Roles of surface tension and Reynolds stresses on the finite amplitude stability of a parallel flow with a free surface. J. Fluid Mech. 1970, 40, 307–314. [Google Scholar] [CrossRef]
- Smyth, W.D.; Carpenter, J.R. Instability in Geophysical Flows; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef]
- Teitel, M.; Schwabe, D.; Gelfgat, A.Y. Experimental and computational study of flow instabilities in a model of Czochralski growth. J. Cryst. Growth 2008, 310, 1343–1348. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).