Dynamics of a Water Droplet Impacting an Ultrathin Layer of Oil Suspended on a Pool of Water
Abstract
1. Introduction
2. Results and Discussions
2.1. Effect of Oil Layer Thickness
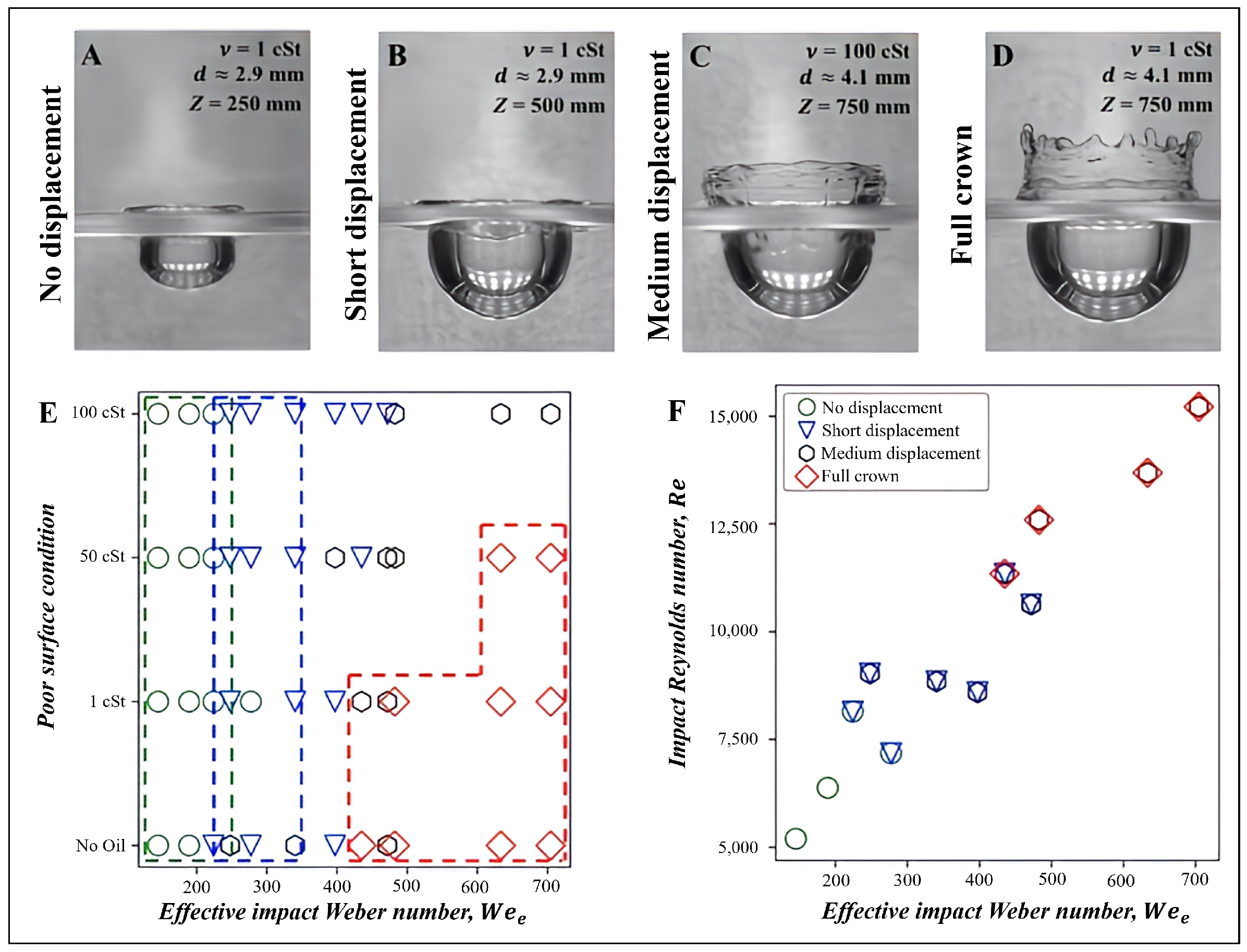
2.2. Vertical Displacement of Liquid and Formation of Crowns
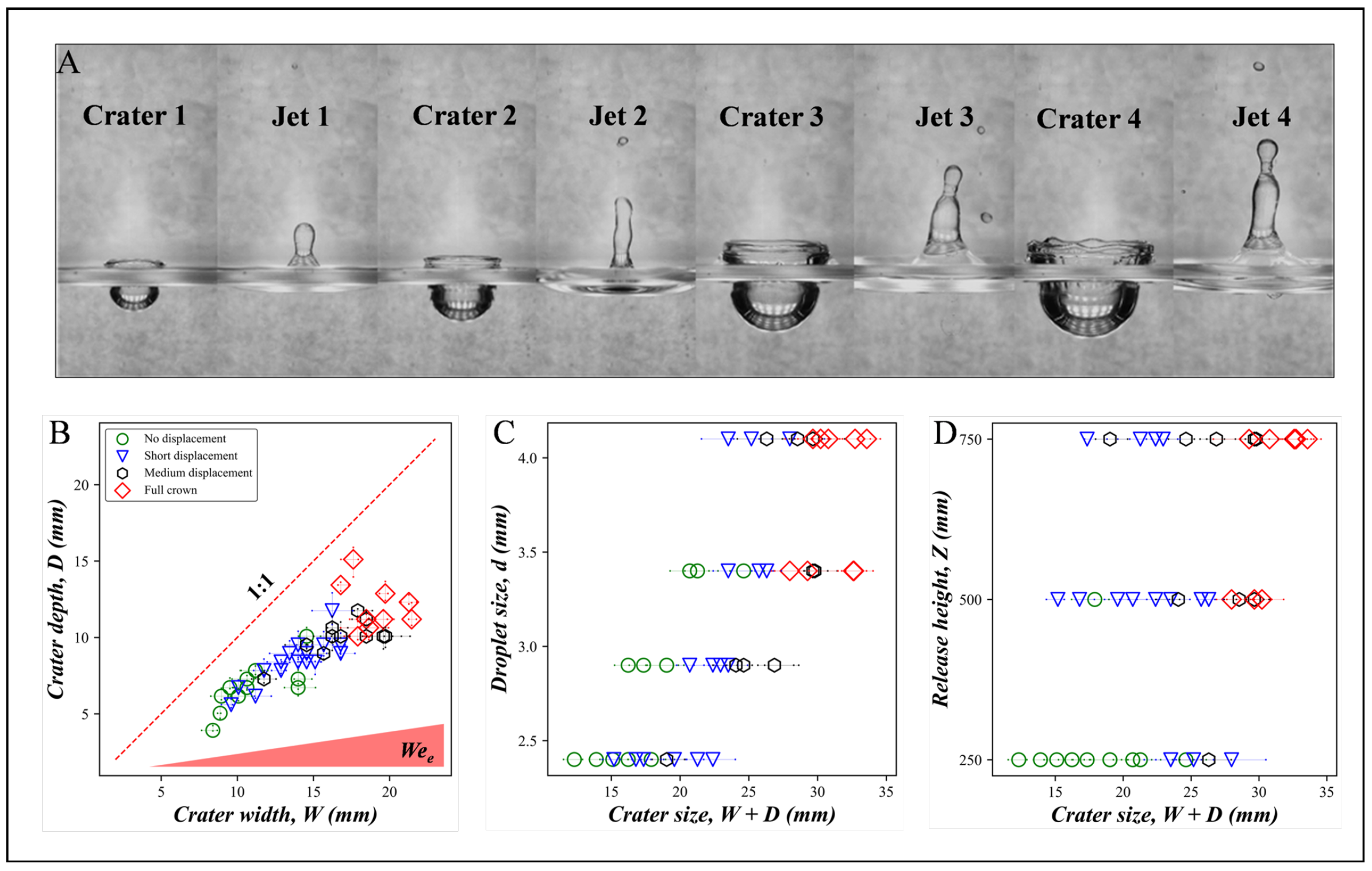
2.3. Crater Formation and Its Characteristics
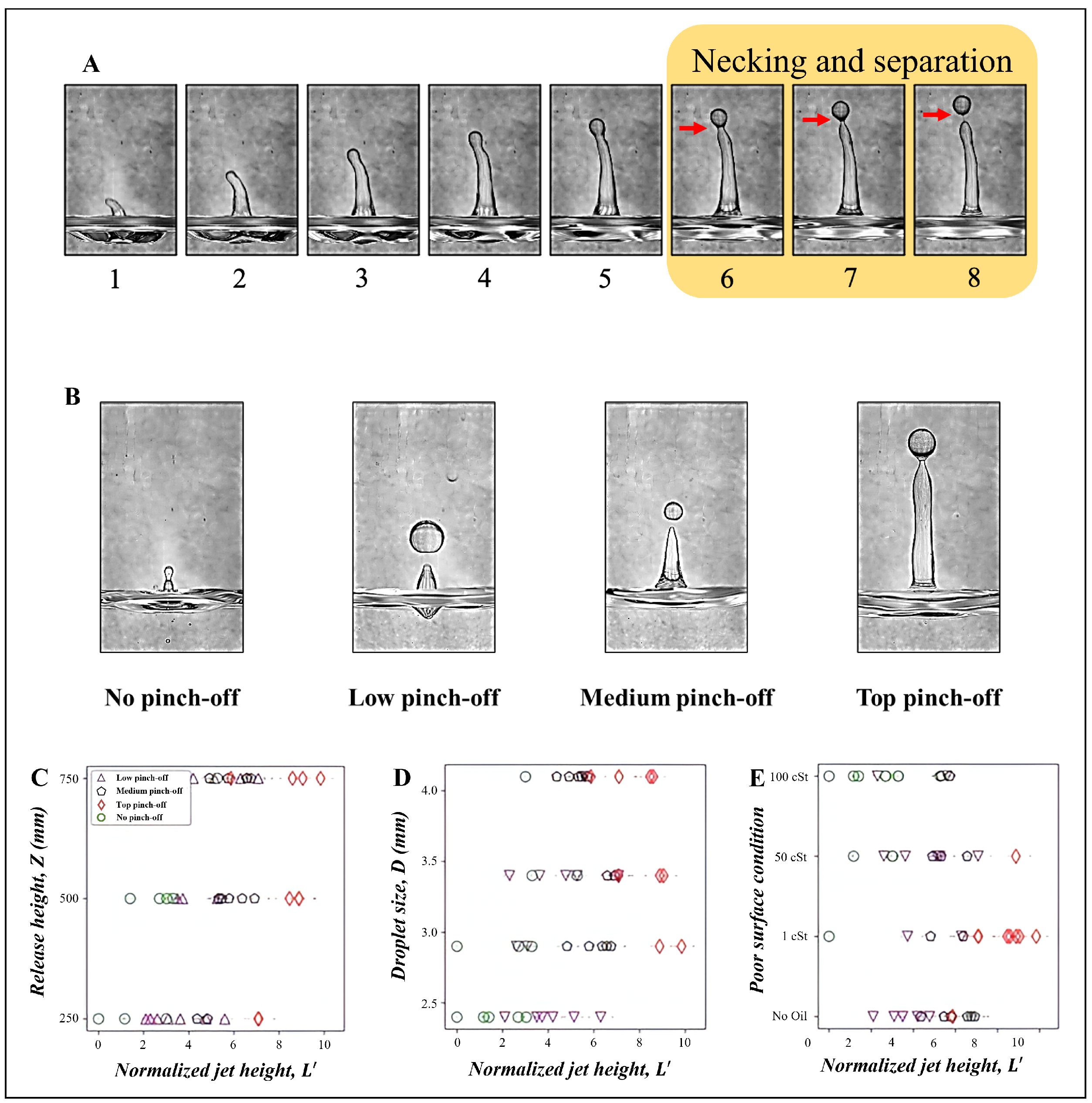
2.4. Jet Pinch-Off Modes
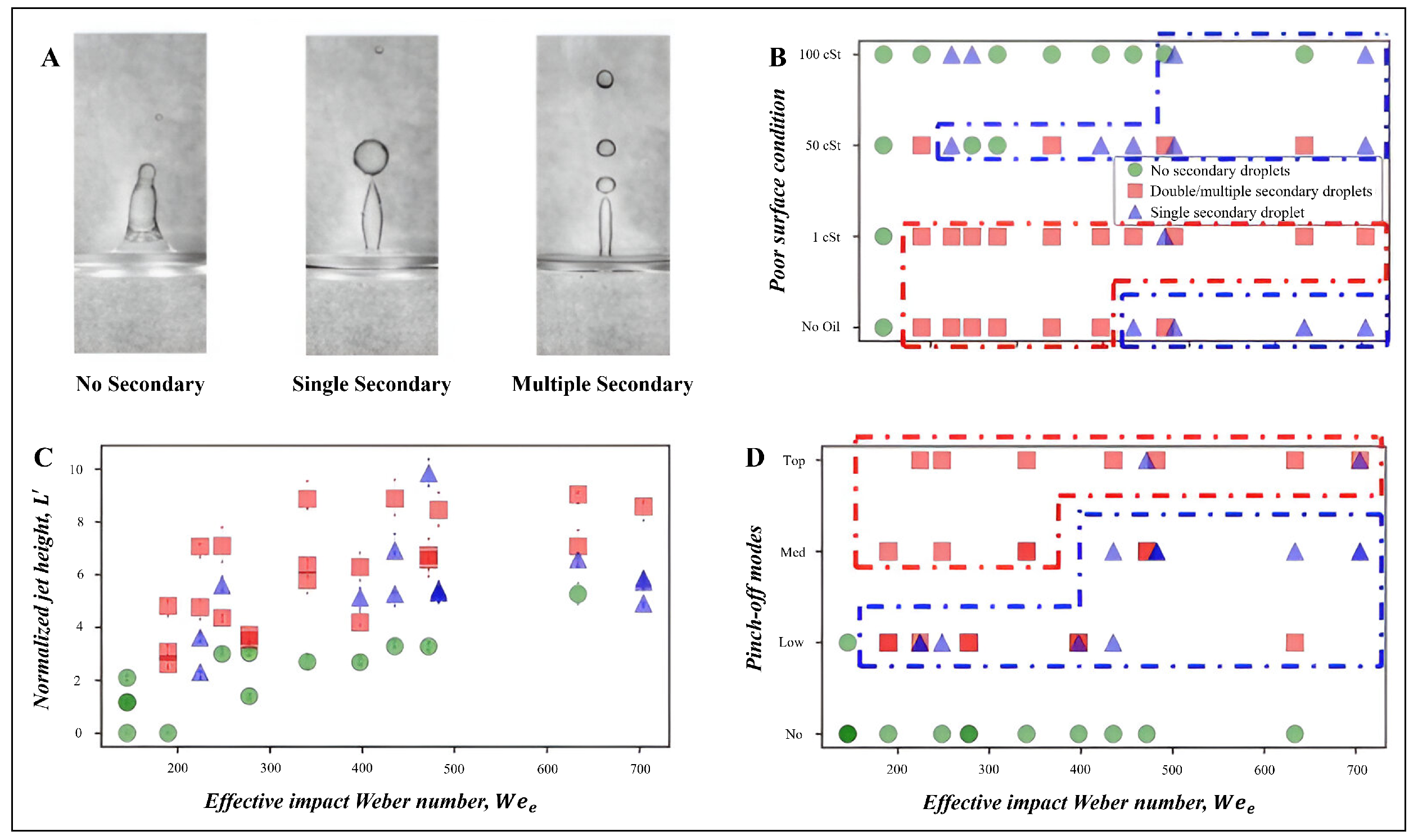
2.5. Secondary Droplet Formation
3. Conclusions
4. Materials and Methods
4.1. Experimental Setup
4.2. Video Processing
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pan, Z.; Weibel, J.A.; Garimella, S.V. Influence of Surface Wettability on Transport Mechanisms Governing Water Droplet Evaporation. Langmuir 2014, 30, 9726–9730. [Google Scholar] [CrossRef] [PubMed]
- Liang, G.; Mudawar, I. Review of Pool Boiling Enhancement by Surface Modification. Int. J. Heat Mass Transfer 2019, 128, 892–933. [Google Scholar] [CrossRef]
- Charalampous, G.; Hardalupas, Y. Collisions of Droplets on Spherical Particles. Phys. Fluids 2017, 29, 103305. [Google Scholar] [CrossRef]
- Luo, K.; Shao, C.; Chai, M.; Fan, J. Level Set Method for Atomization and Evaporation Simulations. Prog. Energy Combust. Sci. 2019, 73, 65–94. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Aziz, S.D.; Chandra, S.; Mostaghimi, J. Cooling Effectiveness of a Water Drop Impinging on a Hot Surface. Int. J. Heat Fluid Flow 2001, 22, 201–210. [Google Scholar] [CrossRef]
- Josserand, C.; Thoroddsen, S.T. Drop Impact on a Solid Surface. Annu. Rev. Fluid Mech. 2016, 48, 365–391. [Google Scholar] [CrossRef]
- Lohse, D. Fundamental Fluid Dynamics Challenges in Inkjet Printing. Annu. Rev. Fluid Mech. 2022, 54, 349–382. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, Y.; Hu, R.; Luo, X. Water Droplet Bouncing Dynamics. Nano Energy 2021, 81, 105647. [Google Scholar] [CrossRef]
- Biroun, M.H.; Rahmati, M.; Tao, R.; Torun, H.; Jangi, M.; Fu, Y. Dynamic Behavior of Droplet Impact on Inclined Surfaces with Acoustic Waves. Langmuir 2020, 36, 10175–10186. [Google Scholar] [CrossRef]
- Hu, Z.; Wu, X.; Chu, F.; Zhang, X.; Yuan, Z. Off-centered Droplet Impact on Single-ridge Superhydrophobic Surfaces. Exp. Therm. Fluid Sci. 2021, 120, 110245. [Google Scholar] [CrossRef]
- Breitenbach, J.; Roisman, I.V.; Tropea, C. From Drop Impact Physics to Spray Cooling Models: A Critical Review. Exp. Fluids 2018, 59, 1–21. [Google Scholar] [CrossRef]
- Weisensee, P.B.; Tian, J.; Miljkovic, N.; King, W.P. Water Droplet Impact on Elastic Superhydrophobic Surfaces. Sci. Rep. 2016, 6, 30328. [Google Scholar] [CrossRef] [PubMed]
- Schutzius, T.M.; Jung, S.; Maitra, T.; Graeber, G.; Köhme, M.; Poulikakos, D. Spontaneous Droplet Trampolining on Rigid Superhydrophobic Surfaces. Nature 2015, 527, 82–85. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Wang, C.; Lu, S. Water Droplet Impacting on Burning or Unburned Liquid Pool. Exp. Therm. Fluid Sci. 2017, 85, 313–321. [Google Scholar] [CrossRef]
- Raiyan, A.; Mohammadian, B.; Sojoudi, H. Droplet Dynamics and Freezing Delay on Nanoporous Microstructured Surfaces at Condensing Environment. Coatings 2021, 11, 617. [Google Scholar] [CrossRef]
- Hasegawa, K.; Nara, T. Energy Conservation during Single Droplet Impact on Deep Liquid Pool and Jet Formation. AIP Adv. 2019, 9, 085218. [Google Scholar] [CrossRef]
- Blanken, N.; Saleem, M.S.; Thoraval, M.-J.; Antonini, C. Impact of Compound Drops: A Perspective. Curr. Opin. Colloid Interface Sci. 2021, 51, 101389. [Google Scholar] [CrossRef]
- Cheng, X.; Sun, T.-P.; Gordillo, L. Drop Impact Dynamics: Impact Force and Stress Distributions. Annu. Rev. Fluid Mech. 2022, 54, 57–81. [Google Scholar] [CrossRef]
- Pasandideh-Fard, M.; Qiao, Y.M.; Chandra, S.; Mostaghimi, J. Capillary Effects during Droplet Impact on a Solid Surface. Phys. Fluids 1996, 8, 650–659. [Google Scholar] [CrossRef]
- Zhang, G.; Quetzeri-Santiago, M.A.; Stone, C.A.; Botto, L.; Castrejón-Pita, J.R. Droplet Impact Dynamics on Textiles. Soft Matter 2018, 14, 8182–8190. [Google Scholar] [CrossRef]
- Liu, Q.; Lo, J.H.Y.; Li, Y.; Liu, Y.; Zhao, J.; Xu, L. The Role of Drop Shape in Impact and Splash. Nat. Commun. 2021, 12, 3068. [Google Scholar] [CrossRef]
- Moghtadernejad, S.; Lee, C.; Jadidi, M. An Introduction of Droplet Impact Dynamics to Engineering Students. Fluids 2020, 5, 107. [Google Scholar] [CrossRef]
- Attinger, D.; Moore, C.; Donaldson, A.; Jafari, A.; Stone, H.A. Fluid Dynamics Topics in Bloodstain Pattern Analysis: Comparative Review and Research Opportunities. Forensic Sci. Int. 2013, 231, 375–396. [Google Scholar] [CrossRef]
- Li, X.J.; Zhou, Y. Microfluidic Devices for Biomedical Applications; Woodhead Publishing: Sawston, UK, 2021. [Google Scholar]
- Manzello, S.L.; Yang, J.C. An Experimental Study of a Water Droplet Impinging on a Liquid Surface. Exp. Fluids 2002, 32, 580–589. [Google Scholar] [CrossRef]
- Castillo-Orozco, E.; Davanlou, A.; Choudhury, P.K.; Kumar, R. Droplet Impact on Deep Liquid Pools: Rayleigh Jet to Formation of Secondary Droplets. Phys. Rev. E 2015, 92, 053022. [Google Scholar] [CrossRef]
- Ding, Q.; Wang, T.; Che, Z. Two Jets during the Impact of Viscous Droplets onto a Less-viscous Liquid Pool. Phys. Rev. E 2019, 100, 053108. [Google Scholar] [CrossRef]
- Che, Z.; Matar, O.K. Impact of Droplets on Immiscible Liquid Films. Soft Matter 2018, 14, 1540–1551. [Google Scholar] [CrossRef]
- Jain, U.; Jalaal, M.; Lohse, D.; van der Meer, D. Deep Pool Water-impacts of Viscous Oil Droplets. Soft Matter 2019, 15, 4629–4638. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.; Lee, J.; Bose, A.; Kim, I.; Lee, J. The Impact of an Oil Droplet on an Oil Layer on Water. J. Fluid Mech. 2021, 906, A5. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Rui, S. Phenomena of Single Water Droplet Impacting a Heptane Layer on Water Pool. Eur. J. Mech. B/Fluids 2022, 92, 65–74. [Google Scholar] [CrossRef]
- Raiyan, A.; McLaughlin, T.S.; Annavarapu, R.K.; Sojoudi, H. Effect of Superamphiphobic Macrotextures on Dynamics of Viscous Liquid Droplets. Sci. Rep. 2018, 8, 15344. [Google Scholar] [CrossRef] [PubMed]
- Yeganehdoust, F.; Attarzadeh, R.; Karimfazli, I.; Dolatabadi, A. A Numerical Analysis of Air Entrapment During Droplet Impact on an Immiscible Liquid Film. Int. J. Multiph. Flow 2020, 124, 103175. [Google Scholar] [CrossRef]
- Wang, W.; Ji, C.; Lin, F.; Wei, X.; Zou, J. Formation of Water in Oil in Water Particles by Drop Impact on an Oil Layer. Phys. Fluids 2019, 31, 037107. [Google Scholar] [CrossRef]
- Wu, Y.; Hannah, C.G.; Thupaki, P.; Mo, R.; Law, B. Effects of Rainfall on Oil Droplet Size and the Dispersion of Spilled Oil with Application to Douglas Channel, British Columbia, Canada. Mar. Pollut. Bull. 2017, 114, 176–182. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, D.F.S.; Silva, A.R.R.; Panão, M.R.O. Insights into Single Droplet Impact Models Upon Liquid Films Using Alternative Fuels for Aero-Engines. Appl. Sci. 2020, 10, 6698. [Google Scholar] [CrossRef]
- Camp, D.W.; Berg, J.C. The Spreading of Oil on Water in the Surface-Tension Regime. J. Fluid Mech. 1987, 184, 445–462. [Google Scholar] [CrossRef]
- Razavi, S.; Hernandez, L.M.; Read, A.; Vargas, W.L.; Kretzschmar, I. Surface Tension Anomaly Observed for Chemically-Modified Janus Particles at the Air/Water Interface. J. Colloid Interface Sci. 2020, 558, 95–99. [Google Scholar] [CrossRef] [PubMed]
- Mohamed, M.H.; Shahbaznezhad, M.; Dehghanghadikolaei, A.; Haque, M.A.; Sojoudi, H. Deformation of Bulk Dielectric Fluids Under Corona-Initiated Charge Injection. Exp. Fluids 2020, 61, 1–12. [Google Scholar] [CrossRef]
- Guo, Y.; Wei, L.; Liang, G.; Shen, S. Simulation of Droplet Impact on Liquid Film with CLSVOF. Int. Commun. Heat Mass Transfer 2014, 53, 26–33. [Google Scholar] [CrossRef]
- Trujillo, M.F.; Lee, C.F. Modeling Crown Formation Due to the Splashing of a Droplet. Phys. Fluids 2001, 13, 2503–2516. [Google Scholar] [CrossRef]
- Bernard, R.; Baumgartner, D.; Brenn, G.; Planchette, C.; Weigand, B.; Lamanna, G. Miscibility and Wettability: How Interfacial Tension Influences Droplet Impact onto Thin Wall Films. J. Fluid Mech. 2021, 908, A36. [Google Scholar] [CrossRef]
- Bernard, R.; Vaikuntanathan, V.; Weigand, B.; Lamanna, G. On the Crown Rim Expansion Kinematics during Droplet Impact on Wall-Films. Exp. Therm. Fluid Sci. 2020, 118, 110168. [Google Scholar] [CrossRef]
- Ersoy, N.E.; Eslamian, M. Phenomenological Study and Comparison of Droplet Impact Dynamics on a Dry Surface, Thin Liquid Film, Liquid Film and Shallow Pool. Exp. Therm. Fluid Sci. 2020, 112, 109977. [Google Scholar] [CrossRef]
- Santra, S.; Das, S.; Chakraborty, S. Electric Field-Induced Pinch-Off of a Compound Droplet in Poiseuille Flow. Phys. Fluids 2019, 31, 062004. [Google Scholar] [CrossRef]
- Almohammadi, H.; Amirfazli, A. Droplet Impact: Viscosity and Wettability Effects on Splashing. J. Colloid Interface Sci. 2019, 553, 22–30. [Google Scholar] [CrossRef]
- Sayyari, M.J.; Naghedifar, S.A.; Esfahani, J.A. Pinch-Off Location and Time during 2D Droplet Impact onto a Wetted Stationary Cylinder Using the Lattice Boltzmann Method. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 1–13. [Google Scholar] [CrossRef]
- Blanco–Rodríguez, F.J.; Gordillo, J.M. On the Jets Produced by Drops Impacting a Deep Liquid Pool and by Bursting Bubbles. J. Fluid Mech. 2021, 916, A37. [Google Scholar] [CrossRef]
- Pan, K.-L.; Hung, C.-Y. Droplet Impact upon a Wet Surface with Varied Fluid and Surface Properties. J. Colloid Interface Sci. 2010, 352, 186–193. [Google Scholar] [CrossRef]
- Huang, K.-L.; Pan, K.-L.; Josserand, C. Pinching Dynamics and Satellite Droplet Formation in Symmetrical Droplet Collisions. Phys. Rev. Lett. 2019, 123, 234502. [Google Scholar] [CrossRef]
- Samenfink, W.; Elsäßer, A.; Dullenkopf, K.; Wittig, S. Droplet Interaction with Shear-Driven Liquid Films: Analysis of Deposition and Secondary Droplet Characteristics. Int. J. Heat Fluid Flow 1999, 20, 462–469. [Google Scholar] [CrossRef]
- Liu, D.; Tan, H.-W.; Tran, T. Droplet Impact on Heated Powder Bed. Soft Matter 2018, 14, 9967–9972. [Google Scholar] [CrossRef] [PubMed]




| Variable | Symbol | Range |
|---|---|---|
| Water droplet diameter (mm) | d | 2.4–4.1 |
| Water droplet release height (mm) | Z | 250–750 |
| Water density (kg/) | 997 | |
| Water kinematic viscosity (cSt) | 1 | |
| Water surface tension (mN/m) | 72.2 | |
| Effective Weber number | 145–704 | |
| Reynolds number | 5195–15,216 | |
| Oil density (kg/) | 962–964 | |
| Oil kinematic viscosity (cSt) | 1–100 | |
| Oil surface tension (mN/m) | 19.8–21.3 |
| We Number Range | Oil Layer Thickness | Jet Pinch-Off | Crater Formation |
|---|---|---|---|
| Low (150–230) | Ultrathin | No/low pinch-off | No displacement |
| Thick | Slight pinch-off | No displacement | |
| Medium (230–400) | Ultrathin | Low to medium pinch-off | Short displacement |
| Thick | Medium pinch-off | Short to medium displacement | |
| High (470–710) | Ultrathin | Medium to high pinch-off | Medium to full crown |
| Thick | Less frequent high pinch-off | Medium, full crown less likely |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dehghanghadikolaei, A.; Abdul Halim, B.; Khoshbakhtnejad, E.; Sojoudi, H. Dynamics of a Water Droplet Impacting an Ultrathin Layer of Oil Suspended on a Pool of Water. Fluids 2024, 9, 82. https://doi.org/10.3390/fluids9040082
Dehghanghadikolaei A, Abdul Halim B, Khoshbakhtnejad E, Sojoudi H. Dynamics of a Water Droplet Impacting an Ultrathin Layer of Oil Suspended on a Pool of Water. Fluids. 2024; 9(4):82. https://doi.org/10.3390/fluids9040082
Chicago/Turabian StyleDehghanghadikolaei, Amir, Bilal Abdul Halim, Ehsan Khoshbakhtnejad, and Hossein Sojoudi. 2024. "Dynamics of a Water Droplet Impacting an Ultrathin Layer of Oil Suspended on a Pool of Water" Fluids 9, no. 4: 82. https://doi.org/10.3390/fluids9040082
APA StyleDehghanghadikolaei, A., Abdul Halim, B., Khoshbakhtnejad, E., & Sojoudi, H. (2024). Dynamics of a Water Droplet Impacting an Ultrathin Layer of Oil Suspended on a Pool of Water. Fluids, 9(4), 82. https://doi.org/10.3390/fluids9040082









