Computation of Real-Fluid Thermophysical Properties Using a Neural Network Approach Implemented in OpenFOAM
Abstract
1. Introduction
Present Contribution
2. Mathematical Models and Implementations
2.1. CFD Model
2.2. Artificial Neural Networks and Multilayer Perceptrons (MLP)
2.3. Training Database
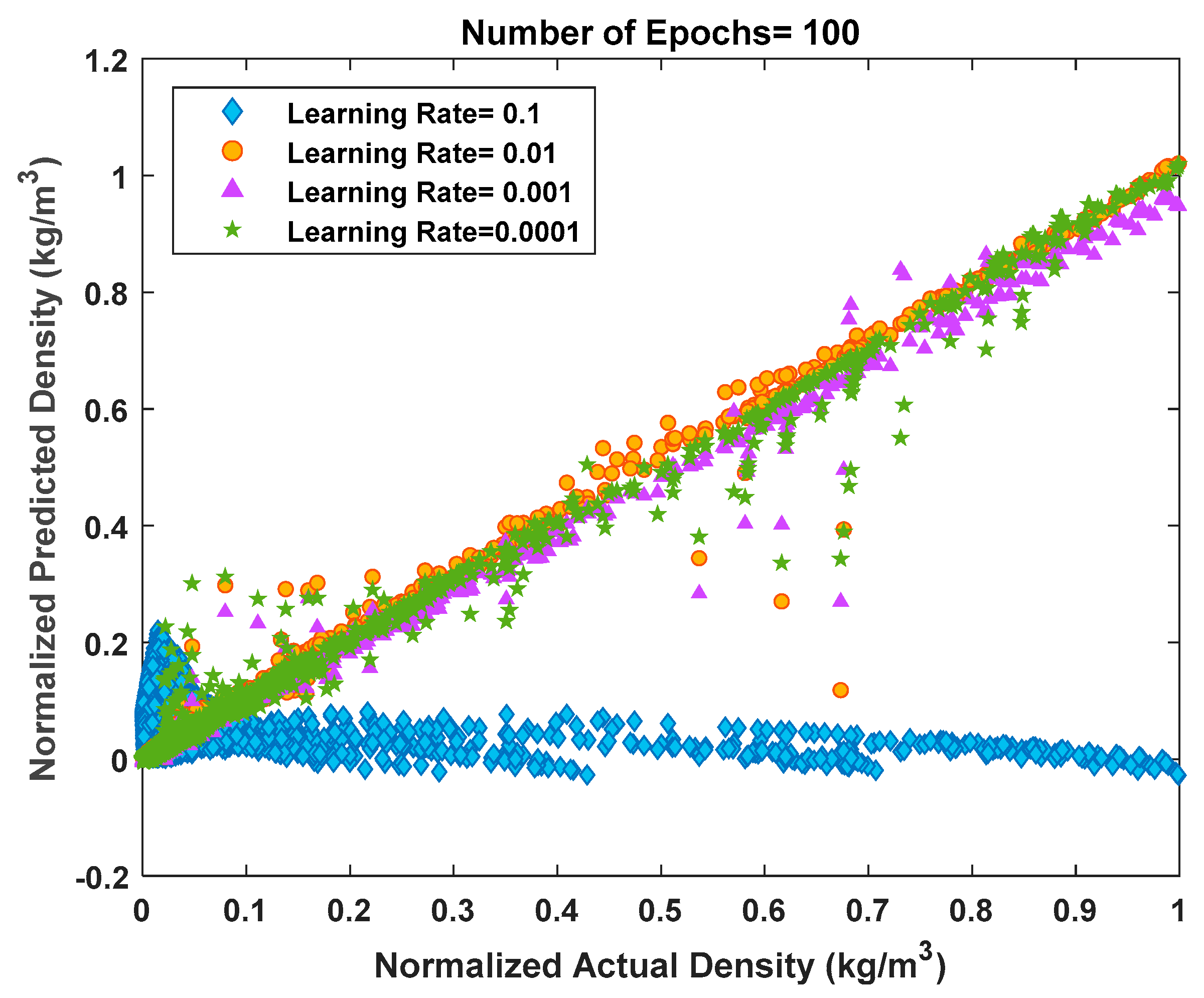
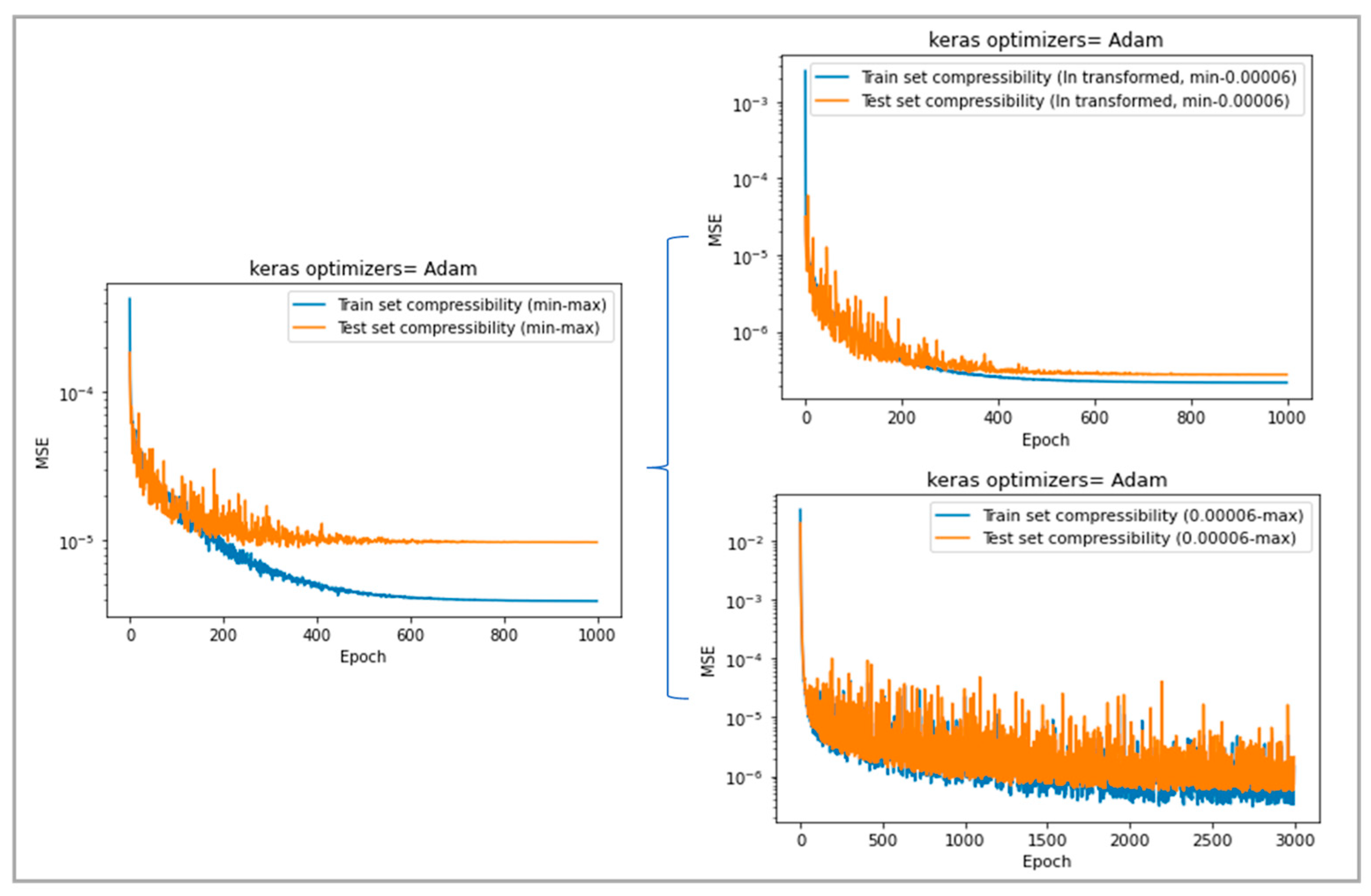
2.4. Model Training
2.5. Implementation of NN Models in OpenFOAM
- In the initialization stage, fields are read from dictionaries and values are used to infer each fluid property through Python-trained NN models via NNICE.
- Then, as shown in the flow chart in Figure 8, at the beginning of a time step, the continuity equation is first solved, and the PIMPLE iteration begins with the momentum predictor step.
- By entering the PISO loop, the species and energy equations are solved. Then, the thermodynamic properties, inferred through the Python-trained NN models with NNICE, replace the original thermo.correct() OpenFOAM function call. In more detail, temperature is first retrieved after the enthalpy equation is solved using information; then, all other properties (density , viscosity , thermal diffusivity , and compressibility ) are updated using the most recent values of .
- Other inferences are then needed inside each PISO loop. Density is first updated with the corresponding NN model before the pressure equation is solved (details of the pressure equation can be found in Figure 8b). Afterwards, density is explicitly updated, solving the continuity equation, and, after checking the continuity error, the velocity field is updated.
- The last step with the PISO loop concerns a new recalculation of the density field via its NN model.
- Outside the PISO loop, turbulence equations are solved, but no additional inferences are needed there. In addition, in this paper we do not include a turbulence model and assume a laminar flow to show the application of the ML method in OpenFOAM.
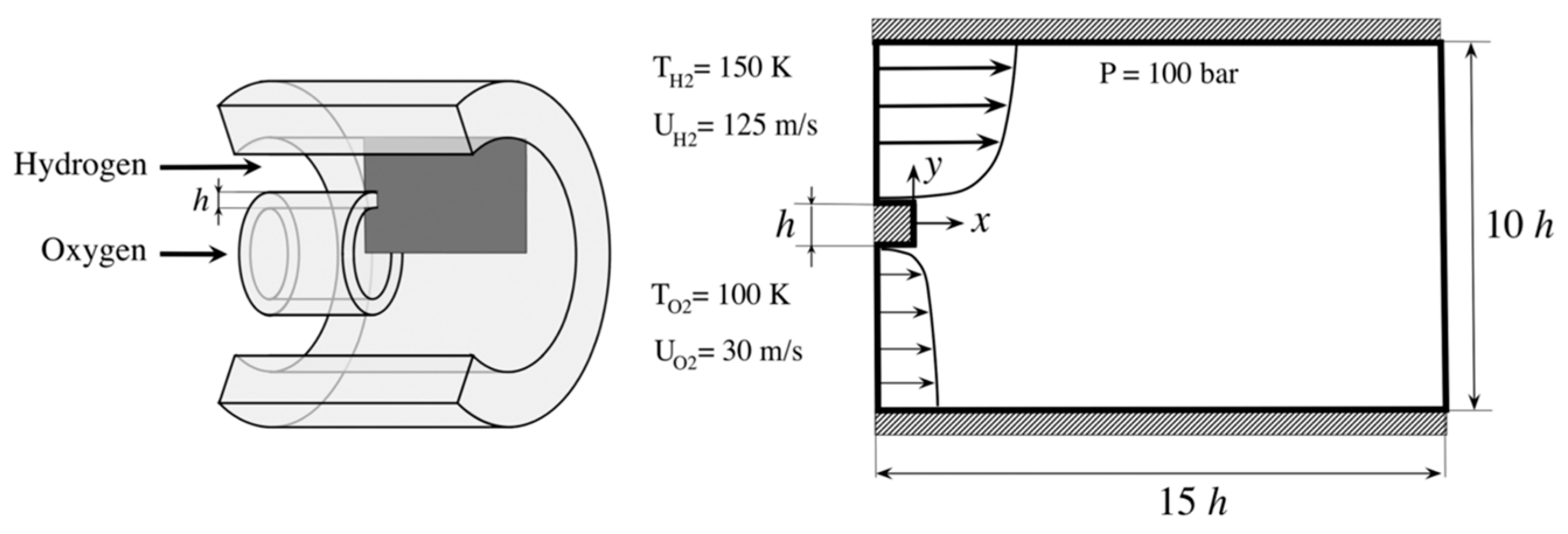
2.6. CFD Case Setup
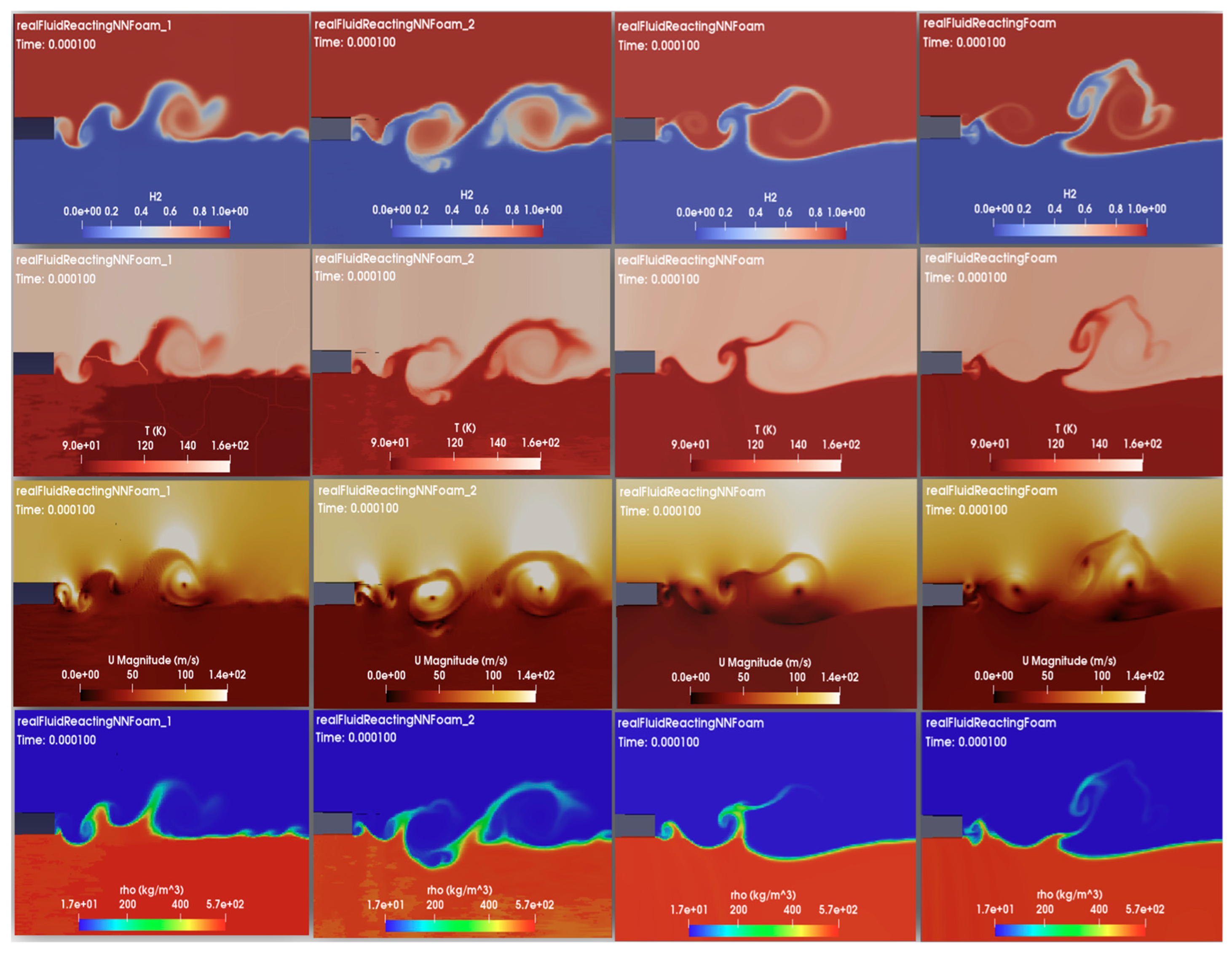
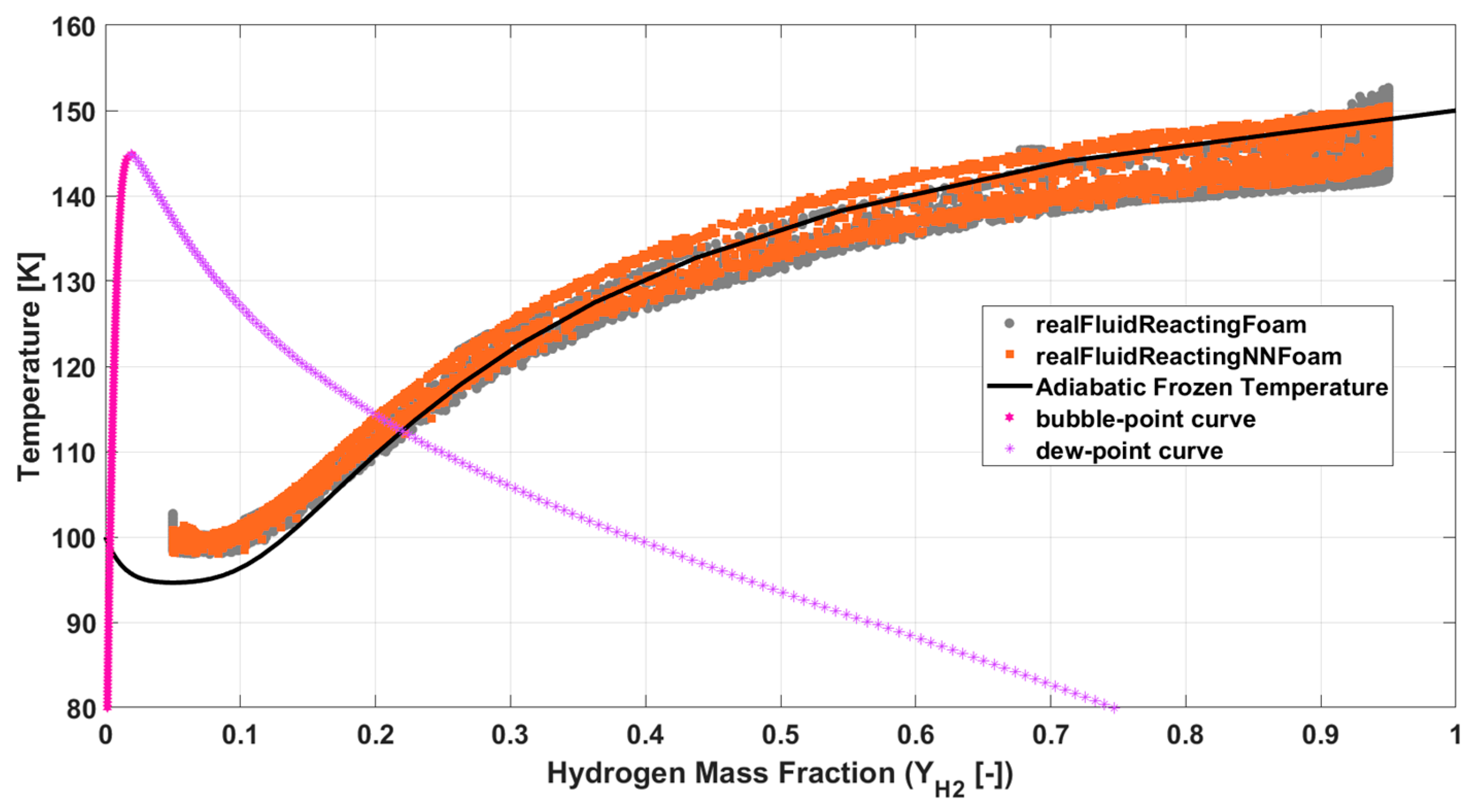
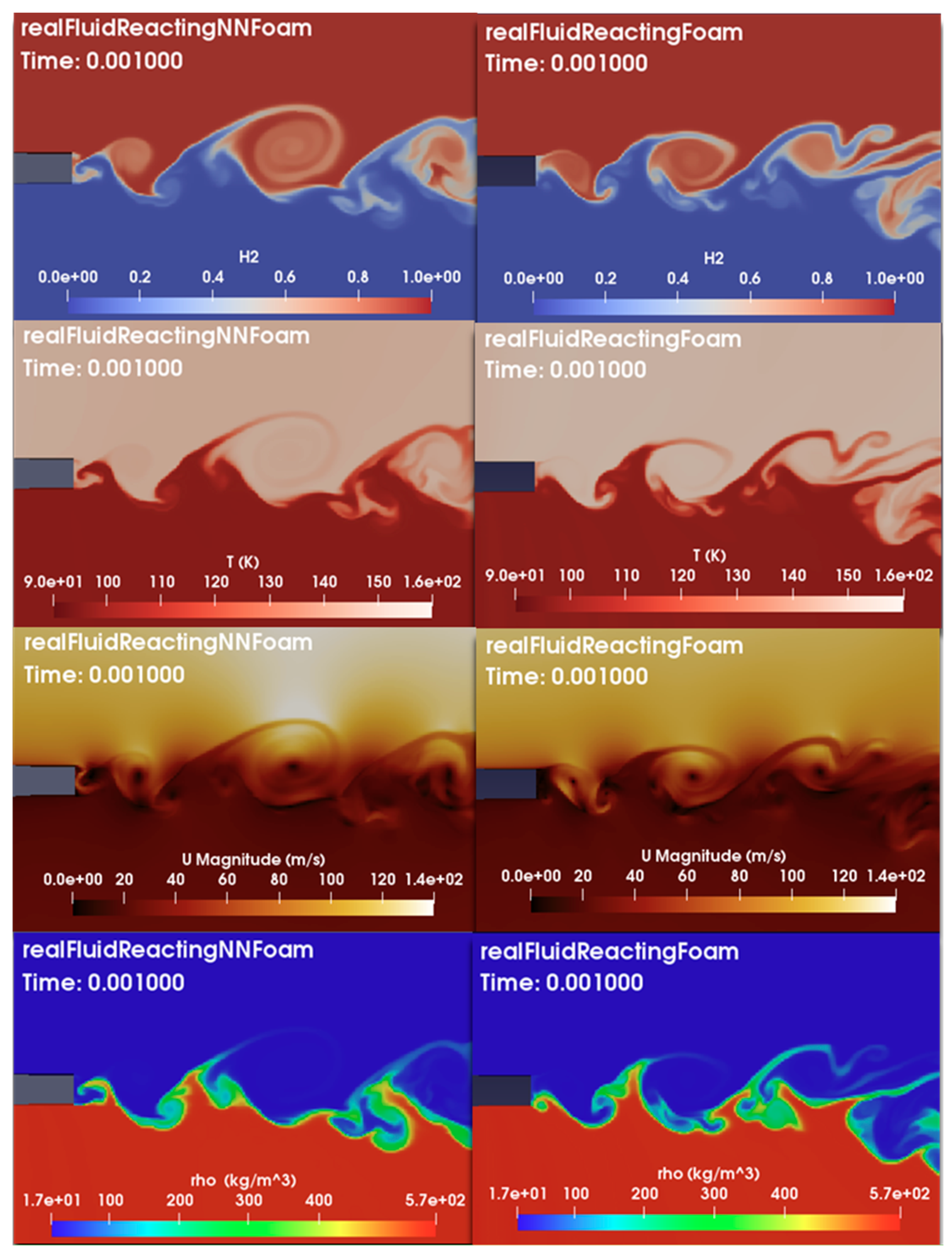
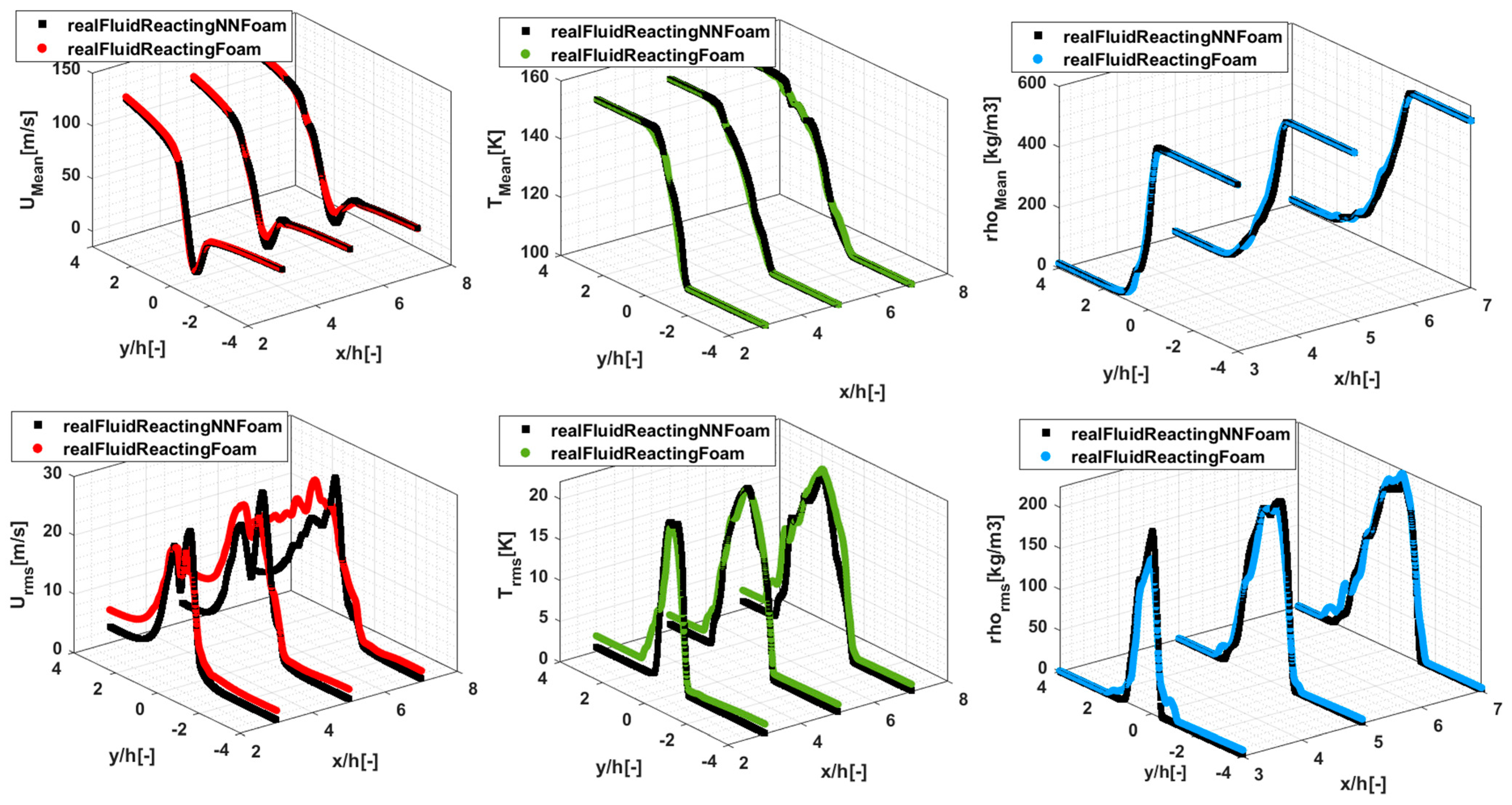
3. Results and Discussion
- The second CFD model is referred to as realFluidReactingNNFoam_1 which adopts a NN approach (referred to here as NN_1 variant) wherein Python-trained NN models and NNICE inference are used to replace original calculations through the RFM.
- The third CFD solver is referred to as realFluidReactingNNFoam_2, which is similar to the second model, but incorporates log transformations for density, compressibility, viscosity, and thermal diffusivity to achieve target accuracy criteria (referred to here as NN_2 variant).
- The last model is referred to as realFluidReactingNNFoam. It is like the previous one, but uses an adapted data range, which means that the data range for training is chosen to be as close as possible to the case study needs to improve network accuracy (referred to here as NN variant).
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, Z.; Shen, Y.; Wang, C.; Zhang, Y.; Wang, Q.; Gavaises, M. Thermophysical properties of n-dodecane over a wide temperature and pressure range via molecular dynamics simulations with modification methods. J. Mol. Liq. 2023, 371, 121102. [Google Scholar] [CrossRef]
- Rahantamialisoa, F.N.; Pandal, A.; Ningegowda, B.M.; Zembi, J.; Sahranavardfard, N.; Jasak, H.; Im, H.G.; Battistoni, M. Assessment of an open-source pressure-based real fluid model for transcritical jet flows. In Proceedings of the International Conference on Liquid Atomization and Spray Systems (ICLASS), Edinburgh, Scotland UK, 30 August 2021; Volume 1. [Google Scholar]
- Qiu, L.; Reitz, R.D. An investigation of thermodynamic states during high-pressure fuel injection using equilibrium thermodynamics. Int. J. Multiph. Flow 2015, 72, 24–38. [Google Scholar] [CrossRef]
- Puissant, C.; Glogowski, M.J. Experimental characterization of shear coaxial injectors using liquid/gaseous nitrogen. At. Sprays 1997, 7, 467–478. [Google Scholar] [CrossRef]
- Mayer, W.; Tamura, H. Propellant injection in a liquid oxygen/gaseous hydrogen rocket engine. J. Propuls. Power 1996, 12, 1137–1147. [Google Scholar] [CrossRef]
- Habiballah, M.; Orain, M.; Grisch, F.; Vingert, L.; Gicquel, P. Experimental studies of high-pressure cryogenic flames on the mascotte facility. Combust. Sci. Technol. 2006, 178, 101–128. [Google Scholar] [CrossRef]
- Rahantamialisoa, F.N.Z.; Zembi, J.; Miliozzi, A.; Sahranavardfard, N.; Battistoni, M. CFD simulations of under-expanded hydrogen jets under high-pressure injection conditions. J. Phys. Conf. Ser. 2022, 2385, 012051. [Google Scholar] [CrossRef]
- Oschwald, M.; Smith, J.J.; Branam, R.; Hussong, J.; Schik, A.; Chehroudi, B.; Talley, D. Injection of fluids into supercritical environments. Combust. Sci. Technol. 2006, 178, 49–100. [Google Scholar] [CrossRef]
- Yang, V. Modeling of supercritical vaporization, mixing, and combustion processes in liquid-fueled propulsion systems. Proc. Combust. Inst. 2000, 28, 925–942. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. Robinson, A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Oefelein, J.C.; Sankaran, R. Large eddy simulation of reacting flow physics and combustion. In Exascale Scientific Applications: Scalability and Performance Portability; Straatsma, T.P., Antypas, K.B., Williams, T.J., Eds.; CRC Press: Boca Raton, FL, USA, 2018; pp. 231–256. [Google Scholar]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- PMilan, P.J.; Li, Y.; Wang, X.; Yang, S.; Sun, W.; Yang, V. Time-efficient methods for real fluid property evaluation in numerical simulation of chemically reacting flows. In Proceedings of the 11th US National Combustion Meeting, 71TF-0396, Pasadena, CA, USA, 24–27 March 2019; pp. 1–10. [Google Scholar]
- Milan, P.J.; Hickey, J.P.; Wang, X.; Yang, V. Deep-learning accelerated calculation of real-fluid properties in numerical simulation of complex flowfields. J. Comput. Phys. 2021, 444, 110567. [Google Scholar] [CrossRef]
- Ruggeri, M.; Roy, I.; Mueterthies, M.J.; Gruenwald, T.; Scalo, C. Neural-network-based Riemann solver for real fluids and high explosives; application to computational fluid dynamics. Phys. Fluids 2022, 34, 116121. [Google Scholar] [CrossRef]
- Jafari, S.; Gaballa, H.; Habchi, C.; de Hemptinne, J.C. Towards understanding the structure of subcritical and transcritical liquid–gas interfaces using a tabulated real fluid modeling approach. Energies 2021, 14, 5621. [Google Scholar] [CrossRef]
- Jafari, S.; Gaballa, H.; Habchi, C.; Hemptinne, J.C.; De Mougin, P. Exploring the interaction between phase separation and turbulent fluid dynamics in multi-species supercritical jets using a tabulated real-fluid model. J. Supercrit. Fluids 2022, 184, 105557. [Google Scholar] [CrossRef]
- Koukouvinis, P.; Rodriguez, C.; Hwang, J.; Karathanassis, I.; Gavaises, M.; Pickett, L. Machine Learning and transcritical sprays: A demonstration study of their potential in ECN Spray-A. Int. J. Engine Res. 2022, 23, 1556–1572. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Maulik, R.; Fytanidis, D.K.; Lusch, B.; Vishwanath, V.; Patel, S. PythonFOAM: In-situ data analyses with OpenFOAM and Python. J. Comput. Sci. 2022, 62, 101750. [Google Scholar] [CrossRef]
- Maulik, R.; Sharma, H.; Patel, S.; Lusch, B.; Jennings, E. Deploying deep learning in OpenFOAM with TensorFlow. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 January 2021; p. 1485. [Google Scholar]
- Kim, J.; Park, C.; Ahn, S.; Kang, B.; Jung, H.; Jang, I. Iterative learning-based many-objective history matching using deep neural network with stacked autoencoder. Pet. Sci. 2021, 18, 1465–1482. [Google Scholar] [CrossRef]
- Liu, Y.-Y.; Ma, X.-H.; Zhang, X.-W.; Guo, W.; Kang, L.-X.; Yu, R.-Z.; Sun, Y.-P. A deep-learning-based prediction method of the estimated ultimate recovery (EUR) of shale gas wells. Pet. Sci. 2021, 18, 1450–1464. [Google Scholar] [CrossRef]
- Rahantamialisoa, F.N.Z.; Gopal, J.V.M.; Tretola, G.; Sahranavardfard, N.; Vogiatzaki, K.; Battistoni, M. Analyzing single and multicomponent supercritical jets using volume-based and mass-based numerical approaches. Phys. Fluids 2023, 35, 067123. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Rahantamialisoa, F.N.Z.; Pandal, A.; Jasak, H.; Im, H.G.; Battistoni, M. Numerical Modeling of Transcritical and Supercritical Fuel Injections Using a Multi-Component Two-Phase Flow Model. Energies 2020, 13, 5676. [Google Scholar] [CrossRef]
- Chung, T.H.; Ajlan, M.; Lee, L.L.; Starling, K.E. Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Eng. Chem. Res. 1998, 27, 671–679. [Google Scholar] [CrossRef]
- Ding, T.; Readshaw, T.; Rigopoulos, S.; Jones, W.P. Machine learning tabulation of thermochemistry in turbulent combustion: An approach based on hybrid flamelet/random data and multiple multilayer perceptrons. Combust. Flame 2021, 231, 111493. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)-a review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Clarendon Press: Oxford, UK, 1995. [Google Scholar]
- Watt, J.; Borhani, R.; Katsaggelos, A.K. Machine Learning Refined: Foundations, Algorithms, and Applications; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Delhom, B.; Faney, T.; Mcginn, P.; Habchi, C.; Bohbot, J. Development of a multi-species real fluid modelling approach using a machine learning method. In Proceedings of the ILASS Europe 2023, 32nd European Conference on Liquid Atomization & Spray Systems, Napoli, Italy, 4–7 September 2023. [Google Scholar]
- Anzanello, M.J.; Fogliatto, F.S. Learning curve models and applications: Literature review and research directions. Int. J. Ind. Ergon. 2011, 41, 573–583. [Google Scholar] [CrossRef]
- Witten, D.; James, G. An Introduction to Statistical Learning with Applications in R; Goodfellow, I., Bengio, Y., Courville, A., Eds.; Deep Learning; Springer Publication, 2013, MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Chen, X.; Mehl, C.; Faney, T.; Di Meglio, F. Clustering-Enhanced Deep Learning Method for Computation of Full Detailed Thermochemical States via Solver-Based Adaptive Sampling. Energy Fuels 2023, 37, 14222–14239. [Google Scholar] [CrossRef]
- Aubagnac-Karkar, D.; Mehl, C. NNICE: Neural Network Inference in C Made Easy, Version 1.0.0; Computer Software. Available online: https://zenodo.org/records/7645515 (accessed on 16 February 2023). [CrossRef]
- Zong, N.; Yang, V. Near-field flow and flame dynamics of LOX/methane shear-coaxial injector under supercritical conditions. Proc. Combust. Inst. 2007, 31, 2309–2317. [Google Scholar] [CrossRef]
- Zong, N.; Yang, V. Cryogenic fluid jets and mixing layers in transcritical and supercritical environments. Combust. Sci. Technol. 2006, 178, 193–227. [Google Scholar] [CrossRef]
- Oefelein, J.C. Mixing and combustion of cryogenic oxygen-hydrogen shear-coaxial jet flames at supercritical pressure. Combust. Sci. Technol. 2006, 178, 229–252. [Google Scholar] [CrossRef]
- Oefelein, J.C. Thermophysical characteristics of shear-coaxial LOX–H2 flames at supercritical pressure. Proc. Combust. Inst. 2005, 30, 2929–2937. [Google Scholar] [CrossRef]
- Oefelein, J.C.; Yang, V. Modeling High-Pressure Mixing and Combustion Processes in Liquid Rocket Engines. J. Propuls. Power 1998, 14, 843–857. [Google Scholar] [CrossRef]
- Ruiz, A.M.; Lacaze, G.; Oefelein, J.C.; Mari, R.; Cuenot, B.; Selle, L.; Poinsot, T. Numerical benchmark for high-reynolds-number supercritical flows with large density gradients. AIAA J. 2016, 54, 1445–1460. [Google Scholar] [CrossRef]
- Ningegowda, B.M.; Rahantamialisoa, F.; Zembi, J.; Pandal, A.; Im, H.G.; Battistoni, M. Large Eddy Simulations of Supercritical and Transcritical Jet Flows Using Real Fluid Thermophysical Properties; SAE Technical Paper 2020-01-1153; SAE: Warrendale, PA, USA, 2020. [Google Scholar]
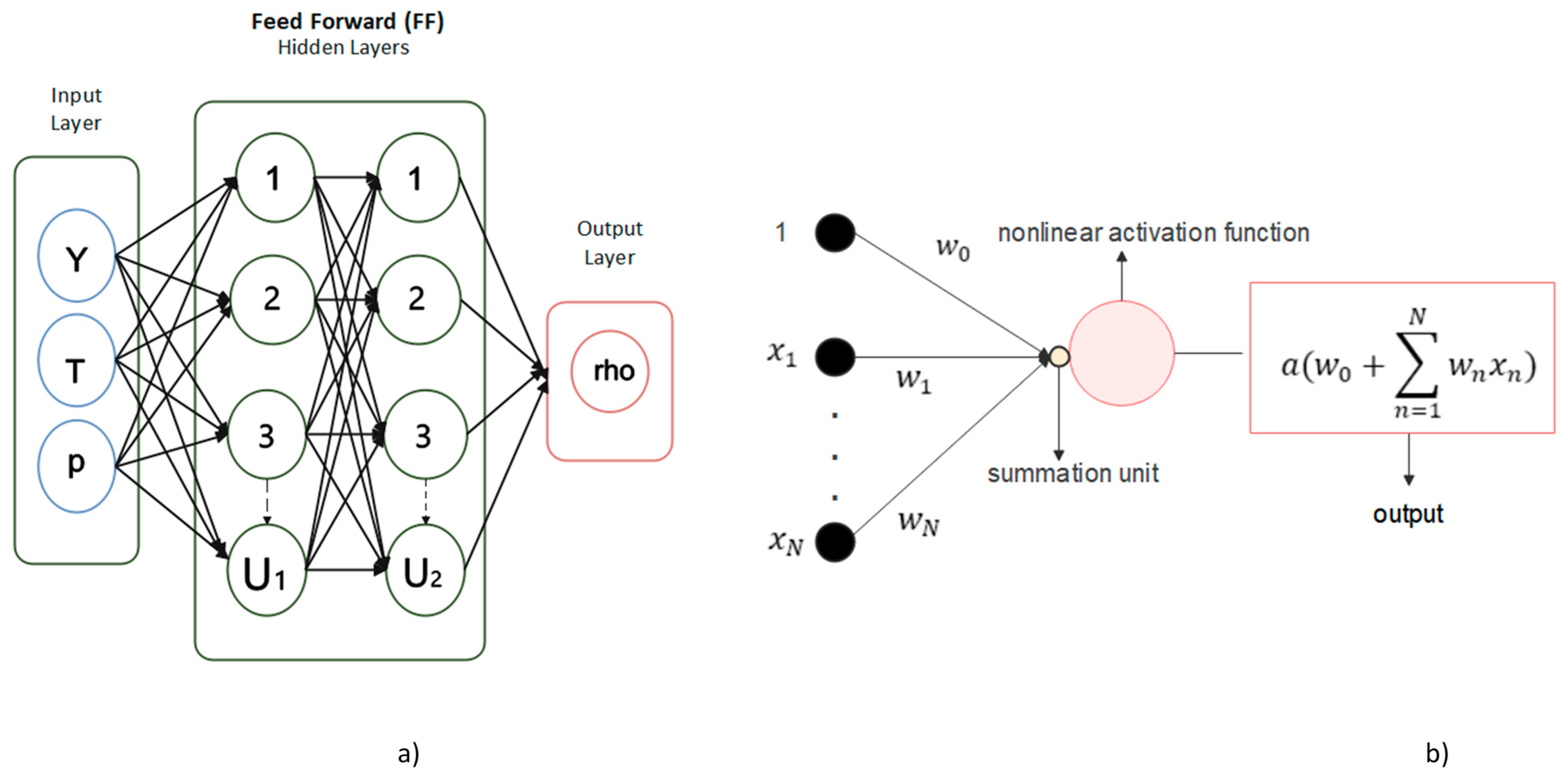




| Inputs | Outputs | |
|---|---|---|
| Variable Symbol (Code Name) | Definition [Units] | |
| Fuel mass fraction [-] | All output variables (except ) | |
| Temperature [K] | All variables (except ) | |
| Pressure [Pa] | All variables (except ) | |
| Enthalpy [J/kg] | ||
| Variable Symbol (Code Name) | Definition [Units] |
|---|---|
| Density [ | |
| Viscosity | |
| Thermal diffusivity [] | |
| Specific enthalpy: [] | |
| Compressibility | |
| Temperature |
| Output (Applied Min-Max Scalar) | Inputs (Applied Min-Max Scalar) | Hidden Layer Size | Activation Function | Solver | Learning Rate | Loss Metrics | Epochs | Batch-Size |
|---|---|---|---|---|---|---|---|---|
| 100 × 100 | ReLU | ADAM | 0.0015 | MSE | 1000 | 256 | ||
| 100 × 100 | ReLU | ADAM | 0.0015 | MSE | 1000 | 256 |
| Solver | Total Execution | Iteration | |||
|---|---|---|---|---|---|
| Time (s) | Speed-Up | Total Number of Iterations | Time/Iter (s/Iter) | Speed-Up | |
| realFluidReactingFoam | 511,096 | 1 | 200,550 | 2.548 | 1 |
| realFluidReactingNNFoam | 179,317 | 2.850 | 523,200 | 0.343 | 7.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahranavardfard, N.; Aubagnac-Karkar, D.; Costante, G.; Rahantamialisoa, F.N.Z.; Habchi, C.; Battistoni, M. Computation of Real-Fluid Thermophysical Properties Using a Neural Network Approach Implemented in OpenFOAM. Fluids 2024, 9, 56. https://doi.org/10.3390/fluids9030056
Sahranavardfard N, Aubagnac-Karkar D, Costante G, Rahantamialisoa FNZ, Habchi C, Battistoni M. Computation of Real-Fluid Thermophysical Properties Using a Neural Network Approach Implemented in OpenFOAM. Fluids. 2024; 9(3):56. https://doi.org/10.3390/fluids9030056
Chicago/Turabian StyleSahranavardfard, Nasrin, Damien Aubagnac-Karkar, Gabriele Costante, Faniry N. Z. Rahantamialisoa, Chaouki Habchi, and Michele Battistoni. 2024. "Computation of Real-Fluid Thermophysical Properties Using a Neural Network Approach Implemented in OpenFOAM" Fluids 9, no. 3: 56. https://doi.org/10.3390/fluids9030056
APA StyleSahranavardfard, N., Aubagnac-Karkar, D., Costante, G., Rahantamialisoa, F. N. Z., Habchi, C., & Battistoni, M. (2024). Computation of Real-Fluid Thermophysical Properties Using a Neural Network Approach Implemented in OpenFOAM. Fluids, 9(3), 56. https://doi.org/10.3390/fluids9030056








