Numerical Analysis of Cambered Plate Configurations under Low Reynolds Numbers and at a Low-Density Condition
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations
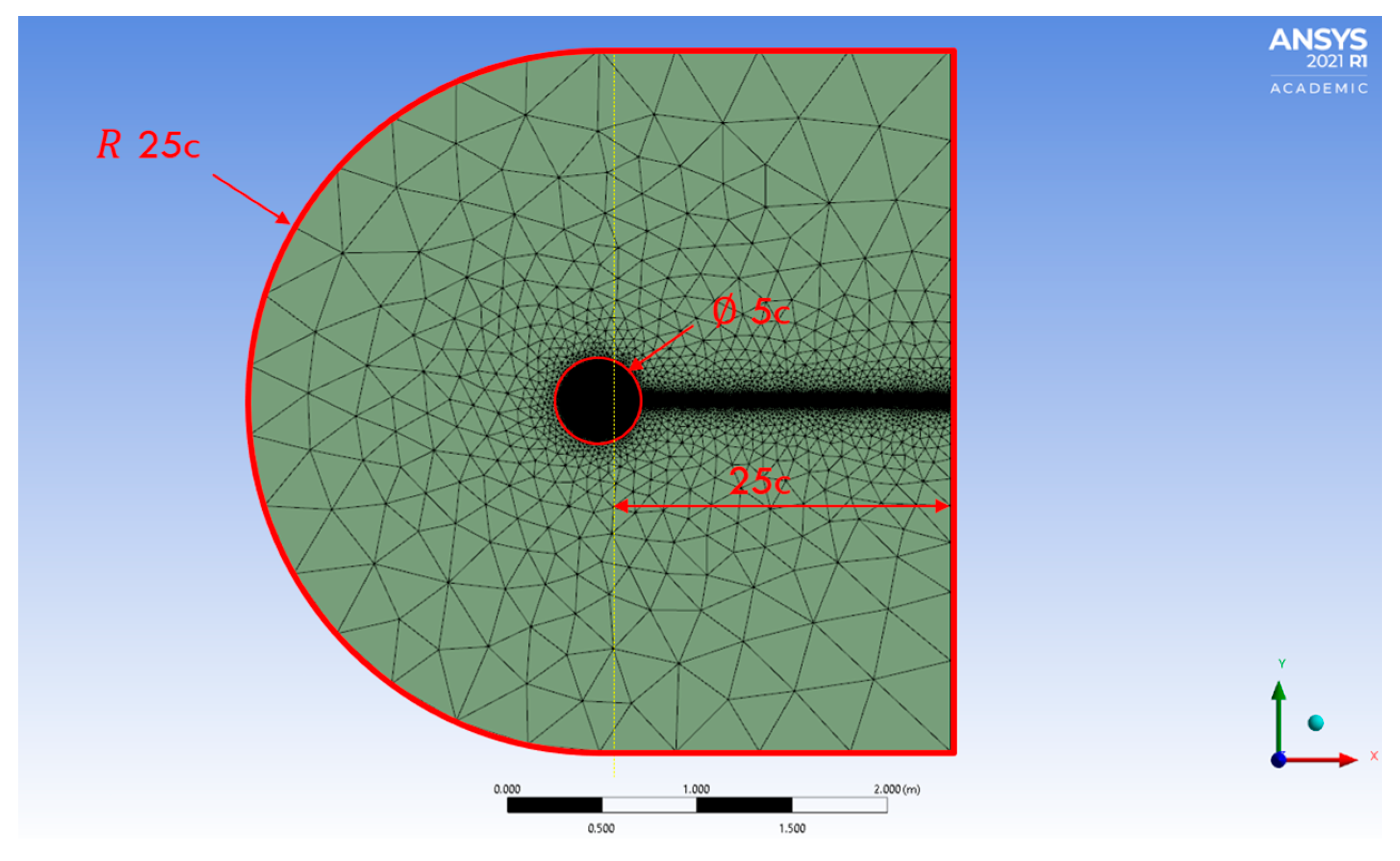
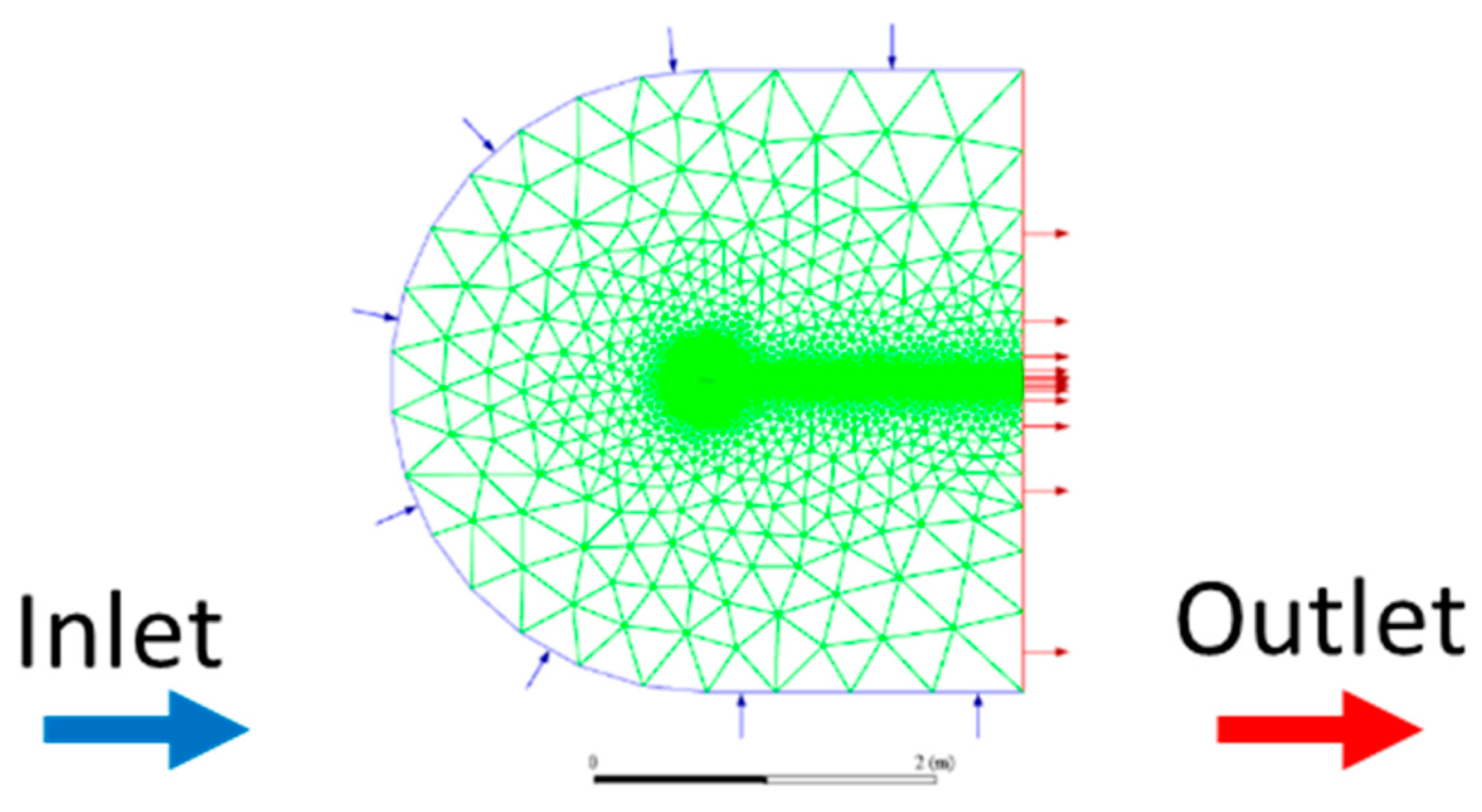
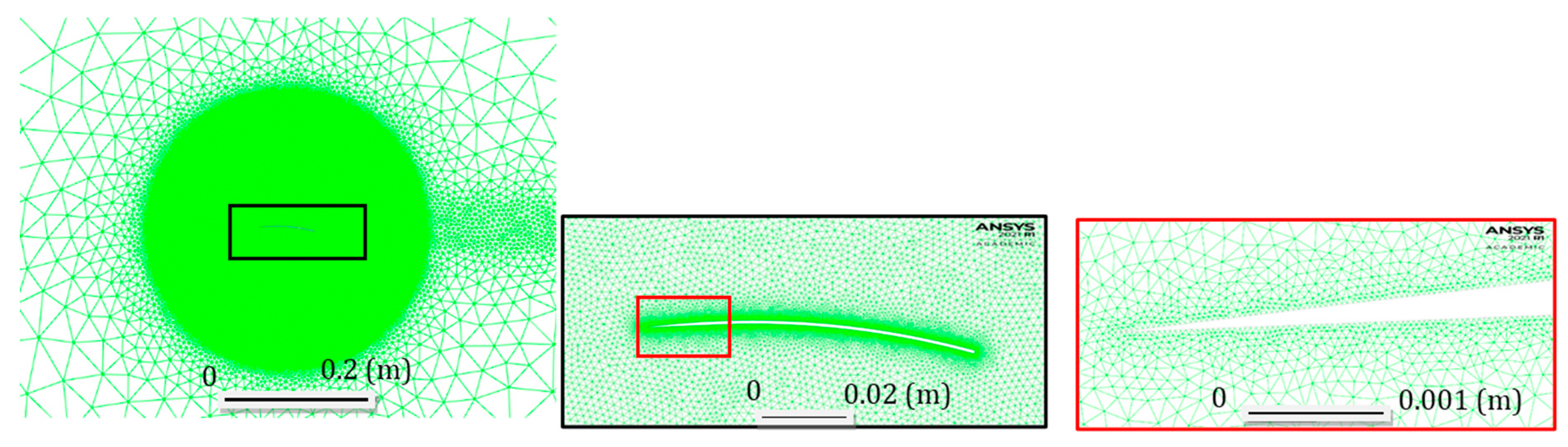
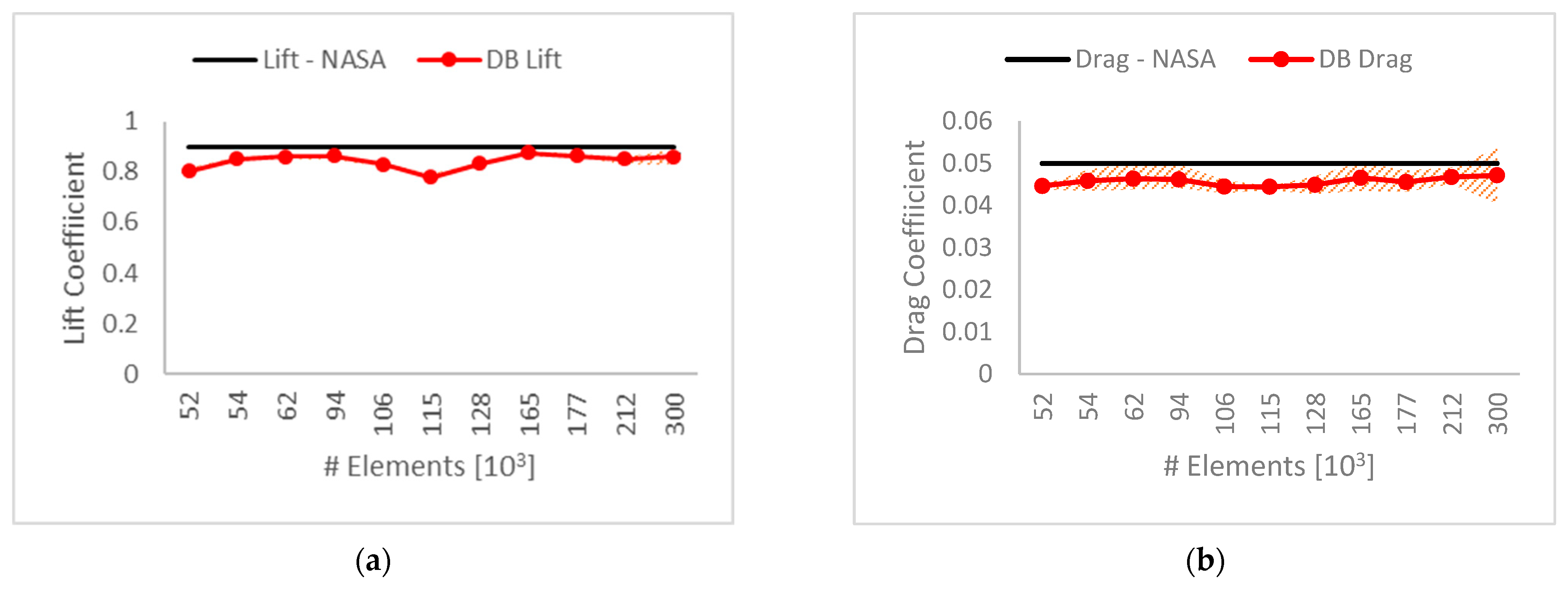
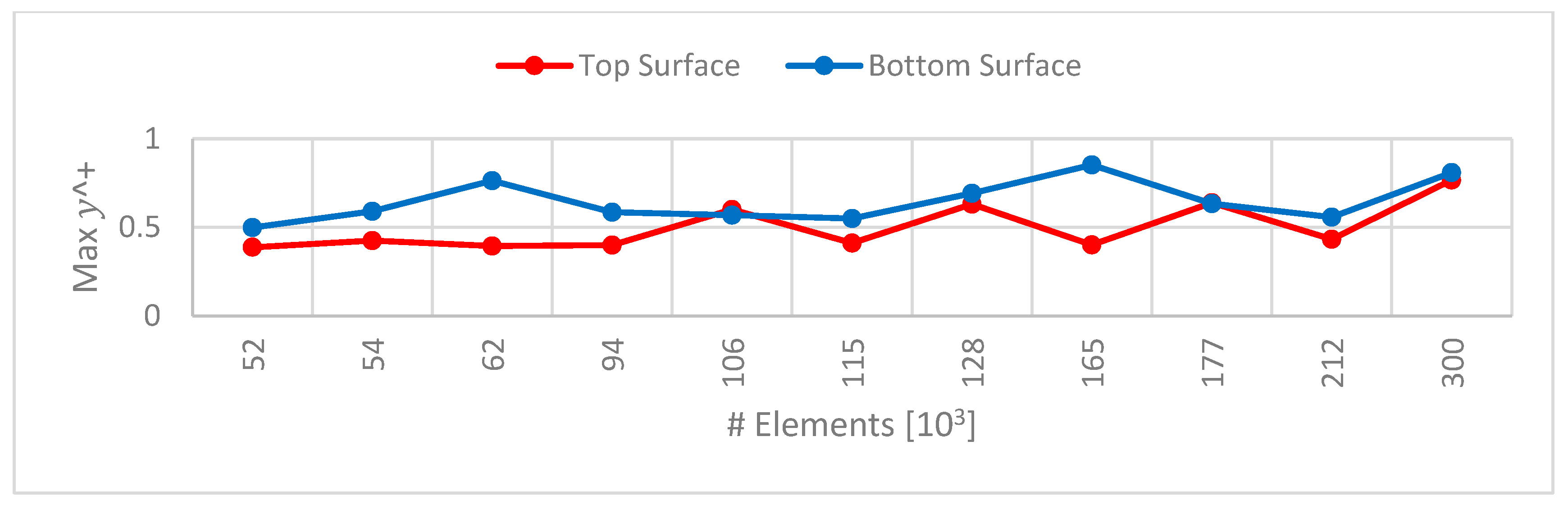
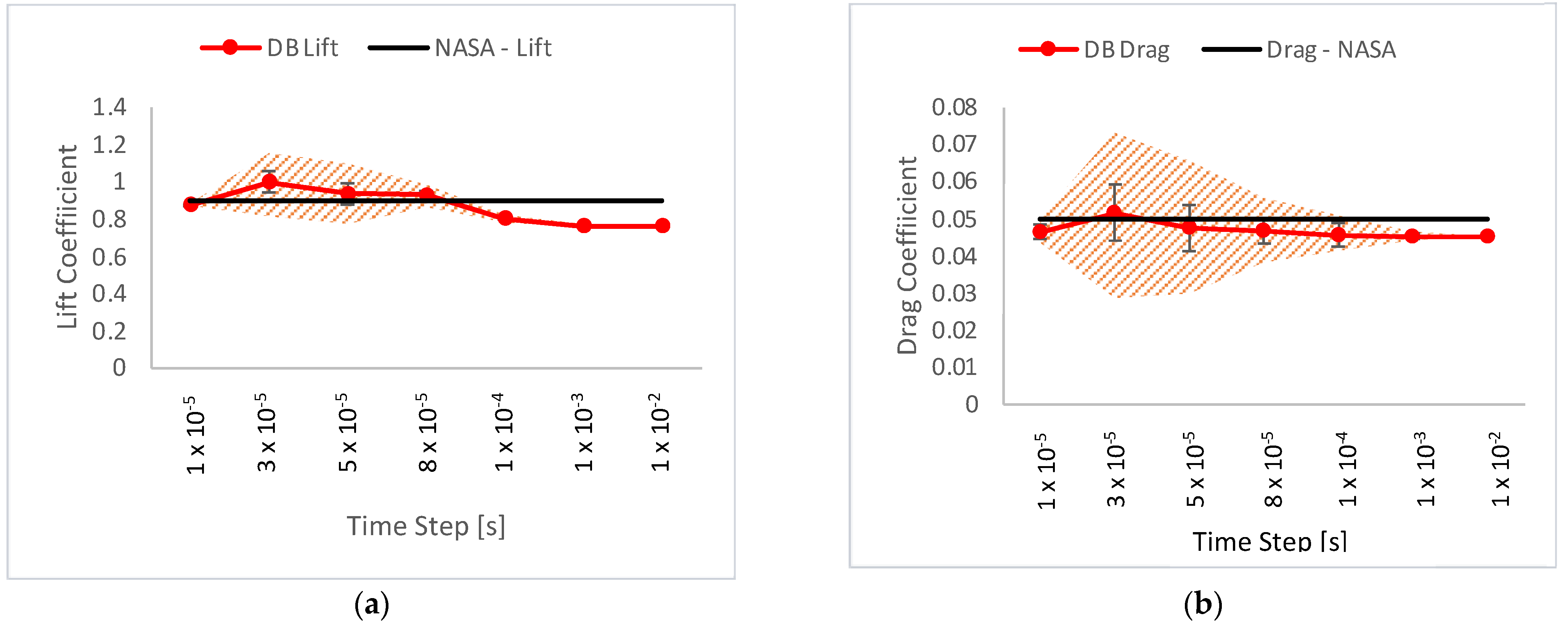
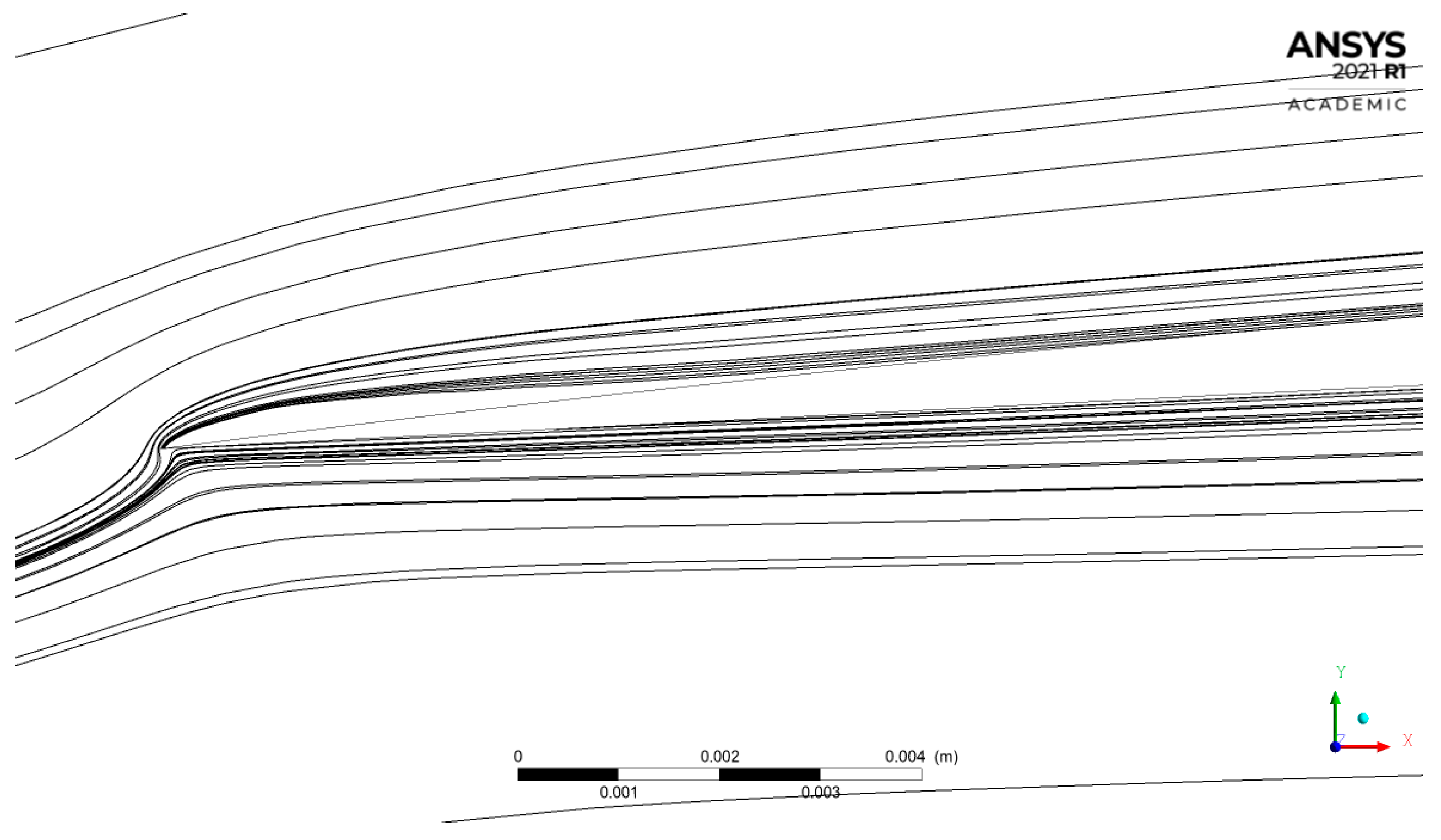
2.2. Model Verification
2.3. Model Validation
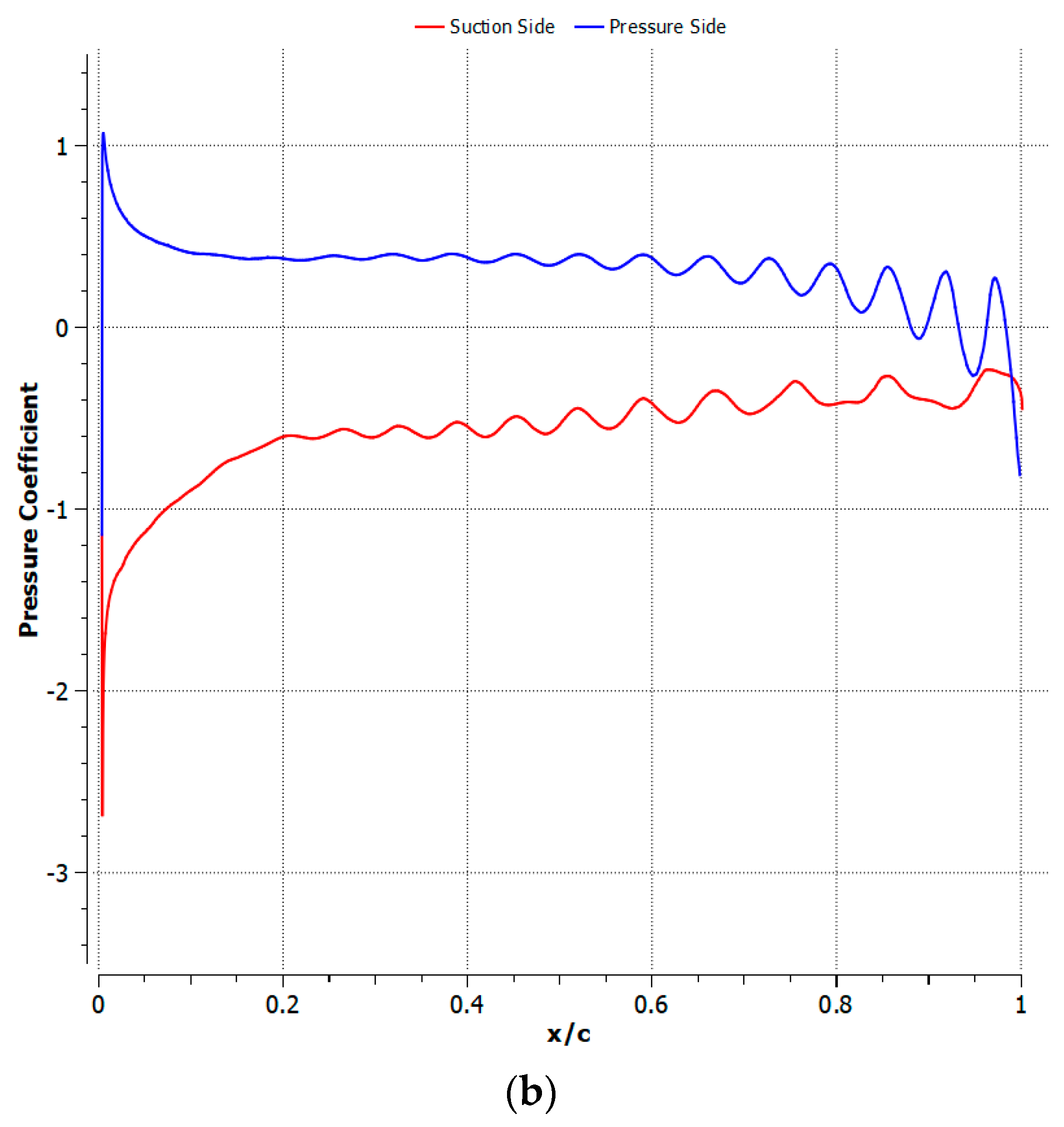
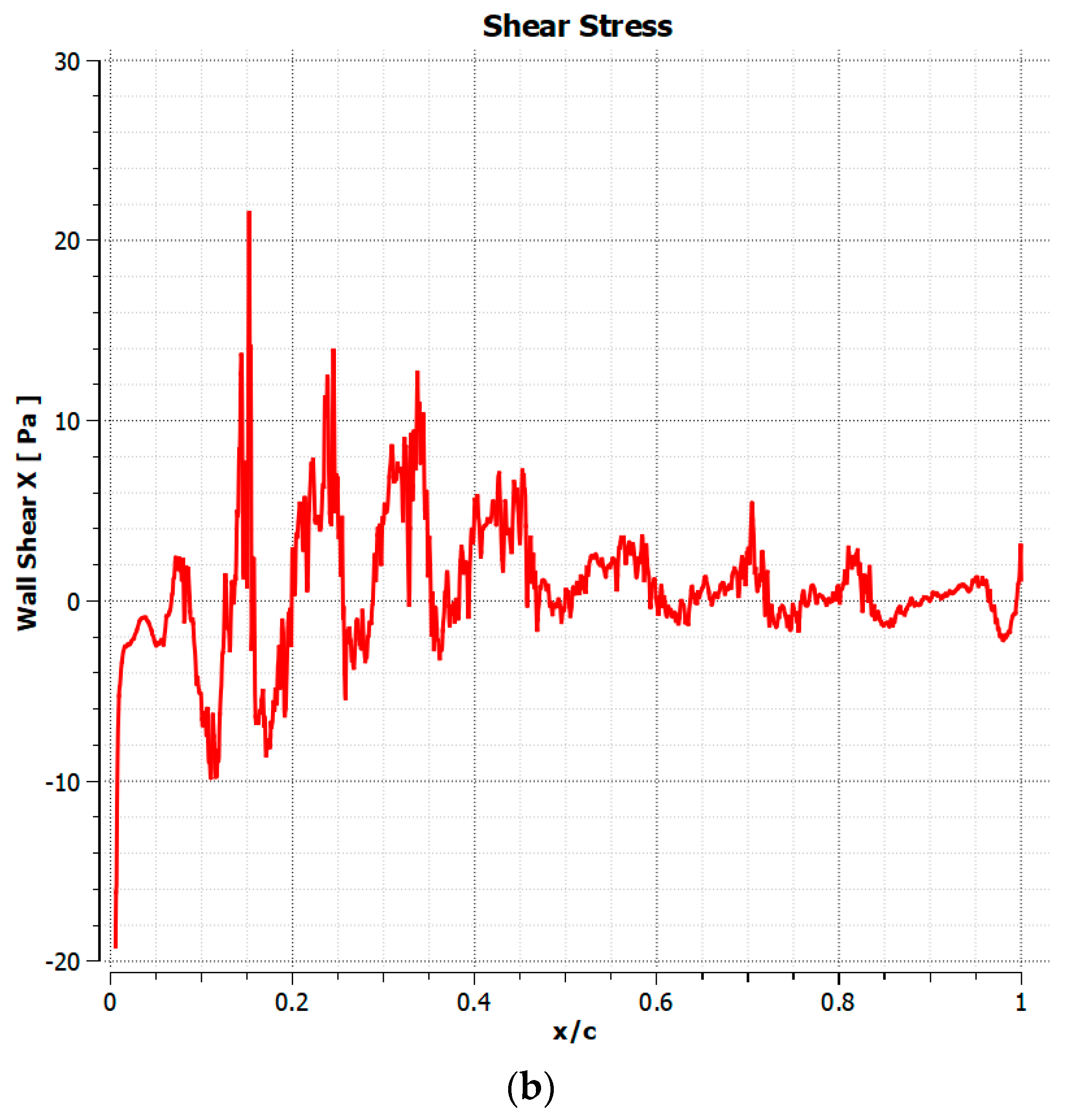
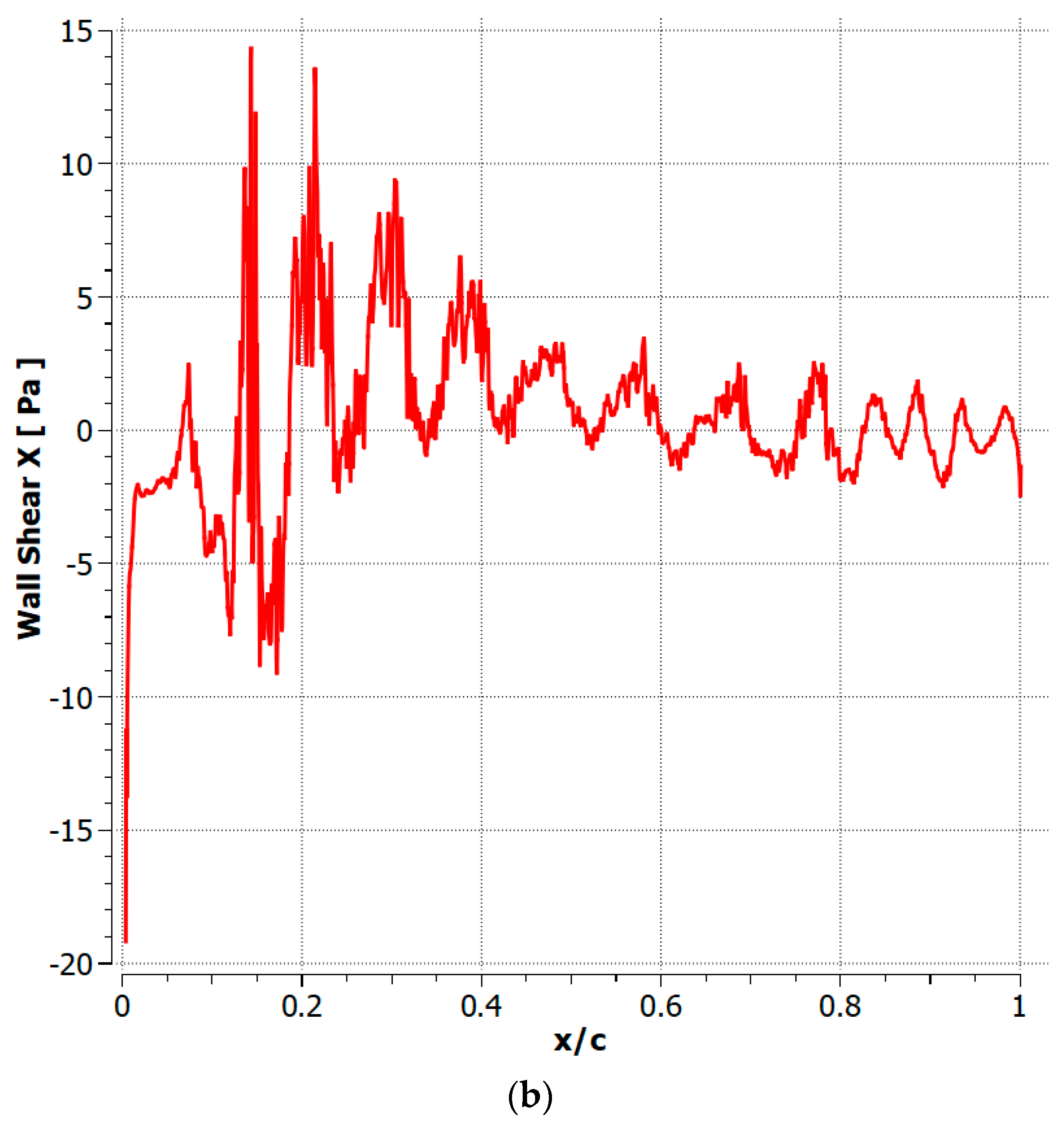
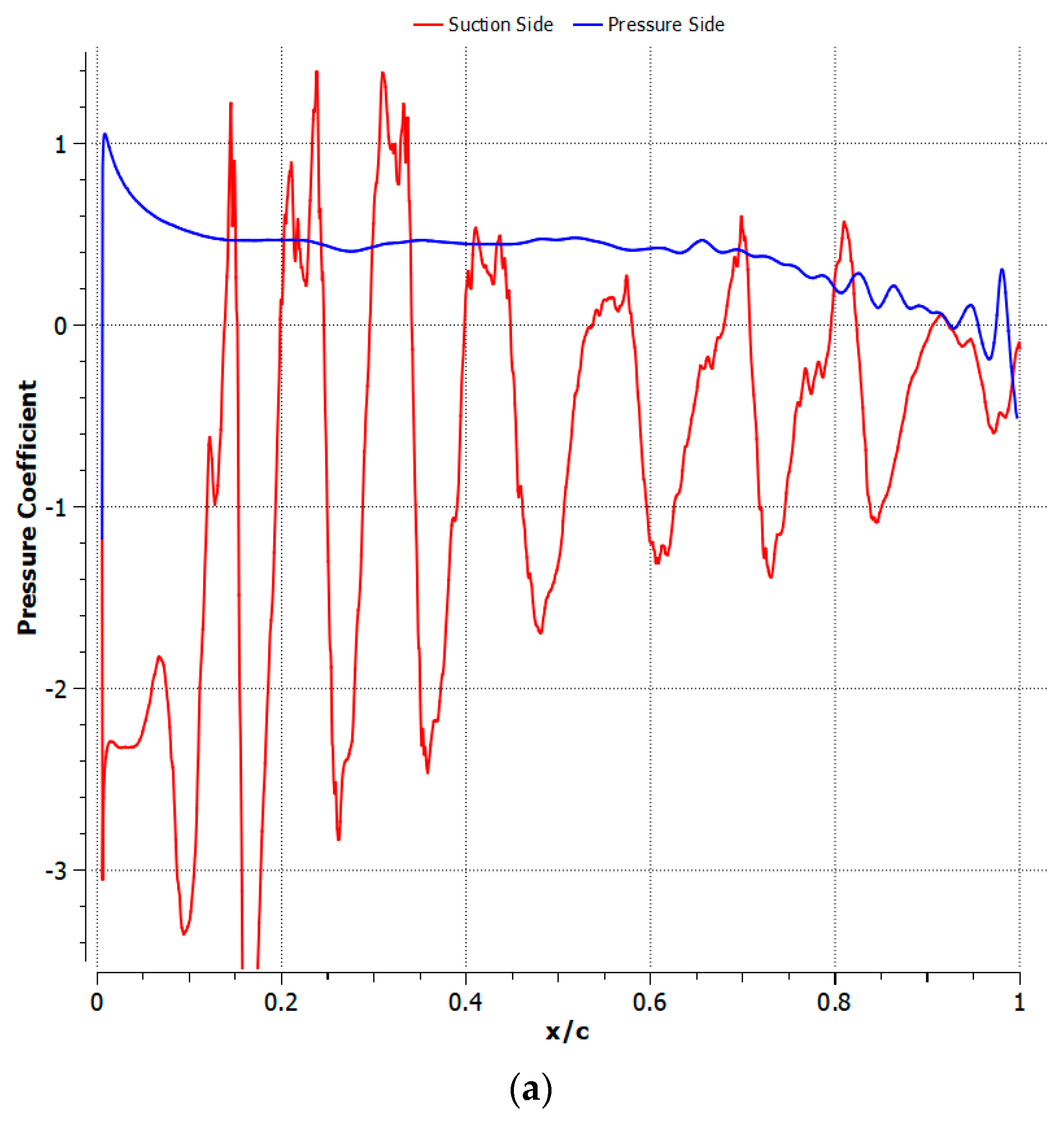
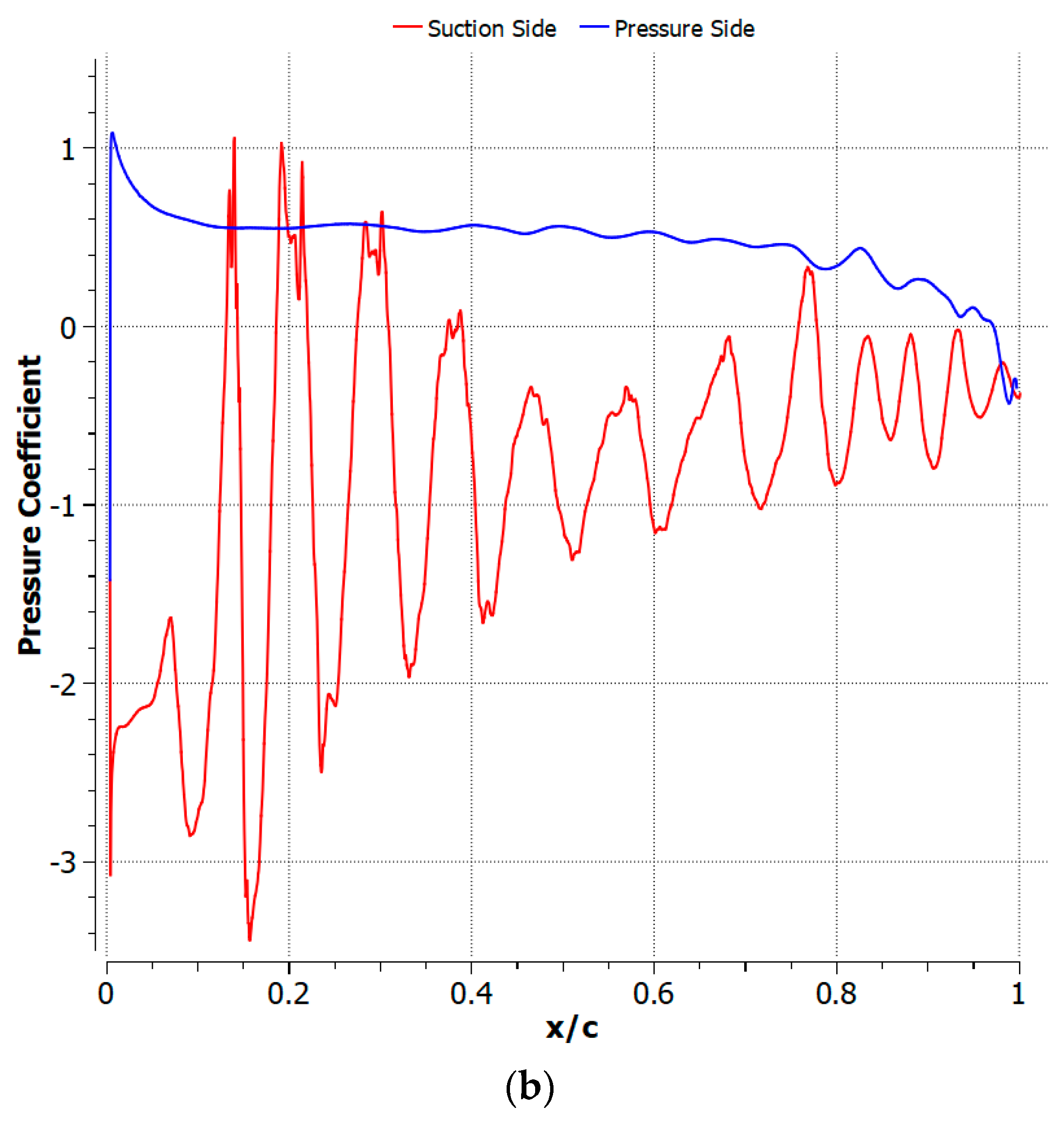
3. Results
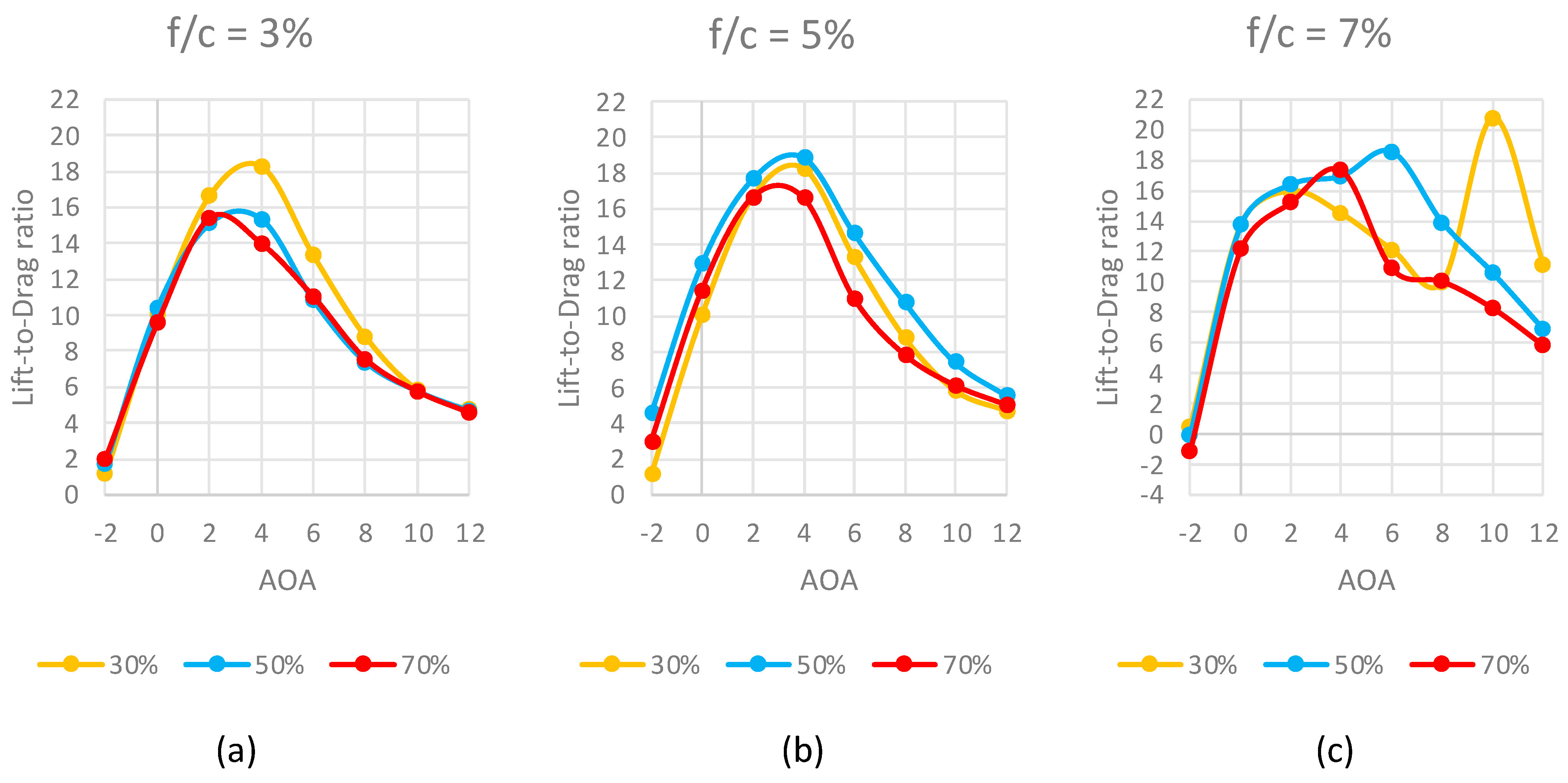
3.1. Parametric Study
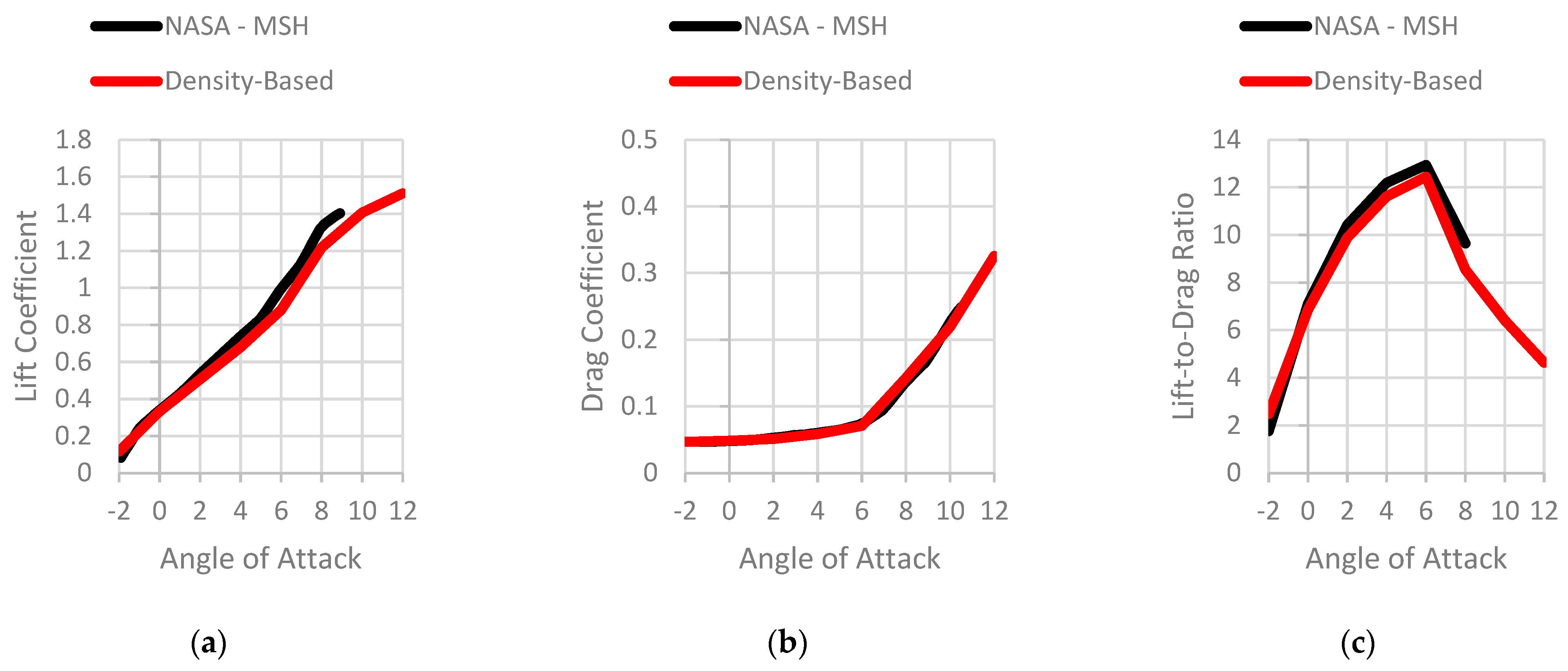
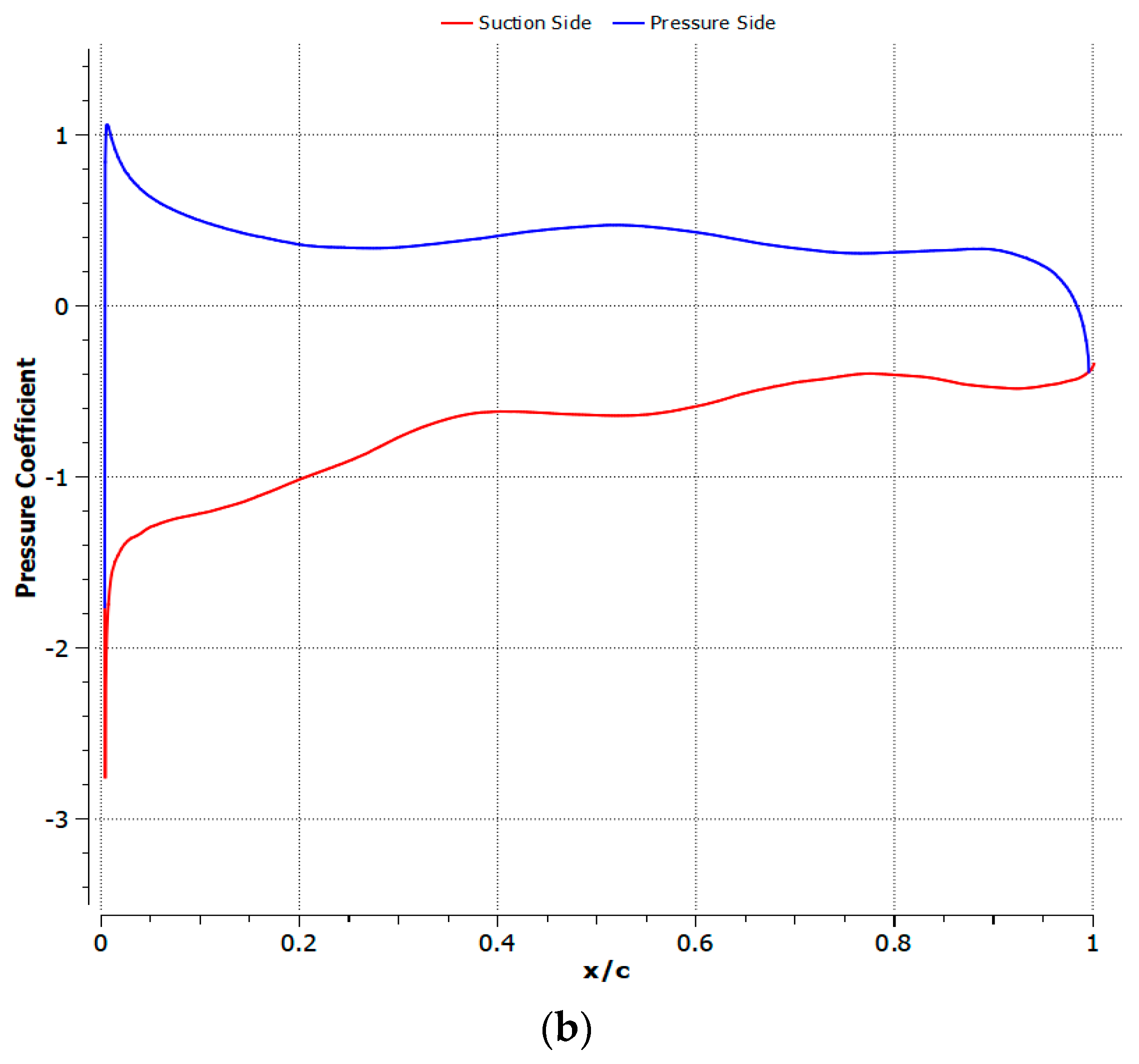
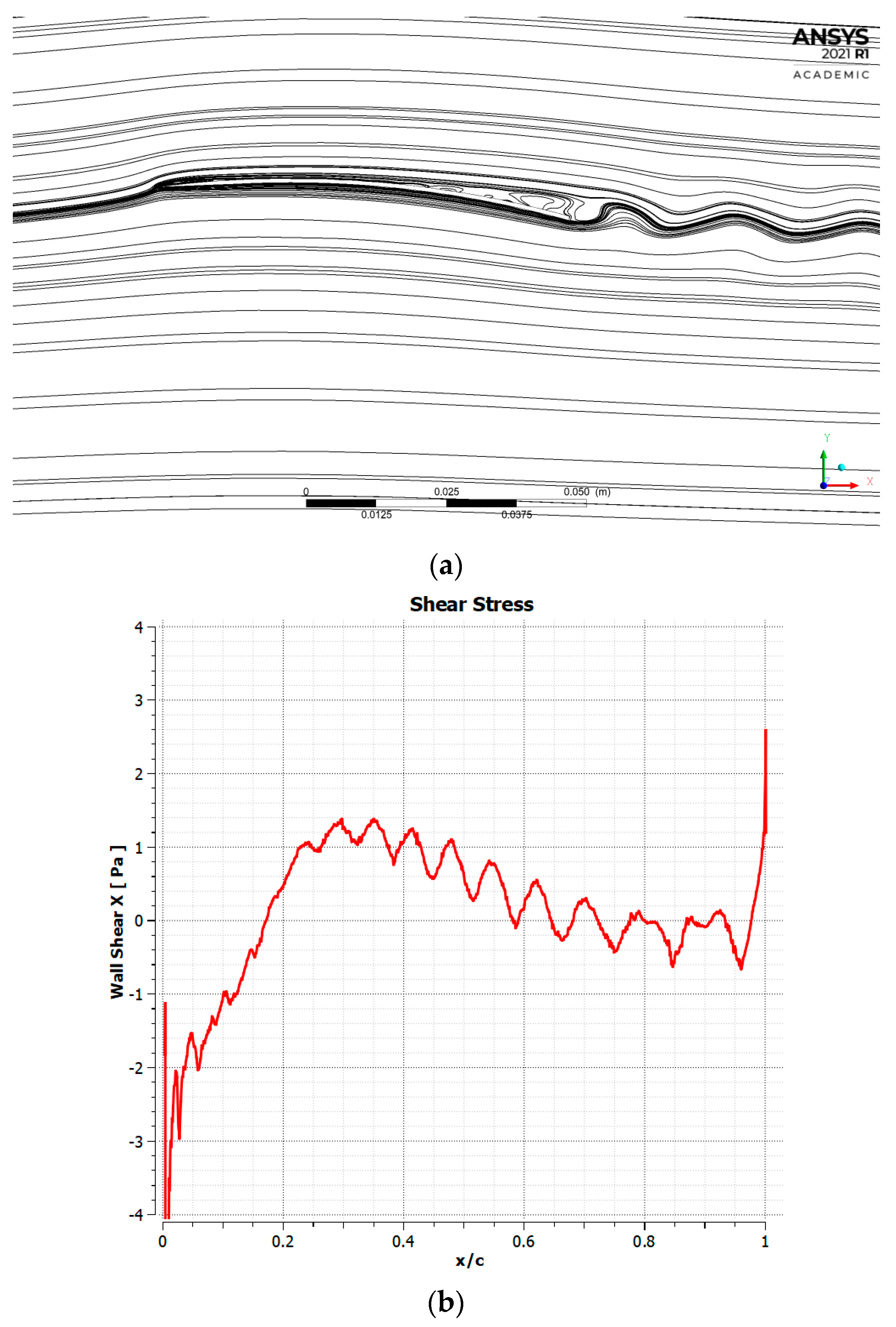
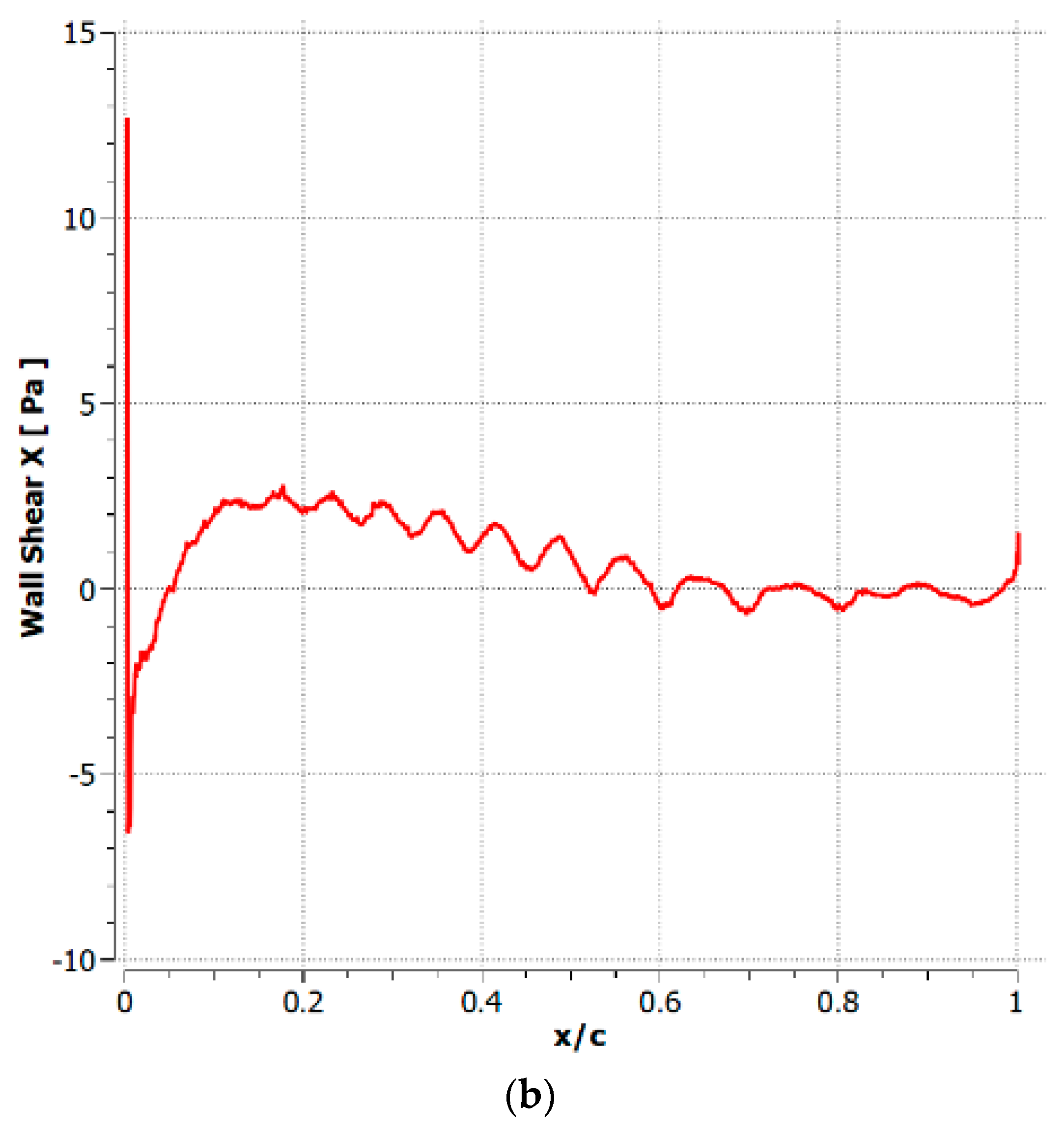
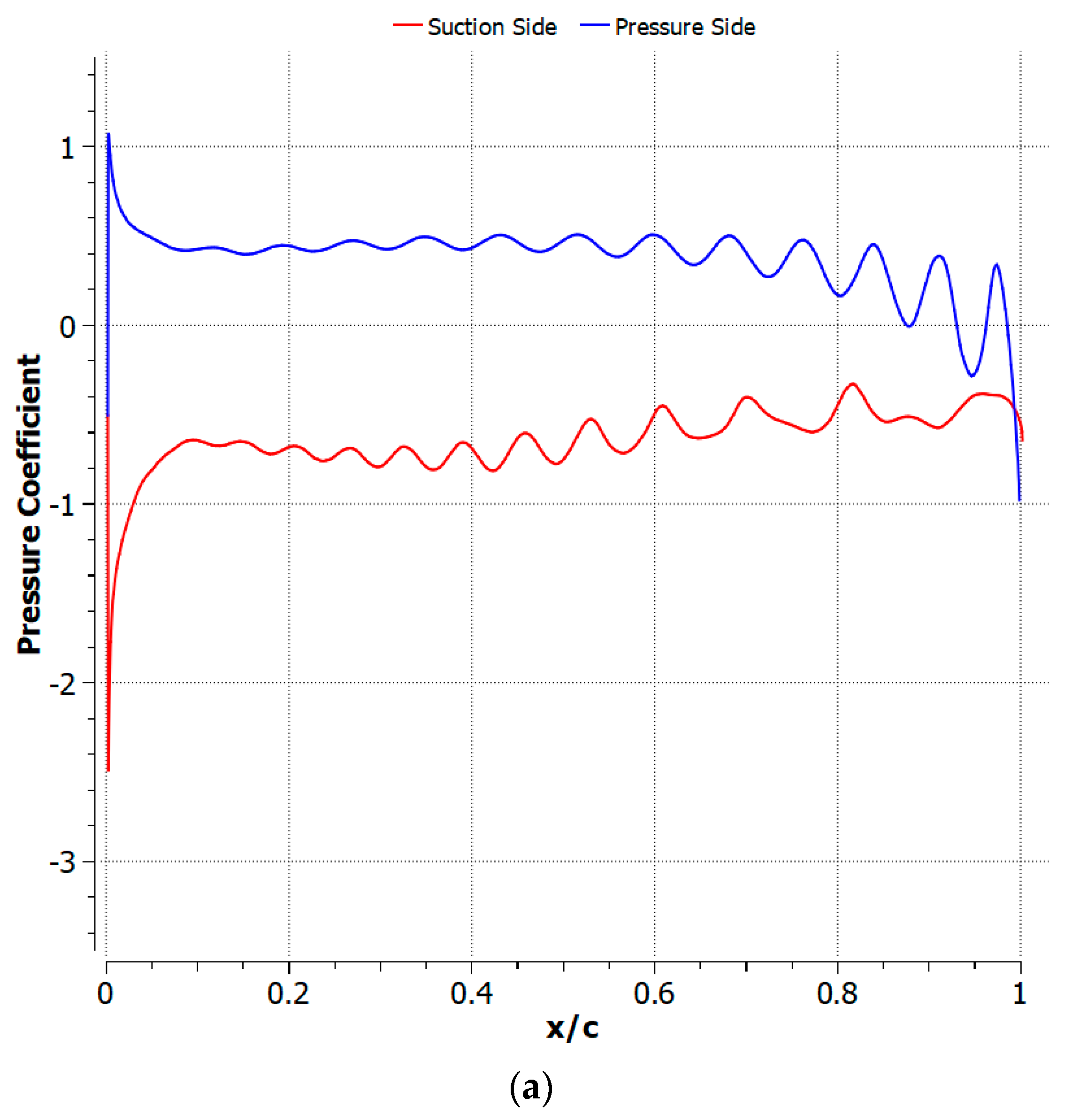
3.2. M = 0.2 Results
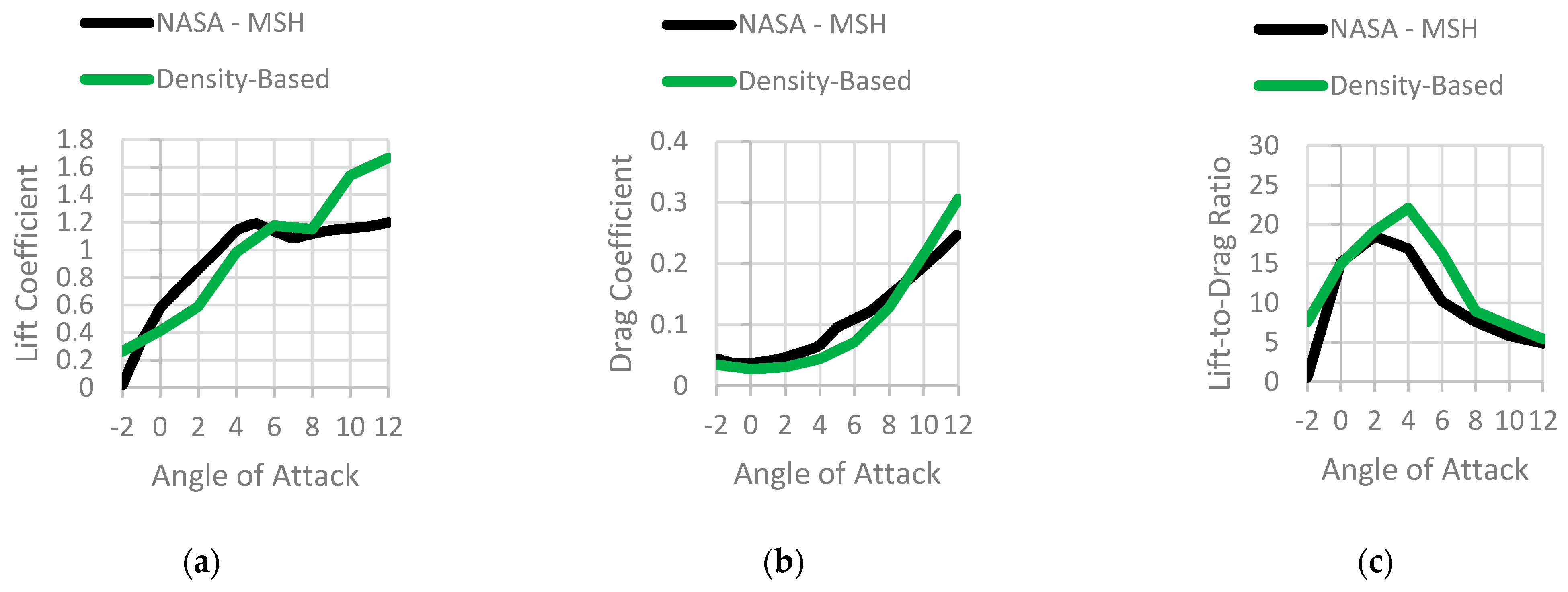
3.3. M = 0.5 Results
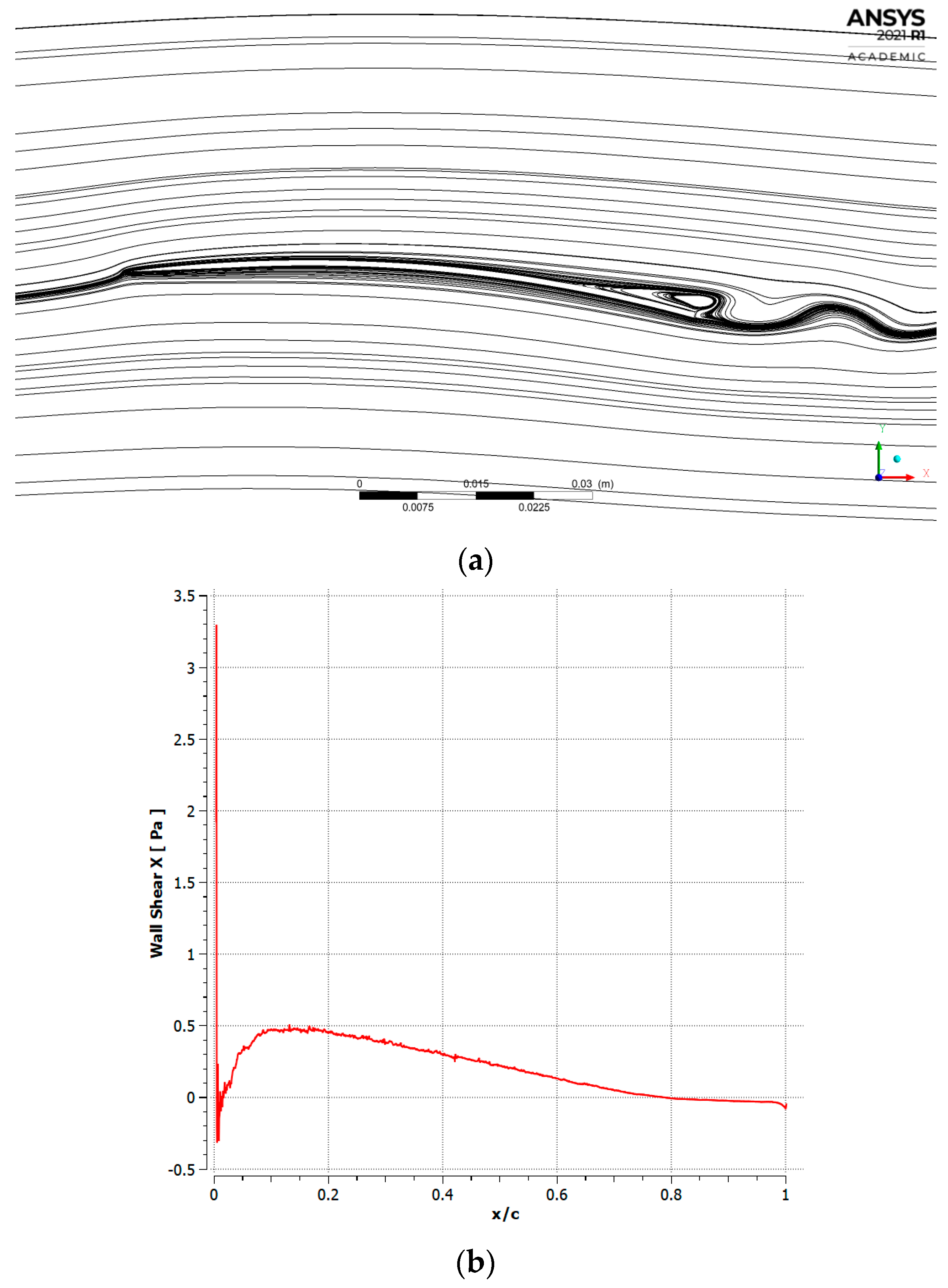
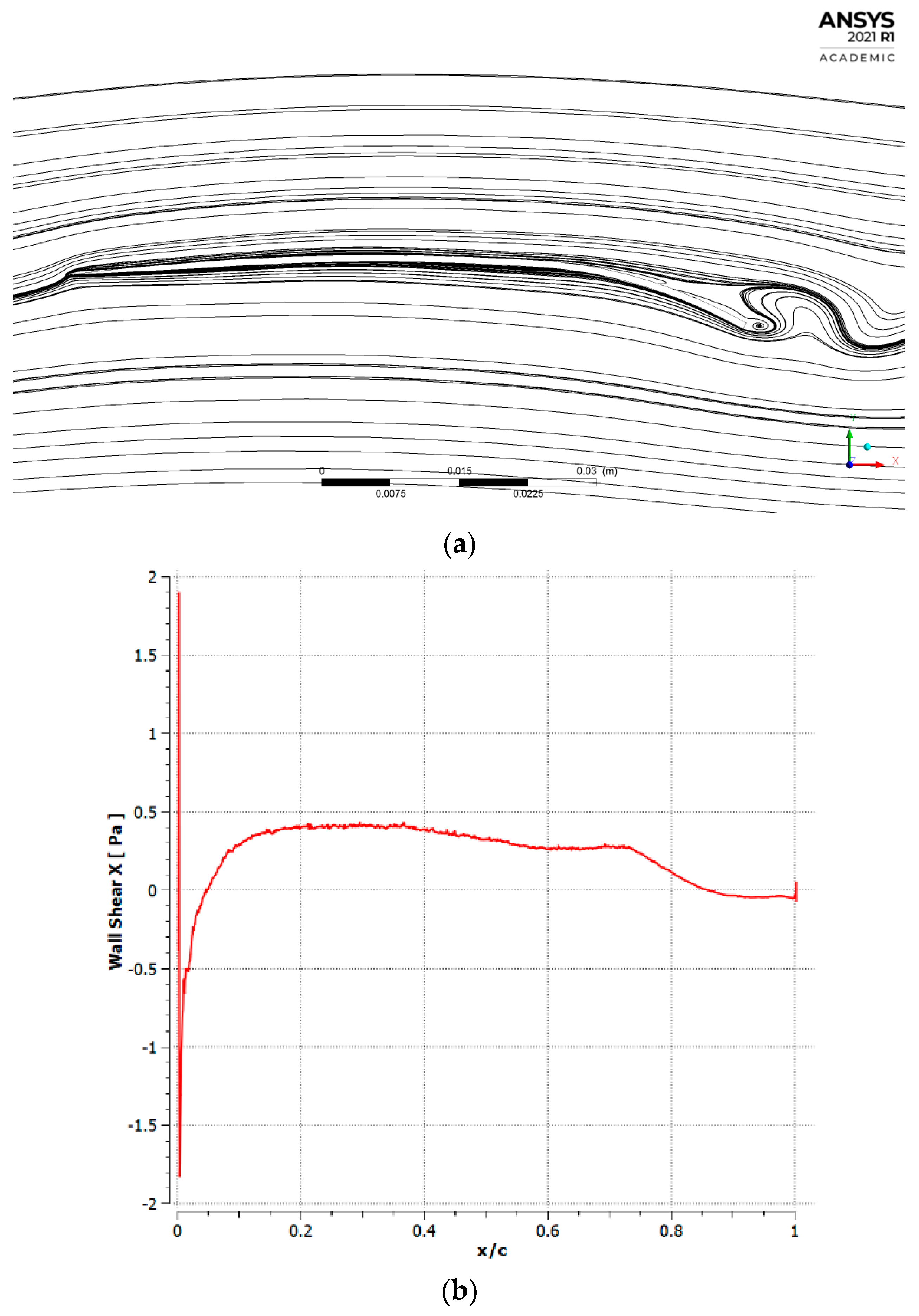
4. Discussion
4.1. Cambered Plate at M = 0.2
4.2. Cambered Plate at M = 0.5
4.3. Cambered Plate at M = 0.7
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| a | Speed of Sound (m/s) |
| c | Chord length |
| cd | Drag coefficient |
| cl | Lift coefficient |
| cp | Pressure coefficient |
| f | Camber height (m) |
| g | Gravity (m/s2) |
| Diffusion flux of species j (mol/m2s) | |
| k | Turbulence kinetic energy (J/kg) |
| Effective conductivity | |
| M | Mach number |
| μ | Dynamic Viscosity (N s/m2) |
| p | Pressure (Pa) |
| R | Gas constant (m2 K/s2) |
| Heat of chemical reactions | |
| T | Temperature (°C) |
| t | Time (s) |
| v | Wind speed (m/s) |
| vt | Turbulent eddy viscosity |
| x | Spatial dimension (m) |
| xc | Camber location from leading edge (m) |
| Dimensionless wall distance | |
| γ | Intermittency |
| ∆ | Grid element size (m) |
| ρ | Density (Kg/m3) |
| Specific dissipation rate |
References
- Gheisari, M.; Irizarry, J.; Walker, B.N. UAS4SAFETY: The Potential of Unmanned Aerial Systems for Construction Safety Applications. In Proceedings of the Construction Research Congress, Atlanta, GA, USA, 19–21 May 2014; pp. 1801–1810. [Google Scholar] [CrossRef]
- Hogan, S.D.; Kelly, M.; Stark, B.; Chen, Y.Q. Unmanned aerial systems for agriculture and natural resources. Calif. Agric. 2017, 71, 5–14. [Google Scholar] [CrossRef]
- Zhang, C.; Kovacs, J.M. The application of small unmanned aerial systems for precision agriculture: A review. Precis. Agric. 2012, 13, 693–712. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Turtle, E.D.; Barnes, J.W.; Trainer, M.G.; Adams, D.S.; Hibbard, K.E.; Sheldon, C.Z.; Zacny, K.; Peplowki, P.N.; Lawrence, D.J. Dragonfly: A rotorcraft lander concept for scientific exploration at Titan. Johns Hopkins APL Tech. Dig. 2018, 34, 14. [Google Scholar]
- Fujita, K.; Karaca, H.; Nagai, H. Parametric Study of Mars Helicopter for Pit Crater Exploration. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar]
- Lacerda, M.; Park, D.; Beard, R.; Schrage, D. Georgia Tech Mars Exploration UAV Collaborative System: A Conceptual Design and Systems Engineering Study; Georgia Institute of Technology: Atlanta, GA, USA, 2017. [Google Scholar]
- González-Jorge, H.; Martínez-Sánchez, J.; Bueno, M. Unmanned aerial systems for civil applications: A review. Drones 2017, 1, 2. [Google Scholar] [CrossRef]
- Vélez-Nicolás, M.; García-López, S.; Barbero, L.; Ruiz-Ortiz, V.; Sánchez-Bellón, Á. Applications of unmanned aerial systems (UASs) in hydrology: A review. Remote Sens. 2021, 13, 1359. [Google Scholar] [CrossRef]
- Irizarry, J.; Costa, D.B. Exploratory study of potential applications of unmanned aerial systems for construction management tasks. J. Manag. Eng. 2016, 32, 05016001. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Pajuelo, M.V.; Mallinis, G.; Dor, E.B.; Helamn, D.; Estes, L.; Ciraolo, G. On the use of unmanned aerial systems for environmental monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
- Wanasinghe, T.R.; Gosine, R.G.; De Silva, O.; Mann, G.K.; James, L.A.; Warrian, P. Unmanned aerial systems for the oil and gas industry: Overview, applications, and challenges. IEEE Access 2020, 8, 166980–166997. [Google Scholar] [CrossRef]
- Canham, B.B.T.; Courtney, D.; Grip, H.F.; Johnson, W.; Maki, J.; Quon, A.; Stern, R.; Zhu, D. Mars Helicopter Technology Demonstrator. In Proceedings of the 2018 AIAA Atmospheric Flight Mechanics Conference, Kissimmee, FL, USA, 8–12 January 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- mars.nasa.gov. Mars Helicopter. Available online: https://mars.nasa.gov/technology/helicopter/ (accessed on 24 February 2022).
- mars.nasa.gov. Flying on Mars Is Getting Harder and Harder. Available online: https://mars.nasa.gov/technology/helicopter/status/334/flying-on-mars-is-getting-harder-and-harder/ (accessed on 24 February 2022).
- Saez, A.; Manzo, M.; Ciarcià, M. Mars Drone Configurations and Approaches to Rotor Design: A Review. In Proceedings of the ASME 2021 International Mechanical Engineering Congress and Exposition, Online, 1–5 November 2021. [Google Scholar] [CrossRef]
- Radotich, M.; Withrow-Maser, S.; de Souza, Z.; Gelhar, S.; Gallagher, H. A Study of Past, Present, and Future Mars Rotorcraft. In Proceedings of the Vertical Flight Society’s 9th Biennial Autonomous VTOL Technical Meeting, Online, 26–28 January 2021; Available online: https://rotorcraft.arc.nasa.gov/Publications/files/Radotich_aVTOL_Tech_Meeting_Final_Revised_012521.pdf (accessed on 24 February 2022).
- Johnson, W.; Withrow-Maser, S.; Young, L.; Malpica, C.; Koning, W.; Kuang, W.; Fehler, M.; Tuano, A.; Chan, A. Datta, Mars Science Helicopter Conceptual Design; National Aeronautics and Space Administration, Ames Research Center: Mountain View, CA, USA, 2020.
- Withrow, S.; Johnson, W.; Young, L.A.; Cummings, H.; Balaram, J.; Tzanetos, T. An Advanced Mars Helicopter Design. In Proceedings of the ASCEND 2020, Online, 16–18 November 2020; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2020. [Google Scholar] [CrossRef]
- Young, L.A.; Aiken, E.W. Vertical Lift Planetary Aerial Vehicles: Three Planetary Bodies and Four Conceptual Design Cases; National Aeronautics and Space Administration: Moffett Field, CA, USA, 2001. Available online: https://apps.dtic.mil/sti/citations/ADA480699 (accessed on 8 March 2021).
- Mars Climate Database v5.3: The Web Interface. Available online: http://www-mars.lmd.jussieu.fr/mcd_python/ (accessed on 13 April 2021).
- mars.nasa.gov. Location Map for Perseverance Rover. Available online: https://mars.nasa.gov/mars2020/mission/where-is-the-rover/ (accessed on 13 May 2021).
- Kroo, I.; Fritz, P.; Shantz, M.; Kunz, P.; Fay, G.; Cheng, S.; Fabian, T.; Partridge, C. The Mesicopter: A Miniature Rotorcraft Concept Phase II Interim Report; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2000. [Google Scholar]
- Koning, W.J.F.; Johnson, W.; Grip, H.F. Improved Mars Helicopter Aerodynamic Rotor Model for Comprehensive Analyses. AIAA J. 2019, 57, 3969–3979. [Google Scholar] [CrossRef]
- Koning, W.J. Airfoil Selection for Mars Rotor Applications; NASA CR: Washington, DC, USA, 2019; Volume 220236.
- Graebel, W. Advanced Fluid Mechanics; Academic Press: Cambridge, MA, USA, 2007; ISBN 9780123708854. [Google Scholar]
- Rodriguez, S. Applied Computational Fluid Dynamics and Turbulence Modeling: Practical Tools, Tips and Techniques; Springer Nature: Berlin/Heidelberg, Germany, 2019; ISBN 978-3-030-28690-3. [Google Scholar]
- Aftab, S.M.A.; Rafie, A.S.M.; Razak, N.A.; Ahmad, K.A. Turbulence Model Selection for Low Reynolds Number Flows. PLoS ONE 2016, 11, e0153755. [Google Scholar] [CrossRef] [PubMed]
- Morgado, J.; Vizinho, R.; Silvestre, M.A.R.; Páscoa, J.C. XFOIL vs CFD performance predic-tions for high lift low Reynolds number airfoils. Aerosp. Sci. Technol. 2016, 52, 207–214. [Google Scholar] [CrossRef]
- Rumsey, C.L.; Spalart, P.R. Turbulence model behavior in low Reynolds number regions of aero-dynamic flowfields. AIAA J. 2009, 47, 982–993. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Low Reynolds Number Aerodynamics; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar]
- ANSYS Inc. ANSYS Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Saez, A.G. Aerodynamic Optimization of a 2D Airfoil for Rotary-Wing Aircraft at Mars Atmospheric Conditions. UNT Digital Library. 2021. Available online: https://digital.library.unt.edu/ark:/67531/metadc1873834/ (accessed on 26 February 2022).
- Withrow-Maser, S.; Koning, W.; Kuang, W.; Johnson, W.R. Recent Efforts Enabling Martian Rotorcraft Missions. In Proceedings of the VFS Aeromechanics for Advanced Vertical Flight Technical Meeting, San Jose, CA, USA, 21–23 January 2020. [Google Scholar]
- Koning, W.J.; Romander, E.A.; Johnson, W. Optimization of Low Reynolds Number Airfoils for Martian Rotor Applications Using an Evolutionary Algorithm. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 0084. [Google Scholar] [CrossRef]
- Koning, W.J.F.; Romander, E.A.; Johnson, W. Performance Optimization of Plate Airfoils for Martian Rotor Applications Using a Genetic Algorithm. In Proceedings of the 45th European Rotorcraft Forum, Warsaw, Poland, 17–20 September 2019; pp. 1–15. [Google Scholar]
- Koning, W.J.; Johnson, W.; Allan, B.G. Generation of Mars Helicopter Rotor Model for Comprehensive Analyses. In Proceedings of the AHS Aeromechanics Design for Transformative Vertical Flight, San Francisco, CA, USA, 16–18 January 2018. [Google Scholar]
- Koning, W.J.F.; Romander, E.A.; Johnson, W. Low Reynolds Number Airfoil Evaluation for the Mars Helicopter Rotor. In Proceedings of the AHS International 74th Annual Forum & Technology Display, Phoenix, AZ, USA, 14–17 May 2018; p. 17. [Google Scholar]











| Property | Units | Range | |
|---|---|---|---|
| T | °C | −29 | −130 |
| P | Pa | 1300 | 87 |
| Density, ρ | kg/m3 | 0.036 | 0.0023 |
| a | m/s | 233.55 | |
| v∞ | m/s | 0 | 23 |
| g | m/s2 | 3.721 | |
| Variable | ESL | MC2 |
|---|---|---|
| Density, ρ [kg/m3] | 1.225 | 0.017 |
| Temperature, T [K] | 288.2 | 223.2 |
| Gas Constant, R [(m2 K)/s2] | 287.1 | 188.9 |
| Specific Heat Ratio | 1.400 | 1.289 |
| μ [N s/m2] | 1.750⋅10−5 | 1.130⋅10−5 |
| Static pressure, p [Pa] | 101,300 | 716.6 |
| Speed of Sound, a [m/s] | 340 | 233.55 |
| Gravity, g [m/s2] | 9.81 | 3.71 |
| Mesh | Element Quality | Aspect Ratio | Skewness | Orthogonal Quality |
|---|---|---|---|---|
| Coarse | 0.92 | 1.35 | 0.12 | 0.93 |
| Medium | 0.95 | 1.25 | 0.08 | 0.95 |
| Fine | 0.96 | 1.22 | 0.07 | 0.96 |
| # | Configuration | Airfoil Shapes |
|---|---|---|
| 1 |  | |
| 2 |  | |
| 3 |  | |
| 4 |  | |
| 5 |  | |
| 6 |  | |
| 7 |  | |
| 8 |  | |
| 9 |  |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saez, A.; Manzo, M.; Ciarcià, M. Numerical Analysis of Cambered Plate Configurations under Low Reynolds Numbers and at a Low-Density Condition. Fluids 2023, 8, 194. https://doi.org/10.3390/fluids8070194
Saez A, Manzo M, Ciarcià M. Numerical Analysis of Cambered Plate Configurations under Low Reynolds Numbers and at a Low-Density Condition. Fluids. 2023; 8(7):194. https://doi.org/10.3390/fluids8070194
Chicago/Turabian StyleSaez, Aleandro, Maurizio Manzo, and Marco Ciarcià. 2023. "Numerical Analysis of Cambered Plate Configurations under Low Reynolds Numbers and at a Low-Density Condition" Fluids 8, no. 7: 194. https://doi.org/10.3390/fluids8070194
APA StyleSaez, A., Manzo, M., & Ciarcià, M. (2023). Numerical Analysis of Cambered Plate Configurations under Low Reynolds Numbers and at a Low-Density Condition. Fluids, 8(7), 194. https://doi.org/10.3390/fluids8070194








