Vortex Model of Plane Couette Flow
Abstract
1. Introduction
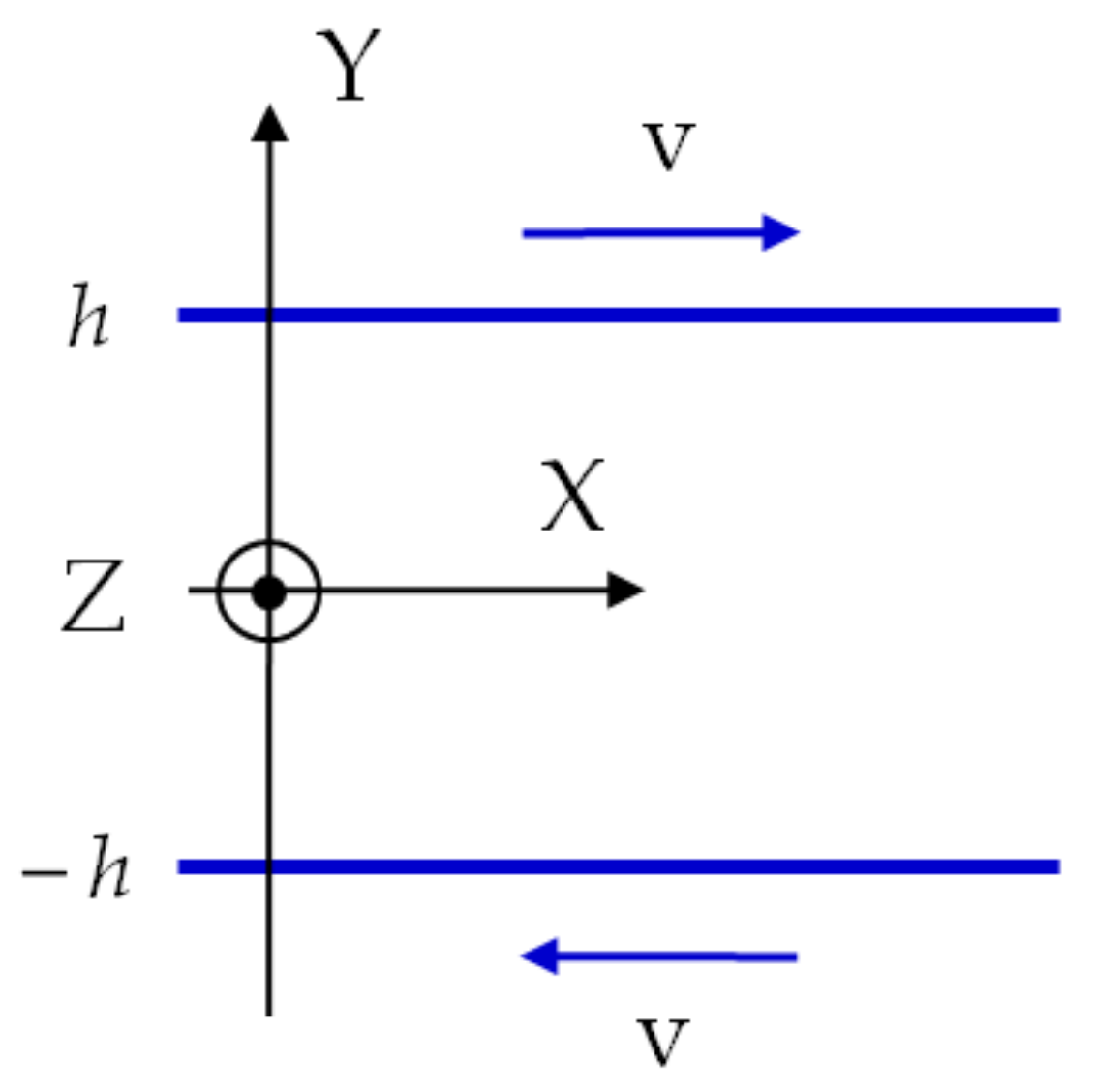
2. Model of Vortex Plane Couette Flow
3. Laminar Plane Couette Flow of Vortex Fluid
3.1. Stationary Flow without Rotation of Vortex Tubes
3.2. Flow with in-Phase Rotation of Vortex Tubes
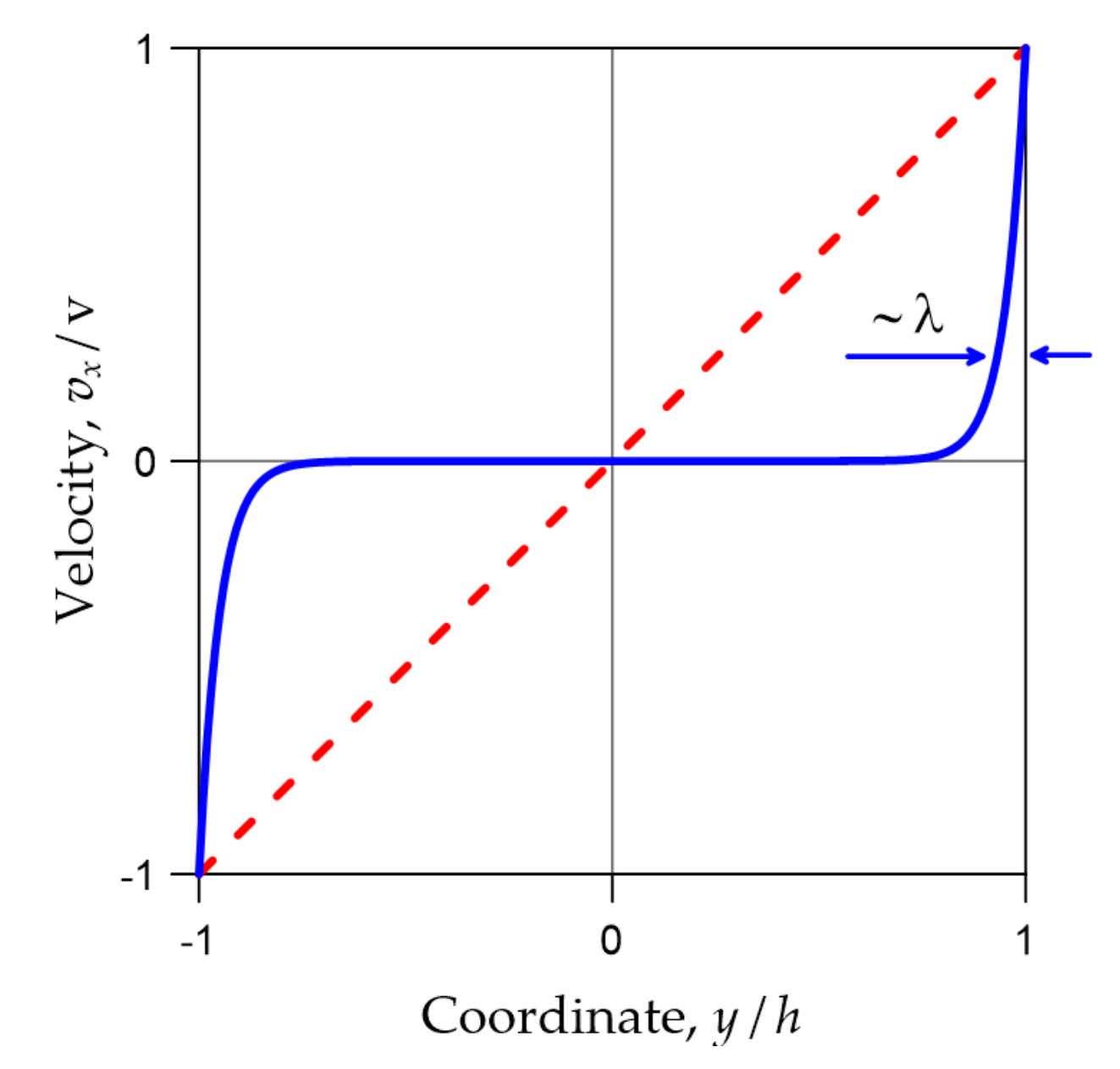
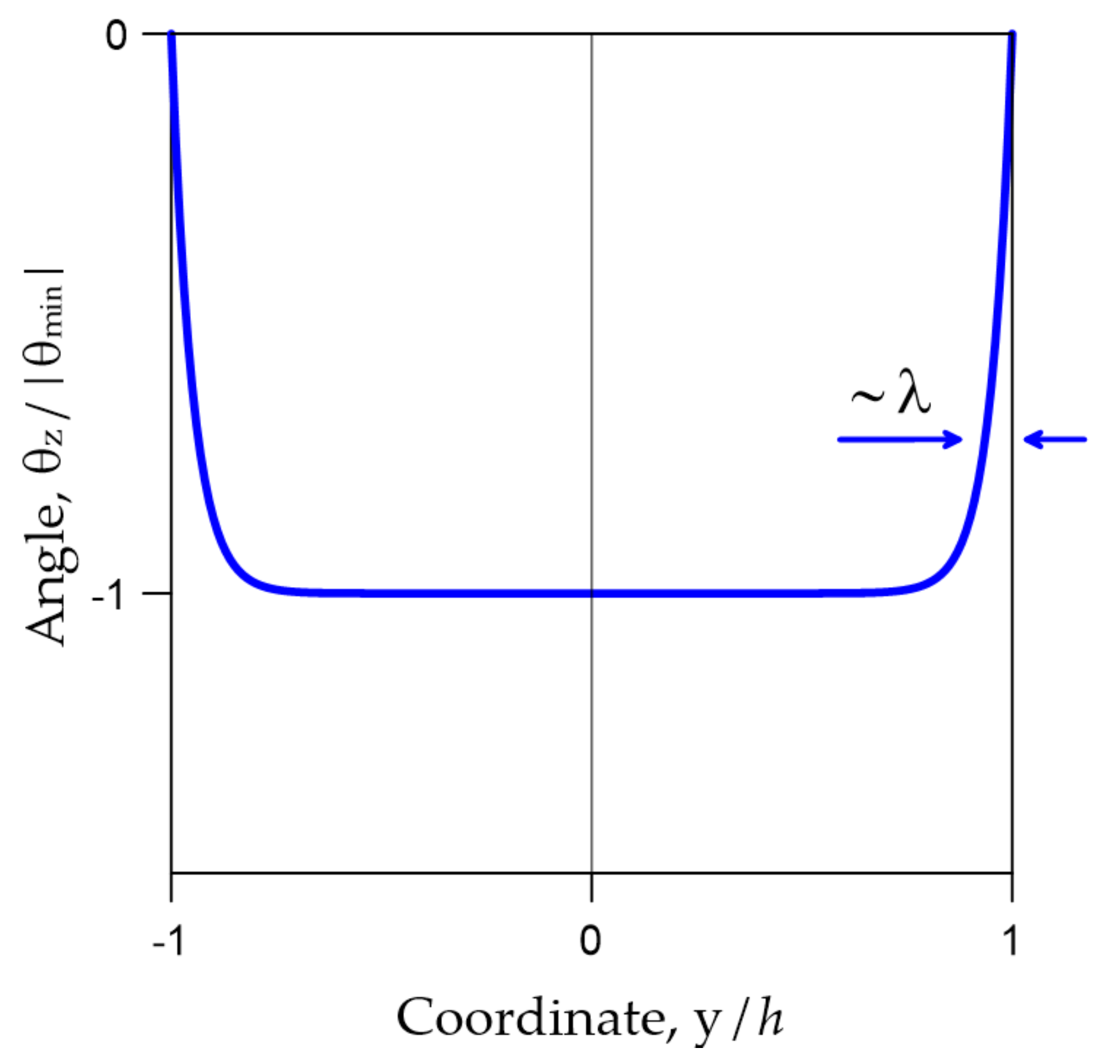
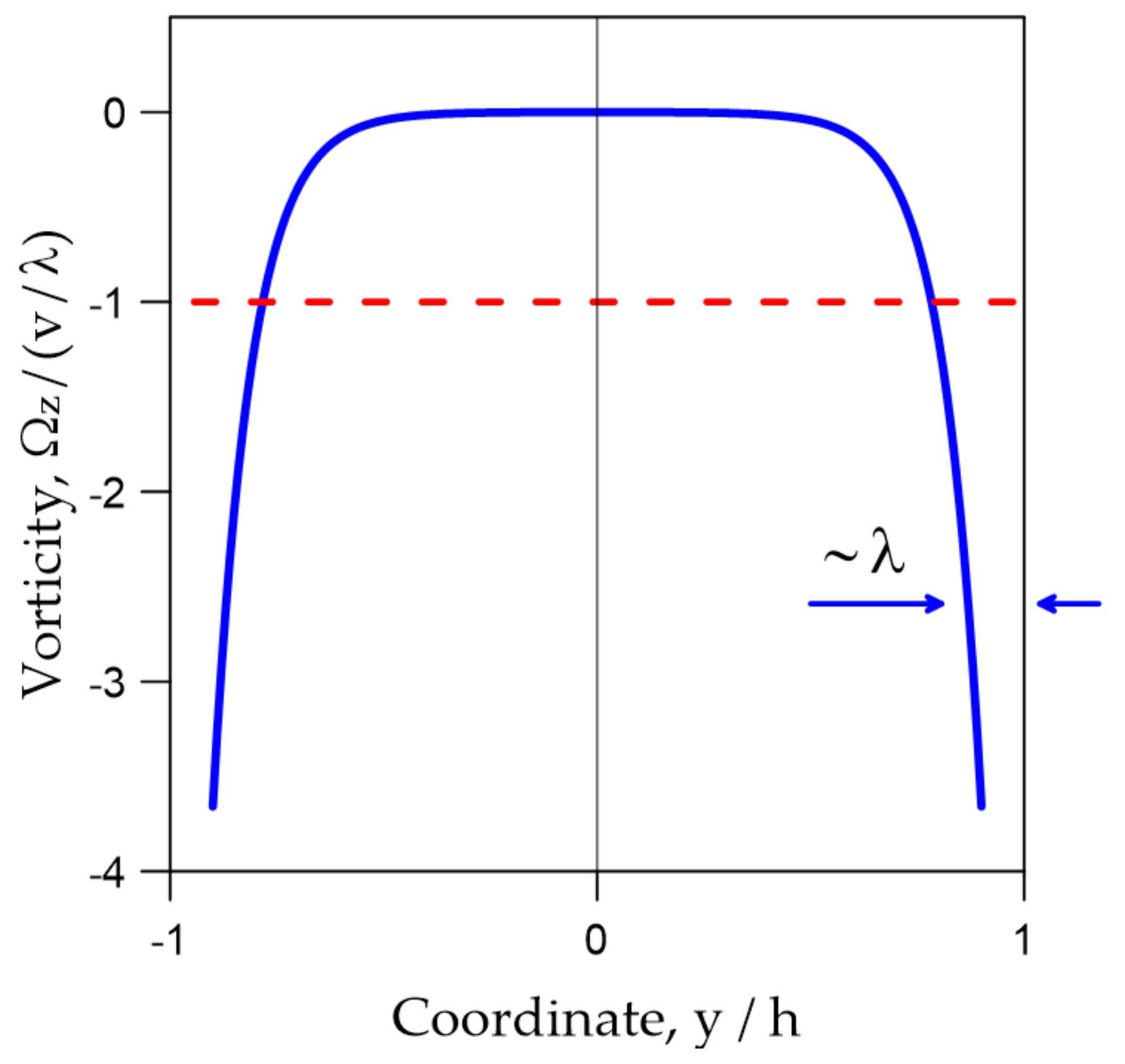
3.3. Case of Vortex Tubes Rotating with Different Phases
4. Turbulent Plane Couette Flow
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kambe, T. A new formulation of equation of compressible fluids by analogy with Maxwell’s equations. Fluid Dyn. Res. 2010, 42, 055502. [Google Scholar] [CrossRef]
- Thompson, R.J.; Moeller, T.M. Numerical and closed-form solutions for the Maxwell equations of incompressible flow. Phys. Fluids 2018, 30, 083606. [Google Scholar] [CrossRef]
- Mendes, C.R.; Takakura, F.I.; Abreu, E.M.C.; Neto, J.A.; Silva, P.P.; Frossad, J.V. Helicity and vortex generation. Ann. Phys. 2018, 398, 146–158. [Google Scholar] [CrossRef]
- Marmanis, H. Analogy between the Navier-Stokes equations and Maxwell’s equations: Application to turbulence. Phys. Fluids 1998, 10, 1428–1437. [Google Scholar] [CrossRef]
- Demir, S.; Tanişli, M. Spacetime algebra for the reformulation of fluid field equations. Int. J. Geom. Methods Mod. Phys. 2017, 14, 1750075. [Google Scholar] [CrossRef]
- Tanişli, M.; Demir, S.; Sahin, N. Octonic formulations of Maxwell type fluid equations. J. Math. Phys. 2015, 56, 091701. [Google Scholar] [CrossRef]
- Demir, S.; Uymaz, A.; Tanışlı, M. A new model for the reformulation of compressible fluid equations. Chin. J. Phys. 2017, 55, 115–126. [Google Scholar] [CrossRef]
- Thompson, R.J.; Moeller, T.M. A Maxwell formulation for the equations of a plasma. Phys. Plasmas 2012, 19, 010702. [Google Scholar] [CrossRef]
- Thompson, R.J.; Moeller, T.M. Classical field isomorphisms in two-fluid plasmas. Phys. Plasmas 2012, 19, 082116. [Google Scholar] [CrossRef]
- Jamil, M.; Ahmed, A. New traveling wave solutions of MHD micropolar fluid in porous medium. J. Egypt Math. Soc. 2020, 28, 23. [Google Scholar] [CrossRef]
- Eshraghi, H.; Gibbon, J.D. Quaternions and ideal flows. J. Phys. A Math. Theor. 2008, 41, 344004. [Google Scholar] [CrossRef]
- Demir, S.; Tanişli, M.; Sahin, N.; Kansu, M.E. Biquaternionic reformulation of multifluid plasma equations. Chin. J. Phys. 2017, 55, 1329. [Google Scholar] [CrossRef]
- Demir, S.; Zeren, E. Multifluid plasma equations in terms of hyperbolic octonions. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850053. [Google Scholar] [CrossRef]
- Chanyal, B.C.; Pathak, M. Quaternionic approach to dual magneto-hydrodynamics of dyonic cold plasma. Adv. High Ener. Phys. 2018, 13, 7843730. [Google Scholar]
- Chanyal, B.C. Quaternionic approach on the Dirac–Maxwell, Bernoulli and Navier– Stokes equations for dyonic fluid plasma. Int. J. Mod. Phys. A 2019, 34, 1950202. [Google Scholar] [CrossRef]
- Helmholtz, H. Über Integrale der hydrodynamischen Gleichungen, welche den Wirbelbewegungen entsprechen. J. Die Reine Angew. Math. 1858, 55, 25–55. [Google Scholar]
- Mironov, V.L.; Mironov, S.V. Generalized sedeonic equations of hydrodynamics. Eur. Phys. J. Plus 2020, 135, 708. [Google Scholar] [CrossRef]
- Mironov, V.L. Self-consistent hydrodynamic two-fluid model of vortex plasma. Phys. Fluids 2021, 33, 037116. [Google Scholar] [CrossRef]
- Mironov, V.L. Self-consistent hydrodynamic model of electron vortex fluid in solids. Fluids 2022, 7, 330. [Google Scholar] [CrossRef]
- Kochin, N.K.; Kibel, I.A.; Roze, N.V. Theoretical Hydrodynamics; John Wiley & Sons: New York, NY, USA, 1964. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1970. [Google Scholar]
- Tillmark, N.; Alfredsson, P.H. Experiments on transition in plane Couette flow. J. Fluid Mech. 1992, 235, 89–102. [Google Scholar] [CrossRef]
- Bech, K.H.; Tillmark, N.; Alfredsson, P.H.; Andersson, H.I. An investigation of turbulent plane Couette flow at low Reynolds numbers. J. Fluid Mech. 1995, 286, 291–325. [Google Scholar] [CrossRef]
- Aydin, E.M.; Leuthersser, H.J. Plane-Couette flow between smooth and rough walls. Experim. Fluids 1991, 11, 302–312. [Google Scholar] [CrossRef]
- Bottin, S.; Chate, H. Statistical analysis of the transition to turbulence in plane Couette flow. Eur. Phys. J. B 1998, 6, 143–155. [Google Scholar] [CrossRef]
- Kitoh, O.; Nakabyashi, K.; Nishimura, F. Experimental study on mean velocity and turbulence characteristics of plane Couette flow: Low-Reynolds-number effects and large longitudinal vortical structure. J. Fluid Mech. 2005, 539, 199–227. [Google Scholar] [CrossRef]
- Reynolds, O. On the dynamical theory of incompressible viscous fluids and the determination of the criterion. Phil. Trans. Royal Soc. London A 1895, 186, 123–164. [Google Scholar]
- McComb, W.D. Theory of turbulence. Rep. Prog. Phys. 1995, 58, 1117–1206. [Google Scholar] [CrossRef]
- Boussinesq, J. Essai sur la Theorie des Eaux Courantes. Memoires Presentes par Divers Savants a l’Academie des Sciences de l’Institut National de France; Tome XXIII, No 1.; Imprimerie Nationale: Paris, France, 1877. [Google Scholar]
- Schmitt, F.G. About Boussinesq’s turbulent viscosity hypothesis: Historical remarks and a direct evaluation of its validity. Comptes Rendus Méc. 2007, 335, 617–627. [Google Scholar] [CrossRef]
- Henry, F.S.; Reynolds, A.J. Analytical solution of two gradient-diffusion models applied to turbulent Couette flow. ASME J. Fluids Eng. 1984, 106, 211–216. [Google Scholar] [CrossRef]
- Nimura, T.; Tsukahara, T. Viscoelasticity-induced instability in plane Couette flow at very low Reynolds number. Fluids 2022, 7, 241. [Google Scholar] [CrossRef]
- Ribau, A.M.; Ferrás, L.L.; Morgado, M.L.; Rebelo, M.; Afonso, A.M. Semi-analytical solutions for the Poiseuille–Couette flow of a generalised Phan-Thien-Tanner fluid. Fluids 2019, 4, 129. [Google Scholar] [CrossRef]
- Baranovskii, E.S.; Burmasheva, N.V.; Prosviryakov, E.Y. Exact solutions to the Navier–Stokes equations with couple stresses. Symmetry 2021, 13, 1355. [Google Scholar] [CrossRef]
- Andersson, H.I.; Pettersson, B.A. Modeling plane turbulent Couette flow. Int. J. Heat Fluid Flow 1994, 15, 447–455. [Google Scholar] [CrossRef]
- Abe, H.; Kawamura, H.; Matsuo, Y. Direct numerical simulation of a fully developed turbulent channel flow with respect to the Reynolds number dependence. ASME J. Fluids Eng. 2001, 123, 382–393. [Google Scholar] [CrossRef]
- Pirozzoli, S.; Bernardini, M.; Orlandi, P. Turbulence statistics in Couette flow at high Reynolds number. J. Fluid Mech. 2014, 758, 327–343. [Google Scholar] [CrossRef]
- Tsukahara, T.; Kawamura, H.; Shingai, K. DNS of turbulent Couette flow with emphasis on the large-scale structure in the core region. J. Turbul. 2006, 7, N19. [Google Scholar] [CrossRef]
- Sherikar, A.; Disimile, P.J. Parametric study of turbulent Couette flow over wavy surfaces using RANS simulation: Effects of aspect-ratio, wave-slope and Reynolds number. Fluids 2020, 5, 138. [Google Scholar] [CrossRef]
- Sarkar, A.; So, R.M.C. A critical evaluation of near-wall two-equation models against direct numerical simulation data. Int. J. Heat Fluid Flow 1997, 18, 197–208. [Google Scholar] [CrossRef]
- Gerodimos, G.; So, R.M.C. Near-wall modeling of plane turbulent wall jets. ASME J. Fluids Eng. 1997, 119, 304–313. [Google Scholar] [CrossRef]
- Tsukahara, T.; Kawamura, H.; Shingai, K. DNS Database of Wall Turbulence and Heat Transfer, Cou3000_A.dat. Available online: https://www.rs.tus.ac.jp/t2lab/db/cou/cou.html#cou3000 (accessed on 4 April 2023).
- Kawamura, H.; Shingai, K.; Matsuo, Y. DNS Database of Wall Turbulence and Heat Transfer, Cou12800_A.dat. Available online: https://www.rs.tus.ac.jp/t2lab/db/cou/cou.html#cou3000 (accessed on 4 April 2023).
- Reichardt, H. Über die Geschwindigkeitsverteilung in einer geradigen turbulenten Couetteströmung. Z. Angew. Math. Mech. 1956, 36, 26–29. [Google Scholar] [CrossRef]
- Stanislas, M.; Perret, L.; Foucaut, J.M. Vortical structures in the turbulent boundary layer: A possible route to a universal representation. J. Fluid Mech. 2008, 602, 327–382. [Google Scholar] [CrossRef]
- Wang, C.; Gao, Q.; Wang, J.; Wang, B.; Pan, C. Experimental study on dominant vortex structures in near-wall region of turbulent boundary layer based on tomographic particle image velocimetry. J. Fluid Mech. 2019, 874, 426–454. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mironov, V.L.; Mironov, S.V. Vortex Model of Plane Couette Flow. Fluids 2023, 8, 165. https://doi.org/10.3390/fluids8060165
Mironov VL, Mironov SV. Vortex Model of Plane Couette Flow. Fluids. 2023; 8(6):165. https://doi.org/10.3390/fluids8060165
Chicago/Turabian StyleMironov, Victor L., and Sergey V. Mironov. 2023. "Vortex Model of Plane Couette Flow" Fluids 8, no. 6: 165. https://doi.org/10.3390/fluids8060165
APA StyleMironov, V. L., & Mironov, S. V. (2023). Vortex Model of Plane Couette Flow. Fluids, 8(6), 165. https://doi.org/10.3390/fluids8060165






