Investigation of Recirculating Marangoni Flow in Three-Dimensional Geometry of Aqueous Micro-Foams
Abstract
1. Introduction
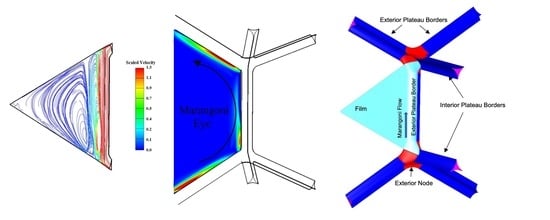
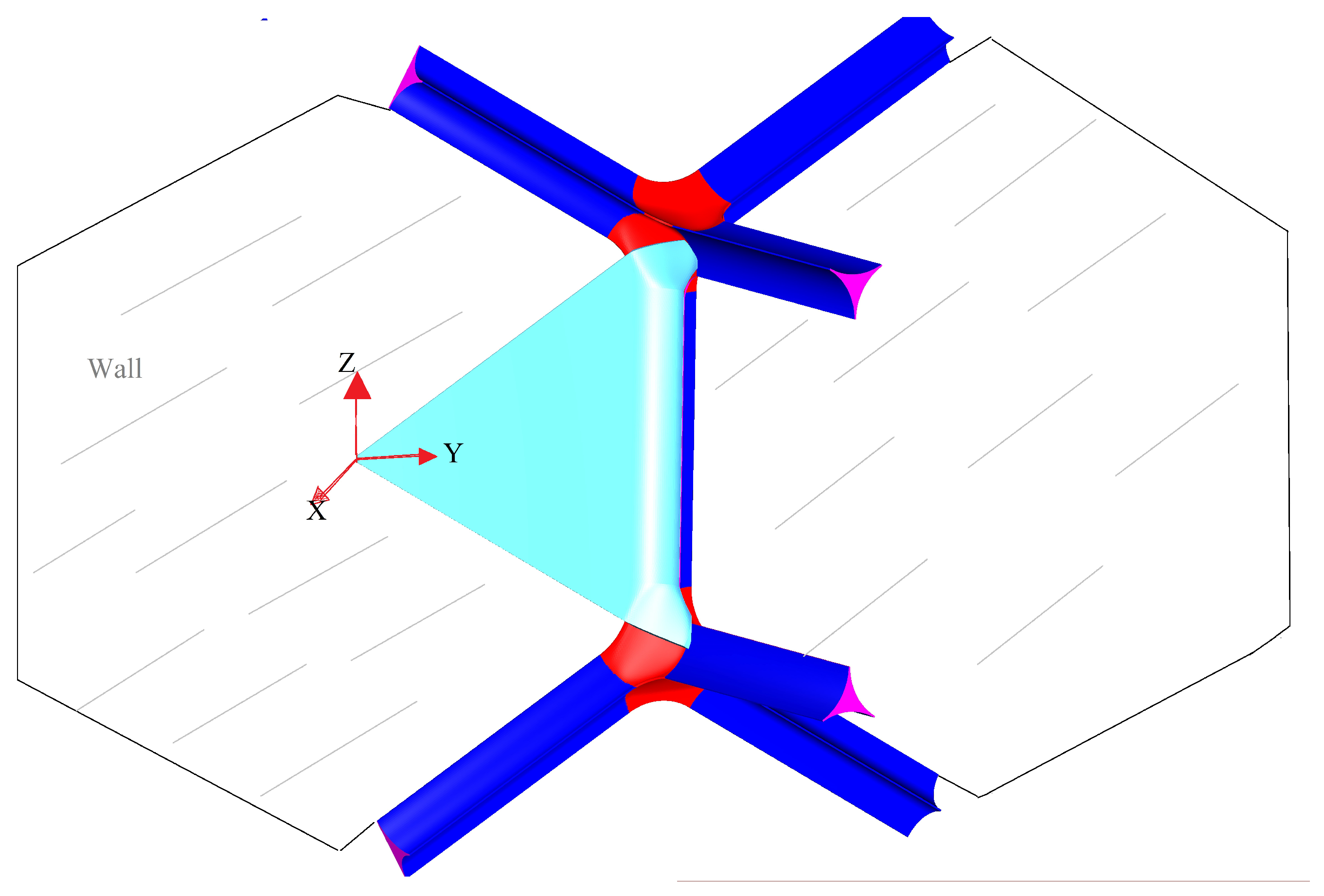
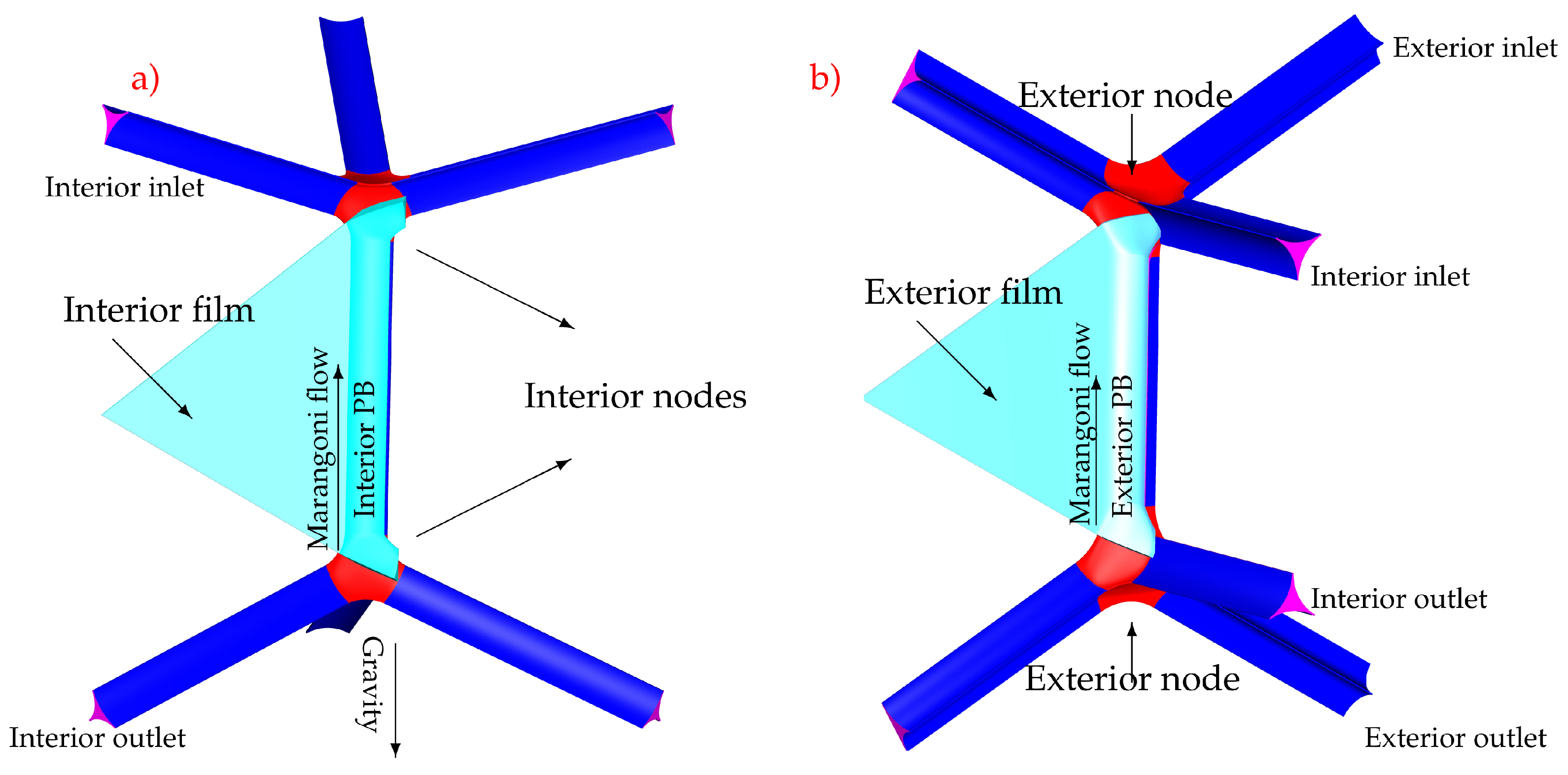
2. Geometrical Model
3. Governing Equations
Boundary Conditions
4. Results and Discussion
4.1. Models Validation
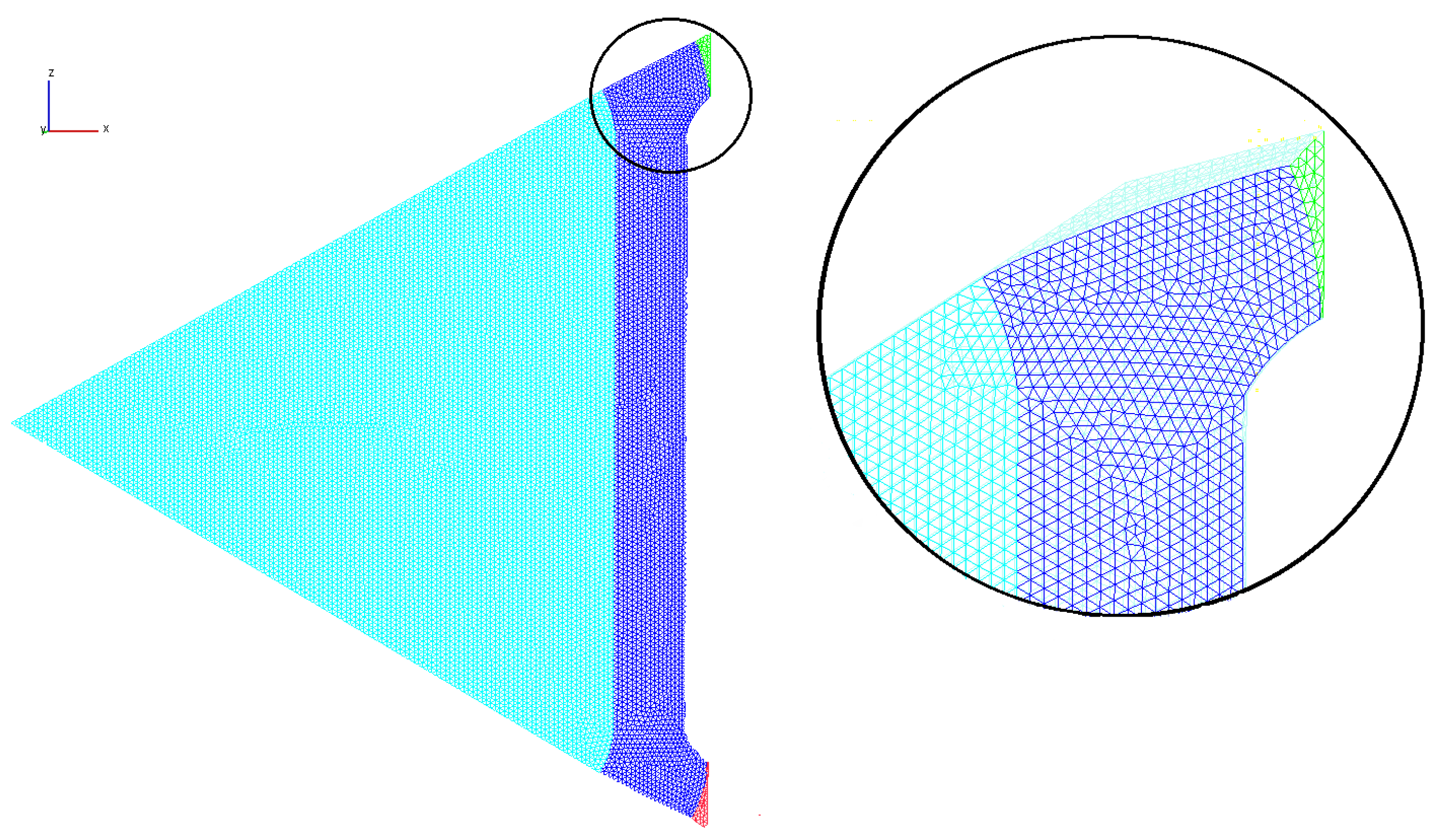
4.1.1. Grid Independency
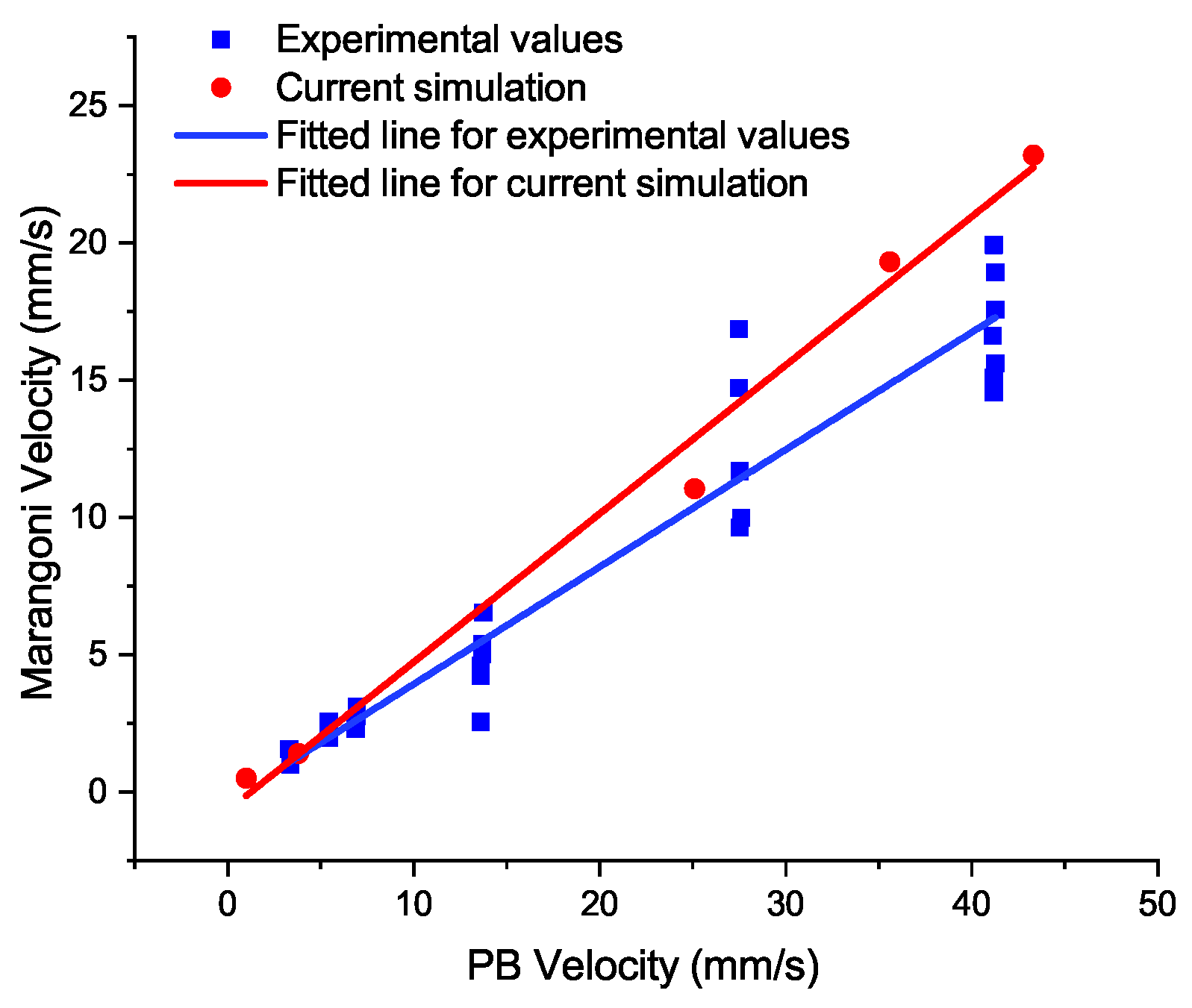
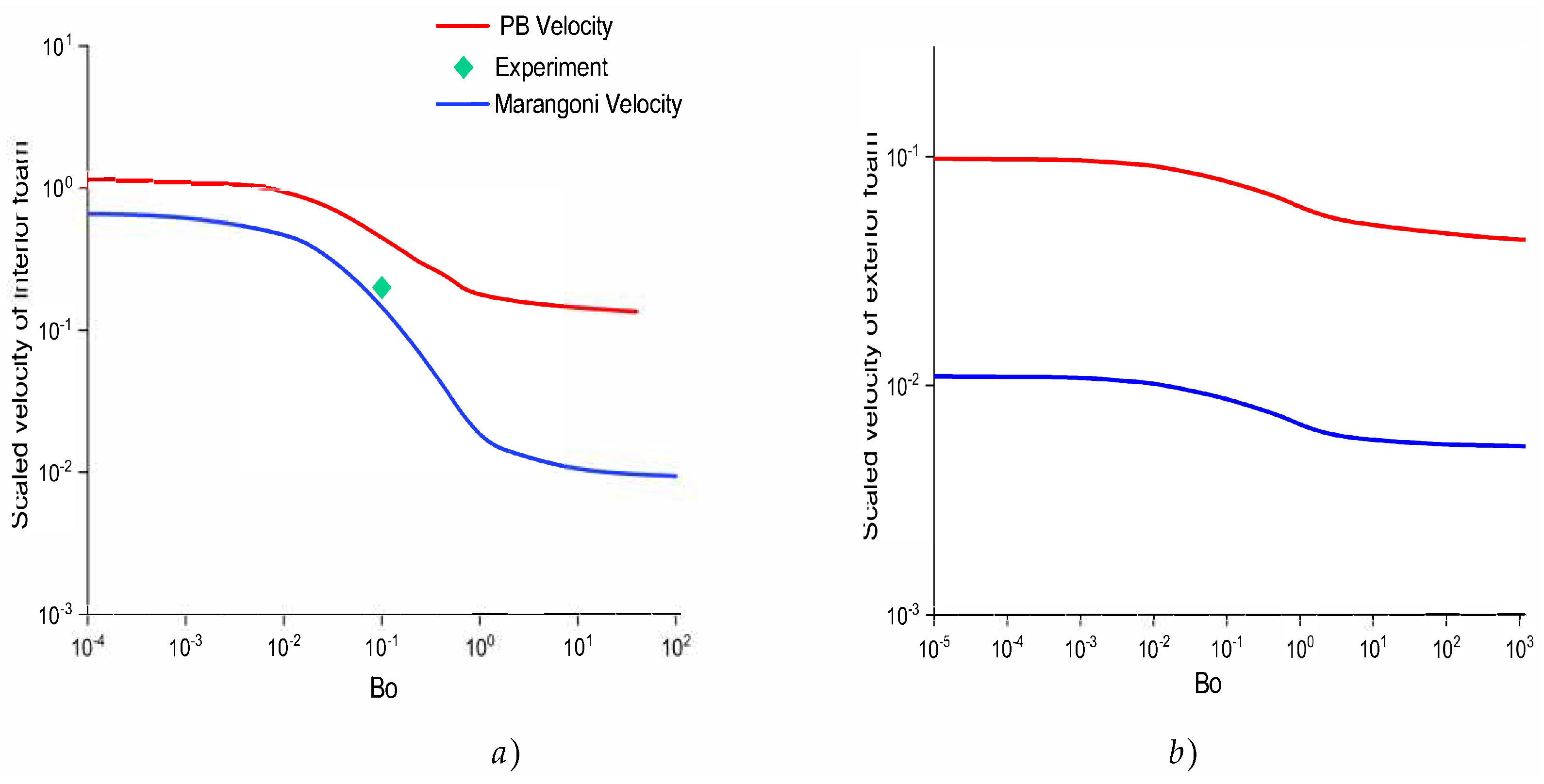
4.1.2. Experimental Validations
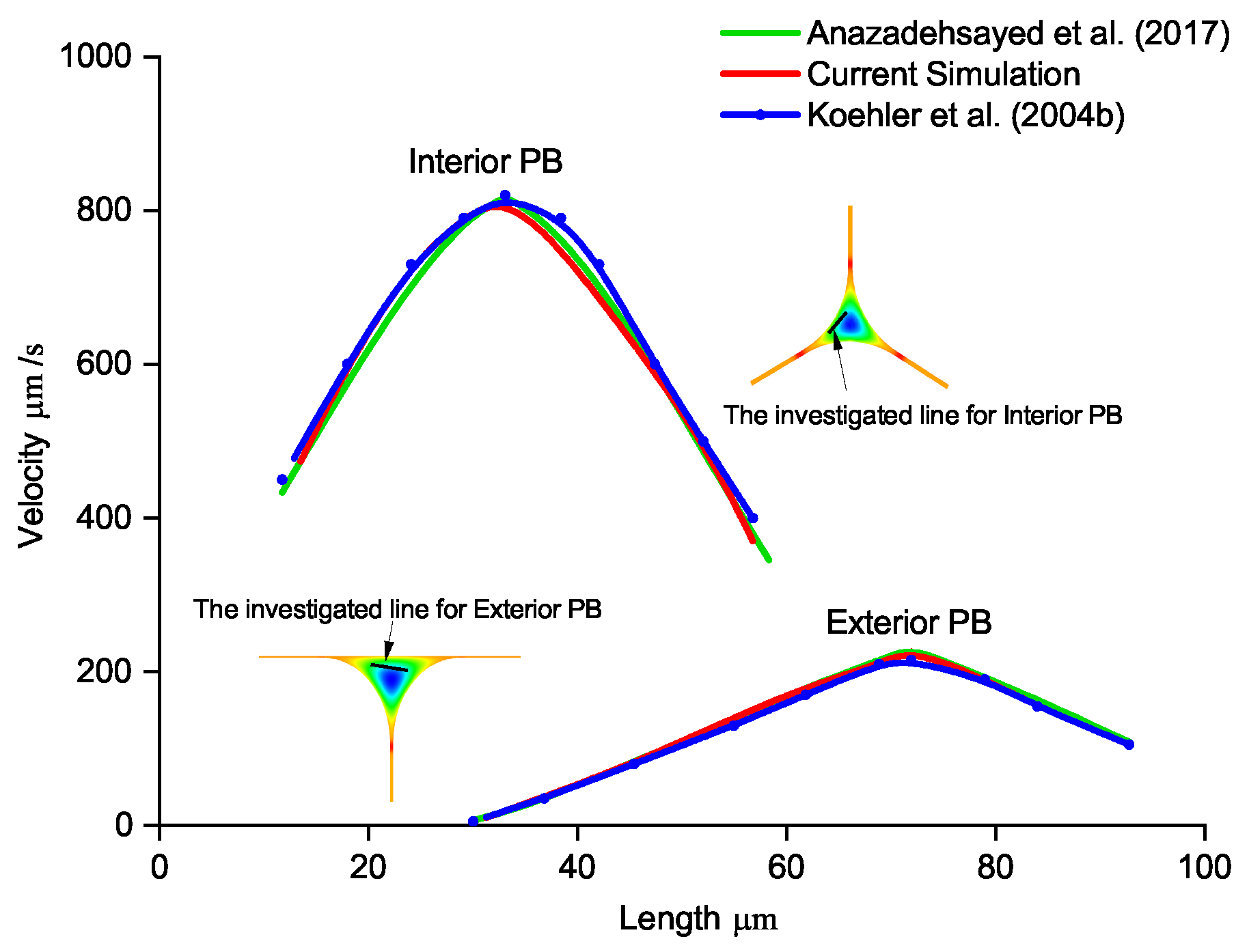
4.1.3. Analytical Validations
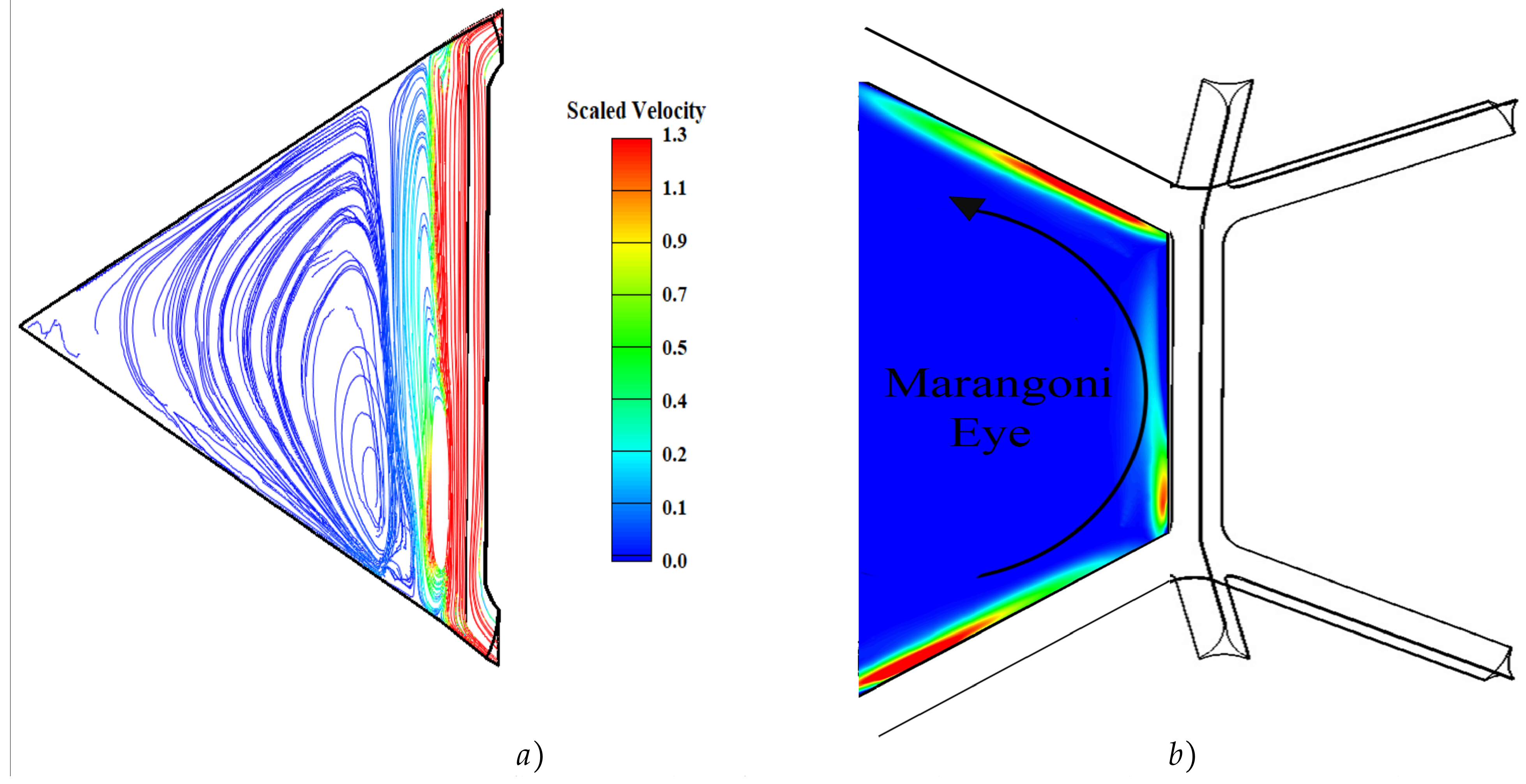
4.2. Recirculation Marangoni Flow
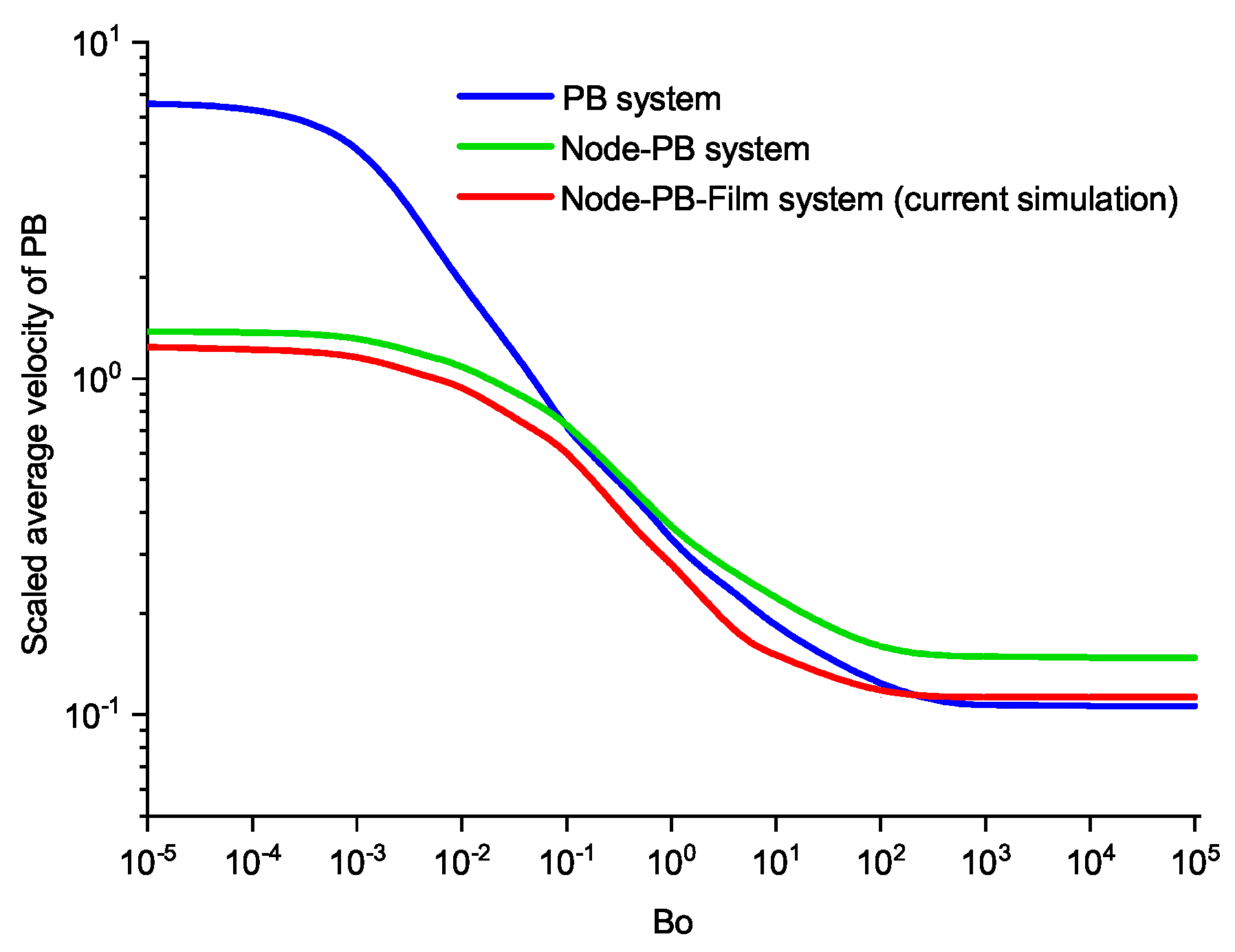
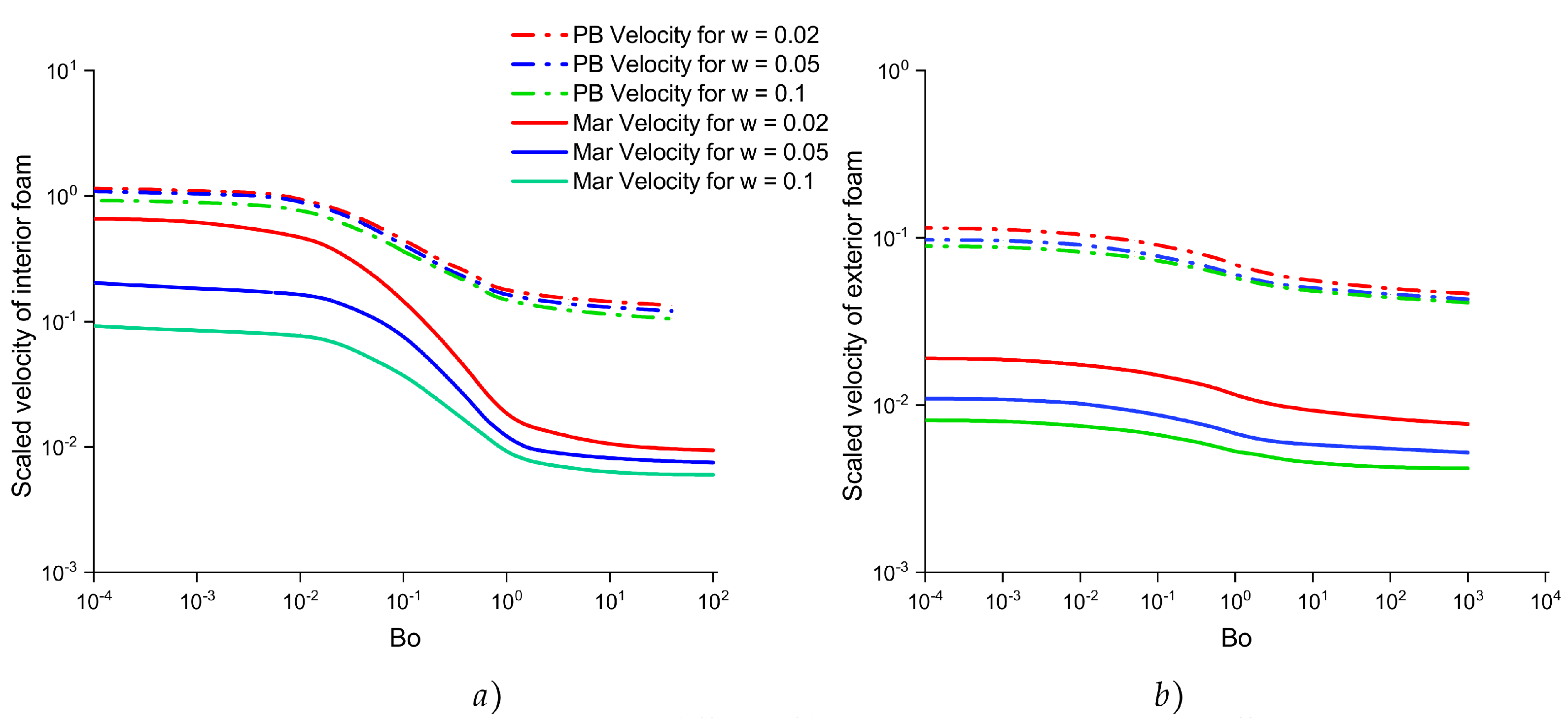
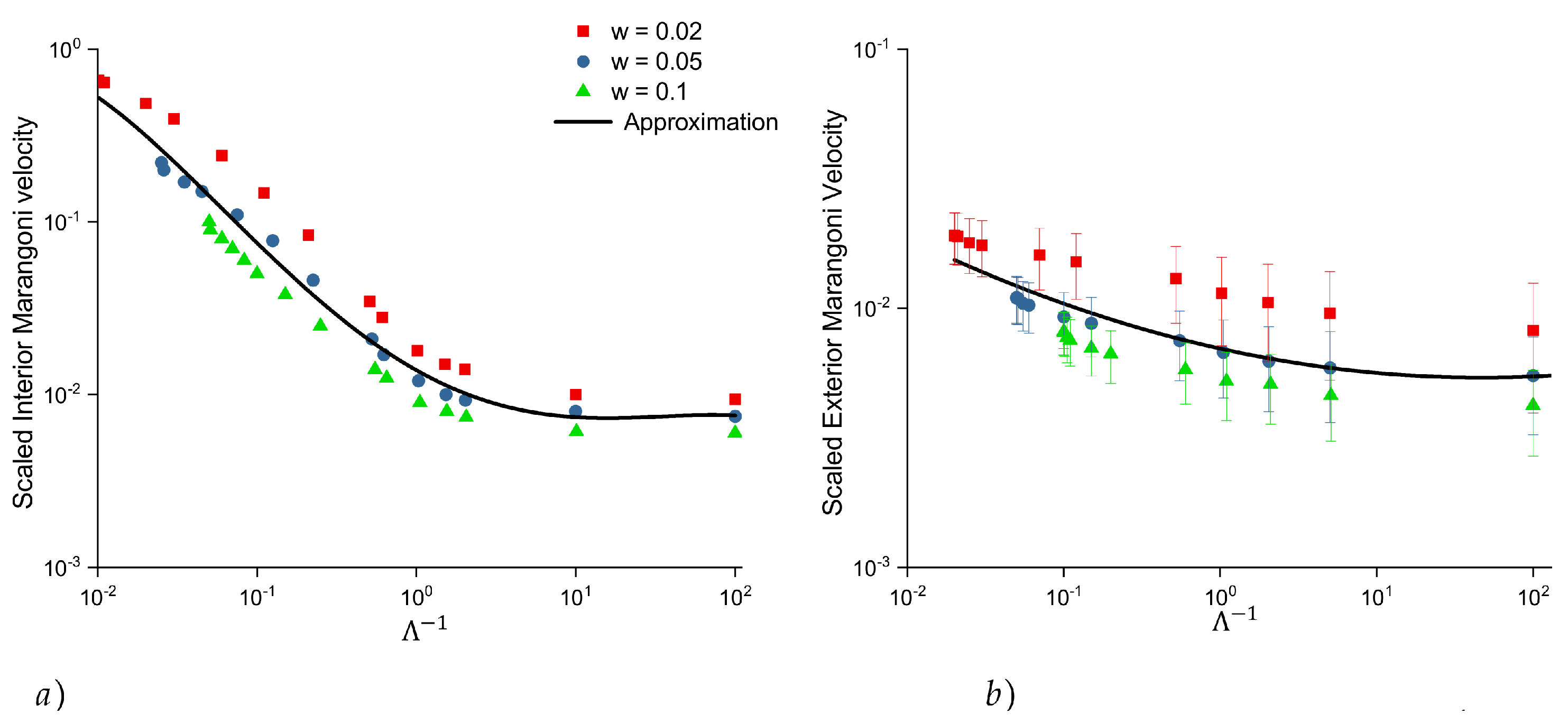
4.3. Effect of Film Thickness on Marangoni Flow
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Hill, C.; Eastoe, J. Foams: From nature to industry. Adv. Colloid Interface Sci. 2017, 247, 496–513. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Yang, W.; Li, S.; Han, G.; Ma, C. Foam Mobility Control for Surfactant Enhanced Oil Recovery. SPE J. 2008, 15, 928–942. [Google Scholar] [CrossRef]
- Simjoo, M.; Dong, Y.; Andrianov, A.; Talanana, M.; Zitha, P.L.J. CT Scan Study of Immiscible Foam Flow in Porous Media for Enhancing Oil Recovery. Ind. Eng. Chem. Res. 2013, 52, 6221–6233. [Google Scholar] [CrossRef]
- Yang, J.; Jovancicevic, V.; Ramachandran, S. Foam for gas well deliquification. Colloids Surf. A 2007, 309, 177–181. [Google Scholar] [CrossRef]
- Koehler, S.; Hilgenfeldt, S.; Stone, H. Foam drainage on the microscale. J. Colloid Interface Sci. 2004, 276, 420–438. [Google Scholar] [CrossRef]
- McKeon, B.J.; Durbin, P.A. The drainage of a foam lamella. J. Fluid Mech. 2002, 458, 379–406. [Google Scholar]
- Anazadehsayed, A.; Naser, J. A combined CFD simulation of Plateau borders including films and transitional areas of liquid foams. Chem. Eng. Sci. 2017, 166, 11–18. [Google Scholar] [CrossRef]
- Nguyen, A. Liquid Drainage in Single Plateau Borders of Foam. J. Colloid Interface Sci. 2002, 249, 194–199. [Google Scholar] [CrossRef]
- Vitasari, D.; Grassia, P.; Martin, P. Surfactant transport onto a foam lamella. Chem. Eng. Sci. 2013, 102, 405–423. [Google Scholar] [CrossRef]
- Wang, Z.; Narsimhan, G. Model for Plateau border drainage of power-law fluid with mobile interface and its application to foam drainage. J. Colloid Interface Sci. 2006, 300, 327–337. [Google Scholar] [CrossRef]
- Fournier, J.; Cazabat, A. Tear of a Disjoining Marangoni Film. EPL (Europhys. Lett.) 1992, 20, 517. [Google Scholar] [CrossRef]
- Myers, T.G. Thin Films with High Surface Tension. SIAM Rev. 1998, 40, 441–462. [Google Scholar] [CrossRef]
- Schick, C. A Mathematical Analysis of Foam Films; Shaker Verlag GmbH: Duren, Germany, 2004; Volume 1, Chapter 1. [Google Scholar]
- Ghosh, P. Colloid and Interface Science; Prentice-Hall Of India Pvt. Limited: Kolkata, India, 2009; Volume 1, Chapter 2. [Google Scholar]
- Bureiko, A.; Trybala, A.; Kovalchuk, N.; Starov, V. Current applications of foams formed from mixed surfactant-polymer solutions. Adv. Colloid Interface Sci. 2015, 222, 670–677. [Google Scholar] [CrossRef] [PubMed]
- Leonard, R.A.; Lemlich, R. A study of interstitial liquid flow in foam. Part II. Experimental verification and observations. AIChE J. 1965, 11, 25–29. [Google Scholar] [CrossRef]
- Martin, P.; Dutton, H.; Winterburn, J.; Baker, S.; Russell, A. Foam fractionation with reflux. Chem. Eng. Sci. 2010, 65, 3825–3835. [Google Scholar] [CrossRef]
- Stevenson, P.; Jameson, G.J. Modelling continuous foam fractionation with reflux. Chem. Eng. Process 2007, 46, 1286–1291. [Google Scholar] [CrossRef]
- Grassia, P.; Ubal, S.; Giavedoni, M.D.; Vitasari, D.; Martin, P.J. Surfactant flow between a Plateau border and a film during foam fractionation. Chem. Eng. Sci. 2016, 143, 139–165. [Google Scholar] [CrossRef]
- Chevallier, E.; Saint-Jalmes, A.; Cantat, I.; Lequeux, F.; Monteux, C. Light induced flows opposing drainage in foams and thin-films using photosurfactants. Soft Matter 2013, 9, 7054–7060. [Google Scholar] [CrossRef]
- Pitois, O.; Louvet, N.; Rouyer, F. Recirculation model for liquid flow in foam channels. Eur. Phys. J. E 2009, 30, 27. [Google Scholar] [CrossRef]
- McMillan, L.; Brown, C.; Garcia, A.; Hughes, M.; Kuhlman, T.; Matsui, Y.; Moya, R.; Lujan, W.; Rader, C.; Coker, J. Sandia National Laboratories. 2010; pp. 1–135. Available online: http://prod.sandia.gov/techlib/access-control.cgi/2010/107501.pdf (accessed on 13 February 2023).
- Lucassen-Reynders, E.; Cagna, A.; Lucassen, J. Gibbs elasticity, surface dilational modulus and diffusional relaxation in nonionic surfactant monolayers. Colloids Surf. A 2001, 186, 63–72. [Google Scholar] [CrossRef]
- Weaire, D.; Hutzler, S. The Physics of Foams; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Zhu, Y.; Aref, H. Dynamics of two-dimensional foam structures. J. Fluid Mech. 2002, 467, 289–311. [Google Scholar]
- Durian, D. Foam mechanics at the bubble scale. Phys. Rev. Lett. 1995, 75, 4780–4783. [Google Scholar] [CrossRef] [PubMed]
- Anazadehsayed, A.; Rezaee, N.; Naser, J. Numerical modelling of flow through foam’s node. J. Colloid Interface Sci. 2017, 504, 485–491. [Google Scholar] [CrossRef]
- Stevenson, P.; Li, X. A viscous-inertial model of foam drainage. Chem. Eng. Res. Des. 2010, 88, 928–935. [Google Scholar] [CrossRef]
- Kallendorf, C.; Cheviakov, A.F.; Oberlack, M.; Wang, Y. Conservation laws of surfactant transport equations. Phys. Fluids 2012, 24, 102105. [Google Scholar] [CrossRef]
- Stone, H.A. Convective-diffusion equation for surfactant transport along a deforming interface. Phys. Fluids Fluid Dyn. 1990, 2, 111–112. [Google Scholar] [CrossRef]
- Slattery, J.C.; Sagis, L.; Oh, E.-S. Interfacial Transport Phenomena; Springer: New York, NY, USA, 2013. [Google Scholar]
- Wong, H.; Rumschitzki, D.; Maldarelli, C. On the surfactant mass balance at a deforming fluid interface. Phys. Fluids 1996, 8, 3203–3204. [Google Scholar] [CrossRef]
- Leonard, R.A.; Lemlich, R. A study of interstitial liquid flow in foam. Part I. Theoretical model and application to foam fractionation. AIChE J. 1965, 11, 18–25. [Google Scholar] [CrossRef]
- Durand, M.; Langevin, D. Physicochemical approach to the theory of foam drainage. Eur. Phys. J. E 2002, 7, 35–44. [Google Scholar] [CrossRef]
- Carrier, V.; Destouesse, S.; Colin, A. Foam drainage: A film contribution? Phys. Rev. E 2002, 65, 061404. [Google Scholar] [CrossRef]
- Cohen-Addad, S.; Hohler, R.; Pitois, O. Flow in Foams and Flowing Foams. Annu. Rev. Fluid Mech. 2013, 45, 241–267. [Google Scholar] [CrossRef]
- Koehler, S.; Hilgenfeldt, S.; Weeks, E.; Stone, H. Foam drainage on the microscale II. Imaging flow through single Plateau borders. J. Colloid Interface Sci. 2004, 276, 439–449. [Google Scholar] [CrossRef] [PubMed]
- Koehler, S.A.; Hilgenfeldt, S.; Weeks, E.R.; Stone, H.A. Drainage of single Plateau borders: Direct observation of rigid and mobile interfaces. Phys. Rev. E 2002, 66, 040601. [Google Scholar] [CrossRef] [PubMed]
- Anazadehsayed, A.; Rezaee, N.; Naser, J. Exterior foam drainage and flow regime switch in the foams. J. Colloid Interface Sci. 2018, 511, 440–446. [Google Scholar] [CrossRef] [PubMed]
- Kumar, D. A Microfluidic Device for Producing Controlled Collisions between Two Soft Particles. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2016. [Google Scholar]
- Motagamwala, A.H. A Microfluidic, Extensional Flow Device for Manipulating Soft Particles. Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2013. [Google Scholar]

| Parameters | Symbols | Values | Unit |
|---|---|---|---|
| Film thickness | 1, 2.5, 5 | ||
| Film length | 800 | ||
| PB length | 1000 | ||
| Liquid viscosity | 0.001 | s | |
| Surface area | A | * | |
| Gibbs parameter | G | 0.01 | m |
| Fluid density | 1000 | ||
| Radius of curvature of the Plateau Border | R | 100 | |
| Initial surfactant surface concentration of the upper stream | m | ||
| Initial surfactant surface concentration of the lower stream | m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezaee, N.; Aunna, J.; Naser, J. Investigation of Recirculating Marangoni Flow in Three-Dimensional Geometry of Aqueous Micro-Foams. Fluids 2023, 8, 113. https://doi.org/10.3390/fluids8040113
Rezaee N, Aunna J, Naser J. Investigation of Recirculating Marangoni Flow in Three-Dimensional Geometry of Aqueous Micro-Foams. Fluids. 2023; 8(4):113. https://doi.org/10.3390/fluids8040113
Chicago/Turabian StyleRezaee, Nastaran, John Aunna, and Jamal Naser. 2023. "Investigation of Recirculating Marangoni Flow in Three-Dimensional Geometry of Aqueous Micro-Foams" Fluids 8, no. 4: 113. https://doi.org/10.3390/fluids8040113
APA StyleRezaee, N., Aunna, J., & Naser, J. (2023). Investigation of Recirculating Marangoni Flow in Three-Dimensional Geometry of Aqueous Micro-Foams. Fluids, 8(4), 113. https://doi.org/10.3390/fluids8040113