Thermal Convection of an Ellis Fluid Saturating a Porous Layer with Constant Heat Flux Boundary Conditions
Abstract
:1. Introduction
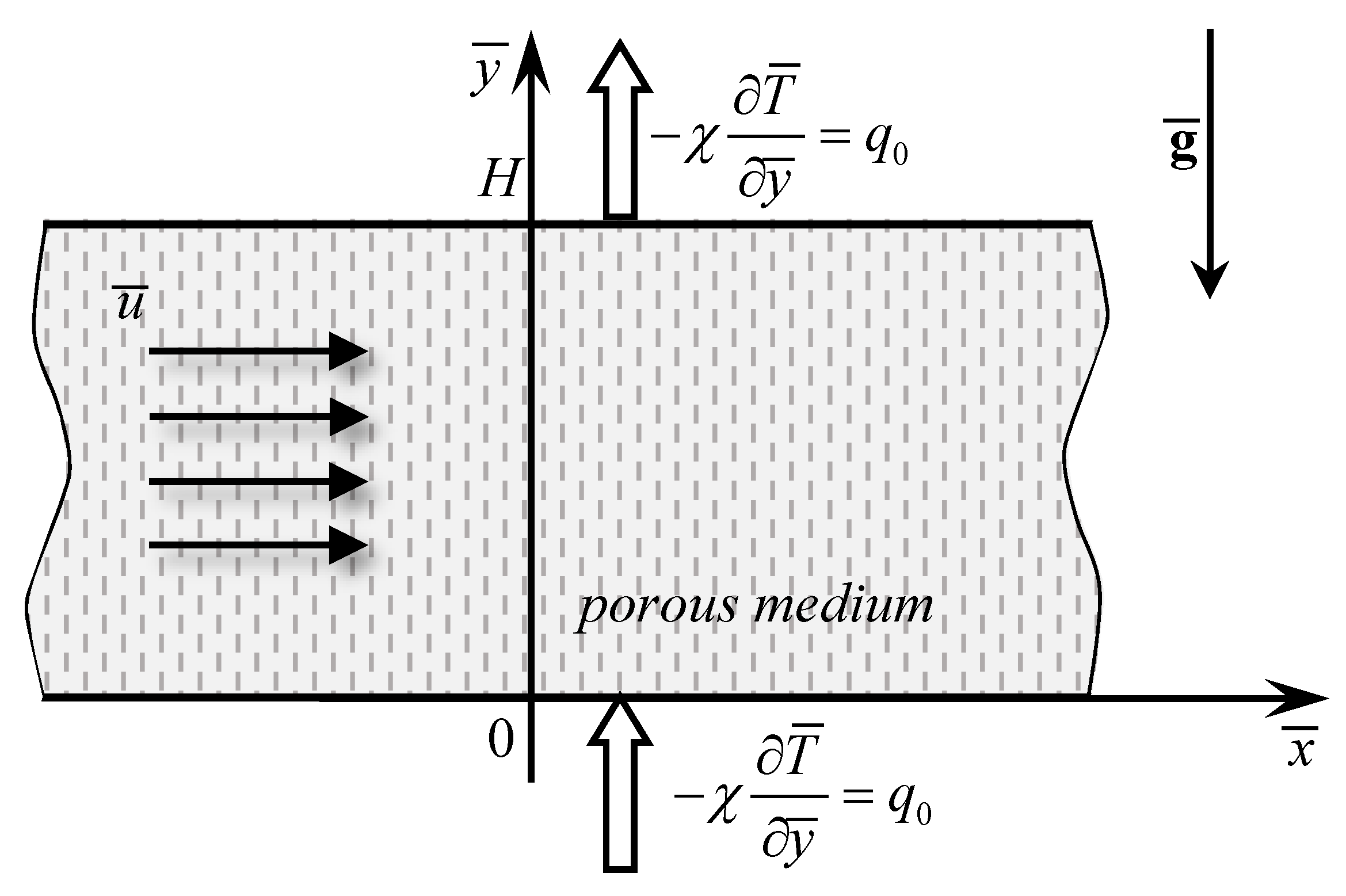
2. Mathematical Formulation
2.1. Rheological Model
2.2. Modified Darcy’s Law
2.3. Governing Equations
2.4. Basic State
2.5. Linear Stability Analysis
3. Asymptotic Analysis for Vanishing Wavenumber
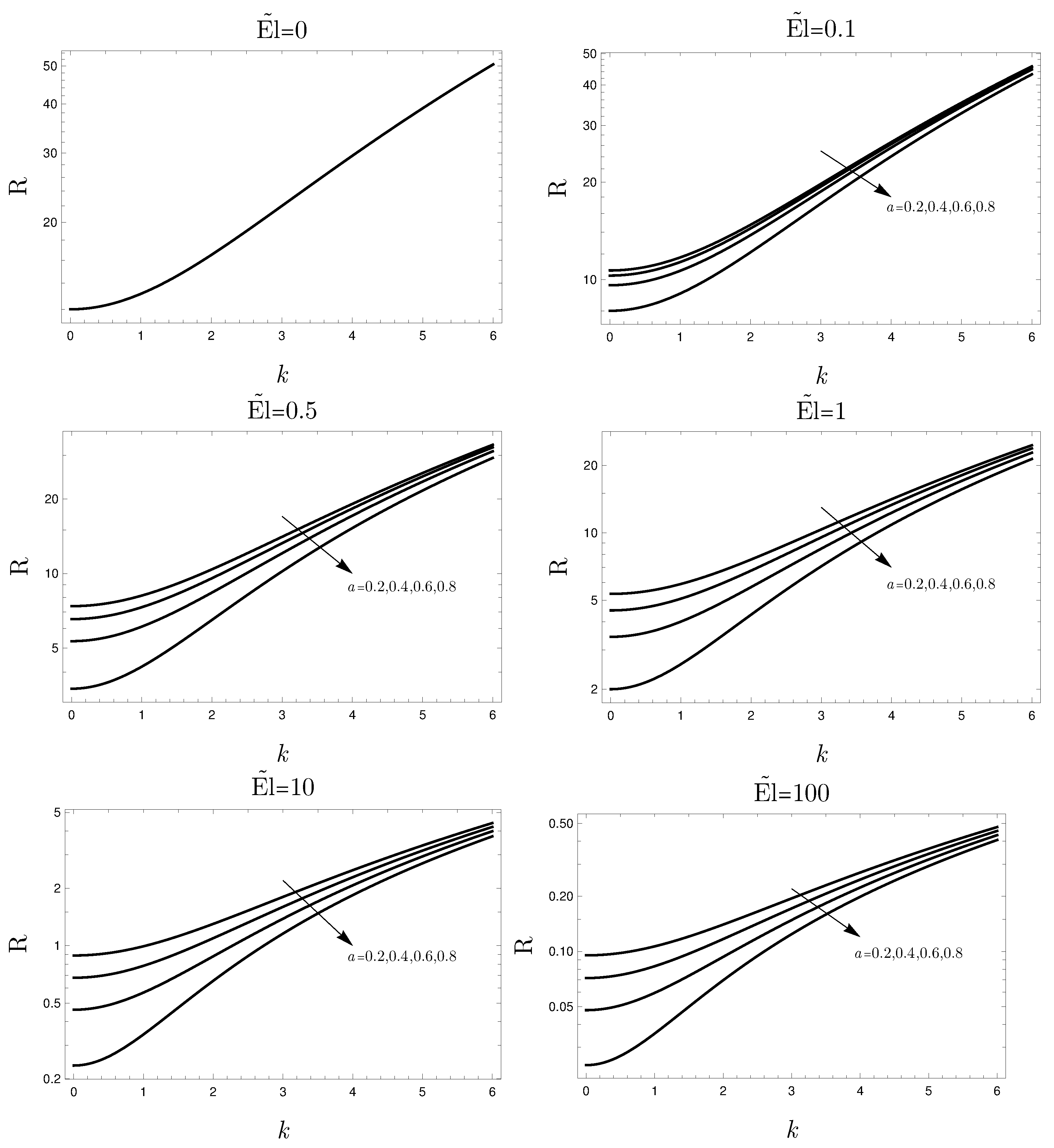
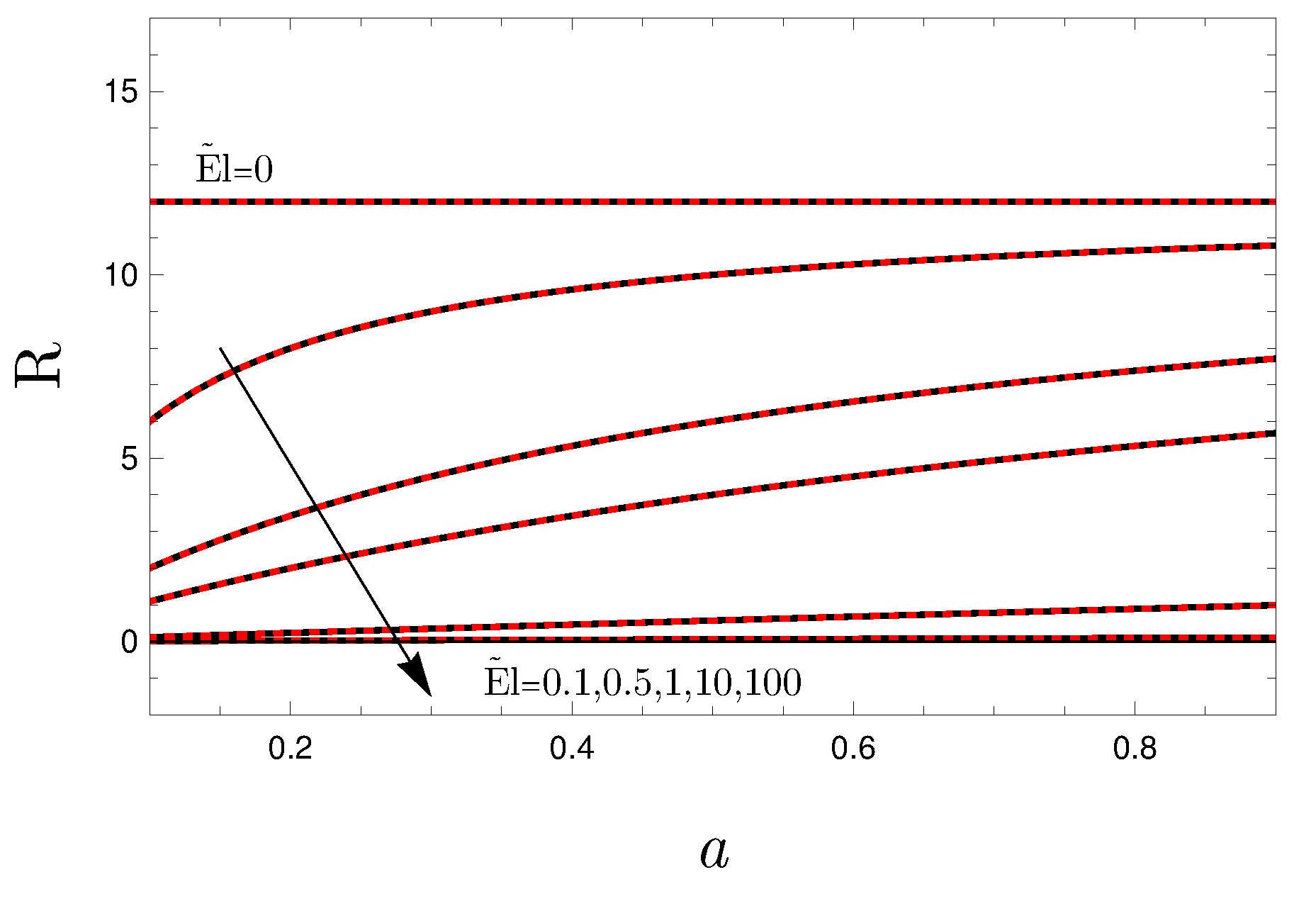
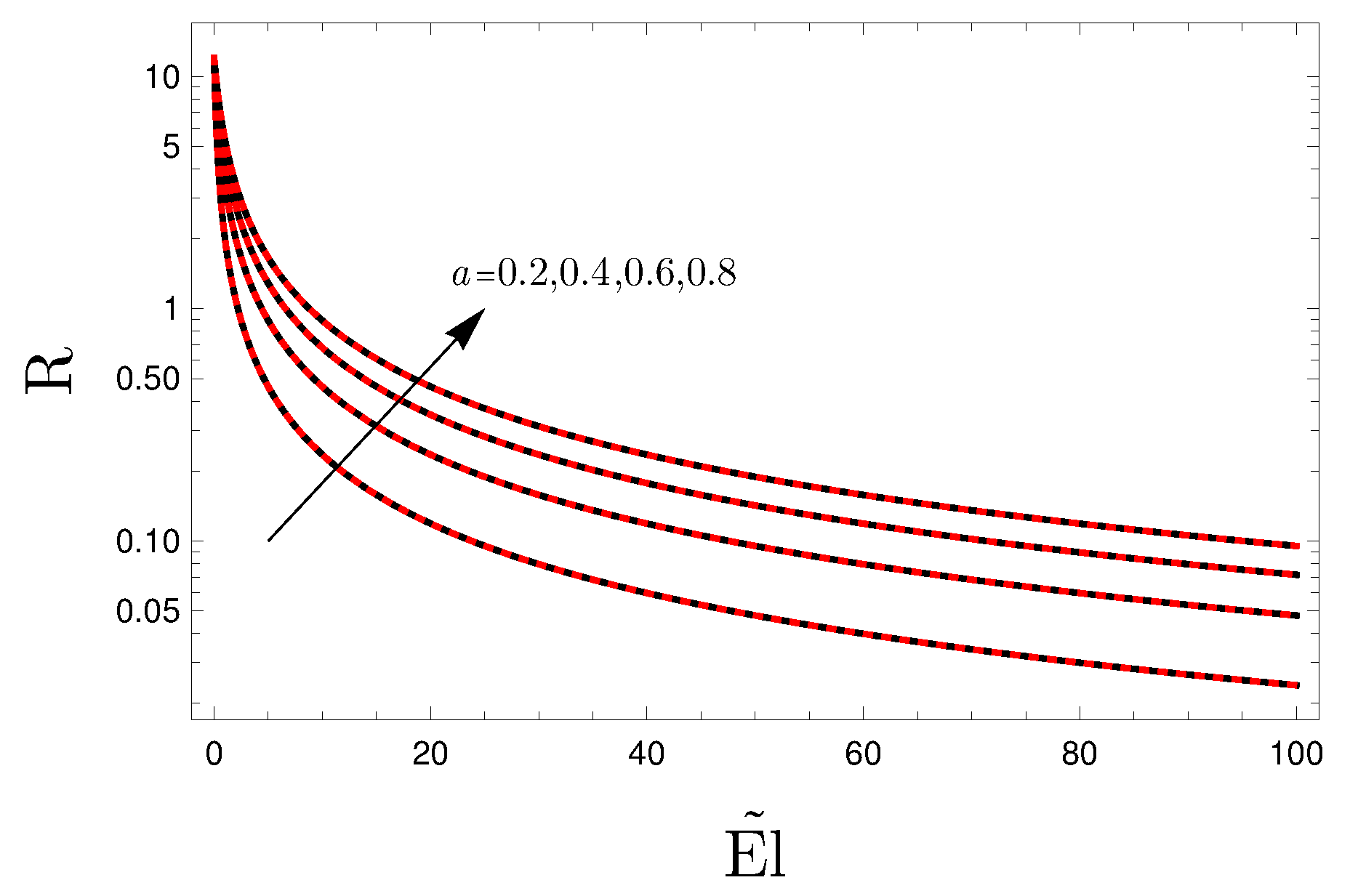
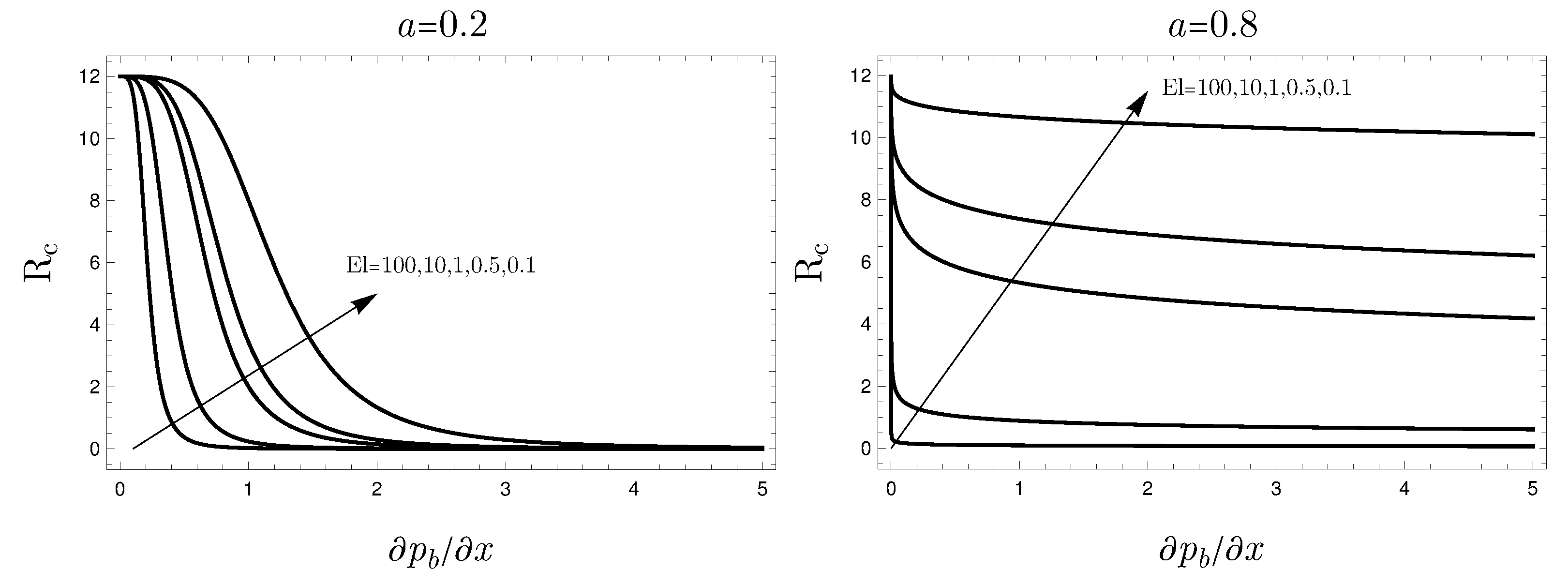
4. Results and Discussion
5. Conclusions
- There exists a suitable variable transformation that yields a compact representation of the stability eigenvalue problem;
- The critical conditions hold always for . The threshold values can be obtained entirely analytically due to an asymptotic analysis performed for ;
- The non-Newtonian character of the fluid plays a destabilizing effect on the convective flow, namely an increasing value of the Ellis number yields a destabilization of the basic flow;
- For , the Ellis index a does not affect the stability conditions and the results coincide with those for the limit of Newtonian fluid already available in the literature ( and );
- For large values of the Ellis number, the power-law behavior is recovered. This means that the critical Rayleigh number tends to zero.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nield, D.A.; Bejan, A. Convection in Porous Media, 5th ed.; Springer: New York, NY, USA, 2017. [Google Scholar]
- Shenoy, A. Non-Newtonian fluid heat transfer in porous media. In Advances in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 1994; Volume 24, pp. 101–190. [Google Scholar]
- Nield, D.A. A note on the onset of convection in a layer of a porous medium saturated by a non-Newtonian nanofluid of power-law type. Transp. Porous Media 2011, 87, 121–123. [Google Scholar] [CrossRef]
- Nield, D.A. A further note on the onset of convection in a layer of a porous medium saturated by a non-Newtonian fluid of power-law type. Transp. Porous Media 2011, 88, 187–191. [Google Scholar] [CrossRef]
- Brandão, P.V.; Ouarzazi, M.N. Darcy–Carreau model and nonlinear natural convection for pseudoplastic and dilatant fluids in porous media. Transp. Porous Media 2021, 136, 521–539. [Google Scholar] [CrossRef]
- Brandão, P.; Ouarzazi, M.; Hirata, S.d.C.; Barletta, A. Darcy–Carreau–Yasuda rheological model and onset of inelastic non-Newtonian mixed convection in porous media. Phys. Fluids 2021, 33, 044111. [Google Scholar] [CrossRef]
- Celli, M.; Barletta, A.; Brandão, P.V. Rayleigh–Bénard instability of an Ellis fluid saturating a porous medium. Transp. Porous Media 2021, 138, 679–692. [Google Scholar] [CrossRef]
- Brandão, P.V.; Celli, M.; Barletta, A. Rayleigh–Bénard instability of an Ellis fluid saturated porous channel with an isoflux Boundary. Fluids 2021, 6, 450. [Google Scholar] [CrossRef]
- Savins, J.G. Non-Newtonian flow through porous media. Ind. Eng. Chem. 1969, 61, 18–47. [Google Scholar] [CrossRef]
- Horton, C.W.; Rogers, F.T. Convection currents in a porous medium. J. Appl. Phys. 1945, 16, 367–370. [Google Scholar] [CrossRef]
- Lapwood, E.R. Convection of a fluid in a porous medium. Proc. Camb. Philos. Soc. 1948, 44, 508–521. [Google Scholar] [CrossRef]
- Prats, M. The effect of horizontal fluid flow on thermally induced convection currents in porous mediums. J. Geophys. Res. 1966, 71, 4835–4838. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Goldstein, R.J.; Jonsson, V.K. Thermal instability in a horizontal fluid layer: Effect of boundary conditions and non-linear temperature profile. J. Fluid Mech. 1964, 18, 513–528. [Google Scholar] [CrossRef]
- Park, H.; Sirovich, L. Hydrodynamic stability of Rayleigh-Bénard convection with constant heat flux boundary condition. Q. Appl. Math. 1991, 49, 313–332. [Google Scholar] [CrossRef]
- Nield, D.A. Onset of thermohaline convection in a porous medium. Water Resour. Res. 1968, 4, 553–560. [Google Scholar] [CrossRef]
- Jones, M.; Persichetti, J. Convective instability in packed beds with throughflow. AIChE J. 1986, 32, 1555–1557. [Google Scholar] [CrossRef]
- Sochi, T. Non-Newtonian flow in porous media. Polymer 2010, 51, 5007–5023. [Google Scholar] [CrossRef]
- Sadowski, T.J.; Bird, R.B. Non-Newtonian flow through porous media. I. Theoretical. Trans. Soc. Rheol. 1965, 9, 243–250. [Google Scholar] [CrossRef]
- Sadowski, T.J. Non-Newtonian Flow through Porous Media. Ph.D. Thesis, The University of Wisconsin-Madison, Madison, WI, USA, 1963. [Google Scholar]
- Wolfram, S. The Mathematica book (3rd ed.). Assem. Autom. 1999, 19, 77. [Google Scholar] [CrossRef]
| k | |
|---|---|
| 12.0114 | |
| 12.0001 | |
| 12.0000 | |
| 0 | 12 |
| 0 | 12 | 12 | 12 | 12 |
| 10.666667 | 10.285714 | 9.6 | 8 | |
| 7.3846154 | 6.5454545 | 5.3333333 | 3.4285714 | |
| 1 | 5.3333333 | 4.5 | 3.4285714 | 2 |
| 10 | 0.88888889 | 0.67924528 | 0.46153846 | 0.23529412 |
| 100 | 0.095238095 | 0.071570577 | 0.047808765 | 0.023952096 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brandão, P.V.; Celli, M.; Barletta, A.; Lazzari, S. Thermal Convection of an Ellis Fluid Saturating a Porous Layer with Constant Heat Flux Boundary Conditions. Fluids 2023, 8, 54. https://doi.org/10.3390/fluids8020054
Brandão PV, Celli M, Barletta A, Lazzari S. Thermal Convection of an Ellis Fluid Saturating a Porous Layer with Constant Heat Flux Boundary Conditions. Fluids. 2023; 8(2):54. https://doi.org/10.3390/fluids8020054
Chicago/Turabian StyleBrandão, Pedro Vayssière, Michele Celli, Antonio Barletta, and Stefano Lazzari. 2023. "Thermal Convection of an Ellis Fluid Saturating a Porous Layer with Constant Heat Flux Boundary Conditions" Fluids 8, no. 2: 54. https://doi.org/10.3390/fluids8020054
APA StyleBrandão, P. V., Celli, M., Barletta, A., & Lazzari, S. (2023). Thermal Convection of an Ellis Fluid Saturating a Porous Layer with Constant Heat Flux Boundary Conditions. Fluids, 8(2), 54. https://doi.org/10.3390/fluids8020054









