Instability Problems and Density-Driven Convection in Saturated Porous Media Linking to Hydrogeology: A Review
Abstract
1. Introduction
2. Mathematical Model
2.1. Equation of State
- density stratification under the gravity force, which is an increase of density in the downward direction due to the own weight of fluid, is not allowed. However even considering large geological scales, this approximation is justified. For example, according to [27], the water density varies from 996.56 kg/m to 1001.0 kg/m if the pressure increases in two orders of magnitude (see two first lines in Table 1). The height of the water column should be km to provide the pressure difference bar. Thus, the density stratification of water at such a huge scale is only about %, which is negligible. As a result, the stratification effect under the gravity force is reduced to a dependence of P on height only. Stratification of P is linear;
- this allows us to consider a fluid as isothermal and eliminate the energy equation in the dynamic model when haline gravity-driven convection is under study. In this way, the set of governing equations is simplified. On the contrary, assuming a dependence of on P and employing the equation of state in the full form of Equation (1), we have to include the energy equation into the set of governing equations to describe heating/cooling due to compression/expansion under pressure gradients even if thermal effects do not influence the convection process generally.
2.2. Mass Balance Equation
2.3. Motion Equation
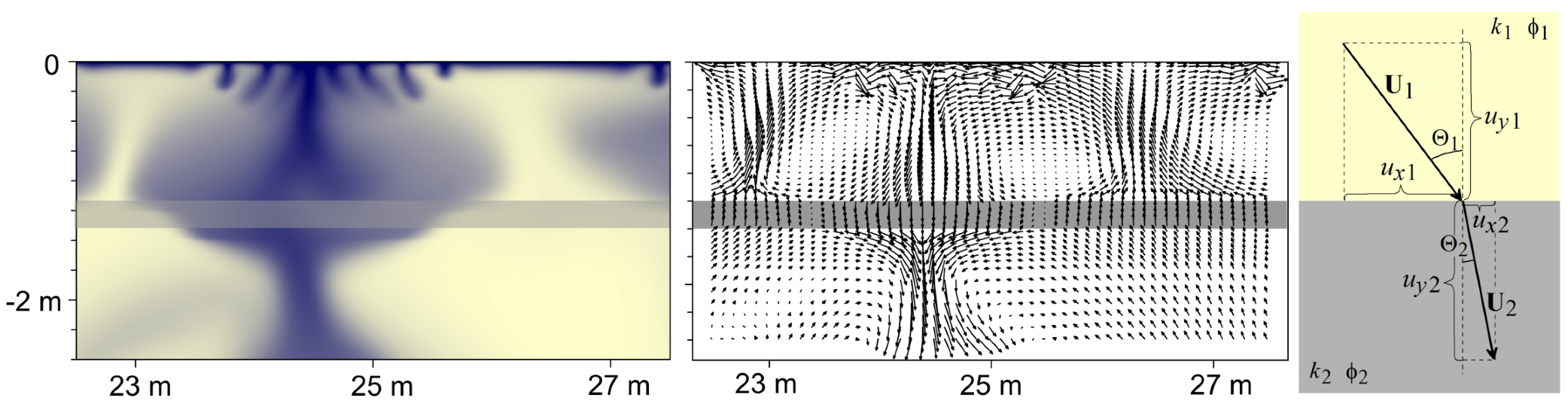
2.4. Physical and Dimensionless Parameters
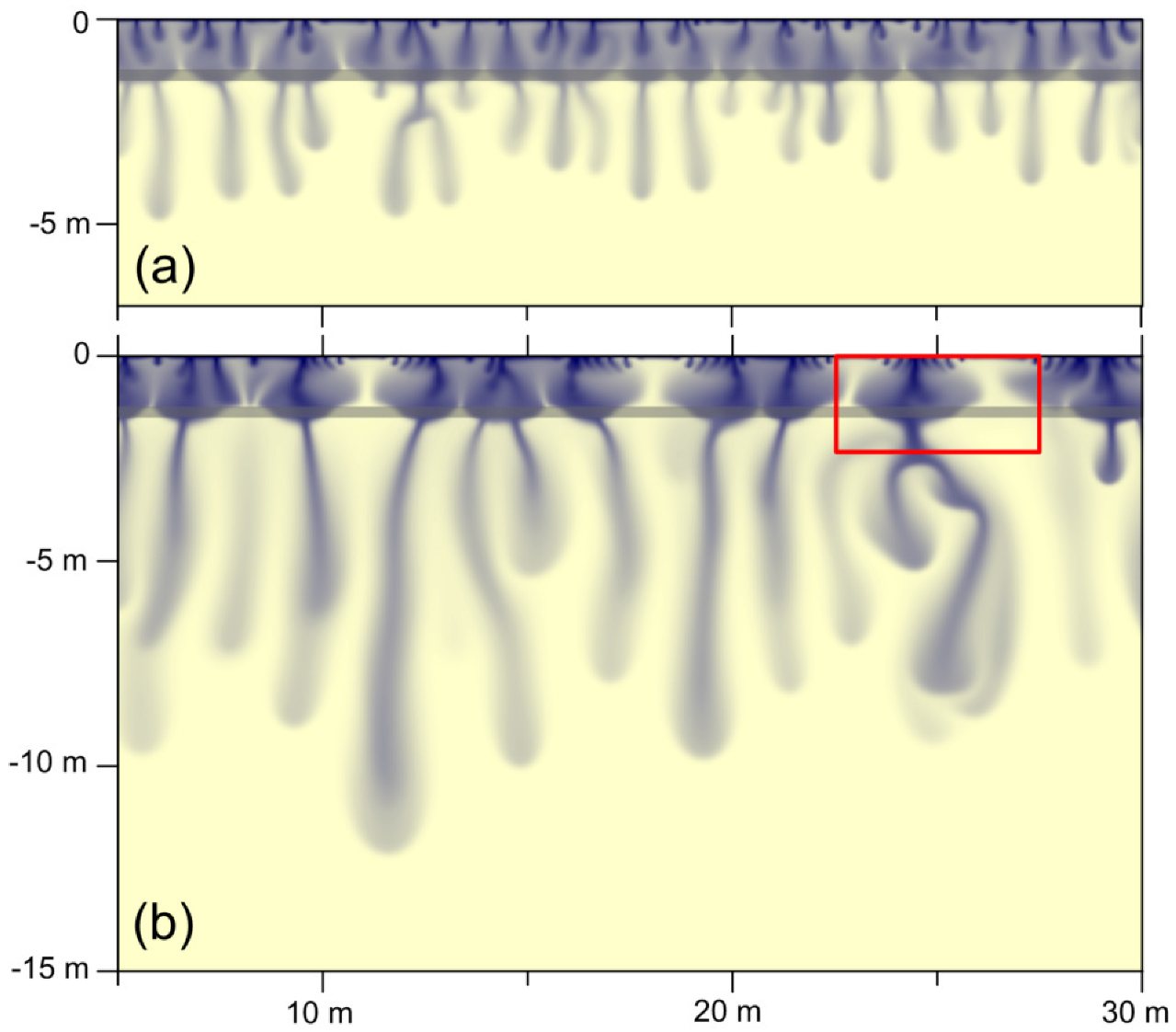
3. Problem I: One-Sided Convection
- An admixture gradually dissolves into a fluid phase and propagates in it due to diffusion. The diffusion layer under the source of admixture extends over time; the width of this layer is proportional to the square-root of time. Fluid remains at rest during this stage.
- Because the diffusion layer is more dense than a pure fluid and hence unstable in the gravity field, this layer is broken. As a result, periodic convective perturbations appear according to theoretical predictions. In numerical simulations and experiments, the onset of convection is associated with quasi-periodic or partially quasi-periodic structures; the last one is observed when groups of quasi-periodic fingers emerge from the diffusion layer in random locations [45,65].
- Convective fingers elongate irregularly, deform randomly, and merge with each other. Stochastic convection occurs.
- the transient diffusive layer is broken and convection starts depending on the initial perturbations of physical parameters;
- the times of convection onset found in theoretical predictions, numerical simulations, and experiments can be different. Therefore, the discrepancies when comparing theoretical, numerical and experimental results can be observed. How to define the critical time in numerical simulations is not obvious.
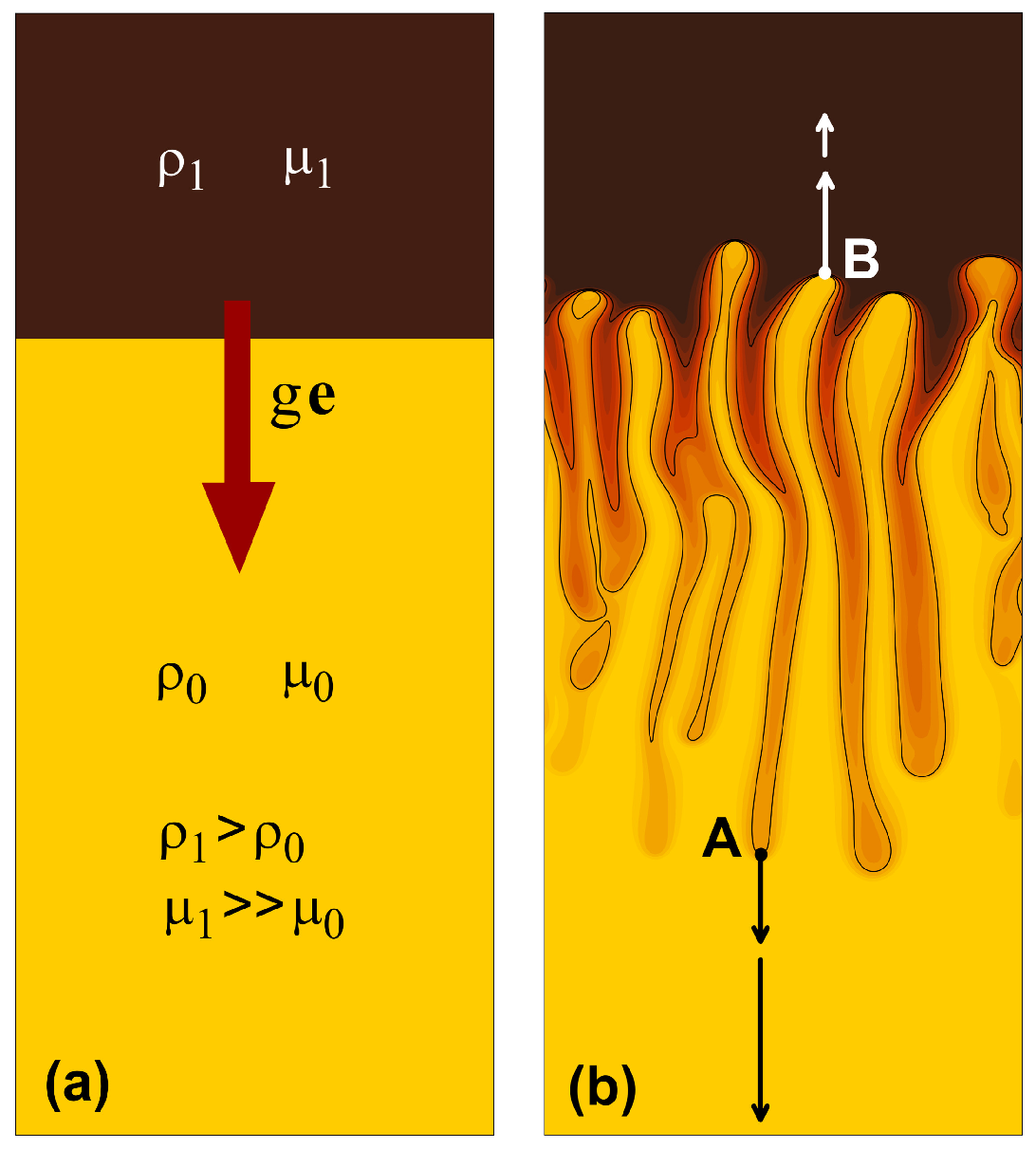
4. Problem II: Two-Sided Convection (Rayleigh–Taylor Problem)
5. Problem III: Convection Caused by Evaporation
6. Methods
7. Future Directions
- As discussed above, the onset of convection depends on initial perturbations of physical parameters. This finding gives the fluid physics community some perspective for controlling the convection onset. By imposing perturbations of prescribed type and amplitude, convection may start sooner or later. The issue of controlling the convection onset with the use of specific perturbations should be clarified.
- The mathematical model treating a solvent as an incompressible fluid provides extensive numerical results on convection flows and mixing. However, including compressibility into account may give the future advancements in modeling density-driven convection in geological conditions and provide novel qualitative effects. This aspect may be significant for considering water flows in deep aquifers where water is in the supercritical state. It also can play a role if the solvent is another fluid, for example, supercritical having a high compressibility.
- Because the Earth spins about its axis, geophysical flows are acted upon an inertial force called the Coriolis force. We did not find any publications reporting that the Coriolis effect is taken into account when density-driven convection in geological conditions is considered. However, this effect should be estimated in analytical and numerical studies especially in the context of solubility trapping.
8. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| c | admixture concentration, |
| D | coefficient of molecular diffusion |
| coefficient of hydrodynamic dispersion (tensor) | |
| unit vector co-directed with the gravity force | |
| g | module of gravity force acceleration |
| H | geometric scale (height of domain) |
| h | height of mixing zone |
| unit tensor | |
| mass flux of admixture (vector) | |
| permeability tensor | |
| k | permeability |
| M | viscosity contrast, = max |
| N | buoyancy ratio |
| P | pressure |
| Peclet number | |
| R | actual Rayleigh-Darcy number |
| r | random number varying in the range: |
| Rayleigh-Darcy number | |
| S | dimensionless admixture density |
| dimensionless admixture density perturbation | |
| T | temperature |
| t | time |
| seepage velocity (vector) | |
| fluid velocity (vector) | |
| V | vertical component of fluid velocity |
| x | horizontal coordinate |
| y | vertical coordinate |
| longitudinal dispersivity | |
| transverse dispersivity | |
| haline contraction coefficient | |
| coefficient of thermal expansion | |
| mass source term | |
| viscosity coefficient | |
| density of fluid phase | |
| density of dissolved admixture | |
| amplitude of density perturbations | |
| tortuosity factor | |
| porosity | |
| Subscripts | |
| b | fluid with dissolved admixture (solution) at initial conditions |
| c | critical conditions |
| d | quantities determined by diffusion |
| g | quantities determined by the gravity force |
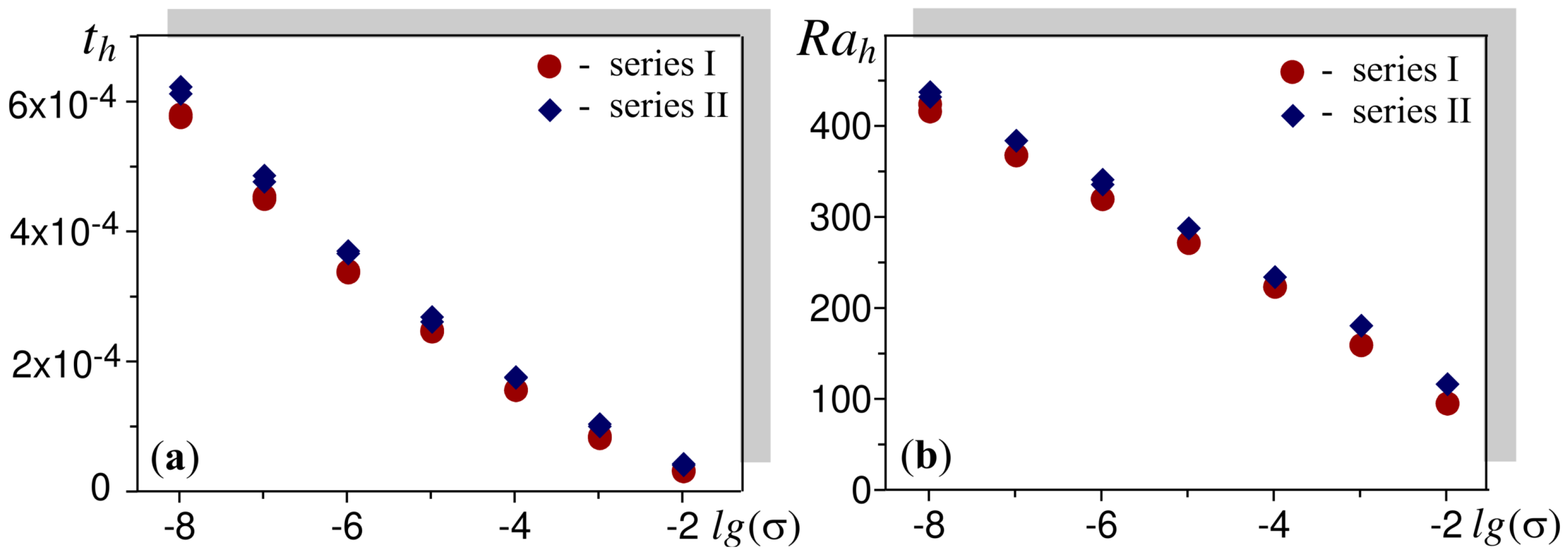
| h | convection onset in numerical simulations determined by the condition: |
| i | hydrostatic conditions |
| 0 | pure fluid |
| Superscripts | |
| 0 | level |
| * | forced flow |
References
- Bear, J.; Cheng, A. Modeling Groundwater Flow and Contaminant Transport; Springer: New York, NY, USA, 2010. [Google Scholar]
- Anderson, L. New Theory of the Earth; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Stanhill, G. Evapotranspiration. In Encyclopedia of Soils in the Environment, 1st ed.; Hillel, D., Ed.; Academic Press: Cambridge, MA, USA, 2004. [Google Scholar]
- McKibbin, R. Modeling heat and mass transport processes in geothermal systems. In Handbook of Porous Media; Vafai, K., Ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2005. [Google Scholar]
- Olasolo, P.; Juárez, M.C.; Morales, M.P.; D’Amico, S.; Liarte, I.A. Enhanced geothermal systems (EGS): A review. Renew. Sust. Energ. Rev. 2016, 56, 133–144. [Google Scholar] [CrossRef]
- Lu, S.-M. A global review of enhanced geothermal system (EGS). Renew. Sust. Energ. Rev. 2018, 81, 2902–2921. [Google Scholar] [CrossRef]
- Phuoc, T.X.; Massoudi, M.; Wang, P.; McKoy, M.L. Exergy of air, CO2, and H2O for use as geothermal fluids. Int. J. Heat Mass Transf. 2018, 126, 448–456. [Google Scholar] [CrossRef]
- Nogara, J.; Zarrouk, S.J. Corrosion in geothermal environment: Part 1: Fluids and their impact. Renew. Sust. Energ. Rev. 2018, 82, 1333–1346. [Google Scholar] [CrossRef]
- Metz, B.; Davidson, O.; De Coninck, H.C.; Loos, M.; Meyer, L.A. IPCC Special Report on Carbon Dioxide Capture and Storage; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2005. [Google Scholar]
- Huppert, H.E.; Neufeld, J.A. The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 2014, 46, 255–272. [Google Scholar] [CrossRef]
- Riaz, A.; Cinar, Y. Carbon dioxide sequestration in saline formations: Part I—Review of the modeling of solubility trapping. J. Petrol. Sci. Eng. 2014, 124, 367–380. [Google Scholar] [CrossRef]
- Riaz, A.; Cinar, Y. Carbon dioxide sequestration in saline formations: Part 2—Review of multiphase flow modeling. J. Petrol. Sci. Eng. 2014, 124, 381–398. [Google Scholar] [CrossRef]
- Abidoye, L.K.; Khudaida, K.J.; Das, D.B. Geological Carbon Sequestration in the Context of Two-Phase Flow in Porous Media: A Review. Crit. Rev. Environ. Sci. Technol. 2015, 45, 1105–1147. [Google Scholar] [CrossRef]
- Emami-Meybodi, H.; Hassanzadeh, H.; Green, C.P.; Ennis-King, J. Convective dissolution of CO2 in saline aquifers: Progress in modeling and experiments. Int. J. Greenh. Gas Control 2015, 40, 238–266. [Google Scholar] [CrossRef]
- Emami-Meybodi, H. Dispersion-driven instability of mixed convective flow in porous media. Phys. Fluids 2017, 29, 094102. [Google Scholar] [CrossRef]
- Saffman, P.G.; Taylor, G.I. The penetration of a fluid into a porous medium or Hele-Shaw cell containing a more viscous liquid. Proc. R. Soc. A 1958, 245, 312–329. [Google Scholar]
- Homsy, G.M. Viscous fingering in porous media. Annu. Rev. Fluid Mech. 1987, 19, 271–311. [Google Scholar] [CrossRef]
- Coskuner, G. Onset of Viscous Fingering for Miscible Liquid-Liquid Displacements in Porous Media. Transp. Porous Media 1993, 10, 285–291. [Google Scholar] [CrossRef]
- Manickam, O.; Homsy, G.M. Fingering instabilities in vertical miscible displacement flows in porous media. J. Fluid Mech. 1995, 288, 75–102. [Google Scholar] [CrossRef]
- De Wit, A.; Homsy, G.M. Viscous fingering in periodically heterogeneous porous media. II. Numerical simulations. J. Chem. Phys. 1997, 107, 9619–9628. [Google Scholar] [CrossRef]
- Scovazzi, G.; Wheeler, M.F.; Mikelić, A.; Lee, S. Analytical and variational numerical methods for unstable miscible displacement flows in porous media. J. Comput. Phys. 2017, 335, 444–496. [Google Scholar] [CrossRef]
- Nijjer, J.S.; Hewitt, D.R.; Neufeld, J.A. Stable and unstable miscible displacements in layered porous media. J. Fluid Mech. 2019, 869, 468–499. [Google Scholar] [CrossRef]
- Sabet, N.; Mohammadi, M.; Zirahi, A.; Zirrahi, M.; Hassanzadeh, H.; Abedi, J. Numerical modeling of viscous fingering during miscible displacement of oil by a paraffinic solvent in the presence of asphaltene precipitation and deposition. Int. J. Heat Mass Transf. 2020, 154, 119688. [Google Scholar] [CrossRef]
- Yuan, Q.; Ling, B.; Aryana, S.A. New phase diagram of miscible viscous fingering instabilities in porous media with dead-end pores. Phys. Fluids 2022, 34, 092109. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Gershuni, G.Z.; Zhukhovitskii, E.M. Convective Stability of Incompressible Fluids; Keter Publishing House: Jerusalem, Israel, 1976. [Google Scholar]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 87th ed.; CRC Press/Taylor and Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Vargaftik, N.B.; Vinogradov, Y.K.; Yargin, V.S. Handbook of Physical Properties of Liquids and Gases Pure Substances and Mixtures, 3rd ed.; Begell House, Inc.: New York, NY, USA, 1996. [Google Scholar]
- Grigoriev, I.S.; Meilikhov, E.Z. Handbook of Physical Quantities, 1st ed.; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Gill, A.E. Atmosphere-Ocean Dynamics; Academic Press: San Diego, CA, USA, 1982. [Google Scholar]
- Nomeli, M.A.; Tilton, N.; Riaz, A. A new model for the density of saturated solutions of CO2–H-2O–NaCl in saline aquifers. Int. J. Greenh. Gas Control 2014, 31, 192–204. [Google Scholar] [CrossRef]
- Bando, S.; Takemura, F.; Nishio, M.; Hihara, E.; Akai, M. Viscosity of aqueous NaCl solutions with dissolved CO2 at (30 to 60) °C and (10 to 20) MPa. J. Chem. Eng. Data 2004, 49, 1328–1332. [Google Scholar] [CrossRef]
- Song, Y.; Chen, B.; Nishio, M.; Akai, M. The study on density change of carbon dioxide seawater solution at high pressure and low temperature. Energy 2005, 30, 2298–2307. [Google Scholar] [CrossRef]
- Morel, C.R.G.; van Reeuwijk, M.; Graf, T. Systematic investigation of non-Boussinesq effects in variable-density groundwater flow simulations. J. Contam. Hydrol. 2015, 183, 82–98. [Google Scholar]
- Nield, D.A.; Bejan, A. Convection in Porous Media; Springer: New York, NY, USA, 2006. [Google Scholar]
- Islam, A.W.; Sharif, M.A.R.; Carlson, E.S. Numerical investigation of double diffusive natural convection of CO2 in a brine saturated geothermal reservoir. Geothermics 2013, 48, 101–111. [Google Scholar] [CrossRef]
- Lyubimova, T.P.; Zubova, N.A. Onset and Nonlinear Regimes of Convection of Ternary Mixture in a Rectangular Porous Cavity Taking into Account the Soret Effect. J. Appl. Math. Tech. Phys. 2020, 61, 1160–1173. [Google Scholar] [CrossRef]
- Soboleva, E. Numerical Simulation of Haline Convection in Geothermal Reservoirs. J. Phys. Conf. Ser. 2017, 891, 012105. [Google Scholar] [CrossRef]
- Papaspyros, J.N.E.; Moutsopoulos, K.N.; Tzavellas, E. Solutions of the Elder problem for a wide range of the Rayleigh number. Eur. Water 2016, 55, 31–40. [Google Scholar]
- Soboleva, E.B. Onset of Rayleigh-Taylor convection in a porous medium. Fluid Dyn. 2021, 56, 200–210. [Google Scholar] [CrossRef]
- Il’ichev, A.T.; Tsypkin, G.G.; Pritchard, D.; Richardson, C.N. Instability of the Salinity Profile during the Evaporation of Saline Groundwater. J. Fluid Mech. 2008, 614, 87–104. [Google Scholar] [CrossRef]
- Soboleva, E.B.; Tsypkin, G.G. Numerical simulation of convective flows in a soil during evaporation of water containing a dissolved admixture. Fluid Dyn. 2014, 49, 634–644. [Google Scholar] [CrossRef]
- Soboleva, E.B.; Tsypkin, G.G. Regimes of Haline Convection during the Evaporation of Groundwater Containing a Dissolved Admixture. Fluid Dyn. 2016, 51, 364–371. [Google Scholar] [CrossRef]
- Soboleva, E.B. Influence of finite-density fluctuations on the development of the Rayleigh-Taylor instability in a porous medium. Theor. Math. Phys. 2022, 211, 724–734. [Google Scholar] [CrossRef]
- Soboleva, E.B. Density-driven convection in an inhomogeneous geothermal reservoir. Int. J. Heat Mass Transf. 2018, 127, 784–798. [Google Scholar] [CrossRef]
- Nick, H.M.; Schotting, R.; Gutierrez-Neri, M.; Johannsen, K. Modeling Transverse Dispersion and Variable Density Flow in Porous Media. Transp. Porous Media 2009, 78, 11–35. [Google Scholar] [CrossRef]
- Danie, D.; Riaz, A. Effect of viscosity contrast on gravitationally unstable diffusive layers in porous media. Phys. Fluids 2014, 26, 116601. [Google Scholar] [CrossRef]
- Raad, S.M.; Hassanzadeh, H. Onset of dissolution-driven instabilities in fluids with nonmonotonic density profile. Phys. Rev. E 2015, 92, 053023. [Google Scholar] [CrossRef]
- Scheidegger, A.E. General theory of dispersion in porous media. J. Geophys. Res. 1961, 66, 3273–3278. [Google Scholar] [CrossRef]
- Matyka, M.; Khalili, A.; Koza, Z. Tortuosity-porosity relation in porous media flow. Phys. Rev. E 2008, 78, 026306. [Google Scholar] [CrossRef]
- Guo, P. Dependency of tortuosity and permeability of porous media on directional distribution of pore void. Transp. Porous Media 2012, 95, 285–303. [Google Scholar] [CrossRef]
- Chou, H.; Wu, L.; Zeng, L.; Chang, A. Evaluation of solute diffusion tortuosity factor models for variously saturated soils. Water Resour. Res. 2012, 48, 10539. [Google Scholar] [CrossRef]
- Porter, M.L.; Valdés-Parada, F.J.; Wood, B.D. Comparison of theory and experiments for dispersion in homogeneous porous media. Adv. Water Resour. 2010, 33, 1043–1052. [Google Scholar] [CrossRef]
- Hunt, A.G.; Skinner, T.E. Predicting Dispersion in Porous Media. Complexity 2010, 16, 43–55. [Google Scholar] [CrossRef]
- Bruining, H.; Darwish, M.; Rijnks, A. Computation of the Longitudinal and Transverse Dispersion Coefficient in an Adsorbing Porous Medium Using Homogenization. Transp. Porous Media 2012, 91, 833–859. [Google Scholar]
- Nguyen, V.; Papavassiliou, D. Hydrodynamic Dispersion in Porous Media and the Significance of Lagrangian Time and Space Scales. Fluids 2020, 5, 79. [Google Scholar] [CrossRef]
- Delgado, J.M.P.Q. A critical review of dispersion in packed beds. Heat Mass Transf. 2006, 42, 279–310. [Google Scholar] [CrossRef]
- Polubarinova-Kochina, P.Y.; Falkovich, S.B. Theory of Filtration of Liquids in Porous Media. Adv. Appl. Mech. 1951, 2, 153–225. [Google Scholar]
- Xu, P.; Yu, B. Developing a new form of permeability and Kozeny-Carman constant for homogeneous porous media by means of fractal geometry. Adv. Water Resour. 2008, 31, 74–81. [Google Scholar] [CrossRef]
- Tang, T.; McDonough, J.M. A theoretical model for the porosity–permeability relationship. Int. J. Heat Mass Transf. 2016, 103, 984–996. [Google Scholar] [CrossRef]
- Vianna, R.S.; Cunha, A.M.; Azeredo, R.B.V.; Leiderman, R.; Pereira, A. Computing Effective Permeability of Porous Media with FEM and Micro-CT: An Educational Approach. Fluids 2020, 5, 16. [Google Scholar] [CrossRef]
- Durlofsky, L.; Brady, J.F. Analysis of the Brinkman Equation as a Model for Flow in Porous Media. Phys. Fluids 1987, 30, 3329–3341. [Google Scholar] [CrossRef]
- Tsypkin, G.G.; Shargatov, V.A. Linear stability of a filtration flow with gas-oil interface within the Brinkman approach. Fluid Dyn. 2022, 57, 273–280. [Google Scholar] [CrossRef]
- Elenius, M.T.; Johannsen, K. On the time scales of nonlinear instability in miscible displacement porous media flow. Comput. Geosci. 2012, 16, 901–911. [Google Scholar] [CrossRef]
- Emami-Meybodi, H.; Hassanzadeh, H. Two-phase convective mixing under a buoyant plume of CO2 in deep saline aquifers. Adv. Water Resour. 2015, 76, 55–71. [Google Scholar] [CrossRef]
- Riaz, A.; Hesse, M.; Tchelepi, H.A.; Orr, F.M. Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 2006, 548, 87–111. [Google Scholar] [CrossRef]
- Rapaka, S.; Chen, S.; Pawar, R.; Stauffer, P.; Zhang, D. Non-modal growth of perturbations in density-driven convection in porous media. J. Fluid Mech. 2008, 609, 285–303. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S.; Zhang, D. Convective stability analysis of the long-term storage of carbon dioxide in deep saline aquifers. Adv. Water Resour. 2006, 29, 397–407. [Google Scholar] [CrossRef]
- Rapaka, S.; Rawar, R.J.; Stauffer, P.H.; Zhang, D.; Chen, S. Onset of convection over a transient base-state in anisotropic and layered porous media. J. Fluid Mech. 2009, 641, 227–244. [Google Scholar] [CrossRef]
- Daniel, D.; Riaz, A.; Tchelepi, H.A. Onset of natural convection in layered aquifer. J. Fluid Mech. 2015, 767, 763–781. [Google Scholar] [CrossRef]
- Rossa, G.B.; Cliffe, K.A.; Power, H. Effects of hydrodynamic dispersion on the stability of buoyancy-driven porous media convection in the presence of first order chemical reaction. J. Eng. Math. 2017, 103, 55–76. [Google Scholar] [CrossRef]
- Kim, M.C.K. Onset of buoyancy-driven convection in a variable viscosity liquid saturated in a porous medium. Chem. Eng. Sci. 2014, 113, 77–87. [Google Scholar] [CrossRef]
- Sabet, N.; Hassanzadeh, H.; Abedi, J. A New Insight into the Stability of Variable Viscosity Diffusive Boundary Layers in Porous Media Under Gravity Field. AIChE J. 2018, 64, 1083–1094. [Google Scholar] [CrossRef]
- Meulenbroek, B.; Farajzadeh, R.; Bruining, H. The effect of interface movement and viscosity variation on the stability of a diffusive interface between aqueous and gaseous CO2. Phys. Fluids 2013, 25, 074103. [Google Scholar] [CrossRef]
- Mahmoodpour, S.; Rostami, B.; Soltanian, M.R.; Amooie, M.A. Effect of brine composition on the onset of convection during CO2 dissolution in brine. Comput. Geosci. 2019, 124, 1–13. [Google Scholar] [CrossRef]
- Bestehorn, M.; Firoozabadi, A. Effect of fluctuations on the onset of density-driven convection in porous media. Phys. Fluids 2012, 24, 114102. [Google Scholar] [CrossRef]
- Farajzadeh, R.; Samili, H.; Zitha, P.L.J.; Bruining, H. Numerical simulation of density-driven natural convection in porous media with application for CO2 injection projects. Int. J. Heat Mass Transf. 2007, 50, 5054–5064. [Google Scholar] [CrossRef]
- Kneafsey, T.J.; Pruess, K. Laboratory Experiments and Numerical Simulation Studies of Convectively Enhanced Carbon Dioxide Dissolution. Energy Proc. 2011, 4, 5114–5121. [Google Scholar] [CrossRef]
- Backhaus, S.; Turitsyn, K.; Ecke, R.E. Convective Instability and Mass Transport of Diffusion Layers in a Hele-Shaw Geometry. Phys. Rev. Lett. 2011, 106, 104501. [Google Scholar] [CrossRef]
- Faisal, T.F.; Chevalier, S.; Bernabe, Y.; Juanes, R.; Sassi, M. Quantitative and qualitative study of density driven CO2 mass transfer in a vertical Hele-Shaw cell. Int. J. Heat Mass Transf. 2015, 81, 901–914. [Google Scholar] [CrossRef]
- Chevalier, S.; Faisal, T.F.; Bernabe, Y.; Juanes, R.; Sassi, M. Numerical sensitivity analysis of density driven CO2 convection with respect to different modeling and boundary conditions. Heat Mass Transf. 2015, 51, 941–952. [Google Scholar] [CrossRef]
- Alipour, M.; De Paoli, M.; Soldati, A. Concentration-based velocity reconstruction in convective Hele–Shaw flows. Exper. Fluids 2020, 61, 195. [Google Scholar] [CrossRef]
- Michel-Meyer, I.; Shavit, U.; Rosenzweig, R. The role of water flow and dispersion in the dissolution of CO2 in deep saline aquifers. Energy Proc. 2017, 114, 4994–5006. [Google Scholar] [CrossRef]
- Wang, L.; Nakanishi, Y.; Hyodo, A.; Suekane, T. Three-dimensional structure of natural convection in a porous medium: Effect of dispersion on finger structure. Int. J. Greenh. Gas Control 2016, 53, 274–283. [Google Scholar] [CrossRef]
- Taheri, A.; Torsæter, O.; Lindeberg, E.; Hadia, N.J.; Wessel-Berg, D. Qualitative and quantitative experimental study of convective mixing process during storage of CO2 in heterogeneous saline aquifers. Int. J. Greenh. Gas Control 2018, 71, 212–226. [Google Scholar] [CrossRef]
- Thomas, C.; Dehaeck, S.; De Wit, A. Convective dissolution of CO2 in water and salt solutions. Int. J. Greenh. Gas Control 2018, 72, 105–116. [Google Scholar] [CrossRef]
- Mojtaba, S.; Behzad, R.; Rasoul, N.M.; Mohammad, R. Experimental study of density-driven convection effects on CO2 dissolution rate in formation water for geological storage. J. Nat. Gas Sci. Eng. 2014, 21, 600–607. [Google Scholar] [CrossRef]
- Ecke, R.E.; Backhaus, S. Plume dynamics in Hele-Shaw porous media convection. Phil. Trans. R. Soc. A 2016, 374, 20150420. [Google Scholar] [CrossRef]
- Slim, A.C.; Bandi, M.M.; Miller, J.C.; Mahadevan, L. Dissolution-driven convection in a Hele-Shaw cell. Phys. Fluids 2013, 25, 024101. [Google Scholar] [CrossRef]
- De Paoli, M.; Zonta, F.; Soldati, A. Dissolution in anisotropic porous media: Modeling convection regimes from onset to shutdown. Phys. Fluids 2017, 29, 026601. [Google Scholar] [CrossRef]
- De Paoli, M.; Zonta, F.; Soldati, A. Influence of anisotropic permeability on convection in porous media: Implications for geological CO2 sequestration. Phys. Fluids 2016, 28, 056601. [Google Scholar] [CrossRef]
- Soltanian, M.R.; Amooie, M.A.; Dai, Z.; Cole, D.; Moortgat, J. Critical Dynamics of Gravito-Convective Mixing in Geological Carbon Sequestration. Sci. Rep. 2016, 6, 35921. [Google Scholar] [CrossRef]
- Scovazzi, G.; Gerstenberger, A.; Collis, S.S. A discontinuous Galerkin method for gravity-driven viscous fingering instabilities in porous media. J. Comput. Phys. 2013, 233, 373–399. [Google Scholar] [CrossRef]
- Doranehgard, M.H.; Dehghanpour, H. Quantification of convective and diffusive transport during CO2 dissolution in oil: A numerical and analytical study. Phys. Fluids 2020, 32, 085110. [Google Scholar] [CrossRef]
- Ju, L.; Shan, B.; Guo, Z. Pore-scale study of convective mixing process in brine sequestration of impure CO2. Phys. Rev. Fluids 2022, 7, 114501. [Google Scholar] [CrossRef]
- Green, C.P.; Ennis-King, J. Steady Flux Regime During Convective Mixing in Three-Dimensional Heterogeneous Porous Media. Fluids 2018, 3, 58. [Google Scholar] [CrossRef]
- Islam, A.; Korrani, A.K.N.; Sepehrnoori, K.; Patzek, T. Effects of geochemical reaction on double diffusive natural convection of CO2 in brine saturated geothermal reservoir. Int. J. Heat Mass Transf. 2014, 77, 519–528. [Google Scholar] [CrossRef]
- Islam, A.; Sun, A.Y.; Yang, C. Reactive Transport Modeling of the Enhancement of Density-Driven CO2 Convective Mixing in Carbonate Aquifers and its Potential Implication on Geological Carbon Sequestration. Sci. Rep. 2016, 6, 24768. [Google Scholar] [CrossRef]
- Soboleva, E.B. Numerical Study of Haline Convection in a Porous Domain with Application for Geothermal Systems. In Physical and Mathematical Modeling of Earth and Environment Processes. SPEES; Karev, V., Klimov, D., Pokazeev, K., Eds.; Springer International Publishing AG: Cham, Switzerland, 2019; pp. 63–74. [Google Scholar]
- Soboleva, E.B. A method for Numerical Simulation of Haline Convective Flows in Porous Media Applied to Geology. Comput. Math. Math. Phys. 2019, 59, 1893–1903. [Google Scholar] [CrossRef]
- Cheng, A.H.-D. Multilayered Aquifer Systems: Fundamentals and Applications; Marcel Dekker: New York, NY, USA, 2000. [Google Scholar]
- Hewitt, D.R.; Neufeld, J.A.; Lister, J.R. High Rayleigh number convection in a porous medium containing a thin low-permeability layer. J. Fluid Mech. 2014, 756, 844–869. [Google Scholar] [CrossRef]
- Drazin, P.G.; Reid, W.H. Hydrodynamic Stability; Cambridge University Press: Cambridge, UK, 1981. [Google Scholar]
- Tsypkin, G.G.; Il’ichev, A.T. Gravitational Stability of the Interface in Water Over Steam Geothermal Reservoirs. Transp. Porous Media 2004, 55, 183–199. [Google Scholar] [CrossRef]
- Il’ichev, A.T.; Tsypkin, G.G. Rayleigh-Taylor Instability of an Interface in a Nonwettable Porous Medium. Fluid Dyn. 2007, 42, 83–90. [Google Scholar] [CrossRef]
- Shargatov, V.A.; Il’ichev, A.T.; Tsypkin, G.G. Dynamics and stability of moving fronts of water evaporation in a porous medium. Int. J. Heat Mass Transf. 2015, 83, 552–561. [Google Scholar] [CrossRef]
- Martin, J.; Rakotomalala, N.; Salin, D. Gravitational instability of miscible fluids in a Hele-Shaw cell. Phys. Fluids 2002, 14, 902–905. [Google Scholar] [CrossRef]
- Elgahawy, Y.; Azaiez, J. Rayleigh–Taylor instability in porous media under sinusoidal time-dependent flow displacements. AIP Adv. 2020, 10, 075308. [Google Scholar] [CrossRef]
- Glimm, J.; Grove, J.W.; Li, X.L.; Oh, W.; Sharp, D.H. A Critical Analysis of Rayleigh–Taylor Growth Rates. J. Comput. Phys. 2001, 169, 652–677. [Google Scholar] [CrossRef]
- De Paoli, M.; Giurgiu, V.; Zonta, F.; Soldati, A. Universal behavior of scalar dissipation rate in confined porous media. Phys. Rev. Fluids 2019, 4, 101501(R). [Google Scholar] [CrossRef]
- De Paoli, M.; Perissutti, D.; Marchioli, C.; Soldati, A. Experimental assessment of mixing layer scaling laws in Rayleigh-Taylor instability. Phys. Rev. Fluids 2022, 7, 093503. [Google Scholar] [CrossRef]
- De Paoli, M.; Zonta, F.; Soldati, A. Rayleigh-Taylor convective dissolution in confined porous media. Phys. Rev. Fluids 2019, 4, 023502. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.S.; Carballido-Landeira, J.; De Wit, A.; Knaepen, B. Relative role of convective and diffusive mixing in the miscible Rayleigh-Taylor instability in porous media. Phys. Rev. Fluids 2017, 2, 012501(R). [Google Scholar] [CrossRef]
- Boffetta, G.; Musacchio, S. Dimensional effects in Rayleigh–Taylor mixing. Phil. Trans. R. Soc. A 2022, 380, 20210084. [Google Scholar] [CrossRef]
- Boffetta, G.; Borgnino, M.; Musacchio, S. Scaling of Rayleigh-Taylor mixing in porous media. Phys. Rev. Fluids 2020, 5, 062501(R). [Google Scholar] [CrossRef]
- Teng, Y.; Jiang, L.; Fan, Y.; Liu, Y.; Wang, D.; Abudula, A.; Song, Y. Quantifying the dynamic density driven convection in high permeability packed beds. Magn. Reson. Imaging 2017, 39, 168–174. [Google Scholar] [CrossRef]
- Wang, L.; Nakanishi, Y.; Teston, A.D.; Suekane, T. Effect of diffusing layer thickness on the density-driven natural convection of miscible fluids in porous media: Modeling of mass transport. J. Fluid Sci. Technol. 2018, 13, 17-00517. [Google Scholar] [CrossRef]
- Suekane, T.; Koe, T.; Barbancho, P.M. Three-Dimensional Interaction of Viscous Fingering and Gravitational Segregation in Porous Media. Fluids 2019, 4, 130. [Google Scholar] [CrossRef]
- Mahardika, M.A.; She, Y.; Koe, T.; Patmonoaji, A.; Nasir, M.; Matsushita, S.; Suekane, T. Competition of gravity and viscous forces in miscible vertical displacement in a three-dimensional porous medium. Phys. Fluids 2022, 34, 073102. [Google Scholar] [CrossRef]
- Moortgat, J. Viscous and gravitational fingering in multiphase compositional and compressible flow. Adv. Water Resour. 2016, 89, 53–66. [Google Scholar] [CrossRef]
- Teng, Y.; Wang, P.; Jiang, L.; Liu, Y.; Song, Y.; Wei, Y. An experimental study of density-driven convection of fluid pairs with viscosity contrast in porous media. Int. J. Heat Mass Transf. 2020, 152, 119514. [Google Scholar] [CrossRef]
- Sabet, N.; Hassanzadeh, H.; De Wit, A.; Abedi, J. Scalings of Rayleigh-Taylor Instability at Large Viscosity Contrasts in Porous Media. Phys. Rev. Lett. 2021, 126, 094501. [Google Scholar] [CrossRef]
- Soboleva, E.B. Comment on “Scalings of Rayleigh-Taylor Instability at Large Viscosity Contrasts in Porous Media”. arXiv 2022, arXiv:2203.16249. [Google Scholar]
- Soboleva, E.B. Numerical Simulation of Haline–Convective Flows with Viscosity Contrast in a Porous Medium. Comput. Math. Math. Phys. 2022, 62, 1942–1954. [Google Scholar] [CrossRef]
- Shokri, N.; Lehmann, P.; Or, D. Liquid-phase continuity and solute concentration dynamics during evaporation from porous media: Pore-scale processes near vaporization surface. Phys. Rev. E 2010, 81, 046308. [Google Scholar] [CrossRef]
- Mejri, E.; Helmig, R.; Bouhlila, R. Modeling of Evaporation-Driven Multiple Salt Precipitation in Porous Media with a Real Field Application. Geosciences 2020, 10, 395. [Google Scholar] [CrossRef]
- Roy, R.; Weibel, J.A.; Garimella, S.V. Modeling the formation of efflorescence and subflorescence caused by salt solution evaporation from porous media. Int. J. Heat Mass Transf. 2022, 189, 122645. [Google Scholar] [CrossRef]
- Wooding, R.A.; Tyler, S.W.; White, I. Convection in groundwater below an evaporating salt lake: 1. Onset of instability. Water Resour. Res. 1997, 33, 1199–1217. [Google Scholar] [CrossRef]
- Wooding, R.A.; Tyler, S.W.; White, I.; Anderson, P.A. Convection in groundwater below an evaporating salt lake: 2. Evolution of fingers or plumes. Water Resour. Res. 1997, 33, 1219–1228. [Google Scholar] [CrossRef]
- Van Duijn, C.J.; Pieters, G.J.M.; Wooding, R.A.; van der Ploeg, A. Stability Criteria for the Vertical Boundary Layer Formed by Throughflow Near the Surface of a Porous Medium. In Environmental Mechanics: Water, Mass and Energy Transfer in the Biosphere. Vol. 129; Raats, P.A.C., Smiles, D., Warrick, A.W., Eds.; AGU: Washington, DC, USA, 2002; pp. 155–169. [Google Scholar]
- Pieters, G.J.M.; van Duijn, C.J. Transient growth in linearly stable gravity-driven flow in porous media. Eur. J. Mech. B/Fluids 2006, 25, 83–94. [Google Scholar] [CrossRef]
- Bringedal, C.; Helmig, R.; Schollenberger, T.; Pieters, G.J.M.; van Duijn, C.J. Evaporation-Driven Density Instabilities in Saturated Porous Media. Transp. Porous Media 2022, 143, 297–341. [Google Scholar] [CrossRef]
- Jones, M.C.; Persichetti, J.M. Convective Instability in Packed Beds with Throughflow. AIChE J. 1986, 32, 1555–1557. [Google Scholar] [CrossRef]
- Nield, D.A. Convective Instability in Porous Media with Throughflow. AIChE J. 1987, 33, 1222–1224. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The Onset of Convection in a Heterogeneous Porous Medium with Vertical Throughflow. Transp. Porous Media 2011, 88, 347–355. [Google Scholar] [CrossRef]
- Nield, D.A.; Kuznetsov, A.V. The Onset of Convection in a Layered Porous Medium with Vertical Throughflow. Transp. Porous Media 2013, 98, 363–376. [Google Scholar] [CrossRef]
- Patil, P.M.; Rees, D.A.S. Linear Instability of a Horizontal Thermal Boundary Layer Formed by Vertical Throughflow in a Porous Medium: The Effect of Local Thermal Nonequilibrium. Transp. Porous Media 2013, 99, 207–227. [Google Scholar] [CrossRef]
- Capone, F.; Gianfrani, J.A.; Massa, G.; Rees, D.A.S. A weakly nonlinear analysis of the effect of vertical throughflow on Darcy-Bénard convection. Phys. Fluids 2022, in press. [CrossRef]
- Geng, X.; Boufadel, M.C. Numerical modeling of water flow and salt transport in bare saline soil subjected to evaporation. J. Hydrol. 2015, 524, 427–438. [Google Scholar] [CrossRef]
- Soboleva, E. Numerical Investigations of Haline-Convective Flows of Saline Groundwater. J. Phys. Conf. Ser. 2017, 891, 012104. [Google Scholar] [CrossRef]
- Soboleva, E.B. Underground Haline Convection Caused by Water Evaporation from the Surface of the Earth. In Processes in GeoMedia. Vol. IV. Springer Geology; Chaplina, T., Ed.; Springer International Publishing AG: Cham, Switzerland, 2022; pp. 109–117. [Google Scholar]
- Homsy, G.M.; Sherwood, A.E. Convective instabilities in porous media with throughflow. AIChE J. 1976, 22, 168–174. [Google Scholar] [CrossRef]
- Moureau, V.; Domingo, P.; Vervisch, L. Design of a massively parallel CFD code for complex geometries. C. R. Mécanique 2011, 339, 141–148. [Google Scholar] [CrossRef]
- Afanasyev, A.; Vedeneeva, E. Compositional modeling of multicomponent gas injection into saline aquifers with the MUFITS simulator. J. Natur. Gas Sci. Eng. 2021, 94, 103988. [Google Scholar] [CrossRef]


| Parameters | Values | Conditions |
|---|---|---|
| Density of water , kg/m | 996.56 [27] | K, bar |
| 1001.0 [27] | K, bar | |
| 958.63 [27] | K, bar | |
| 761.82 [27] | K, bar | |
| Viscosity of water , Pa s | [28] | K, bar |
| [28] | K, bar | |
| Saturation concentration of c, - | [27] | K, bar |
| [27] | K, bar | |
| Saturation density of dis- solved , kg/m | 330.2 1 | K, bar |
| Diffusion coefficient of D, m/s | [29] | K, bar, |
| Haline contraction coefficient , - | 0.753 2 | K, bar |
| Porosity of soils and rocks , - | [1] | |
| Permeability of pervious and semipervious soils and rocks k, m | [1] | |
| Geometric scale H, m | ||
| Rayleigh-Darcy number , - |
| Analytical Methods | Numerical Methods | Experimental Techniques |
|---|---|---|
| Linear stability analysis: [41,47,66,68,70,71,72,73,74,75,76,107,108,130,132,133,134,135,136,137] | Finite-difference and finite-volume methods: [36,40,42,43,45,71,73,77,80,81,100,102,113,124,128,129,144] | Hele-Shaw cell: [75,78,79,80,82,83,85,86,87,88,89,111,113,128,129] |
| Other methods: [67,68,69,130,131,138] | Finite element method: [64,75,92,93,96,120,139] | X-ray computed tomography: [84,117,118,119] |
| Spectral method: [67,90,91,108,110,111,112,114,115] | Magnetic resonance image technique: [116,121] | |
| Hybrid method: [76,122] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soboleva, E. Instability Problems and Density-Driven Convection in Saturated Porous Media Linking to Hydrogeology: A Review. Fluids 2023, 8, 36. https://doi.org/10.3390/fluids8020036
Soboleva E. Instability Problems and Density-Driven Convection in Saturated Porous Media Linking to Hydrogeology: A Review. Fluids. 2023; 8(2):36. https://doi.org/10.3390/fluids8020036
Chicago/Turabian StyleSoboleva, Elena. 2023. "Instability Problems and Density-Driven Convection in Saturated Porous Media Linking to Hydrogeology: A Review" Fluids 8, no. 2: 36. https://doi.org/10.3390/fluids8020036
APA StyleSoboleva, E. (2023). Instability Problems and Density-Driven Convection in Saturated Porous Media Linking to Hydrogeology: A Review. Fluids, 8(2), 36. https://doi.org/10.3390/fluids8020036







