Abstract
Theoretical and experimental aspects of the project were conducted to investigate the effect of the mixing of a swirling steam jet into cross-flowing water. It was observed that based on the theoretical adiabatic estimations for the equilibrium temperature of steam–water mixing and by varying Psteam = 1–3 bar, Pwater = 1 bar and RPM = 60–300 around 97% (experimentally compared to the area it has at initial condition) and 85% (CFD study compared to the area it has at initial condition), an increase in the area under the influence of perfect adiabatic mixing was found. A virtual cover over the steam duct was seen. The area of this virtual cover based on the void fraction of swirling steam had a weak relationship with the total area of the region, inhibiting the perfect mixing for which an analytical relationship had been developed. The effect of mixing on the stability of swirling steam–water cross-flows was overall more than twice that of the effect on the area under the influence of the stability profile protrusions. Thus, an overall rise in inlet pressure contributed to improper mixing, whereas a rise in the RPM contributed to proper mixing inside a fixed window of observations. The effect of spatial scaling of a swirling steam trajectory on mixing in cross-flowing water was also investigated across the vertical plane. Also, the scaling of the vertical trajectories of the swirling steam jets under all operating conditions resulted in merging the regions of perfect mixing to some extent. Thus, the area under the influence of perfect mixing was reduced to around 3–4.7% under all operating conditions with scaling. This type of scaling has enormous potential for the characterization of larger fluid domains in environmental and process engineering studies.
1. Introduction
Mixing two fluids via injection of one fluid into a flowing stream of another fluid in a cross-flow configuration has immense importance in engineering applications. Based on the differences between their inlet pressures, velocities and mass flow rates, myriad such scenarios are encountered in daily life, ranging from the ejection of exhaust gases from chimneys of processing plants into the atmosphere and turbo machinery (film cooling of turbine blades) to jets injected into combustors, waste discharges into flowing streams of water, and many more. The mixing via subsonic cross-flow in a confined environment is another facet of this problem, which includes examples such as premixing of fuel and air, injection of sorbents, and combustion with emission control—a few of the more prominent among countless issues. A huge number of studies have been conducted on the topic of cross-flow characterization [1], with few discussing some specialized aspects of this topic experimentally, like the scaling of the local velocities, temperature, and concentration maxima [2,3]. They have derived relations to infer collapse of the various profiles [4,5] for scaling and effective penetration depths, as well as effects of the boundary layer thickness on the initial profile of the jet [6]. In another category of these types of studies, the profiles of the cross-flow jet after the onset of its interaction with the flowing stream have been discussed [7,8,9,10]. The turbulent flows may also be generated when the jets have been exposed to the cross-flowing fluids. It has been found that these flows contain four basic structures that include the vortices produced by the jet shear layers [7], which create an interface between the jet and the cross-flowing fluid, the horseshoe vortices produced above the jet in upstream surfaces [7,9], whereas the counter-rotating vortices are generated following the tilting of the jet’s progression by the cross-flowing fluid [10], and the wake vortices [4] that are produced on the leeside of the jet situated in the far downstream fluid mixture. Among earlier studies that have been performed regarding the jet characteristics in the cross-flow field, most have focused on the identification of the scaling laws for the jet’s trajectory. In this regard, earlier reviewers [11] provided much insight into a gas jet’s flow characteristics in the cross-flow. In these works, an important parameter like jet penetration was also characterized. In addition, other parameters like the length scale, which provides information on the collapse of the center-line trajectory of the circular jets, were also investigated [2,3,5]. The behavior of the initial jet profiles and the boundary layers in the case of jets in cross-flowing fluids was also investigated in much detail. Both theoretical and experimental aspects of the project has been investigated to highlight the influence of mixing of the subsonic swirling steam jet with cross-flowing water. Possible further outcomes from this study should determine the influence of mixing phenomena on the interactive stability between the swirling subsonic steam and cross-flowing water. Also, it will attempt to find the trajectory associated with the spatial scaling of swirling steam, affecting the flow of cross-water stream. Despite the huge volume of research conducted on the topic of cross-flows, to our knowledge, no studies that inter-relate the extent of mixing of swirling steam with water in a subsonic confined configuration with cross-flow orientation have been performed or cited elsewhere.
We anticipate very complex flow dynamics in the region of interest (ROI—where the subsonic swirling steam jet interacts with the cross-flowing water). Here, in the present experimental setup, ROI refers to two orthogonal planes, with one along the plane sheet on which LM35 sensor arrays were mounted (termed the plane of symmetry), and the other a vertical plane across which LM35 temperature sensors [12] and HFA sensors [13] traversed. The domain thus characterized is under the influence of varying hydrodynamic operating conditions, and hence, with turbulence being involved, inhibits complex flow phenomena. Without a complete understanding of these conditions, a clear and realistic picture of the phenomena taking place across these planes, where subsonic steam in a swirling configuration interacts with cross-flowing water, cannot be approximated. Thus, our knowledge will remain hampered considerably without a detailed study on this topic. The present manuscript is an effort in this regard. The details of the experimental setup, and the results thus drawn, are discussed in the following sections.
2. Experimental Setup
The experimental setup comprised a cylindrical vessel, as shown in Figure 1a, with a length of 3 m and diameter ~0.4572 m (45.72 cm). The length of the experimental setup was around 3 m. The flow rig was manufactured with this dimension because it was intended to ensure a smooth flow of the cross-flowing water, without any disturbance that might occur due to sudden ejection from the inlet orifices. Secondly, better mixing was achieved owing to the water and steam jet interaction at these length scales, which provided promising results. The cylindrical vessel was manufactured from grade 316 (13-gauge) stainless steel and had two sections. The first section was a horizontal section with a length of 3 m, and the second section was an inclined, vertically downward diverted (45° to the horizontal axial axis) section, as shown in Figure 1b. Water was injected from the left-hand side of the vessel and collected at the end of the downward diverted section. Steam was injected into the flow vessel by using a vertical pipe (diameter = 3.5 cm, length = 7.62 cm, from the base of the rig, oriented along the radial direction of the flow vessel) that had a propeller fixed at its exit. The water, being warmed by mixing with the steam, was run through the titled pipe into the water reservoir, and the hot water was pumped into the cold reservoir before being sent into the horizontal pipe. The propeller was rotated by using a motor that had a fine adjustment for controlled propeller RPM. The propeller was attached with a shaft that extended on the backend to a bevel gear that was rotated using an external motor. The objectives served by the propeller were not only to inject the steam into a swirling configuration, but also to help recover the pressure loss incurred inside the nozzle and propeller assembly. Steam was injected into the nozzle at a pressure of 1–3 bars, whereas the propeller was rotated at a speed varying from 60 to 300 RPM. The operating conditions are given in Table 1. The whole setup was closed and wrapped heavily from the outside using Teflon and sponge layers so that the temperature of the water inside the rig would not be affected by the external environment temperature. To safeguard against any accidental pressure buildup, the whole setup was kept at a pressure of “0 bar of gauge pressure” using a pressure sensor and pressure safety valves (Figure 1b). The measurements for the velocity profiles were acquired using a total of 20 Hot Film Anemometers (Dantec HFA-D55R11 series [13]), as shown in Figure 2. These sensors have up to three components of velocity measurement, a small probe size, the ability to measure in increments of 1 mm for fast frequency response, a sampling frequency of up to 400 kHz, and flow rates of around 2–10 m/sec.
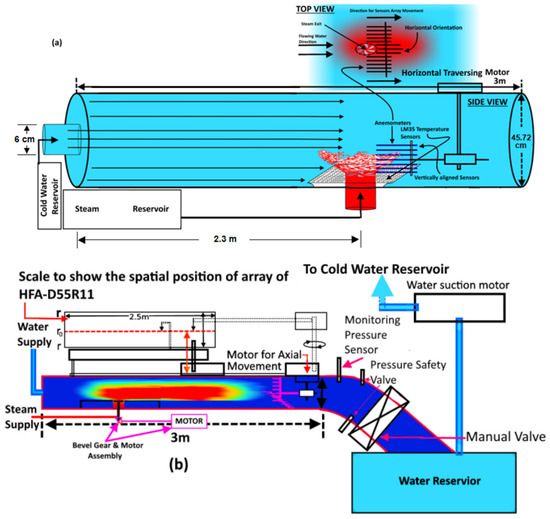
Figure 1.
A schematic of (a) the flow rig and (b) complete experimental rig.

Table 1.
Operating conditions.
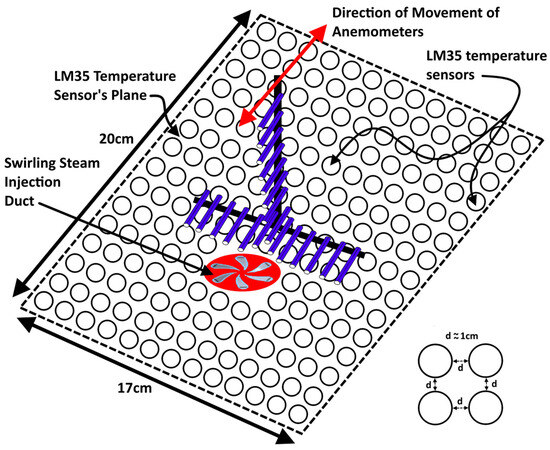
Figure 2.
Plane sheet for temperature sensors.
The measurements for recording the extent of mixing were performed using a total of 217 LM35 temperature sensors [12]. The LM35 device draws only 60 µA from the power supply and has very low self-heating of less than 0.1 °C in still air. The LM35 device is rated to operate over a −55 °C to 150 °C temperature range, while the LM35C device is rated for a −40 °C to 110 °C range (−10° with improved accuracy). Out of the 217 LM35 temperature sensors, 189 were used at a sampling speed of 5 kHz for 5 min and were mounted on the plane sheet to acquire the time-averaged temperature data from the fluid flowing over the plane sheet. The 28 remaining LM35 temperature sensors were used at the same sampling rate and duration (with a total sampling time at each respective position of 0.1 cm each step) and mounted with a vertical rod to acquire the time-averaged temperature data along the vertical plane. While the velocity measurements were being conducted, 20 LM35 sensors were mounted with HFA sensors, and of those, 13 were mounted along the horizontal direction and 7 were mounted along the vertically mounted HFA sensors. These 20 LM35 temperature sensors provided measurements of the temperature of the fluid present within the vicinity of the sensor at the time of velocity measurements. These measurements were used afterwards to obtain an estimate of the value of the density of the fluid as well. Thus, these 20 LM35 temperature sensors were also used to calibrate the HFA sensors as well. All LM35 temperature sensors mounted on the plane sheet had their sensing sides in an upright direction, whereas those mounted with a vertical rod had their faces oriented in the direction opposite to that of the flowing water and steam mixture. All HFA sensors were mounted on a straight perforated rod, as shown in Figure 2. Using an external electronically controlled switching setup, both the temperature and HFA sensors were placed in operating mode at the same time and had the same operating times.
The rod had a perforated structure to minimize disturbances in the measurements due to the flow-induced disturbances among the neighboring HFA sensors. The disturbances were further minimized by mounting the velocity-measuring sensors at a reasonable height from the body of the rod (i.e., 4 cm). The sampling rate for the HFA sensors was 5 kHz, and the total sampling time at each respective position (0.1 cm each step) was 5 min. The movement of the vertical rod inside the rig was controlled by the motor, which had a movement arm traversing through the body of the rig, across a lip seal to avoid possible leakage. The rotation of the rod inside the rig contributed to traversing the vertical rod along the axial direction of the rig through a shaft with a fine pitch of 0.1 cm. The motor, regulated by a regulator and transformer and used for the rotation of the propeller, was calibrated for the frictional and inertial losses using a tachometer [14]. It was observed that in the water at 15 °C, the error in the RPM measured by the tachometer ranged from 0.05 to 0.06% (3–18 rpm) at varying rotational speeds of 60–300 RPM, which was corrected by increasing the RPM of the motor in corresponding experimental phases to rotate the mixture of steam and water at the given RPM (Table 1).
As the experimental setup was closed to record the spatial position of each of the sensors along with the axial and radial directions, a parallel graduated scale was provided, as shown in Figure 1b. The vessel was filled with cold water at 15 °C, and during all experimental phases, the vessel was kept filled with the water at the same temperature. The mass fraction added by the injection of steam and water was drained using a manual valve at the right-hand side of the vessel, as shown in Figure 1b. Due to possible ambiguity in the measurements by the HFA probes due to the flow of water, the measurements were undertaken with flowing water only. It was observed that the maximum amplitude of the fluctuations as measured by the HFA sensors was 0.5 cm; thus, this value of the amplitude was subtracted from the measurements by the HFA probes, which were recorded after the onset of the swirling steam injection. This was performed to show a clear picture of the flow processes that take place due to the swirling injection of steam only. Initially, the rig was filled with the water at 15 °C, then afterward, water at the same temperature was injected into it for all phases of the experimentation. This was exercised to avoid disturbances in the measurements by the HFA sensors at their measuring faces due to the boiling of water. The hot-film anemometers use for the velocity measurements in steam–water two-phase flows had been proved in previous studies [15,16]. The HFA sensors were calibrated for the known inlet pressures of steam (i.e., 1–3 bars) and water (1 bar). The relation used for the velocity calculation using the present conditions is as follows [17]
The value of the local density was estimated based on the temperature of the fluid present at the time of measurement and the spatial location of the LM35 temperature sensor, which was attached with each HFA sensor during calibration. For comparison the value of for average velocity was estimated by the following relation [17]
using the fluctuation data from each of the HFA sensors. It was found that a relative error existed in the measurements collected by the sensors, which was below 4%, corresponding to the velocity fluctuations against the inlet pressure of steam and water (1–3 bars and 1 bar, respectively) at a 5 kHz sampling rate of the sensors; the measurements were repeated 5 times with a sampling duration of 5 min in each phase of experimentation to confirm the value of the relative error. The corresponding error values were subtracted from each measurement by each sensor before drawing the results. The magnitude and sign of the error in velocity fluctuations were determined by setting the confidence interval of the velocity fluctuation values, and any deviation from this was treated as the magnitude and sign of the error in velocity fluctuations. The LM35 sensors’ relative errors ranged from −0.75 °C to +0.75 °C, as mentioned in the manual for these sensors [12]. Values for the velocity calculations were obtained using Equations (1) and (2) [12,13,16]. It should be noted that the most confusing parameter, i.e., the density of the fluid at that time in the observed section, was measured with the help of the temperature measurement. We took the temperature measurement, then, with the help of the confidence interval, or, in case of too much fluctuation, by using averaging, we calculated the temperature of the steam–water mixture at that time point. For the density values, the STEAM DATA TABLES [18] were consulted.
Measurements based on the temperature values were adjusted based on these error ranges. The hydrodynamics of the flow and thus the selection of the given parameter provided the best possible way to determine the flow characteristics using the available equipment. All of the related equipment used in the current investigations was calibrated with the standard procedures for each instrument. All abbreviations thus used for the calculations are tabulated at the end of the manuscript in Appendix A. The results thus drawn are given in the following sections.
3. Results and Discussion
The results have been categorized into three sections The first section deals with the extent of mixing and velocity profiles in a swirling steam injection into cross-flowing water along two orthogonal planes. In the second section, the effect of mixing on the stability of the flow domain is reported and discussed. In the third section, we discuss the effect of scaling of the vertical trajectory of the swirling steam jet on the mixing under all operating conditions. It should be noted that the measured results for the temperature and velocity have been supported by the CFD outcomes wherever necessary.
3.1. The Extent of Mixing and the Velocity Profiles for Swirling Steam Injection into Cross-Flowing Water
The steam was injected into the cross-flowing water at 1 bar of gauge pressure initially, at varying rpm ranging from 60–300 rpm. The water was injected at the same 1 bar of gauge pressure; the manual valve was used to adjust the pressure inside the flow vessel. Measurements were obtained by using the LM35 temperature sensors [12] mounted on the plane sheet. It should be noted that all LM35 temperature sensors were mounted on the plane sheet in such a way that their measurement faces were flush with the surface of the plane sheet. The corresponding time-averaged temperature measurements for the time duration (i.e., 5 min) recorded by each of the LM35 temperature sensors are shown by the color contours on each sensor in Figure 3.
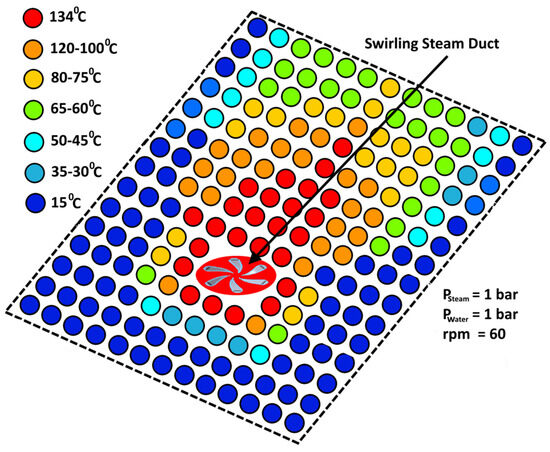
Figure 3.
Temperature distribution by color contours of each sensor.
The color contours inside each circle show the rounded-off, time-averaged value of the temperature recorded by the respective LM35 temperature sensor. As the flow vessel was heavily wrapped with Teflon and sponge tape, on an adiabatic basis, the theoretical equilibrium temperature of the resultant mixture of steam and water at the varying inlet pressure, neglecting friction losses and height differences, was given by Equations (3)–(6), as follows,
where is the mass flowrate (kg/s) of water, is the mass flowrate (kg/s) of steam, is the temperature of water at the inlet (°C), is the temperature of steam at the inlet (°C), is the inlet pressure of steam or water (Pa), is the outlet pressure of steam or water (Pa), represents steam or water, is volumetric flowrate (m3/s), and is the universal gas constant (J/mol.K). Based on these estimations, the adiabatic equilibrium temperature at varying operating conditions ranged from 57.5 to 74.5 °C. So, the average temperature value recorded by each of the LM35 temperature sensors, which was within the given temperature range at the respective operating conditions, provided the information related to the extent of mixing as well as the area patches on the plane sheet that inhibited proper mixing between the swirling steam and cross-flowing water. In other words, the color contours belong to the temperature ranges that showed the extent of mixing of the swirling steam and water in terms of area inhibiting the mixing phenomenon. A Matlab-based code written for color recognition and pixel counting [19] was used to recognize different colors based on their RGB intensity as well as to estimate the area based on their colors. It should be noted that the experimental values of the average temperature recorded by each LM35 sensor constructed a 2D plane sheet having different color patches based on the difference in the average temperature values. The experimental values were compared/supported by using the computational fluid dynamic (CFD) studies, in which the direct contact condensation (DCC) model [20] was applied to our previous steam–water studies [12,21,22]. The associated boundary conditions for the CFD study are given in Table 2. A total mesh number of 4.89 million along the two orthogonal planes provided grid independence at all operating conditions. The perfect mixing zones based on the experimental as well as theoretical studies at the initial conditions (i.e., Psteam = 1 bar, Pwater = 1 bar, and rpm = 60) can be seen in Figure 4a. Perfect mixing is outlined by the even distribution of steam bubbles across the cross-flowing water, and even distribution of steam is reduced. It should be noted that the experimental measurements were placed in an overlapping configuration over the CFD-based profiles after equating the aspect ratios of the two figures (one figure contains experimental profiles, and other contains CFD profiles) showing the orthogonal planes. A clear difference existed between the theoretical and experimental values of the temperature profiles. A possible reason for this difference may be the spatial resolution of the temperature sensors on the plane of symmetry as well as vertical planes while acquiring the experimental data, as the distance between two adjacent LM35 temperature sensors left a void region between them. This region may have contained some meaningful data regarding mixing that was not acquired within the allowed time due to limitations in the data acquisition system used in the present experiment.

Table 2.
Boundary conditions and details of the models used.
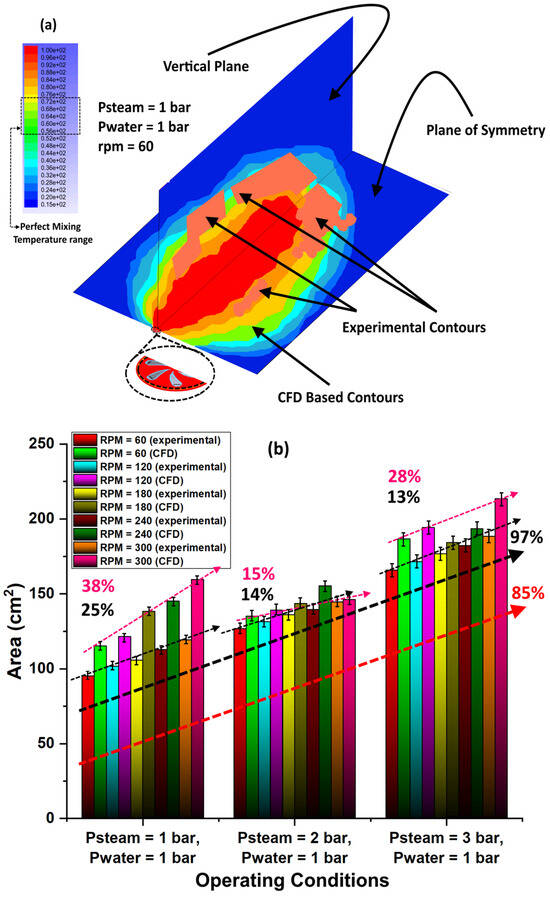
Figure 4.
(a) Experimental and CFD temperatures. (b) Area under perfect mixing between steam contours and water at varying conditions. Error bar has more length at elevated steam pressure due to fluctuating nature of the flow.
Contrarily, in simulation studies, no region was left without characterization. It should also be noted that in the CFD studies, a number of suppositions led to regular nature profiles, whereas in the experimental studies, there were myriad hidden factors that were not incorporated into the CFD studies, including the non-uniformity of the flow profiles in connection with the surface of the plane of symmetry, the effect of the wake profile and insertion of the surrounding cold water inside the leeward section. It should be noted that, in the experimental profiles, regions inhibiting perfect mixing have been shown only, whereas in the CFD profiles, such area patches have been shown by a dotted square around a portion in the legend. The corresponding area patches have been shown by color contours in the CFD profile along the vertical and horizontal planes.
The variation in the area patches inhibiting the perfect mixing of swirling steam inside the cross-flowing water under the varying operating conditions on an experimental as well as theoretical basis is shown by the bar charts in Figure 4b. The centralized dark region is the maximized mixing area, whereas the zones surrounding this represent inhibited mixing areas shown by the color, which is lightened as it is displaced away from the center of the steam pipe’s exit. It was found that the rotational speed of the propeller, as well as the inlet pressure of the and water, contributed to a rise in the area under the influence of approximate perfect mixing. With an increase in rotational speed from 60 to 300 RPM in steps of 60 RPM, the percentage increase in the area under the influence of perfect mixing ranged from 13 to 25% on an experimental basis and 15 to 38% on a theoretical basis. Overall, by varying the operating conditions from Psteam, Pwater = 1 bar each and RPM = 60 to Psteam = 3 bars, Pwater = 1 bar and RPM = 300, a 97% (on experimental basis) and 85% (on theoretical basis) increase in the area was estimated, which was under the influence of perfect adiabatic mixing. In the experimental study, a higher percentage of rise in the area under the influence of perfect mixing than in the CFD study was noted. However, in fact, there was a tendency toward narrowing the difference between experimental and CFD results within a fixed aspect ratio plane. The experimental results shown in Figure 4b are reproducible with varying errors depending upon the accurateness of the experimental setups. In the present setup, the errors shown in Figure 4b ranged from 4 to 7%. The velocity variations were measured using the 20 HFA sensors, of which 13 were oriented in the horizontal direction with respect to the plane sheet and seven were mounted in the vertical direction with respect to the plane sheet. For characterizing the fluid region based on the velocity distribution across the plane of symmetry as well as a vertical plane, the velocity data were recorded by using the HFA sensors along the plane of symmetry as well as vertical plane. The amplitudes of the velocity fluctuations were computed using a fast Fourier transform (FFT). As the data were acquired for the whole length of the plane sheet, only the time-averaged amplitudes at an axial distance of 1 cm along the axial direction over the plane sheet were plotted symbolically with the similar experimental and CFD aspect ratio-based temperature profiles, as shown in Figure 5. The actual values of the amplitudes can be seen in the legend in Figure 5. Here, two important observations were made. First, the time-averaged amplitudes of the velocity profiles had higher values in the crossing regions than the mainstream velocity, whereas the water/steam mixed region was directed toward the windward side, and the velocities were toward the leeward side of the swirling steam duct. A possible reason for this behavior is that the swirling steam jet may provide a virtual cover over the exit of the duct, which leads to bending of the mainstream flow. This lead toward an accelerated flow within this region, which contributes to an increase in the velocity of the swirling steam–water mixture in these regions. These regions are depicted by Regions R1 and R2 in Figure 5. Another observation was that when the duct was raised above the surface of the plane sheet to a height of h ≈ d/2, the velocity amplitudes initially had lower values than the values of the velocity amplitudes in the mainstream region area, as well as compared to the regions R1 and R2 on the plane of symmetry, but afterward, these amplitude values restored their strength, starting from a distance of 2.3 r ≈ 4.0 cm up to 3.6 r ≈ 6.3 cm. This led to the amplitudes being reduced to the end of the plane sheet. A possible reason for the velocity amplitude decrease followed by an increasing trend is due to the deflection of the streamlines with the body of the duct inhibiting the propeller, and this was raised to the height of h ≈ d/2. After the deflection zone, the streamlines converged toward the wake region, thus giving rise to the amplitudes of the velocity fluctuations.
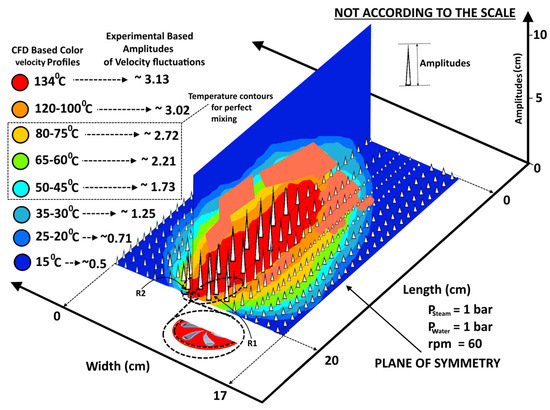
Figure 5.
Experimental and CFD-based temperature profiles showing regions of perfect mixing and experimentally based time-averaged velocity amplitudes in swirling steam–water cross-flows across orthogonal planes (aspect ratios equated for experimental and CFD study-based planes).
It was observed that in all given hydrodynamic operating conditions, there were multiple mixing zones that inhibited the extent of good mixing. These mixing zones prevailed over different sizes of area patches, which in the present research project were measured by using color recognition and pixel-counting Matlab-based code. It was observed that in each phase of experimentation, there was a virtual cover based on the void fraction of the swirling steam spread and the surroundings of the duct inhibiting the propeller. The area stretch of this virtual cover was defined based on the colored pixels recorded on an experimental and theoretical CFD basis. The area of this virtual cover had a weak relationship with the total area of the region inhibiting the perfect mixing. The area of such a virtual cover under all hydrodynamic operating conditions is shown in Figure 6.
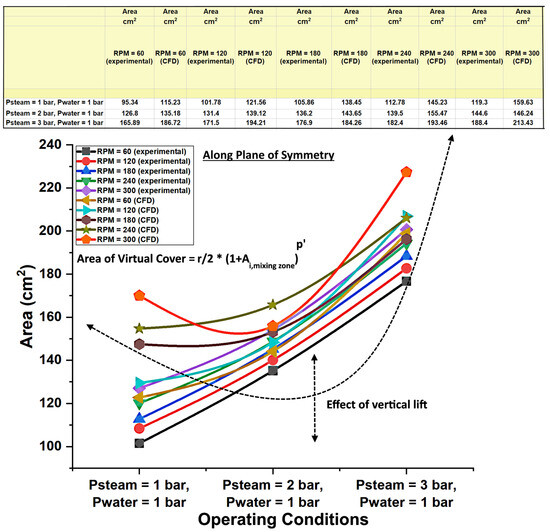
Figure 6.
Area of virtual cover under the influence of varying operating conditions.
The relationship of the area of virtual cover with the area of perfect mixing can be represented by an analytical relation, as shown in Equation (7).
where, is the area of the virtual cover, = 0.875 cm, is experimentally or CFD based, is the area under the influence of perfect mixing (either experimentally or theoretically based), and is the power factor (~1.03). With increasing inlet pressure of steam, it was observed that along the plane of symmetry, a proportional rise to the area under the influence of virtual cover resulted. Also, it was observed that with increasing RPM, the area along the plane of symmetry showed a decreasing trend. This may be attributed to the effect of vertical lift acting on the swirling steam jet. In addition, close similarity was observed between the experimental and CFD studies, under operating conditions (Psteam = 2 bars, Pwater = 1 bar), in terms of the total area of the virtual cover surrounding the exit of the duct, which may be associated with the higher degree of vertical lift action by the swirling steam on the cross-flowing water.
3.2. Effect of Mixing on the Stability of Swirling Steam–Water Cross-Flows
Swirling steam was injected into cross-flowing water. It was found that the swirling steam mixed with the cross-flowing water, which resulted in the formation of multiple regions surrounding the swirling steam, and the flow phenomena within these regions tended to be complex. However, before discussing the effect of the mixing on the stability in the flow domain, there is a need to discuss some norms from the cited literature, based on which the analysis of the flow domain for its stability can become easier task.
The radius of curvature was taken as positive when the jet was bending outward or upward and considered negative when the jet was bending inward or downward [2]. Thus, based on this observation, the plane of symmetry around the swirling steam jet exit was divided into four regions, as shown in Figure 7a. In addition, the stability of the flow domain could be defined based on the velocity variation trends inside the fluid domain. If the velocity decreases in the direction of the radius of curvature, it shows that the flow domain tends towards instability. But when the velocity increases in the direction of the radius of curvature, then the flow domain tends toward stability in that region [2]. The area at the exit of the duct was divided into small area elements dA/dx, as shown in Figure 7b. The dotted arrows indicate the radius of curvature, whereas the dotted circles indicate acceleration, dissipation and retardation.
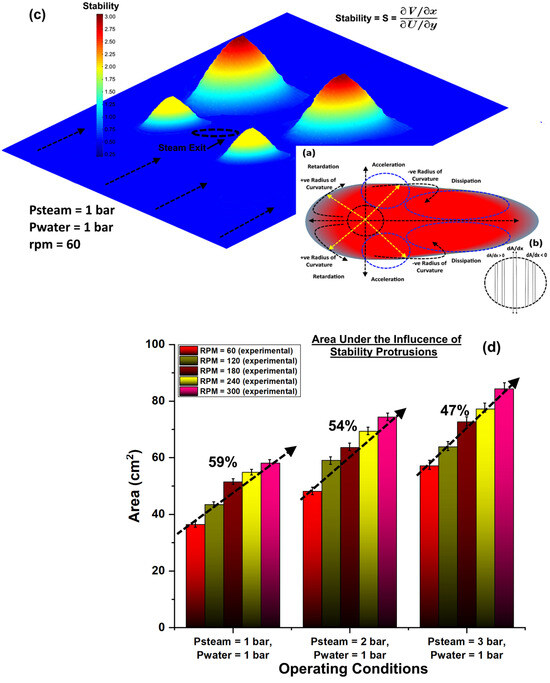
Figure 7.
(a) Radius of curvature, acceleration and retardation potential areas (bottom-right), (b) small area elements dA/dx segmentation (bottom-right), and (c) experimental data-based stability profiles across the plane of symmetry (top-left). (d) Area under the influence of stability protrusions. Error bar has more length at elevated steam pressure due to fluctuating nature of the flow.
On the plane of symmetry, the behavior of the velocity profiles seems strongly dependent on this small area dA/dx variation across the exit of the steam duct. It was observed that the value of the dA/dx shifted from positive to negative across the duct exit. This imparts an effect on the velocity profiles along the plane of symmetry, which can be realized upon the distribution of the perfect mixing zones, as shown in Figure 5. Under all operating conditions initially, this gradient of area element, where blocking the cross-stream flow resulted in deacceleration, subsequently diverted it along the radial direction on both sides of the duct and accelerated it in the downward direction around the jet, eventually dissipating in the far-off fluid domain along the axial direction, as shown in Figure 5. The stability plot based on the experimental data across the plane of symmetry is shown in Figure 7c.
It was observed that the stability profiles follow the criteria set for the flow stability in the cited literature [2], where the accelerating flows in the direction of the radius of curvature contribute to a stable flow, and the retarding flows contribute to the flow instabilities. It should also be noted that the flow stability had similar values in the surroundings of the steam jet exit duct as well as in the downstream part of the flow domain across the plane sheet. S ≈ (∂V/∂x)/(∂U/∂y) provides a measure of the rotational intensity of the steam swirl. Relatively smaller values of dA/dx point toward an unstable region, and larger values point toward an unstable uniform region.
The rotational intensity of the swirl is determined by determining the strength of the swirl, which is defined as the ratio of the axial flux of angular momentum to the axial flux of axial momentum. The rotational intensity of the swirl, S, is expressed mathematically as,
where is the axial flux of linear momentum, is the axial flux of angular momentum, R is the radius of the pipe through which the steam was injected, and and are the axial and tangential velocities.
The first two protrusions around the swirling steam exit duct may be attributed to the bending over the mainstream of water due to the virtual cover around the swirling steam jet exit duct where the flow accelerates. Another contribution may be due to the velocity fluctuations that are due to the inception and collapse of the steam bubbles, as shown in Figure 7c. The last two protrusions are due to the contribution of the inward bending of the surrounding fluids; thus, after the wake region, the inward flow contributes to the velocity of the flow, which provides more stable flow within the regions, as shown by Figure 7c. The flow in the leeward region was found to be more stable, which indicates the dominant role of the inward deflecting flow on the flow stability. The stability had a higher value on the left side than the right-hand side in the leeward section. The possible reason may be the head-on collision of the steam wave accompanied by the swirler fin. This results in more blockage by the virtual cover on the left-hand side than the right-hand side within the vicinity of the nozzle, which eventually converges with surrounding water at higher speed on the left-hand side of the leeward section than the right-hand side.
On the right-hand side, the fin almost supports the flowing water direction; thus, the two protrusions are large enough but have comparable sizes. The presence of flow instabilities is essential for the proper mixing of the two fluids if these interact with each other in such a manner that one fluid exerts a shearing effect upon the other one. The mixing will occur under the effect of a highly time-driven sequence of small-scale instabilities, whose strength depends on the structure of the shear layers. For this reason, on the plane of symmetry, the stability has lower values in the regions where the shear layers act in a more dominant way, thus generating retardation due to the blockage by the swirling steam in the adjacent windward quadrants, and their curvatures have positive values (Figure 7b). The downstream area and surroundings of the swirling steam jet in the duct showed no protrusions; thus, regions with unstable flow domains, due to the highly time-driven sequence of small-scale instabilities, promote proper mixing [2]. Overall, the total flow patches under the influence of stability protrusions, fulfilling all hydrodynamic conditions, can be seen in Figure 7d. The experimental results shown in Figure 7d are reproducible with varying errors depending upon the accuracy of the experimental setup. In the present setup, the errors in Figure 7d range from 3 to 8%.
With increasing RPM at fixed operating inlet pressure, a decreasing trend toward instability occurred in the fluid domain across the plane sheet, and hence, a growing tendency toward proper mixing, which was governed and influenced dominantly by the small-scale instabilities, whereas overall, the variations in operating conditions had more than twice the effect on the area under the influence of these stability protrusions. Thus, an overall rise in inlet pressure contributed to improper mixing, whereas a rise in the RPM contributed to proper mixing.
3.3. Effect of Spatial Scaling of Swirling Steam Trajectory on Mixing in Cross-Flows
The swirling steam was injected into the cross-flowing water at varying inlet steam gauge pressures in the range of 1–3 bars and at a constant inlet gauge pressure of 1 bar of water. To examine the effect of the mixing on the spatial scaling of the swirling steam trajectory inside the cross-flowing water along the horizontal and vertical planes, the velocity data gathered by the HFA sensors were analyzed. It should be noted that in the current phase of experimentation, we had a total of 60 million data points (spatial resolution ~50 mm), which were collected for each sensor along the horizontal as well as vertical directions. The jet trajectory along the horizontal and vertical planes was based on the windward and leeward jet trajectory lines, as shown in Figure 8a. It should be noted that the windward and leeward boundaries were drawn based on the time-averaged velocity values at 0.5 cm each. In previous studies [2], different scaling methods were adopted, with the majority of the time scaling relying on the parameters stated as rd and r2d ( , d is the diameter of the steam duct exit).
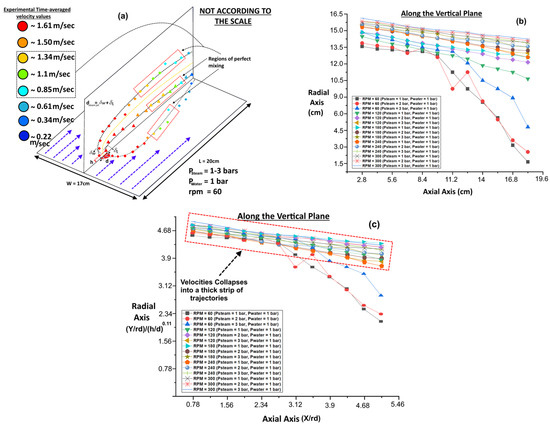
Figure 8.
(a) Experimental time-averaged velocity contours. Velocity distribution along (b) the vertical plane and (c) the vertical plane after scaling.
In the present case, the jet trajectory was scaled by using the same methodology as adopted in the cited literature [2,3,5,11,23], first by calculating the height at which the jet remained vertical and after that point deflected to the right-hand direction. If it is considered that the steam exit has a diameter, d, and height, h, to the point that it remains vertical, the pressure gradient can be computed using the relation expressed as,
The vertical momentum flux in the present case can be given as,
Now the deflection of the steam jet under the influence of the cross-flowing water can be valid if the vertically acting momentum flux is comparable to the pressure gradient along the axial direction. This condition is given by the relation,
where (in the present case ≈ 0.017) is the constant of proportionality. Now, if the velocity of the steam jet has been presented in terms of the effective diameter , which is the diameter of the jet, density of steam jet , and time-averaged velocity of the steam jet the relation is given as,
Now, in the present case, where an effective diameter has been calculated as 1–1.09, under all operating conditions, the effective diameter allows us to compare the jet trajectories under all operating conditions having the same values of but different velocities. Simplifying Equations (11) and (12) results in the following,
Thus, from Equation (13), it is inferred that when the value of r is raised (in the present case by raising the inlet pressure of steam) on the right-hand side, the value of will be raised also, to satisfy Equation (13), and thus, on physical grounds, the swirling steam jet will deflect to the right-hand side after gaining some penetration/vertical lift, which is denoted by . It was observed that the rise in the RPM (60–300) contributed to the rise in the vertical penetration of the jet (15–19%). The penetration depth bears a relationship [6] with the hydraulic diameter of the steam duct exit as well as with the ratio r, expressed as,
In our case, this condition was approximately satisfied with the value of when it is lower than the value of at RPM = 60 and 120 and Psteam, Pwater = 1 bar each. For higher values, the relation is given as,
This condition was approximately satisfied under the rest of the operating conditions (RPM = 180–300, Psteam = 2 and 3 bars, and Pwater = 1 bar). By parameterizing the axis using the same scaling technique as proposed in the cited literature [6], i.e., scaling of the axial and radial axes by rd = rdsteam (dsteam = , the velocity distribution was obtained along the vertical plane, as shown in Figure 8b. Using the scaled axis, the vertical trajectories of the velocities were collapsed into a tick strip composed of the velocity trajectories of the vertical jet along the vertical plane at all operating conditions, as shown in Figure 8c. As the values of the proportionality constant, and the penetration depth were obtained from experiments. Upon further adjustment, i.e., scaling by r2d with the corrected value of r, i.e., = 0.16–0.31 (for all operating conditions) for the vertical steam jet trajectory scaling, the velocity profiles collapsed nearer to each other, as shown in Figure 8d. It was observed that the amended value of r is well suited for scaling the vertical trajectories of the swirling steam jet in cross-flowing water.
The scaling imparts a proportional effect on the calculated area under the effect of the perfect mixing. Although the vertical swirling impingement of the steam jet tried to recover the pressure loss at the steam duct exit with the help of the swirler, after the onset of the impingement, an irrecoverable loss of pressure, and hence, the kinetic energy inside the cross-flowing water, was observed [6,24]. It was observed that, based on the velocity points that represent the regions for perfect mixing, the scaling of the vertical trajectories of the swirling steam jets under all operating conditions merged the regions of perfect mixing to some extent. Thus, it was observed that by scaling the trajectories along the vertical plane, the area under the influence of perfect mixing was reduced to around 3–4.7% under all operating conditions. This method could be helpful for a number of flow-related studies involved in chemical and environmental fluid mechanics, where a large area needs to be studied. As in the environmental engineering domain, we can compare the different injection mechanisms of the brine from desalination plants inside flowing water reservoirs as the improper mixing of the brine, resulting in higher salinity near the brine exit into the flowing water [5]. Thus, our observed flow domain size, as well as characterization requirements, would be reduced to inlet pressure/velocity of the brine and the resulting area under the influence of perfect mixing only, whereas in such cases, the discerning factor would be the relative concentration of salts inside the domain under observation.
4. Conclusions
In the present study, theoretical and experimental research was conducted to investigate the effect of the mixing of a swirling steam jet into cross-flowing water. Steam was injected into cross-flowing water at varying steam inlet pressures, i.e., Psteam = 1–3 bars, and RPM = 60–300, through a vertical duct using a swirler whose RPM was controlled by using an external motor. A plane of symmetry comprising LM35 temperature sensors and an array of hot-film anemometers was used for the characterization of the fluid domain. Based on the theoretical adiabatic calculations, perfect mixing was calculated for a temperature range of 57.5–74.50 C. Overall, by varying Psteam = 1–3 bar, Pwater = 1 bar, and RPM = 60–300, a 97% (on experimental basis) and 85% (on theoretical basis) increase in the area under the influence of perfect adiabatic mixing was calculated. It was observed that there is a virtual cover based on the steam void fraction on and in the surroundings of the duct inhibiting the propeller. The area of this virtual cover has a weak relationship with the total area of the region inhibiting the perfect mixing, for which an analytical relationship was devised. The effect of mixing on the stability of swirling steam–water cross-flows was also investigated. It was observed that the stability profiles followed the criteria as set for the flow stability in previous studies, where the accelerating flows in the direction of the radius of curvature contributed to a stable flow and the retarding flows contributed to flow instabilities. Overall, the variations in the operating conditions yielded more than twice the effect on the area under the influence of these stability protrusions. Thus, an overall rise in inlet pressure contributed to improper mixing, and a rise in RPM contributed to proper mixing. The effect of spatial scaling of the swirling steam trajectory on mixing in cross-flowing water was also investigated. It was observed that the scaling of the vertical trajectories of the swirling steam jets under all operating conditions merged the regions of perfect mixing to some extent. Thus, the area under the influence of perfect mixing was reduced to around 3–4.7% under all operating conditions with the scaling of the jet trajectories.
Author Contributions
Conceptualization, H.A.G. and A.K.; methodology, K.S.; validation, A.K. and K.S.; formal analysis, A.K. and H.A.G.; investigation, K.S. and H.A.G.; resources, K.S. and H.A.G.; data curation, A.K. and V.V.S.; writing—original draft preparation, A.K. and K.S.; writing—review and editing, V.V.S. and K.S.; visualization, A.K. and K.S.; supervision, K.S. and H.A.G.; project administration, H.A.G.; funding acquisition, H.A.G., V.V.S., K.S. and A.K. All authors have read and agreed to the published version of the manuscript.
Funding
The project was funded by Deanship of Scientific Research (DSR) at Jazan University, Jazan, Kingdom of Saudi Arabia under Grant No. W43-063. The authors gratefully acknowledge DSR for technical and financial support. We are also thankful to the Ministry of Science and Higher Education of the Russian Federation (project No. FENU-2023-0010) for supporting this work.
Data Availability Statement
Data will be available upon request.
Acknowledgments
The authors are thankful to the Deanship of Scientific Research (DSR) at Jazan University, Jazan, Kingdom of Saudi Arabia for supporting this work through Grant No. W43-063, the Ministry of Science and Higher Education of the Russian Federation for supporting this work (through project No. FENU-2023-0010) and Dongguan University of Technology (DGUT), Sino-French United Institute (DCI) for their support and cooperation.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
| Symbol | Details |
| local density (Kg/m3) | |
| Pressure at the inlet (Pa or Bar) | |
| Pressure at the outlet (Pa or Bar) | |
| Velocity (m/s) | |
| Average velocity (m/s) | |
| Acceleration due to gravity ((m/s2) | |
| Height (m) | |
| Mass flow rate of water (Kg/m2-s) | |
| Temperature of water (°C) | |
| Mass flow rate of steam (Kg/m2-s) | |
| Temperature of steam (°C) | |
| Velocity at the outlet (m/s) | |
| Volumetric flow rate (Kg/m3-s) | |
| Universal gas constant (J/K/mole) | |
| Pressure of steam (Pa or Bar) | |
| Pressure of water (Pa or Bar) | |
| rpm | Revolution per minute (n/s) |
| Area of the virtual cover (m2) | |
| Area under the influence of perfect mixing (m2) | |
| Area variation (m2/m) | |
| rotational intensity of the steam swirl (m2/s2) | |
| Axial flux of linear momentum (kg-m2/s) | |
| Axial flux of angular momentum (kg-m2/s) | |
| Radius (m) | |
| Axial velocities (m/s) | |
| Tangential velocities (m/s) | |
| Constant of proportionality |
References
- Holdeman, J.D. Mixing of Multiple Jets with a Confined Subsonic Crossflow. Prog. Energy Combust. Sci. 1993, 19, 31–70. [Google Scholar] [CrossRef]
- Kamotani, Y.; Greber, I. Experiments on a Turbulent Jet in a Cross Flow. AIAA J. 1972, 10, 1425–1429. [Google Scholar] [CrossRef]
- Smith, S.H.; Mungal, M.G. Mixing, Structure and Scaling of the Jet in Crossflow. J. Fluid. Mech. 1998, 357, 83–122. [Google Scholar] [CrossRef]
- Keffer, J.F.; Baines, W.D. The Round Turbulent Jet in a cross-wind. J. Fluid. Mech. 1963, 15, 481–496. [Google Scholar] [CrossRef]
- Pratte, B.D.; Baines, W.D. Profiles of the Round Turbulent Jet in A Cross Flow. J. Hydraul. Div. 1967, 93, 53–64. [Google Scholar] [CrossRef]
- Muppidi, S.; Mahesh, K. Study of trajectories of jets in crossflow using direct numerical simulations. J. Fluid. Mech. 2005, 530, 81–100. [Google Scholar] [CrossRef]
- Fric, T.F.; Roshko, A. Vortical structure in the wake of a transverse jet. J. Fluid. Mech. 1994, 279, 1–47. [Google Scholar] [CrossRef]
- Kelso, R.M.; Smits, A.J. Horseshoe vortex systems resulting from the interaction between a laminar boundary layer and a transverse jet. Phys. Fluids 1995, 7, 153–158. [Google Scholar] [CrossRef]
- Kelso, R.M.; Lim, T.T.; Perry, A.E. An experimental study of round jets in cross-flow. J. Fluid. Mech. 1996, 306, 111–144. [Google Scholar] [CrossRef]
- Baker, C.J. The laminar horseshoe vortex. J. Fluid. Mech. 1979, 95, 347–367. [Google Scholar] [CrossRef]
- Margason, R.J. Fifty Years of Jet in Cross Flow Research. Ceaj. 1993. Available online: https://ui.adsabs.harvard.edu/abs/1993ceaj.agar.....M/abstract (accessed on 22 August 2023).
- Instrumentation, T. LM35 Precision Centigrade Temperature Sensors. Available online: https://www.ti.com/product/LM35?keyMatch=LM35&tisearch=search-everything&usecase=GPN-ALT (accessed on 22 August 2023).
- Hot-Wire and Hot-Film Probes—Dantec Dynamics. Available online: https://www.dantecdynamics.com/components/hot-wire-and-hot-film-probes/ (accessed on 22 August 2023).
- Engineering, O. Digital 4-in-1 Tachometer System | Omega Engineering. Available online: https://www.omega.com/en-us/control-monitoring/motion-and-position/speed-sensors/p/OMDC-DM8000-Series (accessed on 22 August 2023).
- Graham, R.; Hsu, Y.; Simon, F. Application of hot-wire anemometry for two- phase flow measurements such as void fraction and slip velocity. In Proceedings of the ASME Winter Annual Meeting, Philadelphia, PA, USA, 17–22 November 1963. [Google Scholar]
- Katarzhis, A.K. Foreign technology div wright-patterson afb ohio. Electr. Method Rec. Stratif. A Steam-Water Mix. 1958. [Google Scholar]
- Galaup, J.M.; Galaup, J.P. Hot-Film Anemometry in Air-Water Flow. Symp. Turbul. Liq. Chem. Biochem. Eng. 1975, 1–9. Available online: https://core.ac.uk/download/pdf/229112982.pdf (accessed on 22 August 2023).
- “STEAM TABLES,” in A-to-Z Guide to Thermodynamics, Heat and Mass Transfer, and Fluids Engineering, Begellhouse. Available online: https://www.scribd.com/document/415267609/Steam-Tables (accessed on 22 August 2023).
- Khan, A.; Sanaullah, K.; Takriff, M.S.; Hussain, A.; Shah, A.; Chughtai, I.R. Void fraction of supersonic steam jet in subcooled water. Flow. Meas. Instrum. 2016, 47, 35–44. [Google Scholar] [CrossRef]
- Shah, A.; Chughtai, I.R.; Inayat, M.H. Numerical Simulation of Direct-contact Condensation from a Supersonic Steam Jet in Subcooled Water. Chin. J. Chem. Eng. 2010, 18, 577–587. [Google Scholar] [CrossRef]
- Khan, A.; Sanaullah, K.; Takriff, M.S.; Zen, H.; Fong, L.S. Inclined Injection of Supersonic Steam into Subcooled Water: A CFD Analysis. Adv. Mat. Res. 2014, 845, 101–107. [Google Scholar] [CrossRef]
- Khan, A.; Sanaullah, K.; Takriff, M.S.; Zen, H.; Rigit, A.R.H.; Shah, A.; Chughtai, I.R. Numerical and experimental investigations on the physical characteristics of supersonic steam jet induced hydrodynamic instabilities. Asia-Pac. J. Chem. Eng. 2016, 11, 271–283. [Google Scholar] [CrossRef]
- Su, L.K.; Mungal, M.G. Simultaneous measurements of scalar and velocity field evolution in turbulent crossflowing jets. J. Fluid. Mech. 2004, 513, 1–45. [Google Scholar] [CrossRef]
- Rajaratnam, N. Turbulent mixing and diffusion of jets. In Encyclopedia of Fluid Mechanics; Gulf Publishing: Houston, TX, USA, 1986; Volume 2, pp. 391–405. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).