Rational Solitons in the Gardner-Like Models
Abstract
:1. Introduction
2. General Approach to Obtaining Rational Solutions of the First Order
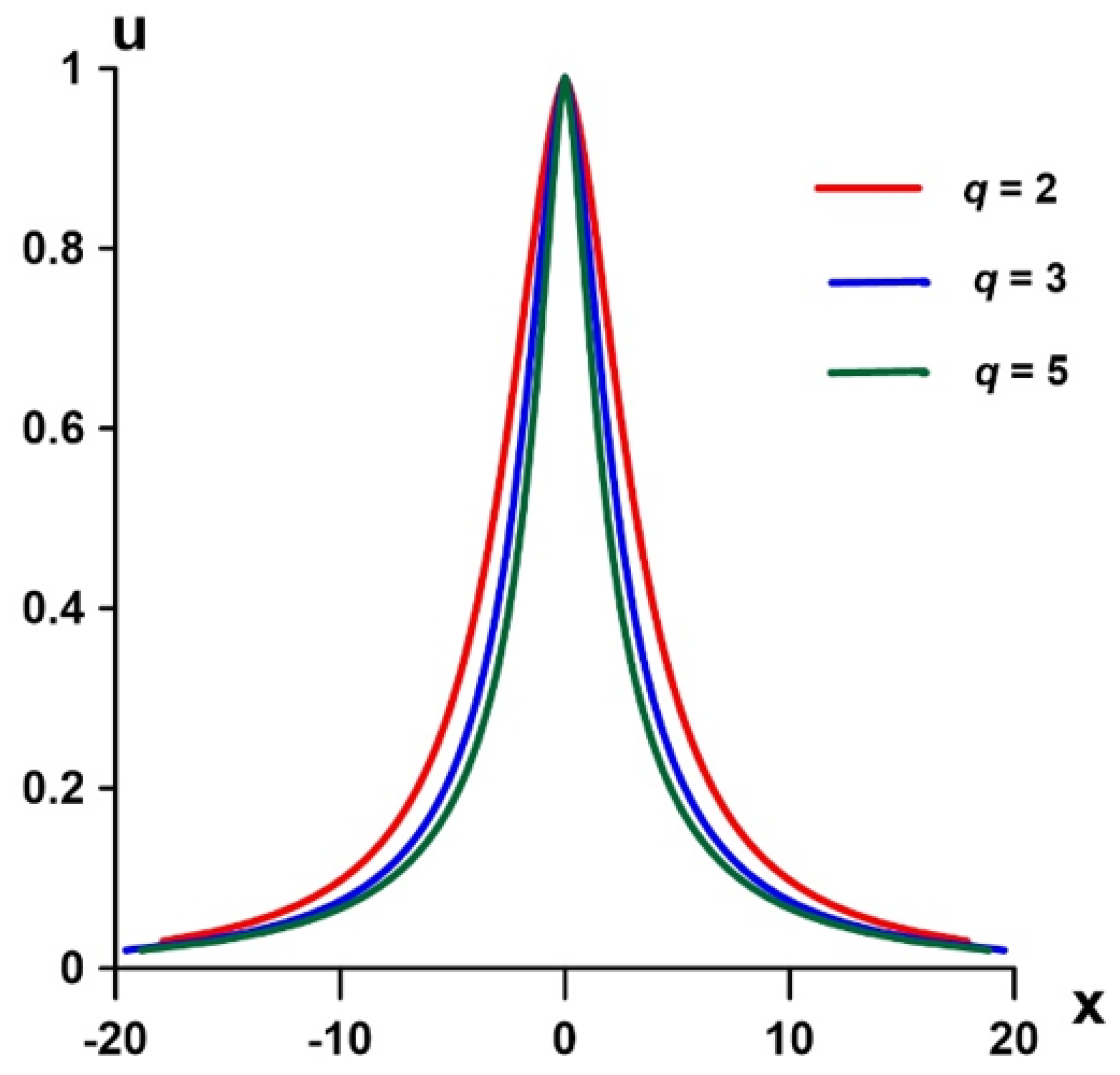
3. Analytical Rational Solitons
4. Rational Solitons in the Korteweg-de Vries Equation with Added High-Order Nonlinearity—Numerical Results
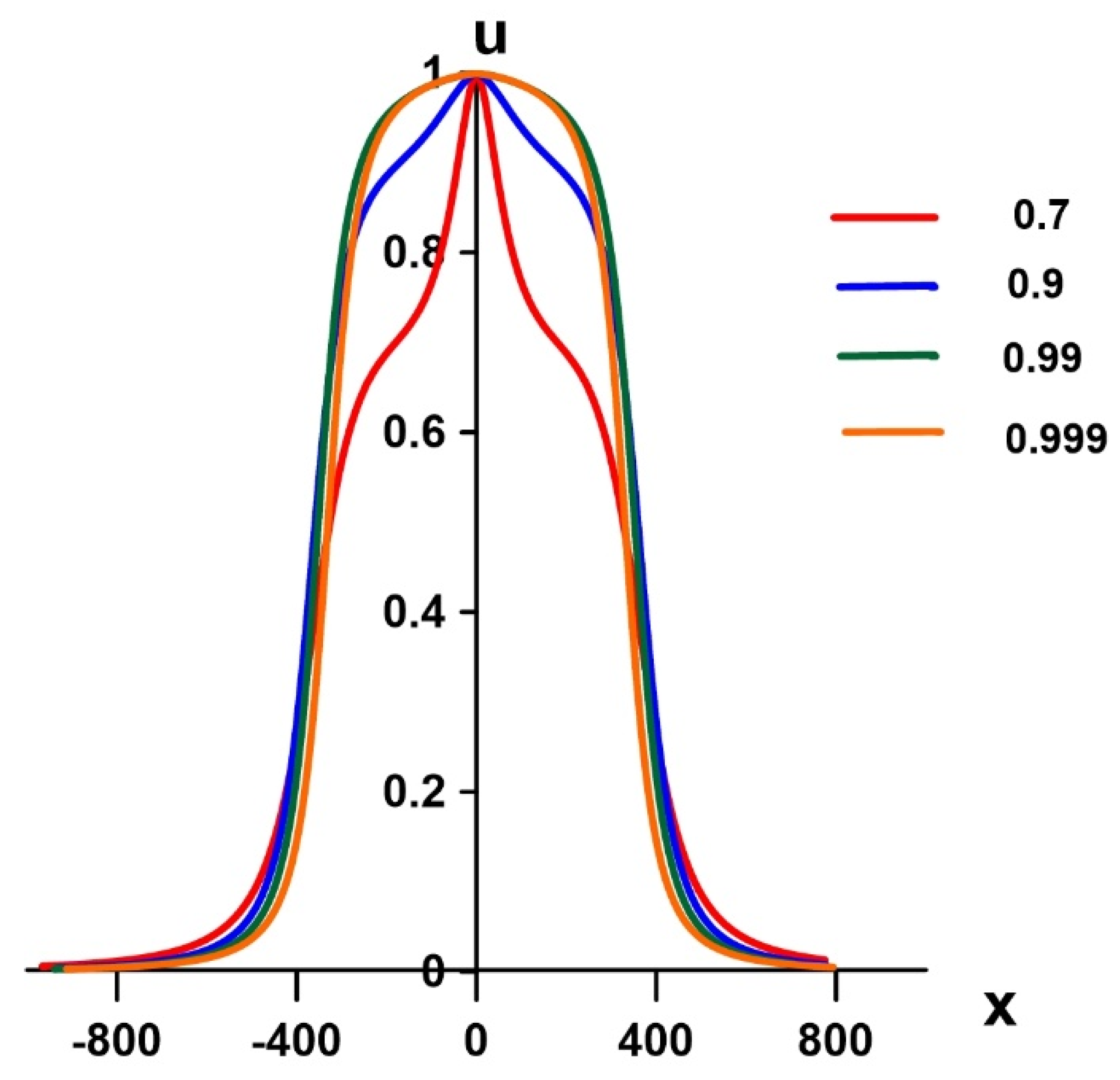
5. Kinks
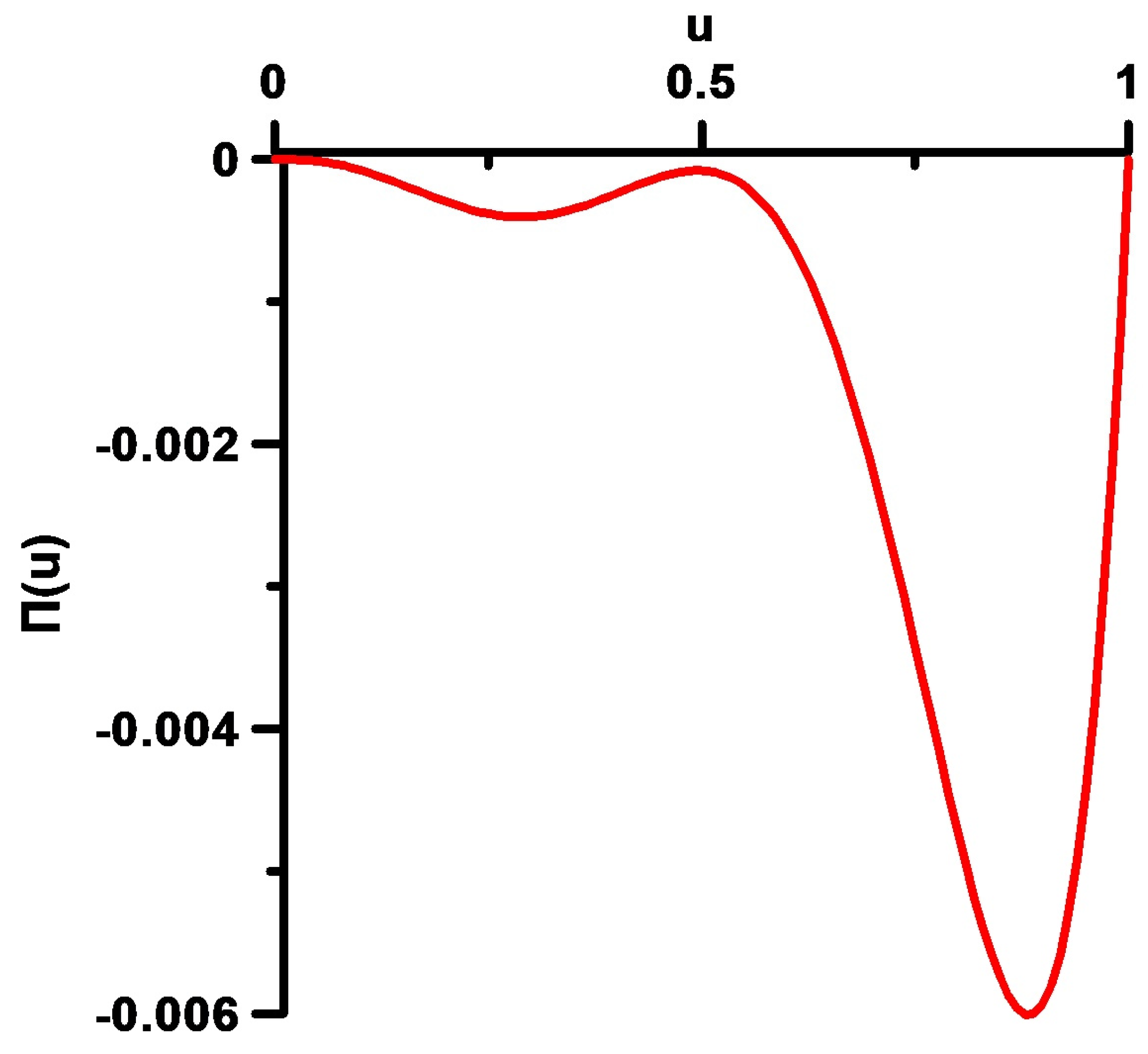
6. Pyramidal Rational Solitons
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Conflicts of Interest
References
- Peregrine, D.H. Water waves, nonlinear Schrödinger equations and their solutions. J. Aust. Math. Soc. Ser. B 1983, 25, 16–43. [Google Scholar] [CrossRef]
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean; Springer: Berlin/Heidelberg, Germany, 2009; 216p. [Google Scholar]
- Onorato, M.; Residori, S.; Bortolozzo, U.; Montinad, A.; Arecchi, F.T. Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 2013, 528, 47–89. [Google Scholar] [CrossRef]
- Shemer, L.; Alperovich, L. Peregrine breather revisited. Phys. Fluids 2013, 25, 051701. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J.M. Rogues waves and rational solutions of nonlinear Schrodinger equation. Phys. Rev. E 2009, 80, 026601. [Google Scholar] [CrossRef]
- Gaillard, P. Families of quasi-rational solutions of the NLS equation and multi-rogue waves. J. Phys. A Meth. Theor. 2011, 44, 435204. [Google Scholar] [CrossRef]
- Gaillard, P. Six-parameters deformations of fourth order Peregrine breather solutions of the NLS equation. J. Math. Phys. 2013, 54, 073519. [Google Scholar] [CrossRef]
- Kedziora, D.J.; Ankiewicz, A.; Akhmediev, N. Classifying the hierarchy of the nonlinear Schrödinger equation rogue waves solutions. Phys. Rev. E 2013, 88, 013207. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 2010, 6, 790–795. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Onorato, M.; Slunyaev, A.; Sergeeva, A.; Pelinovsky, E.; Akhmediev, N. Observation of a hierarchy of up to fifth-order rogue waves in a water tank. Phys. Rev. E 2012, 86, 056601. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Onorato, M.; Akhmediev, N. Super rogue waves: Observation of a higher-order breather in water waves. Phys. Rev. X 2012, 2, 011015. [Google Scholar] [CrossRef] [Green Version]
- Dudley, J.M.; Genty, G.; Mussot, A.; Chabchoub, A.; Dias, F. Rogue waves and analogies in optics and oceanography. Nat. Rev. Phys. 2019, 1, 675–689. [Google Scholar] [CrossRef]
- He, Y.; Suret, P.; Chabchoub, A. Phase evolution of the time- and space-like Peregrine Breather in a laboratory. Fluids 2021, 6, 308. [Google Scholar] [CrossRef]
- Benjamin, T.B. Internal waves of permanent form in fluids of great depth. J. Fluid Mech. 1967, 29, 559. [Google Scholar] [CrossRef]
- Ono, H. Algebraic solitary waves in stratified fluids. J. Phys. Soc. Jpn. 1975, 39, 1082–1091. [Google Scholar] [CrossRef]
- Pelinovsky, D.E. Rational solutions of the Kadomtsev-Petviashvili hierarchy and the dynamics of their poles. I. New form of a general rational solution. J. Math. Phys. 1994, 35, 5820–5830. [Google Scholar] [CrossRef]
- Gaillard, P. Rational solutions to the KPI equation and multi rogue waves. Ann. Phys. 2016, 367, 1–5. [Google Scholar] [CrossRef]
- Akhmediev, N.; Ankiewicz, A.; Soto-Crespo, J.M. Rogue Waves and rational solutions of the Hirota equation. Phys. Rev. E 2010, 81, 046602. [Google Scholar] [CrossRef]
- Ankiewicz, A.; Akhmediev, N.; Lederer, F. Approach to first-order exact solutions of the Ablowitz-Ladik equation. Phys. Rev. E 2011, 83, 056602. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, W.X. Rational solutions to a kdv-like equation. Appl. Math. Comput. 2015, 256, 252–256. [Google Scholar] [CrossRef]
- Chowdury, A.; Ankiewicz, A.; Akhmediev, N. Periodic and rational solutions of modified Korteweg-de Vries equation. Eur. Phys. J. D 2016, 70, 104. [Google Scholar] [CrossRef]
- Bokaeeyan, M.; Ankiewicz, A.; Akhmediev, N. Bright and dark rogue internal waves: The Gardner equation approach. Phys. Rev. E 2019, 99, 062224. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Pelinovsky, D.E. Periodic travelling waves of the modified KdV equation and rogue waves on the periodic background. J. Nonlinear Sci. 2019, 29, 2797–2843. [Google Scholar] [CrossRef]
- Crabb, M.; Akhmediev, N. Complex Korteweg-de Vries equation: A deeper theory of shallow water waves. Phys. Rev. E 2021, 103, 022216. [Google Scholar] [CrossRef]
- Matveev, V.B. Positons: Slowly decreasing analogues of solitons. Theor. Math. Physis 2002, 131, 483–497. [Google Scholar] [CrossRef]
- Gaillard, P. Rational Solutions to the Boussinesq Equation. Fundam. J. Math. Appl. 2019, 2, 349–369. [Google Scholar] [CrossRef]
- Pelinovsky, D.; Grimshaw, R. Structural transformation of eigenvalues for a perturbed algebraic soliton potential. Phys. Lett. A 1997, 229, 165–172. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T. Solitary wave transformation in a medium with sign-variable quadratic nonlinearity and cubic nonlinearity. Phys. D 1999, 132, 40–62. [Google Scholar] [CrossRef]
- Grimshaw, R.; Pelinovsky, E.; Talipova, T.; Kurkina, O. Internal solitary waves: Propagation, deformation and disintegration. Nonlinear Process. Geophys. 2010, 17, 633–649. [Google Scholar] [CrossRef]
- Kurkina, O.E.; Kurkin, A.A.; Soomere, T.; Pelinovsky, E.N.; Ruvinskaya, E.A. Higher-order (2 + 4) Korteweg-de Vries-like equation for interfacial waves in a symmetric three-layer fluid. Phys. Fluids 2011, 23, 116602. [Google Scholar] [CrossRef]
- Derzho, O. Multiscaled solitary waves. Nonlinear Processes Geophys. 2017, 24, 695–700. [Google Scholar] [CrossRef] [Green Version]
- Derzho, O. Large internal solitary waves on a week shear. Chaos 2022, 32, 063130. [Google Scholar] [CrossRef] [PubMed]
- Ruderman, M.S.; Talipova, T.; Pelinovsky, E. Dynamics of modulationally unstable ion-acoustic wavepackets in plasmas with negative ions. J. Plasma Phys. 2008, 74, 639–656. [Google Scholar] [CrossRef]
- El-Tantawy, S.A.; Salas, A.H.; Albalawi, W. New localized and periodic solutions to a Korteweg–de Vries equation with power law nonlinearity: Applications to some plasma models. Symmetry 2022, 14, 197. [Google Scholar] [CrossRef]
- Tamang, J.; Saha, A. Bifurcations of small-amplitude supernonlinear waves of the mKdV and modified gardner equations in a three-component electron-ion plasma. Phys. Plasmas 2020, 27, 012105. [Google Scholar] [CrossRef]
- Wang, G.; Wazwaz, A.-M. On the modified Gardner type equation and its time fractional form. Chaos Solitons Fractals 2022, 155, 111694. [Google Scholar] [CrossRef]
- Rosenau, P.; Oron, A. Flatons: Flat-top solitons in extended Gardner-like equations. Commun. Nonlinear Sci. Numer. Simul. 2020, 19, 1329. [Google Scholar] [CrossRef]
- Pelinovsky, E.; Talipova, T.; Soomere, T. The structure of algebraic solitons and compactons in the generalized Korteweg-de Vries equation. Phys. D 2021, 419, 132785. [Google Scholar] [CrossRef]
- Schamel, H. A modified Korteweg–de Vries equation for ion acoustic waves due to resonant electrons. J. Plasma Phys. 1973, 9, 377–387. [Google Scholar] [CrossRef]
- Mushtaq, A.; Shah, H.A. Study of non-maxwellian trapped electrons by using generalized (r, q) distribution function and their effects on the dynamics of ion acoustic solitary wave. Phys. Plasmas 2006, 13, 012303. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pelinovsky, E.; Talipova, T.; Didenkulova, E. Rational Solitons in the Gardner-Like Models. Fluids 2022, 7, 294. https://doi.org/10.3390/fluids7090294
Pelinovsky E, Talipova T, Didenkulova E. Rational Solitons in the Gardner-Like Models. Fluids. 2022; 7(9):294. https://doi.org/10.3390/fluids7090294
Chicago/Turabian StylePelinovsky, Efim, Tatiana Talipova, and Ekaterina Didenkulova. 2022. "Rational Solitons in the Gardner-Like Models" Fluids 7, no. 9: 294. https://doi.org/10.3390/fluids7090294
APA StylePelinovsky, E., Talipova, T., & Didenkulova, E. (2022). Rational Solitons in the Gardner-Like Models. Fluids, 7(9), 294. https://doi.org/10.3390/fluids7090294









