Taichi-LBM3D: A Single-Phase and Multiphase Lattice Boltzmann Solver on Cross-Platform Multicore CPU/GPUs
Abstract
:1. Introduction
- -
- It is relatively simple to implement. LBM relies on particle group distributions. The interaction between nodes are fully linear, while the nonlinearity enters into a local collision process within each node [29]
- -
- The LBM algorithm is mostly local, leading to efficiency and scalability on a parallel computer [30]
- -
- Robust handling of complex geometries.
2. Algorithm
- Initialisation of the distribution function
- Collision step: A time iteration takes the populations from their state at time t to the next state , where is a constant discrete time step:
- 3.
- Streaming step:Different boundary conditions, e.g., simple bounce-back and periodic, were implemented.
- 4.
- Computation of macroscopic hydrodynamic quantities, density, and momentum are conserved values that can be calculated from:
Multicomponent Lattice Boltzmann Models
- Single phase collision using MRT scheme
- Surface tension perturbation to obtaining
- Recolouring
- Streaming.
| Listing 1. Example of collision operator in Taichi-LBM3D for single phase flow problem. |
 |
| Listing 2. Examples of dense and sparse memory allocation in Taichi-LBM3D. |
 |
3. Numerical Benchmark
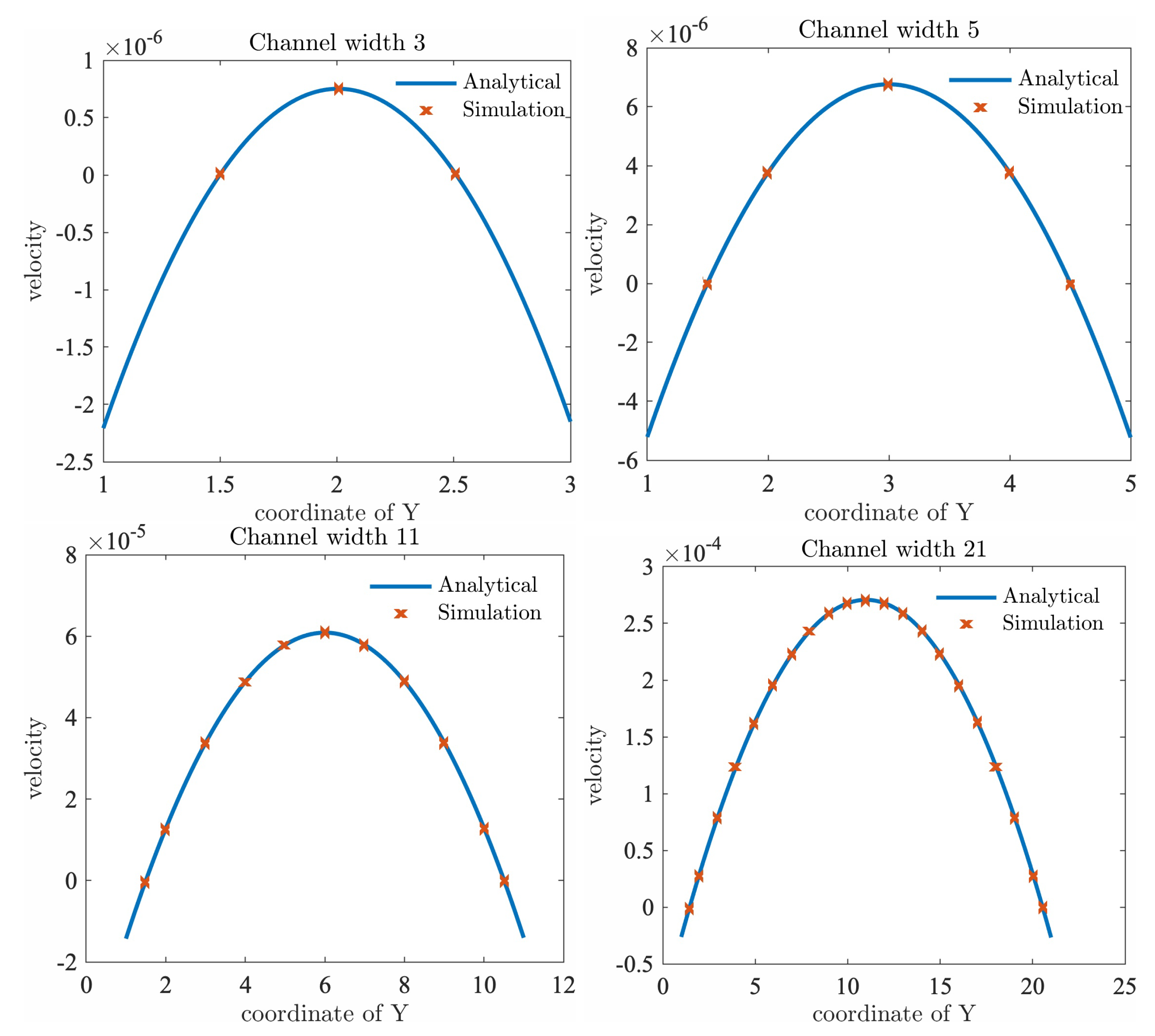
3.1. Stokes Flow
3.2. Lid-Driven Flow
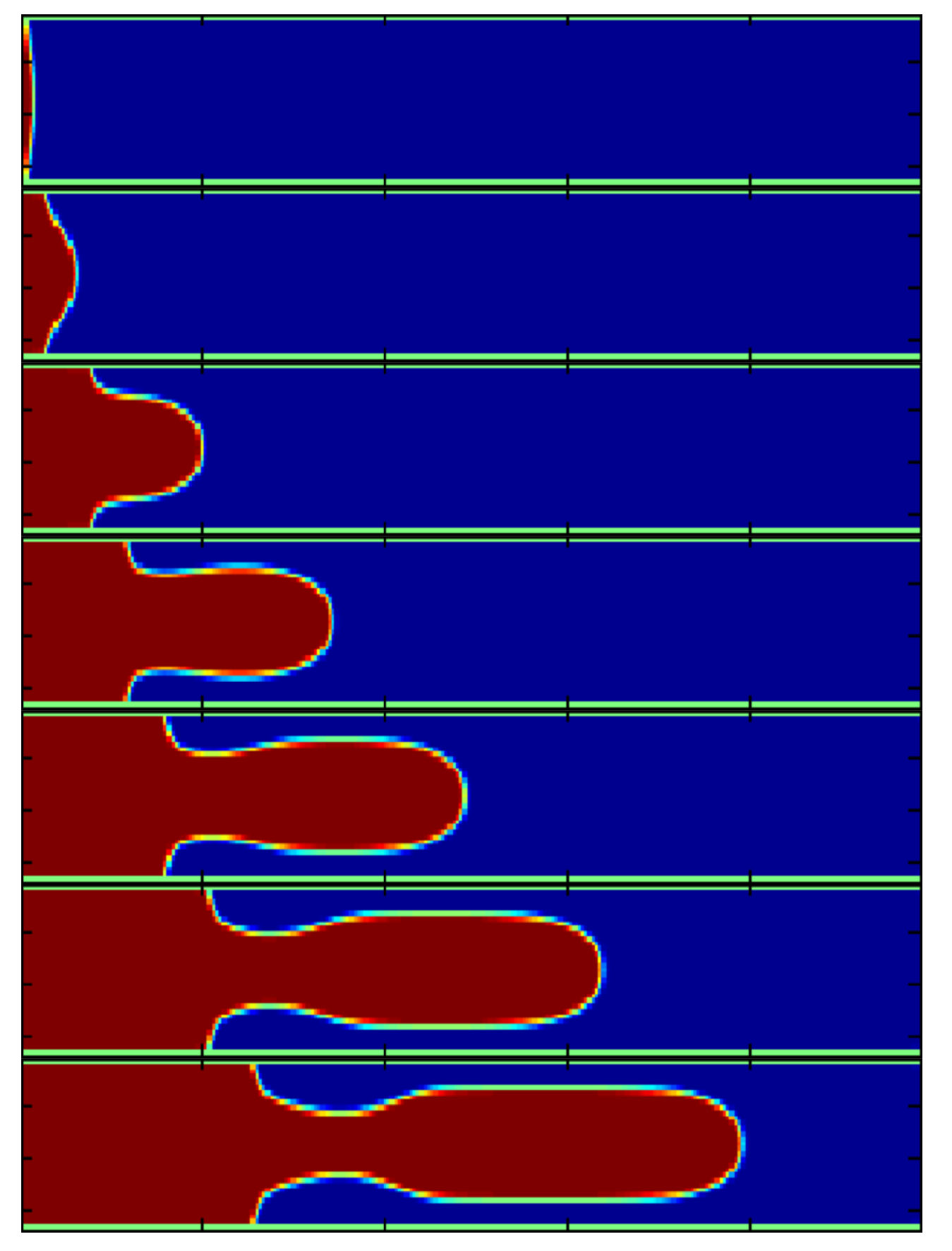
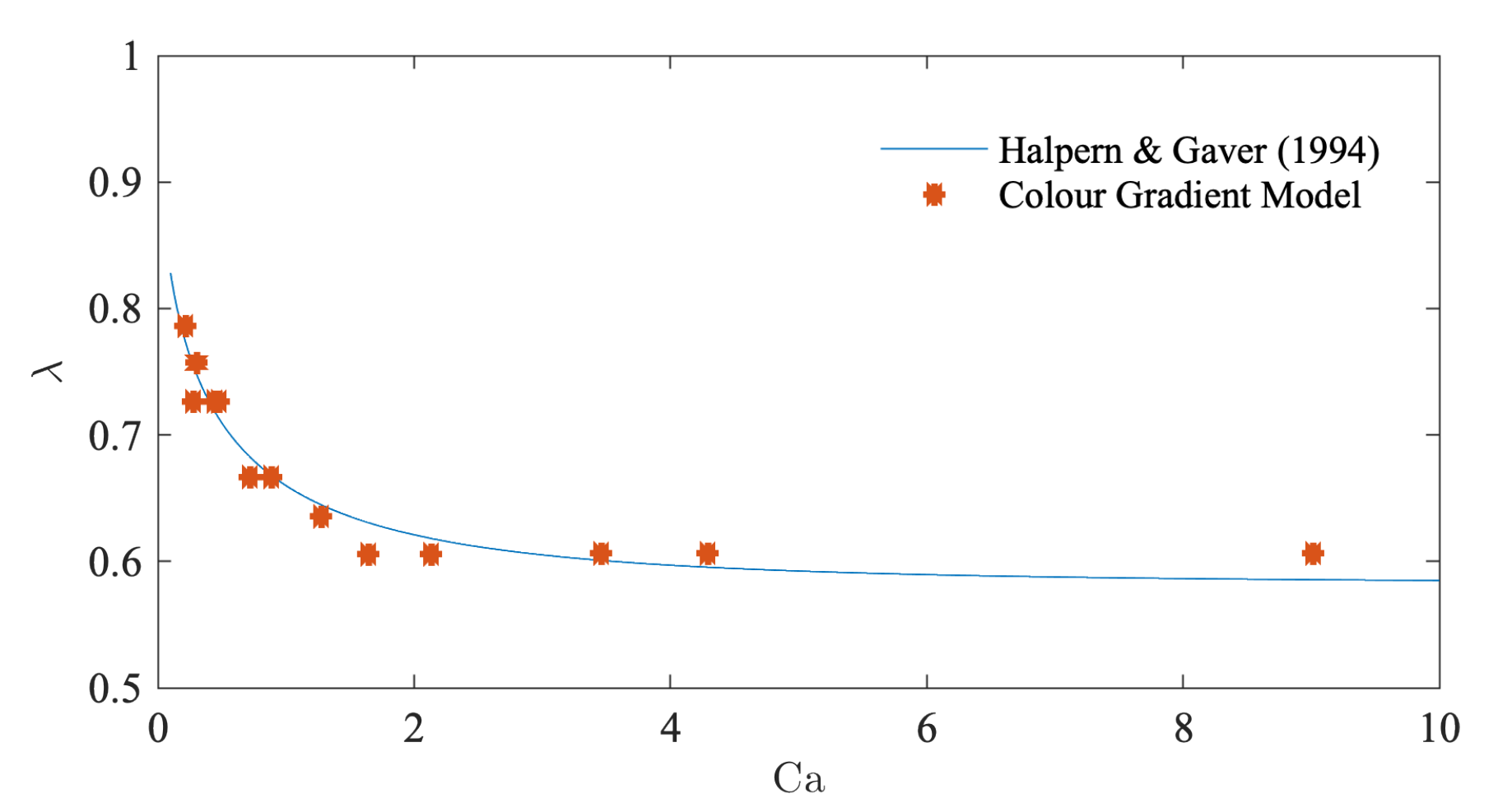
3.3. Capillary Fingering
4. Engineering Applications
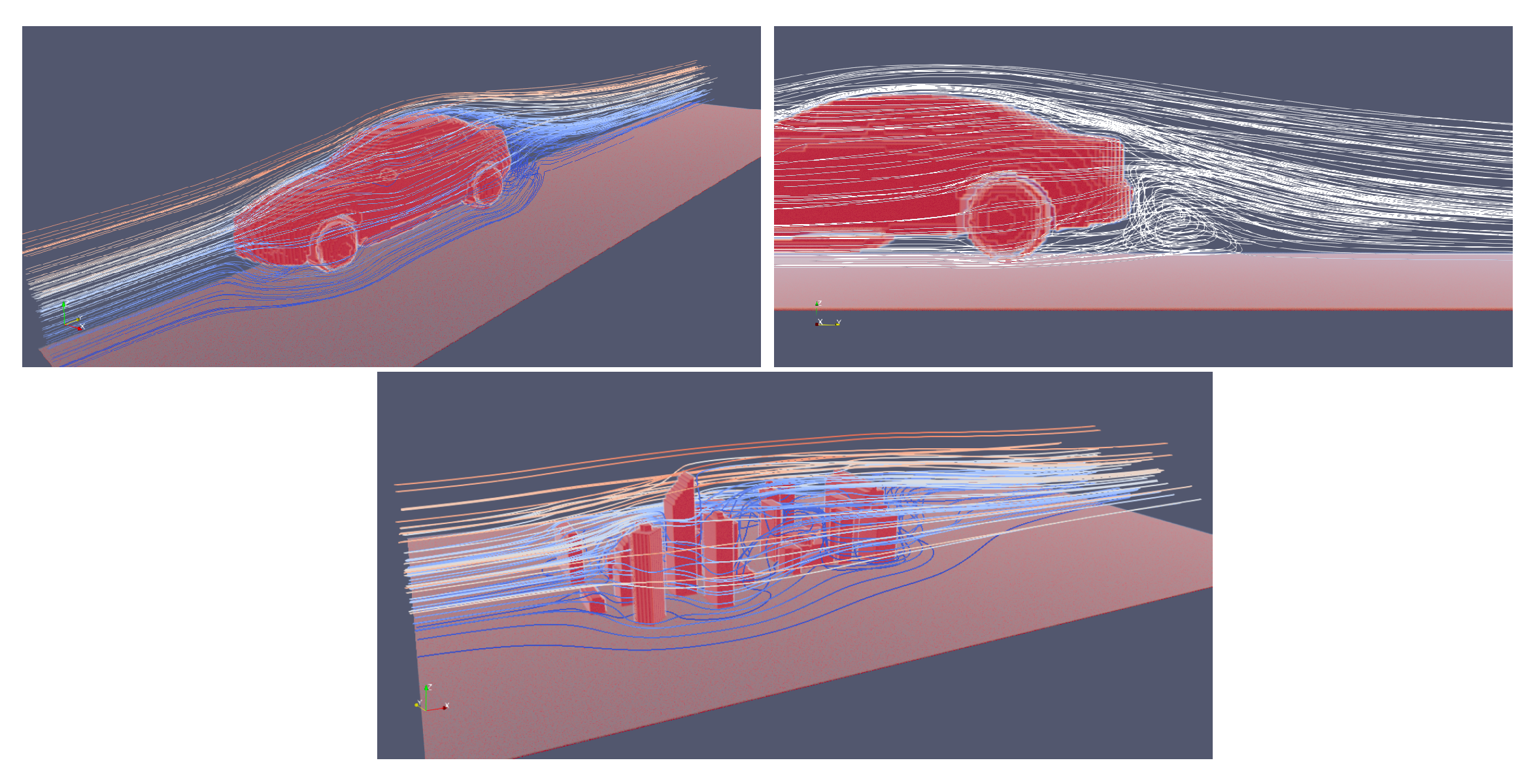
4.1. Single Phase Flow
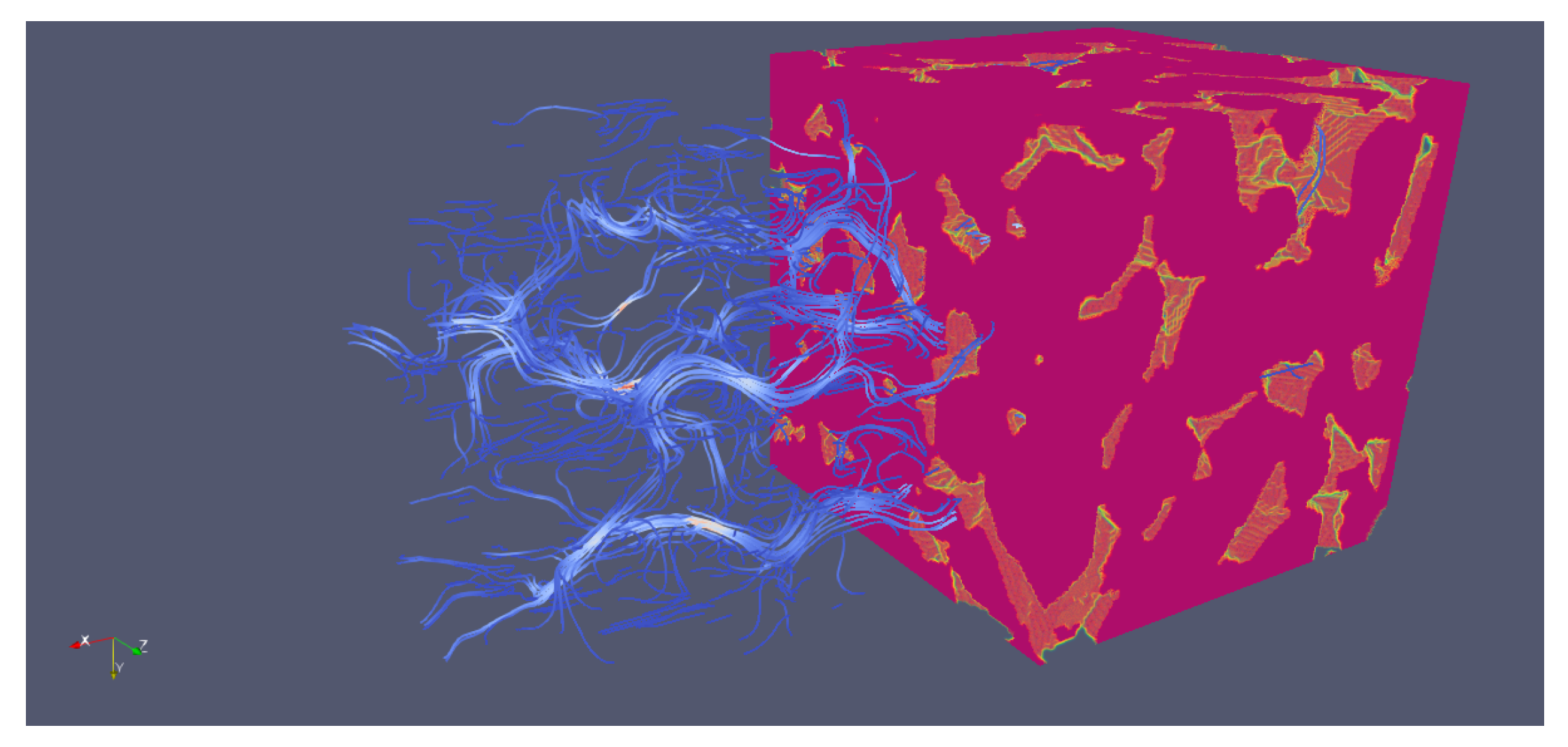
4.2. Simulation of Single-Phase Flow in Porous Media with Sparse Data Storage
4.3. Two-Phase Flow with Sparse Data Storage for Porous Medium
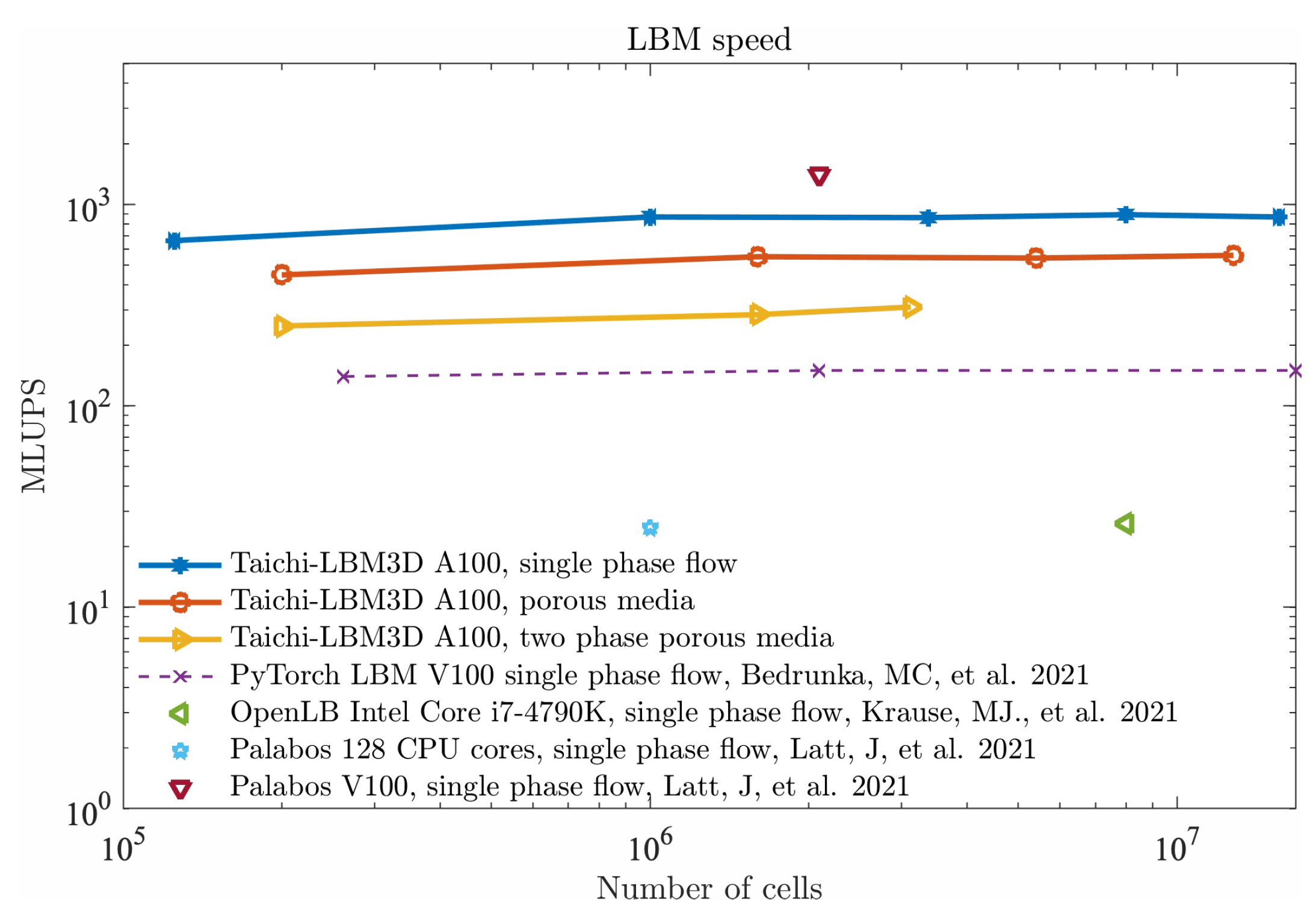
4.4. Performance Tests on Parallel Platforms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CPU | Central processing unit |
| GPU | Graphics processing unit |
| CFD | Computational fluid dynamics |
| BGK | Bhatnagar–Gross–Krook |
| OpenGL | Open Graphics Library |
| CUDA | Compute unified device architecture |
| LBM | Lattice Boltzmann method |
| HPC | High performance computing |
| MRT | Multiple-relaxation-time |
| MLUPS | Million lattice updates per second |
| D3Q19 | Three-dimensional lattice stencil with 19 discrete velocity directions in each node |
References
- Higuera, F.J.; Jiménez, J. Boltzmann approach to lattice gas simulations. EPL Europhys. Lett. 1989, 9, 663. [Google Scholar] [CrossRef]
- McNamara, G.R.; Zanetti, G. Use of the Boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 1988, 61, 2332. [Google Scholar] [CrossRef] [PubMed]
- Benzi, R.; Succi, S.; Vergassola, M. The lattice Boltzmann equation: Theory and applications. Phys. Rep. 1992, 222, 145–197. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef] [Green Version]
- Frisch, U.; Hasslacher, B.; Pomeau, Y. Lattice-gas automata for the Navier–Stokes equation. Phys. Rev. Lett. 1986, 56, 1505. [Google Scholar] [CrossRef] [Green Version]
- Chen, H.; Chen, S.; Matthaeus, W.H. Recovery of the Navier–Stokes equations using a lattice-gas Boltzmann method. Phys. Rev. A 1992, 45, R5339. [Google Scholar] [CrossRef]
- Ladd, A.J. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 1. Theoretical foundation. J. Fluid Mech. 1994, 271, 285–309. [Google Scholar] [CrossRef] [Green Version]
- d’Humières, D.; Lallemand, P.; Frisch, U. Lattice gas models for 3D hydrodynamics. EPL Europhys. Lett. 1986, 2, 291. [Google Scholar] [CrossRef]
- Higuera, F.; Succi, S.; Benzi, R. Lattice gas dynamics with enhanced collisions. EPL Europhys. Lett. 1989, 9, 345. [Google Scholar] [CrossRef]
- Qian, Y.H.; d’Humières, D.; Lallemand, P. Lattice BGK models for Navier–Stokes equation. EPL Europhys. Lett. 1992, 17, 479. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 1954, 94, 511. [Google Scholar] [CrossRef]
- d’Humières, D. Multiple–relaxation–time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. Lond. Ser. Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef] [PubMed]
- Lallemand, P.; Luo, L.S. Theory of the lattice Boltzmann method: Dispersion, dissipation, isotropy, Galilean invariance, and stability. Phys. Rev. E 2000, 61, 6546. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gunstensen, A.K.; Rothman, D.H.; Zaleski, S.; Zanetti, G. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 1991, 43, 4320. [Google Scholar] [CrossRef]
- Grunau, D.; Chen, S.; Eggert, K. A lattice Boltzmann model for multiphase fluid flows. Phys. Fluids A Fluid Dyn. 1993, 5, 2557–2562. [Google Scholar] [CrossRef] [Green Version]
- Lishchuk, S.; Care, C.; Halliday, I. Lattice Boltzmann algorithm for surface tension with greatly reduced microcurrents. Phys. Rev. E 2003, 67, 036701. [Google Scholar] [CrossRef]
- Latva-Kokko, M.; Rothman, D.H. Diffusion properties of gradient-based lattice Boltzmann models of immiscible fluids. Phys. Rev. E 2005, 71, 056702. [Google Scholar] [CrossRef]
- Ahrenholz, B.; Tölke, J.; Lehmann, P.; Peters, A.; Kaestner, A.; Krafczyk, M.; Durner, W. Prediction of capillary hysteresis in a porous material using lattice-Boltzmann methods and comparison to experimental data and a morphological pore network model. Adv. Water Resour. 2008, 31, 1151–1173. [Google Scholar] [CrossRef]
- Swift, M.R.; Osborn, W.; Yeomans, J. Lattice Boltzmann simulation of nonideal fluids. Phys. Rev. Lett. 1995, 75, 830. [Google Scholar] [CrossRef] [Green Version]
- Swift, M.R.; Orlandini, E.; Osborn, W.; Yeomans, J. Lattice Boltzmann simulations of liquid-gas and binary fluid systems. Phys. Rev. E 1996, 54, 5041. [Google Scholar] [CrossRef]
- Inamuro, T.; Konishi, N.; Ogino, F. A Galilean invariant model of the lattice Boltzmann method for multiphase fluid flows using free-energy approach. Comput. Phys. Commun. 2000, 129, 32–45. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shan, X.; Chen, H. Simulation of nonideal gases and liquid-gas phase transitions by the lattice Boltzmann equation. Phys. Rev. E 1994, 49, 2941. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sbragaglia, M.; Benzi, R.; Biferale, L.; Succi, S.; Sugiyama, K.; Toschi, F. Generalized lattice Boltzmann method with multirange pseudopotential. Phys. Rev. E 2007, 75, 026702. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Luo, K.; Li, X. Lattice Boltzmann modeling of multiphase flows at large density ratio with an improved pseudopotential model. Phys. Rev. E 2013, 87, 053301. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Chen, S.; Zhang, R. A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh–Taylor instability. J. Comput. Phys. 1999, 152, 642–663. [Google Scholar] [CrossRef]
- Inamuro, T.; Ogata, T.; Tajima, S.; Konishi, N. A lattice Boltzmann method for incompressible two-phase flows with large density differences. J. Comput. Phys. 2004, 198, 628–644. [Google Scholar] [CrossRef]
- Li, Q.; Luo, K.; Gao, Y.; He, Y. Additional interfacial force in lattice Boltzmann models for incompressible multiphase flows. Phys. Rev. E 2012, 85, 026704. [Google Scholar] [CrossRef] [Green Version]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E.M. The Lattice Boltzmann Method; Springer: Berlin/Heidelberg, Germany, 2017; Volume 10, pp. 4–15. [Google Scholar]
- Succi, S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Latt, J.; Malaspinas, O.; Kontaxakis, D.; Parmigiani, A.; Lagrava, D.; Brogi, F.; Belgacem, M.B.; Thorimbert, Y.; Leclaire, S.; Li, S.; et al. Palabos: Parallel lattice Boltzmann solver. Comput. Math. Appl. 2021, 81, 334–350. [Google Scholar] [CrossRef]
- Krause, M.J.; Kummerländer, A.; Avis, S.J.; Kusumaatmaja, H.; Dapelo, D.; Klemens, F.; Gaedtke, M.; Hafen, N.; Mink, A.; Trunk, R.; et al. OpenLB—Open source lattice Boltzmann code. Comput. Math. Appl. 2021, 81, 258–288. [Google Scholar] [CrossRef]
- Feichtinger, C.; Götz, J.; Donath, S.; Iglberger, K.; Rüde, U. WaLBerla: Exploiting massively parallel systems for lattice Boltzmann simulations. In Parallel Computing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 241–260. [Google Scholar]
- Huang, C.; Shi, B.; Guo, Z.; Chai, Z. Multi-GPU based lattice Boltzmann method for hemodynamic simulation in patient-specific cerebral aneurysm. Commun. Comput. Phys. 2015, 17, 960–974. [Google Scholar] [CrossRef]
- Hu, Y.; Li, T.M.; Anderson, L.; Ragan-Kelley, J.; Durand, F. Taichi: A language for high-performance computation on spatially sparse data structures. ACM Trans. Graph. 2019, 38, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Bedrunka, M.C.; Wilde, D.; Kliemank, M.; Reith, D.; Foysi, H.; Krämer, A. Lettuce: Pytorch-based lattice boltzmann framework. In Proceedings of the International Conference on High Performance Computing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 40–55. [Google Scholar]
- Hu, Y.; Anderson, L.; Li, T.M.; Sun, Q.; Carr, N.; Ragan-Kelley, J.; Durand, F. Difftaichi: Differentiable programming for physical simulation. arXiv 2019, arXiv:1910.00935. [Google Scholar]
- Yang, J.Y.; Yang, S.C.; Chen, Y.N.; Hsu, C.A. Implicit weighted ENO schemes for the three-dimensional incompressible Navier–Stokes equations. J. Comput. Phys. 1998, 146, 464–487. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Badia, S.; Codina, R. A pseudo-compressible variational multiscale solver for turbulent incompressible flows. Comput. Mech. 2016, 58, 1051–1069. [Google Scholar] [CrossRef] [Green Version]
- Halpern, D.; Gaver, D., III. Boundary element analysis of the time-dependent motion of a semi-infinite bubble in a channel. J. Comput. Phys. 1994, 115, 366–375. [Google Scholar] [CrossRef]
- Bacciaglia, A.; Ceruti, A.; Liverani, A. A systematic review of voxelization method in additive manufacturing. Mech. Ind. 2019, 20, 630. [Google Scholar] [CrossRef] [Green Version]
- Thorpe, D.B. Cad2Vox. 2022. Available online: https://github.com/bjthorpe/Cad2vox (accessed on 1 June 2022).
- Yang, L.; Yang, J.; Boek, E.; Sakai, M.; Pain, C. Image-based simulations of absolute permeability with massively parallel pseudo-compressible stabilised finite element solver. Comput. Geosci. 2019, 23, 881–893. [Google Scholar] [CrossRef]
- Nillama, L.B.A.; Yang, J.; Yang, L. An explicit stabilised finite element method for Navier–Stokes-Brinkman equations. J. Comput. Phys. 2022, 457, 111033. [Google Scholar] [CrossRef]


| Test Cases | NVIDIA A100 | AMD Radeon Pro 5300 | 3.3 GHz 6-Core Intel i5 12 Threads |
|---|---|---|---|
| Memory | 40 GB | 4 GB | 64 GB |
| 662 | 189 | 13.6 | |
| 870 | 192 | 13.5 | |
| 861 | ∖ | 13.5 | |
| 900 | ∖ | 13.5 | |
| 890 | ∖ | 13.5 | |
| 1-phase | 449 | 110 | 12.1 |
| 1-phase | 550 | 115 | 14.5 |
| 1-phase | 550 | ∖ | 14.5 |
| 1-phase | 550 | ∖ | 14.5 |
| 2-phase | 250 | 70 | |
| 2-phase | 283 | ∖ | 7.7 |
| 2-phase | 310 | ∖ | 7.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, J.; Xu, Y.; Yang, L. Taichi-LBM3D: A Single-Phase and Multiphase Lattice Boltzmann Solver on Cross-Platform Multicore CPU/GPUs. Fluids 2022, 7, 270. https://doi.org/10.3390/fluids7080270
Yang J, Xu Y, Yang L. Taichi-LBM3D: A Single-Phase and Multiphase Lattice Boltzmann Solver on Cross-Platform Multicore CPU/GPUs. Fluids. 2022; 7(8):270. https://doi.org/10.3390/fluids7080270
Chicago/Turabian StyleYang, Jianhui, Yi Xu, and Liang Yang. 2022. "Taichi-LBM3D: A Single-Phase and Multiphase Lattice Boltzmann Solver on Cross-Platform Multicore CPU/GPUs" Fluids 7, no. 8: 270. https://doi.org/10.3390/fluids7080270
APA StyleYang, J., Xu, Y., & Yang, L. (2022). Taichi-LBM3D: A Single-Phase and Multiphase Lattice Boltzmann Solver on Cross-Platform Multicore CPU/GPUs. Fluids, 7(8), 270. https://doi.org/10.3390/fluids7080270






