Numerical Investigation of 3D Flow Properties around Finite Emergent Vegetation by Using the Two-Phase Volume of Fluid (VOF) Modeling Technique
Abstract
1. Introduction
2. The Volume of Fluid Model (Air–Water) Two-Phase Flow
- (a)
- when the qth fluid fills the whole cell demonstrating that the cell is filled with water.
- (b)
- when the qth fluid does not occupy the whole cell means that the cell is filled with air.
- (c)
- indicates that where the cell has an interface between the qth fluid, i.e., free surface between air and water layer.
3. Turbulence Modeling (RANS)
4. Material and Methods
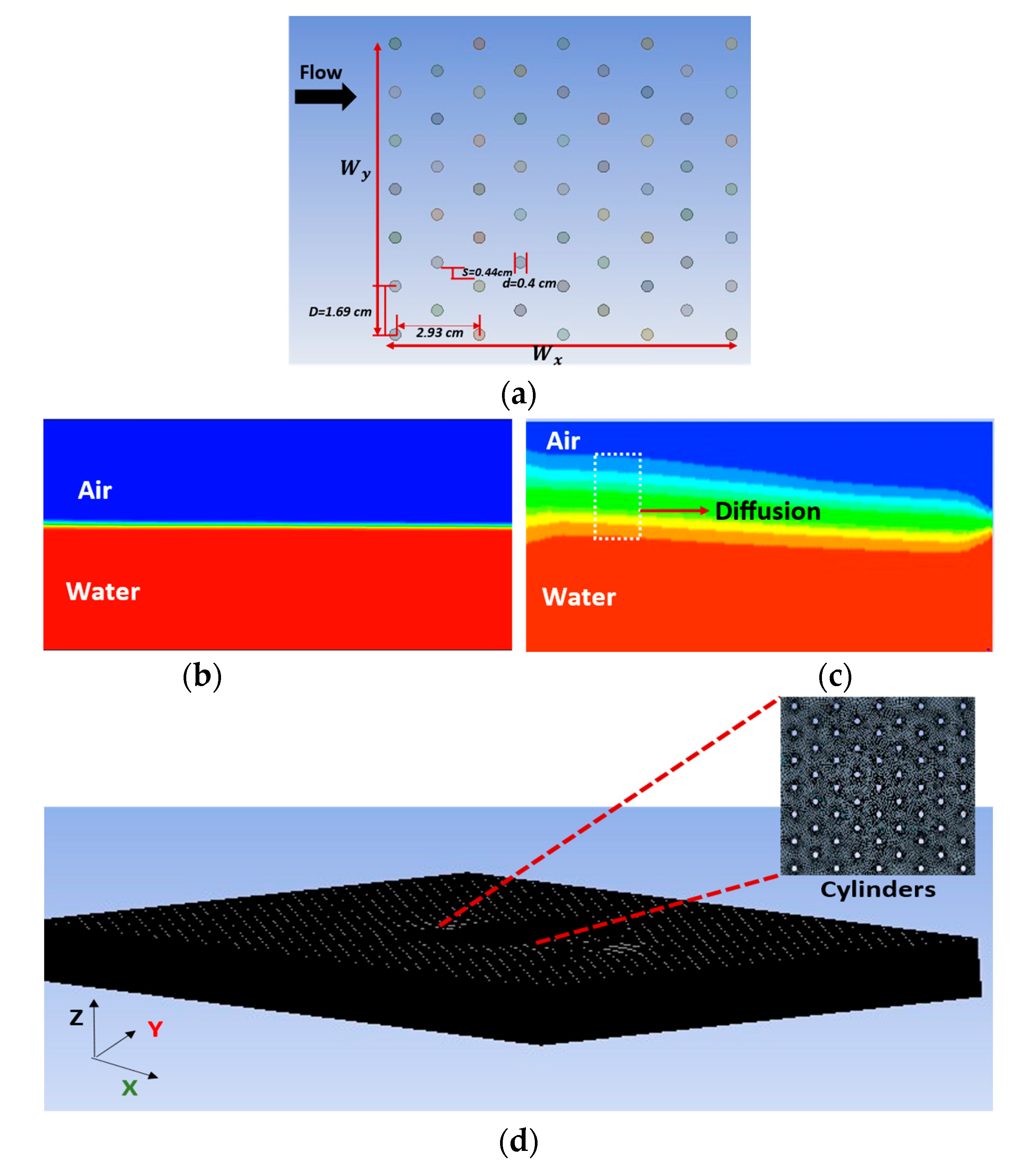
4.1. Conditions for Numerical Simulation
4.1.1. Flow Conditions
4.1.2. Vegetation Conditions
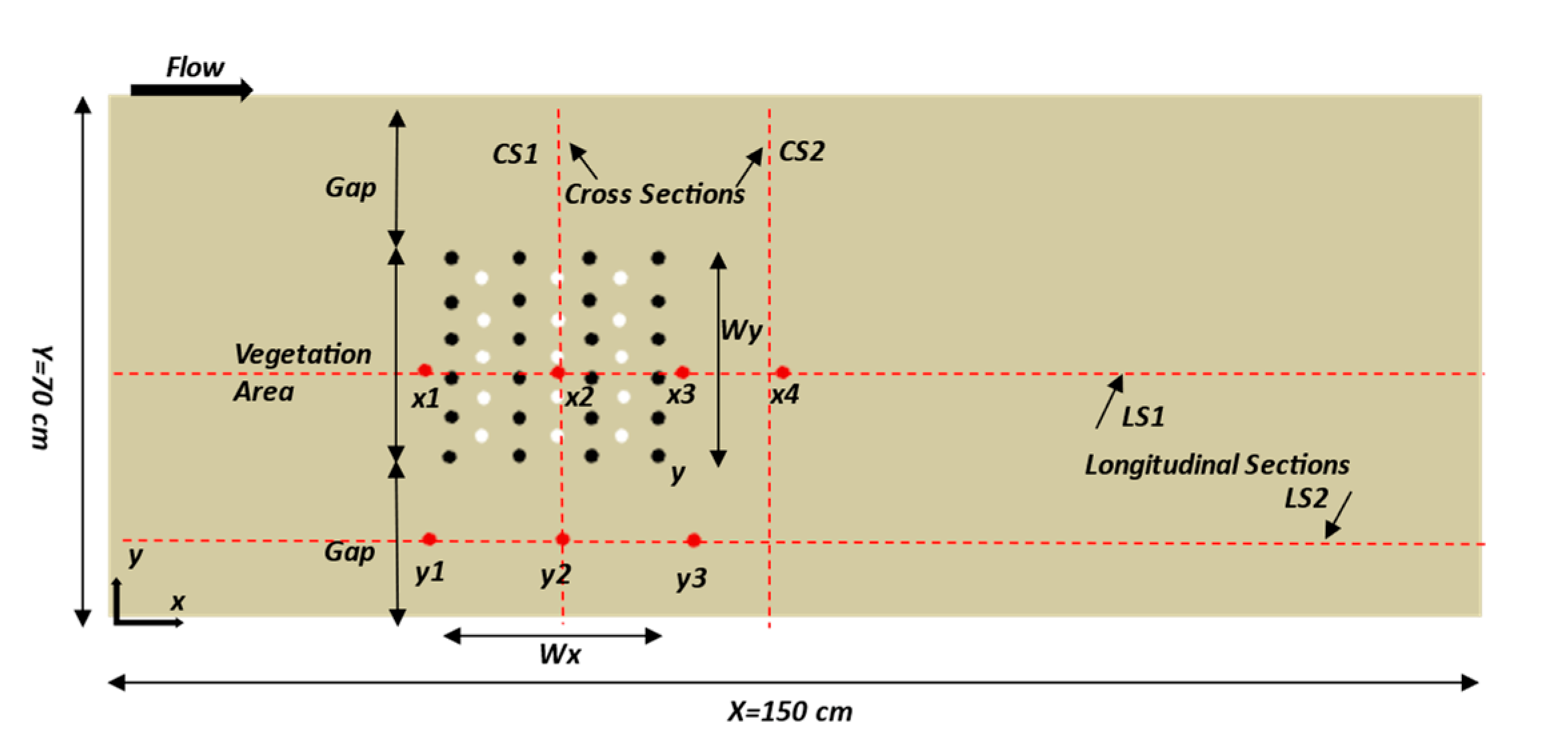
4.1.3. Measurement Locations
4.2. Preprocessing and Postprocessing
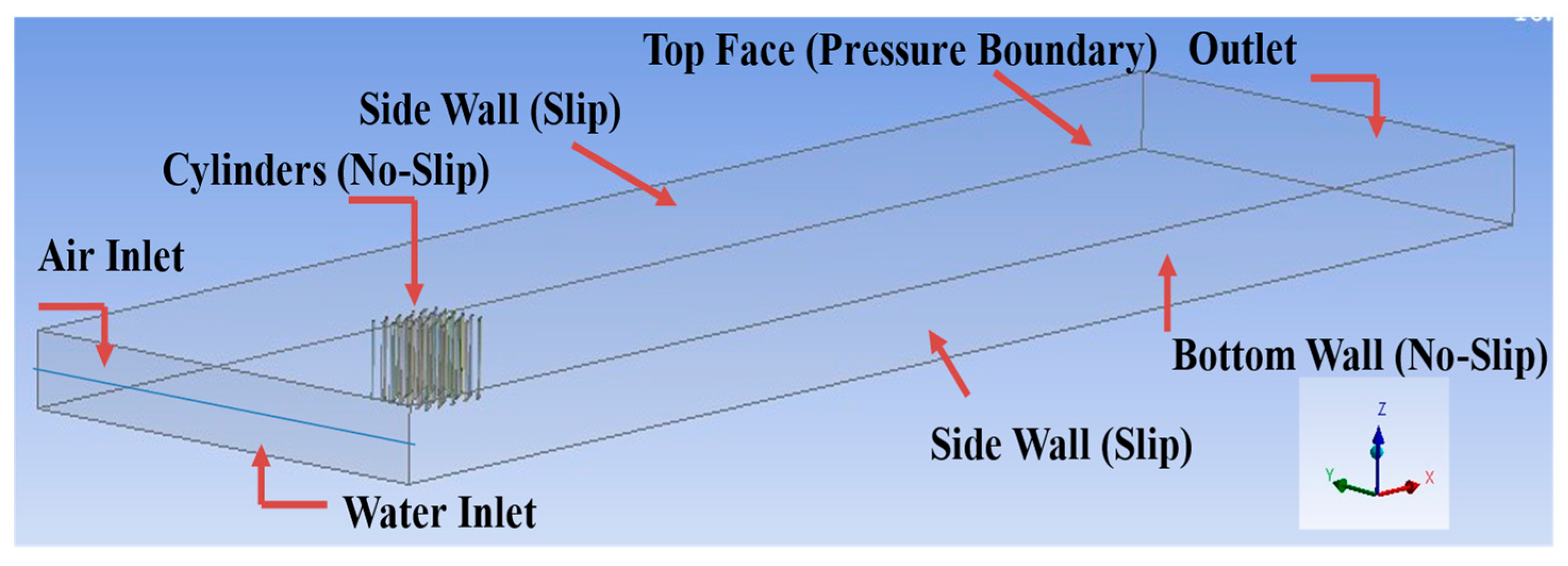
4.2.1. Preprocessing
4.2.2. Postprocessing
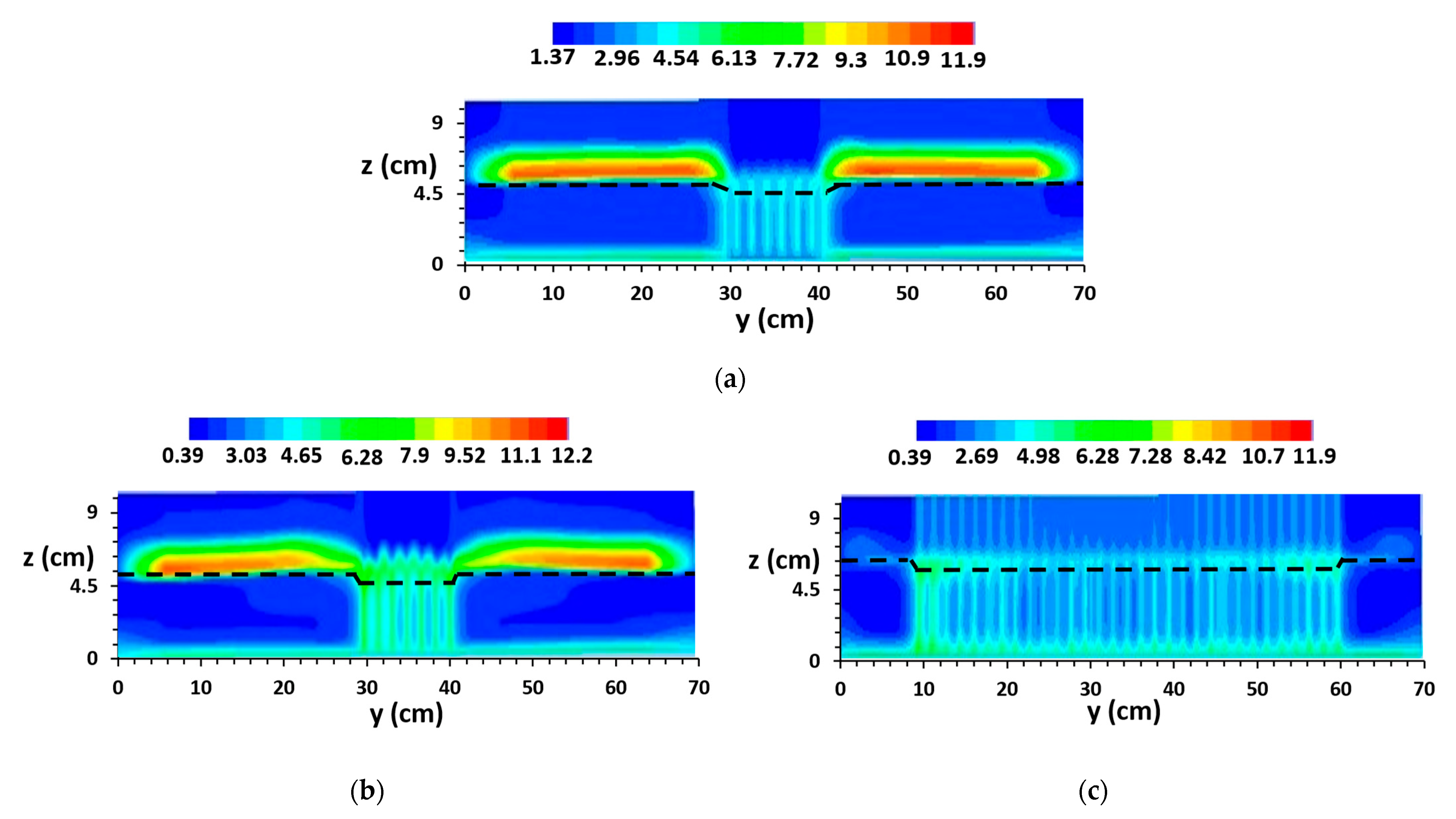
5. Results and Discussion
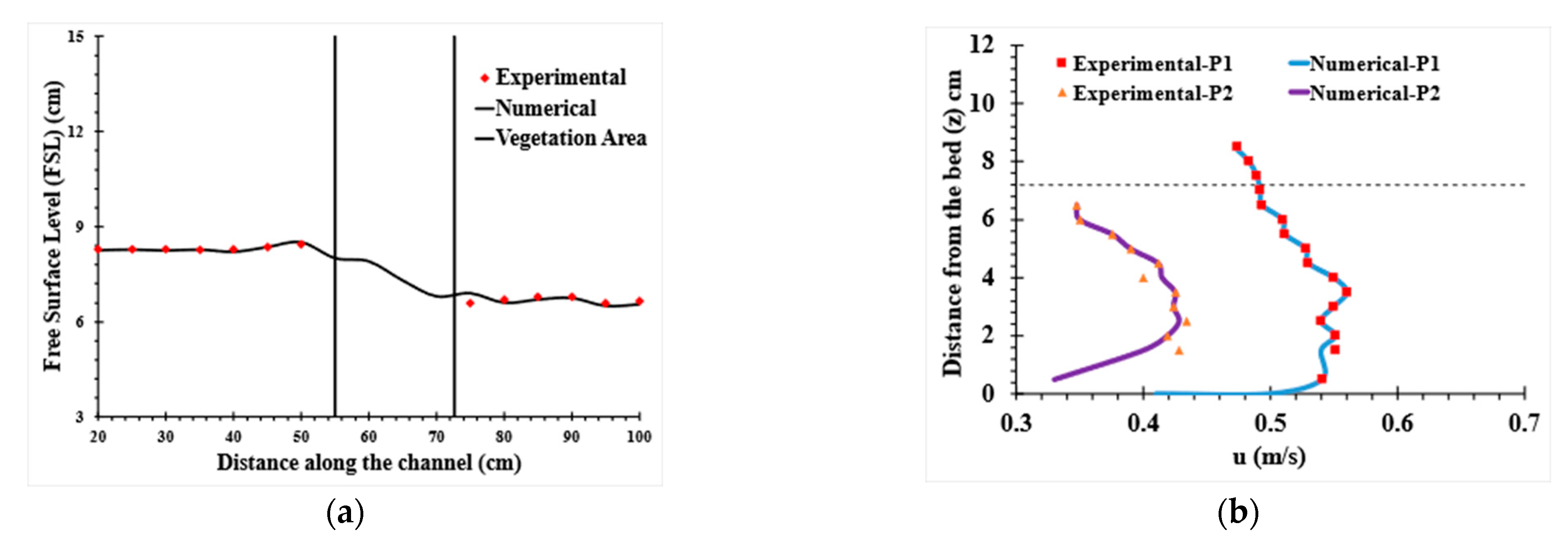
5.1. Model Validation
5.2. Flow Characteristics
5.2.1. Free Surface Profiles
5.2.2. Velocity Distribution of Streamwise Velocity Profiles
5.2.3. Velocity Profiles along the Longitudinal Sections
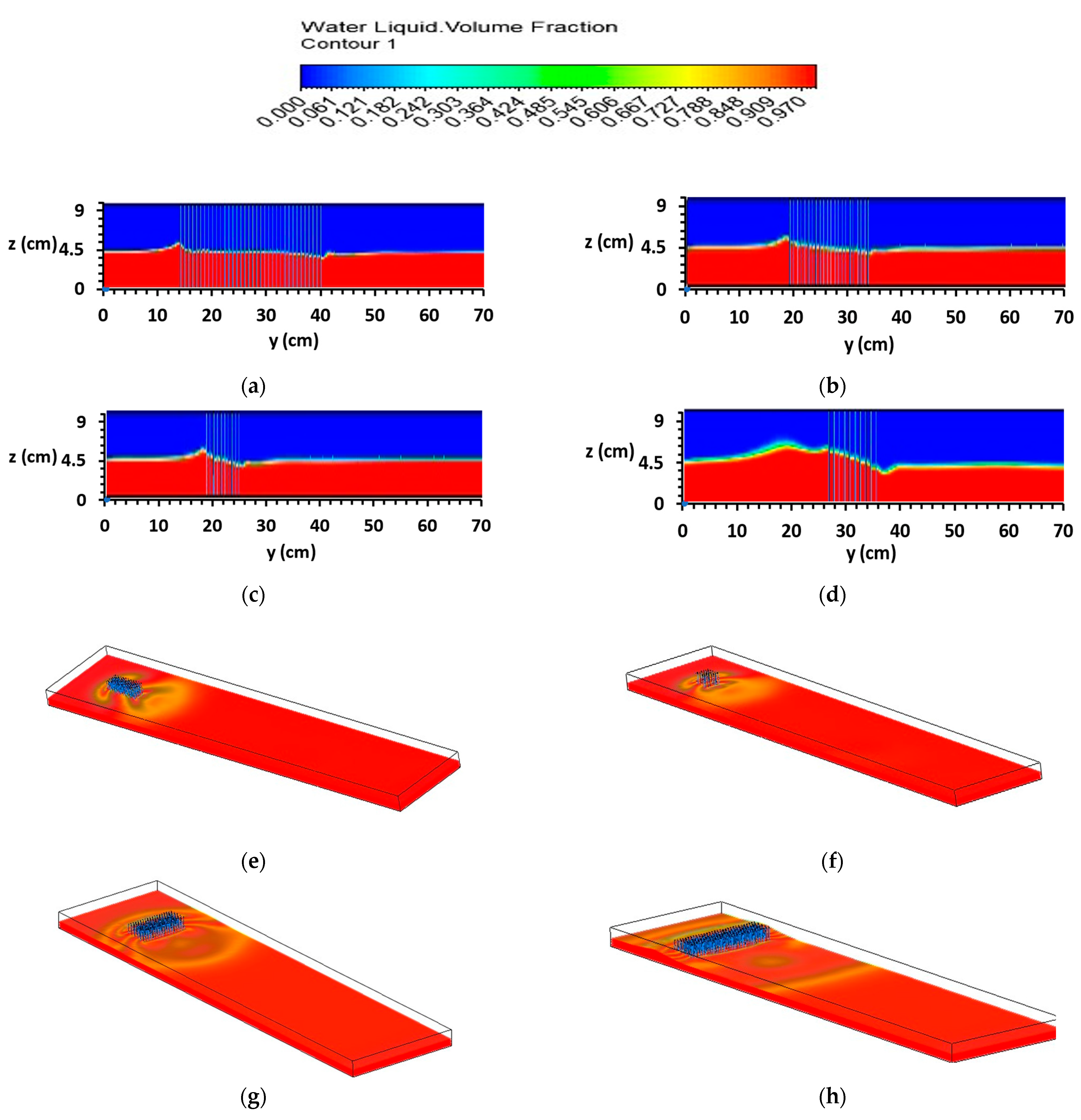
5.2.4. Simulated Contour Plot Distribution of Streamwise Velocity
5.2.5. Flow Movement of Water and Air Phase
5.2.6. Turbulent Intensity Distribution of Air–Water Phase
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shuto, N. The effectiveness and limit of tsunami control forests. Coast. Eng. Jpn. 1987, 30, 143–153. [Google Scholar] [CrossRef]
- Fadly, U.; Murakami, K. Study on reducing tsunami inundation energy by the modification of topography based on local wisdom. J. Jpn. Soc. Civ. Eng. Ser. B3 2013, 68, 66–71. [Google Scholar] [CrossRef]
- Kathiresan, K.; Rajendran, N. Coastal mangrove forests mitigated tsunami. Estuar. Coast. Shelf Sci. 2005, 65, 601–606. [Google Scholar] [CrossRef]
- Yanagisawa, H.; Koshimura, S.; Goto, K.; Miyagi, T.; Imamura, F.; Ruangrassamee, A.; Tanavud, C. The reduction effects of mangrove forest on a tsunami based on field surveys at Pakarang Cape, Thailand and numerical analysis. Estuar. Coast Shelf Sci. 2009, 81, 27–37. [Google Scholar] [CrossRef]
- Harada, K.; Kawata, Y. Study on tsunami reduction effect of coastal forest due to forest growth. Ann. Disaster Prev. Res. Inst. 2005, 48, 161–165. [Google Scholar]
- Irtem, E.; Gedik, N.; Kabdasli, M.S.; Yasa, N.E. Coastal Forest effects on tsunami run-up heights. Ocean Eng. 2009, 36, 313–320. [Google Scholar] [CrossRef]
- Tanaka, N. Vegetation bio shields for tsunami mitigation: Review of effectiveness, limitations, construction, and sustainable management. Landsc. Ecol. Eng. 2009, 5, 71–79. [Google Scholar] [CrossRef]
- Tanaka, N.; Jinadasa, K.; Mowjood, M.I.M.; Fasly, M.S.M. Coastal vegetation planting projects for tsunami disaster mitigation: Effectiveness evaluation of new establishments. Landsc. Ecol. Eng. 2011, 7, 127–135. [Google Scholar] [CrossRef]
- Ismail, H.; Abd Wahab, A.K.; Alias, N. Determination of man- grove forest performance in reducing tsunami run-up using physical models. Nat. Hazards 2012, 63, 939–963. [Google Scholar] [CrossRef]
- Thuy, N.B.; Tanimoto, K.; Tanaka, N. Flow and potential force due to runup tsunami around a coastal forest with a gap, Experiments and numerical simulations. Sci. Tsunami Hazards 2010, 29, 43–69. [Google Scholar]
- Iimura, K.; Tanaka, N. Numerical simulation estimating effects of tree density distribution in coastal forest on tsunami mitigation. Ocean Eng. 2012, 54, 223–232. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Undular hydraulic jump formation and energy loss in a flow through emergent vegetation of varying thickness and density. Ocean Eng. 2017, 141, 308–325. [Google Scholar] [CrossRef]
- Tanaka, N. Effectiveness and limitations of coastal forest in large tsunami: Conditions of Japanese pine trees on coastal sand dunes in tsunami caused by Great East Japan Earthquake. J. Jpn. Soc. Civil. Eng. Ser. B1 2012, 68, II_7–II_15. [Google Scholar] [CrossRef]
- Rashedunnabi, A.H.M.; Tanaka, N. Effectiveness of double-layer rigid vegetation in reducing the velocity and fluid force of a tsunami inundation behind the vegetation. Ocean Eng. 2020, 201, 107142. [Google Scholar] [CrossRef]
- Iimura, K.; Tanaka, N. Dangerous zone formation behind finite-length coastal forest for tsunami mitigation. J. Earthq. Tsunami 2013, 7, 1350034. [Google Scholar] [CrossRef]
- Pasha, G.A.; Tanaka, N. Effectiveness of Finite Length Inland Forest in Trapping Tsunami-Borne Wood Debris. J. Earthq. Tsunami 2016, 10, 1650008. [Google Scholar] [CrossRef]
- Thuy, N.B.; Tanimoto, K.; Tanaka, N.; Harada, K.; Iimura, K. Effect of open gap in coastal forest on tsunami run-up-investigations by experiment and numerical simulation. Ocean Eng. 2009, 36, 1258–1269. [Google Scholar] [CrossRef]
- Nandasena, N.A.K.; Tanaka, N.; Tanimoto, K. Perspective of coastal vegetation patches with topography variations for tsunami protection in 2D numerical modeling. Annu. J. Hydraul. Eng. JSCE 2008, 52, 138. [Google Scholar] [CrossRef][Green Version]
- Vandenbruwaene, W.; Temmerman, S.; Bouma, T.J.; Klaassen, P.C.; De Vries, M.B.; Callaghan, D.P.; Van Steeg, P.; Dekker, F.; Van Duren, L.A.; Martini, E.; et al. Flow interaction with dynamic vegetation patches: Implications for bio geomorphic evolution of a tidal landscape. J. Geophys. Res. Earth Surf. 2011, 116, F01008. [Google Scholar] [CrossRef]
- Irish, J.L.; Weiss, R.; Yang, Y.; Song, Y.K.; Zainali, A.; Marivela Colmenarejo, R. Laboratory experiments of tsunami run-up and withdrawal in patchy coastal forest on a steep beach. Nat. Hazards 2014, 74, 1933–1949. [Google Scholar] [CrossRef]
- Ghani, U.; Anjum, N.; Pasha, G.A.; Ahmad, M. Numerical investigation of the flow characteristics through discontinuous and layered vegetation patches of finite width in an open channel. Environ. Fluid Mech 2019, 19, 1469–1495. [Google Scholar] [CrossRef]
- Hasnain, T.; Usman, G.; Naveed, A.; Ghufran, A.P. 3D Numerical modeling of flow characteristics in an open channel having in-line circular vegetation patches with varying density under submerged and emergent flow conditions. J. Hydrol. Hydromech. 2022, 70, 128–144. [Google Scholar]
- Muhammad, A.; Usman, G.; Naveed, A.; Ghufran, A.P.; Muhammad, K.U.; Afzal, A. Investigating the flow hydrodynamics in a compound channel with layered vegetated floodplains. Civ. Eng. J. 2020, 6, 860–876. [Google Scholar]
- Maji, S.; Pal, D.; Hanmaiahgari, P.R.; Gupta, U.P. Hydrodynamics and turbulence in emergent and sparsely vegetated open channel flow. Environ. Fluid Mech. 2017, 17, 853–877. [Google Scholar] [CrossRef]
- Stoesser, T.; Kim, S.J.; Diplas, P. Turbulent Flow through Idealized Emergent Vegetation. J. Hydraul. Eng. 2010, 136, 1003–1017. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. Citeseer 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Chen, Q.; Dai, G.; Liu, H. Volume of Fluid Model for Turbulence Numerical Simulation of Stepped Spillway Overflow. J. Hydraul. Eng 2002, 128, 683–688. [Google Scholar] [CrossRef]
- Xiangju, C.; Chen, Y.; Luo, L. Numerical simulation of air-water two-phase flow over stepped spillways. Sci. China Ser. E Technol. Sci. 2006, 49, 674–684. [Google Scholar]
- Zhenwei, M.; Zhang, Z.; Zhao, T. Numerical simulation of 3-D flow field of spillway based on VOF method. Procedia Eng. 2012, 28, 808–812. [Google Scholar] [CrossRef]
- Eghbalzadeh, A.; Javan, M. Comparison of Mixture and VOF models for numerical simulation of Air-Entrainment in skimming flow over stepped spillways. Procedia Eng. 2012, 28, 657–660. [Google Scholar] [CrossRef]
- Zhan, J.; Zhang, J.; Gong, Y. Numerical investigation of air-entrainment in skimming flow over stepped spillways. Theory Appl. Mech. Lett. 2016, 6, 139–142. [Google Scholar] [CrossRef]
- Ramamurthy, A.S.; Qu, J.; Vo, D. Volume of fluid model for an open channel flow problem. Can. J. Civ. Eng 2005, 32, 996–1001. [Google Scholar]
- Patel, T.; Gill, L. Volume of fluid model applied to curved open channel flows. WIT Trans. Eng. Sci 2006, 52, 361–369. [Google Scholar]
- Carrier, G.; Wu, T.T.; Yeh, H. Tsunami run-up and draw-down on a plane beach. J. Fluid Mech. 2003, 475, 79–99. [Google Scholar] [CrossRef]
- Yang, Y.; Irish, J.L.; Weiss, R. Impact of patchy vegetation on tsunami dynamics. J. Waterw. Port C-ASCE 2017, 143, 04017005. [Google Scholar] [CrossRef]
- Zainali, A.; Marivela, R.; Weiss, R.; Yang, Y.; Irish, J.L. Numerical simulation of nonlinear long waves in the presence of discontinuous coastal vegetation. Mar. Geol. 2018, 396, 142–149. [Google Scholar] [CrossRef]
- Ali, H.M.; El-Gendy, M.M.; Mirdan, A.M.H.; Ali, A.A.M.; Abdelhaleem, F.S.F. Minimizing downstream scour due to submerged hydraulic jump using corrugated aprons. Ain. Shams Eng. J. 2014, 5, 1059–1069. [Google Scholar] [CrossRef]
- Fritz, H.M.; Borrero, J.C.; Synolakis, C.E.; Yoo, J. 2004 Indian Ocean tsunami flow velocity measurements from survivor videos. Geophys. Res. Lett. 2006, 33, L24605. [Google Scholar] [CrossRef]
- Tanaka, N.; Yagisawa, J.; Yasuda, S. Breaking pattern and critical breaking condition of Japanese pine trees on coastal sand dunes in huge tsunami caused by Great East Japan Earthquake. Nat. Hazards 2013, 65, 423–442. [Google Scholar] [CrossRef]
- Salaheldin, T.M.; Imran, J.; Chaudhry, M.H. Numerical Modeling of Three-Dimensional Flow Field Around Circular Piers. J. Hydraul. Eng 2004, 130, 91–100. [Google Scholar] [CrossRef]
- Tanaka, N.; Yasuda, S.; Iimura, K.; Yagisawa, J. Combined effects of coastal forest and sea embankment on reducing the washout region of houses in the Great East Japan tsunami. J. Hydro–Environ. Res. 2014, 8, 270–280. [Google Scholar] [CrossRef]
- Lee, J.; Suh, J.; Sung, H.J.; Pettersen, B. Structures of turbulent open-channel flow in the presence of an air-water interface. J. Turbul. 2014, 13, N18. [Google Scholar] [CrossRef]
- Bayon, A.; Toro, J.P.; Bombardelli, F.A.; Matos, J.; Lopez-Jimenez, P.A. Influence of VOF technique, turbulence model and discretization scheme on the numerical simulation of the non-aerated, skimming flow in stepped spillways. J. Hydro-Environ. Res. 2017, 19, 137–149. [Google Scholar] [CrossRef]
- Naik, B.; Khatua, K.K.; Wright, N.; Sleigh, A.; Singh, P. Numerical modeling of converging compound channel flow. ISH J. Hydraul. Eng. 2018, 24, 285–297. [Google Scholar] [CrossRef]
- Fluent Inc User's Guide; Release 19.2; ANSYS, Inc.: Canonsburg, PA, USA, 2020.
- Okamoto, S.; Okamoto, T. Theoretical study of blockage effect of wind-tunnel on wake of two-dimensional flat plate normal to plane wall. Trans. Jpn. Soc. Aero. Space Sci. 1984, 27, 134–144. [Google Scholar]
- Okajima, A.; Yi, D.; Kimura, S.; Kiwata, T. The blockage effects for an oscillating rectangular cylinder at moderate Reynolds number. J. Wind Eng. Ind. Aerodyn. 1997, 69, 997–1011. [Google Scholar] [CrossRef]
- White, B.L.; Nepf, H.M. A vortex-based model of velocity and shear stress in a partially vegetated shallow channel. Water Resour. Res. 2007, 44, 1–15. [Google Scholar] [CrossRef]
- Raupach, M.R.; Finnigan, J.J.; Brunet, Y. Coherent eddies and turbulence in vegetation canopies: The mixing-layer analogy. Bound.-Layer Meteorol 1996, 78, 351–382. [Google Scholar] [CrossRef]
- Ricardo, A.M.; Koll, K.; Franca, M.J.; Schleiss, A.J.; Ferreira, R.M.L. The terms of turbulent kinetic energy budget within random arrays of emergent cylinders. Water Resour. Res 2014, 50, 4131–4148. [Google Scholar] [CrossRef]
- Savelsberg, R.; Van De Water, W. Turbulence of a free surface. Phys. Rev. Lett 2008, 100, 034501. [Google Scholar] [CrossRef]
- Cain, P. Measurements Within Self-Aereated Flow on Large Spilway. Ph.D. Thesis, University of Canterbury, Christchurch, New Zealand, 1978. [Google Scholar]
- Chanson, H. Air-water flows in water engineering and hydraulic structures. Basic processes and metrology. Dam. Eng. 2004, 1, 3–16. [Google Scholar]
- Baldy, S. A generation-dispersion modal of ambient and transient bubbles in the close vicinity of breaking waves. Geophys. Res. 1993, 98, 18. [Google Scholar] [CrossRef]
- Ma, G.F. Multiscale Numerical Study of Turbulent Flow and Bubble Entrainment in the Surf Zone. Ph.D. Thesis, University of Delaware, Newark, DE, USA, 2012. [Google Scholar]
- Thompson, E.; Piecuch, P.R.; Merrifield, C.G.; McCreary, M.A.; Firing, J.P. Turbulent flow field and air entrainment in laboratory plunging breaking waves. J. Geophys. Res. Ocean 2016, 121, 6762–6778. [Google Scholar] [CrossRef]
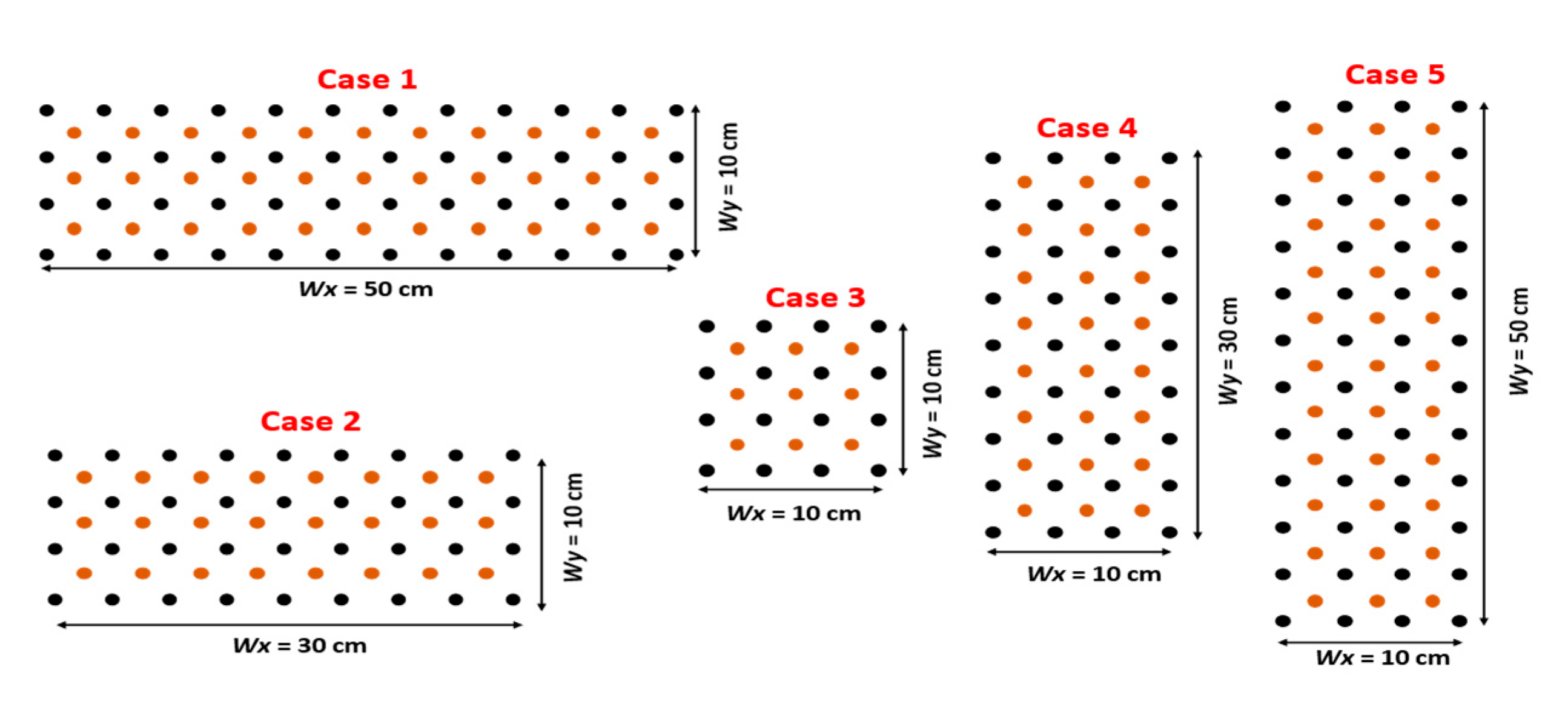

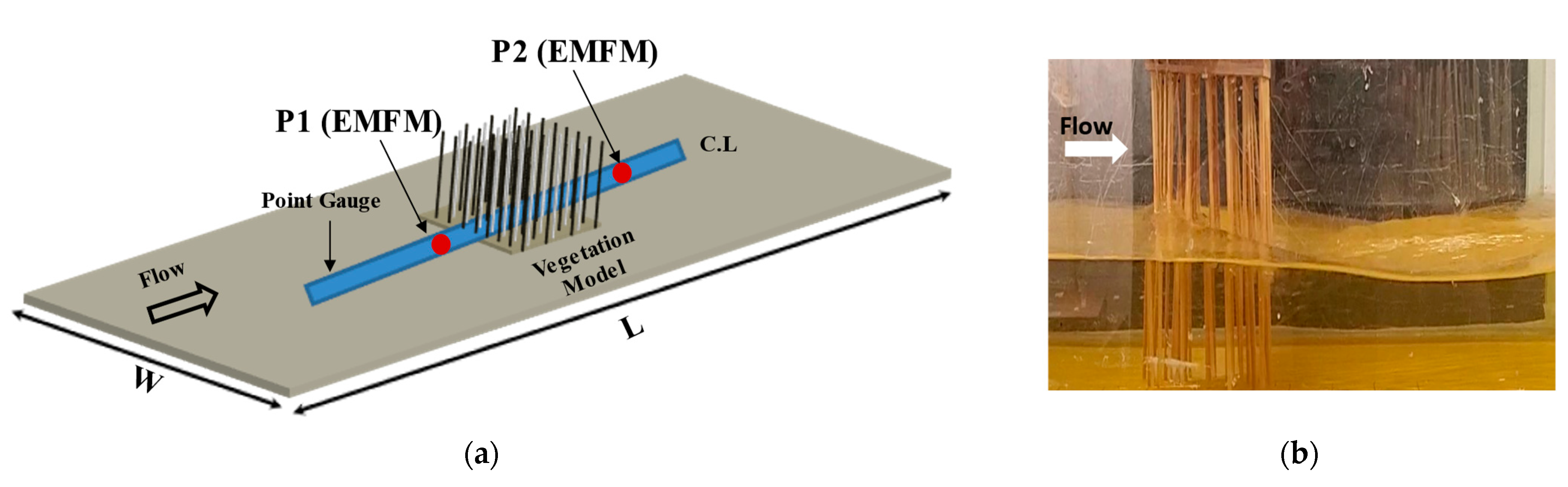
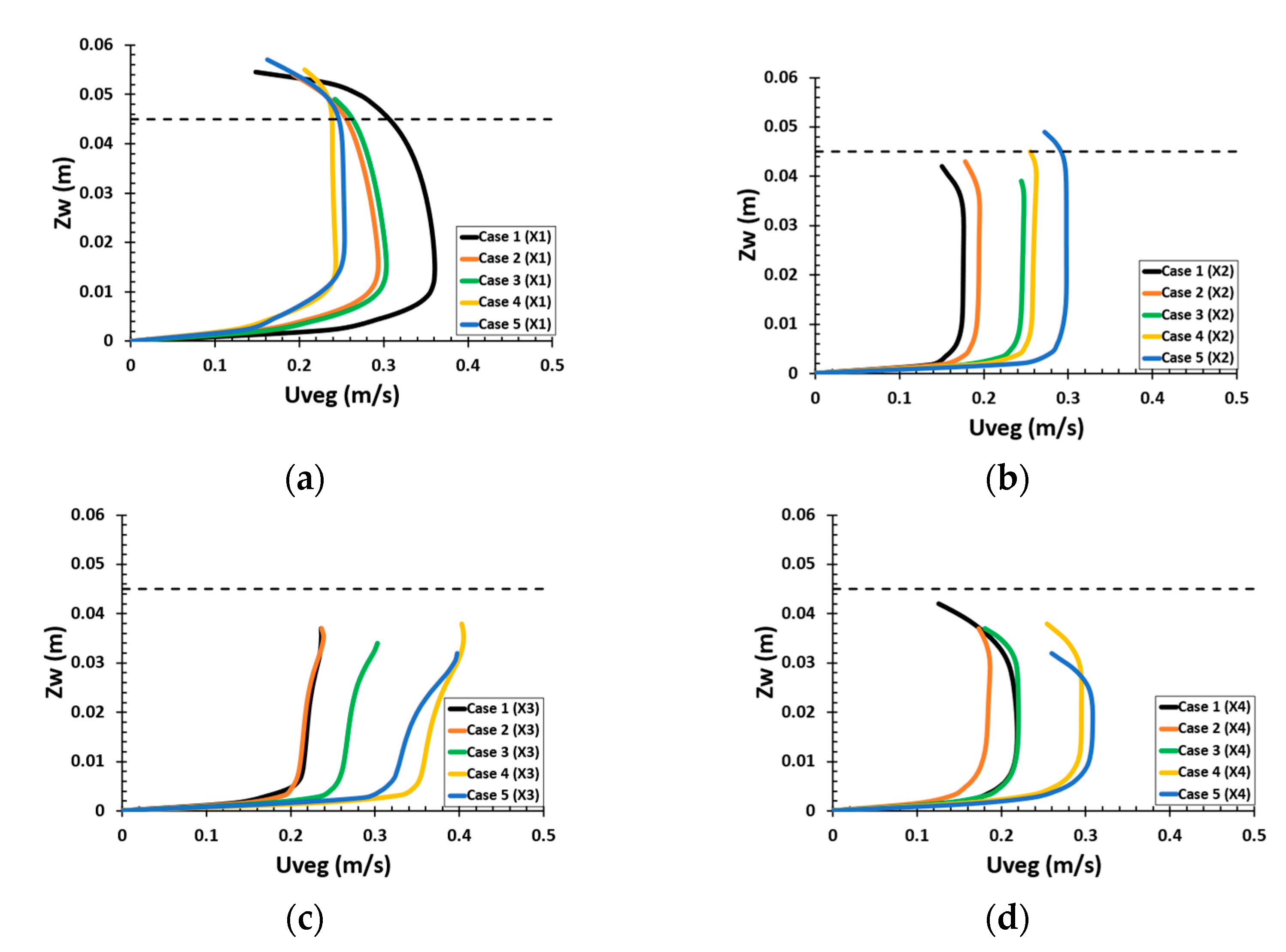
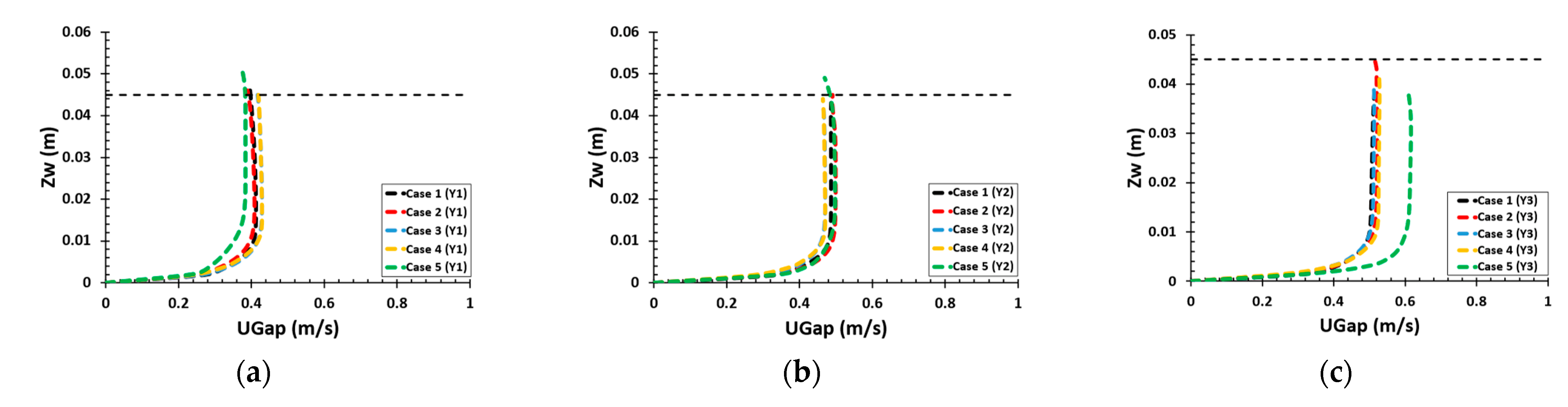
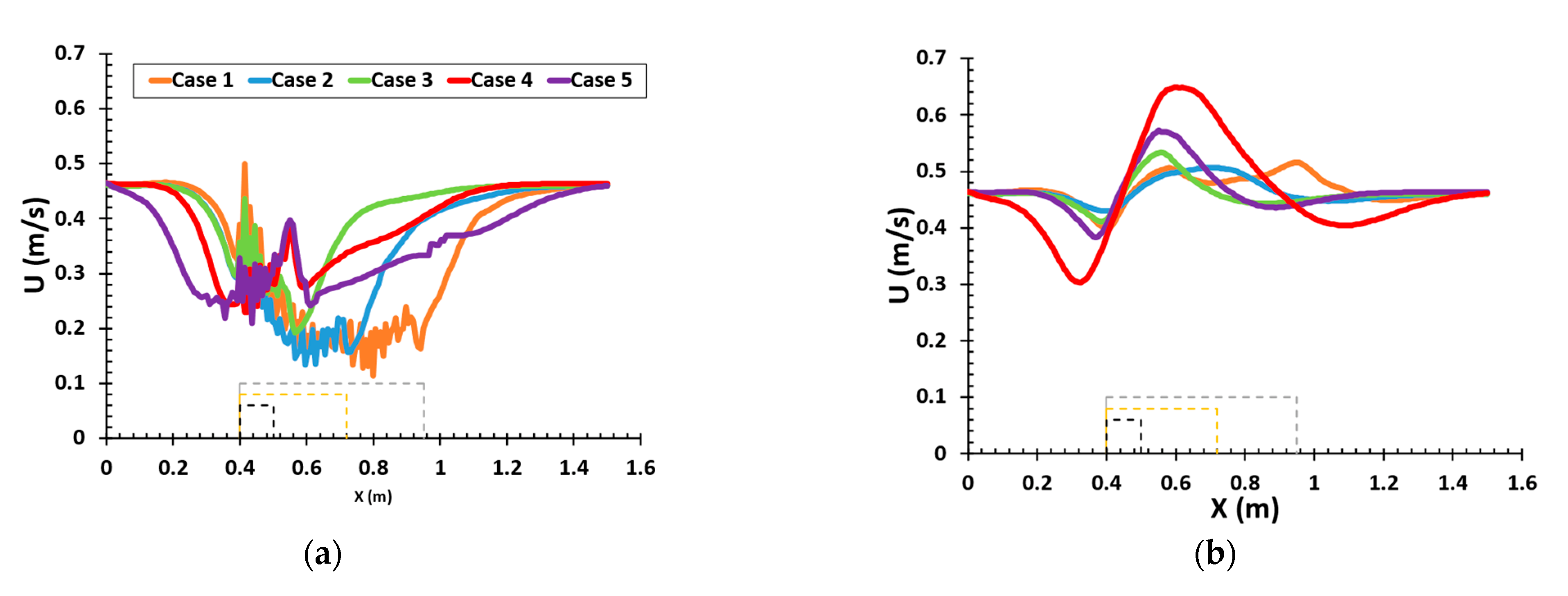

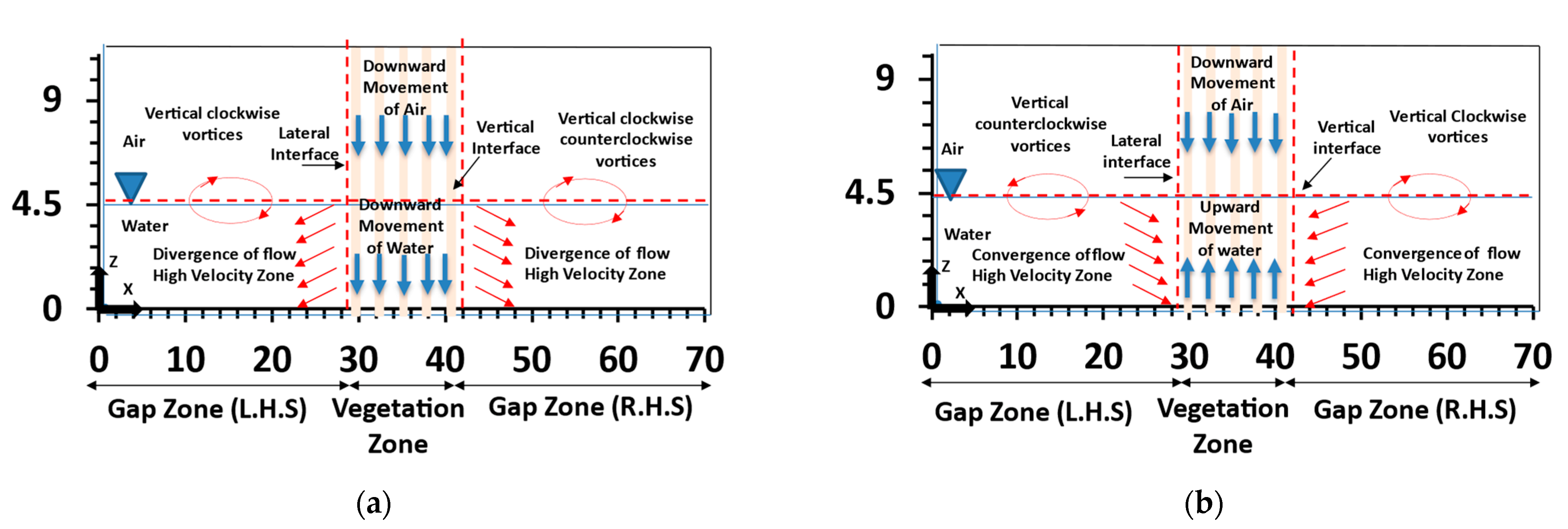
| Cases | AR | Wx (cm) | Wy (cm) | Fr | S/d | Dw (cm) | U (m/s) | |
|---|---|---|---|---|---|---|---|---|
| Longer Vegetation Patch | 1 | 0.2 | 50 | 10 | 0.7 | 1.03 | 4.5 | 0.465 |
| 2 | 0.3 | 30 | 10 | 0.7 | 1.03 | 4.5 | 0.465 | |
| 3 | 1 | 10 | 10 | 0.7 | 1.03 | 4.5 | 0.465 | |
| Wider Vegetation Patch | 4 | 3 | 10 | 30 | 0.7 | 1.03 | 4.5 | 0.465 |
| 5 | 5 | 10 | 50 | 0.7 | 1.03 | 4.5 | 0.465 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amina; Tanaka, N. Numerical Investigation of 3D Flow Properties around Finite Emergent Vegetation by Using the Two-Phase Volume of Fluid (VOF) Modeling Technique. Fluids 2022, 7, 175. https://doi.org/10.3390/fluids7050175
Amina, Tanaka N. Numerical Investigation of 3D Flow Properties around Finite Emergent Vegetation by Using the Two-Phase Volume of Fluid (VOF) Modeling Technique. Fluids. 2022; 7(5):175. https://doi.org/10.3390/fluids7050175
Chicago/Turabian StyleAmina, and Norio Tanaka. 2022. "Numerical Investigation of 3D Flow Properties around Finite Emergent Vegetation by Using the Two-Phase Volume of Fluid (VOF) Modeling Technique" Fluids 7, no. 5: 175. https://doi.org/10.3390/fluids7050175
APA StyleAmina, & Tanaka, N. (2022). Numerical Investigation of 3D Flow Properties around Finite Emergent Vegetation by Using the Two-Phase Volume of Fluid (VOF) Modeling Technique. Fluids, 7(5), 175. https://doi.org/10.3390/fluids7050175






