Modal Decomposition Techniques: Application in Coherent Structures for a Saccular Aneurysm Model
Abstract
:1. Introduction
2. Background
3. Experimental Setup
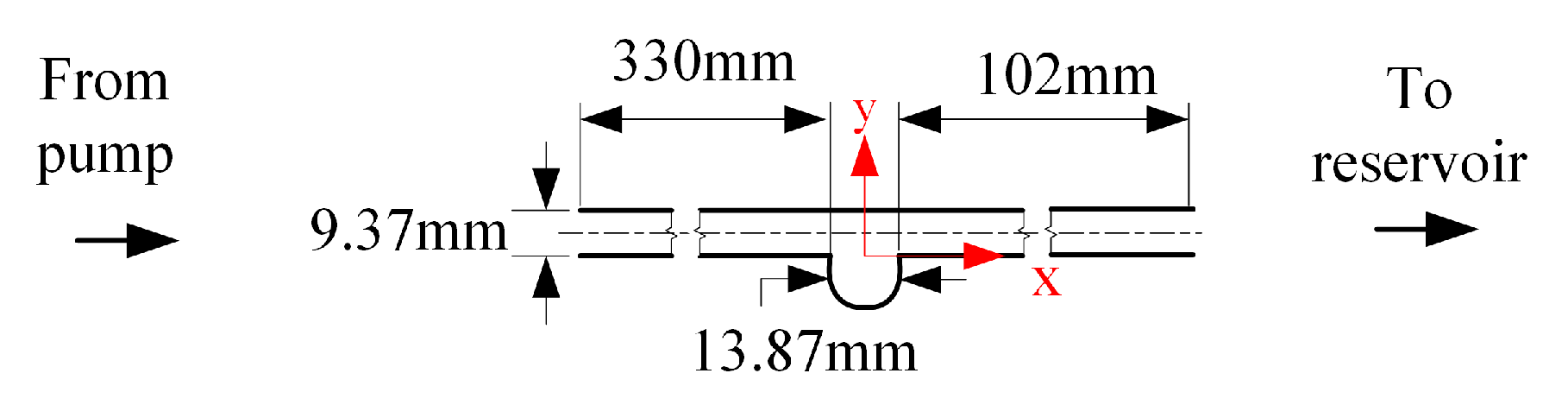
3.1. Aneurysm Model and Fluid
3.2. Velocity Field Measurements
3.3. Pump System
4. Approach
4.1. Proper Orthogonal Decomposition
4.2. Dynamic Mode Decomposition
5. Results
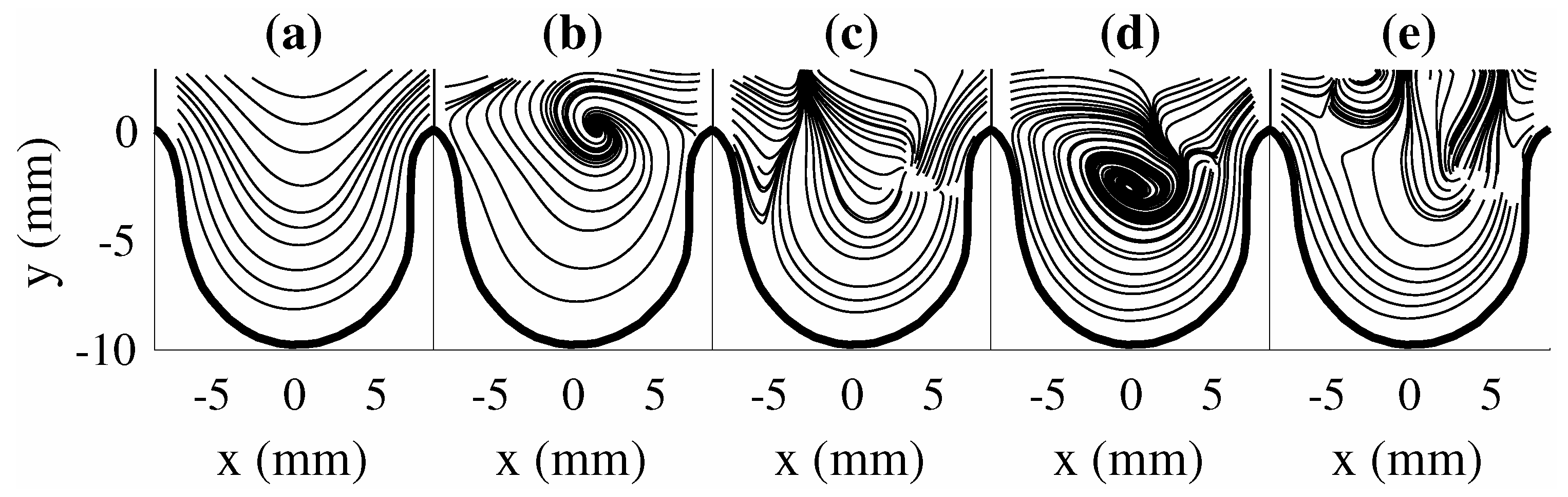
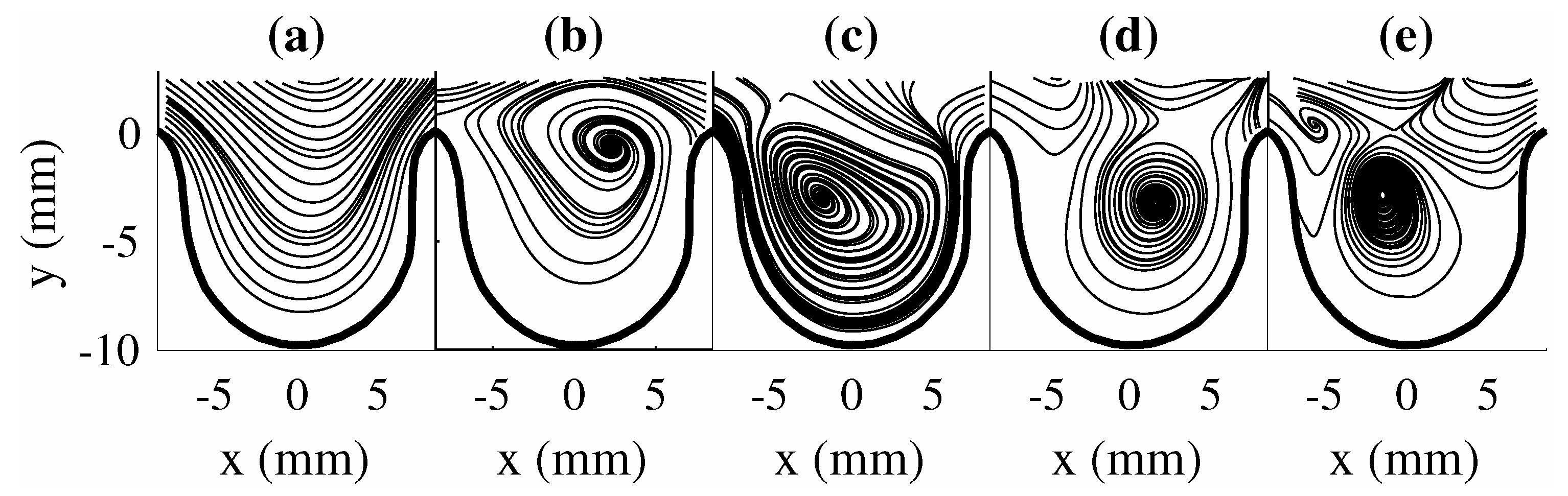
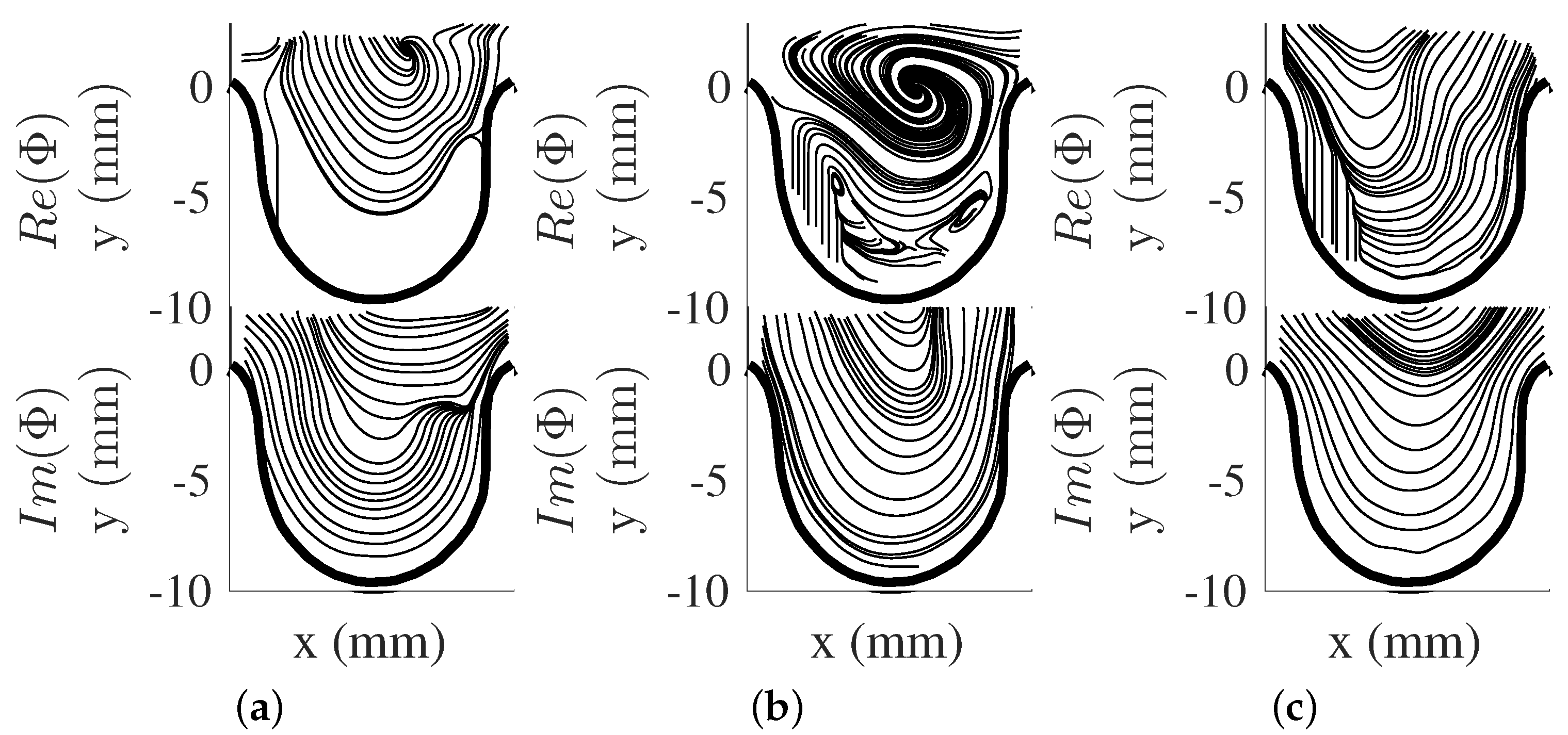
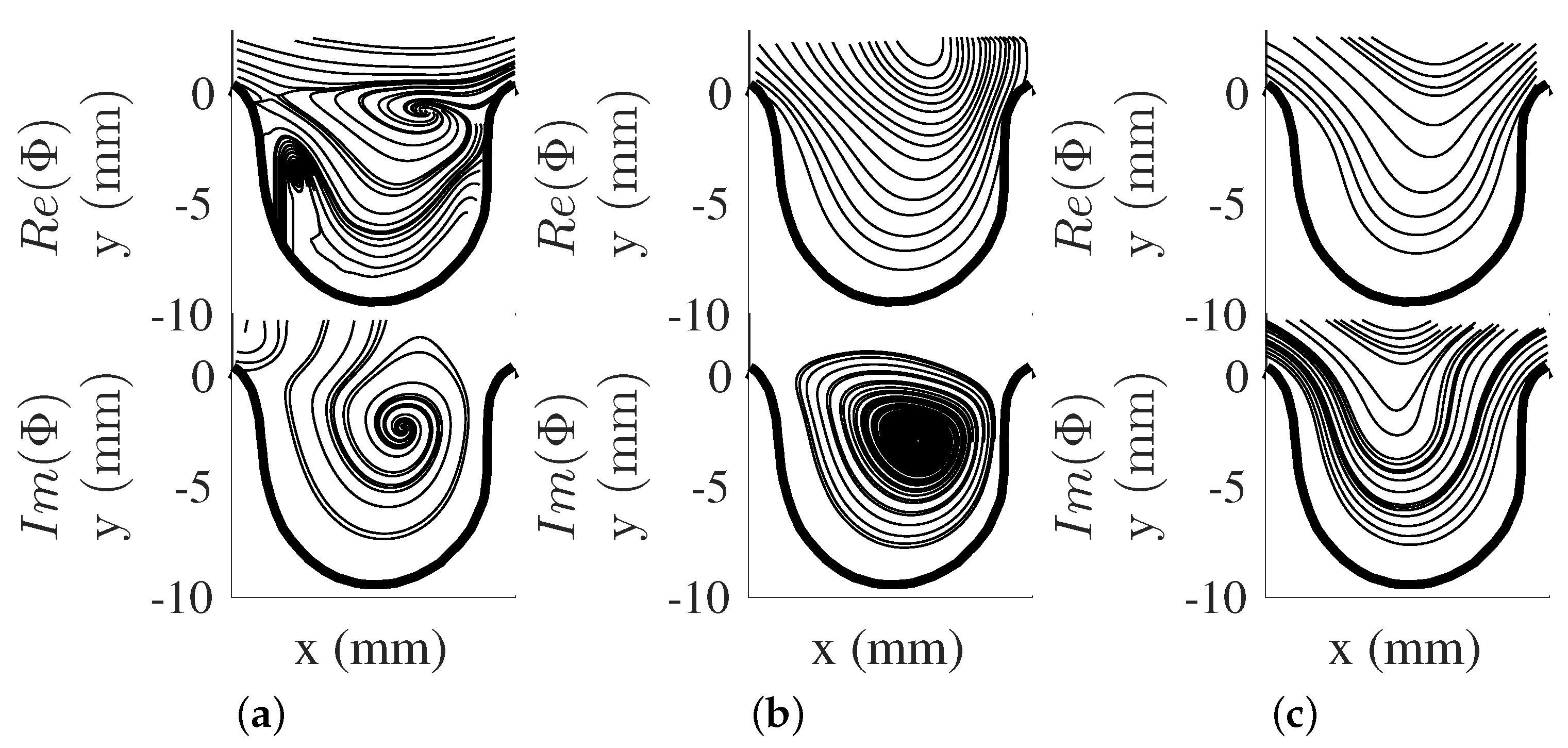
5.1. POD and DMD Modes
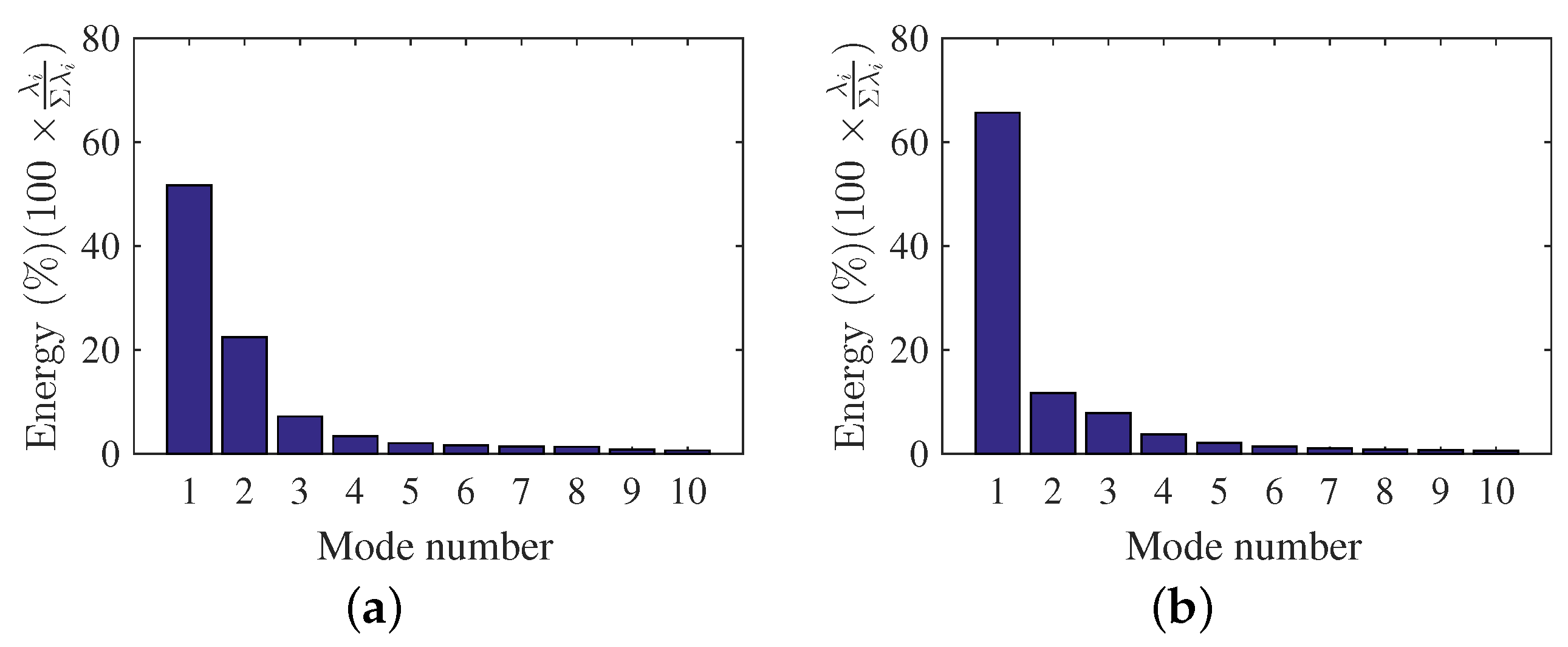
5.2. POD and DMD Energies
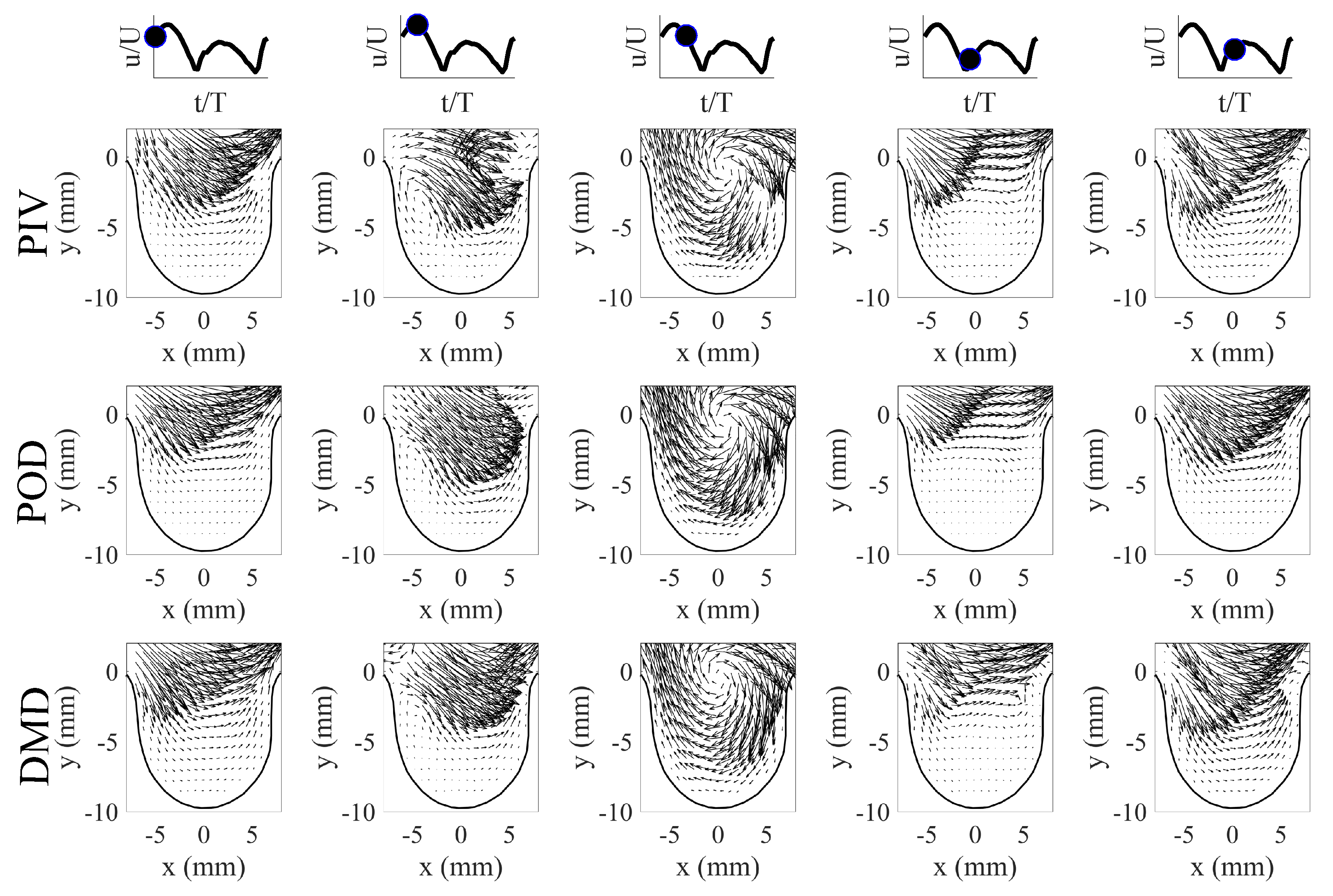
6. Flow field Reconstruction
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | Linear coefficient operator matrix |
| Approximated linear coefficient operator matrix to A | |
| Computational Fluid Dynamics | |
| Pipe diameter (m) | |
| D | Data set containing snapshot to |
| Data set containing snapshot to | |
| DMD | Dynamic Mode Decomposition |
| m | Number of snapshots |
| Particle Image Velocimetry | |
| Proper Orthogonal Decomposition | |
| ith velocity field snapshot | |
| Peak Reynolds number | |
| t | Time (s) |
| T | Time period (s) |
| u | Velocity component in x-direction (m/s) |
| Right singular vector from SVD | |
| v | Velocity component in y-direction (m/s) |
| Left singular vector from SVD | |
| Maximum centerline velocity in the pipe (m/s) | |
| Eigenvectors of | |
| Cartesian coordinates | |
| Womersley number | |
| DMD amplitudes | |
| kth DMD amplitude | |
| Time step (s) | |
| Eigenvalues of | |
| ith eigenvalue of | |
| DMD decay rate from ith real component of | |
| DMD frequency from ith imaginary component of | |
| Blood kinematic viscosity (m/s) | |
| Kinematic viscosity (m/s) | |
| DMD modes | |
| ith DMD mode | |
| Blood density (kg/m) | |
| Fluid density (kg/m) | |
| Rectangular diagonal matrix from SVD | |
| Angular frequency (rad/s) | |
| Vandermonde matrix | |
| ith POD mode | |
| Streamwise component of ith POD mode | |
| Transverse component of ith POD mode | |
| Domain of interest | |
| ⊗ | Tensor product |
| Ensemble averaging |
References
- Byrne, G.; Mut, F.; Cebral, J. Quantifying the large-scale hemodynamics of intracranial aneurysms. Am. J. Neuroradiol. 2014, 35, 333–338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Daroczy, L.; Abdelsamie, A.; Janiga, G.; Thevenin, D. State Detection and Hybrid Simulation of Biomedical Flows. In Proceedings of the Tenth International Symposium on Turbulence and Shear Flow Phenomena, Chicago, IL, USA, 7–9 July 2017; Begel House Inc.: Danbury, CT, USA, 2017. [Google Scholar]
- Janiga, G. Quantitative assessment of 4D hemodynamics in cerebral aneurysms using proper orthogonal decomposition. J. Biomech. 2019, 82, 80–86. [Google Scholar] [CrossRef] [PubMed]
- Yu, P.; Durgesh, V.; Xing, T.; Budwig, R. Application of Proper Orthogonal Decomposition to Study Coherent Flow Structures in a Saccular Aneurysm. J. Biomech. Eng. 2021, 143, 061008. [Google Scholar] [CrossRef] [PubMed]
- Habibi, M.; Dawson, S.; Arzani, A. Data-driven pulsatile blood flow physics with dynamic mode decomposition. Fluids 2020, 5, 111. [Google Scholar] [CrossRef]
- Le, T.B. Dynamic modes of inflow jet in brain aneurysms. J. Biomech. 2021, 116, 110238. [Google Scholar] [CrossRef]
- Arzani, A.; Dawson, S.T. Data-driven cardiovascular flow modelling: Examples and opportunities. J. R. Soc. Interface 2021, 18, 20200802. [Google Scholar] [CrossRef]
- Yu, P.; Durgesh, V. Application of Dynamic Mode Decomposition to Study Temporal Flow Behavior in a Saccular Aneurysm. J. Biomech. Eng. 2022, 144. [Google Scholar] [CrossRef]
- Munson, B.R.; Okiishi, T.H.; Huebsch, W.W.; Rothmayer, A.P. Fluid Mechanics; Wiley: Singapore, 2013. [Google Scholar]
- Shankar, P.; Deshpande, M. Fluid mechanics in the driven cavity. Annu. Rev. Fluid Mech. 2000, 32, 93–136. [Google Scholar] [CrossRef] [Green Version]
- Ku, D.N. Blood flow in arteries. Annu. Rev. Fluid Mech. 1997, 29, 399–434. [Google Scholar] [CrossRef]
- Lasheras, J.C. The biomechanics of arterial aneurysms. Annu. Rev. Fluid Mech. 2007, 39, 293–319. [Google Scholar] [CrossRef] [Green Version]
- Sakalihasan, N.; Limet, R.; Defawe, O.D. Abdominal aortic aneurysm. Lancet 2005, 365, 1577–1589. [Google Scholar] [CrossRef]
- Pressler, V.; McNamara, J.J. Thoracic aortic aneurysm Natural history and treatment. J. Thorac. Cardiovasc. Surg. 1980, 79, 489–498. [Google Scholar] [CrossRef]
- Brisman, J.L.; Song, J.K.; Newell, D.W. Cerebral aneurysms. N. Engl. J. Med. 2006, 355, 928–939. [Google Scholar] [CrossRef] [Green Version]
- WJ, G.; SP, B. Intra-aneurysmal hemodynamics: Turbulence. Trans. Am. Neurol. Assoc. 1954, 13, 163–165. [Google Scholar]
- Jain, K. Mechanism of rupture of intracranial saccular aneurysms. Surgery 1963, 54, 347–350. [Google Scholar]
- Kallmes, D.F.; Altes, T.; Vincent, D.; Cloft, H.; Do, H.; Jensen, M. Experimental side-wall aneurysms: A natural history study. Neuroradiology 1999, 41, 338–341. [Google Scholar] [CrossRef]
- McCormick, W.F.; Acosta-Rua, G.J. The size of intracranial saccular aneurysms: An autopsy study. J. Neurosurg. 1970, 33, 422–427. [Google Scholar] [CrossRef]
- International Study of Unruptured Intracranial Aneurysms Investigators. Unruptured intracranial aneurysms—Risk of rupture and risks of surgical intervention. N. Engl. J. Med. 1998, 339, 1725–1733. [Google Scholar]
- Ujiie, H.; Tachi, H.; Hiramatsu, O.; Hazel, A.L.; Matsumoto, T.; Ogasawara, Y.; Nakajima, H.; Hori, T.; Takakura, K.; Kajiya, F. Effects of size and shape (aspect ratio) on the hemodynamics of saccular aneurysms: A possible index for surgical treatment of intracranial aneurysms. Neurosurgery 1999, 45, 119–130. [Google Scholar]
- Ma, B.; Harbaugh, R.E.; Raghavan, M.L. Three-dimensional geometrical characterization of cerebral aneurysms. Ann. Biomed. Eng. 2004, 32, 264–273. [Google Scholar] [CrossRef]
- Raghavan, M.L.; Ma, B.; Harbaugh, R.E. Quantified aneurysm shape and rupture risk. J. Neurosurg. 2005, 102, 355–362. [Google Scholar] [CrossRef] [PubMed]
- Burleson, A.C.; Strother, C.M.; Turitto, V.T. Computer modeling of intracranial saccular and lateral aneurysms for the study of their hemodynamics. Neurosurgery 1995, 37, 774–784. [Google Scholar] [CrossRef] [PubMed]
- Bluestein, D.; Niu, L.; Schoephoerster, R.; Dewanjee, M. Steady flow in an aneurysm model: Correlation between fluid dynamics and blood platelet deposition. J. Biomech. Eng. 1996, 118, 280–286. [Google Scholar] [CrossRef] [PubMed]
- Asgharzadeh, H.; Borazjani, I. Effects of Reynolds and Womersley numbers on the hemodynamics of intracranial aneurysms. Comput. Math. Methods Med. 2016, 2016, 7412926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferguson, G.G. Physical factors in the initiation, growth, and rupture of human intracranial saccular aneurysms. J. Neurosurg. 1972, 37, 666–677. [Google Scholar] [CrossRef] [PubMed]
- Egelhoff, C.; Budwig, R.; Elger, D.; Khraishi, T.; Johansen, K. Model studies of the flow in abdominal aortic aneurysms during resting and exercise conditions. J. Biomech. 1999, 32, 1319–1329. [Google Scholar] [CrossRef]
- Yu, S.; Zhao, J. A particle image velocimetry study on the pulsatile flow characteristics in straight tubes with an asymmetric bulge. Proc. Inst. Mech. Eng. Part C: J. Mech. Eng. Sci. 2000, 214, 655–671. [Google Scholar] [CrossRef]
- Bouillot, P.; Brina, O.; Ouared, R.; Lovblad, K.; Pereira, V.M.; Farhat, M. Multi-time-lag PIV analysis of steady and pulsatile flows in a sidewall aneurysm. Exp. Fluids 2014, 55, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Budwig, R.; Elger, D.; Hooper, H.; Slippy, J. Steady flow in abdominal aortic aneurysm models. J. Biomech. Eng. 1993, 115, 418–423. [Google Scholar] [CrossRef]
- Fukushima, T.; Matsuzawa, T.; Homma, T. Visualization and finite element analysis of pulsatile flow in models of the abdominal aortic aneurysm. Biorheology 1989, 26, 109–130. [Google Scholar] [CrossRef]
- Yu, S.; Zhao, J. A steady flow analysis on the stented and non-stented sidewall aneurysm models. Med. Eng. Phys. 1999, 21, 133–141. [Google Scholar] [CrossRef]
- Le, T.B.; Borazjani, I.; Sotiropoulos, F. Pulsatile flow effects on the hemodynamics of intracranial aneurysms. J. Biomech. Eng. 2010, 132, 111009. [Google Scholar] [CrossRef] [PubMed]
- Taira, K.; Brunton, S.L.; Dawson, S.T.; Rowley, C.W.; Colonius, T.; McKeon, B.J.; Schmidt, O.T.; Gordeyev, S.; Theofilis, V.; Ukeiley, L.S. Modal analysis of fluid flows: An overview. AIAA J. 2017, 55, 4013–4041. [Google Scholar] [CrossRef] [Green Version]
- Lumley, J.L. The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation; Yaglom, A.M., Tartarsky, V.I., Eds.; Nauka: Tokyo, Japan, 1967; pp. 166–177. [Google Scholar]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Holmes, P.; Lumley, J.L.; Berkooz, G.; Rowley, C.W. Turbulence, Coherent Structures, Dynamical Systems and Symmetry; Cambridge University Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Rowley, C.W.; Mezi, I.; Bagheri, S.; Schlatter, P.; Henningson, D. Spectral analysis of nonlinear flows. J. Fluid Mech. 2009, 641, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Taira, K.; Hemati, M.S.; Brunton, S.L.; Sun, Y.; Duraisamy, K.; Bagheri, S.; Dawson, S.T.; Yeh, C.A. Modal analysis of fluid flows: Applications and outlook. AIAA J. 2020, 58, 998–1022. [Google Scholar] [CrossRef]
- Rowley, C.W.; Dawson, S.T. Model reduction for flow analysis and control. Annu. Rev. Fluid Mech. 2017, 49, 387–417. [Google Scholar] [CrossRef] [Green Version]
- Yu, P.; Durgesh, V. Comparison of Flow Behavior in Saccular Aneurysm Models Using Proper Orthogonal Decomposition. Fluids 2022, 7, 123. [Google Scholar] [CrossRef]
- Cheng, N.S. Formula for the viscosity of a glycerol- water mixture. Ind. Eng. Chem. Res. 2008, 47, 3285–3288. [Google Scholar] [CrossRef]
- Volk, A.; Kähler, C.J. Density model for aqueous glycerol solutions. Exp. Fluids 2018, 59, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Steiger, H.; Poll, A.; Liepsch, D.; Reulen, H.J. Haemodynamic stress in lateral saccular aneurysms. Acta Neurochir. 1987, 86, 98–105. [Google Scholar] [CrossRef] [PubMed]
- Gobin, Y.; Counord, J.; Flaud, P.; Duffaux, J. In vitro study of haemodynamics in a giant saccular aneurysm model: Influence of flow dynamics in the parent vessel and effects of coil embolisation. Neuroradiology 1994, 36, 530–536. [Google Scholar] [CrossRef] [PubMed]
- Ugron, Á.; Farinas, M.I.; Kiss, L.; Paál, G. Unsteady velocity measurements in a realistic intracranial aneurysm model. Exp. Fluids 2012, 52, 37–52. [Google Scholar] [CrossRef]
- Womersley, J.R. Method for the calculation of velocity, rate of flow and viscous drag in arteries when the pressure gradient is known. J. Physiol. 1955, 127, 553–563. [Google Scholar] [CrossRef]
- Steiger, H.J.; Poll, A.; Liepsch, D.; Reulen, H.J. Basic flow structure in saccular aneurysms: A flow visualization study. Heart Vessel. 1987, 3, 55–65. [Google Scholar] [CrossRef]
- Liou, T.M.; Liou, S.N. A review on in vitro studies of hemodynamic characteristics in terminal and lateral aneurysm models. Proc. Natl. Sci. Counc. Repub. China. Part B Life Sci. 1999, 23, 133. [Google Scholar]
- White, F.M.; Corfield, I. Viscous Fluid Flow; McGraw-Hill: New York, NY, USA, 2006; Volume 3. [Google Scholar]
- Sirovich, L. Turbulence and the dynamics of coherent structures. I. Coherent structures. Q. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Durgesh, V.; Naughton, J. Multi-time-delay LSE-POD complementary approach applied to unsteady high-Reynolds-number near wake flow. Exp. Fluids 2010, 49, 571–583. [Google Scholar] [CrossRef]
- Durgesh, V.; Naughton, J.W.; Whitmore, S.A. Experimental investigation of base-drag reduction via boundary-layer modification. AIAA J. 2013, 51, 416–425. [Google Scholar] [CrossRef]
- Tu, J.H.; Rowley, C.W.; Luchtenburg, D.M.; Brunton, S.L.; Kutz, J.N. On dynamic mode decomposition: Theory and applications. arXiv 2013, arXiv:1312.0041. [Google Scholar]
- Kutz, J.N.; Brunton, S.L.; Brunton, B.W.; Proctor, J.L. Dynamic Mode Decomposition: Data-Driven Modeling of Complex Systems; SIAM: Philadelphia, PA, USA, 2016. [Google Scholar]
- Chen, K.K.; Tu, J.H.; Rowley, C.W. Variants of dynamic mode decomposition: Boundary condition, Koopman, and Fourier analyses. J. Nonlinear Sci. 2012, 22, 887–915. [Google Scholar] [CrossRef]
- Wynn, A.; Pearson, D.; Ganapathisubramani, B.; Goulart, P.J. Optimal mode decomposition for unsteady flows. J. Fluid Mech. 2013, 733, 473–503. [Google Scholar] [CrossRef] [Green Version]
- Jovanović, M.R.; Schmid, P.J.; Nichols, J.W. Sparsity-promoting dynamic mode decomposition. Phys. Fluids 2014, 26, 024103. [Google Scholar] [CrossRef]
- Proctor, J.L.; Brunton, S.L.; Kutz, J.N. Dynamic mode decomposition with control. SIAM J. Appl. Dyn. Syst. 2016, 15, 142–161. [Google Scholar] [CrossRef] [Green Version]

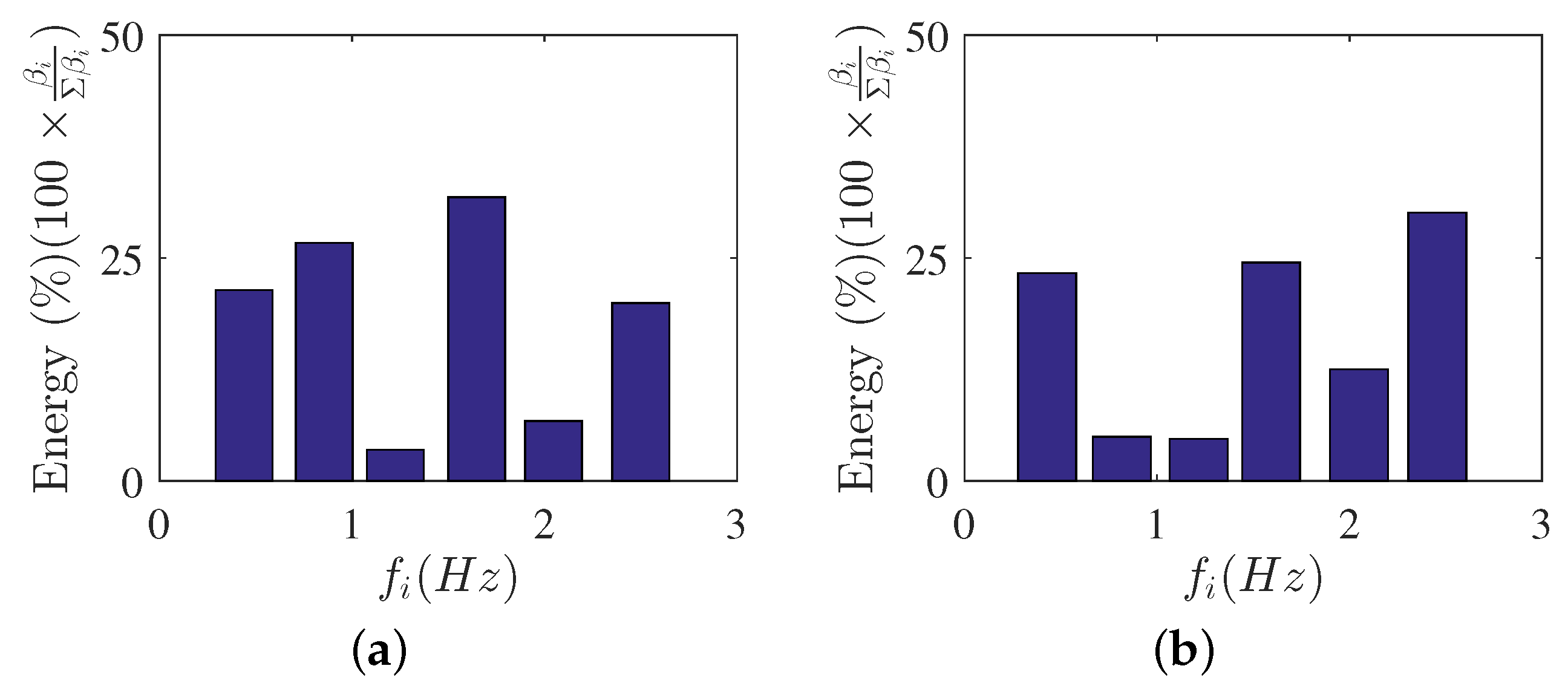
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, P.; Durgesh, V. Modal Decomposition Techniques: Application in Coherent Structures for a Saccular Aneurysm Model. Fluids 2022, 7, 165. https://doi.org/10.3390/fluids7050165
Yu P, Durgesh V. Modal Decomposition Techniques: Application in Coherent Structures for a Saccular Aneurysm Model. Fluids. 2022; 7(5):165. https://doi.org/10.3390/fluids7050165
Chicago/Turabian StyleYu, Paulo, and Vibhav Durgesh. 2022. "Modal Decomposition Techniques: Application in Coherent Structures for a Saccular Aneurysm Model" Fluids 7, no. 5: 165. https://doi.org/10.3390/fluids7050165
APA StyleYu, P., & Durgesh, V. (2022). Modal Decomposition Techniques: Application in Coherent Structures for a Saccular Aneurysm Model. Fluids, 7(5), 165. https://doi.org/10.3390/fluids7050165





