Abstract
In this paper, we discuss some well-known experimental observations on self-organization in dissipative systems. The examples range from pure fluid flow, pattern selection in fluid–solid systems to chemical-reaction-induced flocking and aggregation in fluid systems. In each case, self-organization can be seen to be a function of a persistent internal gradient. One goal of this article is to hint at a common theory to explain such phenomena, which often takes the form of the extremum of some thermodynamic quantity, for instance the rate of entropy production. Such variational theories are not new; they have been in existence for decades and gained popularity through the Nobel Prize-winning work of theorists such as Lars Onsager and Ilya Prigogine. The arguments have evolved since then to include systems of higher complexity and for nonlinear systems, though a comprehensive theory remains elusive. The overall attempt is to bring out examples from physics, chemistry, engineering, and biology that reveal deep connections between variational principles in physics and biological, or living systems. There is sufficient evidence to at least raise suspicion that there exists an organization principle common to both living and non-living systems, which deserves deep attention.
1. Introduction
The modern, hard-science perspective of nature draws from the successes of Twentieth Century science and sees quantification as the dominant approach to questions of epistemology. The alternative approach, based on qualitative explanations, typically adopted in the humanities and social sciences, is considered subsidiary to quantitative methods. The post-modern view [1,2] argues for a systemic explanation drawn by a melding of quantitative and qualitative approaches. Likewise, contention between linear causality and circular causality, physics and biology, and art and science have set up false dualities, which hinder progress in our ability to approach fundamental issues such as a definition of “life” in a meaningful way. On this question, the mechanistic (i.e., information-based) view defines life as a machine [3,4], while perception–action-based models [1,5,6] suggest a broader, non-local definition, whereby a living system needs to be characterized more holistically through its connection to its environment. We do not pretend to know the answer to this question and therefore cannot advocate for any particular viewpoint; there are certainly valuable insights on either side. This paper is an attempt to further examine the non-dual perspective advocated by Gibson and Rosen, albeit in much simpler, tractable systems. The literature on self-organization is extremely broad, and it is not our aim to review this literature. We are more narrowly focused on specific examples of self-organization that are observed in dissipative systems that are insightful with regard to establishing links between physics and biology. Our sentiments were well articulated by Goldenfeld and Woese [7], who stated that the “...key issues of how rapidly evolution occurs, and its coupling to ecology have not been satisfactorily addressed and formulated”, thereby arguing for the need for a synergistic theory of physics–biology, especially when it comes to understanding evolution, self-organization, and pattern formation.
The case for our undertaking to find a common ground between biology and physics was brilliantly made by Vitas and Dobovisek [8] in their article, where they painstakingly scoured the literature to formulate a definition of life: “Life is a far from equilibrium self-maintaining chemical system capable of processing, transforming and accumulating information acquired from the environment”, which is grounded in the fundamental laws of thermodynamics and built upon the more isolated view of living systems that had been previously suggested.
1.1. Dissipative Structures and Organisms
The objective of this paper is to delve deeper into the thermodynamic aspect of dissipative systems and explore some examples of such self-organization in nature. More specifically, the goal of this article is to demonstrate by argument and example that fluids are ideal systems to illustrate the notion of self-organization in a complex system and to highlight thermodynamics as the underlying self-organizing principle of any system that lies outside thermal equilibrium. We chose to make our case by means of some examples in fluid mechanics. Since fluids are dissipative systems, they are “thermodynamically analogous” [9] to living systems and provide insight into the mechanism of self-organization, not only in physics, but also in biology. In this regard, our approach is more in line with the Gibsonian rather than the Fristonian philosophy [6], where the environment plays a significant role in determining the fate of the system. This work is by no means an exhaustive review of the subject. It specifically focuses on some very interesting phenomena that exemplify the thermodynamic basis of self-organization. While it has correctly been pointed out that complexity and self-organization can be traits of physical systems that are not living [8], what is somewhat lacking in the literature is a nuanced examination and categorization of the specific physical examples where self-organization is displayed and their overlaps with biological systems. While our contribution is also somewhat restricted in this regard, it is the start of such a venture to which we hope there will be more contributions in the years ahead.
Dissipative structures have been long recognized for their similarity to biological organisms [10,11,12]. Oscillating chemical reactions, or chemical clocks, are widely present in the biological world. Chemical pattern formations in dissipative structures were clues to how morphogenesis might occur in biological development. More recently, it was discovered that non-living dissipative structures can also exhibit bio-analog behavior [13,14]. This has further strengthened the view that biological organisms are a subset of dissipative structures. To make this point clear, it would help to contrast dissipative structures/organisms with machines. The contrast is particularly important to address the question: are organisms complex machines, or are they a different class of systems such as dissipative structures? Let us look at the fundamental differences between dissipative structures and machines:
- The structure and function of a dissipative structure arises from processes within the system, while the structure of a machine is a result of external design;
- A dissipative structure is created and maintained by entropy-generating and Gibbs- or Helmholtz-energy-dissipating irreversible processes. In contrast, a machine’s structure does not require any entropy generation, and in fact, a machine becomes more efficient with decreasing entropy generation: an ideal machine has no losses and produces no entropy. It is a fundamental difference between the two classes of systems;
- Generally, the design of a machine is based on reversible laws of mechanics, while dissipative structures are described using irreversible thermodynamic processes. It could be argued that mechanics gave us machines, while the thermodynamic theory of dissipative structures is the foundation for a science of biological organisms;
- Dissipative structures are stable and self-healing in the sense that if the structure is perturbed, the processes that created it can also restore it. The processes that create the structure also “heal” the structure from damage, an important property of all living organisms. With rare exceptions that we discuss below, machines are generally not self-healing;
- Machines are designed to perform a specific function, which they do independent of the context. End-directed behavior in dissipative structures shows context-dependent behavior [15].
Thus, two fundamental differences distinguish machines from dissipative structures among others: (i) Entropy generating irreversible processes create a dissipative structure; when these processes cease to operate, entropy production reduces to zero, thermodynamic equilibrium is reached, and the dissipative structure ceases to exist. The structure of a machine does not require continuous generation of entropy for it to exist. While a machine is functioning or during its assembly, entropy may be generated; but once assembled, the existence of a machine does not require continuous entropy generation. As noted above, entropy generation during its operation only reduces a machine’s efficiency. (ii) In most cases, an ideal machine is one that does not generate any entropy during its operation. Its operation is described by reversible laws of mechanics. Dissipative structures, on the other hand, are described using irreversible thermodynamic laws. In this manner, machines are coupled with mechanics, while dissipative structures are coupled with thermodynamics. Regarding self-healing, we note that it is a consequence of the stability of a dissipative structure. Within limits, when a dissipative structure is momentarily perturbed, the structure is restored to its original state. Since an equilibrium state is also stable, a component of a machine that is in an equilibrium state can restore its structure after a momentary perturbation. For example, a spring or pressure-controlled component of a machine can restore its structure after a perturbation. However, a broken spring does not heal itself as a muscle does. In dissipative structure, such as a chemical clock, the entire structure (temporal in this case) and its function are restored after a perturbation.
These important differences between dissipative structures and machines, on the one hand, and the similarities between dissipative structures and organisms, on the other, make it clear that organisms are a class of dissipative structures, not complex machines. René Descartes famously claimed that animals are complex machines (soulless and emotionless and incapable of suffering). As machines that humans build became more complex, the machine metaphor became dominant in describing organisms: the brain as a computer, DNA as an information-carrying molecule, a “blueprint” of an organism, the eye as a camera, and living cells as molecular machines. While the machine paradigm is not universally accepted, a clear alternative paradigm is important to identify. In our view, dissipative structures provide a distinctly different paradigm. Now, we even have examples of bio-analog behavior emerging in dissipative structures. Could there be any ambiguity between dissipative structures and machines? Could animals be complex machines and also dissipative structures? We do not think there is any ambiguity between machines and dissipative structures: either the existence of a structure requires the production of entropy or it does not. Dissipative structures require the production of entropy; machines do not.
We would also like to note that the practical use of a dissipative structure does not make it a machine: we use a dog for its ability to smell and a horse to pull a cart. However, that does not make a dog nor a horse a machine. Our ability to control and manipulate biological organisms do not make them machines. Indeed, we hope our understanding and study of dissipative structures will lead to the discovery and creation of dissipative structures that are of practical use. It is our opinion, however, that they should be clearly distinguished from the traditional machines and identified as dissipative structures with practical utility.
Since this paper has a fundamentally ambitious goal, we also feel it is necessary to include a discussion about certain philosophical aspects of science that would be essential to capture the behavior of self-organizing systems, i.e., end-directedness, which has a controversial history in the sciences.
1.2. Optimality and Final Cause
Theoretical arguments about ontology are usually related to optimality arguments. Variational principles abound in physics and point to the beauty and elegance of scientific theories [16]. While such principles are often discussed in the physics classroom, they have largely been valued for their utility alone. Linear causal thinking still dominates theorizing in physics with the Newtonian laws providing the underlying mechanistic structure. However, there is no apparent reason to attribute primacy status to the Newtonian, causal world view [1,17]. In the words of Braithwait [18]: “Both causation and purpose appear to be psychological primitives that we naturally use to make sense of our surrounding world. It remains unclear which of these two crucial concepts is epistemologically more objective or valid”. This issue has still not been settled. Variational arguments such as Hamilton’s least action principle can be used to derive the governing equations of classical and quantum mechanics [19]. Furthermore, the Euler–Lagrange equation, to a large extent, under the appropriate conditions (i.e., Lagrangian), appears to be a generalization of well-known dynamical laws. They do, however, concern the end-directed nature of the variational theories, which has stymied their progress [16]. In the past several decades, certain key elements about the nature of “purpose” in science and nature have emerged [13,20,21] that provide a new way of thinking about nature’s optimality and possibly even to fundamental ontological questions.
In a 1991 paper, Schoemaker [22] argued that the optimality principle is “most systematically and successfully used in the physical sciences where its case is weakest...and least in social sciences...where its case is strongest(because of the conscious striving of people and the presence of competition and selection)”. However, from the point of view of Gibsonian psychology, the common-place interpretation of end-directedness and “conscious striving” that is attributed to human action are cast in doubt [6]. Ecological psychology hypothesizes that [9] “...behavior can be explained without recourse to internal models or mediating constructs residing within the agents”. Accordingly, insights into human behavior can be sought through the laws of physics, which govern the feedback of interactions between agents and their environment. More recently, ecological psychologists have offered that some forms of biological end-directedness, especially foraging for resources and structural self-maintenance, is best modeled as the optimization of a physical variable, rather than reducing goals to a system’s internal states [15]. In trying to explain several organizational structures in animal social interactions, the laws of thermodynamics have been found to potentially have a say [9,14]. Kugler et al. [21] went even further, synthesizing the behavior of living and non-living systems as falling under gradient-based laws and differentiated by purely thermodynamic or also including informational gradients. The ultimate litmus test for optimization is the Occam’s razor principle: “We allow that Nature may generalize its operational principles, but believe it honors parsimony too much to violate them wantonly simply because intentions evolve” [21].
Wiener et al. [20] argued that one useful way of classifying “active behavior” was in terms of its purpose or lack thereof, where “The term purpose is meant to denote that the act or behavior may be interpreted as directed to the attainment of a goal...”. A fundamentally significant idea that emerged in Wiener’s work on Cybernetics was the idea of feedback, which was considered synonymous with the idea of purpose, and therefore, his notion of teleology was distinct, but not contrary to the deterministic notions of the scientific community. More recently, optimization arguments rooted in the idea of feedback and optimization have been utilized to explain behavior and organization in living systems [3]. Another related concept that needs to be discussed is that of “side-effects”, which sets the stage for “entropy” as a significant player in emergent self-organization.
1.3. Side-Effects and Control
The second law of thermodynamics, or the entropy law, is perhaps one of the deepest and most insightful statements of physics. Confusion about what entropy actually means has given rise to various definitions and interpretations; one powerful way of thinking about entropy, from the point of view of classical thermodynamics, is as a side-effect. Every act of doing work produces a side-effect (or entropy), usually in the form of unrecoverable heat, which is dissipated in the larger system, bringing it back, just a little closer, to a state of thermal equilibrium. The aim of thermodynamics can therefore be described as an attempt to preserve thermal equilibrium. According to non-equilibrium thermodynamics, when the system is outside thermal equilibrium, it is the rate at which entropy is produced that is pertinent. Consequently, when thermal disequilibrium persists, the dissipation of heat energy in the system is enacted in such a way to result in emergent structures. In a manner of speaking, in systems out of thermal equilibrium, side-effects can be said to control the system.
Such notions are not new: Wiener’s Cybernetic theory [20,23] pointed to the significance of feedbacks in a system. These feedbacks show up as causing a reconfiguration of the entire system as a result of the constant dissipative heat flow produced in and out of the equilibrium system. This sort of circularly causal connection results in an eventual mechanical equilibrium (in physical systems), which persists as a result of the thermal disequilibrium. The formation of self-organizing patterns is therefore a central feature of all thermo-mechanical systems and speaks to the significance of side-effects produced by the particular configuration and constraints present in the system.
Therefore, in seeking to understand and explain pattern formation and self-organization, one must examine the “agent”, as well as the system in which it is embedded. Take, for instance, the example of a rigid object falling freely in a fluid medium (air, water, etc.), which will be discussed in further detail in the following section. The central object of attention is the rigid body, while the background environment is the fluid that must also be accounted for. As the rigid body falls in the liquid, it displaces the liquid, thereby activating the internal friction within, as the liquid moves. There is thermal disequilibrium in the system, between the boundary of the rigid body and fluid and parts of the fluid domain that are far away from the body. The feedback cycle of energy exchange plays itself out thusly: an increase in the kinetic energy of the body causes a change (say, drop) in the potential energy of the body, which is countered by a change (increase) in the potential energy of the fluid followed by a change in the kinetic energy of the fluid. This cycle continues until, in the steady state, the kinetic energies are maintained at a steady state, and only potential energy exchange participates as the cause of frictional heat loss. The movement of the body and fluid work towards bringing the system closer to thermal equilibrium (see Figure 1).
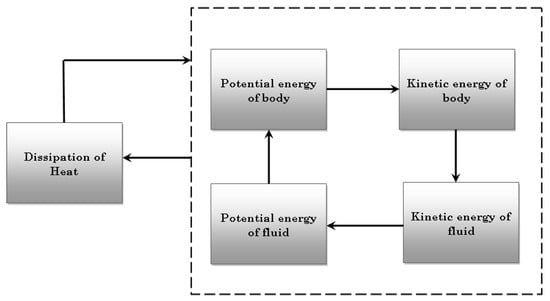
Figure 1.
Energy feedback and dissipation mechanism in the case of a sedimenting body in a fluid. The feedback process can only stop when each component of the system stops moving, as a result of which no dissipation occurs. This is the state of zero entropy production.
Another system demonstrating such agent–environment reciprocities is an electrically-driven self-organizing dissipative system. In this system, metal ball bearings are placed in a glass dish with a shallow bath of oil [24,25]. A metal ring connected to a grounding electrode lines the edge of the dish, surrounding the metal beads. Electrical charges are sprayed out over the beads from a source electrode above the dish, separated by a 5 cm air gap. The beads collect charges, become dipoles, and spontaneously self-organize into branching chains of beads, called trees, rooted on the grounding ring. With sufficiently high voltage, these trees will tend to move through the oil, translating along the grounding ring, bending and swaying their limbs. There is a wealth of evidence supporting that the system self-selects for morphologies and dynamics that increase the rate of entropy production through the system, as measured via the electrical current. Crucially, this flow of charges and the irreversible entropy-producing processes within the system provide the forces that maintain the trees’ stability. This constitutes a rudimentary teleology for the system where it is end-directed to maximize the entropy production and, thus, end-directed to maintain its own stability. This system displays remarkably sophisticated lifelike behaviors stemming from this teleology, including self-healing, coordination among trees, and even an analogue of learning [9,15,24,25,26].
Whether optimality principles are real or not will be debated and argued about for much longer. For now, they are and should continue to be used as a positive heuristic [22] and for their various affordances [16]. What they do allow us to see are common underlying features in seemingly different physical (and biological) systems. Thermodynamics in particular has been observed to play a major role in organizing the behavior of complex physical dissipative systems [27,28]. More specifically, we will see that thermodynamic variables such as free energy and the rate of entropy production contain information about the stability of the system; in fact, the extremum of these quantities in several examples discussed below serve as selection principles for the most stable from among the permitted steady states. The rest of the paper focuses on the theory of dissipative systems and specific examples of dissipative structures in physical and biological systems that appear to be governed by similar underlying principles.
2. Theory of Dissipative Systems
Experimental evidence from our studies [13,14,29,30,31,32] in different systems and those in the literature point to the fact that complex dissipative systems are capable of revealing a host of stable and metastable equilibria, which can be mathematically investigated and explained through relevant dynamical equations and their stability. The larger goal of developing an overarching theory of self-organization first took form through the Nobel Prize-winning work of Onsager [33,34] and Prigogine [28], who put forth a thermodynamics-based variational argument for irreversible dissipative systems. The rate of entropy production has been identified to be such a powerful objective function synthesizing the common physical traits of the class of dissipative systems and can be given by the expression
where corresponds to the “driving force” in the system and represents the flux, which have specific meanings in different physical systems. Curie’s principle generalizes these relationships allowing the rate of entropy production to be written in general for any collection of forces and fluxes, as a product of tensor, vector, or scalar expressions:
Phenomenological relations, for systems slightly out of thermodynamic equilibrium, allow us to write the fluxes in terms of the forces, that is,
where are constants subject to Onsager’s reciprocity relations [33,34]. As a result, Equation (1), for instance, becomes
which has contributed to the discovery of principles such as the Minimum Rate of Entropy Production by Prigogine and co-workers. Since then, some notable advancements have been made under slightly different out-of-equilibrium conditions, such as the Maximum Rate of Entropy Production by Has Ziegler [35], where the force is prescribed and is extremized with respect to the flux. However, a generalized theory has proven to be elusive. The larger goals of this study are therefore to identify and evaluate the possibility of developing a generalized variational argument for dissipative, self-organized systems based on observed commonalities between recent developments in this area. Another objective of such a study would be to categorize and classify the multitude self-organizing dissipative phenomena in the literature along with their physical characteristics and thermodynamic profiles in the hopes that it might be insightful in bridging the physics–biology gap.
3. Self-Organization in Fluids
Fluids are dissipative systems; a flowing fluid naturally generates internal heat due to its viscosity, which puts it in constant thermal disequilibrium with its surroundings. Therefore, when studying fluids, it is appropriate to apply the laws of non-equilibrium thermodynamics, which require that we examine the time rate of change of entropy, i.e., the rate of entropy production (REP). The literature on fluid mechanics is rich with examples of self-organization, and these problems are often insightful in gaining an understanding of other larger, more complex systems. We contend that problems of fluid flow or fluid–solid interactions provide simple and insightful examples of pattern formation, which can guide our understanding of physics, biology, and all that lies at the intersection of the these two disciplines. In the rest of this section, we give a few examples that illustrate these points clearly. Another point that needs to be emphasized is that the cases being discussed in this article indeed constitute a complex system, despite in some cases possessing only two components. The complexity of such a system comes from the sophisticated internal structure of the two components, described by the coupled governing equations, which include the fluid flow and heat equation in example 1 and the fluid flow and rigid body motion equations in examples 2 and 3. The feedback (see Figure 1) between the dynamics of the two components is what gives rise to self-organization in these systems.
3.1. Benard Convection
One problem of self-organization in fluid mechanics that has been studied extensively is the problem of Benard convection [36,37,38,39]. The out-of-equilibrium state of a fluid heated from below, upon sufficiently large departure from thermal equilibrium, results in convection in the fluid, giving rise to organized motion and the well-known Rayleigh–Benard cells on the liquid’s surface (see Figure 2). It has been argued that convective rolls serve the purpose of dissipating the excess thermal energy within the system, at the fastest rate possible, when the system is sufficiently far from thermodynamic equilibrium () [40]; below this threshold (), conductive heat transfer suffices. From a thermodynamic perspective, the particular mechanism of energy flow in systems not too far from thermal equilibrium has been described by the Constructal Law [40,41,42] as being “tree-like”, which is precisely how conduction is typically visualized. A comparison of the rate of entropy production (indicated as ) between conduction and convection shows that:
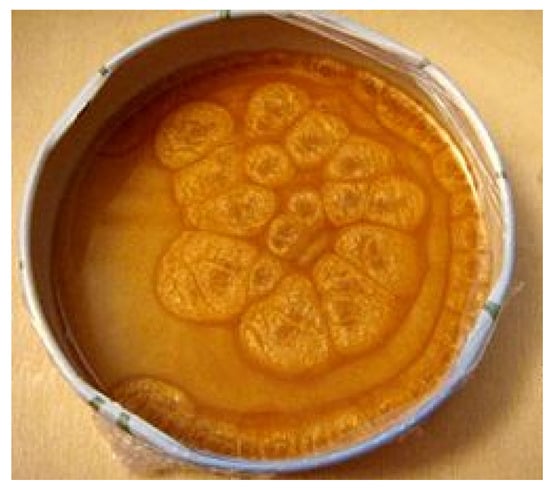
Figure 2.
Benard convection cells observed in gold paint heated from below. Image taken from [43].
A simple mathematical way to illustrate the point made by Equation (5) is using the example of Hamiltonian paths (HP) on a graph. Consider the question of defining the path of least time for a point traversing on an graph. A Hamiltonian path touches all nodes in a lattice just once, i.e., without any crossings. In general, this is a hard counting problem, and a simple recurrence formula cannot be readily found. Therefore, in this paper, based on computations performed on smaller graphs, we enumerate the total number of such paths, which are shown in Table 1. The question of interest here is to identify the paths that best correspond to the convection-type patterns. While this is a mathematical simplification of the real physical situation, one can draw valuable insights from such an analysis. The task is now to classify the types of paths one observes while keeping track of some of their properties. Figure 3 illustrates this idea for a 3 × 3 graph, which has eight total allowable HPs.

Table 1.
Number of Hamiltonian paths in a rectangular grid of dimension .
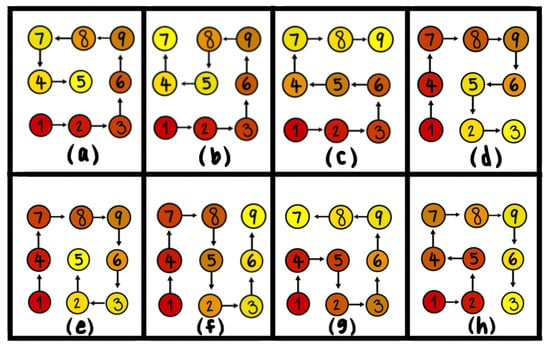
Figure 3.
The panels (a–h) in this schematic present various possible Hamiltonian (non-overlapping) paths in a graph, starting at the cell ’1’. The darker cells indicate locations of greater energy. The path from dark red to orange to yellow indicates the arrow of time. The Table 1 reveals the number of such Hamiltonian paths for a general system.
While this approach has the appearance of a mathematical abstraction, the number of turns in the HP is a way of introducing some physics into the problem. The reciprocal of the number of turns in any given path can be thought of as being proportional to the time taken to traverse this path. In the particular case of the 3 × 3 graph, a simple visual inspection reveals that the path of least time is a spiral (Figure 3a,e) or a wave (Figure 3c,f). Computations for all HPs depicted in Table 1 denote the same overall trend; the path of least time in all of these cases is a spiral or wave. Such modes of energy dispersal are ubiquitous in nature and have been discussed in detail in a review article by Makela and Anilla [44]. Whether, in this particular case, the path of least time is symptomatic of a more general variational principle is not clear, and more work needs to be performed for confirmation. The example presented here says nothing about the transition from conduction to convection, which is a far more nuanced issue than can be handled using these methods. However, a simple heuristic argument about the possible pathways for convection can be quite revealing and point to underlying optimality in the system. Earlier studies have shown that the maximum rate of entropy production to correlate the transition from conduction to convection as a means of dispersing energy to the system.
3.2. Pattern Selection of a Rigid Body in a Fluid
A second example of fluid self-organization for a two-component system involves a fluid flow around an immersed rigid body.
Symmetric bodies such as spheroids and cylinders, when moving in a Newtonian fluid, orient themselves in a steady configuration such that their longer axis is perpendicular to the direction of the flow (see Figure 4). This mechanical steady state depends on the shape, size, density of the rigid body, and nature of the surrounding fluid [45]. To probe further, we define a critical parameter, the Reynolds number () (the Reynolds number is given by the expression where is the density of the fluid, U is the characteristic velocity of the fluid, L is the characteristic scale, and is the dynamic viscosity of the fluid), which describes the competing effects of inertia to viscosity. Experiments have shown that in the case when , referred to as creeping flow (Stokes regime), any orientation of the body is permitted, i.e., there are infinitely many allowable configurations of the rigid body. However, there are critical Reynolds numbers, , , so that for , a symmetric body such as a cylinder or spheroid, orients itself with its longest axis perpendicular to the direction of gravity (or flow) [46]. However, as is increased beyond , the fluid–solid system becomes highly nonlinear, and the effect of inertia, as a result of vortex shedding (see Figure 5), is seen to give rise to bifurcations from the steady orientation to periodic oscillations [46], which eventually leads to autorotation, i.e., complete and sustained flow-induced rotation.
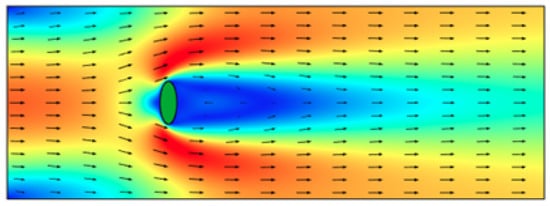
Figure 4.
A numerical computation (using Comsol) of the velocity field around a static ellipse placed at the centerline of a parallel channel. The color in this graph indicates the normalized flow speed, with blue indicating zero speed and red indicating the maximum speed of unity. The entrance velocity is prescribed to be parabolic, and flow along the wall boundaries is taken to be perfect slip.

Figure 5.
This experimental figure shows a two-dimensional slice of the wake vortex structure formed behind a spheroidal body. The wake is illuminated using a a laser sheet, which is scattered by the micron-sized glass powder, which seeds the fluid, thereby illuminating and revealing the vortex spiral. This can be thought of as a zoomed-in image of the computational wake image shown in Figure 4.
While rigorous dynamics-based explanations have been provided for several of these observations [45], in this paper, we focus on the thermodynamic perspective. Some recent studies [30] have shown that the entropy production of such a system, given by
where is the symmetric part of the fluid velocity gradient, is the fluid domain, is the effective mass, T is the ambient temperature, is the acceleration due to gravity, and is the velocity of the body, captures the mechanical steady states of the rigid body, thereby showing potential for consideration as an overarching organizing principle. The first integral term is the dissipation energy of the fluid, while the second term on the right-hand side is relevant in the case when the body is falling freely due to gravity and is not considered in an equivalent variation of the study when the body is hinged and flow driven past it. In any case, it is worth noting at the outset that this term does not contribute to the eventual outcome of the study. In the Stokes case, i.e., when , Equation (6) correctly predicts that any orientation is allowed, since the flow is reversible and the entropy production rate is zero. In the case when the flow speed increases beyond , which is sensitive to the geometric features of the immersed body, wake structures emerge, giving rise to symmetry breaking in the flow. In the case of cylinders and spheroids, when goes past this critical limit, calculations show that the maximum rate of entropy production corresponds to the experimentally observed equilibrium state [32] (as shown in Figure 4). Furthermore, the rate of entropy production is also effective in selecting the experimentally observed stable equilibrium configurations of bodies with fewer symmetries such as a half-cylinder [32]. In such a case, at least in the one example that has been reported on, the maximum rate of entropy production is replaced by the min–max of the rate of entropy production, i.e., while the equilibria of the system correspond to the configuration of the maximum REP, the stable state is the min of the set of maximum REPs. Additional examples of such systems possessing multiple equilibria are needed to verify the generality of this result.
Other self-organizing patterns of free-falling bodies in fluids reveal that orientational configurations, cooperative flocking, and a general response to the environment of a body moving in a Newtonian fluid [32] is clearly influenced by the thermodynamic state of the system and especially by the REP. The following section discusses a classic self-organizing behavior observed in fluids with implications in biology.
3.3. The Segré–Silberberg Effect
We now examine an example of natural pattern formation, the Segré–Silberberg effect; first observed by its eponyms in 1961 [47], the Segré–Silberberg effect has hence become the subject of a large body of fundamental and applied research. The Segré–Silberberg effect describes the behavior of neutrally buoyant sedimenting particles carried through flow in a bounded domain. The Segré–Silberberg effect corresponds to particle settling at a particular distance from the walls. The first experimental observations of this natural pattern selection showed that spheres suspended in Poiseuille flow tend to settle at a position within a channel equal to about 0.6–0.7-times the radius of the channel [47].
The stable settling positions depend on the size of the particle, the speed of the flow, and the material properties of the fluid. Many studies have uncovered the Segré–Silberberg radial equilibrium displacements for different flow parameter regimes [48]. Parabolic flow profiles give rise to translational and rotational forces exerted on a sedimenting particle, which in turn give rise to rich dynamical motions such as tumbling and spinning [49,50,51]. In nature, the effects of the Segré–Silberberg effect are felt when cells tumble through blood vessels, contaminants move through plumbing systems, or in the sedimentary motion in rivers.
The existence of a translational force toward the boundary of flow would suggest that all sedimenting particles tend toward the boundary and would quickly crash into the wall. However, a “wall effect” felt by particles near the boundaries of flow allow particles to settle in an equilibrium position away from the wall. This near-wall interaction is mostly driven by the viscous property of fluids in the vicinity of the boundary. Many studies have shown the potential for varying equilibrium positions, dependent mostly on the viscous properties of the fluid. Groups of sedimenting particles and particles of varying size have equilibrium positions within the Segré–Silberberg radius [52]. In a neatly constrained system such as a pipe, particles are seen to suspend in stable positions in the Segré–Silberberg radial band (as shown in Figure 6).
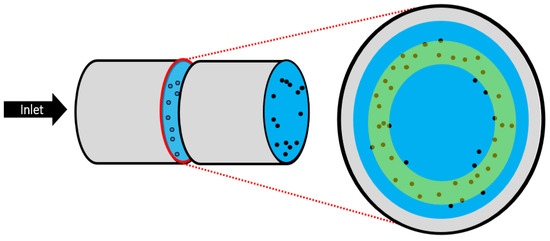
Figure 6.
Sample diagram of particles settling near the Segré–Silberberg radius (the shaded region).
In order to model this effect, COMSOL 4.3’s CFD - Laminar Flow module was used. A circle was placed within a walled channel of fluid at varying displacements from the center of the channel. The sedimenting object in our model was held fixed as the fluid flows by it, simulating buoyancy. The fluid’s density was taken to be , and its viscosity was . The diameter of the channel was 0.4 m. Inlet velocities were assigned such that the Reynolds number was varied between . Many particle sizes were investigated. The length of the channels were tested between 1.1 m and 6.6 m.
To model the near-wall dynamics of the sedimenting particle, we prescribe a slip velocity to mimic the angular velocity for the circlerepresenting the particle. The angular velocity is given by [53]:
Here, a is the radius of the particle, l is the distance from the particle to the wall, and U is the defined inlet velocity.
In Figure 7, the two-component system of concern is shown. A particle spins as it is placed at varying radial positions inside the channel. The particle’s angular velocity depends on the inlet speed, the particle’s radius, and its distance from the wall. A thermodynamic approach was taken to examine the stability of the Segré–Silberberg radius. As a function of particle placement and the resulting dynamics, we can determine the thermodynamic landscape of the fluid for particular configurations. To this end, we calculated the rate of entropy production (REP) contained in the entire system. Thus, one can determine if the placement of the particle in the channel correlates with the overall system’s maximum REP. Therefore, our approach can establish a link between the tail (the thermodynamic landscape of the system including the sedimenting particle and its surrounding fluid) wagging the dog (the Segré–Silberberg effect).
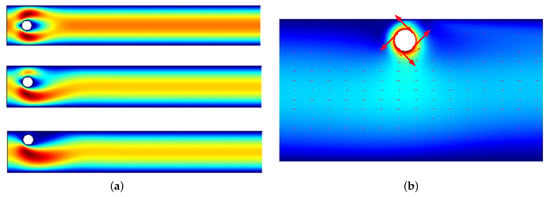
Figure 7.
Panel (a) depicts the results of our numerical computation of the pressure gradients surrounding the model of a sedimenting particle; (b) numerical computation of fluid velocity fields surrounding a sedimenting particle. The color scheme in (a) represents the flow speed, with blue corresponding to zero speed and red to the maximum speed. Flow velocity at the channel walls are taken to correspond to no-slip velocity, while perfect slip conditions are prescribed on the boundary of the cylinder.
Calculations of the REP were carried out using the deformation function. The REP in the case of a sedimenting particle in a viscous fluid can be expressed in the functional form [32]:
where is the constant ambient temperature, is the Cauchy stress tensor, is the symmetric part of the velocity gradient, is the fluid velocity field, represents a three-dimensional volume integral, and is the far-field velocity of the fluid as . Further, the stress tensor can be decomposed into , with p being the isotropic pressure and the viscous coefficient. Furthermore, is the effective mass with , where is the volume of the sedimenting particle and and are the density of the body and the fluid, respectively. is the flow domain where , and is the volume occupied by the particle. In the case of a hinged body in horizontal flow, the gravitational term can be neglected; thus, the REP is identical to the dissipation in the system.
The exchange of kinetic and potential energies in the fluid flow can adequately define the rate of entropy production, as shown in previous work [31], as it satisfies three key conditions: (i) is positive over the entire domain; (ii) 0 as the Reynolds number tends to zero in the reversible, Stokes case; (iii) satisfies Onsager’s reciprocity relations [30]. The results for a particle of radius of 0.024 m for various Reynolds numbers are shown in Figure 8. Displacement is equal to zero in the center of the channel. Here, we see a peak in the REP when the particle is placed within the Segré–Silberberg radial band.
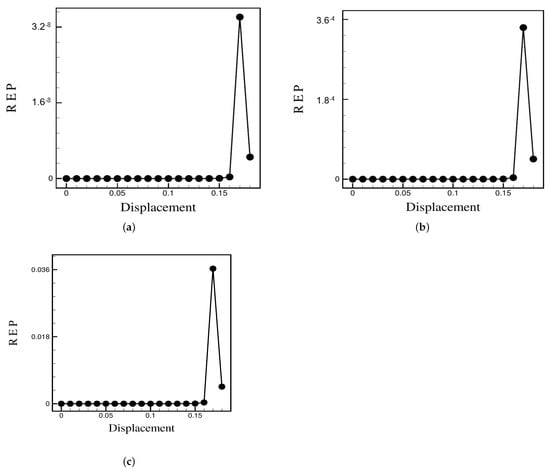
Figure 8.
The rate of entropy production versus the non-dimensional wall distance from the center of the channel to one of the walls at (a) , (b) , and (c) . The rate of entropy production shows a maximum near the outer wall, which agrees well with the observations.
Preliminary results on low Reynolds number flows have suggested that a system realizes a maximum REP when the particle is placed near the Segré–Silberberg radius. These results bode well in an attempt for a thermodynamic explanation of the formation of the Segré–Silberberg equilibrium position. Our results suggest that the pattern formation observed regularly in experiments and simulations could be attributed to the system’s search for a state corresponding to the maximum rate of entropy production.
3.4. Benzoquinone Particles at the Air–Water Interface
This system consists of a collection of Benzoquinone (BQ) particles at the air–water interface in a Petri dish [54,55]. The BQ particles slowly dissolve in water and, in doing so, generate heterogeneous interfacial surface tension gradients. As a result of these gradients, the BQ particles move on the surface of the medium. The motion of the BQ particles can be understood as an example of the Marangoni effect; there are interfacial tension variations along the solid–liquid–air interfaces. A single BQ particle will move continuously, eventually slowing as the particle decays. However, when the system comprises multiple particles, things become more interesting. If the particles are irregular in shape, we see collective behavior in the form of “flocks” (irregularly shaped particles are formed by breaking up larger circular particles, and thus, they have complex edges, jagged points, etc.). Flocks are loose collections of particles, in which the particles continue to move about, but tend to remain in close proximity with each other (see Figure 9). Individual particles may join or leave a flock, but the flocks generally persist for extended periods of time.
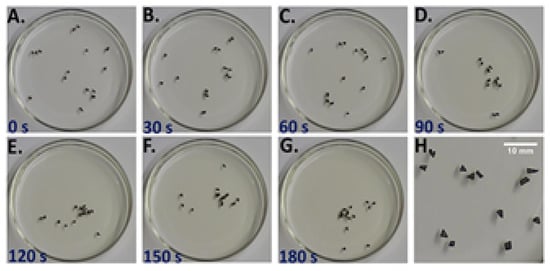
Figure 9.
An example of flocking. The panels (A–H) show the time evolution of the development of a flock with 15 irregular BQ particles. Reprinted with permission from Satterwhite-Warden, J.E., Kondepudi, D.K., Dixon, J.A. and Rusling, J.F., 2019. Thermal-and Magnetic-Sensitive Particle Flocking Motion at the Air–Water Interface. The Journal of Physical Chemistry B, 123(17), pp. 3832–3840. Copyright 2019 American Chemical Society.
A rather different set of dynamics arises if the particles are circular (rather than irregularly shaped). With circularly shaped particles, we see non-random behavior, both in terms of trajectories and events (e.g., collisions), but flocks rarely form, even for a short period of time [54]. The formation of flocks was something of a mystery at first, since upon first consideration, it seems that particles should mutually repel each other in systems such as this one (for a detailed example, see [56]). As a particle dissolves, it increases the local concentration, thereby lowering the local surface tension; any neighboring particle should move away from that particle, toward regions of higher surface tension. Thus, two nearby particles should move away from each other, all other things being equal.
It is proposed that the observed flocks are dissipative structures whose spatio-temporal organizations are formed and maintained by dissipative processes. Consistent with this hypothesis, it was found that the dissolution rate constant, k, which approximates the rate of entropy production, was higher for irregular particles compared to regular particles [55]. More recently, using a mass action kinetic framework, it was shown that both the flocking and non-flocking behaviors (in the irregular and circular particles, respectively) could be explained as a consequence of minimizing the Gibbs free energy, which indirectly is equivalent to the maximization of the rate of entropy production (these results converge on a thermodynamic explanation (optimality principle) for the collective behavior of the particles in this system). Figure 10 shows the results of the free energy computations for the patterns revealed by the BQ interaction dynamics. For the sake of computational convenience, the analysis was performed by binning the flocks into fives sizes, denoted “A” through “E” in progression of increasing size. The figure appears to show that irregularly shaped particles have a greater propensity to form very large flocks (since the free energy is a minimum for the “E” flocks in this case), while regularly shaped, disk-like BQ particles are more likely to stabilize at intermediate sizes (indicated by the free energy being minimized for a “C” flock). If we accept that a thermodynamic optimality principle is responsible for the behavior of the particles and, thus, the flocks, then, it follows that more complex behaviors of BQ flocks may also be due to this optimality principle. We discuss two of these behaviors, emphasizing their commonalities with biological phenomena.
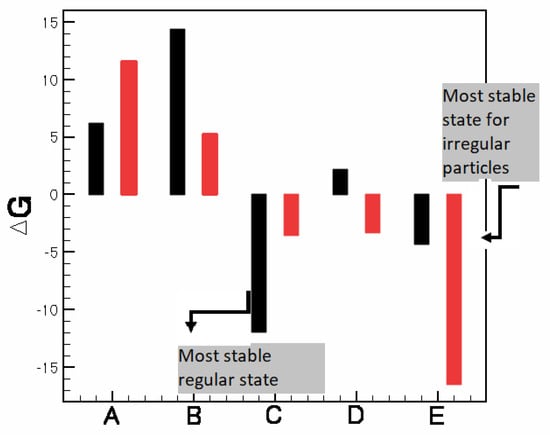
Figure 10.
This graph shows the change in the Gibbs free energy for the various flock sizes for regular (black) and irregular (red) BQ particles. is required for the stability of the configuration with the most stable state corresponding to the most negative. It is clear that in the case of regular particles, the most stable are the mid-sized “C” flocks, while the irregular particles tend towards the larger, “E” flocks.
Sensitivity to thermal gradients. In another set of experiments, we asked whether BQ flocks would be sensitive to environmental conditions that were relevant to their energy consumption [55], keeping in mind that as dissipative structures, their existence depends on energy consumption. When a hot or cold probe is placed near the air–water interface, it creates a thermal gradient on the surface. Flocks of irregular BQ particles will migrate down a cold gradient and up a warm gradient (see Figure 11). One explanation of this phenomenon is that the dissipation rate is higher in warmer regions; thus, the flock moves in accord with the optimality principle (REP or min free energy). By doing so, it seems likely that the flock increases its stability.
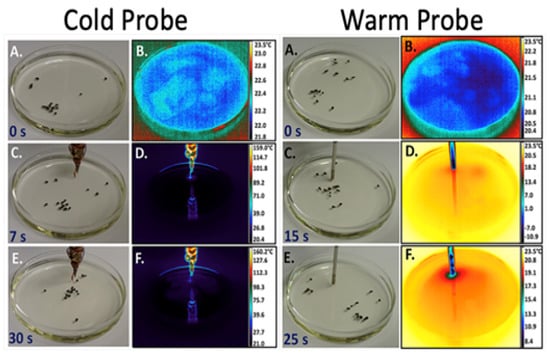
Figure 11.
The two columns of panels on the left show the response of a flock to the introduction of a cold probe (Panels A, C, and E) and corresponding thermal images (Panels B, D, and F). The two columns of panels on the right show the response of a flock to the introduction of a warm probe and corresponding thermal images. Reprinted with permission from Satterwhite-Warden, J.E., Kondepudi, D.K., Dixon, J.A. and Rusling, J.F., 2019. Thermal-and Magnetic-Sensitive Particle Flocking Motion at the Air–Water Interface. The Journal of Physical Chemistry B, 123(17), pp. 3832–3840. Copyright 2019 American Chemical Society.
Flocks with sensors. In another set of experiments, we asked if a flock could become sensitive to a low-energy gradient, much as biological systems are [55]. Biological systems respond disproportionally to very-low-energy gradients (e.g., chemical gradients, acoustic vibrations, light). Further, it is often the case that an element in the biological system has unique sensitivity to that specific gradient. These elements are usually called “sensors” and the very-low-energy gradients are often called “information”. To make a candidate sensor, a single irregular BQ particle was infused with iron oxide nanopowder and included with 14 additional typical BQ particles on the air–water interface. After a flock had formed, a very-low-energy gradient was imposed by positioning a magnet at a predetermined height above the surface of the water. (The height was set at the minimum height, such that the magnet field would not control the behavior of a single iron oxide with no other particles in the dish.) Only the sensor (i.e., iron-oxide-infused) particle was sensitive to this low-energy gradient, but the entire flock moved to the region below the magnet (see Figure 12). A control condition with 15 irregular BQ particles, but no sensor particle, showed that the sensor particle was indeed required for sensitivity to the gradient. An additional control condition with 15 circular BQ particles (that do not flock), one of which was infused with iron oxide, showed that flocking was also necessary for sensitivity to the gradient. This set of experiments demonstrates how a system that is maintaining itself far from equilibrium may be able to use very small energy gradients in ways that are analogous to biological systems.

Figure 12.
The panels (A–F) show the response of the flock to the introduction of a low-energy magnetic field at different times. The single sensor particle is highlighted in red. Reprinted with permission from Satterwhite-Warden, J.E., Kondepudi, D.K., Dixon, J.A. and Rusling, J.F., 2019. Thermal-and Magnetic-Sensitive Particle Flocking Motion at the Air–Water Interface. The Journal of Physical Chemistry B, 123(17), pp. 3832–3840. Copyright 2019 American Chemical Society.
4. Self-Organization in Nature
Dispersal of seeds happens in a variety of ways [57]; therefore, wind dispersal in particular is pertinent to the discussion here. Recent studies have borne out the fact that trees and forests are quite intelligent systems, which are capable of: “consciousness” at various levels including the ability to respond to external stimuli and their environment; cooperative behavior; self-replication, etc., all traits commonly associated with complex biological, living systems. Therefore, the argument we are making is that trees are part of a Darwinian evolutionary process, which is the cornerstone of biology, and the evolution of the various variety of seed shapes is nature’s selection process to find shapes that maximize the potential to survive through the invocation of thermodynamic principles.
Two modes of dispersal have been identified thus far: (i) parachuting motion and (ii) winged flight, which includes gliding, rocking, and spinning (or autorotation) [57,58] (see Figure 13). The mathematics of these modes of motion have been quite well studied in the past decades. What is striking about this biological event is the similarity between this event and the discussion in Section 3.2. Biologists and scientists attribute “intention” to dispersal mechanics. Minami and Azuma [58], for instance, remarked that “Each flying seed is designed to have a small rate of descent and to float in the air current as long as possible, according to their environmental conditions”. Of course, this could be passed off as merely a manner of speaking about the adaptation of trees. After all, we have a natural affinity toward anthropomorphize. There are ecological advantages to local dispersal by wind, the most significant perhaps being that it prevents competition and seed mortality near the parent plant [57]. This example of seeds is significant in explaining how a complex biological system bound by the laws of thermodynamics evolves to have the best selective advantage for reproduction. While it might be a stretch to argue that the laws of thermodynamics and entropy production rates are the underlying rules of living and non-living systems alike, it appears reasonable to say, based on these examples, that living systems take advantage of such optimal principles for their survival. After all, given the environmental constraints that a tree has to contend with, the seeds are produced with shapes that lead to the lowest rate of descent or those experiencing maximum drag, which coincides with the configuration of the maximum rate of entropy production. In some recent work exploring the connections between Darwin’s theory of natural selection and Hamilton’s principle of least action [59,60], it is argued that the two are very likely to be similar and may be bound together by the fastest energy flows across the respective energy landscapes.

Figure 13.
A sketch of the shapes of wind-dispersed seeds.
Another intriguing example from biology comes from the work of Vallino and Huber [61], who applied the maximum rate of entropy production principle to model and explain microbial organization in Siders Pond in Falmouth, Massachussettes, USA, and the response of the microbial community to changes in the environment. The model considers a network of coupled redox reactions among phytoplankton, sulfur bacteria, aerobic and anaerobic grazers, aerobic organoheterotrophic bacteria, sulfate-reducing bacteria, photoheterotrophs, and sulfide-oxidizing bacteria through a system of nonlinear dynamical equations. The model is built on the assumption that “microbial systems organize to use all available energy sources...”, which they identified as the Gibbs free energy, which is another way of recasting the MEP principle. While predictive models have been successfully used in such contexts, they face considerable challenges in efficiently being able to resolve highly complex systems; the systems-based thermodynamic approach proves to be an effective alternative approach in this regard. In their paper, the MEP principle was used as an optimization argument to determine the rate constants of the system, as a result of which, the computational results were in good agreement with the observations.
Yet another example can be found by surveying the foraging capabilities of bacteria. The stability and persistence of organisms are intrinsically tied to their ability to maintain an in-flux of energetic resources (food) that drive physiological processes, maintain structure, and power behaviors. All such maintenance processes are irreversible entropy-producing processes [62], and thus, the importing of food is substantively related to the entropy production within living systems. Foraging, the behaviors associated with detecting, navigating to, and ingesting energetic resources, should similarly be related to the entropy production of organisms.
For example, bacteria will follow increasing concentration gradients of metabolizable resources such as sugar. In one set of famous experiments by Adler [63], a long, narrow tube was filled with a uniform distribution of sugar. A bacterial colony was placed at one end of the tube. The bacteria consumed local supplies of sugar, which generated a concentration gradient, which they then followed throughout the length of the tube. This induced concentration gradient drives them to move up-gradient, consume sugar, and generate new gradients. There is thus a circular relationship between the activity of the organisms and the state of the environment, much like the preceding cases discussed herein. The feedback effects between colony and sugar gradients drove the system to a steady state of consuming sugar while moving up the concentration gradient. A recent thermodynamic analysis of this behavior provides evidence that the chemotactic and reproductive dynamics are consistent with the bacterial colony’s entropy production being maximized [64]. Both the circular causal structure of dissipative systems and the intimate relation to entropy production are likely to be evident in many other biological examples [65,66].
5. Conclusions
We made the case here through multiple examples in dissipative, fluid systems that thermodynamic variational arguments provide essential clues about self-organization in complex systems. Such complex systems can be non-living or even living systems, as in the cases discussed in Section 4. While these cases are independent, for the most part, there are recurring physical traits that make the case for an underlying structure for all of nature quite compelling (see also the summary in Table 2). One of these common traits is the emergence of spiral patterns. In convection, energy distribution is seen to best happen along a spiral path. The spiral pattern is also key to the energy dissipation of the fluid in our second example; Figure 5 shows a close up image of a primary wake vortex behind a spheroid in its steady orientation in a flowing liquid.

Table 2.
The table summarizes the various examples of self-organization in dissipative systems and fluid–solid interaction that have been tackled by us, where the maximum REP or related thermodynamic variational principle appears to correspond to the stable steady state. The table also provides the various forces and gradients that drive the system to its emergent steady configuration. Here, MEP refers to the maximum REP, CT to constructal theory, and MFE is the minimum free energy of the system. Note that in invoking variational arguments such as the max REP, we are in fact making an argument about stability, namely of the various configurations or self-organized states that a system allows for; the stable one is seen to the one that maximizes the rate of entropy production.
A very detailed and insightful discussion in the papers by Annila and co-workers (see, for instance, [44,59]) was provided on the prevalence of specific patterns in nature through which energy is dispersed. The natural selection of a small subset of patterns from the plethora that could be conceived of points to a fundamental, preferred pattern. It is argued that nonequilibrium systems seek to “consume free energy in the least time” [44]. Spirals are not the only patterns we see: tree-like paths of energy distribution occur in several physical systems. However, in such systems, energy flow occurs from a source to multiple sinks or vice versa, giving rise to the tree-/fractal-like structures [40].
The biggest drawback in convincing biologists and physicists alike of the underlying unity of these two fields is the concept of “purpose”, which we discussed in detail in the earlier parts of this paper. However, it must be noted that the kind of purposive action that we refer to in living systems where a direct correlation can be made between the intent and action are simple ones; in most of these cases, there is a direct, linear connection between the two events. For instance, the intent to travel from point A to point B can lead to a direct action and successful enactment of the intent. In more complex cases, “purposefulness” may be irrelevant, and intent may have no bearing on the outcome of the action. It is plausible that in these nonlinear cases, a host of complexly tied events, the environment, etc., may result in some emergent consequences. This is where the laws of complexity theory and non-equilibrium thermodynamics may be able to provide valuable insights.
Author Contributions
Methodology, B.J.C., J.P. and A.V.; experiments, B.D.B., J.D. and D.K.; discussion, B.D.B., J.D., D.K. and A.V. All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially made possible through support by the National Science Foundation’s INSPIRE Track 1 Program, Grant No. BCS- 1344725. Author A.V. also acknowledges National Science Foundation Grant 1802641 for their support.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The paper is dedicated to our co-author Bong Jae Chung, who passed away unexpectedly in February 2021. The authors thank Mehrdad Massoudi and Jonathan Cutler for valuable discussions. Section 3.1 is partially based on the work of former student Wayne Ernst. Author names are listed in alphabetical order. Thanks to Sanya Vaidya for her help in creating some of the figures in the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rosen, R. Life Itself: A Comprehensive Inquiry into the Nature, Origin, and Fabrication of Life; Columbia University Press: Columbia, UK, 1991. [Google Scholar]
- Rosen, R. Essays on Life Itself; Columbia University Press: Columbia, UK, 2000. [Google Scholar]
- Friston, K. Life as we know it. J. R. Soc. Interface 2013, 10, 20130475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dawkins, R. The Selfish Gene; Oxford University Press: Oxford, UK, 2016. [Google Scholar]
- Bertalanffy, L.V. General system theory: Foundations, development, applications. JAMA 1969, 208, 870. [Google Scholar] [CrossRef]
- Gibson, J.J. The Ecological Approach to Visual Perception: Classic Edition; Psychology Press: New York, NY, USA, 2014. [Google Scholar]
- Goldenfeld, N.; Woese, C. Life is physics: Evolution as a collective phenomenon far from equilibrium. Annu. Rev. Condens. Matter Phys. 2011, 2, 375–399. [Google Scholar] [CrossRef] [Green Version]
- Vitas, M.; Dobovišek, A. Towards a general definition of life. Orig. Life Evol. Biosph. 2019, 49, 77–88. [Google Scholar] [CrossRef]
- Davis, T.J.; Kay, B.A.; Kondepudi, D.; Dixon, J.A. Spontaneous interentity coordination in a dissipative structure. Ecol. Psychol. 2016, 28, 23–36. [Google Scholar] [CrossRef]
- Prigogine, I.; Nicolis, G.; Babloyantz, A. Thermodynamics of Evolution. Phys. Today 1972, 25, 23. [Google Scholar] [CrossRef]
- Nicolis, G.; Prigogine, I. Self-Organization in Non-Equilibrium Systems; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Prigogine, I.; Stengers, I. Order Out of Chaos: Man’S New Dialogue with Nature; Bantam Books: New York, NY, USA, 1984. [Google Scholar]
- Kondepudi, D.; Kay, B.; Dixon, J. End-directed evolution and the emergence of energy-seeking behavior in a complex system. Phys. Rev. E 2015, 91, 050902. [Google Scholar] [CrossRef] [Green Version]
- Kondepudi, D.; Kay, B.; Dixon, J. Dissipative structures, machines, and organisms: A perspective. Chaos 2017, 27, 104607. [Google Scholar] [CrossRef]
- Dixon, J.A.; Kay, B.A.; Davis, T.J.; Kondepudi, D. End-directedness and context in nonliving dissipative systems. In Contextuality from Quantum Physics to Psychology; Dzhafarov, E., Jordan, S., Zhang, R., Cervantes, V., Eds.; World Scientific: Singapore, 2016. [Google Scholar]
- Chung, B.J.; McDermid, K.; Vaidya, A. On the affordances of the MaxEP principle. Eur. Phys. J. B 2014, 87, 20. [Google Scholar] [CrossRef]
- Doll, W.E., Jr. Foundations for a post-modern curriculum. J. Curric. Stud. 1989, 21, 243–253. [Google Scholar] [CrossRef]
- Braithwait, R.B. Causal and teleological explanation. In Purpose in Nature; Canfield, J.V., Ed.; Prentice Hall: Hoboken, NJ, USA, 1966; pp. 27–47. [Google Scholar]
- Feynman, R.P.; Robert, B.L.; Matthew, S. The principle of least action. Feynman Lect. Phys. 1964, 2, 19-1. [Google Scholar]
- Wiener, N.; Rosenbluth, A.; Bigelow, J. Behavior, Purpose and Teleogie. Philos. Sci. 1943, 1, 18–24. [Google Scholar]
- Kugler, P.N.; Shaw, R.E.; Vincente, K.J.; Kinsella-Shaw, J. Inquiry into intentional systems I: Issues in ecological physics. Psychol. Res. 1990, 52, 98–121. [Google Scholar] [CrossRef]
- Schoemaker, P.J. The quest for optimality: A positive heuristic of science? Behav. Brain Sci. 1991, 14, 205–215. [Google Scholar] [CrossRef]
- Wiener, N. Cybernetics or Control and Communication in the Animal and the Machine; MIT Press: Cambridge, MA, USA, 1961; Volume 25. [Google Scholar]
- De Bari, B.; Paxton, A.; Kondepudi, D.K.; Kay, B.A.; Dixon, J.A. Functional Interdependence in Coupled Dissipative Structures: Physical Foundations of Biological Coordination. Entropy 2021, 23, 614. [Google Scholar] [CrossRef] [PubMed]
- De Bari, B.; Dixon, J.A.; Kay, B.A.; Kondepudi, D. Oscillatory dynamics of an electrically driven dissipative structure. PLoS ONE 2019, 14, e0217305. [Google Scholar] [CrossRef]
- De Bari, B.; Dixon, J.; Pateras, J.; Rusling, J.; Satterwhite-Warden, J.; Vaidya, A. A thermodynamic analysis of end-directed particle flocking in chemical systems. Commun. Nonlinear Sci. Numer. Simul. 2021, 106, 106107. [Google Scholar] [CrossRef]
- Martyushev, L.M.; Seleznev, V.D. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Prigogine, I.; Isabelle, S. Order out of Chaos: Man’s New Dialogue with Nature; Verso Books: London, UK, 2018. [Google Scholar]
- Chen, T.; Kondepudi, D.K.; Dixon, J.A.; Rusling, J.F. Particle Flock Motion at Air–Water Interface Driven by Interfacial Free Energy Foraging. Langmuir 2019, 35, 11066–11070. [Google Scholar] [CrossRef]
- Chung, B.J.; Ashwin, V. An optimal principle in fluid–structure interaction. Phys. D Nonlinear Phenom. 2008, 237, 2945–2951. [Google Scholar] [CrossRef]
- Chung, B.J.; Ashwin, V. Non-equilibrium pattern selection in particle sedimentation. Appl. Math. Comput. 2011, 218, 3451–3465. [Google Scholar] [CrossRef]
- Chung, B.J.; Blas, O.; Ashwin, V. Entropy production in a fluid–solid system far from thermodynamic equilibrium. Eur. Phys. J. E 2017, 40, 105. [Google Scholar] [CrossRef] [PubMed]
- Onsager, L. Reciprocal relations in irreversible processes. I. Phys. Rev. 1931, 37, 405. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. II. Phys. Rev. 1931, 38, 450. [Google Scholar] [CrossRef] [Green Version]
- Ziegler, H. An Introduction to Thermomechanics; North-Holland: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Bodenschatz, E.; Werner, P.; Guenter, A. Recent developments in Rayleigh–Benard convection. Annu. Rev. Fluid Mech. 2000, 32, 709–778. [Google Scholar] [CrossRef] [Green Version]
- Busse, F.H. Non-linear properties of thermal convection. Rep. Prog. Phys. 1929, 41, 1929. [Google Scholar] [CrossRef]
- Chatterjee, A.; Mears, N.; Yadati, Y.; Iannacchione, G.S. An overview of emergent order in far-from-equilibrium driven systems: From kuramoto oscillators to rayleigh–bénard convection. Entropy 2020, 22, 561. [Google Scholar] [CrossRef]
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851. [Google Scholar] [CrossRef] [Green Version]
- Bejan, A. Shape and Structure, from Engineering to Nature; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bejan, A.; Marden, J.H. Unifying constructal theory for scale effects in running, swimming and flying. J. Exp. Biol. 2006, 209, 238–248. [Google Scholar] [CrossRef] [Green Version]
- Bejan, S.; Lorente, S. The constructal law of design and evolution in nature. Philos. Trans. R. Soc. B 2010, 365, 1335–1347. [Google Scholar] [CrossRef] [Green Version]
- File: Benard Cells Convection.ogv. (23 September 2013). Wikimedia Commons, the Free Media Repository. Available online: https://commons.wikimedia.org/w/index.php?title=File:B%C3%A9nard_cells_convection.ogv\&oldid=105140182 (accessed on 2 July 2018).
- Makela, T.; Annila, A. Natural patterns of energy dispersal. Phys. Life Rev. 2010, 7, 477–498. [Google Scholar] [CrossRef] [PubMed]
- Galdi, G.P. On the Motion of a Rigid Body in a Viscous Fluid: A Mathematical Analysis with Applications. In Handbook of Mathematical Fluid Mechanics; Elsevier Science: Amsterdam, The Netherlands, 2002; pp. 653–791. [Google Scholar]
- Chung, B.J.; Cohrs, M.; Ernst, W.; Galdi, G.P.; Vaidya, A. Wake-cylinder interaction at low and intermediate Reynolds numbers. Arch. Appl. Mech. 2016, 86, 627–641. [Google Scholar] [CrossRef]
- Segre, G.; Silberberg, A. Radial particle displacements in Poiseuille flow of suspensions. Nature 1961, 189, 209–210. [Google Scholar] [CrossRef]
- Choi, C.R.; Kim, C.N. Inertial migration and multiple equilibrium positions of a neutrally buoyant spherical particle in Poiseuille flow. Korean J. Chem. Eng. 2010, 27, 1076–1086. [Google Scholar] [CrossRef]
- Mitchell, H.W.; Spagnolie, S.E. Sedimentation of spheroidal bodies near walls in viscous fluids: Glancing, reversing, tumbling, and sliding. J. Fluid Mech. 2015, 772, 600–629. [Google Scholar] [CrossRef] [Green Version]
- Shao, X.; Yu, Z.; Sun, B. Inertial migration of spherical particles in circular Poiseuille flow at moderately high Reynolds numbers. Phys. Fluids 2008, 20, 103307. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.H.; Wang, J.; Joseph, D.D.; Hu, H.H.; Pan, T.W.; Glowinski, R. Migration of a sphere in tube flow. J. Fluid Mech. 2005, 540, 109–131. [Google Scholar] [CrossRef] [Green Version]
- Morita, Y.; Itano, T.; Sugihara-Seki, M. Equilibrium radial positions of neutrally buoyant spherical particles over the circular cross-section in Poiseuille flow. J. Fluid Mech. 2017, 813, 750–767. [Google Scholar] [CrossRef]
- Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics: With Special Applications to Particulate Medial; Springer Science and Business Media: New York, NY, USA, 2012; Volume 1. [Google Scholar]
- Satterwhite-Warden, J.E.; Kondepudi, D.K.; Dixon, J.A.; Rusling, J.F. Co-operative motion of multiple benzoquinone disks at the air–water interface. Phys. Chem. Chem. Phys. 2015, 17, 29891–29898. [Google Scholar] [CrossRef]
- Satterwhite-Warden, J.E.; Kondepudi, D.K.; Dixon, J.A.; Rusling, J.F. Thermal-and Magnetic-Sensitive Particle Flocking Motion at the Air–Water Interface. J. Phys. Chem. B 2019, 123, 3832–3840. [Google Scholar] [CrossRef]
- Kohira, M.I.; Hayashima, Y.; Nagayama, M.; Nakata, S. Synchronized self-motion of two camphor boats. Langmuir 2001, 17, 7124–7129. [Google Scholar] [CrossRef]
- Howe, H.F.; Smallwood, J. Ecology of seed dispersal. Annu. Rev. Ecol. Syst. 1982, 13, 201–228. [Google Scholar] [CrossRef]
- Minami, S.; Azuma, A. Various flying modes of wind-dispersal seeds. J. Theor. Biol. 2003, 225, 1–14. [Google Scholar] [CrossRef]
- Kaila, V.R.; Annila, A. Natural selection for least action. R. Soc. Lond. Math. Phys. Eng. Sci. 2008, 464, 3055–3070. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Annila, A. Natural process? Natural selection. Biophys. Chem. 2007, 127, 123–128. [Google Scholar] [CrossRef] [Green Version]
- Vallino, J.J.; Huber, J.A. Using maximum entropy production to describe microbial biogeochemistry over time and space in a meromictic pond. Front. Environ. Sci. 2018, 6, 100. [Google Scholar] [CrossRef] [Green Version]
- Kondepudi, D. Self-organization, entropy production, and physical intelligence. Ecol. Psychol. 2012, 24, 33–45. [Google Scholar] [CrossRef]
- Adler, J. Chemotaxis in bacteria. Science 1966, 153, 708–716. [Google Scholar] [CrossRef]
- Dobovišek, A.; Županović, P.; Brumen, M.; Juretić, D. Maximum entropy production and maximum Shannon entropy as germane principles for the evolution of enzyme kinetics. In Beyond the Second Law; Springer: Berlin/Heidelberg, Germany, 2014; pp. 361–382. [Google Scholar]
- Goldbeter, A. Dissipative structures and biological rhythms. Chaos 2017, 27, 104612. [Google Scholar] [CrossRef]
- Goldbeter, A. Biochemical Oscillations and Cellular Rhythms. In The Molecular Bases of Periodic and Chaotic Behaviour; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Horne, C.; Smith, C.A.; Karamcheti, K. Aeroacoustic and Aerodynamic Applications of the Theory of Nonequilibrium Thermodynamics; NASA Technical Paper 3118; NASA: Washington, DC, USA, 1991. [Google Scholar]
- Ghesselini, R. Elastic free energy of an upper convected maxwell fluid undergoing fully developed planar poiseuille flow: A variational result. J. Non-Newton. Fluid Mech. 1993, 46, 229–241. [Google Scholar] [CrossRef]
- Niven, R.K. Steady state of a dissipative flow-controlled system and the maximum entropy production principle. Phys. Rev. E 2009, 80, 2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vaidya, A. MaxEP and Stable Configurations in Fluid Solid Interactions, Beyond the Second Law: Entropy Production and Non-Equilibrium Systems; Book Series: Understanding Complex Systems; Dewar, R.C., Lineweaver, C., Niven, R., Regenauer-Lieb, K., Eds.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Galdi, G.P.; Vaidya, A.; Pokorný, M.; Joseph, D.D.; Feng, J. Orientation of symmetric bodies falling in a second-order liquid at nonzero Reynolds number. Math. Models Methods Appl. Sci. 2002, 12, 1653–1690. [Google Scholar] [CrossRef] [Green Version]
- Allaire, R.; Guerron, P.; Nita, B.; Nolan, P.; Vaidya, A. On the equilibrium configurations of flexible fibers in a flow. Int. J. Non-Linear Mech. 2015, 69, 157–165. [Google Scholar] [CrossRef]
- Joseph, D.D.; Liu, Y.J.; Poletto, M.; Feng, J. Aggregation and dispersion of spheres falling in viscoelastic liquids. J. Non-Newton. Fluid Mech. 1994, 54, 45–86. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).