The Radiation Problem of a Submerged Oblate Spheroid in Finite Water Depth Using the Method of the Image Singularities System

Abstract

This study examines the hydrodynamic parameters of a unique geometry that could be used effectively for wave energy extraction applications. In particular, we are concerned with the oblate spheroidal geometry that provides the advantage of a wider impact area on waves, closer to the free surface where the hydrodynamic pressure is higher. In addition, the problem is formulated and solved analytically via a method that is robust and most importantly very fast. In particular, we develop an analytical formulation for the radiation problem of a fully submerged oblate spheroid in a liquid field of finite water depth. The axisymmetric configuration of the spheroid is considered, i.e., the axis of symmetry is perpendicular to the undisturbed free surface. In order to solve the problem, the method of the image singularities system is employed. This method allows for the expansion of the velocity potential in a series of oblate spheroidal harmonics and the derivation of analytical expressions for the hydrodynamic coefficients for the translational degrees of freedom of the body. Numerical simulations and validations are presented taking into account the slenderness ratio of the spheroid, the immersion below the free surface and the water depth. The validations ensure the correctness and the accuracy of the proposed method. Utilizing the same approach, the whole process is implemented for a disc as well, given that a disc is the limiting case of an oblate spheroid since its semi-minor axis approaches zero.

1. Introduction

The method of the Image Singularities System for an oblate spheroid relies on the distribution of singularities on the disk of the spheroid. Mathematically, the method is represented by Miloh’s oblate spheroid theorem. The proof of this theorem was given recently in the book of Chatjigeorgiou [1]. This method allows for the expression of the fundamental solution of the Laplace equation in terms of spheroidal harmonics and enables the employment of the hydrodynamic analysis with respect to the associated coordinate system. A similar method can be applied for a prolate spheroid. In that case, the method relies on the uniform distribution of singularities along the major axis of the prolate spheroid between the two foci. The relevant proof was rigorously obtained by Miloh [2].

Conducting a review of the literature, it is seen that the method of the image singularities system has been applied mainly to prolate spheroids. The pioneer who established this method was Havelock [3,4]. In the former study, he considered the moment on a fully submerged moving prolate spheroid, while in the latter study he extended his work in order to investigate the forces and the moments acting on a moving body under waves. Chatjigeorgiou and Miloh [5,6,7,8,9] studied all the hydrodynamic problems, namely, the diffraction, radiation and wave resistance problem for a submerged prolate spheroid assuming both finite and infinite water depth. They investigated both the axisymmetric and the non-axisymmetric configuration, i.e., the symmetrical axis parallel and perpendicular to the undisturbed free surface, respectively.

So far, the method of the Image Singularities System for oblate spheroids has been used in [10,11,12,13]. Chatjigeorgiou et al. [10], and Anastasiou and Chatjigeorgiou [11], investigated the solution of the diffraction problem when the oblate spheroid was situated in a liquid field of infinite [10] and finite water depth [11]. Anastasiou et al. [12,13] solved the radiation problem for an oblate spheroid assuming infinite water depth. In all these studies [10,11,12,13], the axisymmetric case of the spheroid was considered, namely, the symmetrical axis being perpendicular to the free surface.

The present study is an extension of the previous efforts aiming to tackle the radiation problem in fixed, finite water depth. The oblate spheroid is considered to perform small amplitude oscillations in the three translational modes of motion. To solve the problem, the governing boundary value problem is first formulated. Accordingly, a suitable Green’s function is determined following Wehausen and Laitone [14], which, originally, is expressed in Cartesian coordinates. The system of the Image Singularities is next employed in order to convert the Green’s function into a series of spheroidal harmonics. Thus, the velocity potential for each mode of motion is expressed as a series of multipoles, which is properly truncated, leading to a semi-analytical solution. The efficacy of the present method is ensured by comparing the associated results with the results of the respected Boundary Integral Equation (BIEΜ) code WAMIT [15]. The present study takes a step further and simulates the oblate spheroid as a disc, studying the radiation problem. The geometries are treated separately, and numerical simulations are presented for both geometries.

This paper is organized as follows: Section 2 formulates the governing boundary value problem. In Section 3, the Green’s function is defined in oblate spheroidal harmonics, and analytical expressions for the hydrodynamic coefficients are obtained. Section 4 is dedicated to the numerical results obtained for the radiation problem of an oblate spheroid. In Section 5, the formulation of the disc’s geometry is discussed and relevant results are presented. Finally, Section 6 includes a discussion and the summary of the present study.

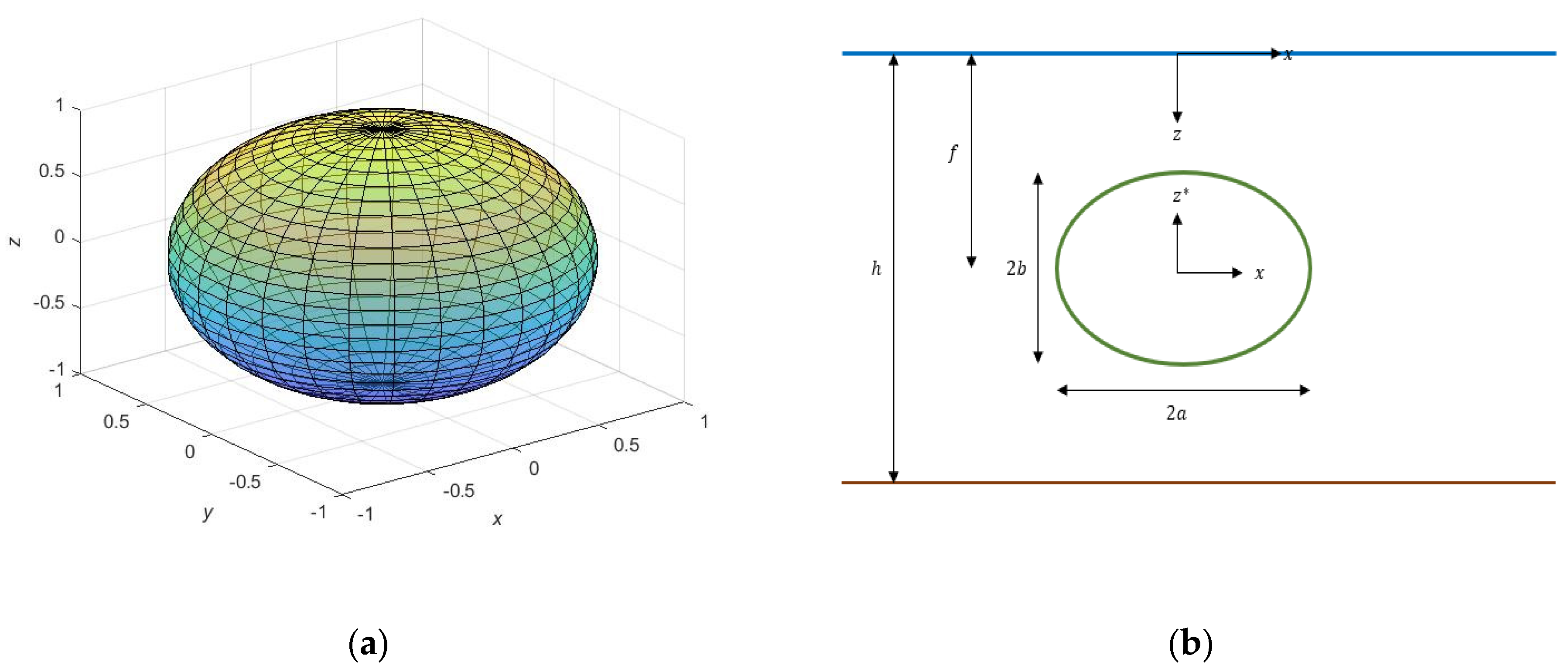
2. The Boundary Value Problem

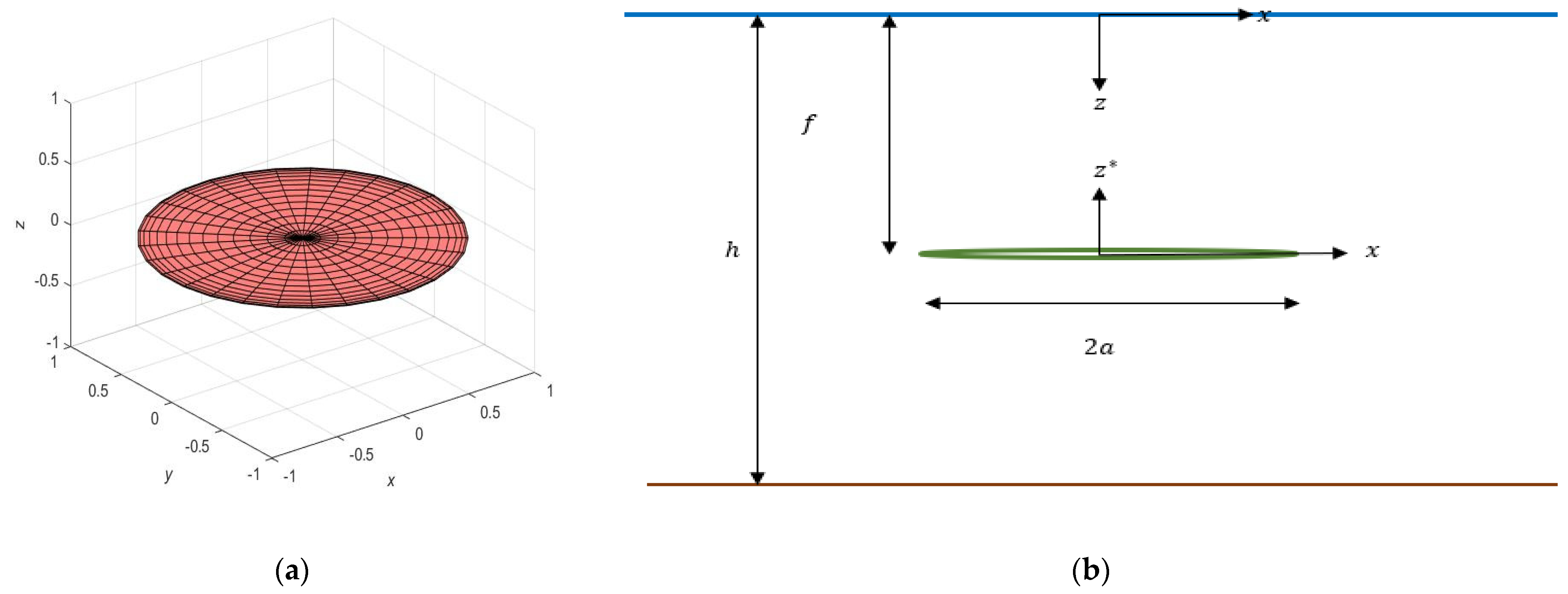
The oblate spheroid is assumed to be immersed at a distance $f$ under the undisturbed free surface and above a flat bottom of finite depth$h$. The axis of symmetry ($z$) is perpendicular to the free surface defining the “axisymmetric” configuration. In the present study, two Cartesian coordinate systems are used. The global ($x,y,z)$ system is fixed on the undisturbed free surface with its vertical z-axis pointing downwards, while the second coordinate system $\left(x,y,z^{*}\right)$ is fixed at the center of the body, with its vertical axis $z^{*}$ pointing upwards so that $z=-z^{*}+f$ (Figure 1).

The expressions that transform the oblate spheroidal coordinates to Cartesian are

$$x=c\cos hu\sin \theta \cos \psi$$

(1)

$$y=c\cos hu\sin \theta \sin \psi$$

(2)

$$z{ }^{*}=c\sin hu\cos \theta$$

(3)

where $0\le u\le \infty$, $0\le \theta \le \pi$, $0\le \psi \le 2\pi$. Additionally, $c$ denotes the half distance between the foci given by $c=\sqrt{\left(a^2-b^2\right)}$, while $a,b$ are the semi-major and the semi-minor axis, respectively. Using $\xi =\sin hu$ and $\mu =\cos \theta$, the transformation formulas are cast into

$$x=c \sqrt{1+{\xi }^2}\sqrt{1-{\mu }^2}\cos \psi$$

(4)

$$y=c \sqrt{1+{\xi }^2}\sqrt{1-{\mu }^2}\sin \psi$$

(5)

$$z^{*}=c\xi \mu$$

(6)

In the sequel, the hydrodynamic boundary value problem for spheroid that is fully immersed in a liquid field of finite water depth is considered. The spheroid undergoes small amplitude oscillations $q_j$, in surge, sway and heave. Accordingly, the velocity and the pressure fields are determined by the velocity potential $\Phi \left(x,y,z,t\right)=Re\left[\phi \left(x,y,z,\right)e^{-i\omega t}\right]$, where $i=\sqrt{-1}$, $\omega$ is the frequency of the body’s oscillation, $t$ is the time and $\phi$ is the spatial complex total radiation potential. The latter is decomposed into the sum of the unit-amplitude radiation potentials, i.e.,

$$\phi =-i\omega \sum _{j=1}^3{q}_j{\phi }_j$$

(7)

where ${\phi }_j, j=1,\dots ,3$ refer to the unit-amplitude individual radiation potentials. Each of these potentials must satisfy the Laplace equation (Equation (8)) in the entire liquid field, the combined linearized boundary condition (kinematic and dynamic) (Equation (9)) on the free surface, $z=0$, the kinematic condition (Equation (10)) on the flat bottom, $z=h$, and the body boundary condition (Equation (11)):

$${\nabla }^2{\phi }_j=0,$$

(8)

$$K{\phi }_j+\frac{\partial {\phi }_j}{\partial z}=0$$

(9)

$$\frac{\partial {\phi }_j}{\partial z}=0$$

(10)

$$\frac{\partial {\phi }_j}{\partial n}=n_j$$

(11)

where $K={\omega }^2/g$, $g$ is the gravitational acceleration and $n=\left(n_1,n_2, n_3\right)$ is the unit vector normal to the boundary of the body. Finally, the radiation potentials should comply with the far-field radiation condition for outgoing waves at infinity.

3. Definition of the Radiation Potential for the Oblate Spheroid

The $jth$ velocity potential is obtained from the following expression

$${\phi }_j=\sum _{n=0}^{\infty }\sum _{m=0}^n{A}_n^m{G}_n^m\left(i\xi ,\mu ,\psi \right),$$

(12)

where $A_n^m$ are the unknown coefficients and $G_n^m$ is the auxiliary Green’s function expressed into a series of spheroidal harmonics, which will be called the multipoles of the Green’s function.

The multipoles of the Green’s function $G_n^m\left(x,y,z\right)$ are obtained by defining the Green’s function and then employing the method of the Image Singularities system. According to the boundary value problem for the radiation problem described in the previous section, the Green’s function satisfies Equations (8)–(10) and is in accord with the radiation condition reads [14]

$$\begin{gathered} G\left(x-x^{\prime },y-y^{\prime },z\right) \\ =\frac{1}{\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2+{\left(z-f\right)}^2}}+\frac{1}{\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2+{\left(z+f-2h\right)}^2}} \\ +\frac{1}{\pi }PV{\int }_0^{\infty }{\int }_{-\pi }^{\pi }Q\left(k,h\right)\cos hk\left(h-z\right) e^{ik\left[\left(x-x^{\prime }\right)\cos \alpha +\left(y-y^{\prime }\right)\sin \alpha \right]}dadk \\ +i{\int }_{-\pi }^{\pi }{Q}_0\left(k_0,h\right)\cos h{k}_0\left(h-z\right)e^{i{k}_0\left[\left(x-x^{\prime }\right)\cos \alpha +\left(y-y^{\prime }\right)\sin \alpha \right]}da, \end{gathered}$$

(13)

while

$$Q\left(k,h\right)=\frac{\left(K+k\right)e^{-kh}\cos hk\left(h-f\right)}{k\sin hkh-K\cos hkh},$$

(14)

$$Q_0\left(k_0,h\right)=\frac{\left(K+k_0\right)e^{-k_{0}h}\cos h{k}_0\left(h-f\right)\sin h{k}_{0}h}{Kh+{\sin h}^2{k}_{0}h}.$$

(15)

Assuming $h \to \infty$, the Green’s function (Equation (13)) leads to the expression related to the infinite water depth (see e.g., [12]).

Here, $\left(x,y,z-f\right)$ denote the coordinates of the source point and $\left(x^{\prime },y^{\prime },0\right)$ denote the coordinates of the field point, the acronym $PV$ denotes the Cauchy Principal Value Integral and $k_0$ is the positive root of the dispersion equation $K=k_0\tan h{k}_{0}h$.

According to Miloh’s theorem for the Image Singularity System, an oblate spheroidal harmonic is obtained by [1].

$$P_n^m\left(\mu \right)Q_n^m\left(i\xi \right)\cos m\psi =\frac{{(-1)}^m}{2\pi P_n^m\left(i0\right)}\frac{\left(n+m\right)!}{\left(n-m\right)!}{\int }_0^{2\pi }{\int }_0^1\frac{P_n^m\left({\mu }^{\prime }\right)\cos m{\psi }^{\prime }}{\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2+{\left(z-f\right)}^2}}d{\mu }^{\prime }d{\psi }^{\prime }.$$

(16)

Note that $z-f$ is the center of the spheroid. Clearly, the flow around the body is symmetrical, and accordingly only the symmetrical, cosine, and harmonics $P_n^m\left(\mu \right)Q_n^m\left(i\xi \right)\cos m\psi$ are retained, where $P_n^m$ and $Q_n^m$ denote the $n$th degree and $m$th order of the associated Legendre functions of the first and the second kind, respectively.

Hence, the auxiliary potentials $G_n^m$ will be given by

$$G_n^m\left(x,y,z\right)=\frac{{(-1)}^m}{2\pi P_n^m\left(i0\right)}\frac{\left(n+m\right)!}{\left(n-m\right)!}{\int }_0^{2\pi }{\int }_0^1{P}_n^m\left({\mu }^{\prime }\right)\cos m{\psi }^{\prime }G\left(x-x^{\prime },y-y^{\prime },z\right)d{\mu }^{\prime }d{\psi }^{\prime }.$$

(17)

Next, using Equations (13), (16) and (17) yields

$$\begin{gathered} G_n^m\left(x,y,z\right)=P_n^m\left(\mu \right)Q_n^m\left(i\xi \right)\cos m\psi \\ +\frac{{(-1)}^m}{2\pi P_n^m\left(i0\right)}\frac{\left(n+m\right)!}{\left(n-m\right)!}{\int }_0^{2\pi }{\int }_0^1\frac{P_n^m\left({\mu }^{\prime }\right)\cos m{\psi }^{\prime }}{\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2+{\left(z+f-2h\right)}^2}}d{\mu }^{\prime }d{\psi }^{\prime } \\ +\frac{{(-1)}^m}{2{\pi }^2{P}_n^m\left(i0\right)}\frac{\left(n+m\right)!}{\left(n-m\right)!}PV{\int }_0^{\infty }{\int }_{-\pi }^{\pi }{\int }_0^1{\int }_0^{2\pi }\cos m{\psi }^{\prime }{P}_n^m\left({\mu }^{\prime }\right)Q\left(k,h\right)\cos hk\left(h+z\right) \\ \times e^{ik\left[\left(x-x^{\prime }\right)\cos a+\left(y-y^{\prime }\right)\sin a\right]}d{\psi }^{\prime }d{\mu }^{\prime }dadk \\ +i\frac{{(-1)}^m}{2\pi P_n^m\left(i0\right)}\frac{\left(n+m\right)!}{\left(n-m\right)!}{\int }_{-\pi }^{\pi }{\int }_0^{2\pi }{\int }_0^1{P}_n^m\left({\mu }^{\prime }\right)\cos m{\psi }^{\prime }{Q}_0\left(k_0,h\right) \\ \times \cos h{k}_0\left(h-z\right)e^{i{k}_0\left[\left(x-x^{\prime }\right)\cos a+\left(y-y^{\prime }\right)\sin a\right]}d{\mu }^{\prime }d{\psi }^{\prime }da. \end{gathered}$$

(18)

In order to express Equation (18) in oblate spheroidal coordinates, more manipulations need to be performed. The integral terms in Equation (18) are denoted by $I_1, I_2$ and $I_3$, respectively. Each of these integrals is treated separately. The analysis starts with $I_1$. Hence,

$$I_1=\frac{{(-1)}^m}{2\pi P_n^m\left(i0\right)}\frac{\left(n+m\right)!}{\left(n-m\right)!}{\int }_0^{2\pi }{\int }_0^1\frac{P_n^m\left({\mu }^{\prime }\right)\cos m{\psi }^{\prime }}{\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2+{\left(z+f-2h\right)}^2}}d{\mu }^{\prime }d{\psi }^{\prime }.$$

(19)

Equation (19) is treated using the Fourier transform of the inverse square root [1] (p. 246).

$$\frac{1}{\sqrt{{\left(x-x^{\prime }\right)}^2+{\left(y-y^{\prime }\right)}^2+{\left(z+f-2h\right)}^2}}=\frac{1}{2\pi }{\int }_0^{\infty }{\int }_{-\pi }^{\pi }{e}^{-k\left(2h-z-f\right)+ik\left[\left(x-x^{\prime }\right)\cos a+\left(y-y^{\prime }\right)\sin a\right]}dadk.$$

(20)

Introducing Equation (20) into Equation (19) gives

$$I_1=\frac{{(-1)}^m}{{\left(2\pi \right)}^2{P}_n^m\left(i0\right)}\frac{\left(n+m\right)!}{\left(n-m\right)!}{\int }_0^{2\pi }{\int }_0^1{\int }_0^{\infty }{\int }_{-\pi }^{\pi }{P}_n^m\left({\mu }^{\prime }\right)\cos m{\psi }^{\prime }{e}^{-k\left(2h-z-f\right)+ik\left[\left(x-x^{\prime }\right)\cos a+\left(y-y^{\prime }\right)\sin a\right]}dadkd{\mu }^{\prime }d\psi ΄,$$

(21)

$I_1$ can be expressed in “axisymmetric” oblate spheroidal coordinates using the following expression for the exponential term [10]:

$$e^{k{z}^{*}+ik\left(x\cos a+y\sin a\right)}=\sum _{s=0}^{\infty }\sum _{t=0}^s{E}_s^t\left(\cos t\psi \cos ta+\sin t\psi \sin ta\right)P_s^t\left(\mu \right)P_s^t\left(i\xi \right),$$

(22)

where

$$E_s^t={\left(-1\right)}^s{i}^{s-t}{\epsilon }_t\left(2s+1\right)\frac{\left(s-t\right)!}{\left(s+t\right)!}\sqrt{\frac{\pi }{2kc}}{J}_{s+1/2}\left(kc\right).$$

(23)

Here, ${\epsilon }_0=1$; ${\epsilon }_t=2, t=1,2,\dots$; and $J_{s+1/2}$ make up the Bessel function of the first kind with fractional order $s+1/2$. Note that the coordinate system that is used on the left-hand side term of Equation (22) concerns the body-fixed system $\left(x,y,z^{*}\right)$, while $z=-z^{*}+f$ (Figure 1b). According to Equation (22), one can write

$$e^{k{z}^{*}-ik\left(x\cos a+y\sin a\right)}=\sum _{s=0}^{\infty }\sum _{t=0}^s{\left(-1\right)}^t{E}_s^t\left(\cos t\psi \cos ta+\sin t\psi \sin ta\right)P_s^t\left(\mu \right)P_s^t\left(i\xi \right).$$

(24)

Therefore, the complex integral term $I_1$ takes the form, after laborious mathematical manipulations,

$$I_1=\sum _{s=0}^{\infty }\sum _{t=0}^s{H}_{ns}^{mt}{P}_s^t\left(\mu \right)P_s^t\left(i\xi \right)\cos t\psi ,$$

(25)

where

$$H_{ns}^{mt}=\frac{{\left(-1\right)}^{n+t}}{4c}{i}^{n-m+s-t}\frac{\left(n+m\right)!}{\left(n-m\right)!}\frac{\left(s-t\right)!}{\left(s+t\right)!}\left(2s+1\right)\frac{2\pi }{{\epsilon }_m}{\epsilon }_t{\delta }_{tm}{\int }_0^{\infty }\frac{e^{-2k\left(h-f\right)}}{k}{J}_{n+1/2}\left(kc\right)J_{s+1/2}\left(kc\right)dk.$$

(26)

using the same reasoning and denoting

$$I_2=\frac{{(-1)}^m}{2{\pi }^2{P}_n^m\left(i0\right)}\frac{\left(n+m\right)!}{\left(n-m\right)!}PV{\int }_0^{\infty }{\int }_{-\pi }^{\pi }{\int }_0^1{\int }_0^{2\pi }\cos m{\psi }^{\prime }{P}_n^m\left({\mu }^{\prime }\right)Q\left(k,h\right)\cos hk\left(h+z\right)e^{ik\left[\left(x-x^{\prime }\right)\cos a+\left(y-y^{\prime }\right)\sin a\right]}d{\psi }^{\prime }d{\mu }^{\prime }dadk$$

(27)

$$I_3=i\frac{{(-1)}^m}{2\pi P_n^m\left(i0\right)}\frac{\left(n+m\right)!}{\left(n-m\right)!}{\int }_{-\pi }^{\pi }{\int }_0^{2\pi }{\int }_0^1{P}_n^m\left({\mu }^{\prime }\right)\cos m{\psi }^{\prime }{Q}_0\left(k_0,h\right)\times \cos h{k}_0\left(h-z\right)e^{i{k}_0\left[\left(x-x^{\prime }\right)\cos a+\left(y-y^{\prime }\right)\sin a\right]}d{\mu }^{\prime }d{\psi }^{\prime }da.$$

(28)

The aforementioned components are elaborated with the aid of Equations (22) and (24) and carrying out the integrations. The relevant expansions in spheroidal harmonics obtain the following form:

$$I_2=\sum _{s=0}^{\infty }\sum _{t=0}^s{D}_{ns}^{mt}{P}_s^t\left(\mu \right)P_s^t\left(i\xi \right)\cos t\psi$$

(29a)

$$I_3=\sum _{s=0}^{\infty }\sum _{t=0}^s{L}_{ns}^{mt}{P}_s^t\left(\mu \right)P_s^t\left(i\xi \right)\cos t\psi$$

(29b)

where

$$\begin{gathered} D_{ns}^{mt}=\frac{{\left(-1\right)}^n}{4c}{i}^{n-m+s-t}\frac{\left(n+m\right)!}{\left(n-m\right)!}\frac{\left(s-t\right)!}{\left(s+t\right)!}\left(2s+1\right){\epsilon }_t\frac{2\pi }{{\epsilon }_m} {\delta }_{tm} \\ \left({\left(-1\right)}^{s}PV{\int }_0^{\infty }Q\left(k,h\right)\frac{e^{k\left(h-f\right)}}{k}{J}_{n+1/2}\left(kc\right)J_{s+1/2}\left(kc\right)dk+{\left(-1\right)}^{t}PV{\int }_0^{\infty }Q\left(k,h\right)\frac{e^{-k\left(h-f\right)}}{k}{J}_{n+1/2}\left(kc\right)J_{s+1/2}\left(kc\right)dk\right) \end{gathered}$$

(30)

and

$$\begin{gathered} L_{ns}^{mt}=\frac{{\left(-1\right)}^n}{4c}{i}^{n-m+s-t+1}{\epsilon }_t\frac{2{\pi }^2}{{\epsilon }_m}{\delta }_{tm}\frac{\left(n+m\right)!}{\left(n-m\right)!}\frac{\left(s-t\right)!}{\left(s+t\right)!}\left(2s+1\right) \\ \times \frac{Q_0\left(k_0,h\right)}{k_0}{J}_{n+1/2}\left(kc\right)J_{s+1/2}\left(kc\right)\left({\left(-1\right)}^s{e}^{k_0\left(h-f\right)}+{\left(-1\right)}^t{e}^{-k_0\left(h-f\right)}\right). \end{gathered}$$

(31)

The final relation that expresses the multipoles of the Green’s function as a series of spheroidal harmonics is

$$G_n^m\left(i\xi ,\mu ,\psi \right)=P_n^m\left(\mu \right)Q_n^m\left(i\xi \right)\cos m\psi +\sum _{s=0}^{\infty }\sum _{t=0}^s{C}_{ns}^{mt}{P}_s^t\left(\mu \right)P_s^t\left(i\xi \right)\cos t\psi ,$$

(32)

while

$$C_{ns}^{mt}=H_{ns}^{mt}+D_{ns}^{mt}+L_{ns}^{mt}.$$

(33)

The individual radiation potentials can now be written as

$${\phi }_j=\sum _{n=0}^{\infty }\sum _{m=0}^n{A}_n^m{P}_n^m\left(\mu \right)Q_n^m\left(i\xi \right)\cos m\psi +\sum _{n=0}^{\infty }\sum _{m=0}^n{A}_n^m\sum _{s=0}^{\infty }\sum _{t=0}^s{C}_{ns}^{mt}{P}_s^t\left(\mu \right)P_s^t\left(i\xi \right)\cos t\psi ,$$

(34)

where $A_n^m$ are unknown expansion coefficients to be obtained by utilizing the body boundary conditions for each mode of motion, namely,

$${\frac{\partial {\varphi }_1}{\partial \xi }|}_{\xi ={\xi }_0}=n_1, \xi ={\xi }_0={\tan h}^{-1}\left(b/a\right),$$

(35)

$${\frac{\partial {\varphi }_3}{\partial \xi }|}_{\xi ={\xi }_0}=n_3, \xi ={\xi }_0={\tan h}^{-1}\left(b/a\right)$$

(36)

where

$$n_1=-\frac{b{P}_1^1\left(\mu \right)\cos \psi }{{\left({\xi }_0^2+{\mu }^2\right)}^{1/2}},$$

(37)

$$n_3=\frac{\alpha P_1^0\left(\mu \right)}{{\left({\xi }_0^2+{\mu }^2\right)}^{1/2}}.$$

(38)

It is worth mentioning that due to the axisymmetric configuration of the spheroid, the surge and the sway oscillations are identical. Hence, only the surge ($j=1)$ and the heave ($j=3)$ modes of motion are considered.

Therefore, taking into account Equations (37) and (38) and utilizing the orthogonality relations of the trigonometric and the associated Legendre functions [16], the following linear systems are obtained for the unknown expansion coefficients of the radiation potentials

$$A_l^r+\sum _{n=0}^{\infty }\sum _{m=0}^n{a}_l^r{A}_n^m{C}_{nl}^{mr}=i\frac{b}{a}\frac{{\delta }_{1r}{\delta }_{1l}}{{\dot{Q}}_l^r\left(i{\xi }_0\right)},$$

(39)

$$A_l^r+\sum _{n=0}^{\infty }\sum _{m=0}^n{a}_l^r{A}_n^m{C}_{nl}^{mr}=-i\frac{{\delta }_{0r}{\delta }_{1l}}{{\dot{Q}}_l^r\left(i{\xi }_0\right)},$$

(40)

where $a_l^r={\dot{P}}_l^r\left(i{\xi }_0\right) /{\dot{Q}}_l^r\left(i{\xi }_0\right)$ and the upper dot denotes differentiation with respect to the argument. Equations (39) and (40) represent a complex linear system that can be solved effectively using standard matrix techniques. The system must be truncated to a finite number of modes that suffice to ensure convergence of the calculations.

The calculation of the unknown coefficients $A_n^m$ completes the solution of the radiation problem in each mode of motion and allows for the derivation of the hydrodynamic added mass and the damping coefficient via the surface integral

$${\mu }_{ij}-\frac{i}{\omega }{\lambda }_{ij}=-\rho {\int }_S^{}{\varphi }_i{n}_{j}dS$$

(41)

where ${\mu }_{ij}$ and${\lambda }_{ij}, i,j=1$, and $3$ denotes the added mass and hydrodynamic damping coefficients, respectively, while $\rho$ is the water density. The integration is performed on the wetted surface $S$ of the spheroid.

The differential area of the spheroid reads

$$dS=c^{2}a {\left({\xi }_0^2+{\mu }^2\right)}^{1/2} d\mu d\psi .$$

(42)

The final expressions that calculate the hydrodynamic added masses and damping coefficients in the surge and heave modes of motion are

$${\mu }_{11}-\frac{i}{\omega }{\lambda }_{11}=\frac{1}{a{\dot{P}}_1^1\left(i{\xi }_0\right)}\left(\frac{i b P_1^1\left(i{\xi }_0\right)}{a}+\frac{2A_1^1}{{\xi }_0^2+1}\right),$$

(43)

$${\mu }_{33}-\frac{i}{\omega }{\lambda }_{33}=\frac{1}{b{\dot{P}}_1^0\left(i{\xi }_0\right)}\left(i P_1^0\left(i{\xi }_0\right)+\frac{A_1^0}{{\xi }_0^2+1}\right).$$

(44)

The added mass and the damping coefficients have been normalized by $4/3\pi \rho b{a}^2$ and$4/3\pi \rho b{a}^2\omega$, respectively.

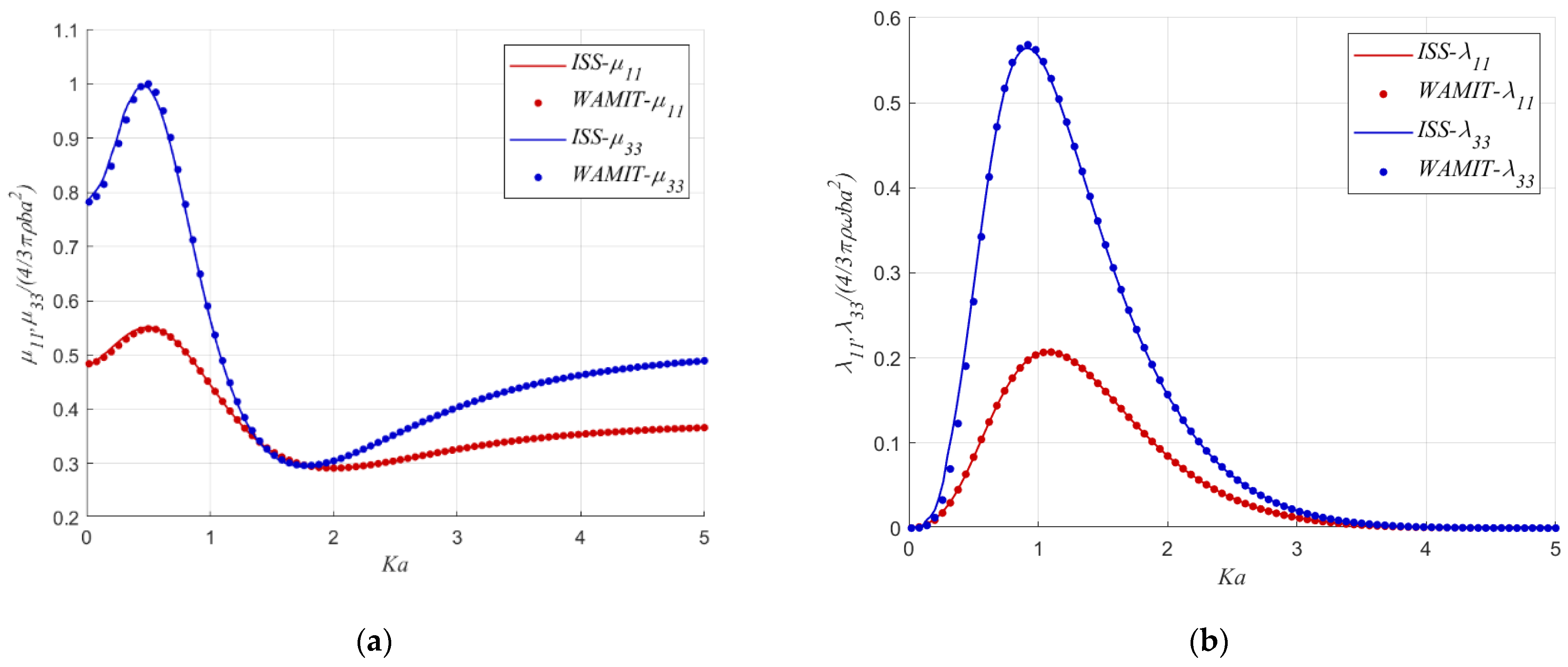
4. Numerical Results

In this section, the accuracy and robustness of the developed semi-analytical solution are represented. In order to achieve this task, the results obtained using the present method are compared with the numerical predictions of the WAMIT code [15], which is based on the well-known Boundary Integral Equation Method (BIEM). The corresponding results are shown in Figure 2, Figure 3 and Figure 4. Figure 2, Figure 3 and Figure 4 show the hydrodynamic added mass and damping coefficient in the surge and the heave directions when the water depth is equal to $h=20a, 10a$ and $5a$. Practically speaking, $h=20a, 10a$and $5a$ represent the infinite, intermediate and shallow water depth cases, respectively. These Figures show an oblate spheroid of slenderness ratio $a/b=$ $1.25$. For $h=20a$ and $h=10a$, the immersion depth is equal to $f=1.5a$, while for $h=5a$ the immersion depth is equal to $f=1.1a$. The abbreviation ISS “Image Singularity System” corresponds to the present semi-analytical solution. Figure 2, Figure 3 and Figure 4 manifest an excellent agreement with the results obtained using WAMIT [15].

The numerical results that appear in Figure 2, Figure 3 and Figure 4 have been obtained by truncating the infinite series. In order to achieve a convergence up to the fourth decimal digit, n = 5 modes (in the semi-analytical formulation) have been employed (

Table 1. Convergence sequence of the normalized surge added mass and damping coefficients for several numbers of modes (oblate spheroid with a/b = 1.25, immersion f = 1.5a and water depth h = 10a).

Ka	n = 2		n = 5		n = 8
	a11	b11	a11	b11	a11	b11
0.00	0.45299	0.00000	0.45301	0.00000	0.45301	0.00000
0.10	0.46103	0.00149	0.46106	0.00149	0.46106	0.00149
0.20	0.47088	0.00759	0.47092	0.00759	0.47092	0.00759
0.30	0.47799	0.01973	0.47804	0.01973	0.47804	0.01973
0.40	0.47986	0.03519	0.47994	0.03521	0.47994	0.03521
0.50	0.47598	0.05071	0.47609	0.05076	0.47609	0.05076
0.60	0.46723	0.06393	0.46736	0.06404	0.46736	0.06404
0.70	0.45525	0.07349	0.45537	0.07368	0.45537	0.07368
0.80	0.44178	0.07897	0.44185	0.07923	0.44185	0.07923
0.90	0.42830	0.08061	0.42829	0.08094	0.42829	0.08094
1.00	0.41585	0.07907	0.41574	0.07943	0.41574	0.07943
2.00	0.37896	0.02194	0.37871	0.02154	0.37871	0.02154
3.00	0.39452	0.00249	0.39471	0.00231	0.39471	0.00231
4.00	0.40311	0.00016	0.40324	0.00014	0.40324	0.00014
5.00	0.40685	0.00001	0.40692	0.00001	0.40693	0.00001

and

Table 2. Convergence sequence of the normalized heave added mass and damping coefficients for several numbers of modes (oblate spheroid with a/b = 1.25, immersion f = 1.5a and water depth h = 10a).

Ka	n = 2		n = 5		n = 8
	a33	b33	a33	b33	a33	b33
0.00	0.70259	0.00000	0.70265	0.00000	0.70265	0.00000
0.10	0.72488	0.00415	0.72498	0.00415	0.72498	0.00415
0.20	0.75257	0.02159	0.75271	0.02160	0.75271	0.02160
0.30	0.77211	0.05691	0.77232	0.05694	0.77232	0.05694
0.40	0.77531	0.10195	0.77560	0.10205	0.77560	0.10205
0.50	0.76051	0.14588	0.76088	0.14612	0.76088	0.14612
0.60	0.73150	0.18087	0.73189	0.18133	0.73189	0.18133
0.70	0.69456	0.20319	0.69487	0.20389	0.69487	0.20389
0.80	0.65572	0.21272	0.65583	0.21365	0.65583	0.21365
0.90	0.61929	0.21154	0.61910	0.21261	0.61910	0.21261
1.00	0.58770	0.20251	0.58715	0.20360	0.58715	0.20360
2.00	0.51163	0.05132	0.51098	0.05004	0.51098	0.05004
3.00	0.55082	0.00593	0.55142	0.00540	0.55142	0.00540
4.00	0.57193	0.00040	0.57233	0.00033	0.57233	0.00033
5.00	0.58123	0.00002	0.58147	0.00001	0.58147	0.00001

). Table 1 and Table 2 present the hydrodynamic coefficients in the surge and the heave motion for an oblate spheroid with slenderness ratio $a/b=$ $1.25$, immersion $f=1.5a$ and water depth $h=10a$.

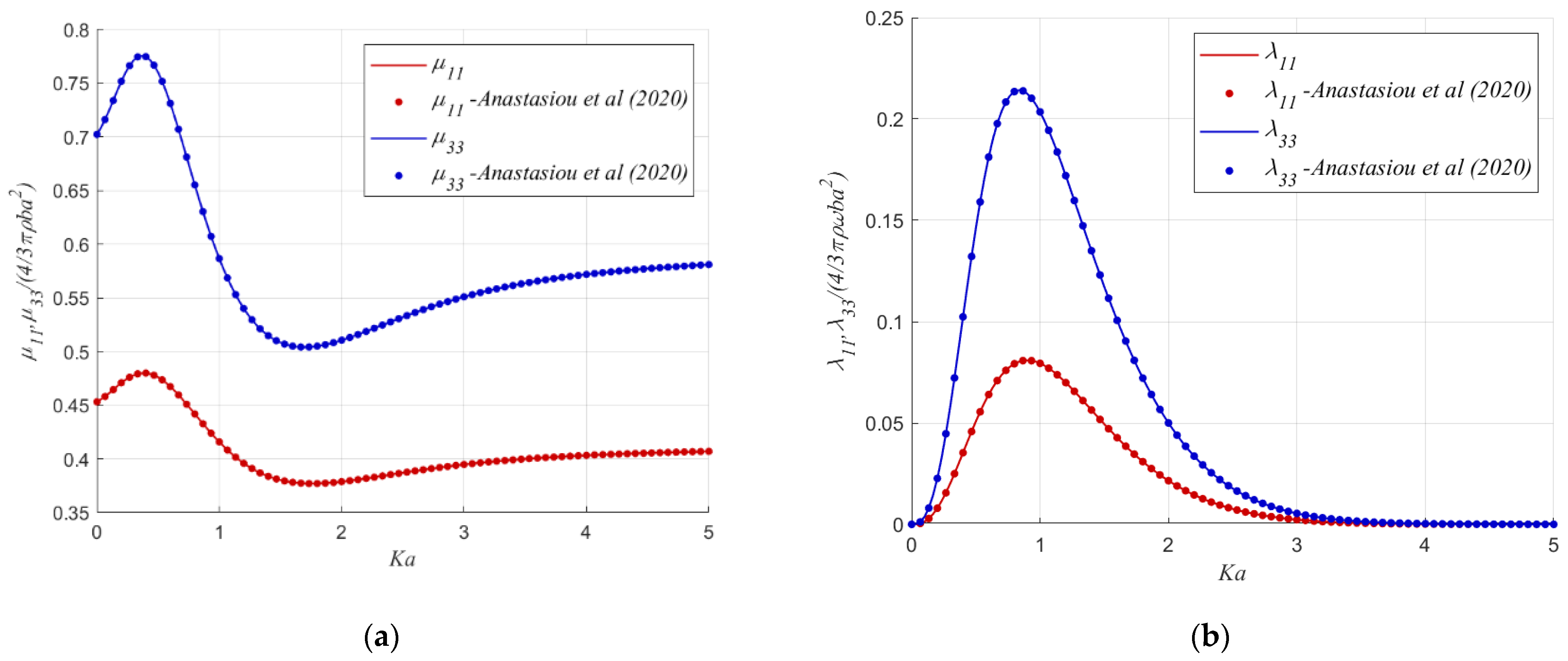
The results that are obtained from the present method are compared against the results reported in [12], which concern the infinite water depth case. Here, the infinite water depth was simulated using $h=50a$. The associated numerical predictions are shown in Figure 5.

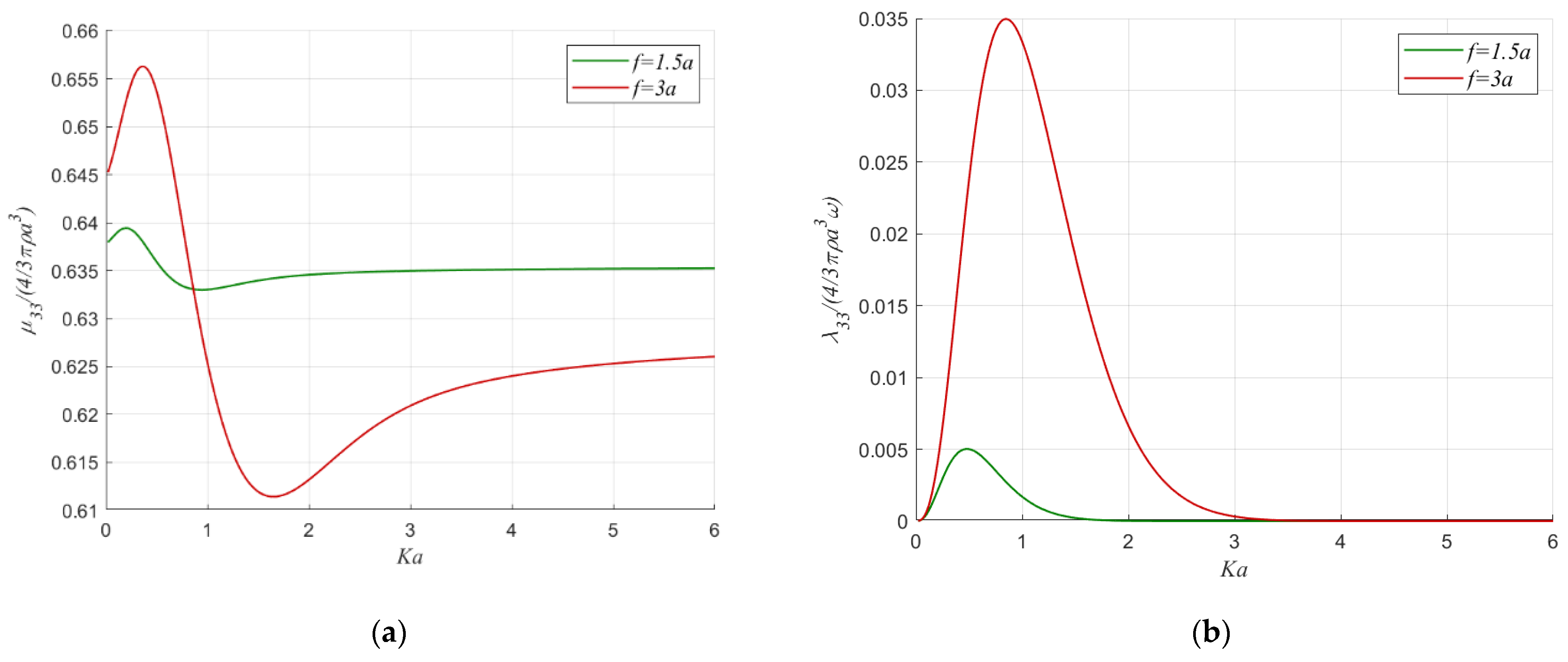
Figure 6 and Figure 7 show the hydrodynamic added mass and damping coefficients in the heave and the surge modes of motion of an oblate spheroid with slenderness ratio $a/b=$ $1.25$, immersion $f=1.01a$ and water depth $h=5a.$ By comparing the results shown in Figure 6 and Figure 7 with those given in Figure 4, it is seen that when the water depth is constant, equal to $h=5a$, and the immersion depth changes, the damping coefficient increases with the decrease of the immersion below the free surface. It is clearly seen that larger immersion depths lead to a smoother variation of the added mass for both modes of motion.

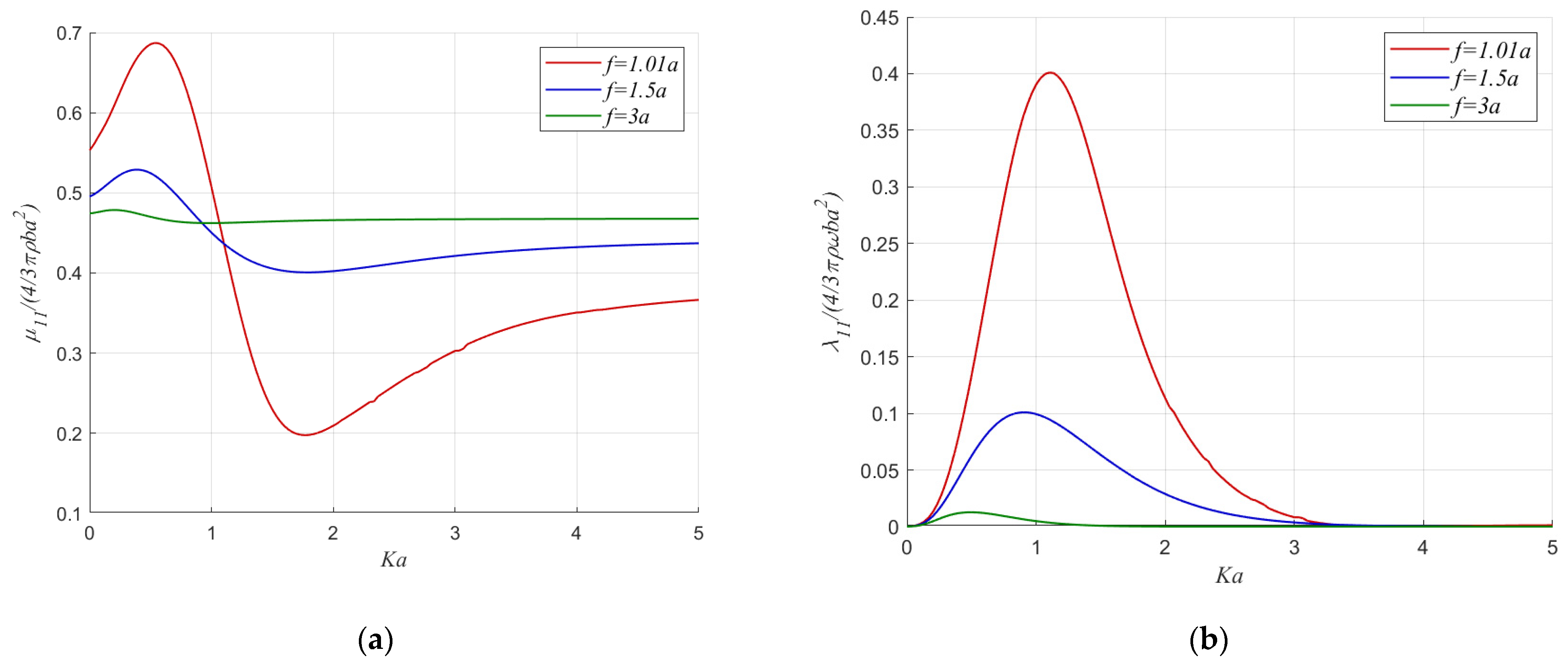
Further, the discussion is extended to the effect of the immersion below the free surface on the surge and the heave hydrodynamic coefficients. The model is a spheroid with slenderness ratio $a/b=$ $1.1$, in a liquid field of $h=10a$. Three different immersions, f, are examined, i.e., $1.01a, 1.5a$, and $3a$ (Figure 8 and Figure 9). In fact, the conclusions drawn previously for the $a/b=$ $1.25$ apply for $a/b=$ $1.1$, as well.

Finally, Figure 10 and Figure 11 investigate an extreme situation where the spheroid nearly touches the bottom. This case is simulated assuming $f=9a$, $h=10a$ and slenderness ratio $a/b=1.1$. It is clearly evident that the added mass is practically constant with the oscillation frequency, while the hydrodynamic damping is negligible.

5. The Special Case of a Disc

The approach taken in the aforementioned sections can be successfully employed for a fully submerged disc since an oblate spheroid can simulate a disc by assuming that the semi-minor axis of the spheroid tends to zero ($b\to 0$). Therefore, the semi-focal distance asymptotes to the semi-major axis, $c\to a$, ${\xi }_0\to 0$. The schematic of the problem is depicted in Figure 12.

The whole formulation described in the aforementioned sections remains the same. Nevertheless, the limiting case ${\xi }_0\to 0$ provides the following closed form expressions for the associate Legendre functions, i.e., [16].

$$P_n^m\left(i{\xi }_0\right)=\frac{2^m{\left(-1\right)}^{-1/2m}\sqrt{\pi }}{\Gamma \left(\frac{1}{2}-\frac{1}{2}n-\frac{1}{2}m\right) \Gamma \left(1+\frac{1}{2}n-\frac{1}{2}m\right)}, {\xi }_0\to 0$$

(45)

$$Q_n^m\left(i{\xi }_0\right)=e^{im\pi }{\pi }^{\frac{1}{2}}{2}^m{\left({\left(i{\xi }_0\right)}^2-1\right)}^{-\frac{1}{2}m}\frac{\Gamma \left(\frac{1}{2}+\frac{n}{2}+\frac{m}{2}\right)}{2\Gamma \left(1+\frac{n}{2}-\frac{m}{2}\right)}{e}^{\pm \frac{i1}{2}\pi }F\left(-\frac{n}{2}-\frac{m}{2},\frac{1}{2}+\frac{n}{2}-\frac{m}{2};\frac{1}{2};{\left(i{\xi }_0\right)}^2\right), {\xi }_0\to 0$$

(46)

where$\Gamma$ is the gamma function and $F$ stands for the hypergeometric function.

Apparently for the disc case, only the heaving oscillations are important. The disc is fully immersed, and the axis of symmetry is perpendicular to the undisturbed free surface. Two immersions depths are studied $(f=1.5a$ and $f=3a),$ and the water depth was assumed to be infinite. The relevant results are shown in Figure 13. The added mass and the damping coefficients have been normalized by $4/3\pi \rho a^3$ and$4/3\pi \rho a^3\omega$, respectively.

6. Conclusions

The present study developed an efficient method for the calculation of the hydrodynamic coefficients of oblate spheroids with vertical axis of symmetry. The motivation behind the analysis conducted is focused on the rigorous computation of added masses and damping coefficients of the spheroids, given that the concerned geometry is very promising for the hydrodynamic interaction of point absorbers for wave energy extraction.

The method of image singularities is used in order to solve the radiation problem of an immersed axisymmetric oblate spheroid in a liquid field of fixed, finite water depth. This method is a powerful tool as it effectively transforms the governing Green’s function into a series of spheroidal harmonics. The latter are assumed to compose the radiation potential. Simple, analytical formulas for the hydrodynamic added mass and damping coefficients are obtained. The numerical results of the present method are validated against the results obtained from a well-known BIEM code. The excellent agreement ensured the accuracy, reliability and robustness of the developed semi-analytical formulation. In addition, numerical simulations have been performed taking into account the immersion depth, the water depth and the slenderness ratio of the spheroid. The obtained results of the study showed that these parameters have a direct impact on the hydrodynamic added mass and the damping coefficients. Finally, a fully submerged disc was investigated, which was simulated by assuming an oblate spheroid of zero semi-minor axis. The calculations were carried out by using the asymptotic expansions of the associate Legendre functions.