Simplified CFD Model for Perforated Tile with Distorted Outflow
Abstract
:1. Introduction
2. Tile Flow Experiment
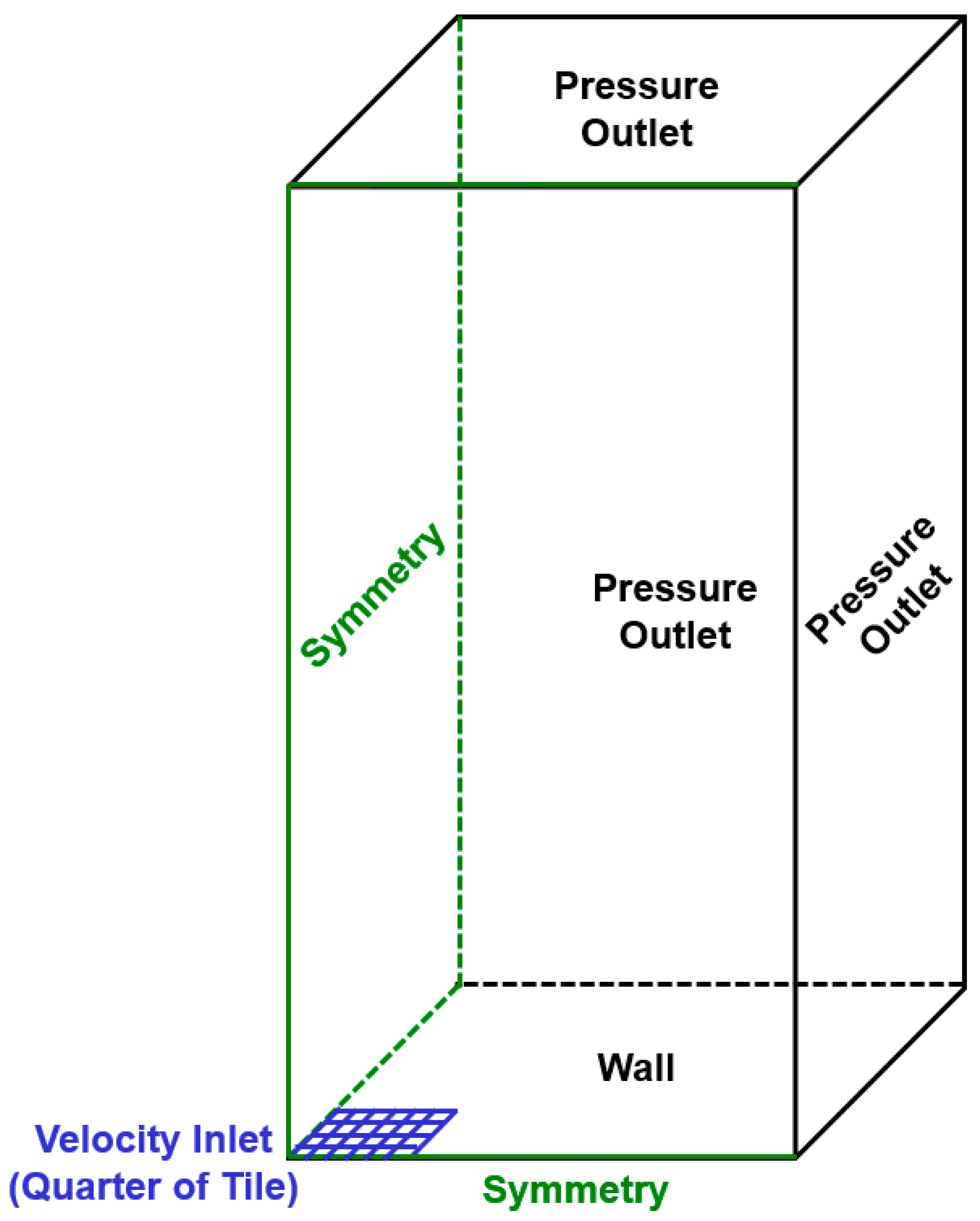
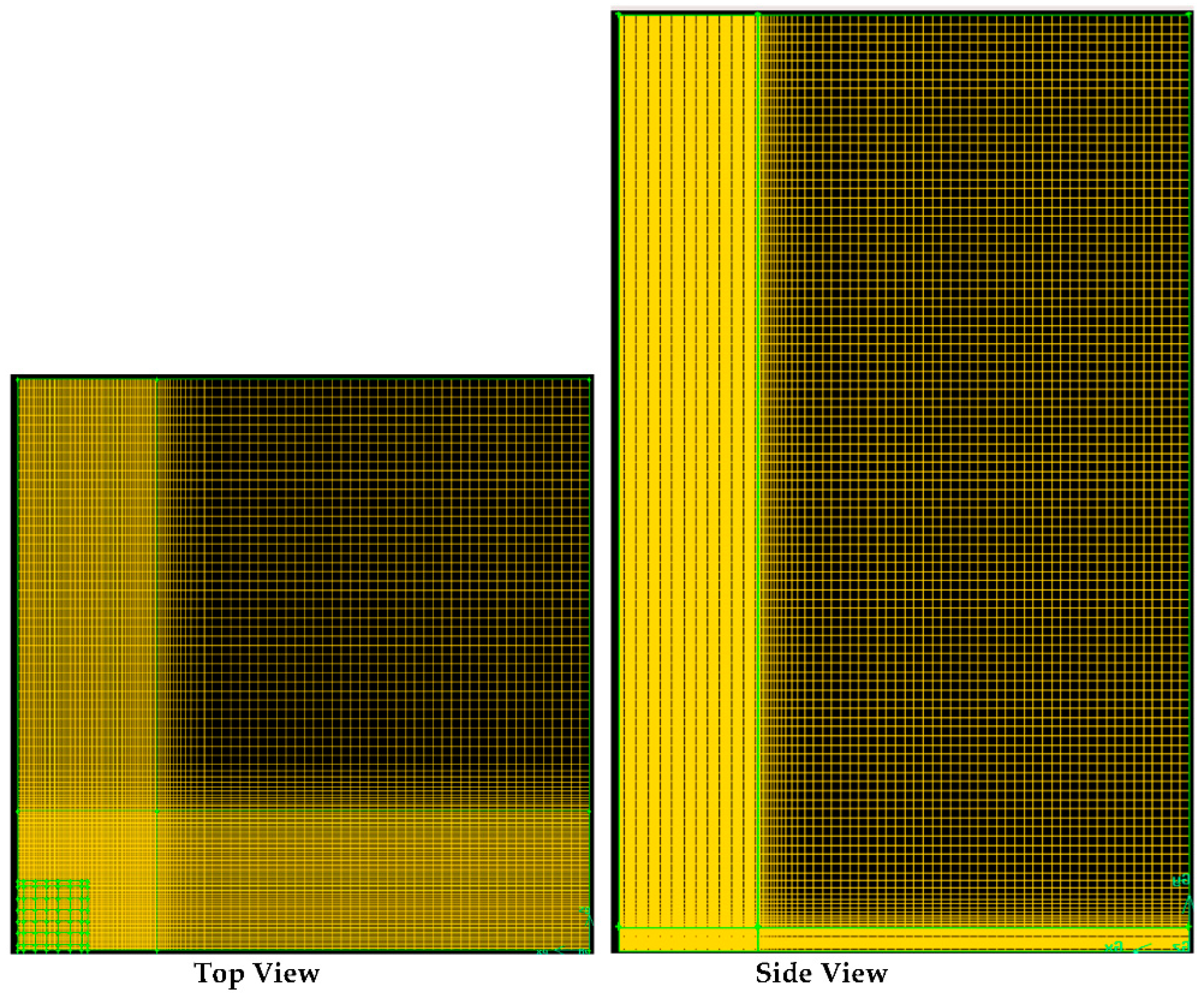
3. Tile Flow Modeling
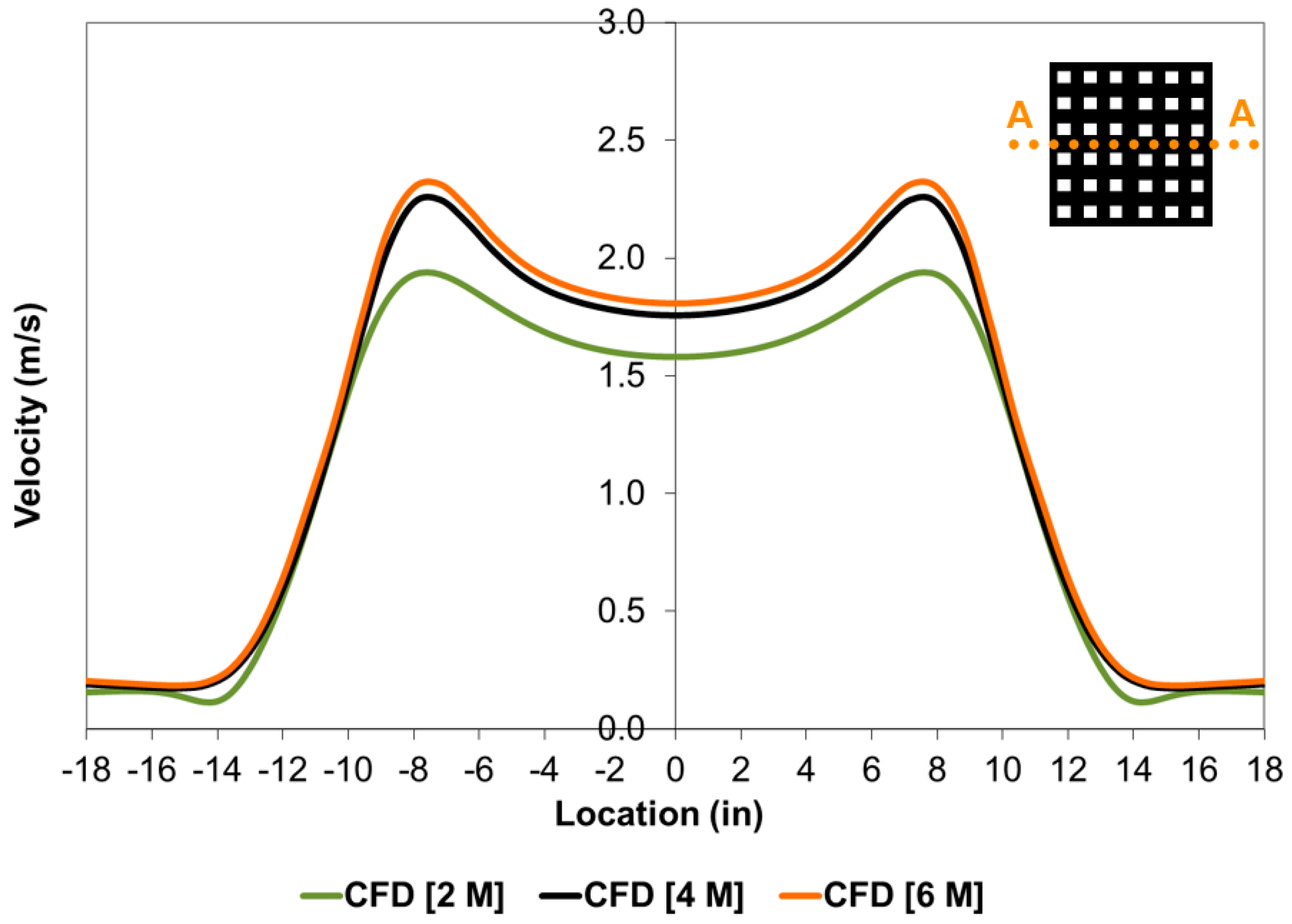
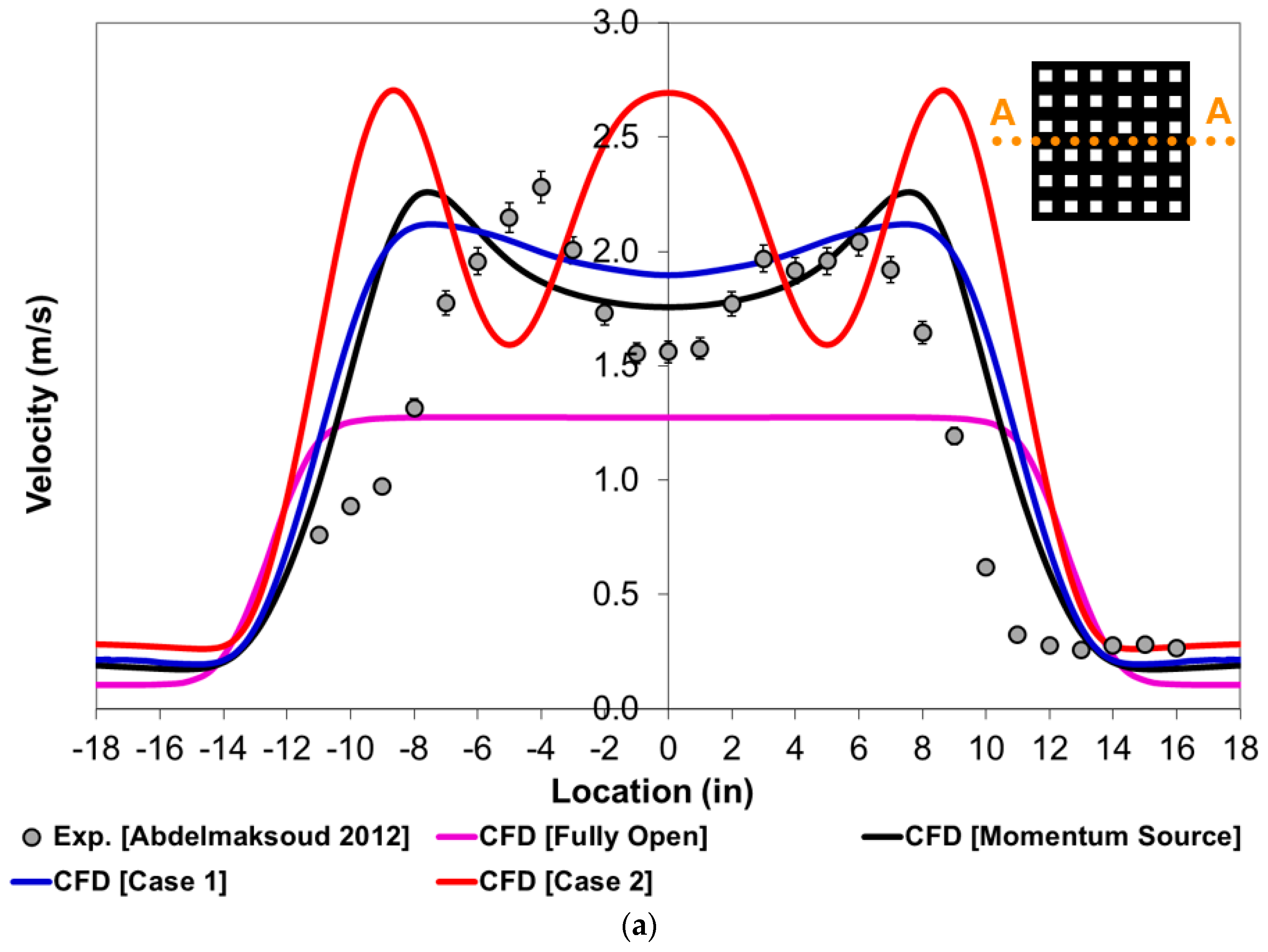
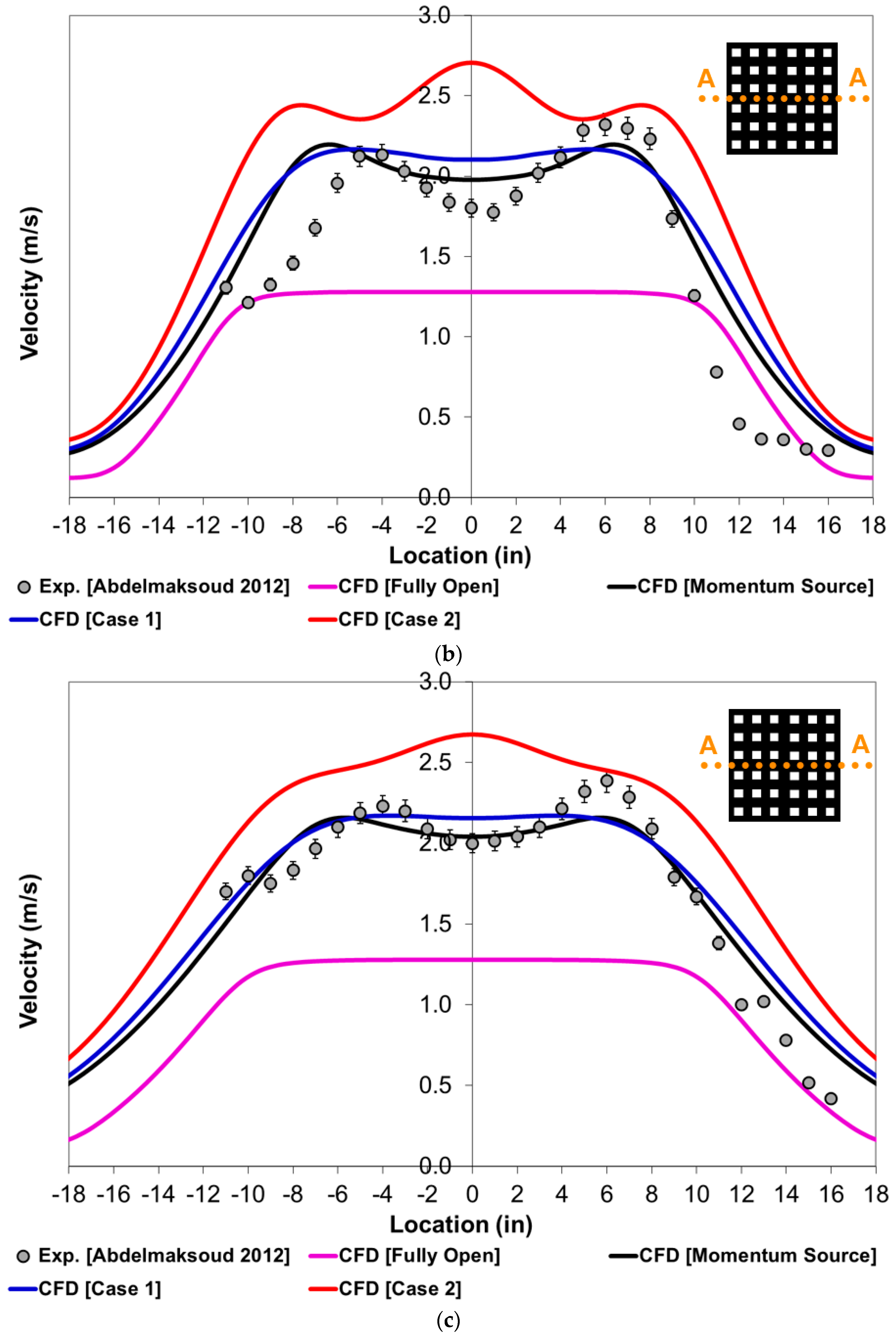
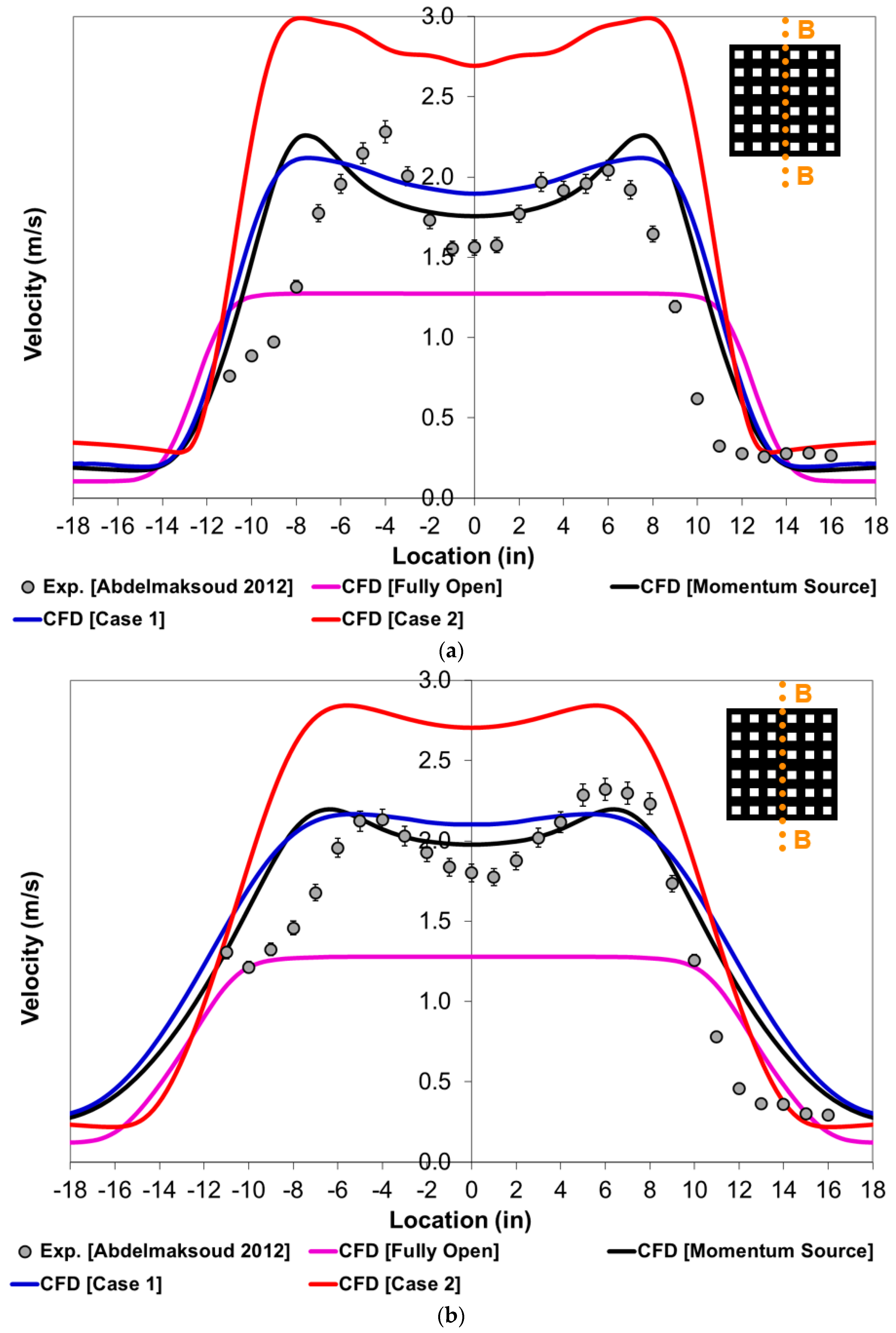
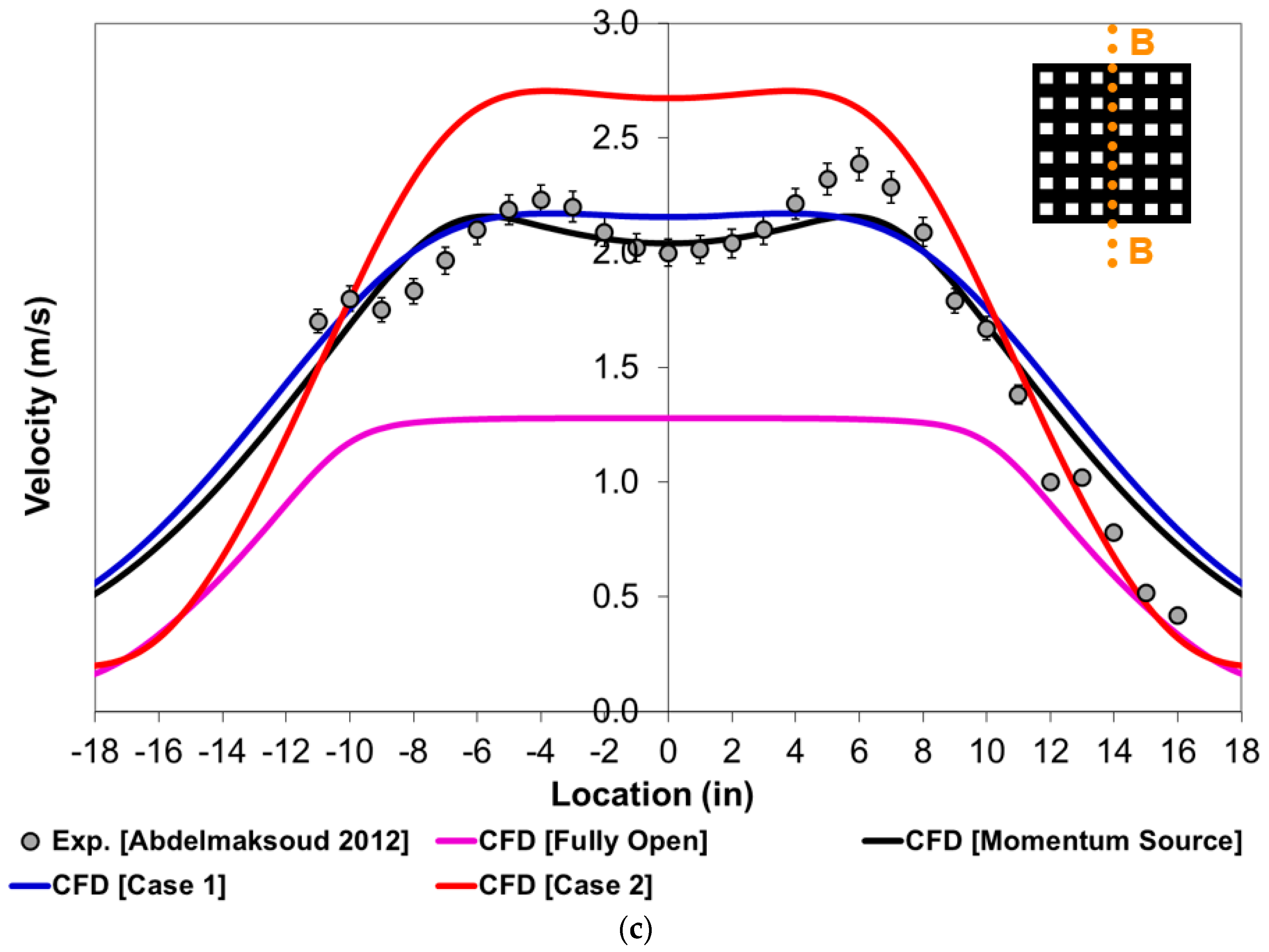
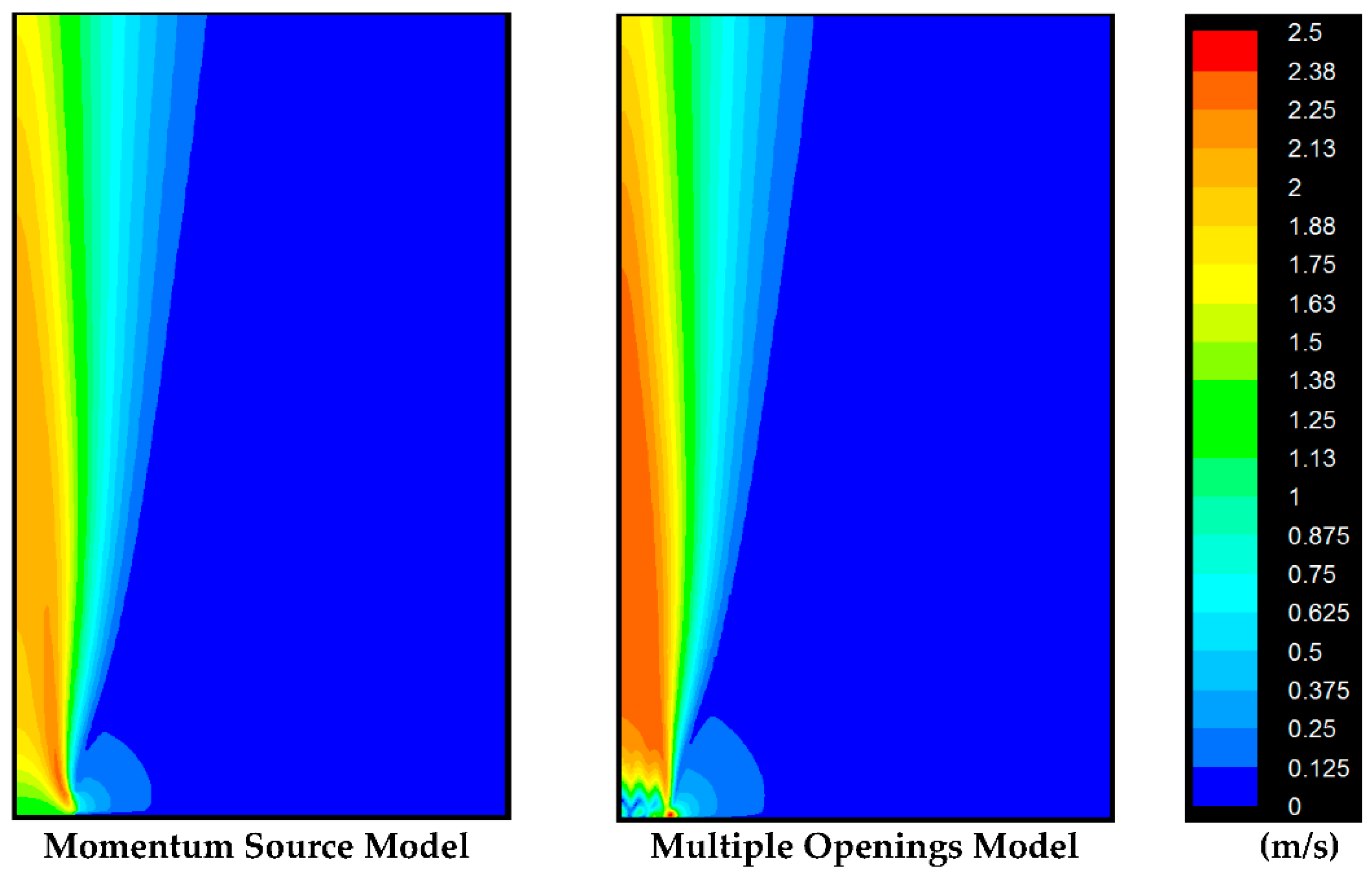
4. Results and Discussion
5. Summary and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CFD | Computational fluid dynamics |
| RANS | Reynolds-averaged Navier–Stokes |
| RMS | Root mean square |
| Volume of body-force field, m3 | |
| A | Perforated tile area, m2 |
| Fy | Body-force-per-unit volume, N/m3 |
| Q | Volume flow rate, m3/s |
| y+ | Dimensionless wall distance |
| xi and xj | Cartesian coordinates, m |
| u | Air velocity, m/s |
| p | Air pressure, Pa |
| C | Body-force adjustment factor due to tile flow distortion |
| k | Turbulent kinetic energy, m2/s2 |
| Gk | Turbulent kinetic energy generation, m2/s2 |
| C2 | Turbulence model constant |
| Greek symbols | |
| ρ | Air density, kg/m3 |
| σ | Fraction of tile perforation |
| μ | Air dynamic viscosity, kg/m.s |
| μt | Turbulent viscosity, kg/m.s |
| ν | Air kinematic viscosity, m2/s |
| ε | Turbulent dissipation rate, m2/s3 |
| σk | Turbulent Prandtl numbers for k |
| σε | Turbulent Prandtl numbers for ε |
References
- Iyengar, M.; Schmidt, R.; Hamann, H.; Van Gilder, J. Comparison between Numerical and Experimental Temperature Distributions in a Small Data Center Test Cell. In Proceedings of the IPACK2007, ASME InterPACK’ 07, Vancouver, BC, Canada, 8–12 July 2007. [Google Scholar]
- Gangisetti, K.; Claridge, D.; Srebric, J.; Paulus, M. Influence of reduced VAV flow settings on indoor thermal comfort in an office space. Build. Simul. 2016, 9, 101–111. [Google Scholar] [CrossRef]
- Abdelmaksoud, W.; Dang, T.; Khalifa, H.; Schmidt, R. Improved Computational Fluid Dynamics Model for Open-Aisle Air-Cooled Data Center Simulations. Electron. Packag. 2013, 135, 030901-1–030901-13. [Google Scholar] [CrossRef]
- Schwarz, W. Integrating ASHRAE-Funded Research into Air Flow Modeling Software. In Proceedings of the Seminar 25, ASHRAE Annual Meeting, Honolulu, HI, USA, 22–26 June 2002. [Google Scholar]
- Chen, Q. Simplified Diffuser Boundary Conditions for Numerical Room Air Flow Models; ASHRAE RP-1009 Final Report; ASHRAE: Atlanta, GA, USA, 2000. [Google Scholar]
- Abdelmaksoud, W.A. Experimental and Numerical Investigations of the Thermal Environment in Air-Cooled Data Centers. Ph.D. Thesis, Department of Mechanical and Aerospace Engineering, Syracuse University, Syracuse, NY, USA, 2012. [Google Scholar]
- Hu, R.; Fanning, T. A Momentum Source Model for Wire-Wrapped Rod Bundles—Concept, Validation, and Application. Nucl. Eng. Des. 2013, 262, 371–389. [Google Scholar] [CrossRef]
- Deng, B.; Wang, J.; Tang, J.; Gao, J. Improvement of the Momentum Method as the Diffuser Boundary Condition in CFD Simulation of Indoor Airflow: Discretization Viewpoint. Build. Environ. 2018, 141, 55–60. [Google Scholar] [CrossRef]
- Phan, L.; Hu, B.; Lin, C. An Evaluation of Turbulence and Tile Models at Server Rack Level for Data Centers. Build. Environ. 2019, 155, 421–435. [Google Scholar] [CrossRef]
- Nielsen, P. Representation of Boundary Conditions at Supply Openings; Technical Report, IEA, Annex 20, Research item 1.11; International Energy Agency: Paris, France, 1989.
- Srebric, J.; Chen, Q. A Method of Test to Obtain Diffuser Data for CFD Modeling of Room Airflow. ASHRAE Trans. 2011, 107, 108–116. [Google Scholar]
- Srebric, J.; Chen, Q. Simplified Numerical Models for Complex Air Supply Diffusers. HVACR Res. 2002, 8, 277–294. [Google Scholar] [CrossRef]
- Huo, Y.; Haghighat, F.; Zhang, J.S.; Shaw, C.Y. A Systematic Approach to Describe the Air Terminal Device in CFD Simulation for Room Air Distribution Analysis. Build. Environ. 2000, 35, 563–576. [Google Scholar] [CrossRef]
- Cehlin, M.; Moshfegh, B. Numerical modeling of a complex diffuser in a room with displacement ventilation. Build. Environ. 2010, 45, 2240–2252. [Google Scholar] [CrossRef]
- Martinez-Almansa, J.J.; Fernandez-Gutierrez, A.; Parras, L.; del Pino, C. Numerical and Experimental Study of a HVAC Wall Diffuser. Build. Environ. 2014, 80, 1–10. [Google Scholar] [CrossRef]
- Yau, Y.H.; Poh, K.S.; Badarudin, A. A Numerical Airflow Pattern Study of a Floor Swirl Diffuser for UFAD System. Build. Environ. 2018, 158, 525–535. [Google Scholar] [CrossRef]
- Deng, B.; Zhang, Y.; Long, F. A Superficial Density Method to Describe the Diffuser Boundary Condition in CFD Simulation of Indoor Airflow. Build. Environ. 2018, 135, 280–285. [Google Scholar] [CrossRef]
- Blocken, B.; Stathopoulos, T.; Carmeliet, J. CFD Simulation of the Atmospheric Boundary Layer: Wall Function Problems. J. Atmos. Environ. 2007, 41, 238–252. [Google Scholar] [CrossRef]
- ANSYS. Lecture 7: Turbulence Modeling Introduction to ANSYS Fluent, Sales Conference Theme and Team Building; ANSYS: Canonsburg, PA, USA, 2015. [Google Scholar]
- ANSYS Inc. ANSYS Fluent 2013 Theory Guide 15; Southpointe 275 Technology Drive; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]


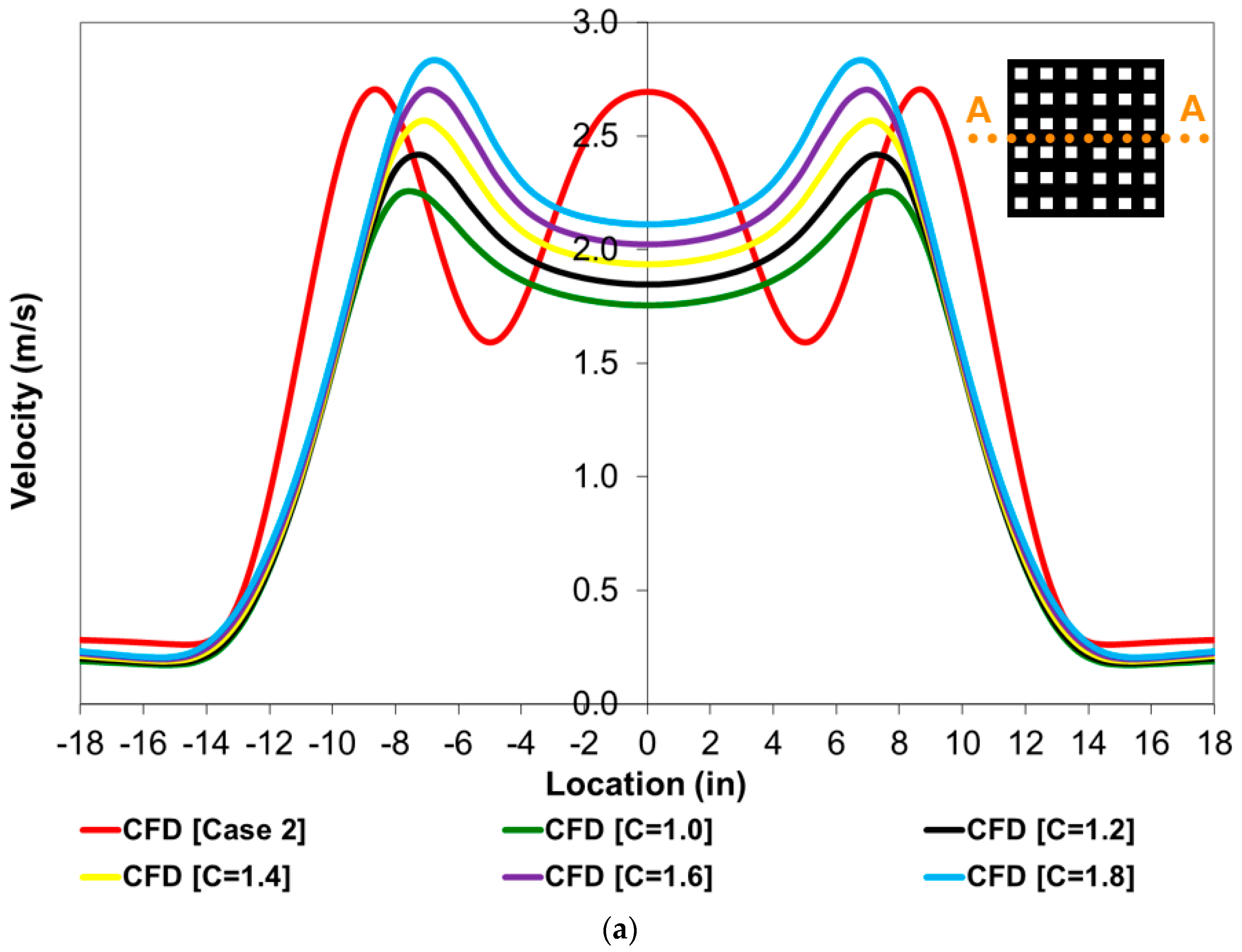
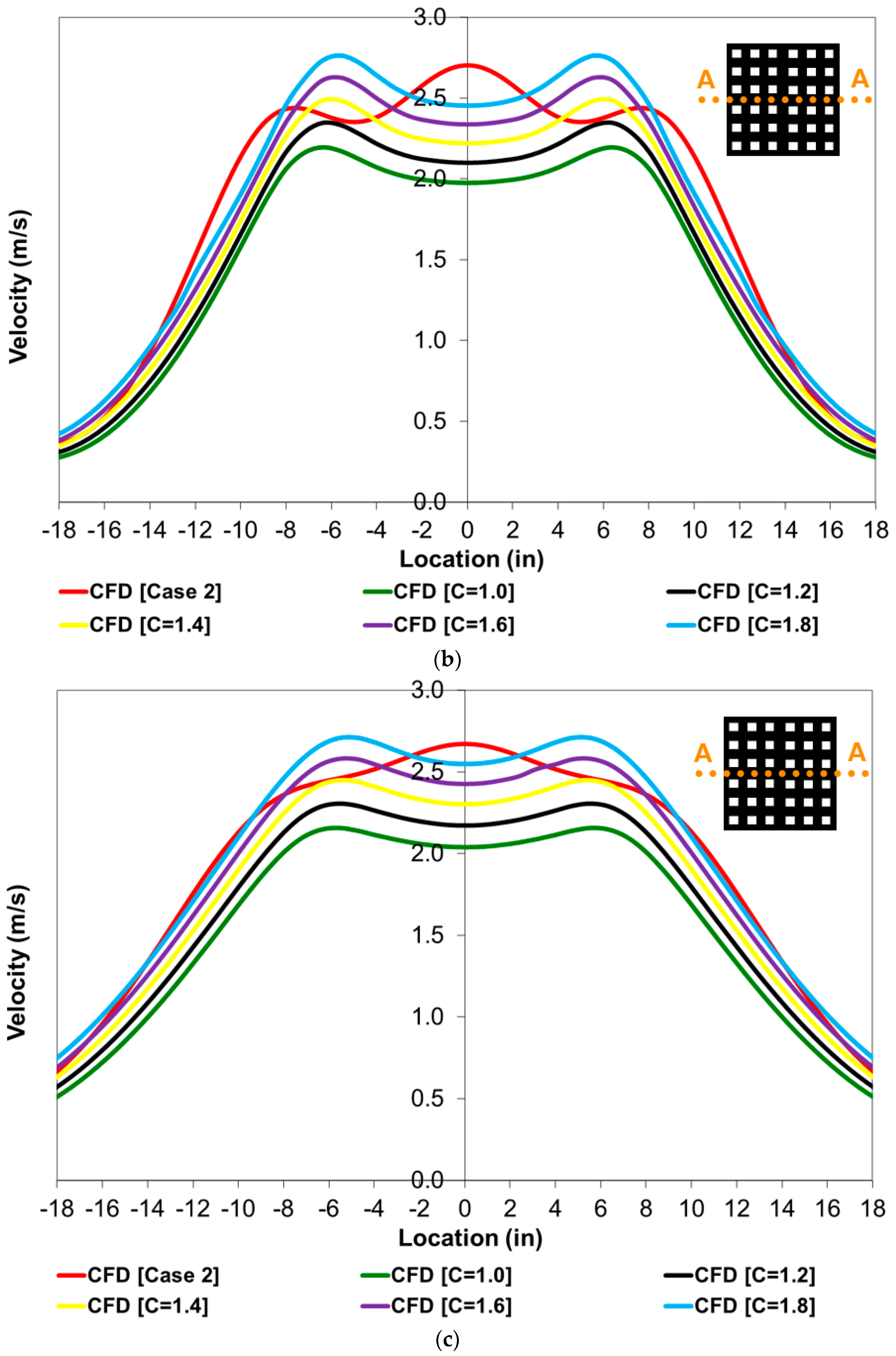
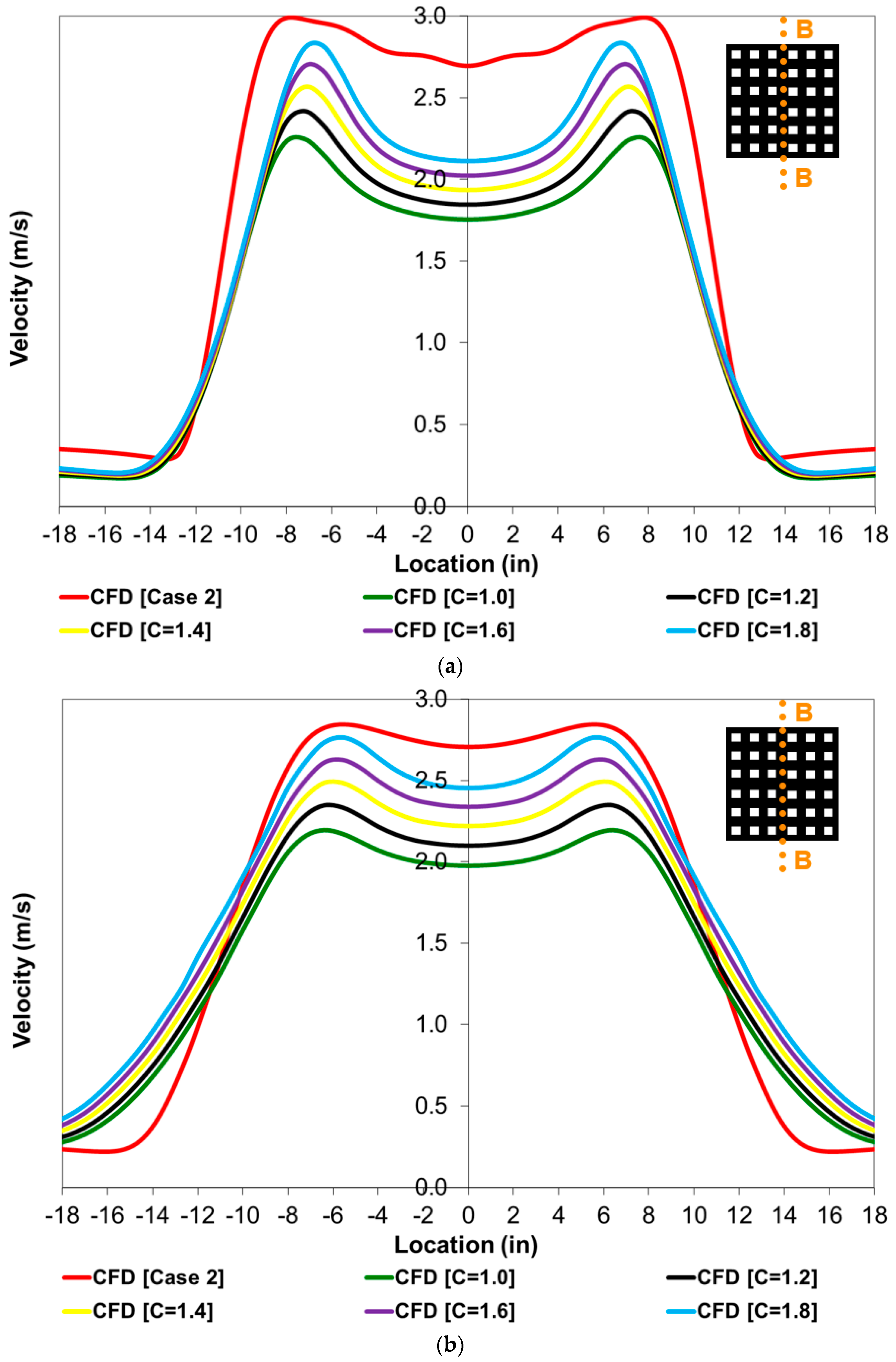
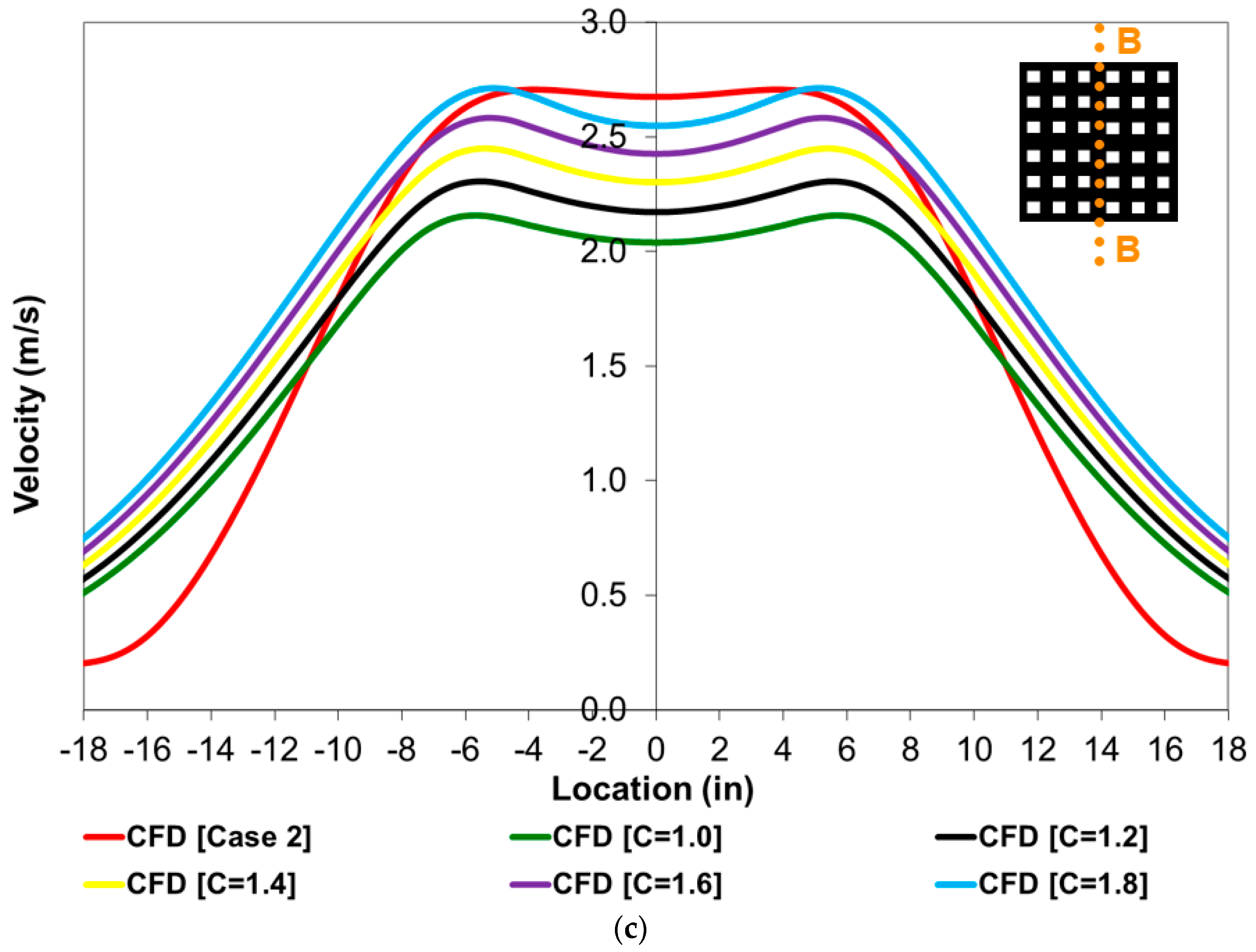
| Parameter | Boundary Condition/Value |
|---|---|
| Cases | Steady, 3D calculations |
| Turbulence model | Realizable k-ε coupled with enhanced wall treatment |
| Tile flow | Velocity inlet (based on 1000 cfm “see Figure 4”) Turbulent intensity (10%) Turbulent length scale (6 mm) |
| Far field boundaries | Pressure outlet (0 gage pressure) |
| Body force (Fy) | 58.36 N/m3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelmaksoud, W.A. Simplified CFD Model for Perforated Tile with Distorted Outflow. Fluids 2022, 7, 112. https://doi.org/10.3390/fluids7030112
Abdelmaksoud WA. Simplified CFD Model for Perforated Tile with Distorted Outflow. Fluids. 2022; 7(3):112. https://doi.org/10.3390/fluids7030112
Chicago/Turabian StyleAbdelmaksoud, Waleed A. 2022. "Simplified CFD Model for Perforated Tile with Distorted Outflow" Fluids 7, no. 3: 112. https://doi.org/10.3390/fluids7030112
APA StyleAbdelmaksoud, W. A. (2022). Simplified CFD Model for Perforated Tile with Distorted Outflow. Fluids, 7(3), 112. https://doi.org/10.3390/fluids7030112





