Abstract
The ever-increasing computational power has shifted direct numerical simulations towards higher Reynolds numbers and large eddy simulations towards industrially-relevant flow scales. However, this increase in both temporal and spatial resolution has severely increased the computational cost of model order reduction techniques. Reducing the full data set to a smaller subset in order to perform reduced-order modeling (ROM) may be an interesting method to keep the computational effort reasonable. Moreover, non-tomographic particle image velocimetry measurements obtain a 2D data set of a 3D flow field and an interesting research question would be to quantify the difference between this 2D ROM compared to the 3D ROM of the full flow field. To provide an answer to both issues, the aim of this study was to test a new method for obtaining POD basis functions from a small subset of data initially and using them afterwards in the ROM of either the complete data set or the reduced data set. Hence, no new method of ROM is presented, but we demonstrate a procedure to significantly reduce the computational effort required for the ROM of very large data sets and a quantification of the error introduced by reducing the size of those data sets. The method applies eigenvalue decomposition on a small subset of data extracted from a full 3D simulation and the obtained temporal coefficients are projected back on the 3D velocity fields to obtain the 3D spatial modes. To test the method, an annular jet was chosen as a flow topology due to its simple geometry and the rich dynamical content of its flow field. First, a smaller data set is extracted from the 2D cross-sectional planes and ROM is performed on that data set. Secondly, the full 3D spatial structures are reconstructed by projecting the temporal coefficients back on the 3D velocity fields and the 2D spatial structures by projecting the temporal coefficients back on the 2D velocity fields. It is shown that two perpendicular lateral planes are sufficient to capture the relevant large-scale structures. As such, the total processing time can be reduced by a factor of 136 and up to 22 times less RAM is needed to complete the ROM processing.
1. Introduction
Studies of turbulent flows have revealed the existence of several coherent structures of different length and time scales in fluid flow fields. Examples of these structures are the vortices shedded in the wake of round and rectangular cylinders [1,2], hairpin vortices in boundary layers [3], the precessing vortex core in swirling jets [4,5] and hairpin vortices shedded from the inner tube of an annular jet or a sphere [6,7]. These coherent structures can have a high kinetic energy content in some flow topologies (such as in the wake of a cylinder), whereas in others, for instance in an annular swirling jet, the energy content is much lower [4,8]. In the latter case, it is much more difficult to extract them as these structures are often only intermittently present in the flow field and, moreover, they exhibit frequency jitter in their dynamics, which results in the smearing of these structures across several modes [4]. Several reduced-order modeling methods exist for the extraction of coherent flow structures from turbulent flow fields. The most widely used ones are classical Fourier decomposition, proper orthogonal decomposition (POD) or its variants [9,10,11], dynamic mode decomposition (DMD) [12,13], spectral proper orthogonal decomposition (SPOD) [14] and non-uniform dynamic mode decomposition [15,16].
Both particle image velocimetry (PIV) and computational fluid dynamics (CFD) simulations have been used to obtain flow data and identify these coherent structures in different flow topologies [17,18,19]. Even though standard PIV obtains only 2D data in a cross-sectional plane (only tomographic PIV can obtain volumetric data) and CFD generates a full 3D data set, both methods seem to be able to extract coherent structures. However, the influence on the accuracy of ROM when reducing a full 3D flow field by means of 2D-PIV measurements for the extraction of these coherent structures is still unknown. Therefore, this paper focuses on the ROM of a reduced data set compared to a full set and the error introduced by this process. To the authors’ knowledge, this error has not been quantified to date and, if not to large, future ROM calculations of 2D data extracted from a 3D data set could be sufficient and would reduce processing (and storage) requirements significantly. The method developed in this paper was tested on the LES data set of an annular swirling jet, which is a representative flow topology for both an axisymmetric-wake flow and a swirling jet.
2. Materials and Methods
In this study, the LES data set of an annular swirling jet, presented in the work of Yang and Vanierschot, is used [8]. For details on the mesh, simulations parameters, boundary conditions, etc., the reader is referred to that study. We apply snapshot SPOD as the ROM technique as it has been shown that it can capture the relevant flow dynamics of the annular jet successfully [4,8]. Similarly to the classical POD approach, the velocity field is decomposed into a mean and fluctuating part, with the latter one written as a set of spatial modes and temporal coefficients as
where is a velocity vector with components u, v and w and the overbar denotes time-averaged quantities. The temporal coefficients and mode energies can be obtained by solving the eigenvalue problem
where the elements of the correlation matrix are given by
The spatial modes are obtained by the projection of the fluctuating velocity fields onto the temporal coefficients as
If periodic coherent structures exist in the flow field, the matrix has a diagonal wave-like structure, also named diagonal similarity [14]. In SPOD, this similarity is augmented by filtering the correlation matrix along the diagonals using a simple low-pass filter. This introduces the correlation matrix , defined as
with being a vector of length 2+1 with filter coefficients and being the filter width. The correlation matrix can be substituted as in Equation (2) and the velocity field is decomposed using instead of . The optimal filter width was shown to be of the order of one or two times the period of the periodic structure in the flow field if it is pronouncedlypresent [14] or four to eight times if intermittently present [4]. In this study, a filter width of 200 samples was chosen in order to focus on the structures with a lower frequency content, as high-frequency structures have already been extensively studied in previous research works [4,8,20]. The calculation of the correlation matrix and the associated eigenvalues in Equations (2) and (5) require the greatest computational effort. This computational effort drastically increases if the data set becomes large, for instance in CFD simulations. In order to reduce this computational effort, a new methodology of ROM is tested here, in which the eigenvalue calculation is performed using information from 2D extracted planes, hereafter called 2D data, from the full 3D data set. Once the temporal coefficients are obtained using Equation (2), the 3D structure of the spatial modes is obtained by projecting those temporal coefficients back on the full 3D velocity fields or on the 2D velocity fields using Equation (4). The choice of projection on either 2D or 3D velocity fields depends upon whether one wants to analyze 3D structures or if 2D structures are sufficient. This method of reducing data for ROM is extensively compared to the ROM of the entire 3D data set in the following section of the paper.
3. Results and Discussion
3.1. Time-Averaged Flow Field
The time-averaged flow field is shown in Figure 1. In the measurement coordinate system, the main jet flow occurs in the x-direction. The black isosurfaces in the figure are isovalues of zero axial velocity and the velocity vectors and contours are shown in a Y-cut section (a cross-sectional plane with the normal in the y-direction) through the 3D domain. Two distinct recirculation zones can be observed: one behind the bluff body and the other one further downstream, i.e., the vortex breakdown bubble. Both structures can also be observed in tomographic PIV measurements at the same swirl number [4]. The recirculation zones exhibit a rich dynamical content with several coherent structures in the flow field. These structures can be successfully extracted via POD or SPOD [8]. However, due to the large size of the data set obtained via CFD, the ROMs are computationally very expensive.
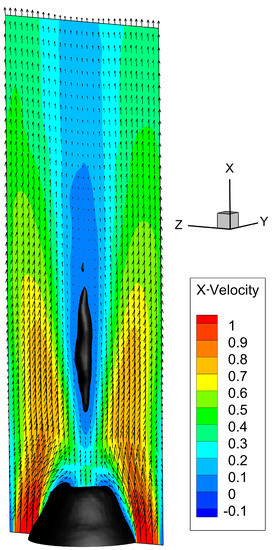
Figure 1.
The time-averaged flow field of an annular jet. The x-direction is the direction of the jet flow.
3.2. ROM of the Full Data Set
The mode pair spectrum of the SPOD decomposition of the full 3D data set is shown in Figure 2 and in the left of Table 1, where the mode pairs are ranked according to their harmonic correlation [14]. The energy content of each mode pair as a percentage of the total kinetic energy can be calculated as:
where i is the index of the modes contained in the specific mode pair considered. In the figure, the 10 mode pairs with the highest harmonic correlation are labeled. As the filter width in this study is larger than the one used in the study of Zhang and Vanierschot [8], structures with the highest harmonic content have Strouhal numbers (based on the average axial velocity and the hydraulic diameter of the jet) of the order of 0.03–0.1, whereas in the latter study the highest ranked modes had Strouhal numbers of 0.21 and 0.52, representing a single and double helical structure. These structures are also present in Figure 2 in mode pairs 5 and 8, albeit at a lower harmonic correlation. As the single and double helix have already been discussed extensively in previously published literature [4,8,20,21], we will focus mainly on the low-frequency structures, namely, the first two mode pairs ( = 0.0311, 0.0729). The quantitative data of the Strouhal number, energy content and harmonic correlation for the 10 highest correlated mode pairs are shown on the left of Table 1.
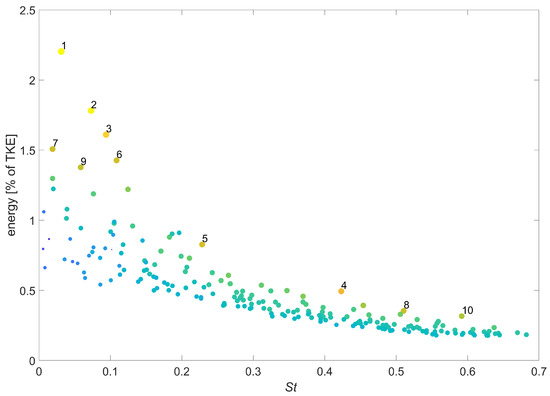
Figure 2.
SPOD spectrum of ROM using the entire 3D data set, where the 10 mode pairs with the highest harmonic correlation are labeled.

Table 1.
The data from the SPOD-analysis of the 3D data set and the YZ-data, colored by their deviation in terms of the Strouhal number between the 2D- and 3D-data.
3.3. ROM of the Reduced Data Sets
There are multiple reduced data sets considered in this study: one Y-cut section (shown in Figure 1), one Z-cut section and a combination of the two, a YZ-cut section. The mode pair spectrum of the SPOD decomposition of these reduced data sets is shown in Figure 3. The filter width was chosen to be equal to the one used in the full data set, namely, 200. The 10 highest-ranked mode pairs according to harmonic correlation are labeled and ranked in decreasing order. All extraction planes capture the first two mode pairs as the most harmonically correlated ones. The other three mode pairs of the 3D data are also captured within the first 10 mode-pairs of each section. However, the mode pairs with the highest harmonic correlation show a different sequence between the different data sets, with the YZ data set showing the best match with the full 3D set (shown in Figure 2). The change in order is more pronounced for the lower harmonic correlation mode pairs, including the single and double helix. Moreover, the average deviations in the Strouhal number of the first five mode pairs compared to the full 3D data for the Y-, Z- and YZ-plane are 3.77%, 4.63% and 2.51%, respectively. Hence, the YZ plane is shown to have the best extraction similarity. This result is to be expected, since the YZ-plane contains the most information subtracted from the full 3D data set. A detailed comparison between the five highest mode pairs in terms of harmonic correlation, plotting their Strouhal number and energy contribution, is shown in Figure 4, which confirms that the YZ data set suffices to extract the dynamics of the coherent structures as the maximum difference of any Strouhal number with the 3D data set is below 10% (error bars are at 10%). Therefore, in the remainder of this paper, the data of a YZ-plane extraction are used in the analysis. The right of Table 1 shows that, for the 2D ROM, the first two highly-ranked mode pairs are equal to the 3D ROM, whereas the third pair in the 3D ROM corresponds to the fourth pair in the 2D ROM.
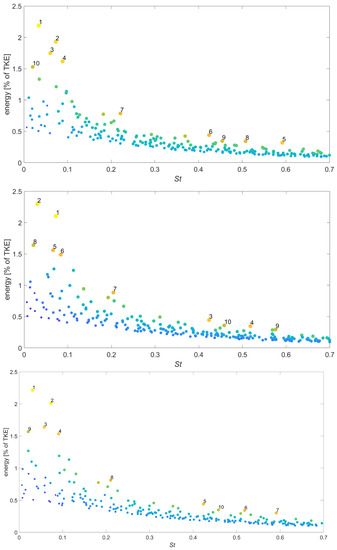
Figure 3.
SPOD spectrum of Y-cut data (top), Z-cut data (middle) and YZ-cut data (bottom), with the 10 highest harmonics labeled.
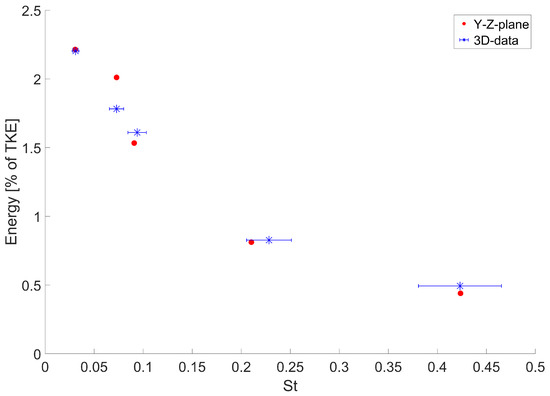
Figure 4.
The Strouhal number and energy content of the 5 highest harmonic correlated modes for the 3D data and 5 closest matches of the Strouhal number of YZ-plane data, with error bars of 10% shown.
3.4. 3D Spatial Mode Reconstruction from 2D ROM
The spatial structure of the SPOD modes of both the 2D and 3D ROM are shown in Figure 5 and Figure 6. For both figures, the first two columns correspond to the 3D spatial structures obtained from 3D ROM, whereas the last two columns represent the spatial structures obtained by projecting the time coefficients obtained by 2D ROM on the 3D velocity fields. For Figure 5, the first row corresponds to the mode pair with = 0.0311, whereas the second row corresponds to = 0.0729. For Figure 6, the first row corresponds to the mode pair with = 0.228, whereas the second row corresponds to = 0.510. Comparing the spatial modes shows that the structures of the modes are very similar between the two data sets. The 2D ROM modes are slightly attenuated for the vortex breakdown bubble (Figure 5), especially for the second mode pair. For the single helix, the 3D ROM is slightly attenuated in comparison to the 2D ROM, and for the double helix, vice versa. The filter width is chosen for the extraction of the low frequency components, i.e., the vortex breakdown bubble, which can be an explanation for the attenuation of the double single helix in the 3D ROM. The spatial similarities between 2D and 3D ROM are clear for every structure. However, there is a huge difference in computational effort. On a standard workstation using two Intel Xeon Gold 6248 processors, it took around 1775 s to perform the ROM on the 3D data set, as shown in Table 2. For the 2D ROM, it took only 13 or 26 s, which is a reduction by a factor of 136 or 68, respectively, for one or two perpendicular 2D planes. Moreover, during the ROM computation, the required RAM capacity was 220 GB for the 3D data, whereas only 10 GB was needed for the 2D data. This is a 22-fold decrease in memory requirements compared to the 3D data set. The projection of the 2D ROM on the 3D data set takes around 250 s. Obtaining these 3D data fields from a 2D ROM is thus six times faster, compared to a full 3D-analysis.
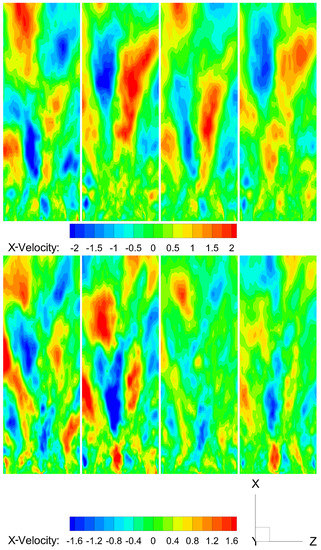
Figure 5.
Axial component [] of the two most harmonically correlated mode pairs using 3D and 2D ROM. The top four pictures correspond to mode pair 1 with a Strouhal number of 0.0311 and 0.0307 for the 3D and 2D ROM respectively. The bottom four pictures correspond to mode-pair 2 with a Strouhal number of 0.0729 for both the 3D and 2D ROM. The first two columns show the two modes of the pair for the 3D ROM, while the last two columns correspond to the 2D ROM.
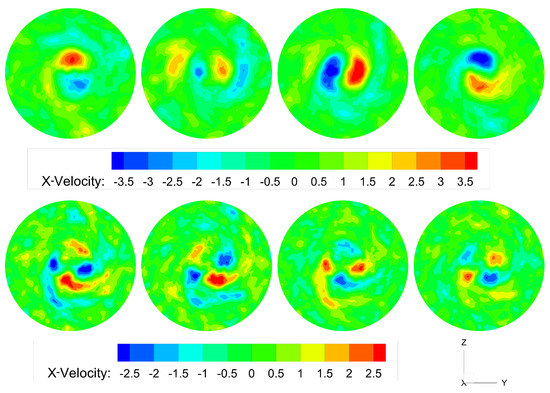
Figure 6.
Axial component () of the single and double helix using 3D and 2D ROM. The top four pictures correspond to the single helix with Strouhal numbers of 0.228 and 0.210 for the 3D and 2D ROM, respectively. The bottom four pictures correspond to the double helix with Strouhal numbers of 0.510 and 0.518 for the 3D and 2D ROM, respectively. The first two columns show the two modes obtained from 3D ROM, whereas the last two columns correspond to the 2D ROM.

Table 2.
Processing time and Strouhal numbers of single and double helices of different input datasets for SPOD.
3.5. Flow Field Reconstruction of Low-Frequency Coherent Structures
To study the dynamics of each mode pair representing a low-frequency coherent structure, the velocity field was reconstructed using Equation (1), only including the modes of the specific pair. The minimal and maximal values of the temporal coefficients of one of the modes of the mode pair was used; the corresponding temporal coefficients of the other mode of this pair was close to zero at this point. The velocity field reconstructed using the first mode pair is shown in Figure 7 for 3D ROM and in Figure 8 for 2D ROM. As can be seen in Figure 7, this mode pair describes the growth/decay of the vortex breakdown bubble (visualized using the iso-contour of zero axial velocity). This dynamic is periodic, with a Strouhal number of . Such intermittent growth and decay has also been observed in transitional swirling jets, where a value of 0.023 has been reported [21]. The velocity field reconstructed using the first mode pair of the 2D ROM is shown in Figure 8. As can be seen, this mode pair also describes the growth/decay of the vortex breakdown bubble. This dynamic is also periodic, with a Strouhal number of , which demonstrates a deviation of 1.29% from the 3D ROM. As shown in Figure 9 and Figure 10, the flow field reconstructed using the second mode pair describes the meandering of the annular jet. Here, the reconstruction is also very similar between both ROM methods. The differences in frequency and in the reconstructed flow fields are only marginal and do not outweigh the gain in computational effort. The difference in extracted structures is equally dependent on the choice of filter width, as it is dependent on processing 2D or 3D data. Therefore, we have shown that the newly presented method works efficiently for an annular swirling flow jet if two perpendicular planes are chosen.
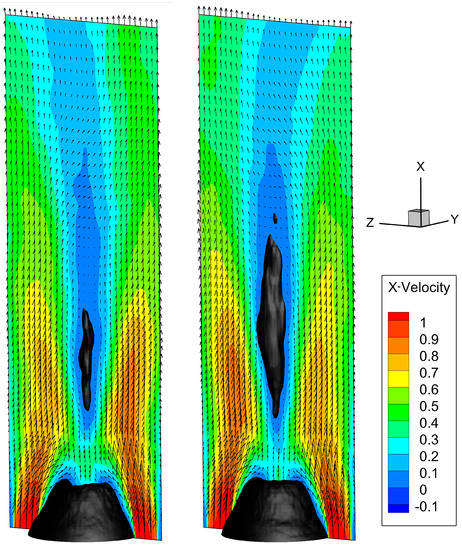
Figure 7.
Reconstruction of the axial velocity fields () by 3D ROM using the first mode pair (), with a black isosurface of zero axial velocity and the velocity vectors shown. Left: Reconstruction with the minimal temporal coefficient. Right: Reconstruction with the maximal temporal coefficient.
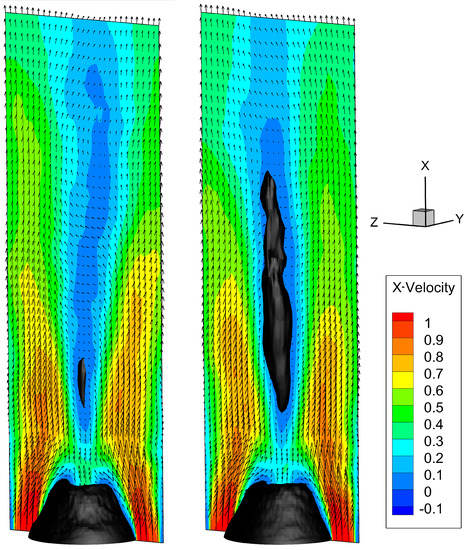
Figure 8.
Reconstruction of the axial velocity fields () by 2D ROM using the first mode pair (), with a black isosurface of zero axial velocity and the velocity vectors shown. Left: Reconstruction with the minimal temporal coefficient. Right: Reconstruction with the maximal temporal coefficient.
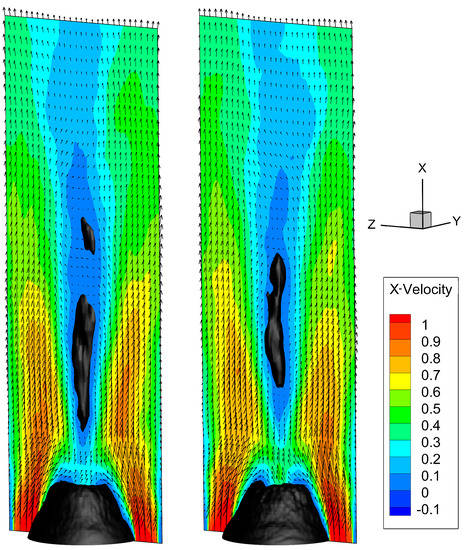
Figure 9.
Reconstruction of the axial velocity fields () by 3D ROM using the second mode pair (), with a black isosurface of zero axial velocity and the velocity vectors shown. Left: Reconstruction with the minimal temporal coefficient. Right: Reconstruction with the maximal temporal coefficient.
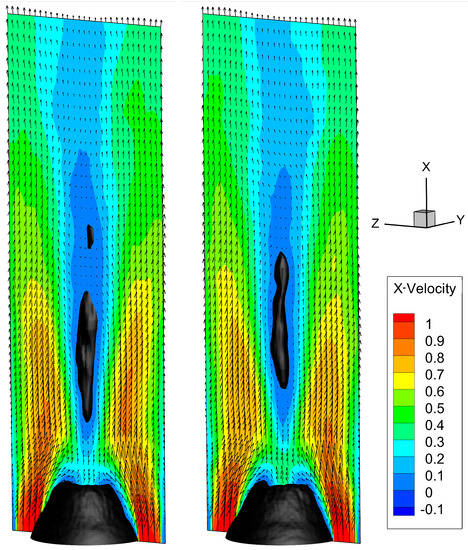
Figure 10.
Reconstruction of the axial velocity fields () by 2D ROM using the second mode pair (), with a black isosurface of zero axial velocity and the velocity vectors shown. Left: Reconstruction with the minimal temporal coefficient. Right: Reconstruction with the maximal temporal coefficient.
4. Conclusions
In this paper, a new method for ROM using CFD simulations was developed and tested. It was shown that in the case of an annular swirling jet flow, which has a rich dynamical content, the coherent structures of interest can be successfully extracted using only a limited amount of data from a full 3D data set. The optimal reduction rate was obtained using data from two perpendicular lateral planes in the 3D domain. The coherent structures were still recognizable in this reduced data set, with an average deviation of 2.51% in terms of the Strouhal number. Using even fewer data—only using data from a Y- or Z-plane—we were still able to recognize the structures of interest within a 5% error interval. It was shown that the differences in performance of this method compared to the ROM of the full 3D data set are only marginal and do not outweigh the gains in computational effort. The necessary RAM capacity was decreased from 220 GB to 10 GB, which is 22 times less. Furthermore, the necessary processing time for the data was decreased from 1775 to just 13 or 26 s, which represents a reduction of a factor of 136 or 68, respectively, for one or two perpendicular 2D-planes. For standard PIV-measurements, this work shows that one should take into account a possible error of a maximum of 10% when extracting coherent structures using PIV data in a cross-sectional plane. However, more research is needed to investigate the applicability of this method to other flow topologies, which is beyond the the scope of the current study. The authors invite other researchers/research groups to perform the same analysis on their CFD data.
Author Contributions
Conceptualization, T.H., Z.Y. and M.V.; methodology, M.V.; software, T.H., Z.Y. and M.V.; validation, T.H. and M.V.; formal analysis, T.H., Z.Y. and M.V.; investigation, T.H. and M.V.; resources, M.V.; data curation, T.H. and M.V.; writing—original draft preparation, T.H. and M.V.; writing—review and editing, T.H., Z.Y. and M.V.; visualization, T.H.; supervision, M.V.; project administration, M.V.; funding acquisition, M.V. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully thank ’Interne Fondsen KU Leuven/Internal Funds KU Leuven’ for funding this research through grant No. C3/19/015.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available by the authors upon request.
Acknowledgments
The authors sincerely thank Yang Zhang for providing the 3D data set of his LES simulations.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Greco, C.S.; Paolillo, G.; Astarita, T.; Cardone, G. The von Karman street behind a circular cylinder: Flow control through synthetic jet placed at the rear stagnation point. J. Fluid Mech. 2020, 901, A39. [Google Scholar] [CrossRef]
- Wang, F.; Lam, K.M. Experimental and numerical investigation of turbulent wake flow around wall-mounted square cylinder of aspect ratio 2. Exp. Therm. Fluid Sci. 2021, 123, 110325. [Google Scholar] [CrossRef]
- Motoori, Y.; Goto, S. Hairpin vortices in the largest scale of turbulent boundary layers. Int. J. Heat Fluid Flow 2020, 86, 108658. [Google Scholar] [CrossRef]
- Vanierschot, M.; Müller, J.; Sieber, M.; Percin, M.; Van Oudheusden, B.; Oberleithner, K. Single- and double-helix vortex breakdown as two dominant global modes in turbulent swirling jet flow. J. Fluid Mech. 2020, 883, A31. [Google Scholar] [CrossRef]
- Sharaborin, D.K.; Savitskii, A.G.; Bakharev, G.Y.; Lobasov, A.S.; Chikishev, L.M.; Dulin, V.M. PIV/PLIF investigation of unsteady turbulent flow and mixing behind a model gas turbine combustor. Exp. Fluids 2021, 62, 96. [Google Scholar] [CrossRef]
- Vanierschot, M.; Percin, M.; van Oudheusden, B.W. Asymmetric vortex shedding in the wake of an abruptly expanding annular jet. Exp. Fluids 2021, 62, 77. [Google Scholar] [CrossRef]
- Tiwari, S.S.; Bale, S.; Patwardhan, A.W.; Nandakumar, K.; Joshi, J.B. Insights into the physics of dominating frequency modes for flow past a stationary sphere: Direct numerical simulations. Phys. Fluids 2019, 31, 045108. [Google Scholar] [CrossRef]
- Zhang, Y.; Vanierschot, M. Determination of single and double helical structures in a swirling jet by spectral proper orthogonal decomposition. Phys. Fluids 2021, 33, 015115. [Google Scholar] [CrossRef]
- Lumley, J.L. Stochastic Tools in Turbulence. Applied Mathematics and Mechanics Series: Volume 12; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Sirovich, L. Turbulence and the dynamics of coherent structures. Part I: Coherent structures. Quat. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef] [Green Version]
- Boreé, J. Extended proper orthogonal decomposition: A tool to analyse correlated events in turbulent flows. Exp. Fluids 2003, 35, 188–192. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A Data-Driven Approximation of the Koopman Operator: Extending Dynamic Mode Decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef] [Green Version]
- Sieber, M.; Paschereit, C.O.; Oberleithner, K. Spectral Proper Orthogonal Decomposition. Fluid Mech. 2016, 792, 798–828. [Google Scholar] [CrossRef] [Green Version]
- Gadalla, M.; Cianferra, M.; Tezzele, M.; Stabile, G.; Mola, A.; Rozza, G. On the Comparison of LES Data-Driven Reduced Order Approaches for Hydroacoustic Analysis. Comput. Fluids 2021, 216, 104819. [Google Scholar] [CrossRef]
- Hall, B.T.; Chou, C.-S.; Chen, J.-P. Using the Nonuniform Dynamic Mode Decomposition to Reduce the Storage Required for PDE Simulations. Int. J. Aerosp. Eng. 2019, 2019, 8291616. [Google Scholar] [CrossRef] [Green Version]
- Sieber, M.; Paschereit, C.O.; Oberleithner, K. Advanced Identification of Coherent Structures in Swirl-Stabilized Combustors. J. Eng. Gas Turbine Power 2017, 139, 021503. [Google Scholar] [CrossRef]
- Zixiang, C. Large-Scale Coherent Structures and Three-Dimensional Velocity Estimation in the Turbulent Wake of a Low Aspect Ratio Surface-Mountede Cone. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 2017. [Google Scholar]
- Vázquez, J.A.R. A Computational Fluid Dynamics Investigation of Turbulent Swirling Burners. Ph.D. Thesis, Universidad De Zaragoza, Zaragoza, Spain, 2012. [Google Scholar]
- Zhang, Y.; Vanierschot, M. Modeling capabilities of unsteady RANS for the simulation of turbulent swirling flow in an annular bluff-body combustor geometry. Appl. Math. Mod. 2020, 89, 1140–1154. [Google Scholar] [CrossRef]
- Vanierschot, M.; Ogus, G. Experimental investigation of the precessing vortex core in annular swirling jet flows in the transitional regime. Exp. Therm. Fluid Sc. 2019, 106, 148–158. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).