Flow Control in Wings and Discovery of Novel Approaches via Deep Reinforcement Learning
Abstract
1. Introduction
1.1. Active Control of Turbulent Flows
1.2. Active Control of Separation
2. Turbulence Simulation Approaches
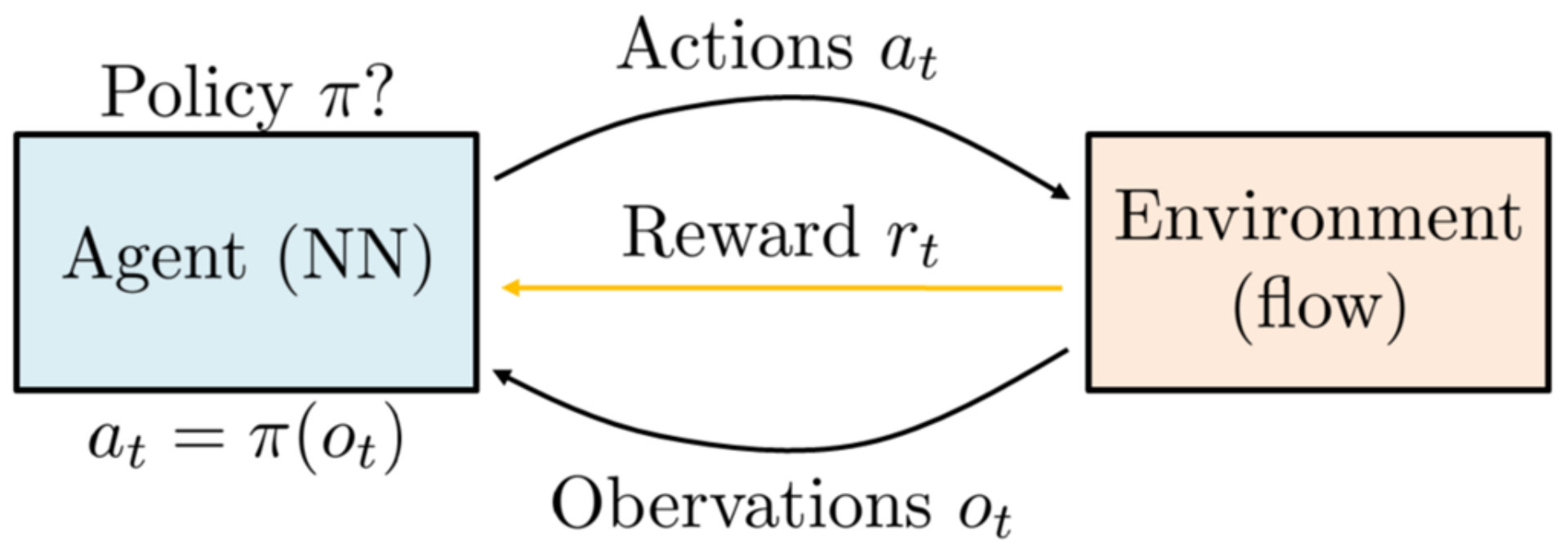
3. Data-Driven Methods for Control and Deep Reinforcement Learning
4. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bouwer, J. Will Airline Hubs Recover from COVID-19? Available online: https://www.mckinsey.com/industries/travel-logistics-and-transport-infrastructure/our-insights/will-airline-hubs-recover-from-covid-19# (accessed on 3 January 2022).
- Liu, J.; Qiao, P.; Ding, J.; Hankinson, L.; Harriman, E.H.; Schiller, E.M.; Ramanauskaite, I.; Zhang, H. Will the aviation industry have a bright future after the COVID-19 outbreak? Evidence from Chinese airport shipping sector. J. Risk Financ. Manag. 2020, 13, 276. [Google Scholar] [CrossRef]
- Owen, B.; Lee, D.S.; Lim, L. Flying into the future: Aviation emissions scenarios to 2050. Environ. Sci. Technol. 2010, 44, 2255–2260. [Google Scholar] [CrossRef] [PubMed]
- Kroo, I. Drag due to lift: Concepts for prediction and reduction. Annu. Rev. Fluid Mech. 2001, 33, 587–617. [Google Scholar] [CrossRef]
- UN General Assembly. Transforming our world: The 2030 Agenda for Sustainable Development. Resolut. A Res. 2015, 25, 1–35. [Google Scholar]
- Vinuesa, R.; Azizpour, H.; Leite, I.; Balaam, M.; Dignum, V.; Domisch, S.; Felländer, A.; Langhans, S.D.; Tegmark, M.; Fuso Nerini, F. The role of artificial intelligence in achieving the Sustainable Development Goals. Nat. Commun. 2020, 11, 233. [Google Scholar] [CrossRef]
- Gupta, S.; Langhans, S.D.; Domisch, S.; Fuso-Nerini, F.; Felländer, A.; Battaglini, M.; Tegmark, M.; Vinuesa, R. Assessing whether artificial intelligence is an enabler or an inhibitor of sustainability at indicator level. Transp. Eng. 2021, 4, 100064. [Google Scholar] [CrossRef]
- Fahland, G.; Stroh, A.; Frohnapfel, B.; Atzori, M.; Vinuesa, R.; Schlatter, P.; Gatti, D. Investigation of blowing and suction for turbulent flow control on airfoils. AIAA J. 2021, 59, 4422–4436. [Google Scholar] [CrossRef]
- Bechert, D.W.; Bartenwerfer, M. The viscous flow on surfaces with longitudinal ribs. J. Fluid Mech. 1989, 206, 105–112. [Google Scholar] [CrossRef]
- Viswanath, P.R. Aircraft viscous drag reduction using riblets. Prog. Aerosp. Sci. 2002, 38, 571–600. [Google Scholar] [CrossRef]
- Gad-el Hak, M. Flow Control—Passive, Active and Reactive Flow Management; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Choi, H.; Jeon, W.P.; Kim, J. Control of flow over a bluff body. Annu. Rev. Fluid Mech. 2008, 40, 113–139. [Google Scholar] [CrossRef]
- Quadrio, M. Drag reduction in turbulent boundary layers by in-plane wall motion. Philos. Trans. R. Soc. A 2011, 369, 1428–1442. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P.; Kim, J. Active turbulence control for drag reduction in wall-bounded flows. J. Fluid Mech. 1994, 262, 75–110. [Google Scholar] [CrossRef]
- Stroh, A.; Frohnapfel, B.; Schlatter, P.; Hasegawa, Y. A comparison of opposition control in turbulent boundary layer and turbulent channel flow. Phys. Fluids 2015, 27, 075101. [Google Scholar] [CrossRef]
- Stroh, A.; Frohnapfel, B.; Schlatter, P.; Hasegawa, Y. Status and perspectives of laminar flow. Aeronaut. J. 2005, 109, 639–644. [Google Scholar]
- Wood, R.M. Impact of advanced aerodynamic technology on transportation energy consumption. SAE Tech. Pap. 2004, 113, 854–874. [Google Scholar]
- Abbas, A.; De Vicente, J.; Valero, E. Aerodynamic technologies to improve aircraft performance. Aerosp. Sci. Technol. 2013, 28, 100–132. [Google Scholar] [CrossRef]
- Hwang, D. A proof of concept experiment for reducing skin friction by using a micro-blowing technique. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997. [Google Scholar]
- Hwang, D. Review of research into the concept of the microblowing technique for turbulent skin friction reduction. Prog. Aerosp. Sci. 2004, 40, 559–575. [Google Scholar] [CrossRef]
- Kornilov, V.I. Current state and prospects of researches on the control of turbulent boundary layer by air blowing. Prog. Aerosp. Sci. 2015, 76, 1–23. [Google Scholar] [CrossRef]
- Park, J.; Choi, H. Effects of uniform blowing or suction from a spanwise slot on a turbulent boundary layer flow. Phys. Fluids 1999, 11, 3095–3105. [Google Scholar] [CrossRef]
- Kametani, Y.; Fukagata, K. Direct numerical simulation of spatially developing turbulent boundary layers with uniform blowing or suction. J. Fluid Mech. 2011, 681, 154–172. [Google Scholar] [CrossRef]
- Kametani, Y.; Fukagata, K.; Örlü, R.; Schlatter, P. Effect of uniform blowing/suction in a turbulent boundary layer at moderate Reynolds number. Int. J. Heat Fluid Flow 2015, 55, 132–142. [Google Scholar] [CrossRef]
- Noorani, A.; Vinuesa, R.; Brandt, L.; Schlatter, P. Aspect ratio effect on particle transport in turbulent duct flows. Phys. Fluids 2016, 28, 115103. [Google Scholar] [CrossRef]
- Bobke, A.; Vinuesa, R.; Örlü, R.; Schlatter, P. History effects and near equilibrium in adverse-pressure-gradient turbulent boundary layers. J. Fluid Mech. 2017, 820, 667–692. [Google Scholar] [CrossRef]
- Vinuesa, R.; Negi, P.S.; Atzori, M.; Hanifi, A.; Henningson, D.S.; Schlatter, P. Turbulent boundary layers around wing sections up to Rec=1,000,000. Int. J. Heat Fluid Flow 2018, 72, 86–99. [Google Scholar] [CrossRef]
- Tanarro, A.; Vinuesa, R.; Schlatter, P. Effect of adverse pressure gradients on turbulent wing boundary layers. J. Fluid Mech. 2020, 883, A8. [Google Scholar] [CrossRef]
- Eto, K.; Kondo, Y.; Fukagata, K.; Tokugawa, N. Assessment of friction drag reduction on a clark-Y airfoil by uniform blowing. AIAA J. 2019, 57, 2774–2782. [Google Scholar] [CrossRef]
- Kornilov, V.I.; Kavun, I.N.; Popkov, A.N. Modification of turbulent airfoil section flow using a combined control action. Thermophys. Aeromech. 2019, 26, 165–178. [Google Scholar] [CrossRef]
- Vinuesa, R.; Schlatter, P. Skin-friction control of the flow around a wing section through uniform blowing. In Proceedings of the European Drag Reduction and Flow Control Meeting (EDRFCM), Rome, Italy, 3–6 April 2017. [Google Scholar]
- Atzori, M.; Vinuesa, R.; Fahland, G.; Stroh, A.; Gatti, D.; Frohnapfel, B.; Schlatter, P. Aerodynamic effects of uniform blowing and suction on a NACA4412 airfoil. Flow Turbul. Combust. 2020, 105, 735–759. [Google Scholar] [CrossRef]
- Albers, M.; Meysonnat, P.S.; Schröder, W. Actively reduced airfoil drag by transversal surface waves. Flow Turbul. Combust. 2019, 102, 865–886. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Vinuesa, R.; Schlatter, P.; Hanifi, A.; Henningson, D.S. Direct numerical simulation of the flow around a wing section at moderate Reynolds number. Int. J. Heat Fluid Flow 2016, 61, 117–128. [Google Scholar] [CrossRef]
- Vinuesa, R.; Hosseini, S.M.; Hanifi, A.; Henningson, D.S.; Schlatter, P. Pressure-gradient turbulent boundary layers developing around a wing section. Flow Turbul. Combust. 2017, 99, 613–641. [Google Scholar] [CrossRef]
- Batikh, A.; Baldas, L.; Colin, S. Application of Active Flow Control on Aircrafts—State of the Art. In International Workshop on Aircraft System Technologies; Shaker: Herzogenrath, Germany, 2017; pp. 1–10. [Google Scholar]
- Khodadoust, A.; Washburn, A. Active control of flow separation on a high-lift system with slotted flap at high Reynolds number. In Collection of Technical Papers—AIAA Applied Aerodynamics Conference; American Institute of Aeronautics and Astronautics Inc.: Reston, VA, USA, 2007; Volume 3, pp. 1645–1669. [Google Scholar] [CrossRef]
- Khün, T.; Ciobaca, V.; Rudnik, R.; Gölling, B.; Breitenstein, W. Active flow separation control on a high-lift wing-body configuration part 1: Baseline flow and constant blowing. In Proceedings of the 29th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 27–30 June 2011. [Google Scholar] [CrossRef][Green Version]
- Radespiel, R.; Burnazzi, M.; Casper, M.; Scholz, P. Active flow control for high lift with steady blowing. Aeronaut. J. 2016, 120, 171–200. [Google Scholar] [CrossRef]
- Fricke, S.; Ciobaca, V.; Kröhnert, A.; Wild, J.; Blesbois, O. Active Flow Control Applied at the Engine-Wing Junction. In Proceedings of the 5th CEAS Air & Aerospace Conference, Delft, The Netherlands, 7–11 September 2015; pp. 1–12. [Google Scholar]
- Schloesser, P.; Soudakov, V.; Bauer, M.; Wild, J. Active separation control at the pylon-wing junction of a real-scale model. AIAA J. 2019, 57, 132–141. [Google Scholar] [CrossRef]
- Hue, D.; François, C.; Dandois, J.; Gebhardt, A. Simulations of an aircraft with constant and pulsed blowing flow control at the engine/wing junction. Aerosp. Sci. Technol. 2017, 69, 659–673. [Google Scholar] [CrossRef]
- Shmilovich, A.; Yadlin, Y.; Whalen, E.A. Active flow control computations: From a single actuator to a complete airplane. AIAA J. 2018, 56, 4730–4740. [Google Scholar] [CrossRef]
- Andino, M.Y.; Lin, J.C.; Roman, S.; Graff, E.C.; Gharib, M.; Whalen, E.A.; Wygnanski, I.J. Active Flow Control on Vertical Tail Models. AIAA J. 2019, 57, 3322–3338. [Google Scholar] [CrossRef]
- Whalen, E.A.; Lacy, D.; Lin, J.C.; Andino, M.Y.; Washburn, A.E.; Graff, E.; Wygnanski, I.J. Performance enhancement of a full-scale vertical tail model equipped with active flow control. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Kara, K.; Kim, D.; Morris, P.J. Flow-separation control using sweeping jet actuator. AIAA J. 2018, 56, 4604–4613. [Google Scholar] [CrossRef]
- Chen, S.; Li, W.; Meng, Q.; Zhou, Z.; Wang, S. Effects of a sweeping jet actuator on aerodynamic performance in a linear turbine cascade with tip clearance. J. Aerosp. Eng. 2019, 233, 4468–4481. [Google Scholar] [CrossRef]
- Aley, K.S.; Guha, T.K.; Kumar, R. Active Flow Control of a High-Lift Supercritical Airfoil with Microjet Actuators. AIAA J. 2020, 58, 2053–2069. [Google Scholar] [CrossRef]
- Glezer, A. Some aspects of aerodynamic flow control using synthetic-jet actuation. Philos. Trans. R. Soc. A 2011, 369, 1476–1494. [Google Scholar] [CrossRef]
- Hartwich, P.M.; Shmilovich, A.; Lacy, D.S.; Dickey, E.D.; Scalafani, A.J.; Sundaram, P.; Yadlin, Y. Refined AFC-Enabled High-Lift System Integration Study; Technical Report CR-2016-219170; Langley Research Center: Hampton, VA, USA, 2016. [Google Scholar]
- Mccormick, D.C. Boundary Layer Separation control with Directed Synthetic Jets. In Proceedings of the 38th Aerospace Sciences Meeting & Exhibit, 2000, Number AIAA 2000-0519, Reno, NV, USA, 10–13 January 2000. [Google Scholar] [CrossRef]
- Amitay, M.; Glezer, A. Role of actuation frequency in controlled flow reattachment over a stalled airfoil. AIAA J. 2002, 40, 209–216. [Google Scholar] [CrossRef]
- Gilarranz, J.L.; Traub, L.W.; Rediniotis, O.K. A New Class of Synthetic Jet Actuators—Part I: Design, Fabrication and Bench Top Characterization. J. Fluids Eng. 2005, 127, 367. [Google Scholar] [CrossRef]
- You, D.; Moin, P. Active control of flow separation over an airfoil using synthetic jets. J. Fluids Struct. 2008, 24, 1349–1357. [Google Scholar] [CrossRef]
- Jabbal, M.; Liddle, S.C.; Crowther, W.J. Active flow control systems architectures for civil transport aircraft. J. Aircr. 2010, 47, 1966–1981. [Google Scholar] [CrossRef]
- Shmilovich, A.; Yadlin, Y. Active Flow Control for Practical High-Lift Systems. J. Aircr. 2009, 46, 1354–1364. [Google Scholar] [CrossRef]
- Bauer, M.; Lohse, J.; Haucke, F.; Nitsche, W. High-Lift Performance Investigation of a Two-Element Configuration with a Two-Stage Actuator System. AIAA J. 2014, 52, 1307–1313. [Google Scholar] [CrossRef]
- Lin, J.C.; Pack Melton, L.G.; Viken, S.; Andino, M.Y.; Koklu, M.; Hannon, J.; Vatsa, V.N. High Lift Common Research Model for Wind Tunnel Testing: An Active Flow Control Perspective. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Lin, J.C.; Melton, L.G.P.; Hannon, J.; Andino, M.; Koklu, M.; Paschal, K.; Vatsa, V.N. Wind Tunnel Testing of Active Flow Control on the High Lift Common Research Model. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Jansen, K.E.; Rasquin, M.; Farnsworth, J.A.; Rathay, N.; Monastero, M.C.; Amitay, M. Interaction of a Synthetic Jet with Separated Flow over a Vertical Tail. AIAA J. 2018, 56, 2653–2668. [Google Scholar] [CrossRef]
- Lehmkuhl, O.; Lozano-Durán, A.; Rodriguez, I. Active flow control for external aerodynamics: From micro air vehicles to a full aircraft in stall. J. Phys. Conf. Ser. 2020, 1522, 012017. [Google Scholar] [CrossRef]
- Johnson, F.T.; Tinoco, E.N.; Yu, N.J. Thirty years of development and application of CFD at Boeing Commercial Airplanes, Seattle. Comput. Fluids 2005, 34, 1115–1151. [Google Scholar] [CrossRef]
- Abbas-Bayoumi, A.; Becker, K. An industrial view on numerical simulation for aircraft aerodynamic design. J. Math. Ind. 2011, 1, 10. [Google Scholar] [CrossRef]
- Spalart, P.R.; Venkatakrishnan, V. On the role and challenges of CFD in the aerospace industry. Aeronaut. J. 2016, 120, 209–232. [Google Scholar] [CrossRef]
- Clark, A.M.; Slotnick, J.P.; Taylor, N.J.; Rumsey, C.L. Requirements and challenges for CFD validation within the High-Lift Common Research Model ecosystem. In Proceedings of the AIAA Aviation 2020 Forum, Online, 15–19 June 2020. [Google Scholar] [CrossRef]
- Recommended Practice: When Flight Modelling Is Used to Reduce Flight Testing Supporting Aircraft Certification (AIAA R-154-2021); AIAA: Reston, VA, USA, 2021. [CrossRef]
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; Technical Report CR–2014-218178; NASA: Washington, DC, USA, 2014. [Google Scholar]
- Lozano-Durán, A.; Bose, S.T.; Moin, P. Performance of Wall-Modeled LES with Boundary-LayerConforming Grids for External Aerodynamics. AIAA J. 2021, J061041. [Google Scholar] [CrossRef]
- Spalart, P.R.; Jou, W.H.; Strelets, M.; Allmaras, S.R. Comments on the feasibility of LES for wings, and on a hybrid RANS/LES approach. Adv. DNS/LES 1997, 1, 4–8. [Google Scholar]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Casey, M.; Wintergerste, T. ERCOFTAC Best Practice Guidelines: ERCOFTAC Special Interest Group on “Quality and Trust in Industrial CFD”; ERCOFTAC; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Rumsey, C.L.; Slotnick, J.P.; Sclafani, A.J. Overview and Summary of the Third AIAA High Lift Prediction Workshop. J. Aircr. 2019, 56, 621–644. [Google Scholar] [CrossRef]
- Rumsey, C.L.; Carlson, J.; Ahmad, N. FUN3D Juncture Flow Computations Compared with Experimental Data. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar] [CrossRef]
- Choi, H.; Moin, P. Grid-point requirements for large eddy simulation: Chapman’s estimates revisited. Phys. Fluids 2012, 24, 011702. [Google Scholar] [CrossRef]
- Piomelli, U.; Balaras, E. Wall-layer models for large-eddy simulations. Annu. Rev. Fluid Mech. 2002, 34, 349–374. [Google Scholar] [CrossRef]
- Cabot, W.H.; Moin, P. Approximate wall boundary conditions in the large-eddy simulation of high Reynolds number flow. Flow Turbul. Combust. 2000, 63, 269–291. [Google Scholar] [CrossRef]
- Larsson, J.; Kawai, S.; Bodart, J.; Bermejo-Moreno, I. Large eddy simulation with modeled wall-stress: Recent progress and future directions. Mech. Eng. Rev. 2016, 3, 15-00418. [Google Scholar] [CrossRef]
- Bose, S.T.; Park, G.I. Wall-Modeled LES for Complex Turbulent Flows. Ann. Rev. Fluid Mech. 2018, 50, 535–561. [Google Scholar] [CrossRef] [PubMed]
- Deardorff, J. A numerical study of three-dimensional turbulent channel flow at large Reynolds numbers. J. Fluid Mech. 1970, 41, 453–480. [Google Scholar] [CrossRef]
- Schumann, U. Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli. J. Comp. Phys. 1975, 18, 376–404. [Google Scholar] [CrossRef]
- Piomelli, U.; Ferziger, J.; Moin, P.; Kim, J. New approximate boundary conditions for large eddy simulations of wall-bounded flows. Phys. Fluids 1989, 1, 1061–1068. [Google Scholar] [CrossRef]
- Balaras, E.; Benocci, C.; Piomelli, U. Two-layer approximate boundary conditions for large-eddy simulations. AIAA J. 1996, 34, 1111–1119. [Google Scholar] [CrossRef]
- Wang, M.; Moin, P. Dynamic wall modeling for large-eddy simulation of complex turbulent flows. Phys. Fluids 2002, 14, 2043–2051. [Google Scholar] [CrossRef]
- Chung, D.; Pullin, D.I. Large-eddy simulation and wall modelling of turbulent channel flow. J. Fluid Mech. 2009, 631, 281–309. [Google Scholar] [CrossRef]
- Bodart, J.; Larsson, J. Wall-modeled large eddy simulation in complex geometries with application to high-lift devices. In Annual Research Briefs; Center for Turbulence Research: Stanford, CA, USA, 2011; pp. 37–48. [Google Scholar]
- Kawai, S.; Larsson, J. Dynamic non-equilibrium wall-modeling for large eddy simulation at high Reynolds numbers. Phys. Fluids 2013, 25, 015105. [Google Scholar] [CrossRef]
- Bermejo-Moreno, I.; Campo, L.; Larsson, J.; Bodart, J.; Helmer, D.; Eaton, J.K. Confinement effects in shock wave/turbulent boundary layer interactions through wall-modelled large-eddy simulations. J. Fluid Mech. 2014, 758, 5–62. [Google Scholar] [CrossRef]
- Park, G.I.; Moin, P. An improved dynamic non-equilibrium wall-model for large eddy simulation. Phys. Fluids 2014, 26, 015108. [Google Scholar] [CrossRef]
- Yang, X.I.A.; Sadique, J.; Mittal, R.; Meneveau, C. Integral wall model for large eddy simulations of wall-bounded turbulent flows. Phys. Fluids 2015, 27, 025112. [Google Scholar] [CrossRef]
- Bose, S.T.; Moin, P. A dynamic slip boundary condition for wall-modeled large-eddy simulation. Phys. Fluids 2014, 26, 015104. [Google Scholar] [CrossRef]
- Lozano-Durán, A.; Bae, H.; Bose, S.; Moin, P. Dynamic wall models for the slip boundary condition. In Annual Research Briefs; Center for Turbulence Research: Stanford, CA, USA, 2017; pp. 229–242. [Google Scholar]
- Bae, H.J.; Lozano-Durán, A.; Bose, S.T.; Moin, P. Dynamic slip wall model for large-eddy simulation. J. Fluid Mech. 2019, 859, 400–432. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.I.A.; Zafar, S.; Wang, J.X.; Xiao, H. Predictive large-eddy-simulation wall modeling via physics-informed neural networks. Phys. Rev. Fluids 2019, 4, 034602. [Google Scholar] [CrossRef]
- Lozano-Durán, A.; Bae, H.J. Self-critical machine-learning wall-modeled LES for external aerodynamics. In Annual Research Briefs; Center for Turbulence Research: Stanford, CA, USA, 2020; pp. 197–210. [Google Scholar]
- Radhakrishnan, S.; Gyamfi, L.A.; Miro, A.; Font, B.; Calafell, J.; Lehmkuhl, O. A data-driven wall-shear stress model for LES using gradient boosted decision trees. In Proceedings of the International Conference on High Performance Computing, St. Louis, MO, USA, 14–19 November 2021; pp. 105–121. [Google Scholar]
- Eivazi, H.; Tahani, M.; Schlatter, P.; Vinuesa, R. Physics-informed neural networks for solving Reynolds-averaged Navier–Stokes equations. arXiv 2021, arXiv:2107.10711. [Google Scholar]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
- Vinuesa, R.; Sirmacek, B. Interpretable deep-learning models to help achieve the Sustainable Development Goals. Nat. Mach. Intell. 2021, 3, 926. [Google Scholar] [CrossRef]
- Li, R.; Noack, B.R.; Cordier, L.; Borée, J.; Harambat, F. Drag reduction of a car model by linear genetic programming control. Exp. Fluids 2017, 58, 103. [Google Scholar] [CrossRef]
- Minelli, G.; Dong, T.; Noack, B.R.; Krajnović, S. Upstream actuation for bluff-body wake control driven by a genetically inspired optimization. J. Fluid Mech. 2020, 893, A1. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Morita, Y.; Rezaeiravesh, S.; Tabatabaei, N.; Vinuesa, R.; Fukagata, K.; Schlatter, P. Applying Bayesian optimization with Gaussian-process regression to Computational Fluid Dynamics problems. arXiv 2021, arXiv:2101.09985. [Google Scholar] [CrossRef]
- Mahfoze, O.A.; Moody, A.; Wynn, A.; Whalley, R.D.; Laizet, S. Reducing the skin-friction drag of a turbulent boundary-layer flow with low-amplitude wall-normal blowing within a Bayesian optimization framework. Phys. Rev. Fluids 2019, 4, 094601. [Google Scholar] [CrossRef]
- Kornilov, V.I.; Boiko, A.V. Efficiency of air microblowing through microperforated wall for flat plate drag reduction. AIAA J. 2012, 50, 724–732. [Google Scholar] [CrossRef]
- Guastoni, L.; Güemes, A.; Ianiro, A.; Discetti, S.; Schlatter, P.; Azizpour, H.; Vinuesa, R. Convolutional-network models to predict wall-bounded turbulence from wall quantities. J. Fluid Mech. 2021, 928, A27. [Google Scholar] [CrossRef]
- Güemes, A.; Discetti, S.; Ianiro, A.; Sirmacek, B.; Azizpour, H.; Vinuesa, R. From coarse wall measurements to turbulent velocity fields through deep learning. Phys. Fluids 2021, 3, 075121. [Google Scholar] [CrossRef]
- Abreu, L.I.; Cavalieri, A.V.G.; Schlatter, P.; Vinuesa, R.; Henningson, D.S. Spectral proper orthogonal decomposition and resolvent analysis of near-wall coherent structures in turbulent pipe flows. J. Fluid Mech. 2020, 900, A11. [Google Scholar] [CrossRef]
- Abreu, L.I.; Tanarro, A.; Cavalieri, A.V.; Schlatter, P.; Vinuesa, R.; Hanifi, A.; Henningson, D.S. Spanwise-coherent hydrodynamic waves around flat plates and airfoils. J. Fluid Mech. 2021, 927, A1. [Google Scholar] [CrossRef]
- Eivazi, H.; Le Clainche, S.; Hoyas, S.; Vinuesa, R. Towards extraction of orthogonal and parsimonious non-linear modes from turbulent flows. arXiv 2021, arXiv:2109.01514. [Google Scholar]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G. An Introduction to Deep Reinforcement Learning. Found. Trends Mach. Learn. 2018, 3, 1–140. [Google Scholar]
- Rabault, J.; Kuchta, M.; Jensen, A.; Réglade, U.; Cerardi, N. Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J. Fluid Mech. 2019, 865, 281–302. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef] [PubMed]
- Gu, S.; Lillicrap, T.; Sutskever, U.; Levine, S. Continuous deep Q-learning with model-based acceleration. In Proceedings of the 33rd International Conference on Machine Learning, ICML, New York, NY, USA, 19–24 June 2016; pp. 4135–4148. [Google Scholar]
- Rabault, J.; Ren, F.; Zhang, W.; Tang, H.; Xu, H. Deep reinforcement learning in fluid mechanics: A promising method for both active flow control and shape optimization. J. Hydrodyn. 2020, 32, 234–246. [Google Scholar] [CrossRef]
- Garnier, P.; Viquerat, J.; Rabault, J.; Larcher, A.; Kuhnle, A.; Hachem, E. A review on deep reinforcement learning for fluid mechanics. Comput. Fluids 2021, 225, 104973. [Google Scholar] [CrossRef]
- Bucci, M.A.; Semeraro, O.; Allauzen, A.; Wisniewski, G.; Cordier, L.; Mathelin, L. Control of chaotic systems by deep reinforcement learning. Proc. R. Soc. A 2019, 475, 20190351. [Google Scholar] [CrossRef]
- Paris, R.; Beneddine, S.; Dandois, J. Robust flow control and optimal sensor placement using deep reinforcement learning. J. Fluid Mech. 2021, 913, A25. [Google Scholar] [CrossRef]
- Beintema, G.; Corbetta, A.; Biferale, L.; Toschi, F. Controlling Rayleigh–Bénard convection via reinforcement learning. J. Turbul. 2020, 21, 585–605. [Google Scholar] [CrossRef]
- Tang, H.; Rabault, J.; Kuhnle, A.; Wang, Y.; Wang, T. Robust active flow control over a range of Reynolds numbers using an artificial neural network trained through deep reinforcement learning. Phys. Fluids 2020, 32, 053605. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, W.; Deng, J.; Rabault, J. Active flow control with rotating cylinders by an artificial neural network trained by deep reinforcement learning. J. Hydrodyn. 2020, 32, 254–258. [Google Scholar] [CrossRef]
- Fan, D.; Yang, L.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Reinforcement learning for bluff body active flow control in experiments and simulations. Proc. Natl. Acad. Sci. USA 2020, 117, 26091–26098. [Google Scholar] [CrossRef]
- Ren, F.; Rabault, J.; Tang, H. Applying deep reinforcement learning to active flow control in weakly turbulent conditions. Phys. Fluids 2021, 33, 037121. [Google Scholar] [CrossRef]
- Rabault, J.; Kuhnle, A. Accelerating deep reinforcement learning strategies of flow control through a multi-environment approach. Phys. Fluids 2019, 31, 094105. [Google Scholar] [CrossRef]
- Belus, V.; Rabault, J.; Viquerat, J.; Che, Z.; Hachem, E.; Reglade, U. Exploiting locality and translational invariance to design effective deep reinforcement learning control of the 1-dimensional unstable falling liquid film. AIP Adv. 2019, 9, 125014. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vinuesa, R.; Lehmkuhl, O.; Lozano-Durán, A.; Rabault, J. Flow Control in Wings and Discovery of Novel Approaches via Deep Reinforcement Learning. Fluids 2022, 7, 62. https://doi.org/10.3390/fluids7020062
Vinuesa R, Lehmkuhl O, Lozano-Durán A, Rabault J. Flow Control in Wings and Discovery of Novel Approaches via Deep Reinforcement Learning. Fluids. 2022; 7(2):62. https://doi.org/10.3390/fluids7020062
Chicago/Turabian StyleVinuesa, Ricardo, Oriol Lehmkuhl, Adrian Lozano-Durán, and Jean Rabault. 2022. "Flow Control in Wings and Discovery of Novel Approaches via Deep Reinforcement Learning" Fluids 7, no. 2: 62. https://doi.org/10.3390/fluids7020062
APA StyleVinuesa, R., Lehmkuhl, O., Lozano-Durán, A., & Rabault, J. (2022). Flow Control in Wings and Discovery of Novel Approaches via Deep Reinforcement Learning. Fluids, 7(2), 62. https://doi.org/10.3390/fluids7020062







