Abstract
Convective velocity perturbations (CVPs) are known to play an important role in the response of flames to acoustic perturbations and in thermoacoustic combustion instabilities. In order to elucidate the flow-physical origin of CVPs, the present study models the response of laminar premixed slit flames to low amplitude perturbations of the upstream flow velocity with a reduced order flow decomposition approach: A linearized G-equation represents the shape and heat release rate of the perturbed flame, while the velocity perturbation field is decomposed into irrotational and solenoidal contributions. The former are determined with a conformal mapping from geometry and boundary conditions, whereas the latter are governed by flame front curvature and flow expansion across the flame, which generates baroclinic vorticity. High-resolution CFD analysis provides values of model parameters and confirms the plausibility of model results. This flow decomposition approach makes it possible to explicitly evaluate and analyze the respective contributions of irrotational and solenoidal flows to the flame response, and conversely the effect of flame perturbations on the flow. The use of the popular ad hoc hypothesis of convected velocity perturbation is avoided. It is found that convected velocity perturbations do not result from immediate acoustic-to-hydrodynamic mode conversion, but are generated by flame-flow feedback. In this sense, models for flame dynamics that rely on ad-hoc models for CVPs do not respect causality. Furthermore, analysis of the flame impulse response reveals that for the configuration investigated, flame-flow feedback is also responsible for “excess gain” of the flame response, that is, the magnitude of the flame frequency response above unity.
1. Introduction
Thermoacoustic instabilities are a cause for concern in combustion applications as diverse as rocket engines, gas turbines, or domestic heaters [1,2,3,4]. Such instabilities can lead to severe mechanical or thermal damage, even catastrophic failure of a combustor. Increased emissions of noise and pollutants—such as oxides of nitrogen, soot, or carbon monoxide—may also result.
Thermoacoustic instabilities result from feedback between acoustic fluctuations and unsteady heat release by the flame. Hydrodynamic flow perturbations, which can be decomposed into irrotational as well as vortical contributions, are understood to play an important intermediate role in acoustic/flow/flame interactions [5,6]. The response of a premixed flame to low amplitude velocity disturbances is generally described by the flame transfer function (FTF) [6,7,8,9]. The FTF relates variations of the heat release rate to those of velocity upstream of the flame. It may be represented in the frequency domain by the frequency response (FR) or in the time domain by the impulse response (IR) [10,11]. Several studies have proposed analytical expressions for the FTF of laminar Bunsen-type flames based on a linearized “G-equation” [8,9,12,13]. Key modeling features in those studies are the respective spatio-temporal distributions of the perturbation velocity, which were not computed from first principles, but simply presumed. Of course, such an ad-hoc approach leaves two important questions open: what is the flow-physical origin of non-trivial spatio-temporal distributions of the perturbation velocity, and what is the proper functional form of this distribution for a given flame configuration?
Fleifil et al. [8] argued that flames are often acoustically compact and presumed a spatially uniform perturbation of axial velocity. Reasonable predictions were obtained for the gain of the FTF; however, the phase saturated at , which does not agree with experiment. To remedy this deficiency, Schuller et al. [9] introduced the so-called “convective velocity model”, which noticeably improved the prediction of the phase of the FTF. However, Cuquel et al. [13] pointed out that the convective velocity model proposed in [9] violates mass conservation and determined the FTF of an “incompressible convective” model, as originally proposed by Baillot et al. [14] to represent a “progressive wave of kinematic disturbance” that was observed to emanate from the flame base during acoustic excitation at low frequencies. Nevertheless, the origin and nature of the “convective wave disruption” remained an open question.
Since the acoustic velocity is an irrotational vector field, an acoustic-to-hydrodynamic mode conversion is required to generate convective velocity perturbations (CVPs). One such mode conversion mechanism is the separation of the flow at a sharp corner, for example at a backward facing step or flame holder. At the point of separation, vorticity that is initially confined to the wall boundary layers is ejected into the flow domain, where it is carried downstream along the shear layer by the flow. The transient (acoustic) entrainment of a separating flow results in unsteady generation and detachment of vortex intensity [15,16]. The velocity field induced by the shear layer vorticity, which is described by the Biot–Savart law, may then influence the flame front in a non-local fashion [17]. Indeed, analysis of high-fidelity computational fluid dynamics (CFD) simulations of unconfined laminar flames by Schlimpert et al. [18] showed that shear layer vortex structures can significantly perturb the flame front—but only in the case of negligible gas expansion across the flame front. For realistic gas expansion, the influence of the vortex structures on the flame perturbations is considerable only at the base of the flame. Similar conclusions were reached by the authors of the present paper for confined flames stabilized at a backward-facing step [19]: Using a low-order model based on a decomposition approach [20,21], it was found that shear layer vorticity only has a negligible influence on the flame response.
These results confirm earlier arguments by Baillot et al. [14], Birbaud et al. [22] and Kornilov et al. [23], who reasoned that convective waves observed within the flame cone are not generated by immediate acoustic-hydrodynamic mode conversion, but result from the influence of flame front deflections on the upstream flow. Blanchard et al. [24] corroborated this hypothesis by coupling a G-equation model for an M-flame with an analytical formulation for flame-flow feedback. The displaced flame front was considered as a sheet of vorticity, with a strength proportional to the gas expansion across the flame and the local gradient of the flame front displacement. The velocity upstream of the vorticity sheet was computed with the Biot-Savart law and, indeed, exhibited convective waves.
The present study revisits the interactions between flow and flame, with the objective of clarifying the flow-physical origin of CVPs and explicating consequences of CVPs for the flame transfer function. In distinction to other studies, a laminar premixed slit flame is investigated, which facilitates the formulation of a 2D flow decomposition model that represents the velocity perturbation field as the sum of irrotational potential and solenoidal contributions. Vorticity generated by acoustic-hydrodynamic mode conversion as well as by perturbations of the flame front, which is represented by a G-equation, may contribute to the latter. In this way, flame-flow interaction is taken into consideration, which is the essential novelty compared to previous studies reviewed above and our earlier work [19]. The validity of the model is cross-checked against high-fidelity CFD simulations.
The flow decomposition approach makes it possible to explicitly evaluate and analyze the respective contributions of the irrotational and solenoidal flows on the flame, and conversely the effect of flame front perturbations on the flow. It is found that the hydrodynamic feedback of the perturbed flame sheet onto the flow contributes in an essential manner to the overall response of the flame to acoustic perturbations. In agreement with Baillot et al. [14], Birbaud et al. [22], Kornilov et al. [23], Blanchard et al. [24] it is concluded that flame/flow interaction generates CVPs upstream of the flame. In other words, CVPs should not be regarded as an input for the evaluation of flame response—as it is commonly done in models based on the G-equation—but instead as a result of flow-flame interaction. Furthermore, analysis of the flame impulse response leads to the conclusion that so-called “excess gain”, that is, the magnitude of the FTF significantly above unity, also results from flame/flow interaction.
The paper is organized as follows: the next section introduces the various components of the flow decomposition modeling approach, which is based on a conformal mapping. Special attention is given to the Kutta condition that is used to suppress flow singularities at the anchoring point of the flame. Then the linearized G-equation model for the flame is presented, analysis of the jump conditions across the flame sheet allow to quantify the vorticity generated by a convoluted flame sheet. Finally, the CFD model of the configuration investigated in the present study, that is, a laminar, premixed slit flame, is described. The results of modeling the flame response to harmonic and impulse velocity perturbations with uni- and bidirectional coupling are then presented. It is emphasized that the flow decomposition model proposed here is not meant to serve as a stand-alone substitute for CFD simulation (indeed the model relies on CFD data to set values of model parameters). Instead, the decomposition approach makes it possible to segregate the various acoustic/flow/flame interaction mechanisms and identify the respective consequences—which would be much more difficult with CFD alone [18]. The results obtained are then contextualized and further interpreted, including an outlook for future studies.
2. Materials and Methods
A set-up as depicted in Figure 1 shall be considered, where a slit flame is stabilized above a planar jet of perfectly premixed, lean fuel/air mixture and excited by upstream velocity perturbations. This configuration may be decomposed into a large-scale hydrodynamic and a thin, quasi-1D combustion zone.
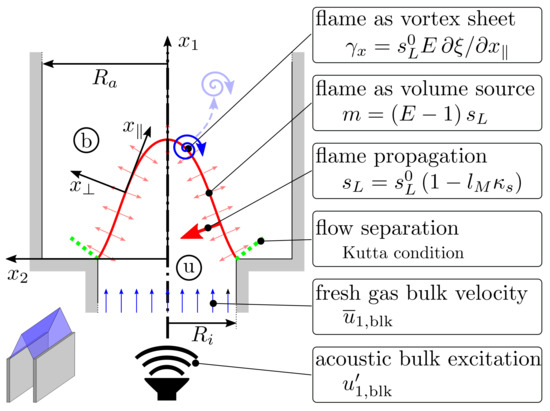
Figure 1.
A laminar slit flame is stabilized above a planar jet of unburned mixture, as illustrated in 3D in the lower left corner of the picture. The unburned (“u”) fuel/air premixture flows with bulk flow velocity and is subjected to upstream bulk velocity perturbations . The flame propagates normal to itself with speed , which may depend on flame front curvature , and acts as a volume source of strength m. Two coordinate systems are used, namely laboratory coordinates and flame-aligned coordinates where points in the local flame normal direction towards the burned gas (“b”).
The goal of the decomposition modeling approach developed within this paper is to identify explicitly mechanisms of acoustics-flame-flow interaction in the limit of small amplitudes, to establish characteristic features of the various mechanisms and to assess their relative importance to overall flame dynamics. This objective naturally suggests a reductionist strategy. A Helmholtz-decomposition is employed, which segregates the flow into two contributions: an irrotational part that obeys a flow potential, and a solenoidal or vortical part that identically satisfies continuity [20,21,25,26]. Such a decomposition makes it possible to “switch off” various components or mechanisms of flow/flame interaction, which facilitates the study of the respective impact on the overall flame dynamics. Chu and Kovasznay [27] showed that far away from any boundaries and in the absence of strong density gradients the irrotational and the vortical flow modes stay well separated in time and space. Hence, one flow mode can be transformed to the other only at the combustor walls and at the flame front.
To fix ideas, consider the configuration depicted in Figure 1. The flow field u is decomposed into irrotational contributions , and a rotational contribution :
The first term on the r.h.s. of (1) is caused by a pressure difference between in- and outlet of the domain. Note that is governed in an instantaneous manner by the geometry and the prevailing boundary conditions. The flow expansion counterpart , on the other hand, results from the density change resulting from combustion and the concomitant acceleration of the flow. It depends on the instantaneous position and strength of the flame. Movement and position of the flame are represented by a linearized G-equation [9,14,28]. Perturbations of the flame shape generate vorticity, which contributes to the vortical part of the velocity field. Additional contributions to may result from vorticity shed due to flow separation from the backward facing step, where the flame is anchored. Contributions and establish a bidirectional feedback between flow and flame, which will in general result in transient phenomena that are not governed instantaneously by the boundary conditions.
Such a flow decomposition-based approach has—in similar form—been solved numerically to model non-linear flame propagation, for example, by Pindera and Talbot [20] or Rhee et al. [21]. Contrary to those studies, the present paper strives to develop a low-order formulation for the dynamics of the resulting flow field perturbations, which is essentially based on four points: (1) The impermeability boundary conditions are satisfied by use of a Schwarz–Christoffel mapping technique; (2) the flow field is decomposed into a finite set of flow field singularities, that is, point sources and point vortices; (3) in order to avoid infinitely high velocities at the anchoring point, a Kutta condition is employed; and (4) the dynamics of the flame front is captured by a G-equation-based model that includes the generation of baroclinic vorticity. All these points are explained in detail in the dissertation of the first author of the present paper [29] and will only be summarized in the following. Points (1)–(3), that is, the modeling approach for the underlying flow field, are covered in Section 2.1. Section 2.2 is solely devoted to point (4), namely the modeling strategy for the flame dynamics.
2.1. Flow Dynamics
2.1.1. Governing Equations
A low Mach number flow is assumed, which is regarded to be dynamically incompressible in the sense that density is only affected by the combustion process [20,21]. Furthermore, the analysis shall be restricted to a 2D ideal fluid (zero viscosity, thermal and mass diffusivities) without any volume or body forces. Viscous effects will be incorporated by use of a Kutta condition. This results in a flow problem governed by
where is the material derivative and u, and p denote flow velocity, density and pressure, respectively.
The right-hand side of the continuity Equation (2) represents a source of volume that vanishes everywhere but in the immediate vicinity of the flame front, where it leads to a volume production rate per unit area of the flame [20,30]. Here, denotes the non-dimensional density increase and the indices “u” and “b” refer to unburned and burned flow, respectively. In line with the analysis of Landau [31], perturbations in the volume source term are neglected in the present paper, although this ignores a mechanism that may destabilize a flame front [32,33]. Consequences of volume source perturbations on acoustic–flame interactions have been explored by Zimmermann [34] and Steinbacher [29], who generated an irrotational contribution to the decomposition (1) by placing a number of discrete volume sources along the flame front. For a corrugated flame sheet, CVPs upstream as well as downstream of the flame result, similar to the effects of flame generated vorticity. For details, the reader is referred to [29]. The neglect of the volume source term also excludes the dilatation term from the vorticity equation, which often mitigates the impact of vortical perturbations that are convected across the flame on the flow field. For the slit flame configuration investigated in this paper, there is no vorticity upstream of the flame front, so this effect is deemed insignificant. To summarize, consequences of flow expansion are neglected, since—at least in the linear regime—they do not add qualitatively new dynamics. Consequently, flame/flow feedback is represented solely in terms of flame generated vorticity and quantitative agreement with high fidelity CFD data can be achieved by fitting an empirical factor, see Section 3.2.
Taking the curl of the momentum Equation (3) leads to a transport equation for vorticity :
Here, the dilatation term was neglected since it is non-zero only right at the flame front and the flow field upstream of the flame is assumed to be free of vorticity. Furthermore, Matalon et al. [35] argued that contributions of this term are negligible across the flame sheet. Thus, for 2D inviscid flows, the dominant source term of the vorticity transport equation is the baroclinic torque, which arises from a misalignment of the pressure and density gradients. From the left-hand side of Equation (4) it becomes clear that vorticity is transported like a mass-less particle.
While the irrotational components each have a potential , the vortical component depends on a stream function via . Application of these relations, together with the decomposition of Equation (1) results in the Poisson equations:
with the Laplace operator . Note that is subject to a line source at , which generates a volume flux through the combustor that is driven by a potential (or pressure) gradient between and . The bulk velocity is given by . All boundaries shall be impermeable and the axial velocity gradients shall vanish far up and downstream the flame: .
In our study, we use this set of equations to model the perturbation velocity field. The only mean field quantities that are required are the stationary shape of the flame front as well as the trajectories and advection speeds of the vorticity that is shed from the burner mouth. Flame front shapes are chosen to match the reference high fidelity CFD data, see Section 2.3. The trajectories are extracted from the CFD data and a constant advection speed of is assumed, as described in more detail in Section 3.1. Furthermore, it is assumed that the perturbation flow field is irrotational before and after the flame front—with the exception of vorticity shed from the burner mouth. Consequently, baroclinic vorticity may only be present right at the flame sheet.
2.1.2. Conformal Mapping-Based Modeling Approach
Following Steinbacher et al. [19], the Poisson Equations (5)–(7) are solved on the geometry of interest by the use of a Schwarz–Christoffel mapping technique. The interior of the physical flow domain is mapped to the imaginary positive half of a complex image domain. By doing so, the flow problem is split into a mapping problem simplifying and unifying the boundary conditions and a canonical flow problem in the image domain.
The coordinate system used to describe the combustor shown in Figure 1 is illustrated in Figure 2. Due to symmetry, we limit ourselves to only one half of the domain. Complex variables are used to describe the 2D problem: Coordinates in the physical domain are represented by where denotes the axial and the transverse direction, perpendicular to the first. Accordingly, velocities are expressed by . In the image domain, the complex variable is used to specify location.
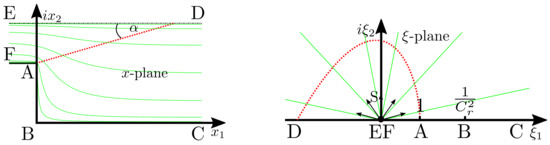
Figure 2.
Illustration of the Schwarz–Christoffel mapping (not to scale). Mean flame position ( ) and straight lines radiating from the origin of the image domain (
) and straight lines radiating from the origin of the image domain ( ), each in the physical domain (left) and the image domain (right).
), each in the physical domain (left) and the image domain (right).
 ) and straight lines radiating from the origin of the image domain (
) and straight lines radiating from the origin of the image domain ( ), each in the physical domain (left) and the image domain (right).
), each in the physical domain (left) and the image domain (right).
All corners of the flow domain are named by capital letters (A to E) and are mapped to points on the real axis of the image domain. At edge A, the feed channel opens into the combustion chamber. This edge is mapped to . Points E and F are located at in the physical domain and are mapped to in the image domain. The mapping is defined by:
with the confinement ratio [36]. This mapping can only be inverted numerically, therefore, evaluation of requires the application of a numerical root finding algorithm.
The complex conjugate, denoted by , of the velocity in the physical domain is computed by application of the chain rule:
The first term in this equation is the derivative of the flow potential with respect to the image domain coordinate , the second the first derivative of the mapping with respect to the physical coordinate x. The latter reads for the combustor geometry:
Using these relations, we are able to compute the velocity field in the physical domain due to any potential given in the image domain. Knowing that any point source or vortex maps to its counterpart in the image domain by conserving its strength—that is, volume production and circulation, respectively—and vice versa, we are able to define a potential field as the superposition of several point sources and vortices. By mapping these points to the image domain, Equation (9) can be used to compute the associated physical velocity field that complies with the boundary conditions. This process is explicated in more detail in the following.
2.1.3. Flow-Field Singularities
Within the proposed modeling approach, the flow field is represented by a finite set of flow field singularities, that is, point sources and vortices. The complex conjugate of the irrotational velocity component due to a point source of strength S at position reads:
Similarly, we get for the solenoidal (vortical) velocity due to a point vortex of strength at the same position:
In the image domain, all walls are mapped to the real axis. Therefore, in order to fulfill the impermeability boundary conditions at all walls, mirror sources of equal strength S are placed in the lower half of the complex plane by mirroring the source locations at the real axis. This simply corresponds to computing the complex conjugate of the original source position . Equivalently, mirror vortices of opposite strength are introduced. In doing so, velocity components normal to the real axis vanish and the volume flux through all walls is zero. This is illustrated in Figure 3 for a single vortex.
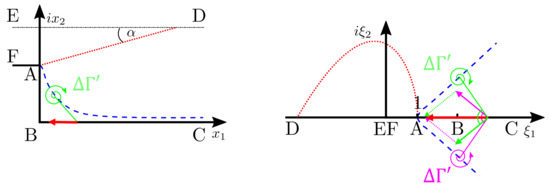
Figure 3.
Illustration of how impermeability boundary conditions are met by use of a mirror vortex (not to scale): the wall normal velocity component of the original vortex of strength (green) is canceled by its mirror counterpart (pink) such that the resulting velocity (red) is parallel to the walls in the physical (left) as well as in the image domain (right). The shear layer and the flame front are shown as blue dashed and red dotted lines, respectively.
In the proposed model, the vortical part of the overall perturbation velocity field is approximated by a finite number of N point vortices of strengths , which induce a velocity in the image domain:
where mirror vortices of opposite circulation have been placed at the complex conjugate coordinates of all vortices.
The potential part of the perturbation velocity field that drives the volume flux through the combustor can be computed by placing a source of strength,
at since all points of are mapped to a single point in the image domain (EF). Following Equation (11), the complex conjugate of the associated velocity field is computed in the image domain as:
Resulting stream lines in the image and in the physical domain, respectively, are shown in green in Figure 2.
2.1.4. Kutta Condition
The flow model for the perturbation velocity field as introduced in the previous sub-section neglects the effects of viscosity. However, it is well understood that in cases where a boundary layer forms and separates from a rigid boundary, the resulting flow field may differ very significantly from completely inviscid flow, and the extent of the region of effectively inviscid flow will be defined by the location of the separated boundary layer [37]. In order to capture the important effects of boundary layer separation, the model for CVPs developed in this paper is supplemented with a Kutta condition, which attaches a vortex sheet to the trailing edge of the burner plate. CFD results are used to set model parameters of the Kutta condition and determine the trajectory of the vortices shed into the flow domain, as described in Section 2.3. The present sub-section provides details on the implementation of the Kutta condition.
According to Equations (9) and (10), the inviscid potential flow in the combustor exhibits an singularity at edge A. This is unrealistic: a viscous flow will not follow the abrupt turn of the wall contour, since this would require an infinitely high pressure gradient. Instead, due to near-wall viscous effects, flow separation at edge A will occur. Pressure gradients remain finite and vorticity, originally confined to the wall boundary layer, is shed into the inner region of the flow domain. Within the inviscid modeling framework adopted here, this singularity is removed by employing a Kutta condition, which recovers a finite-valued velocity at the edge by imposing
see Equation (9). In order to satisfy this condition, vorticity is introduced in the vicinity of edge A, which implies the formation of an infinitely thin shear layer. It should be pointed out that in the case of an anchored flame, eliminating the singularity is compulsory since otherwise the infinitely high velocity at the anchoring would lead to unbounded displacement amplitudes at the flame base.
Following [15,16,38,39], the Kutta condition is implemented with a single panel method, which attaches a vortex sheet (the panel) to the trailing edge. The values of length and strength of this panel depend on the instantaneous flow field and are set such that the edge singularity is removed. At each time step, the circulation confined to the panel is condensed into one point vortex and advected by the local flow velocity.
The length of the panel is set to the distance a fluid parcel placed at edge A would be advected during one time step . In order to avoid the computation of the mean flow state, it is assumed this fluid parcel propagates with a constant speed . Thus, the panel length in the physical domain becomes . Its counterpart in the image domain, that is, , is then numerically evaluated as the root of:
where a parametrization of the curve representing the Kutta panel is used (note that here t denotes the parametrization variable, not the time). This approach implicitly assumes a block flow profile in the feed channel and zero velocity in the recirculation zone. Besides the length , there is a second geometrical parameter of the vortex sheet, that is, its angle with respect to the real axis , see Figure 4. The angle of the panel in the image domain is set to , such that the flow follows the wall contour of the feed duct.
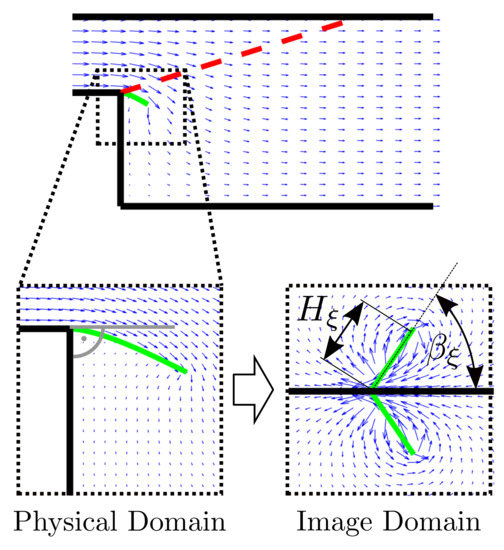
Figure 4.
Flow field in a combustor with resulting from a source at and a Kutta panel (green). Close up views of the Kutta panel and are shown in the physical (bottom left) and the image domain (bottom right).
The strength of a vortex sheet in the physical domain is given by:
where is the circulation, defined as the integral of vorticity over an area A. In order to achieve an (approximately) constant distribution of vorticity along the panel, a sheet strength of
is imposed, which is parametrized by a constant .
The value of this constant is set such that Condition (16) is fulfilled, thus:
where denotes the potential associated with the Kutta condition and the potential resulting from all other flow field singularities (sources and vortices). This relation together with the definition of (not specified here; for details see [29]) allows us to determine the unknown constant to:
Having computed and and following Equation (9), we can now evaluate the complex conjugate of the resulting overall flow velocity in the physical domain,
A flow field as illustrated in Figure 4 evolves.
2.2. Flame Dynamics
2.2.1. Linearized G-Equation for the Flame Front
Following [28,40], the evolution of the flame sheet may be described by a 1D linearized G-equation:
where denotes the mean flow velocity in flame-parallel direction and the Markstein length. A Dirichlet boundary condition anchors the flame at the burner edge. Furthermore, curvature at the flame tip is set to zero, that is, and hence the tip is allowed to move [41].
2.2.2. Jump Conditions across a Flame Sheet
Fluxes of mass and momentum are conserved across a flame sheet,
Here, the squared brackets denote the change of a quantity across the flame front: . Furthermore, the Einstein summation convention is employed: , and denote the -component of the flow velocity, the local flame normal and flame tangential vectors respectively; the local mass flux across the flame sheet is denoted by m.
If the flame front is represented by a linearized G-Equation (23), the jump conditions Equation (24) may be written as [31,42]:
These relations are evaluated at the mean flame position, which is, per definition, fixed in space and time. This simplification imposes an error that scales with the displacement amplitude and the inverse of the perturbation wave length.
Evaluation of the jump conditions Equation (25) requires the computation of the velocity components tangential and normal to the flame front. The linear analysis presented in the following shall be limited to perturbation wave lengths that are large compared to the convective-diffusive length scale in order to avoid significant levels of flame stretch or significant 2D effects. This limits the analysis to large Péclet numbers . Furthermore, flame displacement amplitudes shall be small . Assuming , where is a small quantity, all terms are negligible and dropped from analysis. Developing all quantities in powers of shifts perturbations with a wavelength much shorter than the flame thickness to higher order in the expansion. Retaining only zeroth order terms, the flame normal and tangential vectors at the perturbed flame are given by:
respectively. Here, a flame-aligned coordinate system as depicted in Figure 1 with mean flow towards the positive -direction is assumed.
A perturbed flame sheet induces perturbations of other flow variables, that is, velocity and pressure [43]. Assuming for the flow of fresh mixture, the flame normal and tangential velocity components just upstream of the flame sheet can be computed from and ,
respectively. Using these equations together with Equation (24), we get for the mean quantities,
where the assumption of a stationary flame front of the unperturbed flow requires and denotes the non-dimensional increase of specific volume. Hence, across the flame front the flow is accelerated by a factor in the -direction and the static pressure decreases by a term . Application of the jump conditions for the perturbed flow field results in:
while the equation governing the flame dynamics leads to
When Landau [31] assessed the stability of planar flames, he neglected stretch effects and assumed a constant flame speed . It follows from Equation (36) that in this case the flame front moves in accord with upstream velocity perturbations . This assumption is in line with the neglect of terms that are of higher than zeroth order in . In the present study, we partly follow this approach: Stretch effects in the jump conditions are neglected while a curvature dependent flame speed in Equation (23) ensures smooth flame shapes. Note that the former is in line with the neglect of consequences of flow expansion described in Section 2.1.1, since stretch imposes a jump of flame normal velocity and pressure across the flame sheet. This effect, which is referred to as “surface compression” by Class et al. [44], further destabilizes the flame sheet. Therefore, stretch effects essentially add new dynamic features only to flame sheet propagation captured by Equation (23). Since the goal of the modeling framework derived here is to achieve qualitative, but not quantitative agreement with high fidelity CFD data, surface compression is neglected.
With the constant flame speed assumption the jump conditions Equations (33)–(35) reduce to:
While pressure and flame-normal velocity fluctuations are continuous across the flame, flame-tangential velocity perturbations change, as stated by Equation (39).
2.2.3. Modeling of Flame Generated Vorticity
Based on the jump conditions derived in the previous section, an expression for the production of vorticity by a perturbed flame sheet shall now be deduced. The tangential velocity component of Equation (39) quantifies the amount of vorticity generated across a flame sheet. This can be shown by computing the circulation around an infinitesimally small volume element, as depicted in Figure 5. The lower side of this rectangle is assumed to be just inside the domain of the unburned fluid, whereas all other sides are inside the burned region.
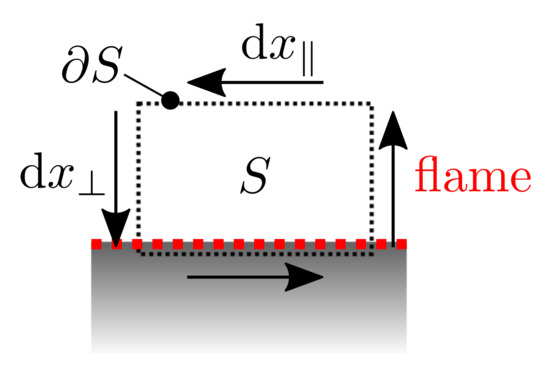
Figure 5.
Illustration of the line integral of Equation (40) along a path enclosing a surface S.
The circulation around this volume element,
where it is assumed that the streamwise component of the flow just upstream of the flame does not vary along the flame sheet, that is, . Furthermore, also the flame tangential velocity is assumed to be constant along the sheet. This results in an expression for the circulation that is related to vorticity by a surface integral . Hence, a perturbed flame acts as a vortex sheet of strength
In line with the arguments presented in the previous subsection, effects of flame stretch on vorticity generation at the flame are not taken into account and hence the first term on the r.h.s. in Equation (41) is neglected in the following. This approximation is further justified by the analysis of Matalon et al. [35], who discuss the dominance of baroclinic vorticity production at a flame front. For a more complete analysis of the generation of vorticity by gas dynamic discontinuities see the work of Hayes [45]. More detailed considerations of flame generated vorticity due to flame stretch are found in [20,21,30,46].
Combining Equation (41) with the jump conditions (37) and (39) yields
which implies that flame generated vorticity is at a maximum at inflection points of the flame displacement. In Figure 6 the effect of this vorticity is indicated by green circular arrows placed at points of . They lead to an acceleration and deceleration of the contracting (red) and expanding (blue) flow tubes, respectively, and thus tend to further increase the corrugation of the flame sheet.
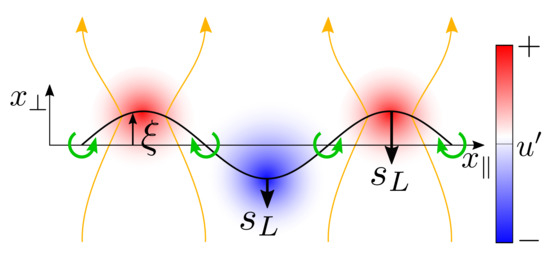
Figure 6.
Flame-generated vorticity at a corrugated flame sheet—indicated by green circular arrows—increases and decreases flow speed, as indicated by the red and blue areas as well as the orange stream tubes. Variations of flame speed as a result of flame stretch are indicated by downward pointing small arrows of various lengths.
The studies of Darrieus and Landau are based on jump conditions (37)–(39), which neglect the effects of flame stretch on flame speed. Thus flame-generated vorticity is identified as the driving mechanisms of the Darrieus–Landau instability [47]. The model of bidirectional flow-flame coupling developed in the present study—see Section 3.2—will build on this result: Vorticity is distributed along the mean flame sheet according to Equation (42) in the form of discrete vortices. In a complete description of vorticity generation and transport, these vortices would subsequently be advected by the mean flow field. This advection process, however, is neglected in the present study. Note that in general, hydrodynamic flame sheet instabilities may result also from additional mechanisms, such as flow expansion, which are not taken into account in the present study.
2.3. Test Case Setup
In the present study, high-fidelity numerical simulations serve as a reference for the aforementioned modeling framework. The simulations rely on well established means of computational fluid dynamics (CFD) of a backward facing step combustor, as shown in Figure 1, and are chosen to be as simple as possible, but without significant compromise in solution accuray.
A perfectly premixed laminar methane-air flame of an equivalence ratio of is stabilized at a sudden expansion of a duct, which connects a feed duct to a combustion chamber, see Figure 7. The feed duct and the combustion chamber have a half-diameter of mm and mm, respectively. At the inlet, a uniform flow profile of axial velocity with a temperature of 300 K is imposed. Further, we assume zero pressure gradients at the inlet and a fixed pressure, as well as a zero axial velocity gradient at the outlet. All walls are no-slip with zero tangential velocity and are set to be adiabatic, except from the feed duct wall, which is set to a fixed temperature of K, and the combustion chamber back plate, which is set to K. This configuration correspond to a Reynolds number of , computed with the mean inlet velocity, the feed duct diameter and the kinematic viscosity of the combustion products.
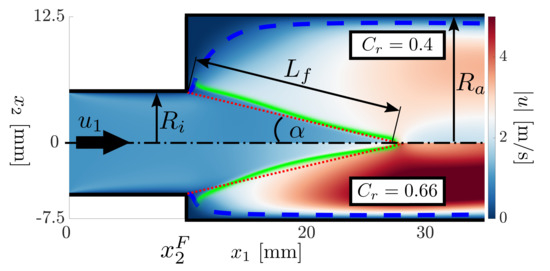
Figure 7.
CFD steady state absolute velocity for a confinement ratio of (upper half) and (bottom half). For both configurations, the location of maximum heat release ( ), the analytically predicted mean flame front (
), the analytically predicted mean flame front ( ) and the approximate location of the shear layer (
) and the approximate location of the shear layer ( ) are also shown.
) are also shown.
 ), the analytically predicted mean flame front (
), the analytically predicted mean flame front ( ) and the approximate location of the shear layer (
) and the approximate location of the shear layer ( ) are also shown.
) are also shown.
Since the setup can be considered to be acoustically compact, a weakly compressible formulation with reference pressure mbar is used, where the density depends on temperature T, but not on the local pressure p. In doing so, possible thermoacoustic instabilities are avoided. The open source software OpenFOAM [48] is employed. Chemical reactions are represented by the reduced chemical kinetic 2-step mechanism (2S-CM2) proposed by Bibrzycki et al. [49], which according to the validation study of Duchaine et al. [50] produces for simple flames as the ones considered here “essentially the same results” as a DNS code with detailed chemistry, for example, GRI-Mech. Schmidt numbers for the six species that comprise the 2S-CM2 mechanism are set according to Duchaine et al. [50]. This solver setup has been used successfully in previous studies for steady state and transient simulations of laminar premixed flames and has been validated with good success in particular for investigation of flame dynamics [51,52,53]. A uniform structured rectangular grid of the 2D domain with a cell density of and a slight increase of the axial cell width towards the outlet boundary after the flame region is adopted. This corresponds to a cell size of in the region of interest, which places approximately 18 cells inside the reactive layer. Note that Duchaine et al. [50] report mesh independence of the solution with 10 cells inside the flame front, which implies that the reaction zone is very well resolved with the present setup. The feed duct has a length of 10 mm and the complete setup, including feed duct and combustion chamber, one of 60 mm (note that Figure 7 only depicts the first 35 mm of the flow domain).
Figure 7 shows steady state solutions for two different confinement ratios of (upper half) and (bottom half). The color denotes absolute velocity and the region of maximum heat release is plotted in green ( ). An estimate of the shear layer position (
). An estimate of the shear layer position ( ) as well as the steady state flame front of length , as predicted by the 1D linearized G-equation approach, (
) as well as the steady state flame front of length , as predicted by the 1D linearized G-equation approach, ( ) are indicated. Note, that other than for conical configurations [13], the confinement ratio does not impact the flame height of 2D Slit flames [54].
) are indicated. Note, that other than for conical configurations [13], the confinement ratio does not impact the flame height of 2D Slit flames [54].
 ). An estimate of the shear layer position (
). An estimate of the shear layer position ( ) as well as the steady state flame front of length , as predicted by the 1D linearized G-equation approach, (
) as well as the steady state flame front of length , as predicted by the 1D linearized G-equation approach, ( ) are indicated. Note, that other than for conical configurations [13], the confinement ratio does not impact the flame height of 2D Slit flames [54].
) are indicated. Note, that other than for conical configurations [13], the confinement ratio does not impact the flame height of 2D Slit flames [54].3. Results—Analysis of Flow/Flame Interactions
The modeling approach introduced in the previous chapter shall now be exploited to model the response of a confined, laminar premixed slit flame with the objective of identifying the origin and importance of CVPs. The reader is reminded that the purpose of the model proposed here is to provide insight into the causality and interdependence of flame/flow interaction. First, flame frequency and impulse responses are computed with a model that relies on unidirectional flow/flame coupling. Results are compared to CFD data, and essential differences are observed. Then the model is extended to bidirectional coupling, which includes flame/flow feedback.
3.1. Unidirectional Coupling
Acoustic perturbations propagate at the speed of sound. Thus, an acoustic-to-hydrodynamic mode conversion is required to generate convective perturbations that propagate with a speed that is of the order of the flow velocity. A possible candidate for such a mode conversion mechanism is the process of flow separation, e.g., at a backward-facing step or bluff body flame holder. At the separation point, vorticity—originally confined to the wall boundary layers—is shed into the interior of the flow domain. Note that transient (acoustic) forcing of a separated flow leads to unsteady generation and shedding of vorticity [15,16,55].
In this subsection, acoustic-flow–flame interactions are scrutinized by decomposing the acoustic velocity disturbance into an irrotational potential and a solenoidal vortical field and analyzing how the respective components interact with the flame. Of particular interest is the impact of vorticity shed from the burner mouth and the question whether this vorticity is indeed the origin of CVPs, which play such an important role in flame dynamics.
In order to suppress the occurrence of vortical structures due to flame-flow feedback, we neglect in this subsection the effects of gas expansion resulting from exothermicity. In other words, we consider an unidirectional coupling (UD) with mode conversion from acoustic to flow fluctuations, which then perturb the flame, but without feedback from the perturbed flame to the flow. Note that the mean flow field, required to compute vortex advection (see below), is nevertheless retrieved from exothermic numerical simulations.
The UD modeling approach employed in the present subsection makes use of the flow decomposition methodology presented in Section 2.1 and may be summarized as follows: The dynamics of an acoustically compact flame anchored on a backward facing step is described by the linearized 1D G-equation of Equation (23). A transient velocity perturbation is imposed, with a spatio-temporal structure that is described by the Poisson Equation (5). A Kutta panel attached to the corner of the backward facing step suppresses a flow field singularity in the vicinity of the flame anchoring point, and sheds vorticity into the flow domain, which is convected along the mean flow shear layer. The position of the mean flow shear layer is taken from the high-fidelity CFD simulations described in Section 2.3. The transport velocity for vorticity along this line is set to the fixed value of [56]. Equation (23) is integrated in time relying on an explicit Euler method together with a first-order upwind discretization scheme for the advection and a second-order central scheme for the diffusion term. The flame sheet is discretized using 100 sample points and the time step width is set such that a mesh Fourier number of is achieved [57].
The spatial distribution of the velocity perturbation depends on the confinement ratio , c.f. Equations (8) and (9). Hence, two configurations with different confinement ratios as introduced in Section 2.3 are analyzed.
3.1.1. Harmonic Forcing
We first present results obtained with the UD model for a confinement ratio and harmonic forcing at a frequency of 80 Hz with an amplitude of . With continuous harmonic forcing, the vorticity bound by the Kutta panel is condensed in each time step into a point vortex that is placed right at the panel end. This vortex then becomes part of the vortical flow field and is advected with velocity along the mean flow shear layer, whose coordinates are deduced from the CFD data, see Figure 7 ( ).
).
 ).
).Figure 8 (top) shows four snapshots of the vorticity distribution and the induced “vortical velocity” in the combustion chamber. The bottom halves of the plots show the irrotational contribution to the perturbation velocity. The respective flame normal velocity perturbations along the flame front ( ) and the resulting flame front displacements (
) and the resulting flame front displacements ( ) generated by the velocity perturbations are also shown. It is evident that the flame front displacements provoked by the irrotational velocity are significantly larger than those generated by the vortical contribution. In other words, vorticity shed at the backward facing step contributes in the present case only in a negligible manner to the response of the flame. Furthermore, it is seen that irrotational velocity perturbations are large near the flame base, and weaken significantly towards the tip of the flame.
) generated by the velocity perturbations are also shown. It is evident that the flame front displacements provoked by the irrotational velocity are significantly larger than those generated by the vortical contribution. In other words, vorticity shed at the backward facing step contributes in the present case only in a negligible manner to the response of the flame. Furthermore, it is seen that irrotational velocity perturbations are large near the flame base, and weaken significantly towards the tip of the flame.
 ) and the resulting flame front displacements (
) and the resulting flame front displacements ( ) generated by the velocity perturbations are also shown. It is evident that the flame front displacements provoked by the irrotational velocity are significantly larger than those generated by the vortical contribution. In other words, vorticity shed at the backward facing step contributes in the present case only in a negligible manner to the response of the flame. Furthermore, it is seen that irrotational velocity perturbations are large near the flame base, and weaken significantly towards the tip of the flame.
) generated by the velocity perturbations are also shown. It is evident that the flame front displacements provoked by the irrotational velocity are significantly larger than those generated by the vortical contribution. In other words, vorticity shed at the backward facing step contributes in the present case only in a negligible manner to the response of the flame. Furthermore, it is seen that irrotational velocity perturbations are large near the flame base, and weaken significantly towards the tip of the flame.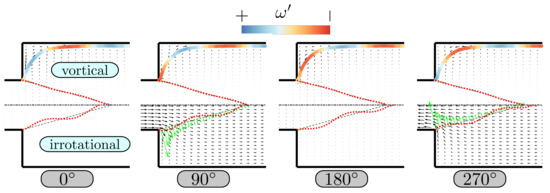
Figure 8.
Predictions of the UD model of a harmonically forced flame (80 Hz, ). Shown are four snapshots taken at phases from to relative to the forcing signal. Displacement of the flame front ( ) is scaled by a factor of 7. Top: vortical flow component, with color along the shear layer indicating the strength of vorticity fluctuations. Bottom: irrotational flow component. The flame normal velocity is represented by green arrows (scaled by a factor of 4 for better visibility).
) is scaled by a factor of 7. Top: vortical flow component, with color along the shear layer indicating the strength of vorticity fluctuations. Bottom: irrotational flow component. The flame normal velocity is represented by green arrows (scaled by a factor of 4 for better visibility).
 ) is scaled by a factor of 7. Top: vortical flow component, with color along the shear layer indicating the strength of vorticity fluctuations. Bottom: irrotational flow component. The flame normal velocity is represented by green arrows (scaled by a factor of 4 for better visibility).
) is scaled by a factor of 7. Top: vortical flow component, with color along the shear layer indicating the strength of vorticity fluctuations. Bottom: irrotational flow component. The flame normal velocity is represented by green arrows (scaled by a factor of 4 for better visibility).
Note that these results fully corroborate the findings of our earlier study [19], which did not rely on a Kutta panel, but instead introduced a simple estimate of the total circulation created by a separating vortex sheet during a time interval [56,58]:
Steinbacher [29] compared the strength of the vortex sheet computed with Equation (43) to the one computed with the Kutta panel and found that for the confinement ratio predictions of the two methods agree very well. On the other hand, for a confinement ratio , i.e., if the flow is more two-dimensional, the amplitude of vorticity fluctuations generated by the Kutta panel is more than twice as large as the one resulting from Equation (43) (see Figure 4.3 in [29]). Despite these quantitative differences, the important conclusions of our earlier and the present study are identical: flame displacement is dominated by the potential contribution to the velocity field, which is most pronounced at and near the flame anchoring point.
3.1.2. Impulse Forcing
In the linear regime, the impulse response (IR) provides a comprehensive description of the flame dynamics [10]. In the present subsection, the conical flame IR is computed with the UD model and compared against CFD results. Details on the CFD setup and the post-processing of the CFD time series are provided above and in [29].
The finding of the previous subsection, i.e., that vorticity shed from the burner mouth has only a negligible impact on the flame response, allows to evaluate the impulse response (IR) of the flame solely from the irrotational part of the velocity perturbation. At first glance, this seems straightforward: an impulsive forcing of amplitude is applied to the combustor and the resulting instantaneous flame displacement is computed from the respective irrotational velocity field by evaluation of the integral .
However, if a Kutta panel is introduced to avoid a flow singularity, the velocity perturbation depends on the panel length , which depends on the time step width of the numerical solver. In particular, shorter time steps will lead to short Kutta panels (see Section 2.1.4). The total circulation of the panel, however, remains unaffected since the impulse acts on an infinitesimal time scale. Figure 9 shows that the flame normal velocity resulting from an impulsive forcing changes significantly with the length of the vortex panel: the shorter the panel, the stronger and the more localized the velocity perturbation. Hence, due to the infinitesimal nature of the impulse forcing, it is not possible to find a numerical time step width that properly resolves the forcing signal and thus leads to meaningful panel lengths .
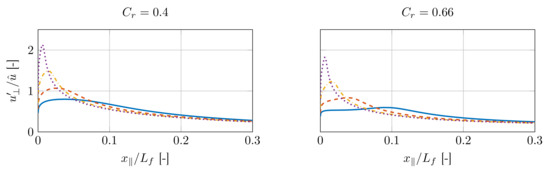
Figure 9.
Flame normal velocity perturbation along the flame length resulting from Kutta conditions with panel lengths ( ), (
), ( ), (
), ( ) and (
) and ( ). is set to for (c.f. Figure 4) and to for , respectively.
). is set to for (c.f. Figure 4) and to for , respectively.
 ), (
), ( ), (
), ( ) and (
) and ( ). is set to for (c.f. Figure 4) and to for , respectively.
). is set to for (c.f. Figure 4) and to for , respectively.
A heuristic approach is chosen in the present study to compute an IR that robustly captures the linear flame dynamics in the inviscid limit: the panel length is set to a value such that the initial flame displacement computed with the Kutta condition corresponds best to CFD results. For details of the procedure, the reader is referred to [29]; here we report only the resulting values of the optimal panel lengths, that is, for and for . The resulting normalized flame displacements is shown in Figure 10. Good agreement between the UD model ( ) and the CFD results (
) and the CFD results ( ) is indeed observed for the initial time .
) is indeed observed for the initial time .
 ) and the CFD results (
) and the CFD results ( ) is indeed observed for the initial time .
) is indeed observed for the initial time .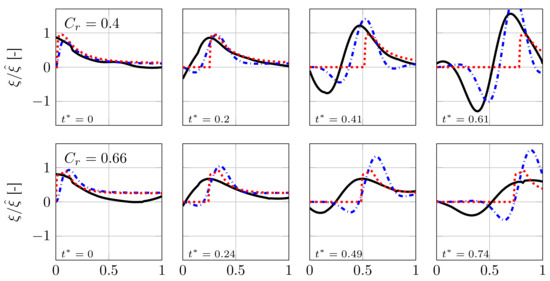
Figure 10.
Four snapshots taken at equidistant instances in time of the normalized flame displacement plotted over resulting from an impulsive velocity forcing at for confinement ratios (top) and (bottom). CFD results ( ); UD model (
); UD model ( ); BD model (
); BD model ( ).
).
 ); UD model (
); UD model ( ); BD model (
); BD model ( ).
).
At later times the flame front displacement moves downstream towards the flame tip, until eventually the original flame shape is restored [10]. Figure 10 shows that with the UD model the shape of the displacement does not change during the restoration process. On the contrary, the CFD results exhibit a spatial growth of the initial displacement amplitude as well as subsequent negative as well as positive excursions.
Figure 11 shows impulse (left) and frequency responses (right) that correspond to the spatio-temporal development of the flame shapes shown in Figure 10. The initial peak in the IR predicted by the UD model ( ) occurs at the right time, however its magnitude is under-predicted. More importantly, subsequent negative and positive strong excursions of the IR shown by the CFD results (
) occurs at the right time, however its magnitude is under-predicted. More importantly, subsequent negative and positive strong excursions of the IR shown by the CFD results ( ) are completely absent in the UD model. One must expect [10,11] that these discrepancies in IR have significant consequences also for the FR. Indeed, while the CFD model develops pronounced “excess gain” with a magnitude of the the frequency response (FR) above unity for frequencies , the FR predicted by the UD model (
) are completely absent in the UD model. One must expect [10,11] that these discrepancies in IR have significant consequences also for the FR. Indeed, while the CFD model develops pronounced “excess gain” with a magnitude of the the frequency response (FR) above unity for frequencies , the FR predicted by the UD model ( ) shows a low pass behavior without excess gain. An almost linearly decaying phase of the FR is captured by all models.
) shows a low pass behavior without excess gain. An almost linearly decaying phase of the FR is captured by all models.
 ) occurs at the right time, however its magnitude is under-predicted. More importantly, subsequent negative and positive strong excursions of the IR shown by the CFD results (
) occurs at the right time, however its magnitude is under-predicted. More importantly, subsequent negative and positive strong excursions of the IR shown by the CFD results ( ) are completely absent in the UD model. One must expect [10,11] that these discrepancies in IR have significant consequences also for the FR. Indeed, while the CFD model develops pronounced “excess gain” with a magnitude of the the frequency response (FR) above unity for frequencies , the FR predicted by the UD model (
) are completely absent in the UD model. One must expect [10,11] that these discrepancies in IR have significant consequences also for the FR. Indeed, while the CFD model develops pronounced “excess gain” with a magnitude of the the frequency response (FR) above unity for frequencies , the FR predicted by the UD model ( ) shows a low pass behavior without excess gain. An almost linearly decaying phase of the FR is captured by all models.
) shows a low pass behavior without excess gain. An almost linearly decaying phase of the FR is captured by all models.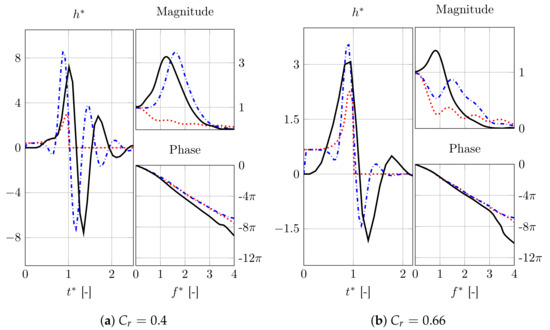
Figure 11.
Impulse responses (left plot in sub-figures (a,b)) and frequency responses (right plots in sub-figures (a,b)). CFD results ( ) vs. predictions of the unidirectional (
) vs. predictions of the unidirectional ( ) and bidirectional (
) and bidirectional ( ) models, that is without and with consideration of flame-generated vorticity ().
) models, that is without and with consideration of flame-generated vorticity ().
 ) vs. predictions of the unidirectional (
) vs. predictions of the unidirectional ( ) and bidirectional (
) and bidirectional ( ) models, that is without and with consideration of flame-generated vorticity ().
) models, that is without and with consideration of flame-generated vorticity ().
3.2. Bidirectional Coupling
The core results of the previous subsection are expressed in Figure 10 and Figure 11, which show not only quantitative, but essential qualitative discrepancies of the UD model ( ) with CFD results (
) with CFD results ( ). The authors of the present study attribute these discrepancies to flame-flow feedback, which is not taken into account by the unidirectional coupling of the UD model. Furthermore, such a feedback may also be responsible for the CVPs, which would run contrary to established G-equation models that impose CVPs of presumed functional form. Support for these hypotheses will be presented in this subsection.
). The authors of the present study attribute these discrepancies to flame-flow feedback, which is not taken into account by the unidirectional coupling of the UD model. Furthermore, such a feedback may also be responsible for the CVPs, which would run contrary to established G-equation models that impose CVPs of presumed functional form. Support for these hypotheses will be presented in this subsection.
 ) with CFD results (
) with CFD results ( ). The authors of the present study attribute these discrepancies to flame-flow feedback, which is not taken into account by the unidirectional coupling of the UD model. Furthermore, such a feedback may also be responsible for the CVPs, which would run contrary to established G-equation models that impose CVPs of presumed functional form. Support for these hypotheses will be presented in this subsection.
). The authors of the present study attribute these discrepancies to flame-flow feedback, which is not taken into account by the unidirectional coupling of the UD model. Furthermore, such a feedback may also be responsible for the CVPs, which would run contrary to established G-equation models that impose CVPs of presumed functional form. Support for these hypotheses will be presented in this subsection.Flame-flow feedback results from the change in density across the flame sheet and supports the growth of flame front disturbances, unless the growth is stabilized by thermal-diffusive or non-linear mechanisms [31,42,47,59]. The corresponding mechanisms of instability are illustrated in Figure 12a,b. Analysis of the jump conditions of mass and momentum across the flame, Equations (37)–(39) elucidates the hydrodynamic mechanism that are at play here: (i) a volume source in the gas expansion related flow component of Equation (2); and (ii) baroclinic vorticity production resulting from the density gradient at the flame front. The consequences of (i) were explored in the dissertation of the first author of the present paper [29]. In the following, we introduce a bidirectional coupling (BD) model that includes the baroclinic source term, see point (ii), and compare results against the UD model and CFD. Note that this approach corresponds to the Darrieus–Landau mechanism of flame front instability, which also relies solely on flame-generated vorticity.
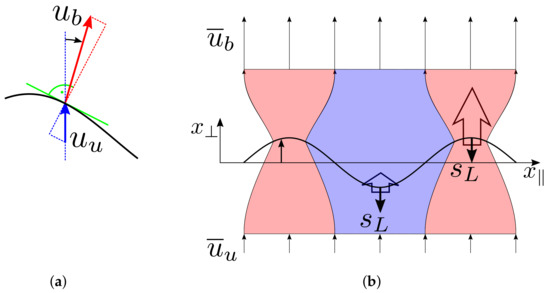
Figure 12.
(a): Downstream of a flame, velocity vectors are bent towards the flame normal direction, since the flow accelerates across the flame front. (b): The instability of a flat flame sheet results from contraction (red) and expansion (blue) of flow tubes across a corrugated flame front that can be linked to consequences of flame generated vorticity (captured by the BD model) and irrotational contributions of flow expansion (not captured).
The proposed BD modeling concept distributes vorticity along the flame front in the form of discrete vortices. According to Equation (35), their strength is proportional to the local flame displacement gradient , the non-dimensional increase of specific volume E and the unstretched flame speed . It follows that maxima of vorticity are found at the inflection points of . Point vortices exhibit a flow field singularity at their center, which results in unbounded velocity magnitudes. To avoid this, viscous “Lamb–Oseen” vortices are used, where the vorticity is not concentrated in one singular point, but spatially distributed according to a Gaussian. This vorticity distribution is obtained as an exact solution of the Navier–Stokes equations for an initially singular point vortex [60]. The complex conjugate of the vortical velocity field of a Lamb–Oseen vortex is written as
where the velocity drops to zero at the vortex center (). The vortex radius specifies the radius where the induced circumferential velocity is maximum. For radii greater than , the velocity distribution asymptotically approaches the one of a singular vortex, see Equation (12).
The vortex sheet assumed by this modeling approach has a thickness of the order of the flame displacement . Hence, the vortex radius is set equal to the prevailing displacement amplitude. The Markstein length , which quantifies the thickness of a flame sheet, may be used as a lower threshold for the vortex radius, i.e., . Specifically, a minimum radius of is assumed in order to avoid an over-prediction of the imposed vortical velocity perturbations at the flame sheet. This choice ensures that the order of magnitude of the kernel radius cannot become smaller than the flame thickness. Nevertheless, has to be regarded as an empirical parameter whose value is not rigorously derived from first principles. Unfortunately, it significantly affects the computed flame response, as will be shown below. As in the previous subsection on the UD model, vorticity generated by the Kutta condition is excluded from the analysis, since it was found to only have a negligible impact on the flame response.
An overview of the flame parameters used for the computations of this section is provided in Table 1. The values for e, and are retrieved from 1D simulations of lean methane-air flames at relying on the software Cantera [61]. The flame thickness is estimated by a diffusion length , where denotes the thermal diffusivity. The stretched flame speed depends on the Markstein length , which is computed from and the Markstein number via . According to Matalon et al. [35], methane-air mixtures exhibit Markstein numbers roughly between 3 and 4. One must expect an over-prediction of displacement amplitudes when including flame-flow feedback into the modeling approach, since only driving, but no damping mechanisms associated, e.g., with flame stretch are considered. In the modeling approach proposed here, we only incorporate consequences of curvature-related stretch for the flame speed. Flow strain as well as stretch generated vorticity are neglected, which might significantly underestimate the damping [30]. Hence, only a qualitative analysis of flame-flow feedback mechanisms is possible and therefore, in a first approximation, a Markstein number of 4 is assumed.

Table 1.
Flame parameters used for the analysis of flame-flow feedback.
To summarize, the BD model relies on the 1D linear representation of the flame dynamics of Equation (23), a Schwarz–Christoffel mapping, a representation of the flow field by a finite number of flow field singularities and a Kutta condition. This corresponds exactly to the setup introduced above, but this time flame–flow feedback is included.
In each time step, Lamb-Oseen vortices are distributed along the mean flame position (one vortex per sampling point, that is, ), with their respective strength being computed from Equation (39). The Kutta condition is applied as described in Section 3.1.2. The run times of the simulations shown in this chapter are of the order of one minute on a personal computer.
Figure 13 and Figure 14 show four snapshots of harmonically forced simulations with the BD model at and , respectively. It is evident that consideration of flame generated vorticity leads to a convective growth of flame front perturbations: right at the anchoring point, flame displacement is very small, whereas the flame tip oscillates with significant amplitude. Comparing the results of the two confinement ratios, we observe that the wave length and maximum displacement amplitude of the resulting flame front perturbations varies: the narrow confinement promotes perturbations of longer wave lengths and lower amplitudes. Furthermore, a considerable impact of the flame on the flow of premixture is observable for both setups. Alternatingly positive and negative axial velocity perturbations propagate from the flame base region to its tip, as reported previously by Baillot et al. [14], Blanchard et al. [24].
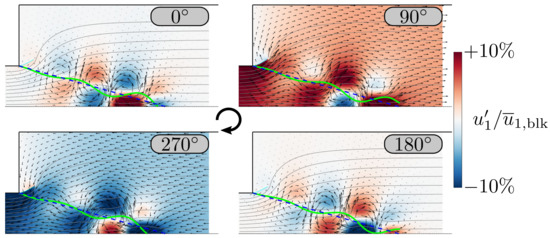
Figure 13.
Predictions obtained with the BD model of a flame with confinement ratio forced harmonically at 120 Hz and an amplitude of . Color raster: axial velocity ; mean flame front position ( ); perturbed flame (
); perturbed flame ( ). Minimum vortex kernel radius .
). Minimum vortex kernel radius .
 ); perturbed flame (
); perturbed flame ( ). Minimum vortex kernel radius .
). Minimum vortex kernel radius .
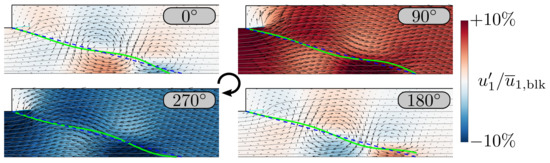
Figure 14.
Results of a simulation as described in Figure 13, but for confinement ratio .
Results of the BD model for the flame shape after an impulse perturbation are depicted in Figure 10. The flame shapes of the UD and BD models agree at , but then increasingly deviate from each other, because the BD model ( ) develops negative and positive secondary excursions, which grow in amplitude while they are advected towards the flame tip. This is in good qualitative agreement with the CFD results (
) develops negative and positive secondary excursions, which grow in amplitude while they are advected towards the flame tip. This is in good qualitative agreement with the CFD results ( ). However, the negative and positive excursions are found slightly too far downstream, and the amplitudes of the excursions are over-predicted by the BD model. Overall, BD model predictions for match the respective CFD results better than for . The damping, presumably imposed by the presence of a rather narrow confinement, seems to be under-predicted for the setup.
). However, the negative and positive excursions are found slightly too far downstream, and the amplitudes of the excursions are over-predicted by the BD model. Overall, BD model predictions for match the respective CFD results better than for . The damping, presumably imposed by the presence of a rather narrow confinement, seems to be under-predicted for the setup.
 ) develops negative and positive secondary excursions, which grow in amplitude while they are advected towards the flame tip. This is in good qualitative agreement with the CFD results (
) develops negative and positive secondary excursions, which grow in amplitude while they are advected towards the flame tip. This is in good qualitative agreement with the CFD results ( ). However, the negative and positive excursions are found slightly too far downstream, and the amplitudes of the excursions are over-predicted by the BD model. Overall, BD model predictions for match the respective CFD results better than for . The damping, presumably imposed by the presence of a rather narrow confinement, seems to be under-predicted for the setup.
). However, the negative and positive excursions are found slightly too far downstream, and the amplitudes of the excursions are over-predicted by the BD model. Overall, BD model predictions for match the respective CFD results better than for . The damping, presumably imposed by the presence of a rather narrow confinement, seems to be under-predicted for the setup.The improved agreement in prediction of perturbed flame shape is reflected by the corresponding impulse and frequency responses of the global heat release rate, shown in Figure 11. For , CFD ( ) and BD (
) and BD ( ) predictions agree well, only small deviations in phase/gain and the impulse response are observed. This supports the hypothesis that flame generated vorticity represents an important mechanism of flame-flow feedback that makes an important contribution to the response of a flame to acoustic perturbations. For , on the other hand, the IR predicted by the BD model deviates significantly from the CFD data right from the beginning, see Figure 11b. Accordingly, the corresponding FTF gain curves are qualitatively different. This suggests that the effects of confinement are not properly captured by the comparatively simplistic implementation of flame-flow feedback, which does not include all possibly important effects [29].
) predictions agree well, only small deviations in phase/gain and the impulse response are observed. This supports the hypothesis that flame generated vorticity represents an important mechanism of flame-flow feedback that makes an important contribution to the response of a flame to acoustic perturbations. For , on the other hand, the IR predicted by the BD model deviates significantly from the CFD data right from the beginning, see Figure 11b. Accordingly, the corresponding FTF gain curves are qualitatively different. This suggests that the effects of confinement are not properly captured by the comparatively simplistic implementation of flame-flow feedback, which does not include all possibly important effects [29].
 ) and BD (
) and BD ( ) predictions agree well, only small deviations in phase/gain and the impulse response are observed. This supports the hypothesis that flame generated vorticity represents an important mechanism of flame-flow feedback that makes an important contribution to the response of a flame to acoustic perturbations. For , on the other hand, the IR predicted by the BD model deviates significantly from the CFD data right from the beginning, see Figure 11b. Accordingly, the corresponding FTF gain curves are qualitatively different. This suggests that the effects of confinement are not properly captured by the comparatively simplistic implementation of flame-flow feedback, which does not include all possibly important effects [29].
) predictions agree well, only small deviations in phase/gain and the impulse response are observed. This supports the hypothesis that flame generated vorticity represents an important mechanism of flame-flow feedback that makes an important contribution to the response of a flame to acoustic perturbations. For , on the other hand, the IR predicted by the BD model deviates significantly from the CFD data right from the beginning, see Figure 11b. Accordingly, the corresponding FTF gain curves are qualitatively different. This suggests that the effects of confinement are not properly captured by the comparatively simplistic implementation of flame-flow feedback, which does not include all possibly important effects [29].When interpreting the results of the BD model, which includes flame-feedback resulting from flame generated vorticity, it should be kept in mind that the model is based on an empirical parameter . In Figure 5.14 of the dissertation of the first author of this paper [29] it is shown that a decrease of the minimum kernel radius by leads to higher velocity amplitudes and, thus, to an increase of the maximum FTF gain of approximately . The opposite behavior can be observed when the radius is increased. Thus we must admit that the predictions of the BD model are rather sensitive to variations in the minimum kernel radius and concede that the quantitative agreement with the reference CFD data relies on setting an optimal value for . On the other hand, the fact that the model can generate qualitatively correct responses for both confinement ratios with the same value of gives confidence that flame generated vorticity is indeed an important mechanism in flow-flame-flow interactions.
4. Discussion
The response of confined, laminar, premixed slit flames stabilized at a backward-facing step to perturbations of velocity was scrutinized. The goal was to establish the origin and nature of so-called CVPs, which are known to play an important role in the flame response to acoustic perturbations, and are a widely-used element of low-order flame response models. Analytical methods from aero-acoustics were combined with a flow decomposition approach to quantify the respective contributions of the irrotational and the vortical parts of the disturbance velocity field to the overall flame impulse and frequency responses. Other than the Michelson–Sivashinsky equation, which was used, for example, by Searby et al. [62] in the study of spatially developing flame instability, the modeling framework proposed here allows to capture confinement induced consequences for the flame response.
At first glance, the present work shares similarities with the work of Lee and Lieuwen [63], who studied the acoustic near-field characteristics of a conical premixed flame by solving two-dimensional (2D) wave equations in zones up- and downstream of the flame and coupled across the flame. Indeed, the velocity perturbation fields computed with this variant of a flow decomposition approach share characteristic similarities with the potential contribution , c.f. Figure 3 in [63] and Figure 8 (bottom). However, a more detailed comparison shows important differences: the conical flames investigated in [63] and the slit flames investigated in the present paper appear deceptively similar, but exhibit important qualitative differences in their response to acoustic perturbations [53]. Note that Lee and Lieuwen [63] apply hydrodynamic matching conditions at the mean flame position, that is, ignore the effects of flame movement and flame wrinkling. Furthermore, the effect of unsteady heat release on the velocity coupling conditions across the flame is neglected and so is the effect of vorticity generation at the flame, which was identified as the root cause of CVPs and excess gain in the present case. In a follow-up study Lee and Lieuwen [64] evaluated the FTF of conical flames resulting from the two-dimensional acoustic disturbance fields. As in the previous study [63], flame/acoustic feedback, mean flow and vorticity shedding or generation were neglected. Somewhat unexpectedly, results obtained matched quite well with a simplified one-dimensional uniform velocity model. Overall, due to the important differences between the flame configurations considered and the methods employed, the direct relevance of the studies of Lee and Lieuwen [63,64] is very limited.
For the cases considered in the present paper—that is, slit flames with a Péclet number of , a thermal expansion ratio of and confinement ratios and , respectively—the irrotational part of the perturbation velocity field was shown to dominate the initial flame displacement, which is most pronounced at and near the flame anchoring point. This behavior prompted Steinbacher et al. [19] to propose a simple “flame base displacement” (FBD) model in the G-equation framework. This model describes the early stage of development of flame perturbations, but fails at later times, because it does not take into account bidirectional coupling.
Vorticity shed from the flame anchoring point plays only a negligible role and cannot account for CVPs in the present configuration. This agrees with the conclusions of Schlimpert et al. [18], who showed that vortical structures significantly affect the shape of an unconfined flame in the case of negligible gas expansion. On the contrary, for realistic gas expansion, a significant influence of shed vorticity was observed only right at the flame base.
Vorticity generated by immediate acoustic-to-hydrodynamic mode conversion was found to have only a negligible effect. On the other hand, baroclinic torque, which results from gas expansion across the flame, generates vorticity along the corrugated flame sheet. Because the flame front perturbations propagate with convective velocity along the flame, the solenoidal velocity generated by baroclinic vorticity manifests itself as a “progressive wave of kinematic disturbance” [14] that moves downstream with a convective velocity. This results in the additional displacement of the flame front and corresponding modulation of the heat release rate. The effects of flame/flow feedback are quite pronounced at later times, and in particular for low confinement ratios. Analysis of the corresponding impulse response functions leads to the conclusion that excess gain in the flame frequency response is a result of flame/flow coupling.
The results presented in this paper corroborate the findings of earlier studies on the convective nature of velocity perturbations within the flame cone [9,14,22,23]. The flow decomposition approach employed identifies explicitly vorticity generated at the flame front due to exothermic effects as an important source of CVPs, in agreement with earlier studies using different methods, and investigating different configurations. Using a linearized compressible Navier–Stokes solver with a one-step chemistry mechanism. Blanchard et al. [24] showed that a perturbed M-flame acts as a vortex source whose upstream influence contributes to the formation of axially convected velocity perturbations. This phenomenon is related to the Darrieus–Landau mechanisms of hydrodynamic instability of a planar flame front. The relevance of this mechanism for the flame response of perturbed, burner-stabilized flames was further confirmed by the studies of Hemchandra [65], Schlimpert et al. [18] and [29]. These studies reported that flame-flow feedback leads to the spatial growth of flame front perturbations, and Hemchandra [65] already conjectured that this mechanism may be responsible for the occurrence of excess gain of the FTF. Analysis of the flame impulse response with its pronounced negative excursions not only confirms this conjecture, but also elucidates the mechanism of excess gain generation by constructive superposition of delayed responses with varying delay times [11].
Oberleithner et al. [66,67] found that the gain of the frequency response of swirl-stabilized flames scales with stability properties of the respective shear layers. It is argued that a Kelvin–Helmholtz-type hydrodynamic instability triggered by acoustic perturbations leads to the formation of large scale coherent structures that interact with the flame and, thus, provoke fluctuations of the global heat release rate. While flame sheets exhibit jumps in normal and tangential velocity, shear layers only show discontinuities in tangential velocity. In their most idealized versions, both entities are unconditionally (convectively) unstable [68,69] and may hence both contribute to the formation of coherent structures that may impact the flame response. Building on the studies [66,67], it would be interesting to analyze the role of flame-flow feedback driven instability mechanisms for technically relevant configurations, in analogy to shear layer instabilities. The Darrieus–Landau mechanism should be analyzed in more detail and clearly demarcated from shear layer instabilities. As a first step, flame-flow feedback related mechanism have been analyzed for laminar flames in this paper.
The Darrieus–Landau mechanism of flame-flow feedback results from flame generated, baroclinic vorticity. There is an additional mechanism of flame-flow feedback that is an immediate consequence of flow expansion, that is, the density change across the flame and the concomitant acceleration of the flow [20,21,25,26,32,33]. As explicated in Section 2.1.1, this effect can be described by an additional irrotational contribution in the decomposition (1). One of the first to explicitly analyze this contribution was Frankel [33], who derived an evolution equation for flame fronts based on a purely irrotational flow field, often referred to as the Frankel equation [70,71,72]. Joulin et al. [72] and also Steinbacher [29] found that such a potential-flow model overestimates growth and amplitudes of flame front perturbations. The cause of this shortcoming and how it can be corrected to achieve quantitative agreement with CFD data is not clear. In this paper we chose a different approach and captured flame-flow interactions solely by flame generated vorticity. By fitting the Markstein number and the minimum vortex radius , good agreement with CFD data was achieved, although the convection of flame generated vorticity was neglected.
The results achieved indicate that essential features of flame/flow feedback are indeed correctly reproduced by our model, but they do not suggest unambiguously that flame generated vorticity is the decisive physical mechanism of flame/flow feedback. Consider that Joulin et al. [72] found that Frankel’s equation generates “a variety of real looking phenomena”, although vorticity was completely neglected. Therefore, it should rather be concluded that flame/flow feedback is a crucial ingredient of flame dynamics and that, at least in the linear regime, its essential consequences can faithfully be described by a vortex sheet that is bound to the flame sheet and proportional to its local displacement. Such a qualitatively correct description may not be unique.
5. Conclusions
The response of confined, laminar, premixed slit flames to acoustic perturbations has been explored with a flow decomposition approach that allows us to judiciously “switch off” various mechanisms of acoustic/flow/flame interactions. The results indicate that flame displacement resulting from imposed acoustic perturbations generates a bidirectional hydrodynamic flame/flow feedback, which has two important consequences, that is, it generates convective velocity perturbations (CVPs) as well as “excess gain” of the flame response. In this sense, models for flame dynamics that rely on ad-hoc models that prescribe CVPs as an immediate result of acoustic-to-hydrodynamic mode conversion do not respect causality.
The model formulation employed in this study has important shortcomings: firstly, it is limited to 2D plane geometries and assumes ideal flame anchoring. Secondly, it ignores the effects of flame stretch and those of vorticity downstream of the flame. Thirdly, it ignores thermal-diffusive mechanisms of flame instability, which might have a noticeable impact on bidirectional acoustics-flame interactions. Finally, it does not account for hydrodynamic flow instabilities, in particular shear layer instabilities, which have also been identified as a possible cause of convective, vortical perturbations. These shortcomings can be addressed in future studies.
Furthermore, it is hoped that the results have convinced the reader that an assessment of the relative importance of the wide variety of acoustic/flow/flame interactions for the dynamics for the generic types of premixed flames (conical, V-, M-flame) should be a worthwhile topic of future studies.
Author Contributions
Conceptualization, T.S. and W.P.; methodology, T.S. and W.P.; software, T.S.; writing—original draft preparation, T.S. and W.P.; writing—review and editing, T.S. and W.P.; visualization, T.S.; funding acquisition, W.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Christopher Douglas gave critical feedback on a draft version of this paper, which is much appreciated.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CFD | Computational Fluid Dynamics |
| CVP | Convective Velocity Perturbation |
| BD | BiDirectional coupling |
| FTF | Flame Transfer Function |
| FR | Frequency Response |
| IR | Impulse Response |
| UD | UniDirectional coupling |
References
- Lieuwen, T.; Yang, V. (Eds.) Combustion Instabilities in Gas Turbine Engines: Operational Experience, Fundamental Mechanisms and Modeling; Number v. 210 in Progress in Astronautics and Aeronautics; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2005. [Google Scholar]
- Candel, S. Combustion Dynamics and Control: Progress and Challenges. Proc. Combust. Inst. 2002, 29, 1–28. [Google Scholar] [CrossRef]
- Culick, F.E.C. Unsteady Motions in Combustion Chambers for Propulsion Systems; Number AC/323(AVT-039)TP/103 in RTO AGARDograph AG-AVT-039, AGARD/NATO; NATO Research and Technology Organization: Neuilly-Sur-Seine, France, 2006. [Google Scholar]
- Poinsot, T. Prediction and Control of Combustion Instabilities in Real Engines. Proc. Combust. Inst. 2017, 36, 1–28. [Google Scholar] [CrossRef]
- Renard, P.H.; Thevenin, D.; Rolon, J.C.; Candel, S. Dynamics of Flame/Vortex Interactions. Prog. Energy Combust. Sci. 2000, 26, 225–282. [Google Scholar] [CrossRef]
- Lieuwen, T.C. Unsteady Combustor Physics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Merk, H. Analysis of Heat-Driven Oscillations of Gas Flows. I. General Considerations. Appl. Sci. Res. Sect. A 1957, 6, 317–336. [Google Scholar] [CrossRef]
- Fleifil, A.; Annaswamy, A.M.; Ghoneim, Z.A.; Ghoniem, A.F. Response of a Laminar Premixed Flame to Flow Oscillations: A Kinematic Model and Thermoacoustic Instability Results. Combust. Flame 1996, 106, 487–510. [Google Scholar] [CrossRef]
- Schuller, T.; Durox, D.; Candel, S. A Unified Model for the Prediction of Laminar Flame Transfer Functions: Comparisons Between Conical and V-Flame Dynamics. Combust. Flame 2003, 134, 21–34. [Google Scholar] [CrossRef]
- Blumenthal, R.S.; Subramanian, P.; Sujith, R.; Polifke, W. Novel Perspectives on the Dynamics of Premixed Flames. Combust. Flame 2013, 160, 1215–1224. [Google Scholar] [CrossRef]
- Polifke, W. Modeling and Analysis of Premixed Flame Dynamics by Means of Distributed Time Delays. Prog. Energy Combust. Sci. 2020, 79, 100845. [Google Scholar] [CrossRef]
- Preetham; Santosh, H.; Lieuwen, T. Dynamics of Laminar Premixed Flames Forced by Harmonic Velocity Disturbances. J. Propuls. Power 2008, 24, 1390–1402. [Google Scholar] [CrossRef]
- Cuquel, A.; Durox, D.; Schuller, T. Scaling the Flame Transfer Function of Confined Premixed Conical Flames. Proc. Combust. Inst. 2013, 34, 1007–1014. [Google Scholar] [CrossRef]
- Baillot, F.; Durox, D.; Prud’homme, R. Experimental and Theoretical Study of a Premixed Vibrating Flame. Combust. Flame 1992, 88, 149–168. [Google Scholar] [CrossRef]
- Disselhorst, J.H.M.; Wijngaarden, L.V. Flow in the Exit of Open Pipes During Acoustic Resonance. J. Fluid Mech. 1980, 99, 293–319. [Google Scholar] [CrossRef][Green Version]
- Peters, M.C.A.M.; Hirschberg, A. Acoustically Induced Periodic Vortex Shedding At Sharp Edged Open Channel Ends: Simple Vortex Models. J. Sound Vib. 1993, 161, 281–299. [Google Scholar] [CrossRef]
- Hirsch, C.; Fanaca, D.; Reddy, P.; Polifke, W.; Sattelmayer, T. Influence of the Swirler Design on the Flame Transfer Function of Premixed Flames. In ASME Turbo Expo 2005: Power for Land, Sea, and Air; GT2005-68195; ASME: Reno, NV, USA, 2005; pp. 151–160. [Google Scholar] [CrossRef]
- Schlimpert, S.; Hemchandra, S.; Meinke, M.; Schröder, W. Hydrodynamic Instability and Shear Layer Effect on the Response of an Acoustically Excited Laminar Premixed Flame. Combust. Flame 2015, 162, 345–367. [Google Scholar] [CrossRef]
- Steinbacher, T.; Albayrak, A.; Ghani, A.; Polifke, W. Response of Premixed Flames to Irrotational and Vortical Velocity Fields Generated by Acoustic Perturbations. Proc. Combust. Inst. 2019, 37, 5367–5375. [Google Scholar] [CrossRef]
- Pindera, M.Z.; Talbot, L. Some Fluid Dynamic Considerations in the Modeling of Flames. Combust. Flame 1988, 73, 111–125. [Google Scholar] [CrossRef]
- Rhee, C.W.; Talbot, L.; Sethian, J.A. Dynamical Behaviour of a Premixed Turbulent Open V-Flame. J. Fluid Mech. 1995, 300, 87–115. [Google Scholar] [CrossRef][Green Version]
- Birbaud, A.; Durox, D.; Candel, S. Upstream Flow Dynamics of a Laminar Premixed Conical Flame Submitted to Acoustic Modulations. Combust. Flame 2006, 146, 541–552. [Google Scholar] [CrossRef]
- Kornilov, V.N.; Schreel, K.R.A.M.; de Goey, L.P.H. Experimental Assessment of the Acoustic Response of Laminar Premixed Bunsen Flames. Proc. Combust. Inst. 2007, 31, 1239–1246. [Google Scholar] [CrossRef]
- Blanchard, M.; Schuller, T.; Sipp, D.; Schmid, P.J. Response Analysis of a Laminar Premixed M-Flame to Flow Perturbations Using a Linearized Compressible Navier-Stokes Solver. Phys. Fluids 2015, 27, 043602. [Google Scholar] [CrossRef]
- Mehta, P.G.; Soteriou, M.C. Combustion Heat Release Effects on the Dynamics of Bluff Body Stabilized Premixed Reacting Flows. In Proceedings of the 41st Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar]
- Erickson, R.; Soteriou, M.; Mehta, P. The Influence of Temperature Ratio on the Dynamics of Bluff Body Stabilized Flames. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar] [CrossRef]
- Chu, B.T.; Kovasznay, L.S.G. Non-Linear Interactions in a Viscous Heat-Conducting Compressible Gas. J. Fluid Mech. 1957, 3, 495–514. [Google Scholar] [CrossRef]
- Boyer, L.; Quinard, J. On the Dynamics of Anchored Flames. Combust. Flame 1990, 82, 51–65. [Google Scholar] [CrossRef]
- Steinbacher, T. Analysis and Low-Order Modeling of Interactions between Acoustics, Hydrodynamics and Premixed Flames. Ph.D. Thesis, TU München, München, Germany, 2019. [Google Scholar]
- Pindera, M.Z.; Talbot, L. Flame Induced Vorticity: Effects of Stretch. Symp. Int. Combust. 1988, 21, 1357–1366. [Google Scholar] [CrossRef][Green Version]
- Landau, L. On the Theory of Slow Combusiton. Acta Physicochim. 1944, 19, 403–411. [Google Scholar] [CrossRef]
- Sivashinsky, G.; Clavin, P. On the Nonlinear Theory of Hydrodynamic Instability in Flames. J. Phys. 1987, 48, 193–198. [Google Scholar] [CrossRef]
- Frankel, M.L. An Equation of Surface Dynamics Modeling Flame Fronts as Density Discontinuities in Potential Flows. Phys. Fluids A Fluid Dyn. 1990, 2, 1879–1883. [Google Scholar] [CrossRef]
- Zimmermann, A. Modeling the Influence of Gas Expansion on the Linear Response of Laminar Premixed Flames. Bachelor’s Thesis, Technische Universität München, München, Germany, 2018. [Google Scholar]
- Matalon, M.; Cui, C.; Bechtold, J.K. Hydrodynamic Theory of Premixed Flames: Effects of Stoichiometry, Variable Transport Coefficients and Arbitrary Reaction Orders. J. Fluid Mech. 2003, 487, 179–210. [Google Scholar] [CrossRef]
- Brown, J.W.; Churchill, R.V. Complex Variables and Applications, 8th ed.; Brown and Churchill Series; McGraw-Hill Higher Education: Boston, MA, USA, 2009. [Google Scholar]
- Batchelor, G. An Introduction to Fluid Mechanics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Pullin, D.I. The Large-Scale Structure of Unsteady Self-Similar Rolled-up Vortex Sheets. J. Fluid Mech. 1978, 88, 401–430. [Google Scholar] [CrossRef]
- Hoeijmakers, H.W.M. Computational Aerodynamics of Ordered Vortex Flows. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 1989. [Google Scholar]
- Ducruix, S.; Durox, D.; Candel, S. Theoretical and Experimental Determinations of the Transfer Function of a Laminar Premixed Flame. Proc. Combust. Inst. 2000, 28, 765–773. [Google Scholar] [CrossRef]
- Wang, H.Y.; Law, C.K.; Lieuwen, T. Linear Response of Stretch-Affected Premixed Flames to Flow Oscillations. Combust. Flame 2009, 156, 889–895. [Google Scholar] [CrossRef]
- Markstein, G.H. Experimental and Theoretical Studies of Flame-Front Stability. J. Aeronaut. Sci. 1951, 18, 199–209. [Google Scholar] [CrossRef]
- Lieuwen, T. Theoretical Investigation of Unsteady Flow Interactions with a Premixed Planar Flame. J. Fluid Mech. 2001, 435, 289–303. [Google Scholar] [CrossRef]
- Class, A.G.; Matkowsky, B.J.; Klimenko, a.Y. A Unified Model of Flames as Gasdynamic Discontinuities. J. Fluid Mech. 2003, 491, 11–49. [Google Scholar] [CrossRef]
- Hayes, W.D. The Vorticity Jump Across a Gasdynamic Discontinuity. J. Fluid Mech. 1957, 2, 595–600. [Google Scholar] [CrossRef]
- Ashurst, W.M.T.; Sivashinsky, G.I.; Yakhot, V. Flame Front Propagation in Nonsteady Hydrodynamic Fields. Combust. Sci. Technol. 1988, 62, 273–284. [Google Scholar] [CrossRef]
- Matalon, M. Flame Dynamics. Proc. Combust. Inst. 2009, 32, 57–82. [Google Scholar] [CrossRef]
- The OpenFOAM Foundation. OpenFOAM 2.3.1. 2017. Available online: https://openfoam.org/ (accessed on 11 May 2017).
- Bibrzycki, J.; Poinsot, T.; Zajdel, A. Investigation of Laminar Flame Speed of CH4/N2/O2 and CH4/CO2/O2 Mixtures Using Reduced Chemical Kinetic Mechanisms. Arch. Combust. 2010, 30, 287–296. [Google Scholar]
- Duchaine, F.; Boudy, F.; Durox, D.; Poinsot, T. Sensitivity Analysis of Transfer Functions of Laminar Flames. Combust. Flame 2011, 158, 2384–2394. [Google Scholar] [CrossRef]
- Jaensch, S.; Merk, M.; Gopalakrishnan, E.; Bomberg, S.; Emmert, T.; Sujith, R.; Polifke, W. Hybrid CFD/Low-Order Modeling of Nonlinear Thermoacoustic Oscillations. Proc. Combust. Inst. 2017, 36, 3827–3834. [Google Scholar] [CrossRef]
- Steinbacher, T.; Meindl, M.; Polifke, W. Modeling the Generation of Temperature Inhomogeneities by a Premixed Flame. Int. J. Spray Combust. Dyn. 2018, 10, 111–130. [Google Scholar] [CrossRef]
- Steinbacher, T.; Albayrak, A.; Ghani, A.; Polifke, W. Consequences of Flame Geometry for the Acoustic Response of Premixed Flames. Combust. Flame 2019, 199, 411–428. [Google Scholar] [CrossRef]
- Mehta, P.; Soteriou, M.; Banaszuk, A. Impact of Exothermicity on Steady and Linearized Response of a Premixed Ducted Flame. Combust. Flame 2005, 141, 392–405. [Google Scholar] [CrossRef]
- Clements, R.R. An Inviscid Model of Two-Dimensional Vortex Shedding. J. Fluid Mech. 1973, 57, 321–336. [Google Scholar] [CrossRef]
- Hirschberg, A.; Hoeijmakers, H. Comments on the Low Frequency Radiation Impedance of a Duct Exhausting a Hot Gas. J. Acoust. Soc. Am. 2014, 136, EL84–EL89. [Google Scholar] [CrossRef] [PubMed]
- Langtangen, H.P.; Linge, S. 3.1 an Explicit Method for the 1D Diffusion Equation. In Finite Difference Computing with PDEs: A Modern Software Approach; Number 16 in Texts in Computational Science and Engineering; Springer Open: Cham, Switzerland, 2017. [Google Scholar]
- Nelson, P.A.; Halliwell, N.A.; Doak, P.E. Fluid Dynamics of a Flow Excited Resonance, Part II: Flow Acoustic Interaction. J. Sound Vib. 1983, 91, 375–402. [Google Scholar] [CrossRef]
- Darrieus, G. Propagation d’un Front de Flamme. Presented at La Technique Moderne Paris, Paris, France, 6–15 March 1938. Unpublished Work. [Google Scholar]
- Saffman, P.G. Vortex Dynamics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Goodwin, D.G.; Moffat, H.K.; Speth, R.L. Cantera: An Object-Oriented Software Toolkit for Chemical Kinetics, Thermodynamics, and Transport Processes. 2016. Available online: http://www.cantera.org (accessed on 13 December 2021).
- Searby, G.; Truffaut, J.M.; Joulin, G. Comparison of Experiments and a Nonlinear Model Equation for Spatially Developing Flame Instability. Phys. Fluids 2001, 13, 3270–3276. [Google Scholar] [CrossRef]
- Lee, D.H.; Lieuwen, T.C. Acoustic Near-Field Characteristics of a Conical, Premixed Flame. J. Acoust. Soc. Am. 2003, 113, 167–177. [Google Scholar] [CrossRef]
- Lee, D.; Lieuwen, T. Premixed Flame Kinematics in a Longitudinal Acoustic Field. J. Propuls. Power 2003, 19, 837–846. [Google Scholar] [CrossRef]
- Hemchandra, S. Premixed Flame Response to Equivalence Ratio Fluctuations: Comparison Between Reduced Order Modeling and Detailed Computations. Combust. Flame 2012, 159, 3530–3543. [Google Scholar] [CrossRef]
- Oberleithner, K.; Schimek, S.; Paschereit, C.O. Shear Flow Instabilities in Swirl-Stabilized Combustors and Their Impact on the Amplitude Dependent Flame Response: A Linear Stability Analysis. Combust. Flame 2015, 162, 86–99. [Google Scholar] [CrossRef]
- Oberleithner, K.; Paschereit, C.O. Modeling Flame Describing Functions Based on Hydrodynamic Linear Stability Analysis. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016; p. V04BT04A009. [Google Scholar] [CrossRef]
- Class, A.G.; Matkowsky, B.J.; Klimenko, A.Y. Stability of Planar Flames as Gasdynamic Discontinuities. J. Fluid Mech. 2003, 491, 51–63. [Google Scholar] [CrossRef]
- Howe, M.S. Hydrodynamics and Sound; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2007. [Google Scholar]
- Joulin, G. Nonlinear Hydrodynamic Instability of Expanding Flames: Intrinsic Dynamics. Phys. Rev. E 1994, 50, 2030–2047. [Google Scholar] [CrossRef] [PubMed]
- Denet, B. Frankel Equation for Turbulent Flames in the Presence of a Hydrodynamic Instability. Phys. Rev. E 1997, 55, 6911–6916. [Google Scholar] [CrossRef]
- Joulin, G.; Denet, B.; El-Rabii, H. Potential-Flow Models for Channelled Two-Dimensional Premixed Flames around near-Circular Obstacles. Phys. Rev. E 2010, 81, 016314. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).