2.1. Mathematical Model
We consider a mathematical model of an isothermal flow of a viscous incompressible fluid. Under the given assumptions, the flow is described by the Navier–Stokes equations in the following form [
18,
19]:
where ρ is the simulated fluid density,
t is the time,
u is the velocity vector of the averaged flow in three-dimensional Cartesian coordinates, τ = τ
μ + τ
t is the sum of the molecular and turbulent components in the viscous part of the stress tensor,
p is the pressure, Γ is the diffusion coefficient, and φ is a scalar quantity.
The system of Equation (1) is solved by numerical integration on a finite-volume grid. As an illustration of the final-volume discretization of Equation (1), consider the discretization of the equation of transfer of scalar quantity φ:
The first term in (2) is an unsteady member, the second one is a convective member, and the next one is a diffusive member. To simplify our presentation below, we consider the diffusion coefficient Γ to be a constant. In the general case, the complete form for the discrete equivalent of the differential equation of transfer of the scalar quantity (2), considering the assumptions above, with the time member approximated by an implicit Eulerian scheme [
20], for the reference volume (cell)
P is given by:
Here, φP is the scalar quantity at the center of cell P at the current time step, is the scalar quantity at the center of cell P at the previous time step, CP is the convective member for cell P at the current time step, and DP is the diffusive member for cell P at the current time step.
In what follows, the method is described for the case of discrete equivalents of the convective CP and diffusive DP members for a matched interface and their modification for an unmatched interface.
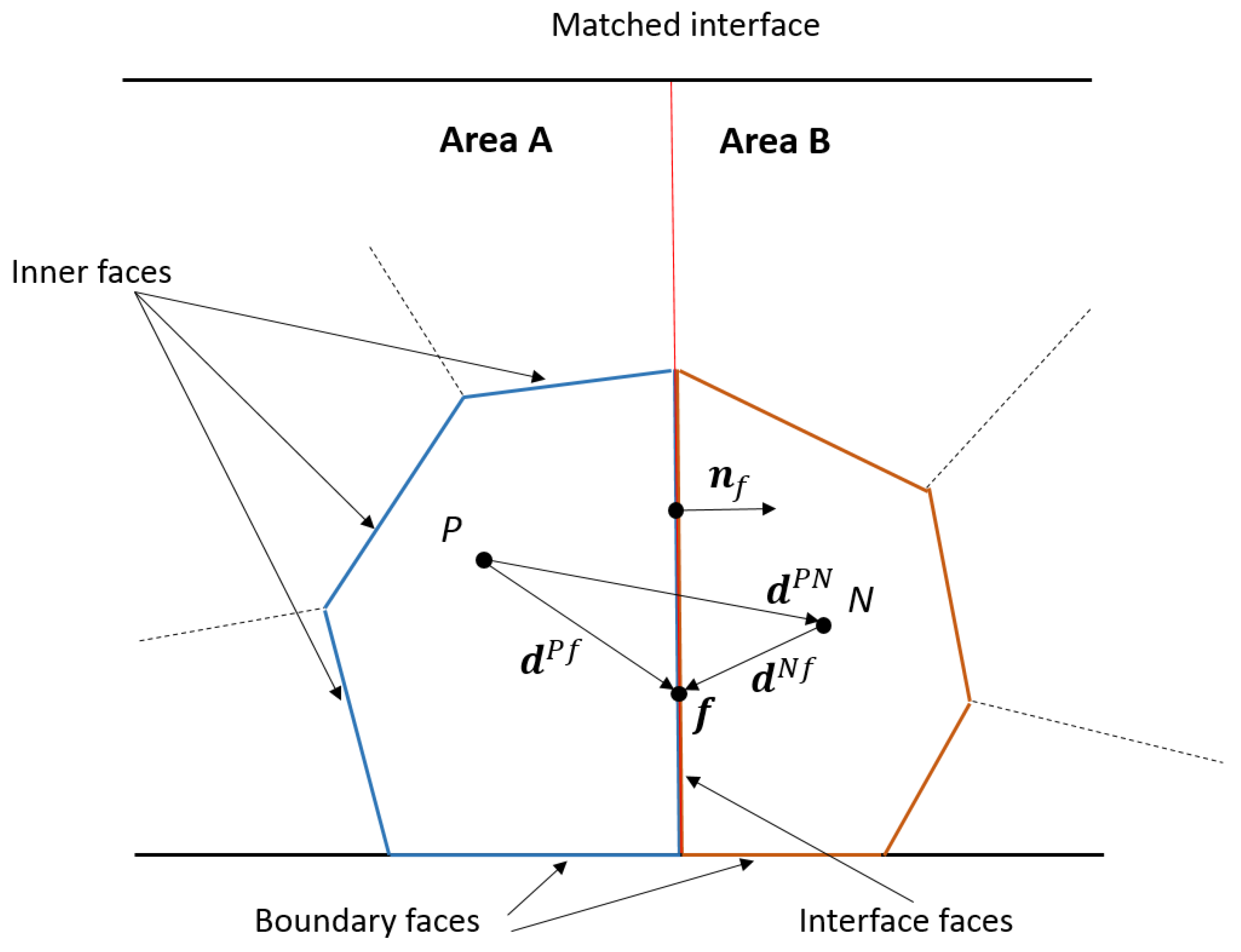
Consider a computational model composed of two grid fragments representing areas
A and
B, the adjacent boundaries of which fit each other in both the number and position of their nodes and create a pair of matched interfaces (
Figure 1).
Approximated on the finite-volume grid, the convective and diffusive members at the current time step for cell
P lying at the matched interface are given by
where
Sf =
Sf nf is the area normal to face
f,
Sf is the area of face
f, φ
f is the scalar quantity at the center of face
f at the current time step,
uf is the velocity at the center of face
f at the current time step,
φ
f is the gradient of the scalar quantity on face
f at the current time step,
f =
face(
Pinner,
Pbound) is summing over all the inner and boundary faces of cell
P, and
f =
face(
Pinterface) is summing over the interface faces of cell
P.
The values of unknowns φ
f and
uf for the inner and interface faces can be calculated by any of the known approximation schemes [
18]. For the approximation scheme CD, the values of φ
f and
uf are determined on face
f assuming the linear variation in φ
f and
uf between the centers of cells
P and
N (
Figure 1), and are defined by
where the value of the geometric interpolation coefficient λ
f is defined as the ratio of distances
fN and
PN projected on face normal
nf for cell
P adjacent to cell
N through face
f (
Figure 1), and is given by
where
dNf and
dPf are the vectors constructed between the cell centers and face center
f (
Figure 1).
The calculations of the gradients on the faces of arbitrary unstructured grids are corrected for nonorthogonality [
21]. The value of gradient
on interface face
f of cell
P (
Figure 1) at the
n-th iteration of the current time step is defined by
where
is the interpolated gradient of the scalar quantity on face
f at the previous iteration.
In turn, gradient
φ
P at the center of cell
P can be calculated by the Green–Gauss algorithm [
18] (the same is for cell
N):
where
f =
face(
P) is summing over all faces of cell
P, including inner, boundary, and interface faces.
The discrete equivalent of the differential equation of transfer of the scalar quantity (3) can finally be represented as a system of algebraic equations, in which the following equation is constructed for each cell
P in the domain (
Figure 1):
where
aP is the diagonal coefficient of cell
P,
aPN is the nondiagonal coefficient relating cells
P and
N through the matched interface,
ai are the nondiagonal coefficients relating cell
P to the cells in domain A through common (inner) faces,
bP is the right-hand member, and
i =
nb(
P) is summing over all neighbor cells
i having common faces with cell
P.
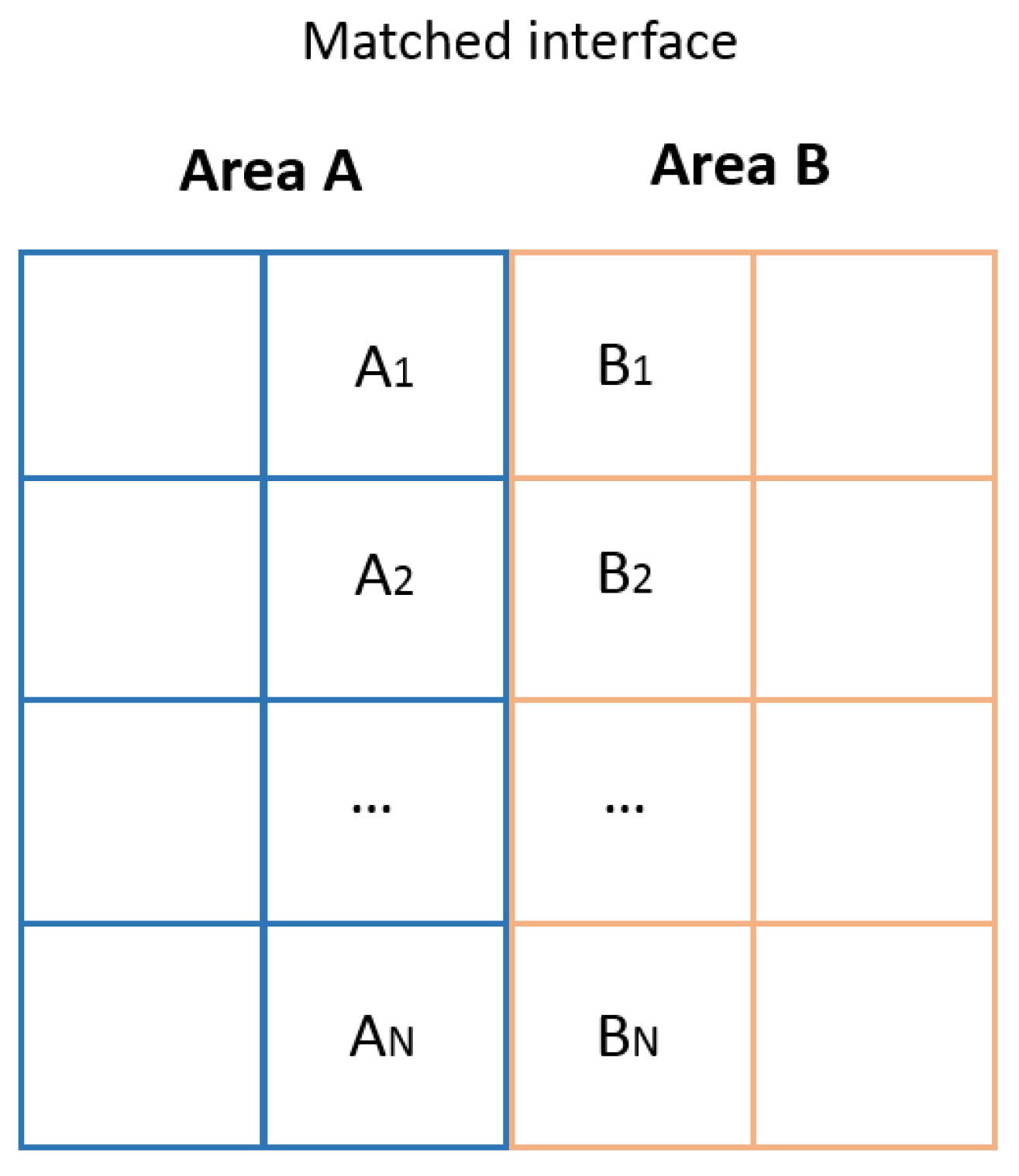
As a result, for the grid model composed of two matched domains A and B (
Figure 2), a system of algebraic equations, (12), is developed, which can be solved by one of the iteration methods [
22]:
where
,
i [1…
N] are the diagonal coefficients of the cells in area
A,
are the diagonal coefficients of the cells in area
B,
are the nondiagonal coefficients relating cells
Ai to cells
Bi through the interface faces, (φ) is the vector of the sought scalar quantity, and (
b) is the vector of the right-hand member.
To simplify the presentation, we do not show the nondiagonal coefficients relating the cells through the inner faces in Equation (12). Let us write the diagonal coefficients in Equation (12) for the cells in area
A (the same is for the cells in area
B) without considering the boundary conditions at the
n-th iteration of the current time step:
where the term
is created due to the adjacency of cell
Ai with the cells in area
A through inner faces
f:
where
Ai is the cell adjacent to cell
Aj through the inner face, the term
is created due to the adjacency of cell
Ai with cell
Bi through interface faces
f:
The nondiagonal coefficients in the system of linear algebraic Equation (12) relating the cells in area
A (the same is for the cells in area
B) through the inner faces at the
n-th iteration of the current time step are given by
The nondiagonal coefficients in the system of linear algebraic Equation (12) relating cell
Ai to cell
Bi through the interface faces at the
n-th iteration of the current time step are given by
The coefficients on the right side of the system of linear algebraic Equation (12) for the cells in area
A (the same is for the cells in area
B) without considering the boundary conditions at the
n-th iteration of the current time step are given by
where
and
are given by
The finite-volume discretization algorithm described above applies to all of the equations in (1). The method can be used in calculations of viscous incompressible flows on grid models of any dimensionality. However, the potential of its application is limited to calculations on models composed of a single grid or a grid composed of matched grid fragments. At present, this limitation makes the method much more difficult to use in most industry-oriented calculations, when grids are built of unmatched fragments to resolve details of specific physical processes. Such calculations require special interfaces, in which quantities φf, uf in (4) and (5), and quantities φf in (9) on the faces belonging to unmatched interfaces cannot be calculated by standard approximation schemes, and the neighborhood of cell P with several cells on the opposite interface must be taken into account.
Below we describe a modification of the numerical method, which considers specific CFD aspects of viscous incompressible flow simulations in the vicinity of interfaces between unmatched grid fragments.
2.2. Unmatched Interface Linking Method
We consider a computational model composed of two grid fragments representing areas
A and
B, the adjacent boundaries of which create a pair of unmatched interfaces (
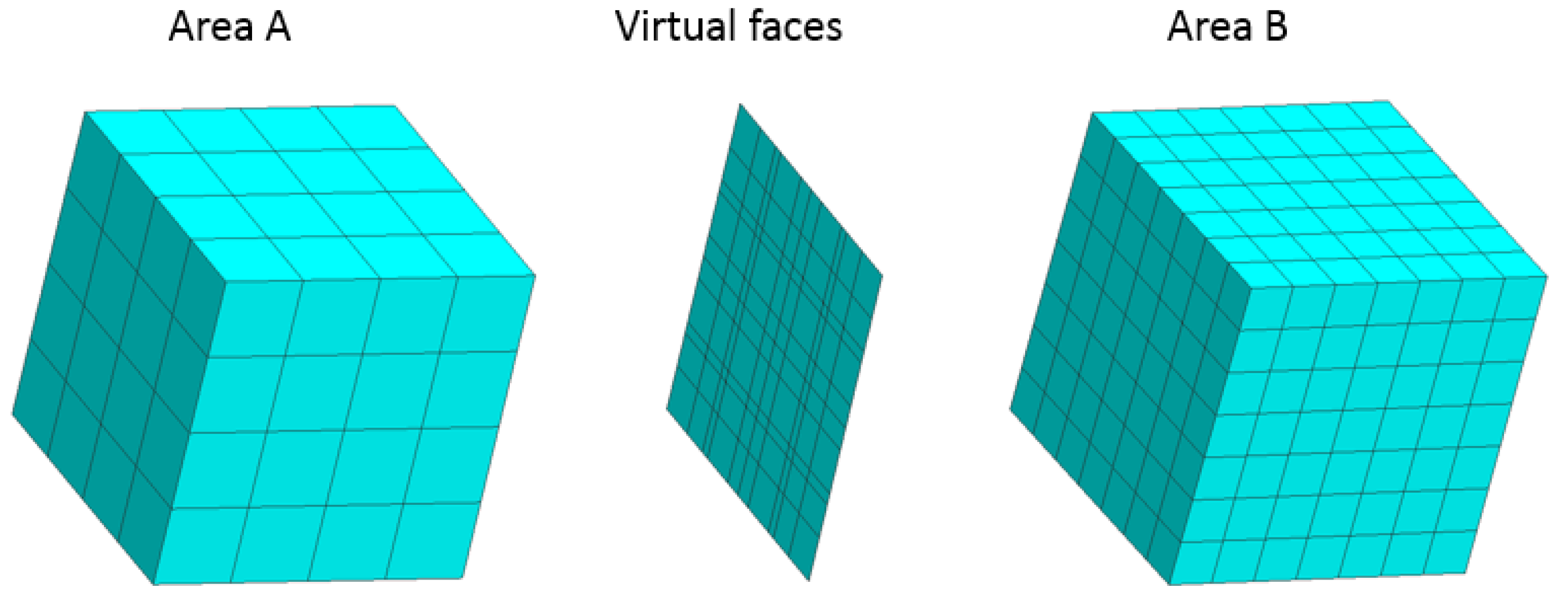
Figure 3). The unmatched interfaces are understood to be adjacent boundaries of unmatched grid fragments, in which the number and position of nodes are different in the general case.
To merge the unmatched interfaces, the original faces are replaced by virtual ones. The geometric parameters of the virtual faces are determined by the successive projection of the original faces in area
A to all of the original faces in area
B. To identify the coordinates of the nodes created at the face intersections, one can use any of the polygon intersection algorithms [
23]. The resulting set of virtual faces constitutes a virtual interface, which links the cells of the unmatched adjacent grid areas (
Figure 3).
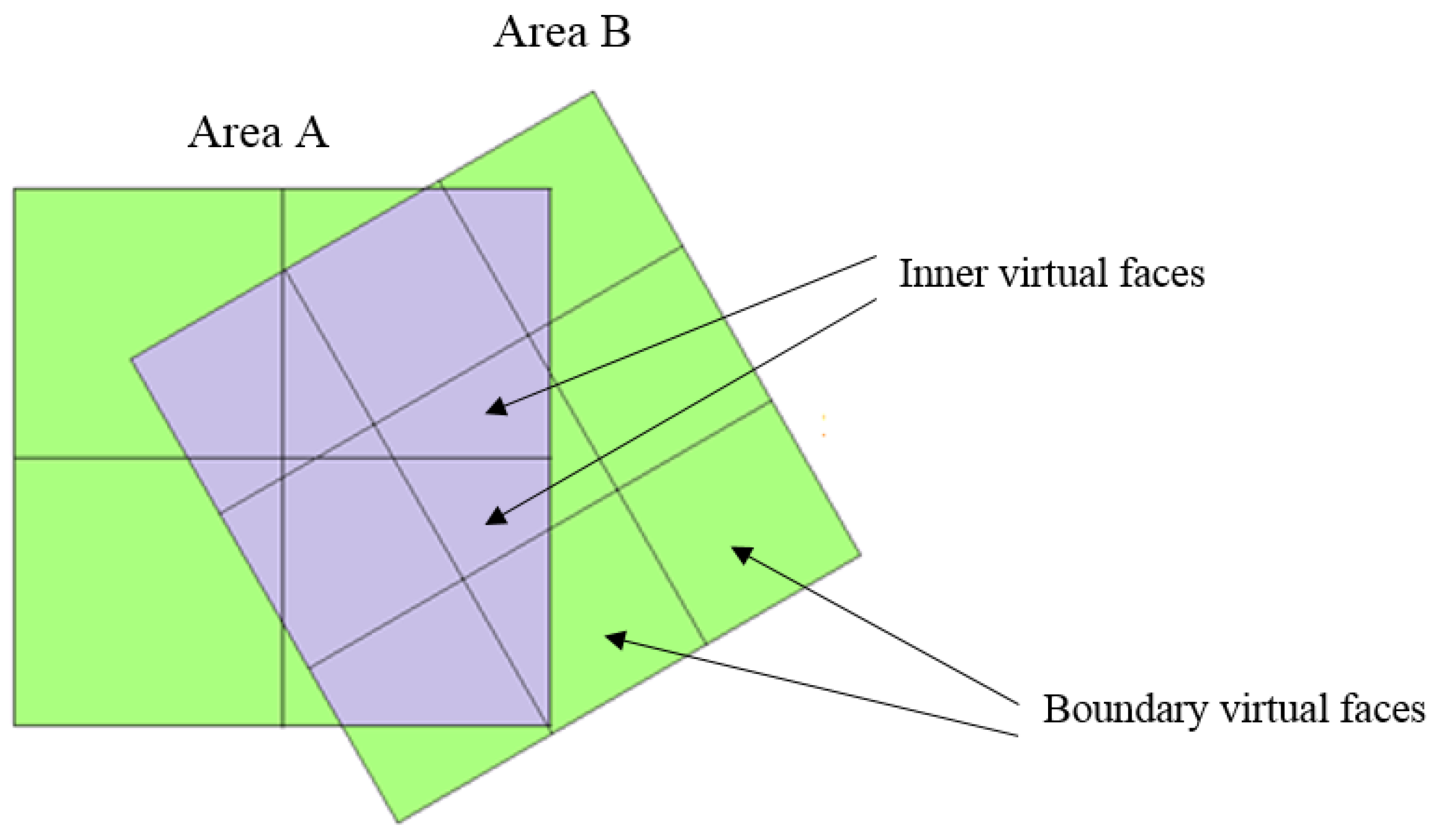
In the general case, the virtual interface consists of a set of inner and boundary virtual faces (
Figure 4). The boundary virtual faces are not linked to the cells on the opposite interface and must be treated in accordance with the chosen boundary conditions. The inner virtual faces create a link between the adjacent cells on the interface.
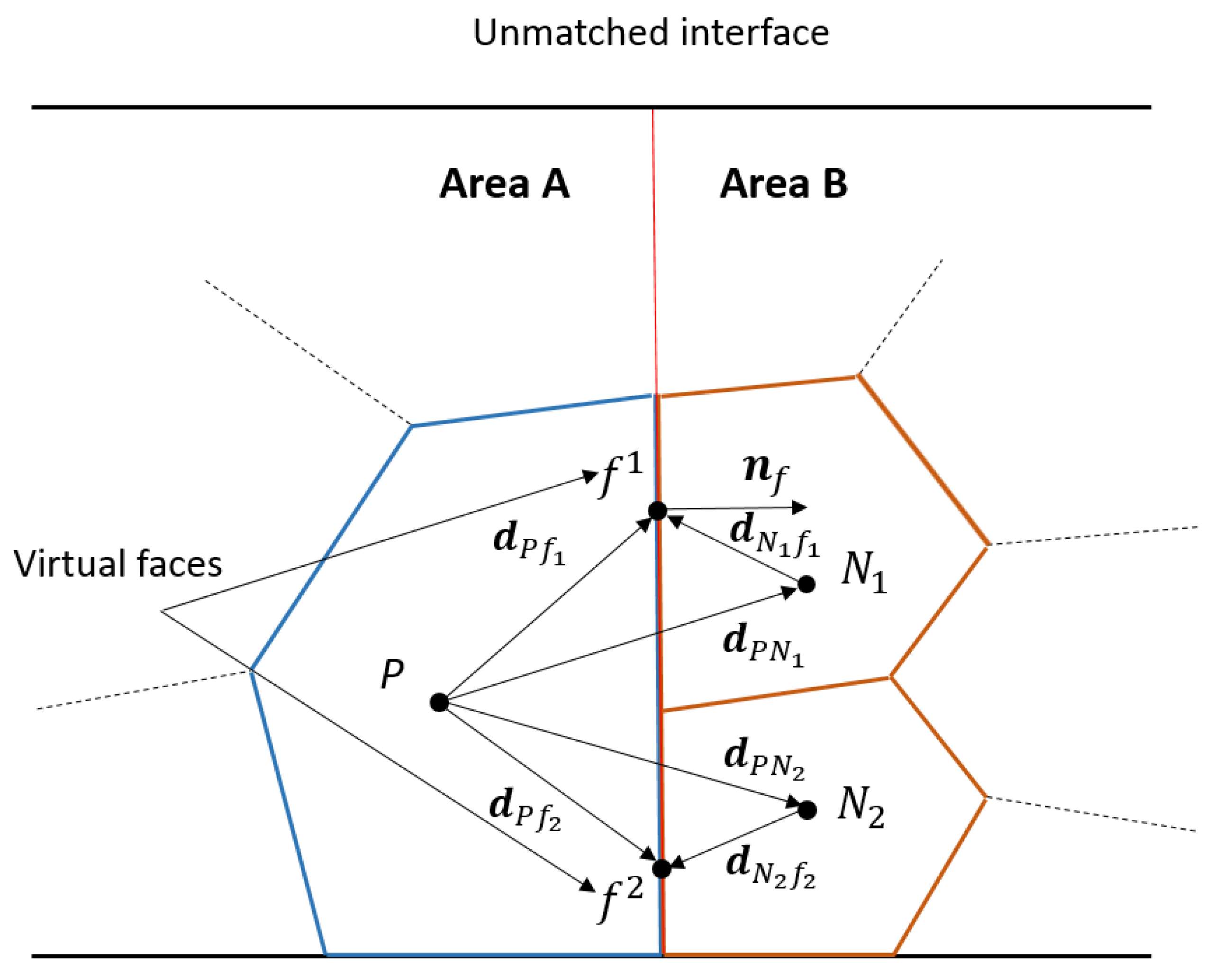
Consider the modification of the diffusive (4) and convective (5) members with a transition from the original to the virtual faces for the case of cell
P belonging to the unmatched interface (
Figure 5).
A discrete equivalent of convective member (4) for cell
P belonging to the unmatched interface is expressed as:
where
and
are the scalar quantity and velocity on virtual face
fv created on original face
f at the current time step, and
is the area of virtual face
fv normal to original face
f.
A discrete equivalent of diffusive member (5) for cell
P belonging to the unmatched interface is expressed as:
where
is the gradient of the scalar quantity on virtual face
fv.
The values of unknowns
,
in (21) belong to the center of virtual face
fv (
Figure 5) and can be calculated by any of the known schemes [
20]. For the approximation scheme CD, the values of
and
are determined on face
fv assuming the linear variation in
and
between the centers of cells
P and
Nv (
Figure 5) and are defined by
where the value of the geometric interpolation coefficient
is defined as the ratio of distances
f Nv and
P Nv projected on face normal
nf for cell
P adjacent to cell
Nv through face
fv (
Figure 5), and is given by
where
and
are the vectors constructed between the cell centers and face center
f (
Figure 5).
Considering the nonorthogonality correction, the value of gradient
on virtual face
fv of cell
P (
Figure 1) at the
n-th iteration of the current time step equals:
where
is the interpolated gradient of the scalar quantity on face
fv calculated at the previous iteration.
The value of gradient
φ
P at the center of cell
P belonging to the unmatched interface is calculated by the Green–Gauss algorithm (the same is for cells
Nv):
where
is the averaged value of the scalar quantity on interface face
f.
As a result of the above transformations, additional terms incorporating the link between the adjacent cells through the virtual faces are included in the discrete equivalent of the equation of transfer (11) for each cell
P belonging to the unmatched interface (
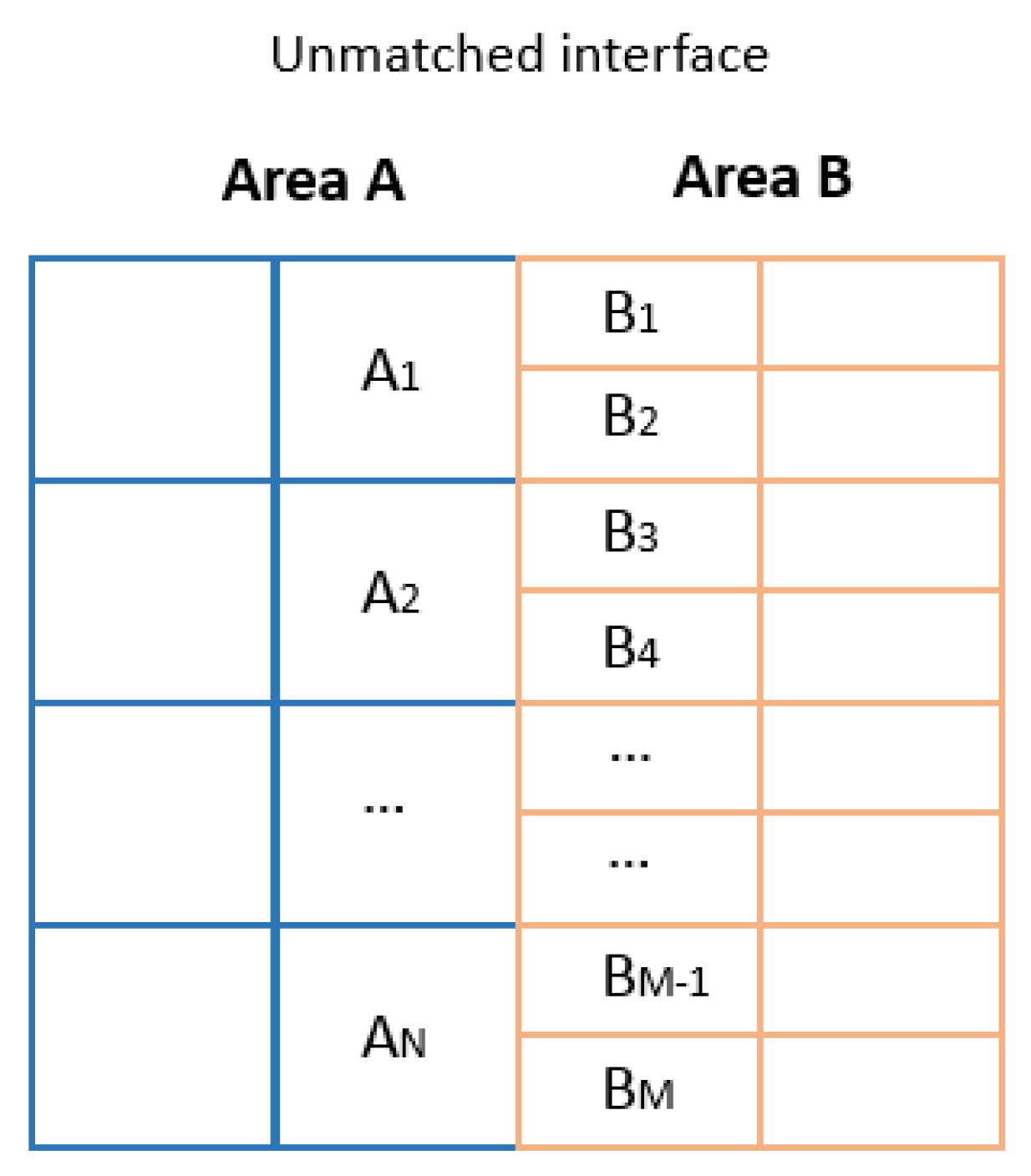
Figure 5). In the general case, for the grid model composed of two unmatched areas
A and
B (
Figure 6), a system of linear algebraic equations, (28), is developed, which can be solved by one of the iteration methods [
22]:
where
,
i [1…
N] are the diagonal coefficients of cells
Ai,
,
j [1…
M] are the diagonal coefficients of cells
Bj,
are the nondiagonal coefficients relating cells
Ai to cells
Bj j through the virtual faces of the unmatched interface, (φ) is the vector of the sought scalar quantity, and (
b) is the vector of the right-hand member.
To simplify the presentation, we do not show the nondiagonal coefficients relating the cells through the inner faces in the system of linear algebraic Equation (28). Let us write the diagonal coefficient in the system of linear algebraic Equation (28) for the cells in area
A without considering the boundary conditions at the
n-th iteration of the current time step (the same is for the cells in area
B):
where
is the term created due to the adjacency of cell
Ai with the cells in area
A through the inner faces, just as in (14), and
is the term created due to the adjacency of cell
Ai with cells
Bi through the virtual faces of the unmatched interface:
Nondiagonal coefficients in the system of linear algebraic Equation (28) relating the cells in area A through the inner faces at the n-th iteration of the current time step are determined identically to (16).
The nondiagonal coefficients in the system of linear algebraic Equation (28) relating cells
Ai to cell
Bj through the virtual faces of the unmatched interface at the
n-th iteration of the current time step are defined by
where
Bj,
j [1…
M] are the cells bordering on cell
Ai through virtual faces
fv.
The coefficients on the right side of the system of linear algebraic Equation (12) for the cells in area
A (the same is for the cells in area
B) without considering the boundary conditions at the
n-th iteration are given by
where
is determined identically to (19), and
is given by
This method combines adjacent unmatched grid fragments into a single domain by means of created virtual interfaces and can be used for all equations in (1). It does not require the modification of the original grid and considers connections between adjacent cells through a set of virtual faces, which creates additional terms in the system of linear algebraic equations of the computational model. Thus, the calculations on models composed of unmatched computational domains by this method are equivalent to the calculations on matched computational models in terms of their computational expenses but are much less expensive in terms of the grid model construction.
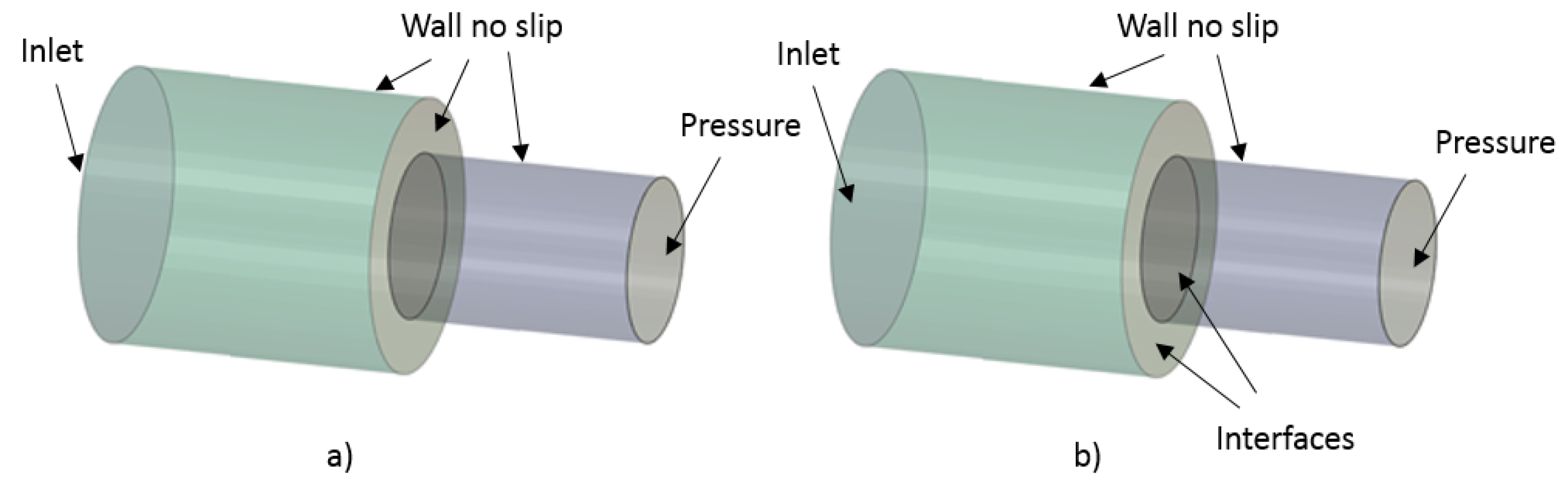
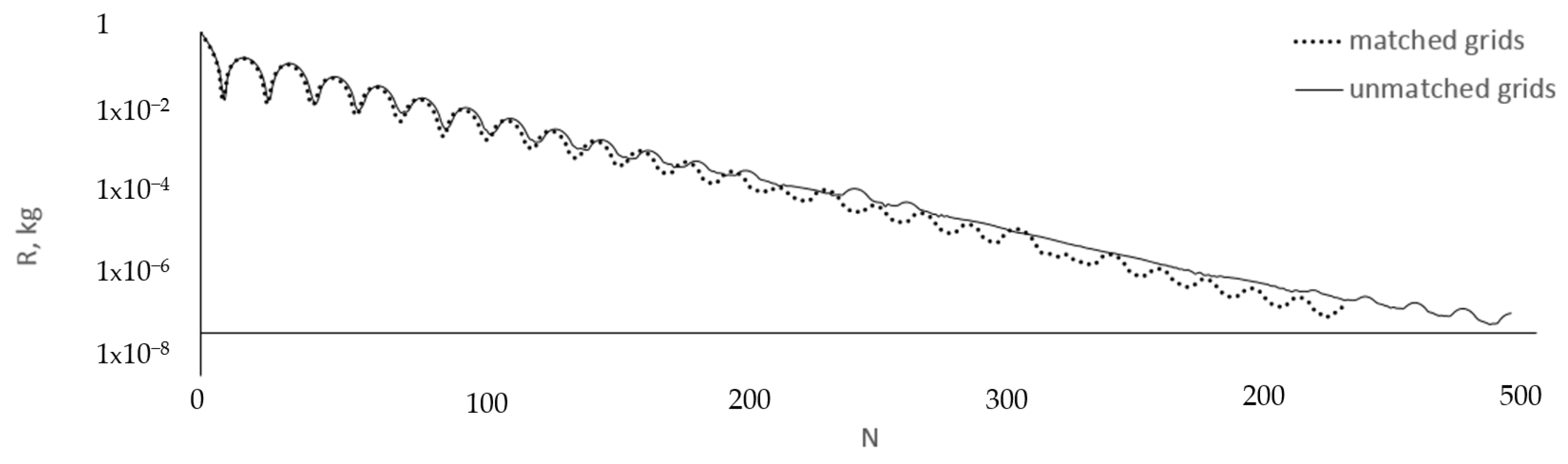
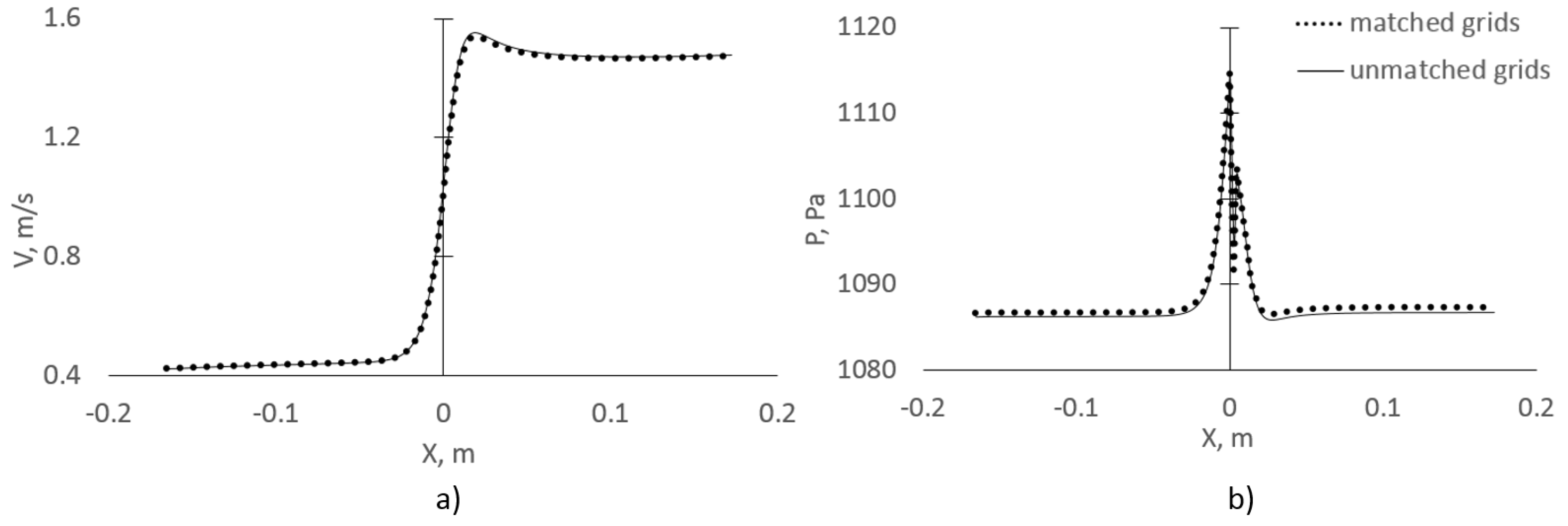
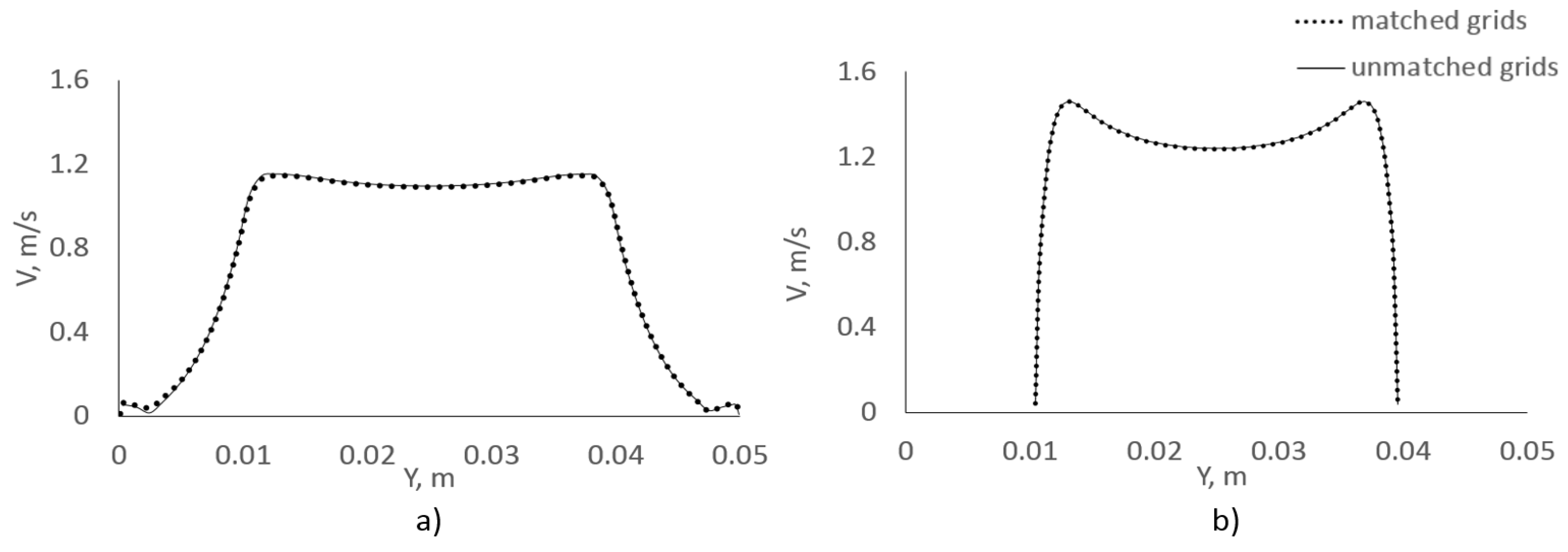
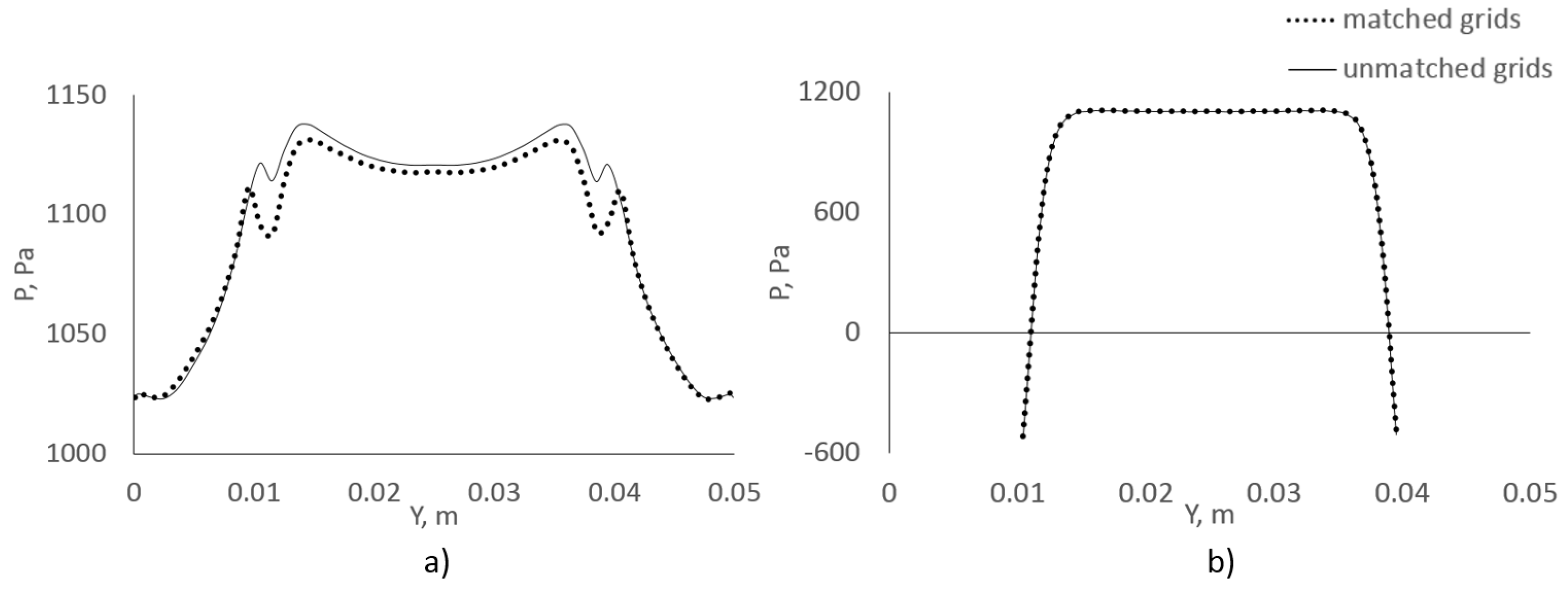
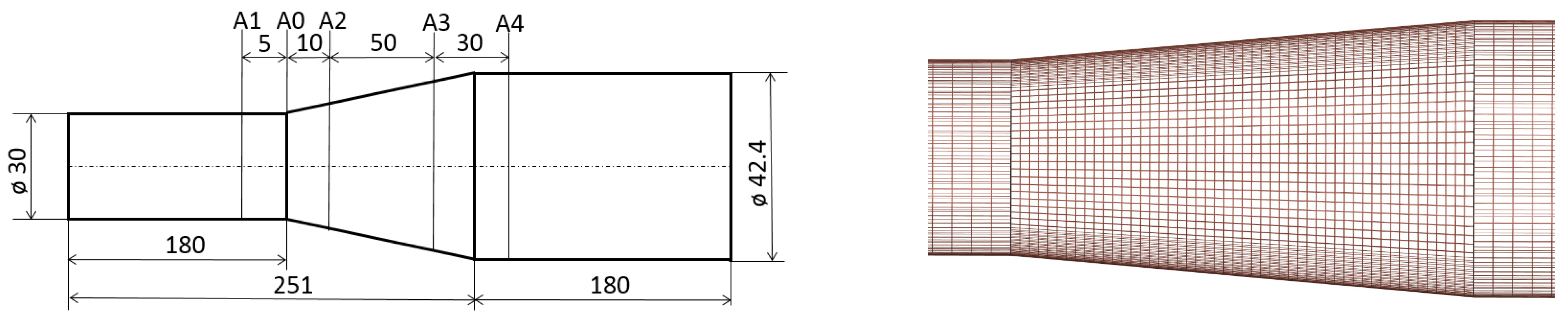
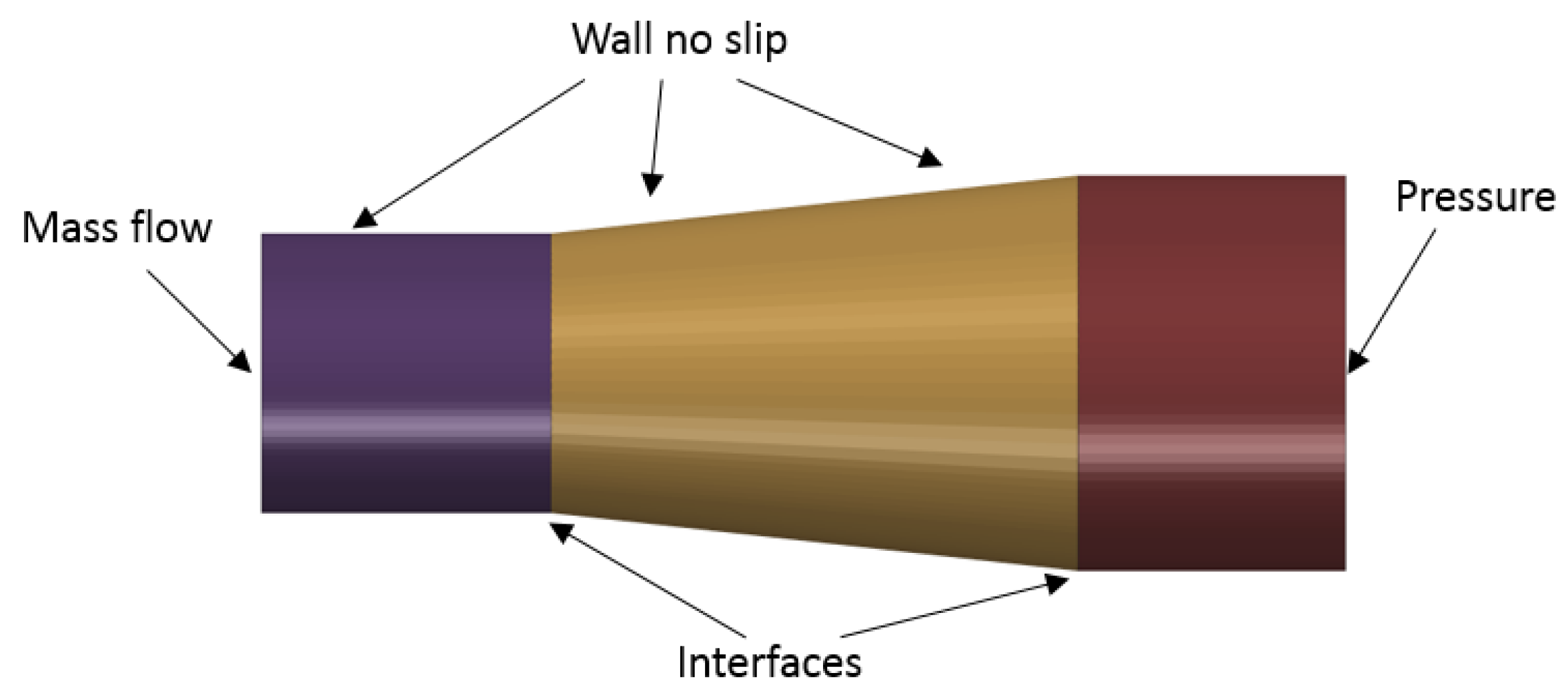
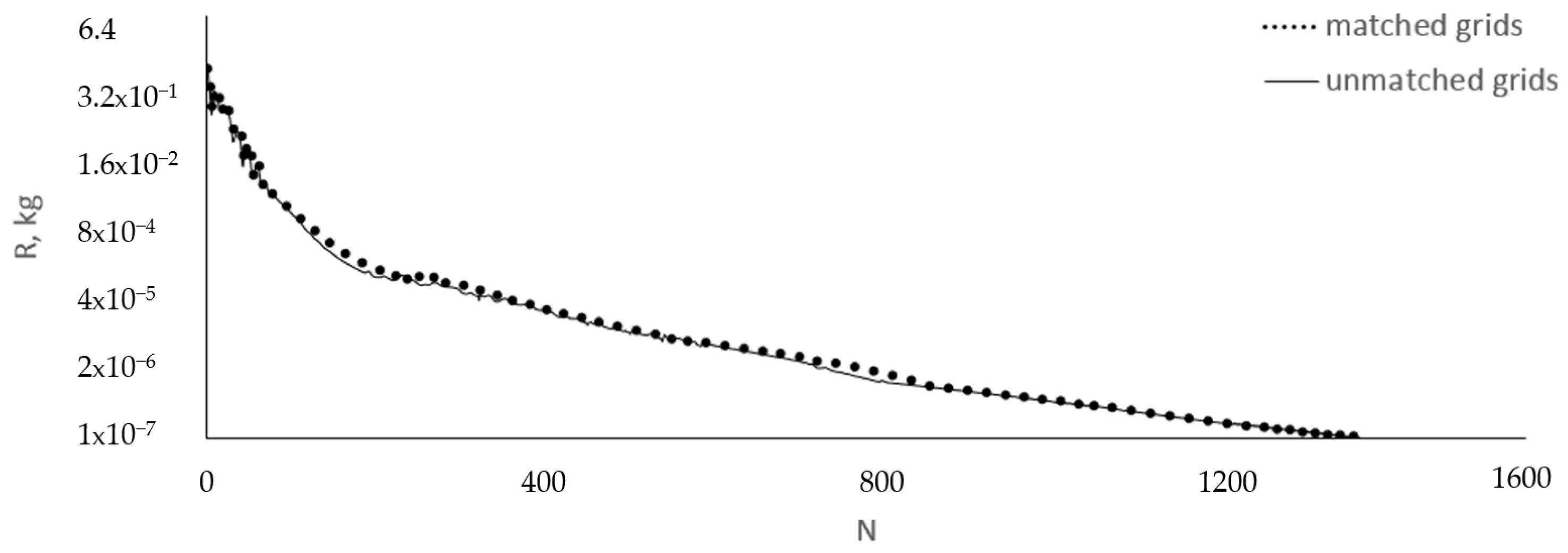
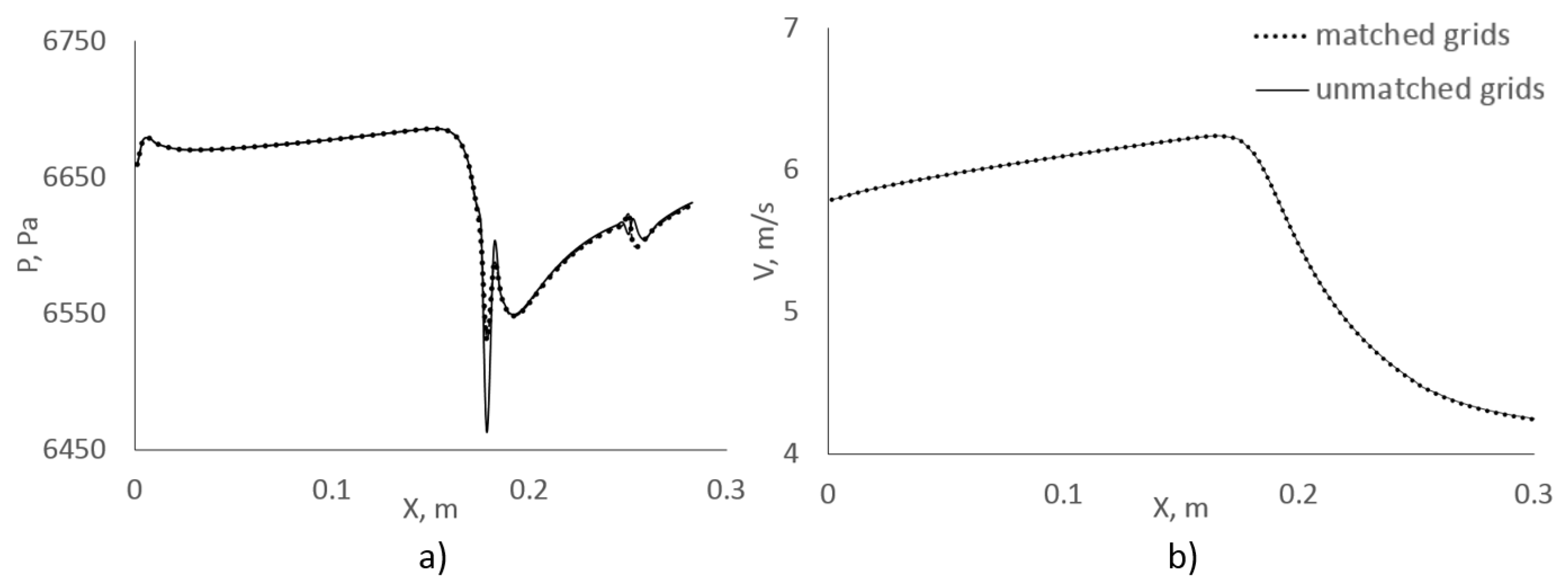
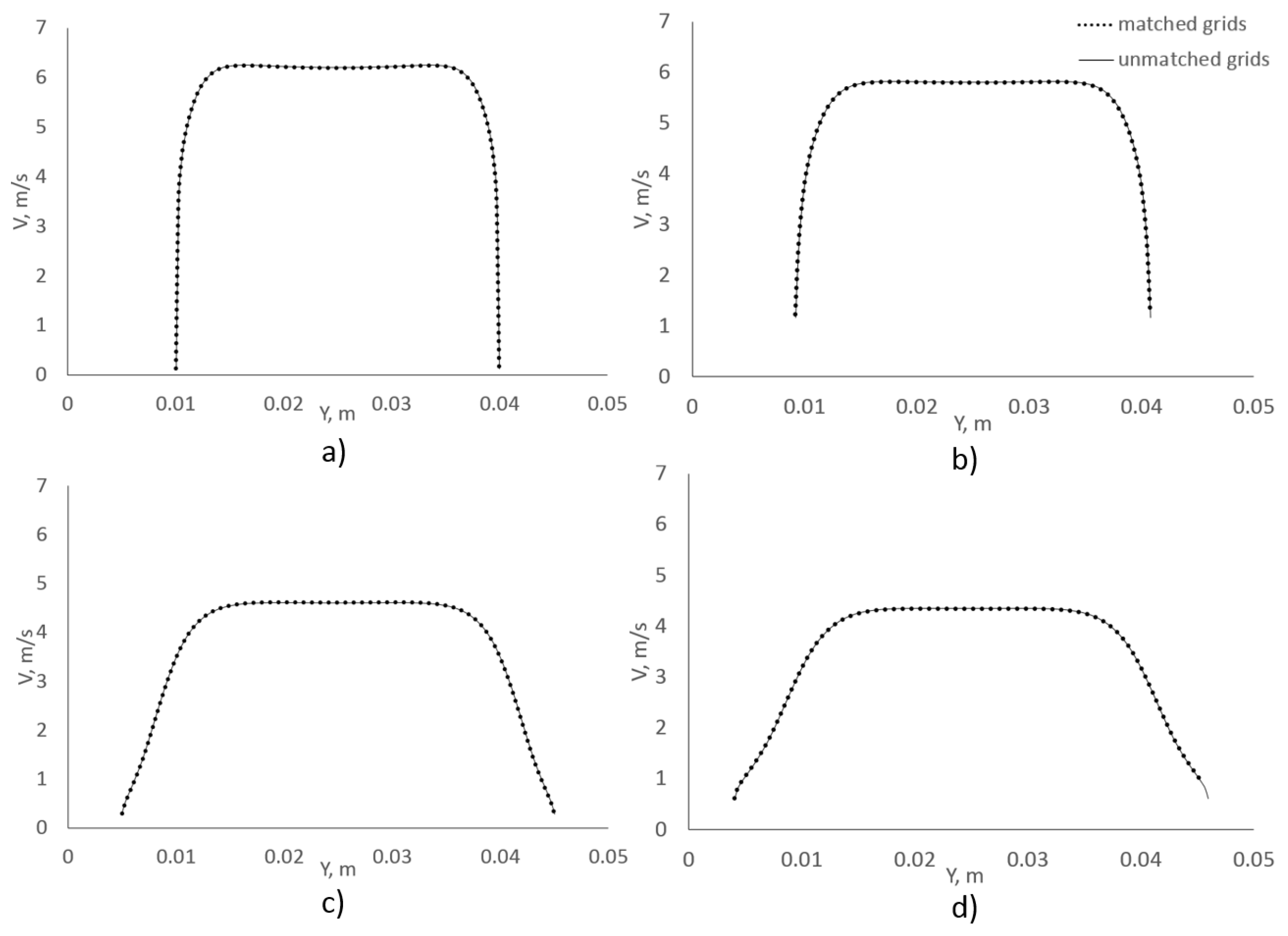
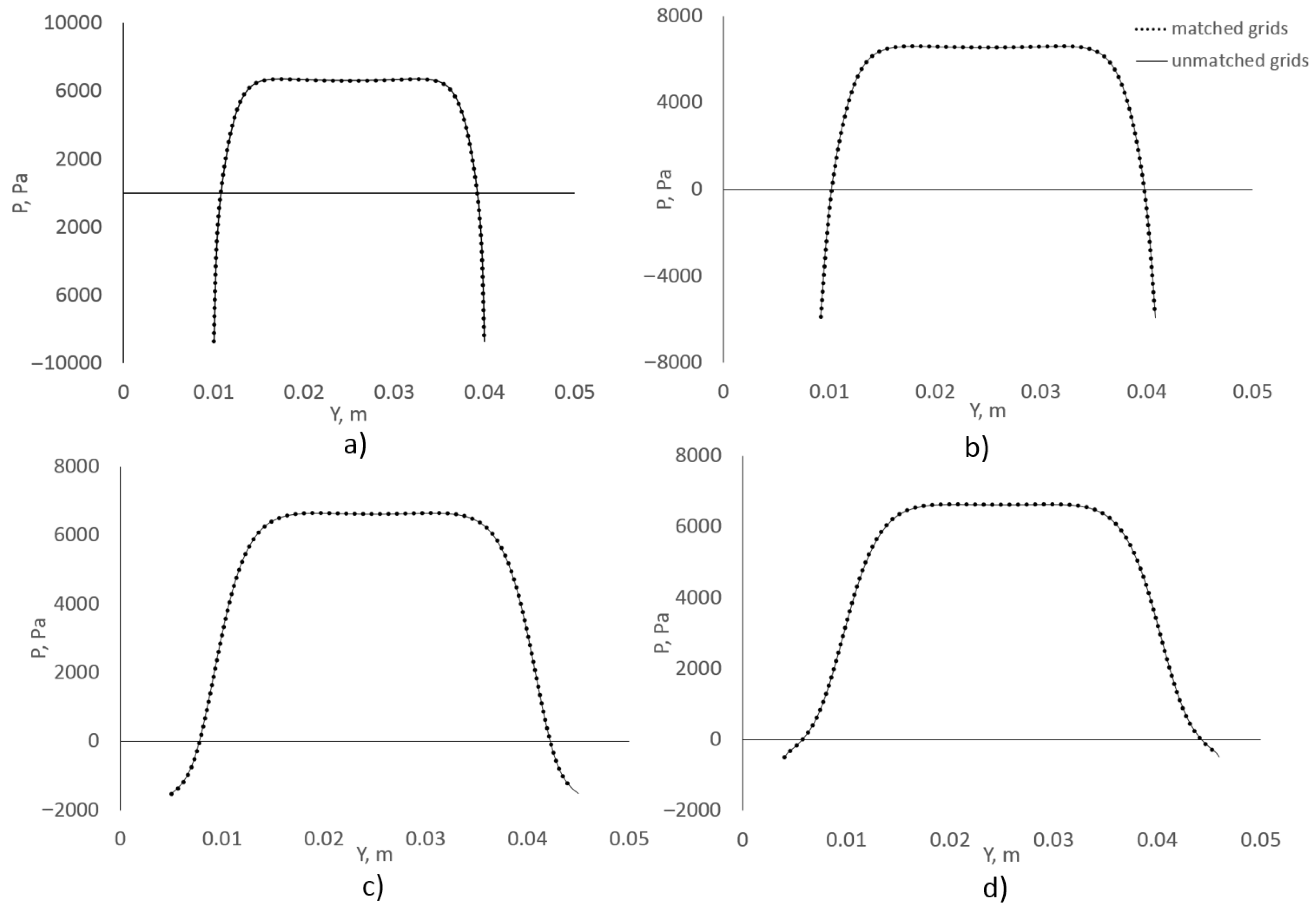
In the section below, we illustrate the performance of our algorithm using simulations of a turbulent flow in a circular pipe with a sudden restriction, and in a round diffuser.