Body Morphology and Drag in Swimming: CFD Analysis of the Effects of Differences in Male and Female Body Types
Abstract
1. Introduction
1.1. Methods of Calculating Drag
1.1.1. Towing
1.1.2. Flume
1.1.3. Inverse Dynamics
1.1.4. Computational Fluid Dynamics (CFD)
1.2. Impact of Morphology on Drag
1.3. Competitive Swimming and Sex Differences
1.4. Rationale
2. Theory
Drag
3. Materials and Methods
3.1. Modeling the Swimmer
3.2. Resizing the Models
3.3. Adapting and Importing the Models
3.4. Manipulating Anthropometry
3.5. Computational Fluid Dynamics (CFD) and Computational Setup
3.6. Calculating Drag
3.7. Mesh Independence
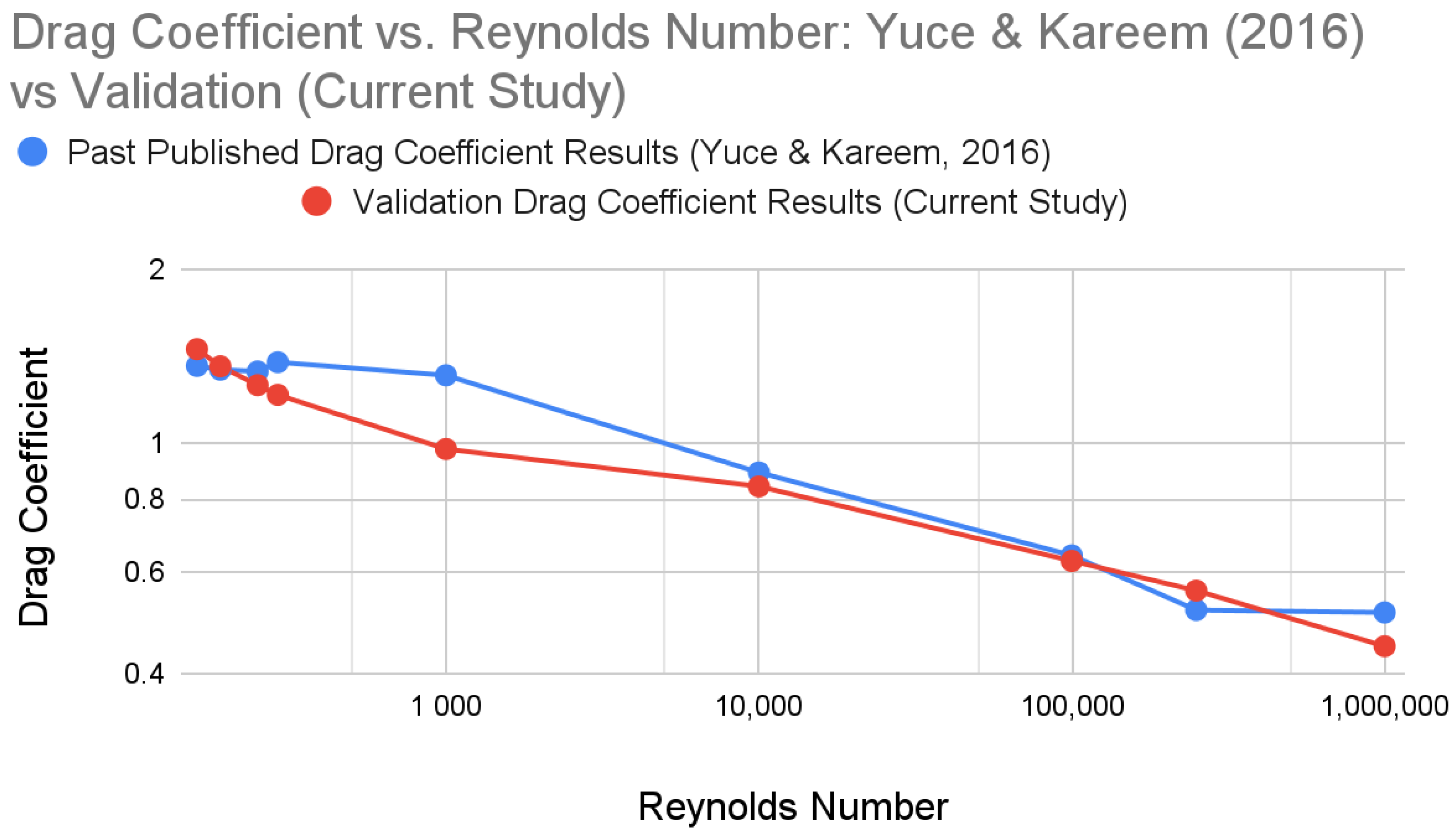
3.8. CFD Validation
4. Results
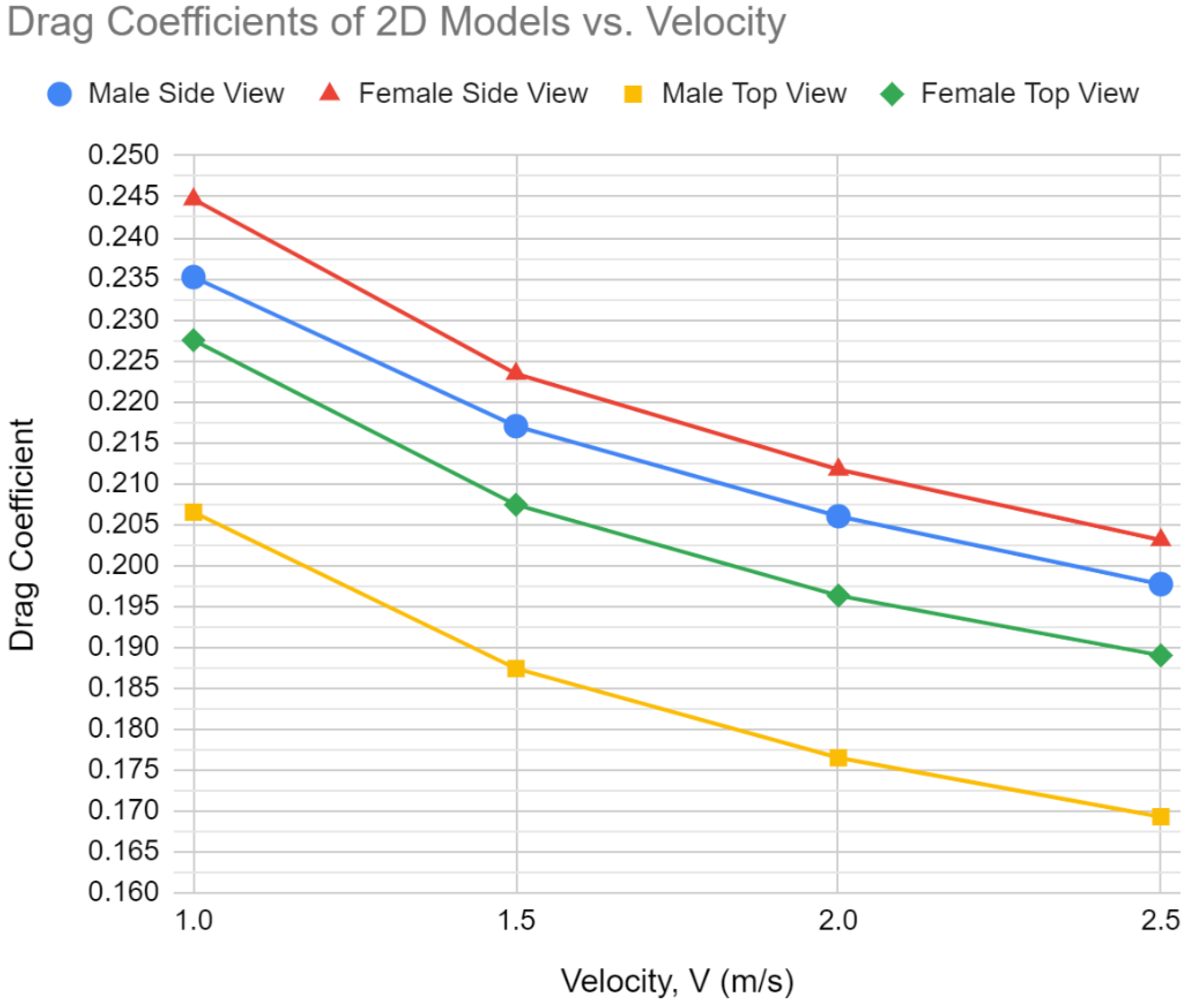
4.1. Male and Female Comparison
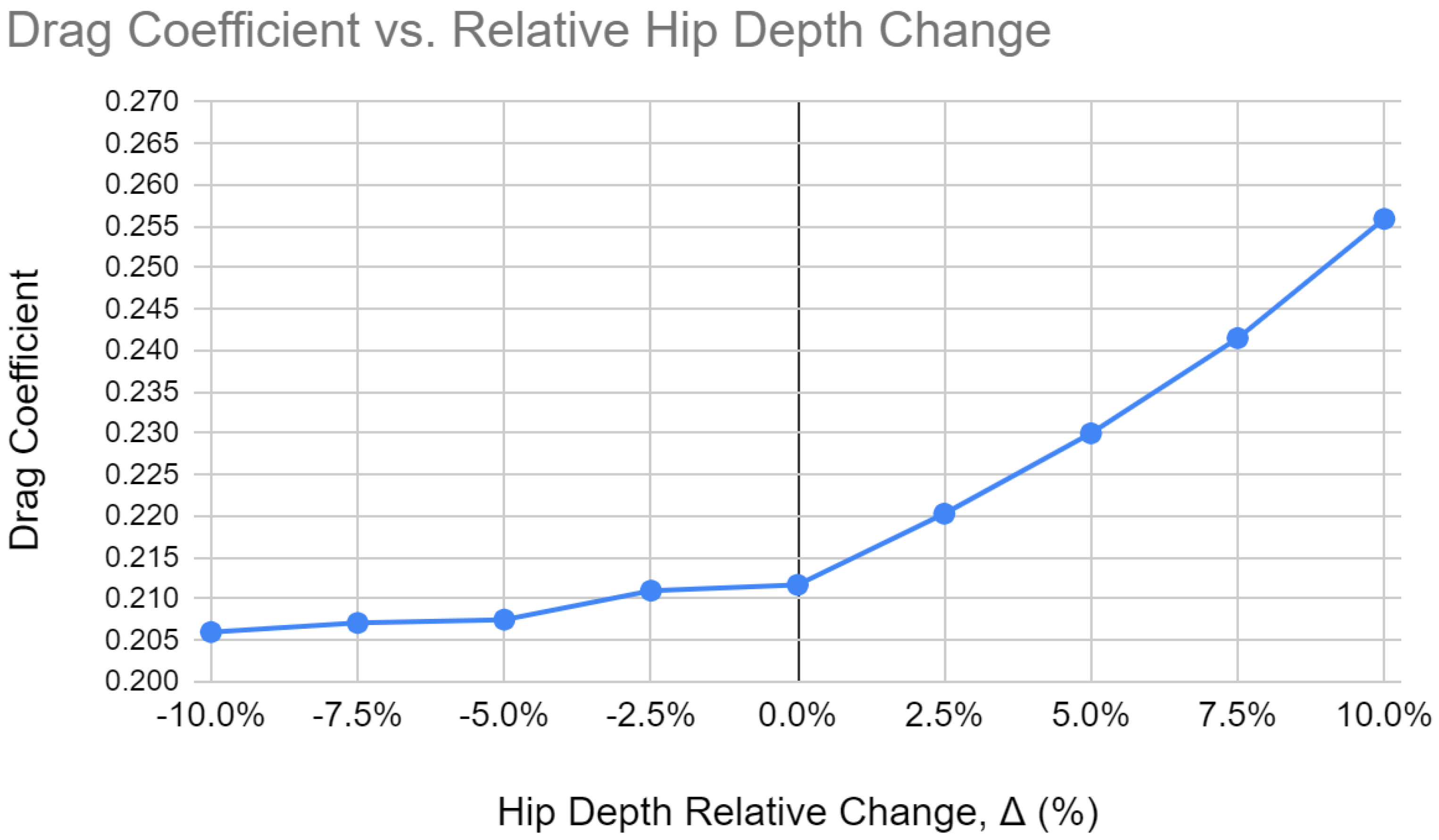
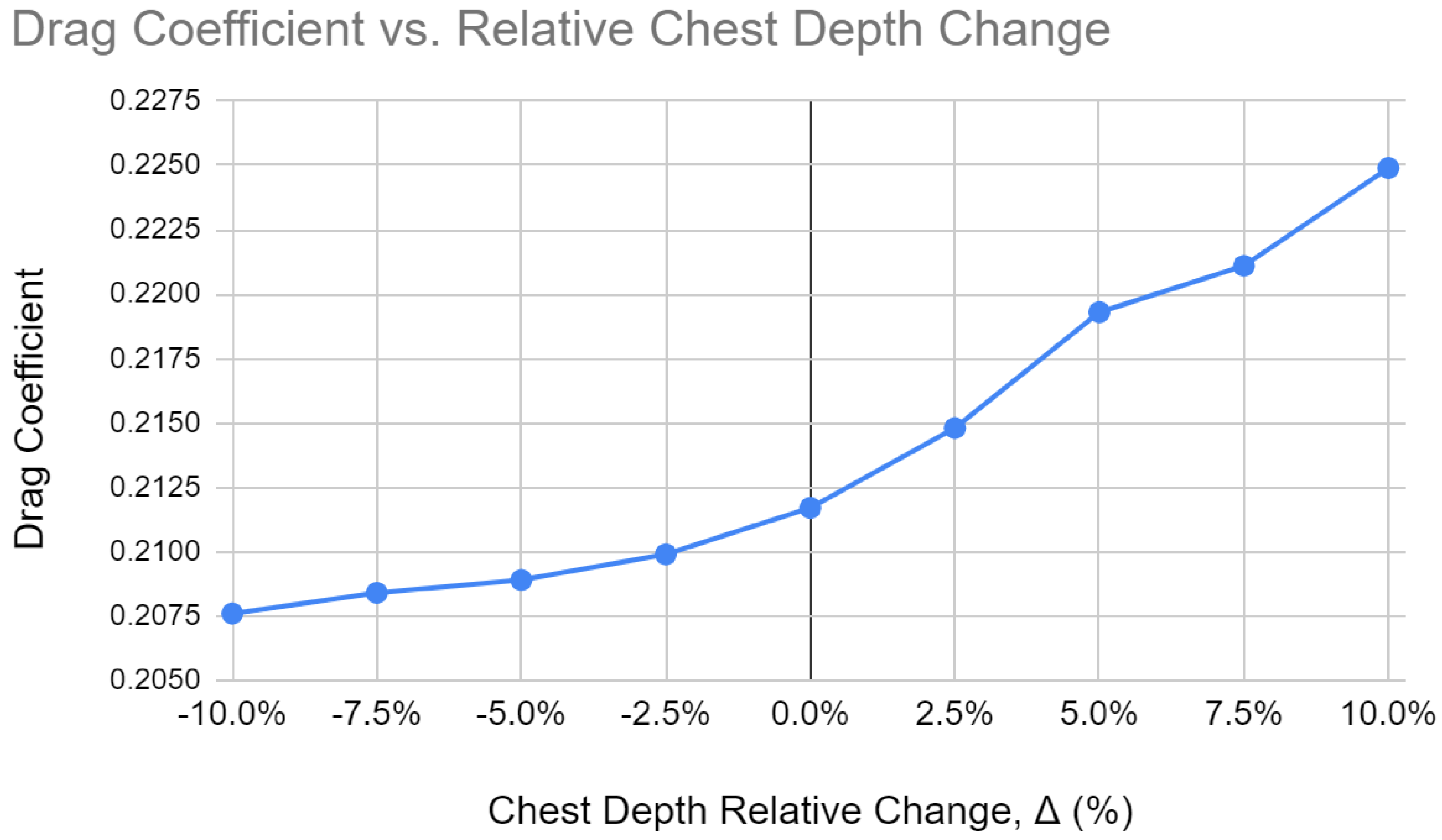
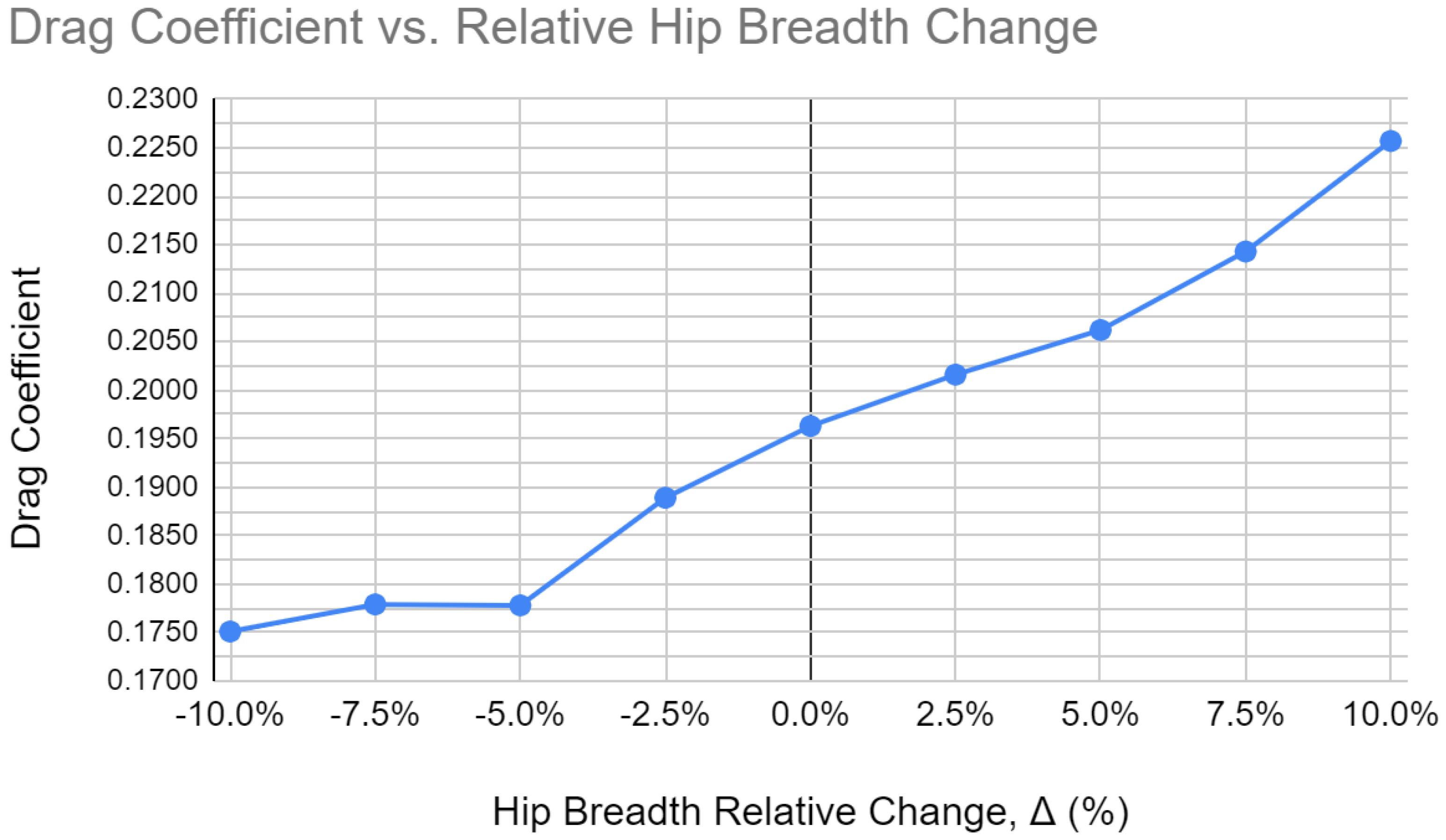
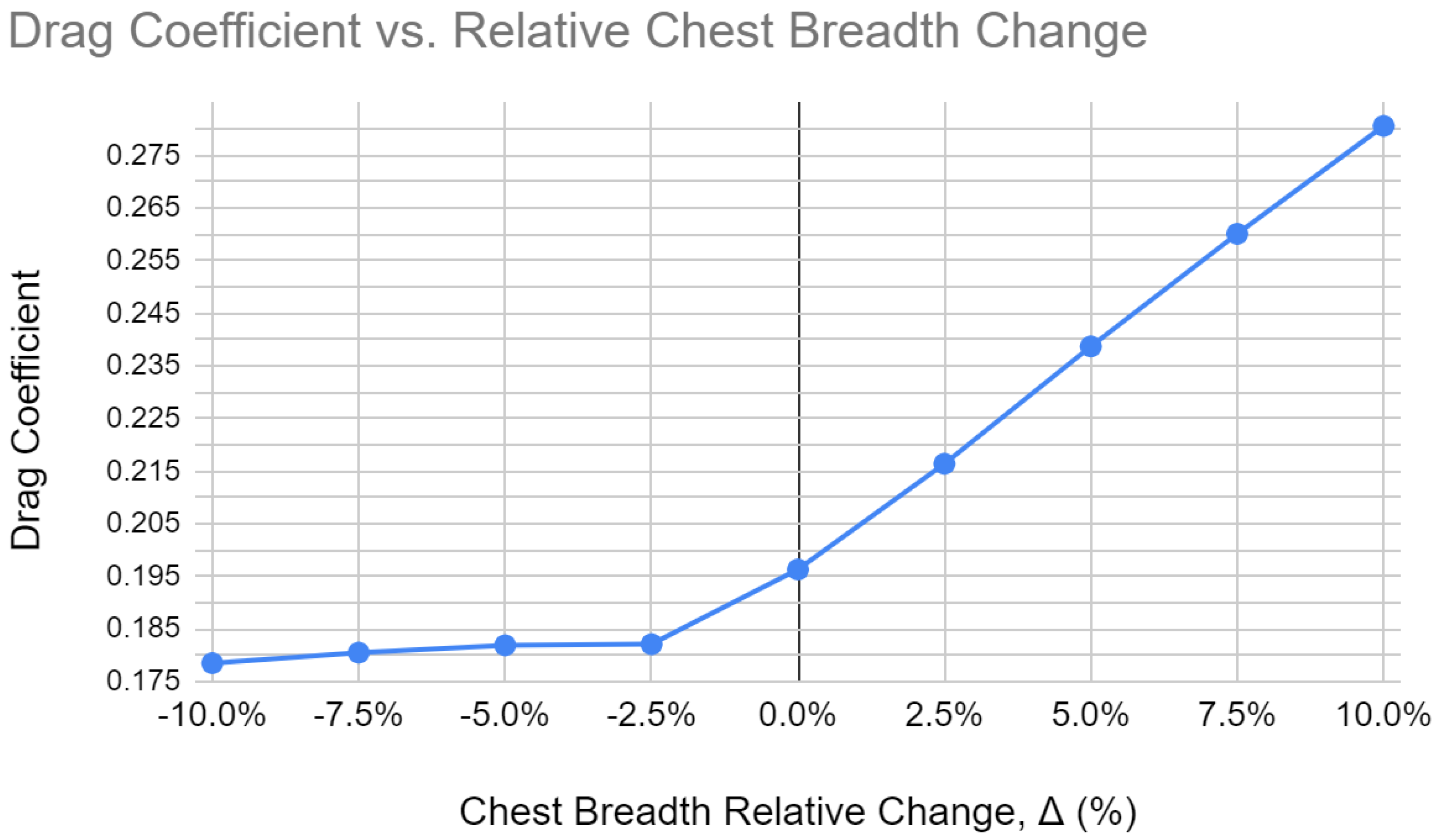
4.2. Manipulating Anthropometry
5. Discussion
5.1. Drag Coefficient and Drag Force Sex Comparison
5.2. Anthropometry and Drag Coefficient Analysis
5.3. Flow Analysis
5.4. Results Comparison
5.5. Differences in Drag on Swimming Performance
6. Conclusions
Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wei, T.; Mark, R.; Hutchison, S. The Fluid Dynamics of Competitive Swimming. Annu. Rev. Fluid Mech. 2014, 46, 547–565. [Google Scholar] [CrossRef]
- Novais, M.; Silva, A.; Mantha, V.; Ramos, R.; Rouboa, A.; Vilas-Boas, J.P.; Luís, S.; Marinho, D. The Effect of Depth on Drag During the Streamlined Glide: A Three-Dimensional CFD Analysis. J. Hum. Kinet. 2012, 33, 55–62. [Google Scholar] [CrossRef] [PubMed]
- Naemi, R.; Easson, W.J.; Sanders, R.H. Hydrodynamic glide efficiency in swimming. J. Sci. Med. Sport 2010, 13, 444–451. [Google Scholar] [CrossRef] [PubMed]
- Vilas-Boas, J.P.; Costa, L.; Fernandes, R.J.; Ribeiro, J.; Figueiredo, P.; Marinho, D.; Silva, A.J.; Rouboa, A.; Machado, L. Determination of the Drag Coefficient during the First and Second Gliding Positions of the Breaststroke Underwater Stroke. J. Appl. Biomech. 2010, 26, 324–331. [Google Scholar] [CrossRef]
- Scurati, R.; Gatta, G.; Michielon, G.; Cortesi, M. Techniques and considerations for monitoring swimmers’ passive drag. J. Sports Sci. 2018, 37, 1168–1180. [Google Scholar] [CrossRef]
- Bixler, B.; Riewald, S. Analysis of a swimmer’s hand and arm in steady flow conditions using computational fluid dynamics. J. Biomech. 2002, 35, 713–717. [Google Scholar] [CrossRef]
- Bixler, B.; Pease, D.; Fairhurst, F. The accuracy of computational fluid dynamics analysis of the passive drag of a male swimmer. Sports Biomech. 2007, 6, 81–98. [Google Scholar] [CrossRef]
- Mantha, V.R.; Marinho, D.A.; Silva, A.J.; Rouboa, A. The 3D CFD study of gliding swimmer on passive hydrodynamics drag. Braz. Arch. Biol. Technol. 2014, 57, 302–308. [Google Scholar] [CrossRef][Green Version]
- Son, H.A.; Lee, S.; Lee, J. Numerical Analysis of Drag Force Acting on 2D Cylinder Immersed in Accelerated Flow. Water 2020, 12, 1790. [Google Scholar] [CrossRef]
- Yuce, M.I.; Kareem, D.A. A Numerical Analysis of Fluid Flow Around Circular and Square Cylinders. J. Am. Water Work. Assoc. 2016, 108, E546–E554. [Google Scholar] [CrossRef]
- Marinho, D.; Barbosa, T.; Rouboa, A.; Silva, A. The Hydrodynamic Study of the Swimming Gliding: A Two-Dimensional Computational Fluid Dynamics (CFD) Analysis. J. Hum. Kinet. 2011, 29, 49–57. [Google Scholar] [CrossRef] [PubMed]
- Hayati, A.N.; Ghaffari, H.; Shams, M. Analysis of free-surface effects on swimming by the application of the computational fluid dynamics method. Proc. Inst. Mech. Eng. Part P J. Sports Eng. Technol. 2016, 230, 135–148. [Google Scholar] [CrossRef]
- Li, T.-Z.; Zhan, J.-M. Hydrodynamic body shape analysis and their impact on swimming performance. Acta Bioeng. Biomech. 2015, 17, 3–13. [Google Scholar] [PubMed]
- Cortesi, M.; Gatta, G.; Michielon, G.; di Michele, R.; Bartolomei, S.; Scurati, R. Passive Drag in Young Swimmers: Effects of Body Composition, Morphology and Gliding Position. Int. J. Environ. Res. Public Health 2020, 17, 2002. [Google Scholar] [CrossRef] [PubMed]
- Benjanuvatra, N.; Blanksby, B.A.; Elliott, B.C. Morphology and Hydrodynamic Resistance in Young Swimmers. Pediatr. Exerc. Sci. 2001, 13, 246–255. [Google Scholar] [CrossRef]
- Naemi, R.; Psycharakis, S.G.; McCabe, C.; Connaboy, C.; Sanders, R.H. Relationships Between Glide Efficiency and Swimmers’ Size and Shape Characteristics. J. Appl. Biomech. 2012, 28, 400–411. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Thibault, V.; Guillaume, M.; Berthelot, G.; Helou, N.E.; Schaal, K.; Quinquis, L.; Nassif, H.; Tafflet, M.; Escolano, S.; Hermine, O.; et al. Women and Men in Sport Performance: The Gender Gap has not Evolved since 1983. J. Sports Sci. Med. 2010, 9, 214–223. [Google Scholar]
- Divers, S.S. How Fast Do Olympic Swimmers Swim? Men vs. Women vs. Average Swimmers. Triathlon Budgeting. 2021. Available online: https://triathlonbudgeting.com/how-fast-do-olympic-swimmers-swim-men-vs-women-vs-average-swimmers (accessed on 14 July 2022).
- Kleinstreuer, C. Fundamental Equations and Solutions. In Fluid Mechanics and Its Applications; Springer: Berlin/Heidelberg, Germany, 2010; pp. 41–98. [Google Scholar] [CrossRef]
- Gatta, G.; Cortesi, M.; Fantozzi, S.; Zamparo, P. Planimetric frontal area in the four swimming strokes: Implications for drag, energetics and speed. Hum. Mov. Sci. 2015, 39, 41–54. [Google Scholar] [CrossRef]
- Vennell, R.; Pease, D.; Wilson, B. Wave drag on human swimmers. J. Biomech. 2006, 39, 664–671. [Google Scholar] [CrossRef] [PubMed]
- Microsoft Corporation. Get Paint 3D from the Microsoft Store. Microsoft Apps. 2022. Available online: https://apps.microsoft.com/store/detail/paint-3d/9NBLGGH5FV99?hl=en-us&gl=US (accessed on 2 August 2022).
- Anthropometric Data for U.S. Adults (All Dimensions in Inches). 2012. Available online: https://www.ergocenter.ncsu.edu/wp-content/uploads/sites/18/2017/09/Anthropometric-Summary-Data-Tables.pdf (accessed on 14 July 2022).
- Ergonomics—Army Public Health Center. 2012. Available online: https://phc.amedd.army.mil/topics/workplacehealth/ergo/Pages/default.aspx (accessed on 14 July 2022).
- Madge, R. Height Analysis of Rio Swimming Finalists. Swimming World News, 24 August 2016. Available online: https://www.swimmingworldmagazine.com/news/height-analysis-of-rio-swimming-finalists (accessed on 14 July 2022).
- Find Co-Ordinates of Contours Using OpenCV: Python. GeeksforGeeks. 2019. Available online: https://www.geeksforgeeks.org/find-co-ordinates-of-contours-using-opencv-python/ (accessed on 1 August 2022).
- Zaidi, H.; Fohanno, S.; Taiar, R.; Polidori, G. Turbulence model choice for the calculation of drag forces when using the CFD method. J. Biomech. 2010, 43, 405–411. [Google Scholar] [CrossRef] [PubMed]
- ANSYS, Inc. Ansys Fluent|Fluid Simulation Software. 2022. Available online: https://www.ansys.com/products/fluids/ansys-fluent (accessed on 2 August 2022).
- Analysis Origins—Fluent, 2019. National Agency for Finite Element Methods and Standards (NAFEMS). Available online: https://www.nafems.org/blog/posts/analysis-origins-fluent/ (accessed on 22 August 2022).
- Greifzu, F.; Kratzsch, C.; Forgber, T.; Lindner, F.; Schwarze, R. Assessment of particle-tracking models for dispersed particle-laden flows implemented in OpenFOAM and ANSYS FLUENT. Eng. Appl. Comput. Fluid Mech. 2015, 10, 30–43. [Google Scholar] [CrossRef]
- Hosseini, S.; Tafreshi, H.V. Modeling particle-loaded single fiber efficiency and fiber drag using ANSYS–Fluent CFD code. Comput. Fluids 2012, 66, 157–166. [Google Scholar] [CrossRef]
- Nair, A.S.; Mathew, M.P. Resistance Estimation of Ships Using GEKO Turbulence Model in ANSYS Fluent; IEEE: Manhattan, NY, USA, 2022; pp. 1–9. [Google Scholar] [CrossRef]
- Kabala, Z.J.; Kim, Y.W. Dynamic Effective Porosity: Numerical Simulations. J. Res. Inst. Eng. Technol. 2011, 30, 91–95. [Google Scholar]
- Kahler, D.M.; Kabala, Z.J. Acceleration of groundwater remediation by deep sweeps and vortex ejections induced by rapidly pulsed pumping. Water Resour. Res. 2016, 52, 3930–3940. [Google Scholar] [CrossRef]
- Benjanuvatra, N.; Dawson, G.; Blanksby, B.; Elliott, B. Comparison of buoyancy, passive and net active drag forces between Fastskin™ and standard swimsuits. J. Sci. Med. Sport 2002, 5, 115–123. [Google Scholar] [CrossRef]
- Chatard, J.-C.; Wilson, B. Effect of Fastskin Suits on Performance, Drag, and Energy Cost of Swimming. Med. Sci. Sports Exerc. 2008, 40, 1149–1154. [Google Scholar] [CrossRef] [PubMed]
- Chatard, J.-C.; Bourgoin, B.; Lacour, J.R. Passive drag is still a good evaluator of swimming aptitude. Eur. J. Appl. Physiol. Occup. Physiol. 1990, 59, 399–404. [Google Scholar] [CrossRef]
- Yuan, Z.-M.; Li, M.; Ji, C.-Y.; Li, L.; Jia, L.; Incecik, A. Steady hydrodynamic interaction between human swimmers. J. R. Soc. Interface 2019, 16, 20180768. [Google Scholar] [CrossRef]
- Afra, B.; Nazari, M.; Kayhani, M.; Delouei, A.A.; Ahmadi, G. An immersed boundary-lattice Boltzmann method combined with a robust lattice spring model for solving flow–structure interaction problems. Appl. Math. Model. 2018, 55, 502–521. [Google Scholar] [CrossRef]
- Afra, B.; Karimnejad, S.; Delouei, A.A.; Tarokh, A. Flow control of two tandem cylinders by a highly flexible filament: Lattice spring IB-LBM. Ocean Eng. 2022, 250, 111025. [Google Scholar] [CrossRef]
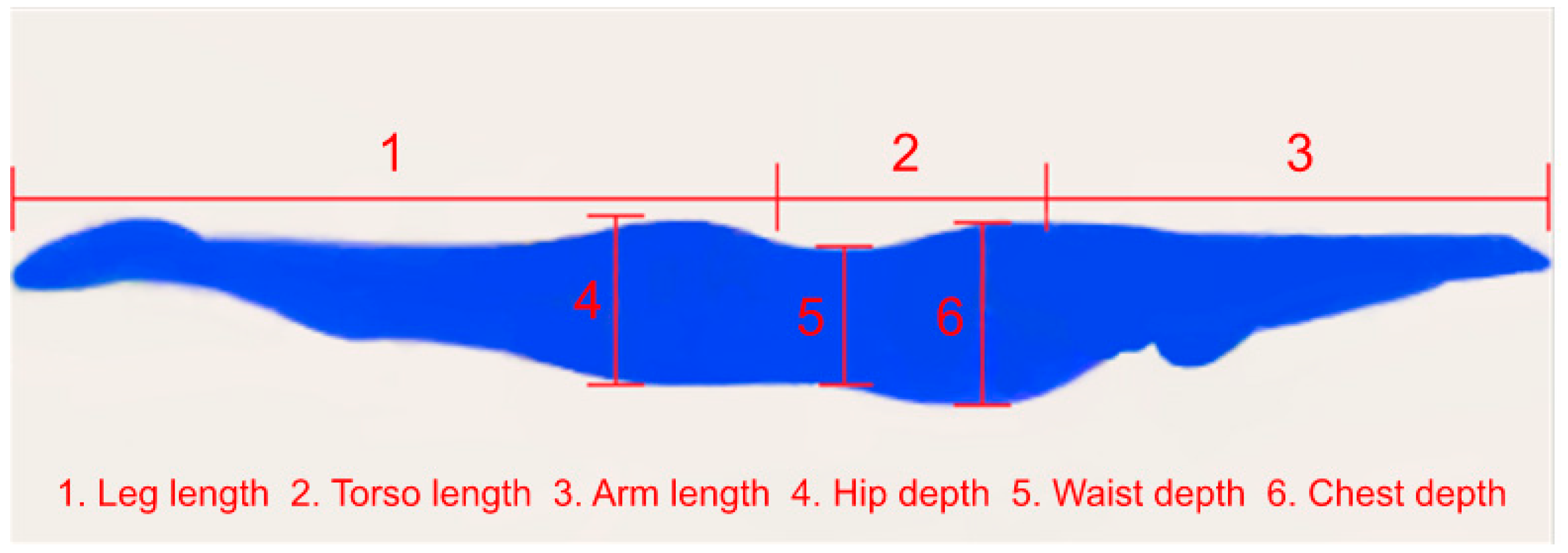
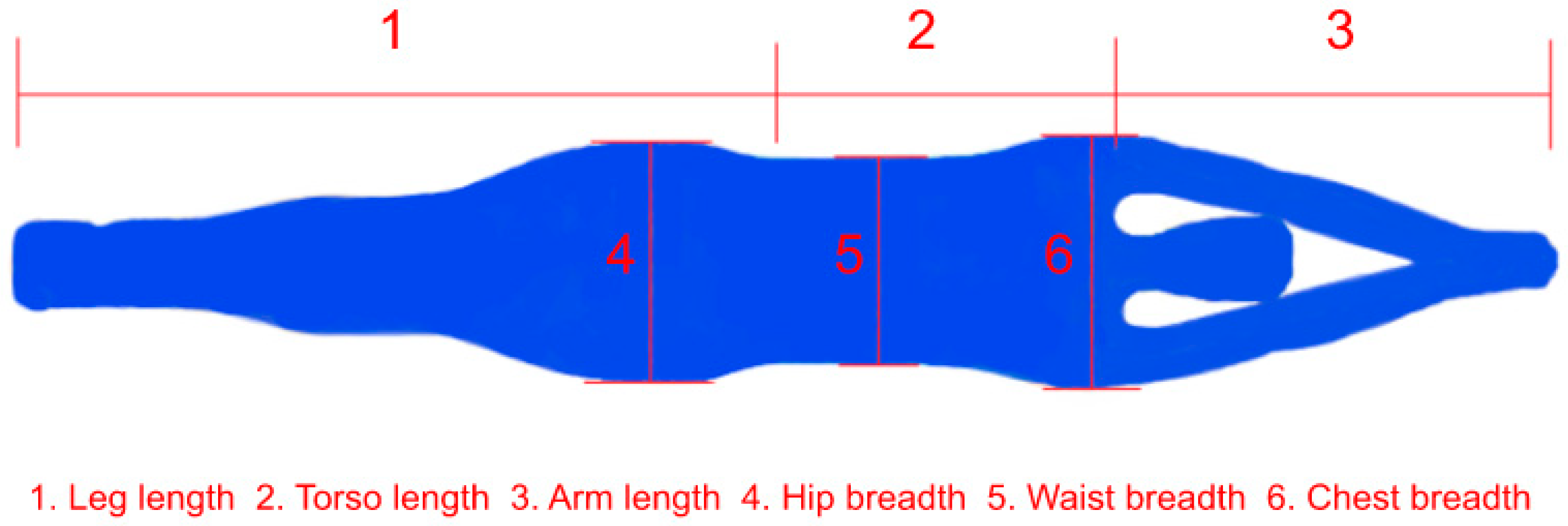






| Leg Length (%) | Torso Length (%) | Arm Length (%) | Hip Breadth (%) | Hip Depth (%) | Waist Breadth (%) | Waist Depth (%) | Chest Breadth (%) 1 | Chest Depth (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Male | 48.55 | 22.41 | 29.03 | 14.27 | 10.20 | 13.55 | 9.87 | 17.22 | 10.53 |
| Female | 49.27 | 22.10 | 28.63 | 15.99 | 10.55 | 13.59 | 9.65 | 16.53 | 11.21 |
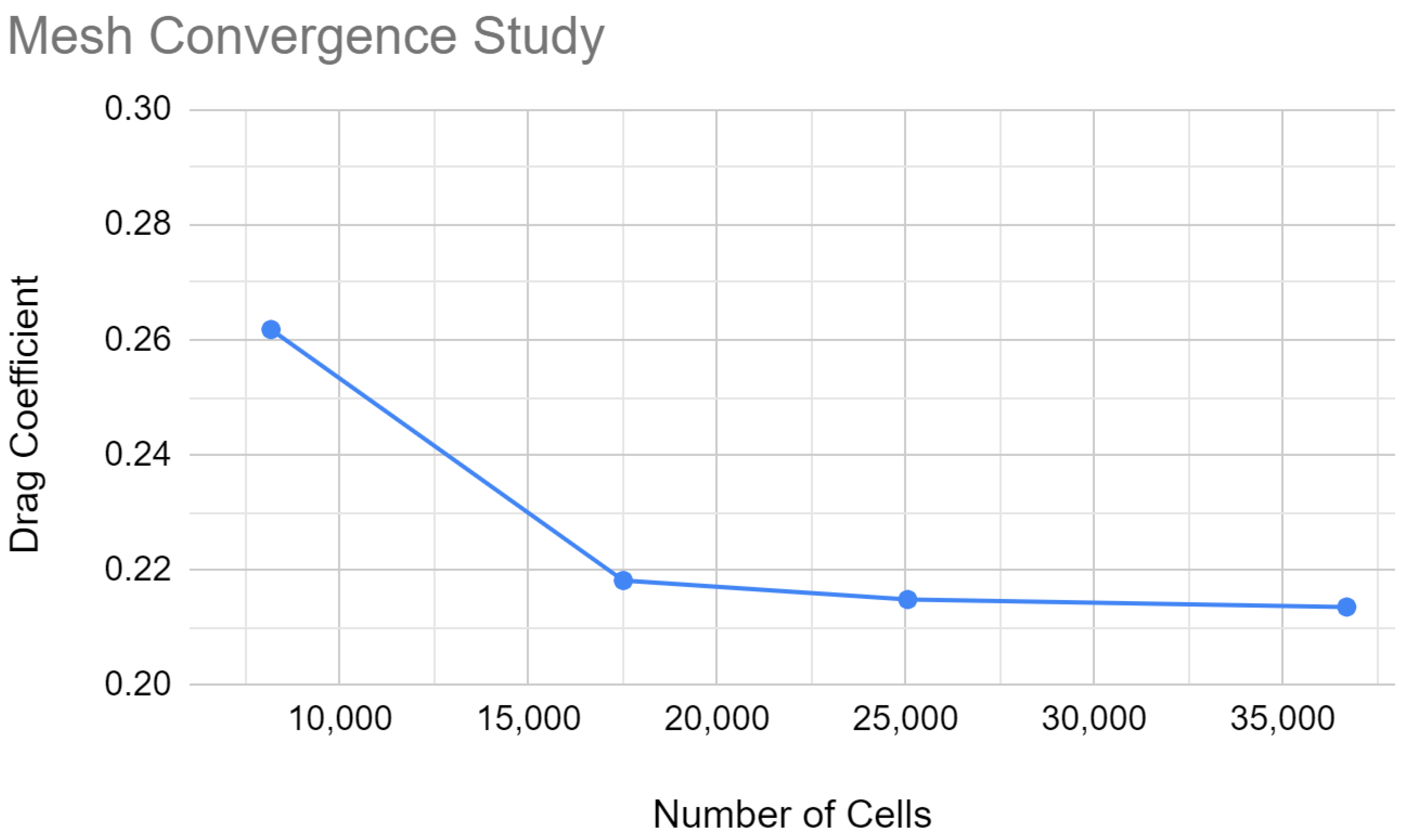
| Mesh Quality | Number of Cells | Drag Coefficient | Change (%) |
|---|---|---|---|
| Very Coarse | 8173 | 0.2618 | N/A |
| Coarse | 17,515 | 0.2182 | 16.7 |
| Medium | 25,055 | 0.2149 | 1.5 |
| Fine | 36,696 | 0.2136 | 0.6 |
| Average Pressure Drag Coefficient | Average Friction Drag Coefficient | Average Drag Coefficient | |
|---|---|---|---|
| Male Side View | 0.1399 | 0.07407 | 0.2140 |
| Female Side View | 0.1471 | 0.07369 | 0.2207 |
| Male Top View | 0.1306 | 0.05436 | 0.1849 |
| Female Top View | 0.1529 | 0.05218 | 0.2051 |
| Average Pressure Drag Force | Average Friction Drag Force | Average Drag Force | |
|---|---|---|---|
| Male Side View | 17.05 | 9.152 | 26.19 |
| Female Side View | 17.84 | 9.123 | 26.96 |
| Male Top View | 15.36 | 6.639 | 22.00 |
| Female Top View | 18.08 | 6.382 | 24.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, A.X.G.; Kabala, Z.J. Body Morphology and Drag in Swimming: CFD Analysis of the Effects of Differences in Male and Female Body Types. Fluids 2022, 7, 332. https://doi.org/10.3390/fluids7100332
Wang AXG, Kabala ZJ. Body Morphology and Drag in Swimming: CFD Analysis of the Effects of Differences in Male and Female Body Types. Fluids. 2022; 7(10):332. https://doi.org/10.3390/fluids7100332
Chicago/Turabian StyleWang, Andrew X. G., and Zbigniew J. Kabala. 2022. "Body Morphology and Drag in Swimming: CFD Analysis of the Effects of Differences in Male and Female Body Types" Fluids 7, no. 10: 332. https://doi.org/10.3390/fluids7100332
APA StyleWang, A. X. G., & Kabala, Z. J. (2022). Body Morphology and Drag in Swimming: CFD Analysis of the Effects of Differences in Male and Female Body Types. Fluids, 7(10), 332. https://doi.org/10.3390/fluids7100332







