Principles of Unsteady High-Speed Flow Control Using a Time-Limited Thermally Stratified Energy Source ^§

Abstract

This study focused on the development of the unsteady impact of a thermally stratified energy source on a supersonic flow around an aerodynamic (AD) body in a viscous heat-conducting gas (air). Research was based on the Navier-Stokes equations. The freestream Mach number was 2. A new multi-vortex mechanism of the impact of a time-limited stratified energy source on the aerodynamic characteristics of a body was described. Almost complete destruction of the bow shock wave in the density field, due to the multiple generation of Richtmyer-Meshkov instabilities in the region of a stratified energy source, was obtained. The dependences of the dynamics of frontal drag and lift forces of a streamlined body on temperature in the source layers were studied. It was determined that, by changing the temperature in the layers of a stratified energy source, it was possible to obtain more intense vortices accompanying the Richtmyer-Meshkov instabilities, causing a temporary decrease in the drag force of an AD body and ensuring the emergence and unsteady change in the magnitude of the lift (pitch) forces. The main principles of unsteady flow control using a stratified energy source were established.

1. Introduction

The problem of high-speed flow control using non-mechanical approaches, and remote energy deposition in particular, currently occupies a leading place among the problems in flow/flight control [1]. Control of supersonic flows by means of electrical discharges, microwave and laser impulses is currently a well-developed area of aerospace engineering (see surveys in [2,3,4]). A historical review of the ideas pertaining to the control of supersonic flow by energy deposition to different points of the flow, which arose several decades ago, was presented in [5]. In a significant number of studies, the effectiveness of energy supply in the form of extended filaments (“hot spikes”) was established for reducing aerodynamic drag [6,7,8]. In air, the effect of microwave discharge was determined by a decrease in stagnation pressure, along with the reduction of a drag force of a blunt cylinder. In the calculations, a vortex mechanism of these phenomena was established [9]. In [10], the curvature of the shock wave was observed during the passage through the region of a plasma zone created by longitudinal pulsed discharge.

The influence of inhomogeneous layered plasma on a reflected shock wave in a supersonic flow was studied in [11]. In these experiments, the blurring and suppression of the reflected shock wave were obtained due to the organization of a system of plasma filaments created by a high-frequency discharge [12,13]. In [14], an array of surface arc plasma actuators were used to control the interaction of the shock wave with the boundary layer in a flow with Mach number 2. As a result, the disappearance of a fragment of the separation shock wave was established. In [15], the authors used a set of heated thin wires for the creation of thermal and density inhomogeneities, which led to the generation of the Richtmyer-Meshkov instability and the formation of a line of vortices due to the Kelvin-Helmholtz instability.

The impact of the ionization strata obtained in the gas discharge plasma region on a plane shock wave was researched in [16]. These experiments attained the curvature, and in some cases, complete disappearance of the shock wave front. In the numerical simulation of the experiment, generation in many points of the Richtmyer-Meshkov instabilities was shown under the action of which the shock wave front (in density field) practically ceased to exist, which explained the results of the experiment [16].

In [17,18], the vortex structure was obtained under the action of a combined energy source, and a double-vortex mechanism of its action on the body was proposed, explaining the additional decrease in the front drag force. It was shown that the generation of the vortices is a result of the manifestation of the Richtmyer-Meshkov instability. A thermally stratified energy source was shown to initiate multiple generation of the Richtmyer-Meshkov instabilities during the interaction with the shock wave front, causing significant density and temperature fluctuations [19]. The redistribution of energy types in a curved shock wave under the conditions of the experiment [16] was estimated for M = 2 and 5 [20], and for hypersonic speeds up to M = 12 [21]. In addition, the influence of a thermally stratified energy source on the supersonic flow around an AD body was investigated, and a new multi-vortex mechanism of the action of the energy source on the body surface has been established [22].

This study focuses on the development of a thermally stratified energy source impacting the flow around supersonic AD bodies in a viscous heat-conducting gas (air). The paper focuses on an unsteady temporary action of a thermally stratified energy source. The research is based on the system of Navier-Stokes equations. The freestream Mach number is 2. Almost complete destruction of the bow shock wave in the density field, through the multiple generation of the Richtmyer-Meshkov instabilities in the region of heated layers of a stratified energy source, is obtained. The dependences of drag and lift (pitch) forces of a streamlined body on temperature in the layers of a stratified energy source are studied. The temperature values in the layers are analyzed and show the possibility of influencing the drag force and the ability to cause the formation and change of the lifting (pitch) force (at zero angle of attack). The main principles of flow control using a stratified energy source are established.

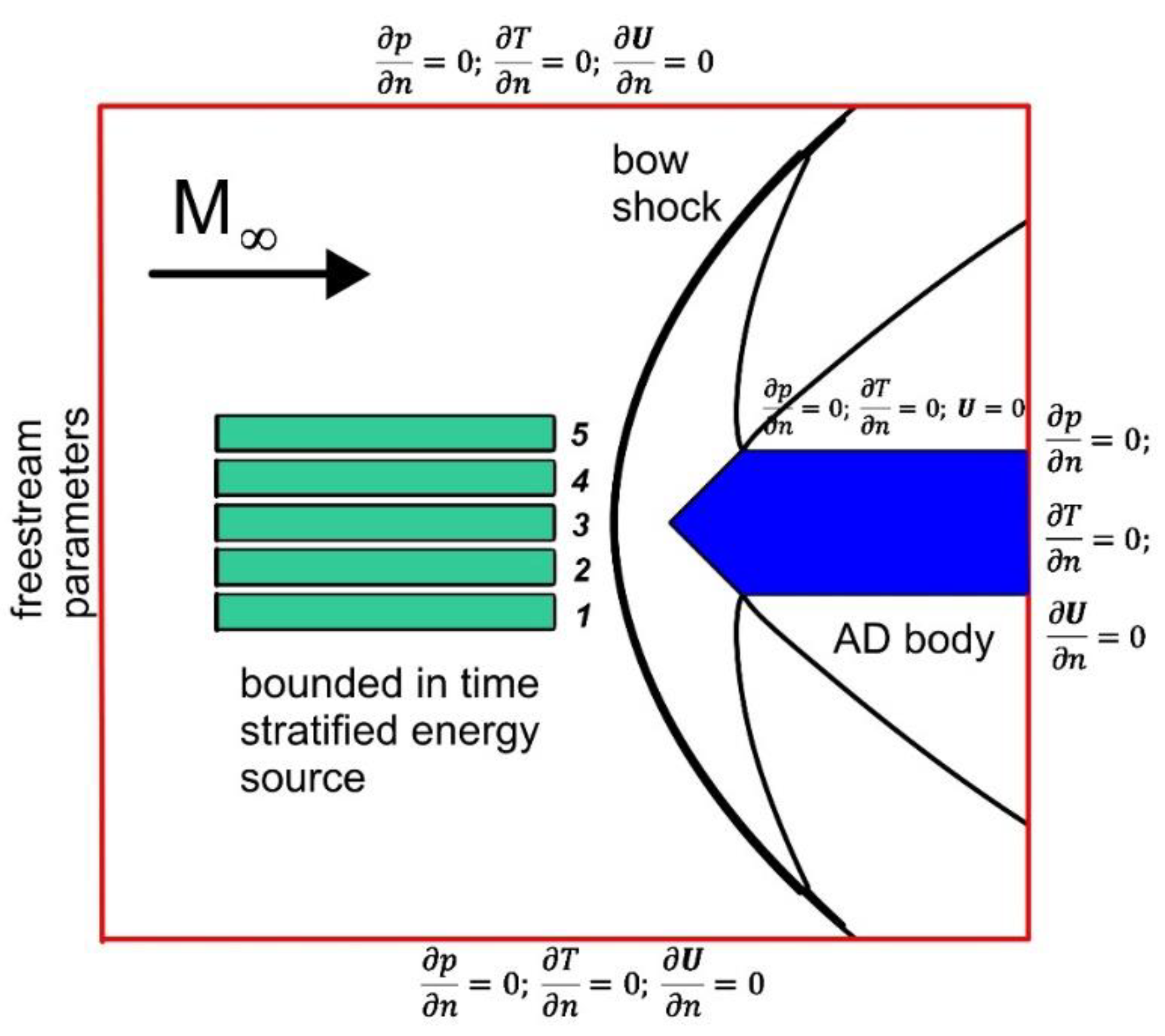
2. Methodology and Statement of the Problem

The impact of a thermally stratified energy source on a supersonic flow past a plate sharpened by a wedge is considered. The angle at the apex of the body is 90° (Figure 1).

The simulations are based on the Navier-Stokes equations for perfect viscous heat conductive gas (air); the ratio of specific heats γ = 1.4. The full Navier-Stokes system of equations in the divergent form for the dimensionless variables [23] is solved numerically:

$$\frac{\partial A}{\partial t}+\frac{\partial \left(B+V\right)}{\partial x}+\frac{\partial \left(C+W\right)}{\partial y}=0,$$

(1)

$$A=\left(\begin{array}{c}\rho \\ \rho u\\ \rho v\\ E\end{array}\right),B=\left(\begin{array}{c}\rho u\\ p+\rho u^2\\ \rho uv\\ u\left(E+p\right)\end{array}\right),C=\left(\begin{array}{c}\rho v\\ \rho uv\\ p+\rho v^2\\ v\left(E+p\right)\end{array}\right),$$

$$V=-\left(\begin{array}{c}0\\ \mu /\mathrm{Re}(4/3u_x-2/3v_y)\\ \mu /\mathrm{Re}(v_x+u_y)\\ \mu {\pi }_1/\mathrm{Re}+\left(1/\mathrm{N}\right)k{T}_x\end{array}\right),W=-\left(\begin{array}{c}0\\ \mu /\mathrm{Re}(v_x+u_y)\\ \mu /\mathrm{Re}(4/3v_y-2/3u_x)\\ \mu {\pi }_2/\mathrm{Re}+\left(1/\mathrm{N}\right)k{T}_y\end{array}\right),$$

$${\pi }_1=u\left(4/3u_x-2/3v_y\right)+v\left(v_x+u_y\right),{\pi }_2=v\left(4/3v_y-2/3u_x\right)+u\left(v_x+u_y\right),$$

$$E=\rho \left(\epsilon +0.5\left(u^2+v^2\right)\right),\mathrm{N}=\mathrm{RePr}(\gamma -1)/\gamma , \epsilon =p/(\rho \left(\gamma -1\right)).$$

Here, ε is the specific internal energy. The following normalizing values for the parameters are accepted:

$${\rho }_n={\rho }_{\infty },p_n=p_{\infty },l_n=k_l^{-1}D,T_n=T_{\infty },u_n={(p_{\infty }/{\rho }_{\infty })}^{0.5},t_n=l_n/u_n.$$

where k_l is the dimensionless value of D. The freestream Mach number is M_∞ = 2, the Reynolds number is Re = 9500, and the Prandtl number is Pr = 0.703.

Sutherland’s law in nondimensional form is used for the dependence of dynamic viscosity on temperature:

$$\mu =T^{1.5}\left(1+s_1\right)/\left(T+s_1\right),$$

s₁ = 0.409556 (120 K). The coefficient of heat conductivity k is supposed to depend on temperature in nondimensional form as follows:

$$k=T^{0.5}.$$

Initial conditions for the problem are the fields of gas parameters in a steady supersonic flow past the body, t = 0.6. At this time, the pressure and density at the apex of the body differ from their theoretical values evaluated with the use of the Bernoulli’s relation by 1.81% and 1.75%, respectively. Here, the converging criterion for the evaluation of the relative errors is used in a form:

$$\mathrm{abs}\left(f_t-f_{t \mathrm{theor}}\right)/ f_{t \mathrm{theor}} *100(\%),$$

where f_t and f_{t theor} are the calculated value at the apex of the body and the theoretical one evaluated from the Bernoulli’s relation.

The boundary conditions provide no-slip conditions for the adiabatic wall at the horizontal boundaries and at the wedge boundaries, and establish the absence of according normal flows on the boundaries of the body:

$$\frac{\partial p}{\partial n}=0; \frac{\partial T}{\partial n}=0; \mathit{U}=0.$$

At the exit boundaries of the computation domain, the absence of reflection in the normal directions is set as follows:

$$\frac{\partial p}{\partial n}=0;\frac{\partial T}{\partial n}=0;\frac{\partial \mathit{U}}{\partial n}=0.$$

The stratified energy source is modeled by a region of rarefied gas layers of the same width located ahead of the bow shock wave front in its immediate vicinity (see Figure 1). The distances between the layers were equal to half the width of the layer. Inside the layers (indicated by the index j), gas density was applied to be reduced,

$${\rho }_j={\alpha }_j{\rho }_{\infty },{\alpha }_j<1,j=1÷N,$$

N is a number of layers in the energy source. The pressure and velocity in the domain of the energy source are set equal to their values in the oncoming flow (indicated by the index ∞),

$$p_j=p_{\infty },u_j=u_{\infty },v_j=0.$$

Therefore, the temperature inside the layers is increased compared to its value in the oncoming flow,

$$T_j={\alpha }_j^{-1}{T}_{\infty }.$$

Thus, a stratified energy source is specified by a set of rarefaction parameters {α_j} = α₁, α₂, _… α_N in its layers. The axis of symmetry of the stratified source is supposed to coincide with the axis of symmetry of the body. The energy source arises instantly in the steady flow at the time instant t_i, and it is assumed that it has a limited duration in time.

A domestic code based on the complex conservative difference schemes of the second order of approximation in space and in time is used in the simulations. Details of construction of the schemes in the computational domain and in the vicinity of the body’s boundaries, are presented in [24]. For increasing the order of approximation in the development of the schemes, the differential consequences of system (1) for the spatial derivatives on x and y are used. The five-point stencil (the stencil of Lax’s scheme) is applied for the scheme construction; therefore the grids used are staggered and uniform everywhere in the computational domain.

The boundaries of a body are introduced into the calculation area without breaking the conservation laws in it (in space and time). For this purpose, the boundaries of the body are included to a structural staggered orthogonal grid, and discrete conservation laws are written for each arising grid configuration. Thus, the schemes are written for 1/4 of a difference cell, 1/2 of a cell and 3/4 of a cell, and are used, as necessary, in accordance with the position of the body’s boundary on the difference grid. In this case, the reflected versions of the schemes are possible, as well as schemes on half cells in the x- and y- directions. This allows the carrying out of calculations conservatively in the entire computational domain, including the regions adjacent to the boundaries of the body [24].

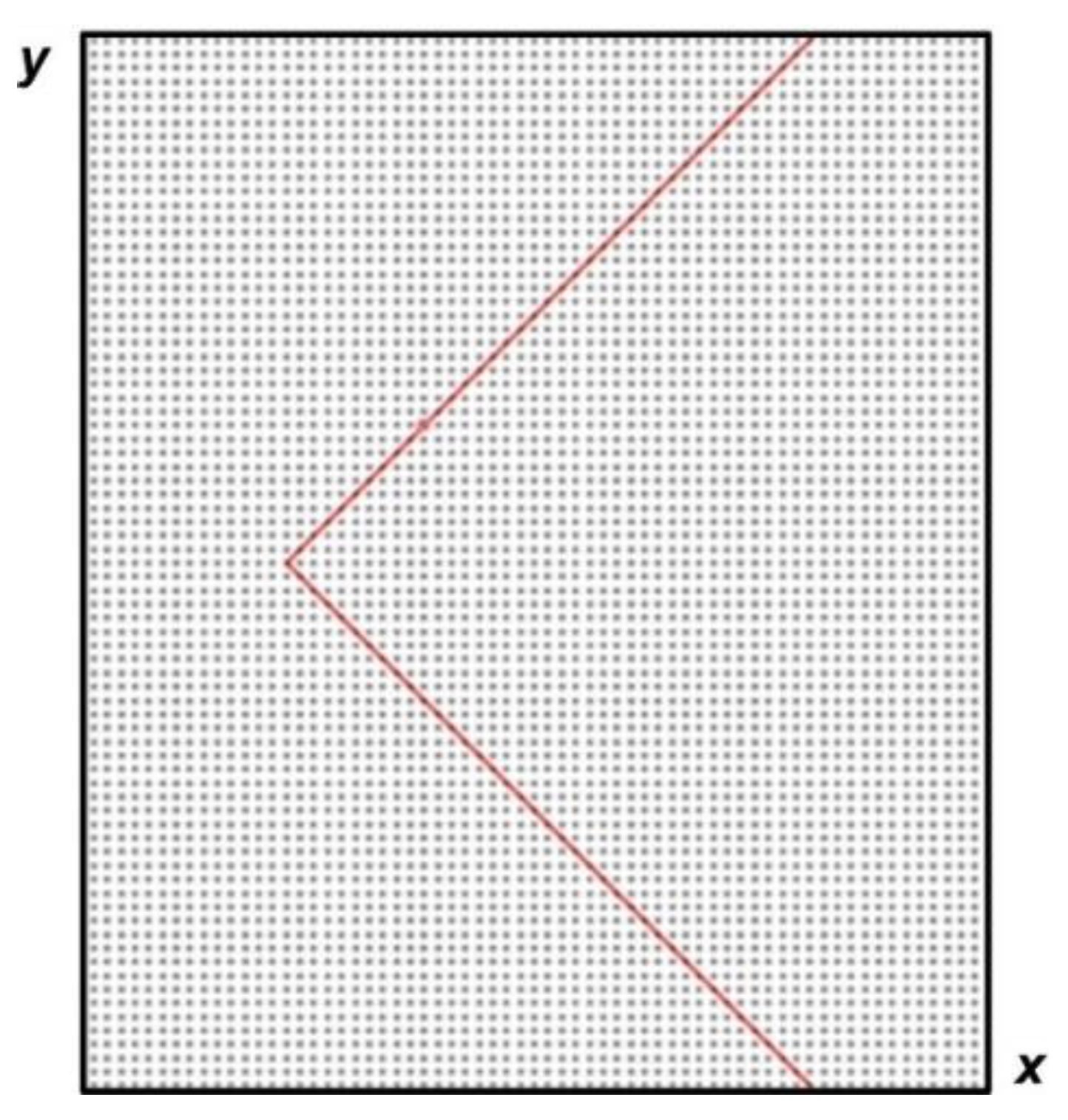
The position of the sharpened part of the body on the grid in an enlarged form is shown in Figure 2. In the calculations, the staggered numerical grids are used with the distance between the nodes at each time level equal to 2h_x, 2h_y (h_x, h_y are the space steps in x- and y-directions). To select the time step, the Courant-Friedrichs-Levy criterion are used.

The numerous test examples for the used numerical methods and developed software are presented in [24]. Comparison with the experimental results was conducted in [25]. Nevertheless, we present some test case analysis below.

3. Method Validation and Grid Convergence Analysis

Figure 3 demonstrates the analysis of the possibilities of the applied numerical code for the resolution of shock waves and contact surfaces (shear layers). The “quasi-one-dimensional” Riemann problem of the decay of an arbitrary discontinuity was chosen for validation. The statement of the problem is schematically shown in Figure 3a. At the initial moment of time t = 0, a heated gas region is set with the rarefaction parameter of α = 0.5 at 0 < x < 1.45, and a plane shock wave with the Mach number of 2 at the point with x = 1.55. At t > 0, the shock wave begins to move from right to left, and at time t = 0.04226 the shock wave begins to interact with the boundary of the heated region at the point with x = 1.45. The emerging flow in the inviscid case is described by the Riemann problem with the formation of a shock wave and a contact discontinuity moving from right to left (and a rarefaction wave propagating to the right) [26]. The numerical density profiles at the axis of symmetry are presented in Figure 3b. Comparison of the locations of shock fronts at different times with the analytical solution (dashed lines) shows a high computational accuracy of the used difference schemes.

For the analysis of grid convergence, the calculations of flow dynamics during the steady state establishment for three difference grids were conducted (

Table 1. Characteristics of the grids and relative errors.

Grid	Steps hx = hy	Sizes	Relative Error *, pt: abs(pt − pt theor)/pt theor × 100%	Relative Error *, ρt: abs(ρt− ρt theor)/ρt theor × 100%
Grid1	0.0005	3400 × 2800	1.81%	1.75%
Grid2	0.001	1700 × 1400	1.17%	2.52%
Grid3	0.002	850 × 700	0.34%	3.61%

* p_{t theor}, ρ_{t theor}—the values calculated using the Bernoulli’s relation.

, t = 0.6). The characteristics of these grids are presented, as well as the relative errors for the stagnation parameters at the apex of the body, in comparison with the theoretically obtained ones from the Bernoulli’s relation.

Figure 4 demonstrates the flow fields in isochores (Figure 4a) and the dynamics of the parameters at the stagnation point (Figure 4b) obtained using these three difference grids. The number of nodes of Grid1 and Grid3 differ by 16 times, and the number of nodes of Grid1 and Grid2 by four times, but nevertheless, one can see that the values at the apex of the body differ from their theoretical values less than by 2% (for Grid1). Additionally, the positions and shapes of the bow shock waves almost coincide (see Figure 4a).

Therefore, all these factors show that grid convergence has taken place. For the simulations, we use Grid1 (h_x = h_y = 0.0005) on two computation domains which contain 9.52 × 10⁶ nodes (3400 × 2800, coordinate of the body’s axis of symmetry y₀ = 0.7) and 12.96 × 10⁶ nodes (3600 × 3600, y₀ = 0.9). Here, the dimensions of the grids are specified counting the middle node of the stencil.

4. Results

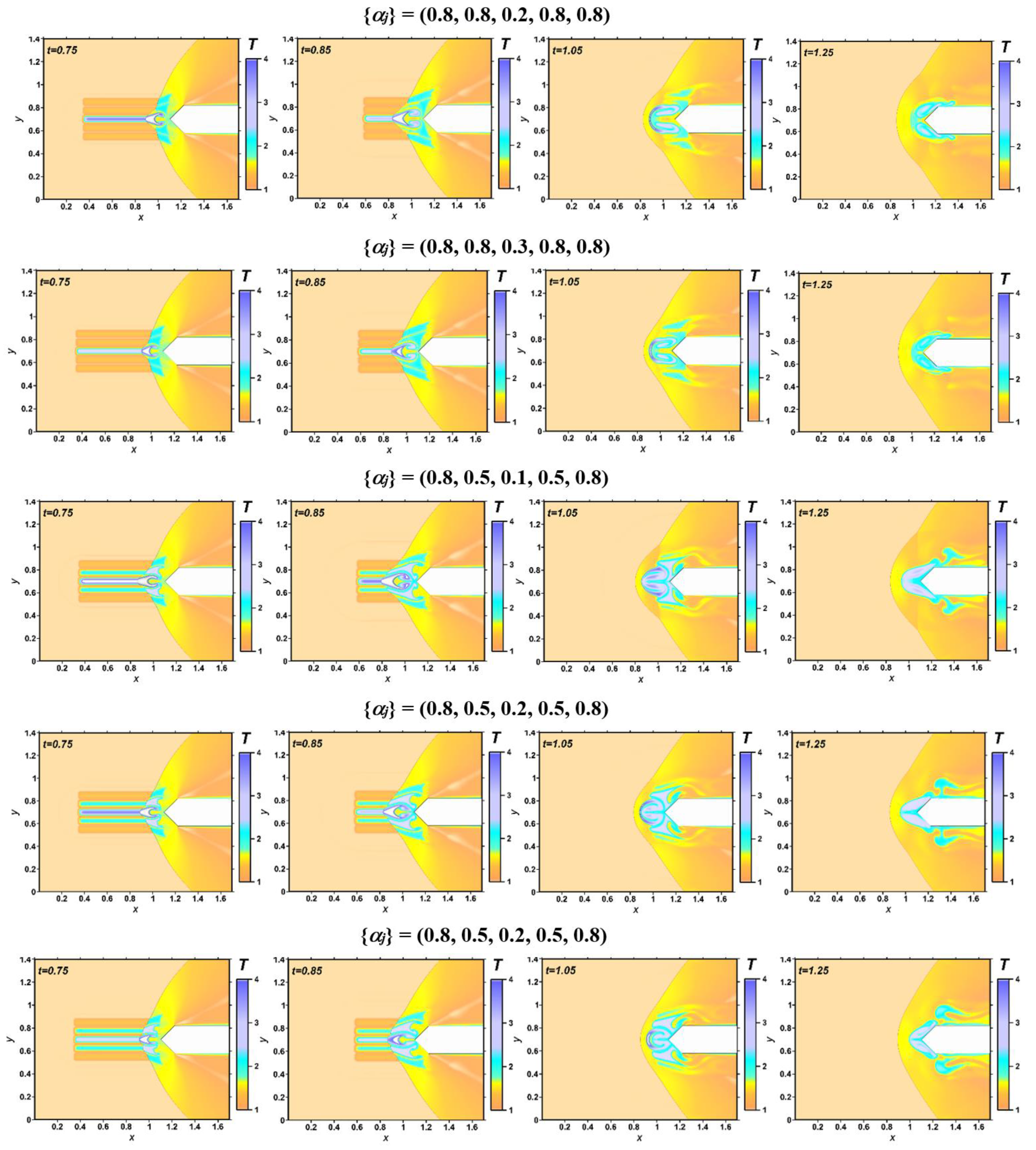
The defining flow parameters used in the simulations are presented in

Table 2. Parameters of the oncoming flow, aerodynamic body and the energy source.

Description	Definition	Value
Freestream Mach number	M∞	2
Ratio of specific heats	γ	1.4
Reynolds number	Re	9500
Prandtl number (20 °C)	Pr	0.703
The body’s width	D	0.24
Coordinate of the body’s axis of symmetry	y0	0.7; 0.9
Number of layers in the energy source	N	5
The width of the layers in the energy source	hj	0.05
Coordinate of the lower boundary of the energy source	yes	0.525; 0.725
Rarefaction parameter in the layer j in the energy source	αj	0.1–0.8

. The energy source specified, as described above, is supposed to instantly arise in the steady flow at the time t_i = 0.601 moves together with the oncoming flow and begins to interact with the bow shock wave. The dynamics of the density fields following this interaction for different symmetrical sets of the values of α_j in the layers of the energy source is presented in Figure 5. Here, the results of two series of the calculations are presented, with sets {α_j} with a heated central layer α₃, and sets {α_j} with the additional layers of reduced density α₂ and α₄.

The first and second lines of images demonstrate the dynamic of the originated vortex structures, which are caused by the sets of layers {α_j} with a heated central layer. One can see the dynamic of a complicated shock structure with two vortices with the decreased density accompanying the Richtmyer-Meshkov instability. The front of the bow shock wave undergoes a significant transformation. As the stratified region of the energy source passes, the diffraction of the shock wave occurs, accompanied by the formation of two symmetrical triple configurations (t = 0.85). During the passage of the stratified pulse, one can see the curvature of the bow shock wave (t = 1.05), which is greater the smaller the value of α₃ (or the higher temperature) in the central layer. After the passage of the stratified pulse, the flow returns to the undisturbed steady mode. These results are consistent with the results of numerous studies on the effect of a heated longitudinal region on a bow shock wave.

Images on other lines in Figure 5 correspond to sets {α_j} with the additional layers of reduced density α₂ and α₄. In this case, the formation of additional vortices and more complex shock-wave structures is seen (t = 0.85, 1.05). The bending of the bow shock wave is almost rectilinear in the source zone. After passing the stratified region, the bending of the bow shock wave is also noticeable, which is greater the lower the values of α_j in the source layers (t = 1.25); at the end of the interaction process, the flow returns to the undisturbed steady flow mode.

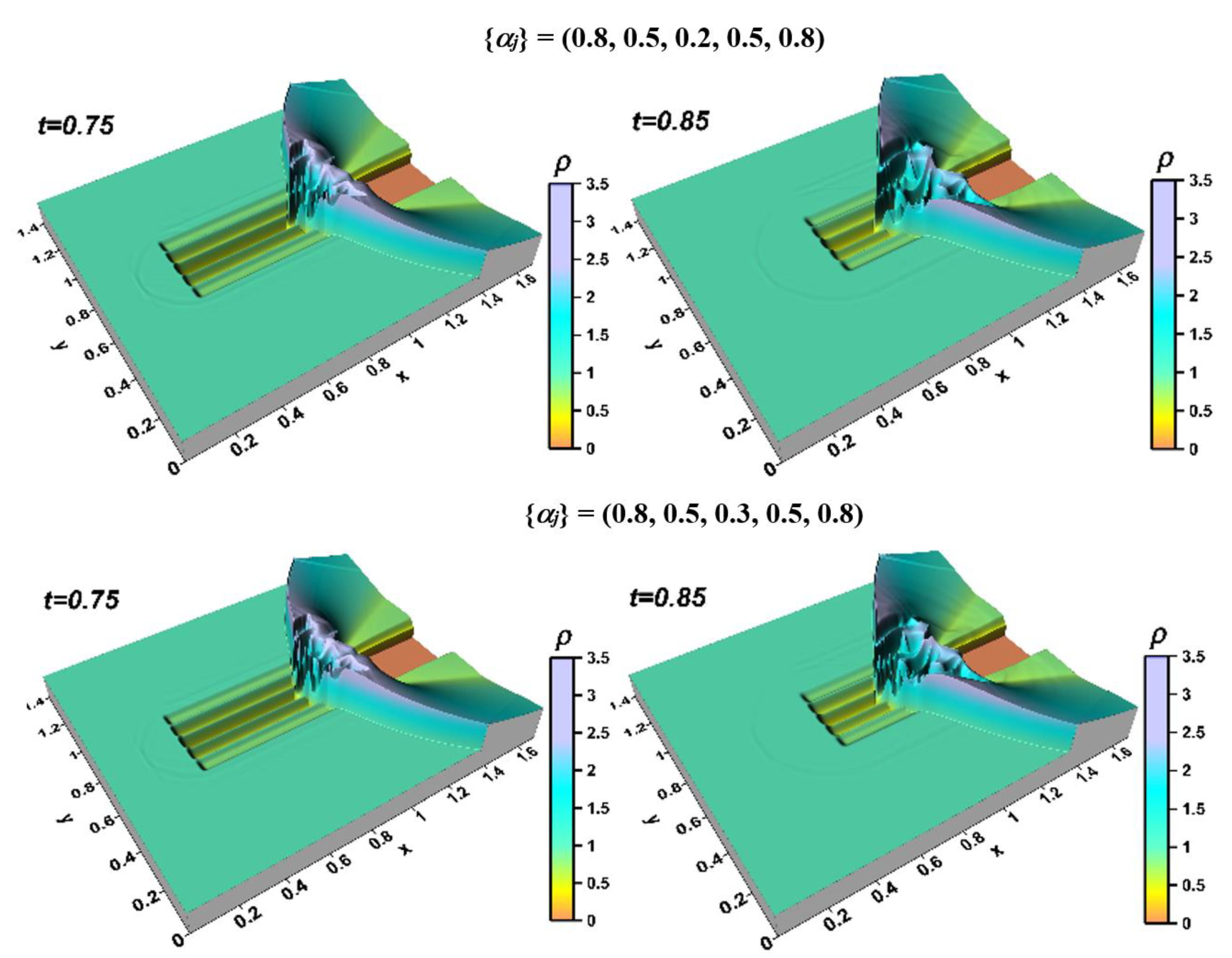
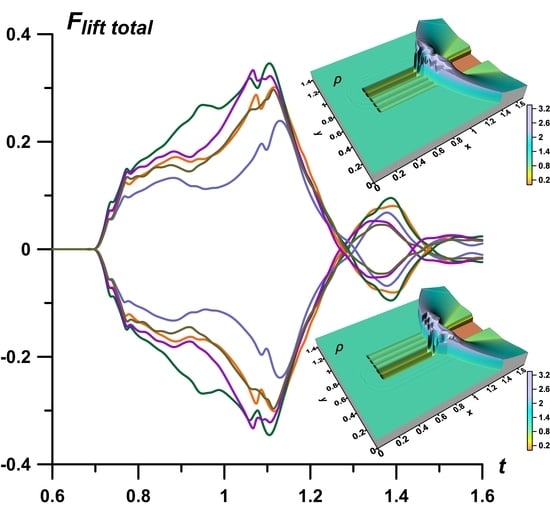
The dynamics of the density fields in surface view is presented in Figure 6. One can see the blurring of the front of the bow shock wave under the action of thermal layers, and for the given several heated layers in the energy source, the front of the bow shock wave practically ceases to exist. This occurs under the influence of the development of multiple Richtmyer-Meshkov instabilities [17,22], which are characterized by the appearance of sharp fluctuations (peaks) of parameters and the formation of the accompanying “mushroom” structures.

The corresponding dynamics of the pressure fields is presented in Figure 7. Since, in the layers of the stratified source, pressure is equal to the freestream pressure, the source layers are not visible in the pressure field. It can be seen that at the beginning of the interaction, the front of the bow shock wave becomes wavy (Figure 7; the fourth and fifth lines of images, t = 0.75). Further, it is deformed, and after the passage of the stratified impulse, the flow comes to an unperturbed stationary state. It can also be seen that inside the formed vortices, the pressure, as well as the density, is reduced (Figure 7 1st line of images, t = 1.05 and t = 1.25).

The dynamics of the temperature fields are presented in Figure 8. One can see that the action of the stratified energy source causes complicated temperature structures inside the shock layer. Temperature fluctuations with high-temperature values (approximately four times higher than the temperature of the oncoming flow) are visible inside the resulting vortex structures (t = 0.85, 1.05). Temperature fluctuations are stronger for hotter layers, and for more number of heated layers in the energy source (third line of the images, t = 1.05); however, these can be expected.

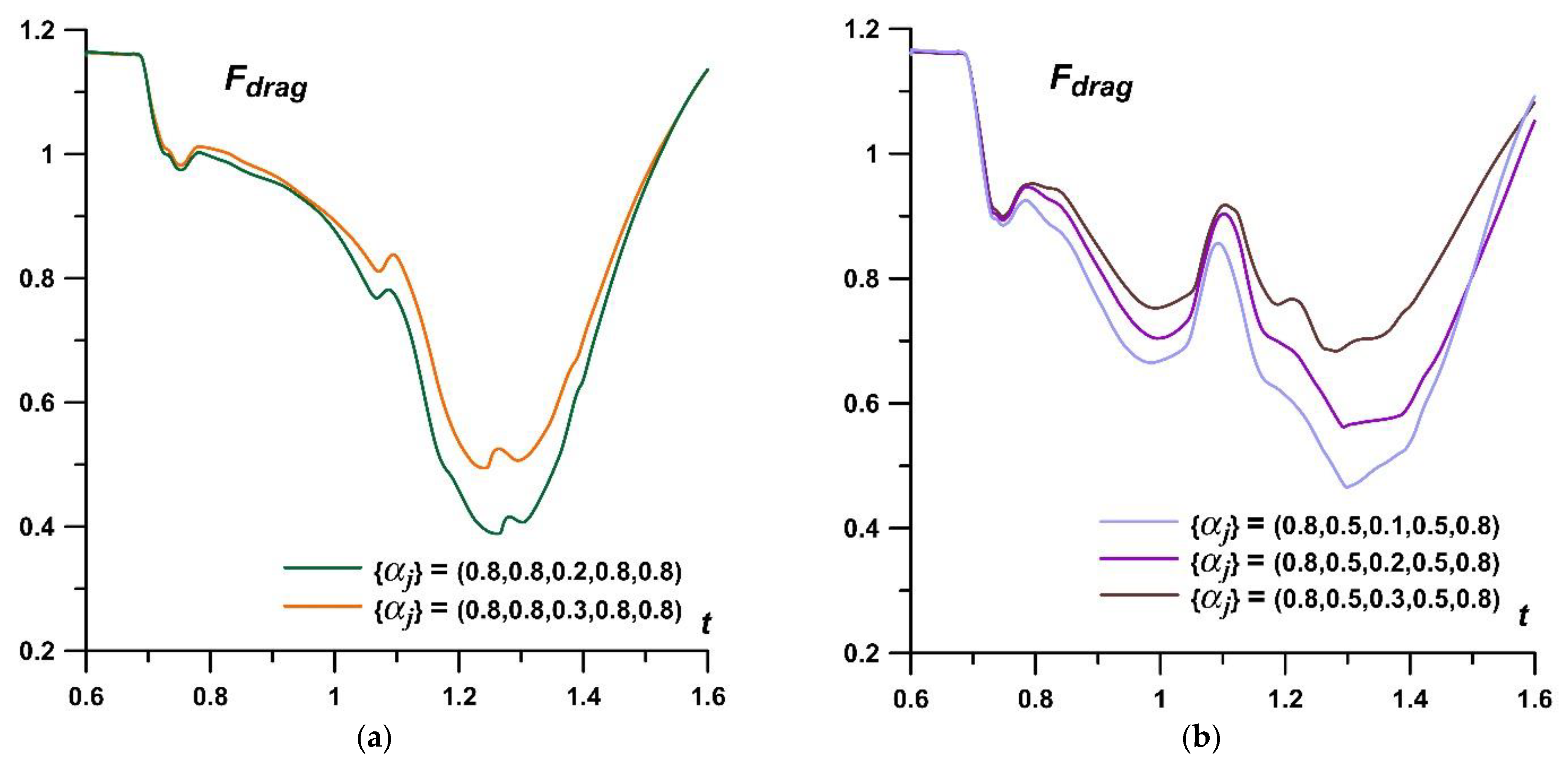
The dynamics of drag force for different symmetrical sets {α_j} are presented in Figure 9. It is seen that the drag force reduction is greater for more rarefied layers in the energy source (with a greater temperature) (Figure 9a). The addition of the heated layers to the stratified source adds oscillation to the drag force dynamic, increasing the time interval on which the drag force is decreased (Figure 9b). Drag reduction is greater (and the longer action in time) the more layers are in the source with the reduced values of α_j (or higher temperatures) in the layers. Thus, it is possible to control the drag force of an AD body surface by changing the temperature values and the number of heated layers in a thermally stratified energy source. Note, that in this case, for symmetrical sets {α_j} in the source, lift forces do not arise, in contrast to asymmetric sets {α_j} in the source, as will be shown below.

The dynamics of the density fields for different asymmetric sets {α_j} in the stratified energy source are presented in Figure 10. One can see the initiation of the asymmetric vortex structures; the drop in densities in these vortices is greater for smaller values of α_j (t = 0.75, 0.85). On hotter layers, the bow shock wave diffracts with the formation of asymmetric triple shock configurations (t = 0.85). After the passage of the stratified pulse, the instabilities weaken, and the front of the bow shock wave is restored, retaining the asymmetric shape (t = 1.05). Furthermore, the shape of the bow shock wave approaches the body and its shape becomes close to symmetrical (t = 1.25). At the end of the process, when the impulse leaves the computational area, the flow returns to its original unperturbed state. Comparing the flow patterns for different sets of {α_j} presented in Figure 10, we can conclude that the drops in densities in the resulting vortices are larger for smaller values of α_j (see the third row of images). In addition, for smaller values of α_j, the action of resulting vortex structures on the lower body surface is stronger for smaller values of α_j, or larger the values of temperature in the layers (see the fourth row).

In Figure 11, the fields of density for asymmetric sets {α_j} are presented. Here, asymmetric (left row of images) and “reflected” asymmetric (right row of images) sets {α_j} are considered; where, in asymmetric sets {α_j} = (α₁, α₂, α₃, α₄, α₅) and in “reflected” asymmetric sets {α_j} = (α₅, α₄, α₃, α₂, α₁). In addition, the structure of the flow is demonstrated by the vector fields of the flow velocity U = (u,v). It is seen that inside the vortex structures the flow is circular. The corresponding flow patterns obtained are directly opposite, which is due to the coincidence of the symmetry axes of the energy source and the body, i.e., it is assumed that the source is rigidly installed symmetrically with respect to the AD body.

The dynamics of unsteady drag forces for different asymmetric sets {α_j} in the stratified energy source are presented in Figure 12. We consider the drag force formed by the wedge part of the body Fdrag, and the drag forces formed by the top and bottom surfaces of the wedge, Fdrag_top and Fdrag_bottom. It can be seen that, as in the case of symmetrical sets {α_j}, the drops in drag force Fdrag are greater for smaller α_j (compare the green, orange and blue curves); here, the rate of change in drag is almost the same. However, using the layers with different α_j, it is possible to set a different rate of change in the drag force, which is greater the greater the difference in α_j (in the temperature values) in the layers (see green, purple and olive curves). One can also see that for asymmetric and “reflected” asymmetric sets {α_j} the drag forces of top and bottom surfaces are of the opposite values, and the total drag forces are the same. This is connected with the fact that the axis of symmetry of the stratified source is supposed to coincide with the axis of symmetry of the body.

In Figure 13 and Figure 14, the dynamics of unsteady lift (pitch) forces for different asymmetric sets {α_j} in the stratified energy source are presented. We consider the lift force formed by the wedge part of the body Flift_wedge, the lift force formed by the horizontal surfaces of the body Flift_horizontal, and the total lift force of the body Flift_total. The dynamics of lift forces Flift_wedge and Flift_horizontal, for asymmetric and “reflected” asymmetric sets {α_j}, are shown in Figure 13a,b, accordingly. It can be seen that the lift (pitch) forces are defined mostly by the wedge part of the body Flift_wedge, and the absolute value of these forces are greater for the sets {α_j} with the more rarefied layers (compare green, orange and blue curves).

Additionally, it is possible to control the rate of change of the lift force Flift_wedge by including differently heated layers in the energy source (compare green, purple and olive curves). It is seen that for two equally heated layers, the rate is strongly increased for smaller α_j (compare blue, orange and green curves for Flift_wedge), but by including the differently heated layers, the difference in the rate can be reduced to a greater extent, and therefore the greater the difference in α_j in the source layers (compare green, purple and olive curves).

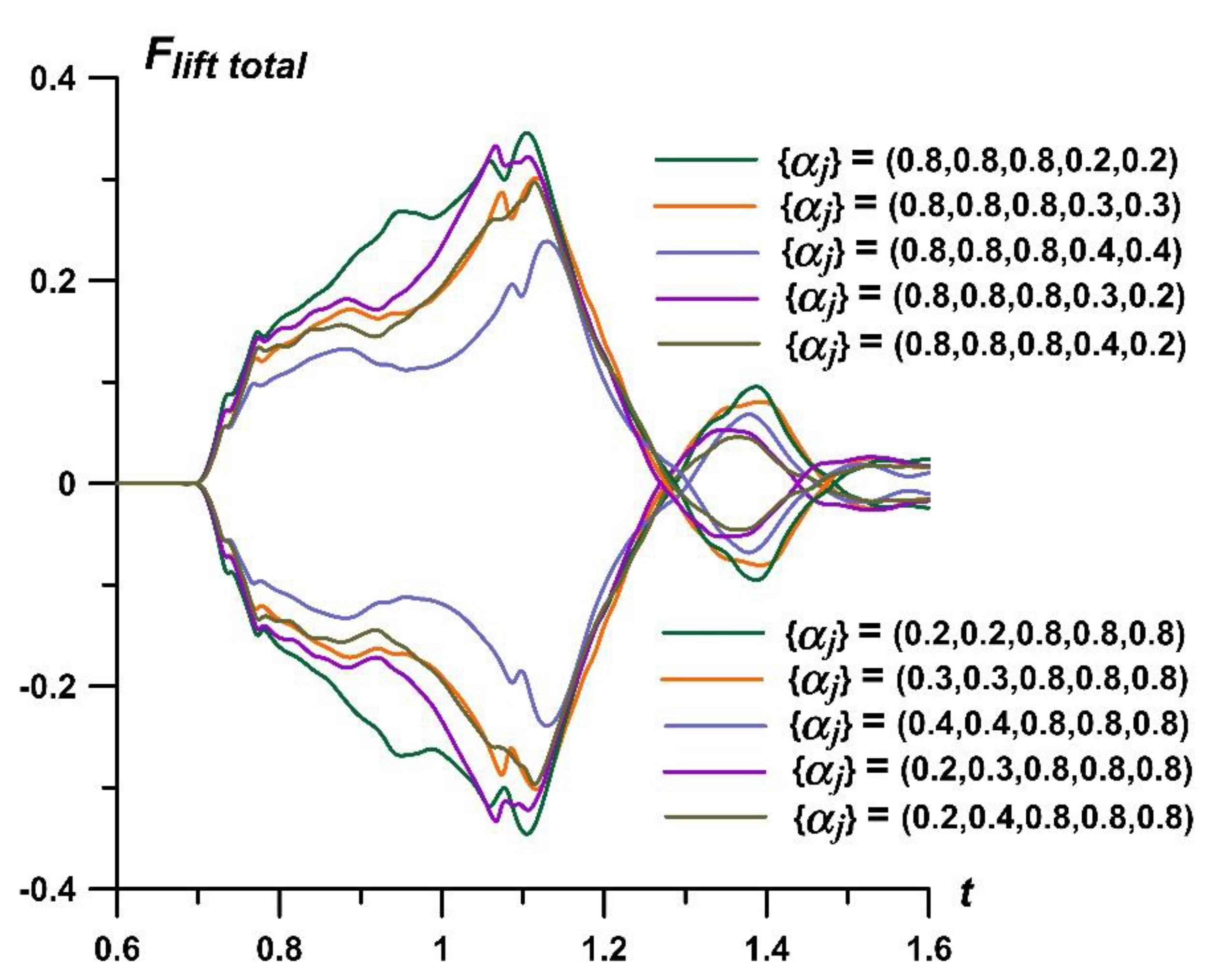
The dynamics of the total lift forces Flift_total for asymmetric and “reflected” asymmetric sets {α_j} are presented in Figure 14. The dynamics of Flift_total are characterized by the same properties that were obtained for Flift_wedge: the absolute value of Flift_total are greater for the sets {α_j} with the more heated layers, with smaller values of α_j (compare green, orange and blue curves), and it is possible to control the rate of change of Flift_total, by including the differently heated layers (compare green, purple and olive curves).

It can be emphasized that the dynamics of lift forces in Figure 13 and Figure 14 are described by the symmetrical curves. Therefore, by replacing the asymmetric set {α_j} with its “reflected” set, it is possible to obtain the oppositely directed lift forces. Thus, lift forces can be created and controlled using a thermally stratified energy source by changing the temperature values in its layers. Notably, it is assumed that the stratified energy source is located symmetrically relative to the AD body (at zero angle of attack).

5. Conclusions

The unsteady effect of a thermally stratified energy source of limited length in time on the supersonic flow past a pointed plate at M = 2 was numerically investigated. The axis of symmetry of the stratified source was supposed to coincide with the axis of symmetry of the AD body. The new results obtained are as follows:

• Almost complete destruction of the bow shock wave in the density field was achieved due to the multiple generation of the Richtmyer-Meshkov instabilities during its interaction with a stratified energy source. The multi-vortex mechanism of the impact of a stratified energy source on the aerodynamic characteristics of an AD body was shown.
• The principles of supersonic flow, local in time control using a stratified energy source of limited length, have been formulated, namely:

• By setting lower values of α_j (higher temperatures) in the layers and larger differences in density values, it is possible to obtain more intensive vortices accompanied the Richtmyer-Meshkov instabilities.
• By setting symmetrical sets {α_j}, one can temporarily decrease the drag force of an AD body. Drag reduction is greater (and the longer action in time) the more layers are in the stratified energy source with the reduced values of α_j (or higher temperatures in the layers).
• By setting asymmetric sets {α_j}, it is possible to create a temporarily lift (pitch) force (at zero angle of attack), which is greater (and the longer action in time) the more layers are in the source with the reduced values of α_j (or of higher temperatures).
• By setting “reflected” asymmetric sets {α_j}, it is possible to create an oppositely directed lift (pitch) force (at zero angle of attack), which is greater (and the longer action in time) the more layers are in the source with the reduced values of α_j. Moreover, the drag forces for the “reflected” asymmetric sets {α_j} remain the same as for the asymmetric sets {α_j} used.
• It is possible to control the rate of change in the drag and lift forces. For equally heated layers, the rate is strongly increased for smaller α_j (or higher temperatures), but by including the differently heated layers (with different α_j) the rate can be reduced to a greater extent, and the greater the difference in α_j in the source layers.